Blood flow and mass transfer regulation of coagulation

Abstract

Blood flow regulates coagulation and fibrin formation by controlling the transport, or mass transfer, of zymogens, co-factors, enzymes, and inhibitors to, from, and within a growing thrombus. The rate of mass transfer of these solutes relative to their consumption or production by coagulation reactions determines, in part, the rate of thrombin generation, fibrin deposition, and thrombi growth. Experimental studies on the influence of blood flow on specific coagulation reactions are reviewed here, along with a theoretical framework that predicts how flow influences surface-bound coagulation binding and enzymatic reactions. These flow-mediated transport mechanisms are also used to interpret the role of binding site densities and injury size on initiating coagulation and fibrin deposition. The importance of transport of coagulation proteins within the interstitial spaces of thrombi is shown to influence thrombi architecture, growth, and arrest.

1. Background

Coagulation is a tightly controlled biochemical network of reactions that leads to the generation of thrombin. This network includes zymogens, enzymes, co-factors, and inhibitors, which quickly generate thrombin at the site of injury and efficiently eliminate it in the peripheral area. Most models of coagulation, such as the cascade or waterfall models¹ and cell-based models,² focus on the biochemical mechanisms that include a series of binding and enzymatic reactions occurring on the subendothelium and the surface of cells and microparticles. These models are useful for describing coagulation in closed systems such as clot time assays and prothrombin time (PT), that take place under static conditions in test tubes or well-plates. They may also be appropriate models for describing clot formation in vivo under conditions of stasis, for example in venous thrombosis. However, blood flow imposes additional biophysical constraints on coagulation and platelet function during intravascular thrombus formation.³

The recognition of the relationship between blood flow and coagulation dates back at least to the 19th century with the description of red clots and white clots.⁴ Red clots are associated with venous thromboembolism and originate in areas of reduced blood flow or stasis as first described by Virchow. White clots are associated with high blood flow in arterial thrombosis as described by Bizzozero in his observations in the first in vitro flow chamber.⁵ The red thrombi-white thrombi nomenclature is a somewhat oversimplified picture because even arterial, white thrombi contain a significant amount of fibrin.⁶ Nevertheless, these initial observations point to blood flow as a key regulator of coagulation, fibrin deposition, and thrombus architecture. Baumgartner and colleagues made the first quantitative measurements of this biophysical regulatory mechanism using in vitro flow chambers.^7–9 An inverse relationship between blood flow and fibrin deposition was observed in whole blood perfusion over the subendothelium of rabbit arteries. Since these initial studies, the influence of flow on individual coagulation reactions, thrombin generation, fibrin formation, and platelet function has been greatly aided by in vitro models, especially more recent models that take advantage of micropatterning and microfluidic technology to define fluid dynamics with spatially controlled presentation of procoagulant surfaces.¹⁰ These technologies provide the tools for determining how geometry, injury size, and more complex flows affect coagulation in environments that mimic in vivo injuries.

The theoretical foundations for how flow influences biochemical reactions on surfaces were developed in support of the burgeoning biotechnology industry in the 1960s and 1970s. Specifically, enzymes immobilized on the wall of tubes serve as bioreactors for food and pharmaceutical processing. In their seminal work, Laidler and colleagues derived modifications to expressions of Michaelis-Menten and other enzyme kinetic models to incorporate the influence of flow on product generation.^11,12 They accounted for the transport of substrates to enzymes immobilized on a surface by convection (flow) and diffusion, which together are referred to hereafter as mass transfer. Nemerson and colleagues applied these mass transfer concepts to coagulation reactions.¹³

This review focuses on the flow-based mechanisms that regulate coagulation reactions, building from a general theory of biochemical reactions on surfaces in order to organize and interpret in vitro and in vivo observations in purified, plasma, and whole blood experiments. The flow-based mechanisms that regulate platelet adhesion and aggregation have been reviewed elsewhere.^3,14 The review is organized as follows: (1) a brief background presented in this section, (2) the theoretical basis of how mass transfer regulates binding and enzyme reactions on surfaces, (3) the application of these theories in purified systems looking at one or a few coagulation or anticoagulation reactions, (4) the effect of injury size and geometry on the extrinsic pathway, (5) the regulation of fibrin polymerization and morphology by flow, (6) interstitial transport as a regulator of thrombus growth, and (7) a summary.

2. Mass transfer regulation of biochemical surface reactions

This section includes the governing equations that describe the relative rates of mass transfer and chemical reactions in order to give the reader the theoretical basis for how the experiments described in Sections 3–6 are interpreted. The intent here is to provide all of these equations in one place, saving the interested reader the time effort of tracking them down across various textbooks and manuscripts. Another motivation is to provide a common language for these biophysical mechanisms that is necessary for ongoing discussions in this field. The definition of all variables and their units can be found in Appendix A.

The concept of a rate-limiting step is a familiar one in describing the kinetics of complex biochemical networks. There are approximately one hundred reactions in coagulation, but there are a few that are particularly slow relative to the rest and limit how fast thrombin is generated. These slowest steps are referred to as rate-limiting. For example, the dissociation of factor Xa (FXa) from a lipid surface before reassociation with FVa on another lipid surface can be the rate-limiting step in thrombin generation.¹⁵ In a closed system, one in which no mass enters or leaves and where procoagulant stimuli are mixed homogenously in solution, we need only consider the intrinsic kinetics of each reaction in the fluid phase. Coagulation assays like PT, activated partial thromboplastin time (APTT), or calibrated automated thrombogram (CAT) are closed systems. Coagulation in an open system, one in which mass can enter or leave, such as in the formation of an intravascular clot, is fundamentally different than closed systems in two ways. First, most reactions occur on the vessel wall rather than in the fluid phase. Even though many coagulation assays in closed systems include phospholipids or platelets as surfaces to promote the assembly of enzyme complexes, these surfaces are suspended homogenously in the fluid phase. Second, these reactions happen in the presence of flowing blood. These features require that models of coagulation reactions under flow consider not only the intrinsic kinetics of each reaction, but also the transport of products and reactants to and from the surface. Under certain conditions that we outline below, transport of products to the surface can be rate-limiting.

Coagulation reactions take place on a variety of surfaces including the subendothelium, endothelial cells, tissue factor (TF) exposing cells or microparticles, and the phosphatidylserine-rich lipid surface of highly activated platelets. There are two general types of surface reactions that are important in coagulation; binding reactions and enzymatic reactions.

Binding reactions are typically modeled with first-order Langmuir kinetics:

$$\frac{\partial C_s}{\partial t}=k_{on}{C}_S(c_{s0}-c_s)-k_{\mathit{off}}{c}_s,$$ (1)

where C_s is the substrate volume concentration in the bulk; c_s is the surface concentration of the bound substrate; c_so is the total number of binding sites per unit area; and k_on and k_off are the association and dissociation rate constants. Note that we use upper case C (e.g., mol/m³) for volume concentration and lower case c (e.g., mol/m²) for surface concentration. Eq. 1 states in the language of differential equations that the change in the bound concentration of the substrate with time (left hand side) is equal to the difference between substrate binding and unbinding events (right hand side). An example is the binding of FVII/FVIIa to its co-factor TF to form the TF:FVIIa (extrinsic tenase) complex.

Enzymatic reactions are typically modeled with Michaelis-Menten kinetics:

$$\frac{\partial C_P}{\partial t}=\frac{V_{\mathit{max}}{C}_s}{K_M+C_S},$$ (2)

where C_P is the product concentration; V_max is the maximum reaction rate at saturating substrate concentrations; and K_M is the Michaelis constant. These include the activation of zymogens to enzymes by complexes formed by binding reaction, for example the conversion of FX to FXa by TF:FVIIa. Both binding and enzymatic reactions depend on the substrate concentration, which is dictated by the relative rate of transport of substrate from the bulk to the wall relative the association rate of the substrate.

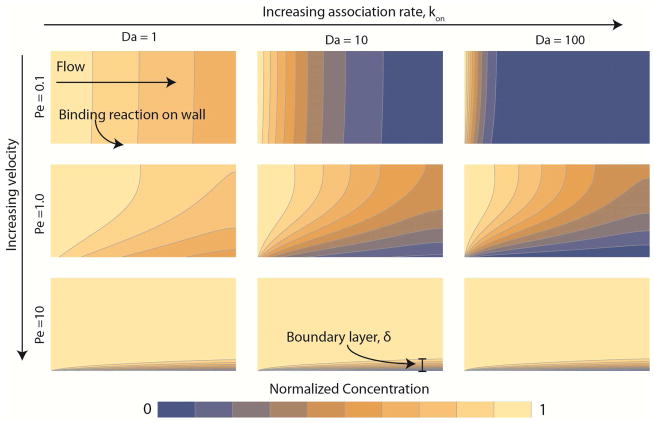
To calculate the rate of transport under flow, we need to consider both diffusion and convection (transport by flow), which are collectively called mass transfer. Mass transfer can be thought of as an additional rate process, which in combination with reaction kinetics, determines the rate of substrate consumption. Fig. 1 depicts the influence of the relative rates of diffusion, convection, and reaction on the substrate consumption by a binding reaction that follows Langmuir kinetics on the lower boundary. Flow moves from left to right between the two walls that make up the upper and lower boundary by a pressure driven flow. The substrate is introduced on the left boundary at a normalized concentration of one. Moving from top to bottom down the columns, the flow goes from low to high. Moving from left to right across the rows, the reaction rate becomes faster. When mass transfer is slow relative to reaction kinetics, we call a system transport-limited. In these cases, the substrate binds to the wall faster than it transports to the wall, leading to a concentration gradient between the surface and the bulk (far-right column of Fig. 1). For an enzymatic reaction that is transport-limited, the substrate concentration is lower near the wall, thus the rate of product formation is reduced. In an experiment, if the measured product generation increases with increasing flow velocity, then it is likely transport-limited. Conversely, when mass transfer is fast relative to reaction kinetics, we call the system reaction-limited. Here, the concentration of the substrate near the surface is close to the concentration in the bulk because it binds at a similar rate that it transports to the wall (far left-hand column of Fig. 1). In an experiment, if product generation is independent of flow velocity, then it is likely reaction-limited. Under reaction-limited conditions, flow can be a potent inhibitor of coagulation by diluting products in the near-wall region that may serve as substrates in subsequent reactions.

Figure 1. The influence of flow and reaction kinetics on the distribution of substrate for a binding reaction.

Flow moves from left to right. The substrate enters the domain on the left at a normalized concentration of unity (yellow) and is consumed by a binding reaction on the bottom wall leading to near-wall concentration of zero (blue). The binding reaction follows Langmuir kinetics (Eq. 1) . The velocity increases going down each column by one order-of-magnitude, and consequently increases the Peclet number (Pe, Eq. 6) by the same amount. Note the formation of a thin boundary layer of thickness δ near the bottom wall at Pe = 10, where convective flux is ten-fold higher than diffusive flux. The binding rate, k_on, increases across each row by one order-of-magnitude, resulting in a higher Dahmkohler number (Da, Eq. 11). For Da greater than unity (middle and right columns), the substrate is completely consumed at the wall leading to a transport-limited regime.

We can estimate whether a system is reaction-limited or transport-limited and reveal other important dynamics about a biochemical reaction or set of reactions by calculating a few dimensionless parameters. These dimensionless parameters come from scaling the conservation of species equation (convection-diffusion equation) by the appropriate geometric and dynamic variables. The details of this scaling procedure are beyond the scope of this review, but interested readers can find an introduction to scaling concepts in textbooks^16,17 and review articles specifically related to scaling arguments in binding and enzymatic reactions.^18–20 In lieu of a rigorous mathematical derivation based on first principles, here we present “engineering approximations” of the relative rates of different transport and reaction processes. These approximations give order-of-magnitude estimates of different rate processes.

We can determine the importance of different rate processes by comparing their fluxes. Flux is defined as the rate that a solute moves through, or is consumed/generated at, a surface and has units of moles or mass per unit time per unit area (e.g. moles s⁻¹ m⁻²). Let’s consider the case of a substrate flowing through a vessel with a diameter, d, and binding to the surface with Langmuir kinetics. The diffusive flux to the surface, j_D, also known as Fick’s law, for a substrate is:

$$j_D=-\mathcal{D}\frac{\mathrm{\Delta }C}{d}=-\mathcal{D}\frac{C_{S,\mathit{wall}}-C_S}{d},$$ (3)

where 𝒟 is the diffusivity of the solute; Δ is the difference operator; d is the vessel diameter; C_s is the bulk concentration; and C_s,wall is the concentration of the substrate near the wall. The maximum diffusion rate will occur when the concentration at the surface is zero, which is comparable to a fast reaction that consumes the substrate instantaneously:

$$j_{D,\mathit{max}}=\mathcal{D}\frac{C_S}{d}.$$ (4)

The convective flux of the substrate, j_C, is:

$$j_C=\frac{C_{S}Q}{A}=C_{S}U=\frac{C_S\gamma d}{8},$$ (5)

where Q is the flow rate; A is the vessel cross-sectional area; U is the average flow velocity; and γ is the shear rate. The velocity and shear rate in a circular tube are related by U = γd/8. Eq. 5 tells us the rate of solutes moving through an area A when carried along by a fluid moving at a velocity U. The ratio of the convective flux to the maximum diffusive flux is called the Peclet number (Pe):

$$Pe=\frac{j_C}{j_D}=\frac{Ud}{\mathcal{D}}=\frac{\gamma d^2}{8\mathcal{D}}.$$ (6)

When Pe < 1, transport is dominated by diffusion (top row of Fig. 1). When Pe = 1, the time it takes for the substrate to diffuse a certain distance is equal to the time it takes to travel that distance by convection. Under most physiological conditions, the Pe≫1 for plasma proteins in blood vessels and thus convection is the dominant mechanism of transport across the vessel. In extravascular hemorrhaging, deep vein thrombosis, and interstitial transport between platelets in a thrombus, the Pe can be near or less than unity, and the contribution of diffusion can be significant or dominant.

In the near-wall region, even at high Pe, the velocity is low (zero at the wall) and diffusion dominates. This is a result of the no-slip condition that states the velocity of a fluid at a solid surface is equal to the velocity of that surface, which in the case of blood vessels is zero. In the near-wall region there are sharp gradients in the velocity and concentration that are termed boundary layers (bottom row of Fig. 1). Because the shear rate is proportional to the velocity gradient, rather than the magnitude of velocity, these sharp gradients in the boundary layer mean that the area with the lowest velocity has the highest shear rate. The thickness of the concentration boundary layer, δ, is related to the Pe by:

$$\delta ~{\left(\frac{d^{2}L}{Pe}\right)}^{1/3},$$ (6)

where L is the length along the wall. Note that the boundary layer thickness is a weak function of the Pe so that a ten-fold increase in velocity (or shear rate) only reduces the thickness two-fold. The boundary layer also grows in thickness so that a longer injury results in greater depletion of the substrate from the bulk, but also greater accumulation of products in the near-wall region. We use the approximation symbol (~) in Eq. 6 because there is typically a coefficient in front of the parenthetical term that depends on channel geometry, but it is typically on the order of one²¹. For cases where a boundary layer exists, the characteristic diffusion length scale is no longer the vessel diameter (d), but rather, the boundary layer thickness (δ). Expressing the diffusive flux in terms of the boundary layer thickness gives an overall mass transfer flux, j_M, which accounts for both convective and diffusive transport:

$$j_M=-\mathcal{D}\frac{C_{S,\mathit{wall}}-C_S}{\delta }=-\mathcal{D}{\left(\frac{Pe}{d^{2}L}\right)}^{\frac{1}{3}}\left(C_{S,\mathit{wall}}-C_S\right)=k_m\left(C_S-C_{S,\mathit{wall}}\right),$$ (7)

Where we define the mass transfer coefficient as:

$$k_c={\left(\frac{{\mathcal{D}}^2\gamma }{8L}\right)}^{\frac{1}{3}}.$$ (8)

Mass transfer coefficients are useful in problems like thrombus formation under flow because they account for convective transport through the shear rate (γ) and diffusive transport through the diffusivity (𝒟).

Turning our attention to reaction rates, the reaction flux depends on the order and type of reaction. For a binding reaction following first-order Langmuir kinetics, the initial reaction flux is

$$j_R=k_{on}{C}_{s,\mathit{wall}}{c}_{s,o}.$$ (9)

To determine substrate concentration at the wall under conditions of high Pe, we equate the mass transfer flux (Eq. 7) to the reaction flux (Eq. 9) and solve for C_S,wall:

$$\frac{C_{S,\mathit{wall}}}{C_S}=\frac{1}{1+k_{on}{c}_{s,o}/k_c}=\frac{1}{1+Da},$$ (10)

where we have defined a new dimensionless number called the Dahmkohler number, Da, as the ratio of the reaction flux to the diffusive flux through the boundary layer:

$$Da=\frac{k_{on}{c}_{s,o}}{k_c}.$$ (11)

When Da ≪1, then the system is considered reaction-limited and the mass transfer does not significantly alter the rate of binding or product formation because the concentration of the solute at the surface is comparable to that in the bulk (C_S,wall ~ C_S ). When Da ≫1, the system is transport-limited and binding or product formation is slower than in the reaction-limited regime because the concentration of the solute at the surface is nearly zero (C_S,wall ~ 0, right column of Fig. 1). In the reaction-limited regime, the lag time to equilibrium is t_lag = (k_onC_s + k_off) ⁻¹. In the transport-limited regime, the lag time is longer due to increased mass transfer resistance such that t_lag = Da(k_onC_s + k_off) ⁻¹.

A similar analysis can be done for an enzyme reaction following Michaelis-Menten kinetics to yield a different form of the Dahmkohler number:²²

$$Da=\frac{V_{\mathit{max}}}{k_c{C}_S}.$$ (12)

Eq. 12 does not account for surface diffusion of the substrate, rather it assumes that substrates bind directly to their enzyme or that surface diffusion of the substrate to the enzyme is fast relative to the enzyme kinetics. However, if the enzyme surface concentration is low then the rate-limiting step for product generation can be diffusion of a substrate on the lipid bilayer to the enzyme.^23,24 In this case, one must consider the binding affinity of the substrate for the lipid surface, its two-dimensional surface diffusivity, and the intrinsic kinetics of the enzyme. The relative association rate of a substrate for an enzyme compared to the substrate surface diffusivity gives a second Dahmkohler number:

$${Da}_{2D}=\frac{k_a{a}^2}{{\mathcal{D}}_{2D}},$$ (13)

where k_a is a first order rate constant; a is the radius of interaction (additive radii of the substrate and enzyme); and 𝒟_2D is the surface diffusivity of the substrate in the lipid bilayer. Surface diffusivities in lipids are typically orders-of-magnitude smaller than volume diffusivities.

Using the Pe and Da we determine whether the rate limiting step in a system is transport or reaction; however, it does not tell us how transport ultimately affects product formation. Laidler and colleagues developed a theory that accounts for transport-limited enzymatic reactions using an apparent Michaelis constant:¹²

$$K_{m,\mathit{app}}=K_m+\frac{V_{\mathit{max}}}{2k_c}.$$ (14)

Note that K_m,app is greater than K_m because a higher bulk substrate concentration is needed to achieve a half-maximal reaction rate in the case of significant transport limitations. In a purely transport-limited regime (Da≫1), the product concentration and reaction rate scales with the 2/3^rd power of the fluid velocity:²⁵

$$C_P~{\left(\frac{\mathcal{D}L}{d^{2}U}\right)}^{2/3}{C}_S$$ (15)

$$\frac{d{C}_p}{dt}~{(U{\mathcal{D}}^2{d}^2{L}^2)}^{2/3}{C}_s$$ (16)

By plotting the product concentration versus velocity (or shear rate) on a double-logarithmic plot, we can determine the degree of transport resistance. If the slope of that line is close to -2/3, then the system is transport-limited. If the slope is close to -1, then the system is reaction-limited. Slopes between these two values mean that the system is partially transport-limited.

In summary, the mass transfer of reactants and products can be thought of as simply another rate process in addition to the biochemical reactions that make up coagulation. The key concept that comes from this section is that under certain conditions mass transfer can be the rate-limiting step for a reaction or reaction network. Here, we have used the defined fluxes for diffusion, convection, and reaction in order to define a set of dimensionless numbers that define the mass transfer and reaction regimes. The mass transfer regime is determined by Pe, which is the ratio between the convective flux and diffusive flux. When Pe is large, mass transfer is dominated by convection, which physically translates to a thin concentration boundary layer near the vessel wall where reactants are depleted and products are generated (bottom row of Fig. 1). For a sense of scale, the boundary layer thickness is 1–10 μm under physiological blood flow conditions. When the Pe is small, mass transfer is dominated by diffusion, and reactants and products can penetrate deep into the lumen of the vessel. The reaction regime is determined by Da, which is the ratio between mass transfer flux and the chemical reaction flux. When the Da is large, the chemical reaction is fast relative to mass transfer, and therefore, the system is transport-limited. A system that is transport-limited will have large concentration gradients near the surface where the reaction occurs because the reactants are being consumed faster than they are being delivered to the surface. In this case, product formation is attenuated compared to the reaction alone. When the Da is small, the chemical reaction is slow relative to mass transfer, and the system is considered reaction-limited. A system that is reaction-limited will not be limited by the transport of reactants and thus product formation will follow reaction kinetics.

3. Mass transfer regulation the tenase and prothrombinase complexes

The scaling arguments from the previous section are easiest to understand in the context of individual reactions in purified systems of coagulation factors. The most extensively studied are the conversion of FX to FXa by TF:FVIIa and the conversion of prothrombin to thrombin by FVa:FXa. Table 1 summarizes several of the key studies on invidual coagulation reactions and their experimental conditions.

Table 1.

Summary of key studies of individual coagulation reactions under flow.

Reaction	Channel diameter or height (mm)	Channel length (mm)	Shear rates (sec−1)	Surface concentration (fmol/cm2)	Substrate concentration	Reference
FVIIa binding to TF, FXa generation on TF:FVIIa	0.34, 0.56,1.1	125,150, 75	4–430	4.58	10 nM FVIIa,100 nM FX	13
FVIIa binding to TF, FXa generation on TF:FVIIa	0.26	125	25–3000	3.73	10 nM FVIIa, 50–800 nM FX	27
FVIIa binding to TF, FXa generation on TF:FVIIa	0.27	127	100, 1600	1–70	10 nM FVIIa, 10–1200 nM FX	29
FXa binding to FVa, IIa generation on FVa:FXa	0.58	127	42, 82	2.4	0.5 nM FXa, 1 μM FII	31
FXa binding to FVa, IIa generation on FVa:FXa	0.29, 0.65	127	20, 300	0.4–1.5	1–80, 500 nM FII	33
IIa generation on	0.2	50	100–1000	1.8	1.4 μM FII	34
FVa:FXa APC generation on TM:IIa	0.1	45	50, 500	60–1400	2 nM FIIa,0.1 μM PC	36

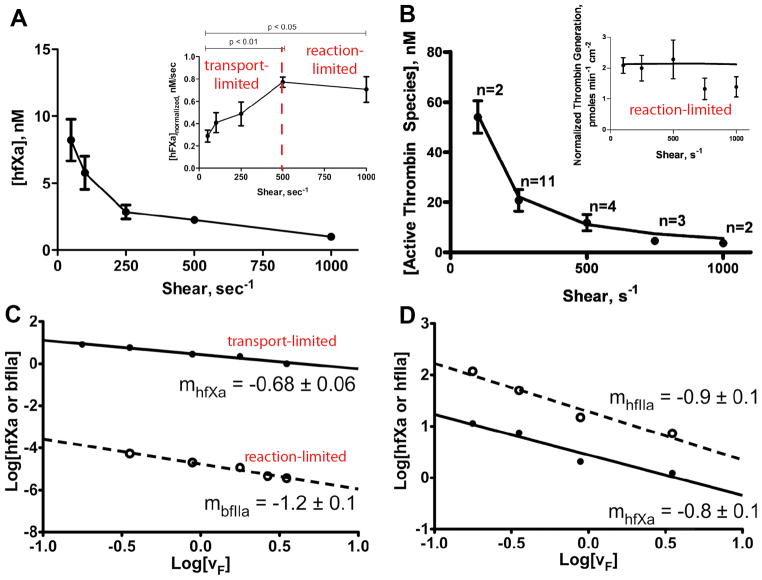
Nemerson and colleagues reported the influence of flow on isolated coagulation reactions in their pioneering work on the formation of the TF:FVIIa (extrinsic tenase) complex and its production of FXa.¹³ In the experiments, a tubular bioreactor is created by coating the inside wall of a glass capillary tube with TF embedded in a phospholipid bilayer consisting of phosphatidylcholine (PC) and phosphatidylserine (PS). A solution of FX and FVII, or FX and FVIIa, is perfused through the tube over a range of shear rates. FXa is measured at the outlet. The transient production of FXa depends on the shear rate to the negative two-thirds power over the range of 26–120 s⁻¹, which as shown in Eq. 16, is indicative of a transport-limited regime. As such, FXa production is dictated not by the kinetics of the TF:FVIIa catalyst, but by transport of FX to the surface and its diffusion within the lipid bilayer. At approximately 500 s⁻¹, FXa production shifts towards a reaction-limited regime as the boundary layer gets thinner with increasing flow (Eq. 6), reducing mass transfer resistance (Fig. 2A).³⁴ A secondary effect of increasing flow is the expedited removal of FXa from near the TF:FVIIa complex. Because FXa binds to TF:FVIIa transiently and reversibly, it acts a competitive inhibitor of binding sites for FX.²⁶

Figure 2. Transport limitations in FXa and thrombin generation in tubular bioreactors.

Purified solutions of zymogens (FX and prothrombin) are perfused through tubular bioreactors that consists of a capillary tube coated with lipid bilayers (PC:PS, 75:25) containing enzyme complexes (TF:FVIIa, FVa:FXa). The effluent is collected and the concentration of enzyme (FXa, thrombin) is measured as function of wall shear rate. A. Human FXa generation on 2.2 fmol/cm² TF:FVIIa crosses over from a transport-limited regime to a reaction-limited regime at a wall shear rate of 500 s⁻¹ owing to a reduction in the boundary layer thickness.³⁵ This transition is characterize by an in increase in FXa flux with shear rate up to 500 s⁻¹ (inset). B. Bovine thrombin generation on 1.7 fmol/cm² FVa:FXa is reaction-limited over the entire range of shear rates. Reduction in thrombin concentration with increasing shear rate is due solely to dilution by flow.³⁴ Note that the thrombin flux is constant over entire range of shear rates (inset). C. Double log plot of FXa and thrombin concentrations exiting the reactor as a function of flow velocity for isolated experiments with FX and thrombin. The slope of −1.2 for thrombin is indicative of a reaction-limited regime. The slope of −0.68 for FXa is indicative of a transport-limited regime (Eq. 5).³⁵ D. Double log plot for simultaneous generation of FXa and thrombin in presence of both TF:FVIIa and FVa:FXa. The slope of −0.8 shows that the competition of FX for binding sites with prothrombin causes a transition in FXa production to a regime where transport rates and reaction rates are on the same order-of-magnitude.³⁵

One way to overcome mass transfer resistance is to increase the substrate flux to the surface by increasing it concentration (C_S) in the bulk (Eq. 7). Increasing the FX concentration from 50 nM to 800 nM drives the system from a transport-limited regime towards a reaction-limited regime even at low shear rates.²⁷ Steady-state FXa production is not a function of FVIIa concentration, but the lag time to steady-state does increase with decreasing concentration of FVIIa. Thus, there are two time scales that dictate FXa production; the time for FVIIa equilibrium with bound TF and the time for FX to diffuse through the boundary layer. Even in the reaction-limited regime where product formation is independent of flow rate, the rate-limiting step in a reaction mechanism can be still be dictated by transport within the lipid bilayer of the surface. For example, under reaction-limited conditions, the rate-limiting step for FXa production on TF bearing epithelial cells is the rate of surface diffusion of FX from its initial binding site to its reaction site with TF:FVIIa.²⁸ In other words, adsorption of FX to the membrane surface and its activation by TF:FVIIa are fast relative to the time it takes between adsorption and collision with TF:FVIIa.

The composition of the lipid bilayer determines when the system crosses from transport-limited to reaction-limited. Lipid bilayers composed of only PC are reaction-limited for shear rates greater than 100 s⁻¹, compared to bilayers of PC:PS (70:30) which are reaction-limited for shear rates greater than 430 s^−1.29 This is likely due to a lower reaction flux on PC, compared to bilayers containing the negatively charged PS, which accelerate reaction rates. Interestingly the lag time to steady state FXa production is reduced on PC bilayers because the binding affinity of FXa to PC is less than to PC:PS surfaces.

A counterintuitive result of transport-limited systems is that increasing enzyme surface concentrations do not result in higher product generation.³⁰ At 100 s⁻¹, well within the transport-limited regime for FX conversion by TF:FVIIa, the FXa generation is independent of TF surface concentration over the range of 30–70 fmol/cm^2.29 An interesting implication of this result is that the surface concentration of enzyme required to reach half-maximal reaction rates depends on mass transfer to the surface, not enzyme kinetics. As a result, relatively low concentrations of enzyme are needed to achieve half-saturation at low transport fluxes.

Similar studies in lipid coated capillary bioreactor show that mass transfer regulates the formation of the prothrombinase complex.³¹ Here, FVa is integrated into a lipid bilayer with PC:PS ratio of 75:25 and FXa and prothrombin are perfused through the tubular reactor. Thrombin, α-thrombin, and miezothrombin (des fragment 1) are measured at the exit of the reactor. The lag time to steady-state thrombin production is reduced by both increasing FXa concentration and increasing the shear rate, both results suggesting that the formation of the prothrombinase complex is a mass transfer-limited. However, even at low wall shear rates (42–82 s⁻¹) where the boundary layer is relatively thick, thrombin generation is independent of flow. Moreover, thrombin generation scales linearly with FVa surface concentration (0.25–2.5 fmol/cm²), but is independent of FXa concentration. These results are indicative of a reaction-limited regime for the conversion of prothrombin to thrombin by the prothrombinase complex.

Mass transfer limitations not only affect the production of coagulation enzymes, but also their inhibition. Thrombin generation is only modestly reduced by antithrombin III (ATIII) and ATIII with heparin in a tubular bioreactor, compared to static experiments when prothrombinase is suspended in a bulk solution.³². This is due to depletion of ATIII by thrombin in the boundary layer region, which effectively reduces the ATIII concentration at the wall compared to the bulk concentration. This result has clinical importance for the use of heparin because it suggests that ATIII/heparin is a strong inhibitor of free thrombin and FXa, but a relatively weak inhibitor of these enzymes on the vessel wall or adhered platelets.

As in the case for TF:FVIIa, whether prothrombin conversion to thrombin is mass transfer limited depends on the surface concentration of prothrombinase, the bulk concentration of FXa and prothrombin, and shear rate.³³ The rate of prothrombinase assembly is limited by transport of FXa at bulk concentration of 1–20 pM because the lag time to steady-state decreases with increasing FXa concentration. Thrombin production is independent of prothrombinase surface concentrations above 1 fmol/cm² (0.05% fractional area), but dependent on prothrombin concentration, indicative of a transport-limited regime. The fact that these arguments hold at low enzyme densities suggest that surface diffusion of prothrombin on the surface is much faster than its flux to the wall.

Haynes et al. examined the production of bovine thrombin on preformed prothrombinase, thus decoupling the kinetics of forming the prothrombinase complex from the kinetics of the prothrombin conversion.³⁴ Over the shear rates of 100–1000 s⁻¹, thrombin generation on 1.8 fmol/cm² of prothrombinase is reaction-limited at physiological concentrations of prothrombin since thrombin wall flux is independent of shear rate (Fig. 2B). The high concentration of prothrombin apparently creates a high enough diffusive flux that there is not significant substrate depletion in the near-wall region. Note that even though the thrombin production is constant, at higher shear rates thrombin concentration on the near-wall region is lower because of dilution by flow. The conversion of prothrombin is a two-step process, where the first step is cleavage at Arg323 to give the intermediate miezothrombin, followed by a second cleavage to give α-thrombin. The ratio of α-thrombin:miezothrombin is 3:2 in the flow reactor and independent of shear rate. Miezothrombin is a less potent platelet agonist and has reduced activity on fibrinogen. The fact that such a high percentage of prothrombin is only converted to miezothrombin under flow reduces the overall procoagulant activity compared to static systems where all miezothrombin eventually is converted to thrombin.

When studied in isolation, at physiological shear rates and zymogen concentrations, and enzyme concentration of 1–2 fmol/cm², FXa production on the TF:FVIIa complex is transport-limited up to wall shear rates of 500 s⁻¹ and thrombin production on the FVa:FXa complex is reaction-limited from 50–1000 s⁻¹ (Table 1, Fig. 2A,B). However these reactions, among others, occur simultaneously in the extrinsic pathway of coagulation, and importantly, compete for binding sites on phospholipid bilayers. Combining these two reactions into a single experiment in a flow reactor led to deviations from behavior observed for each individual reaction.³⁵ In the experiments, extrinsic tenase (TF:FVIIa) and FVa were preassembled in supported bilayers in a rectangular bioreactor followed by perfusion of a mixture of prothrombin, FX, and in some experiments, FVa at 50–1000 s⁻¹. The authors measured K_m,app and using the formalism introduced by Laidler and colleagues (Eqs. 15–16) to determine whether FXa and thrombin production were transport-limited or reaction-limited and additionally integrated the competition of prothrombin, FX, and FXa for binding sites (Fig. 2C–D). When prothrombin and FX are perfused together, FXa production deviated from the purely transport-limited regime observed when FX is perfused alone. In these experiments prothrombin outcompetes FXa for binding sites, thus reducing both the surface bound and free FXa. When FX has to compete with prothrombin for binding sites, the rate-limiting step for FXa production shifts from transport to the surface through the boundary layer to binding to the lipid surface.

Anticoagulation mechanisms like the protein C pathway are subject to similar mass transfer limitations as coagulation reactions. Tseng et al. developed a method to cross-link a thrombomodulin (TM) containing lipid bilayer to a polyelectrolyte multilayer as an antithrombotic surface coating.³⁶ To determine the catalytic efficacy of this preparation, TM coated glass slides were placed in a parallel plate flow chamber and thrombin and protein C were perfused over the surface at 50 and 500 s⁻¹. At low TM concentration, activated protein C (APC) production is reaction-limited. At high TM concentrations, APC production is transport-limited. The TM surface concentration that leads to a cross-over to a transport-limited regime depends on shear rate, 400 fmol/cm² at 50 s⁻¹ and 800 fmol/cm² at 500 s⁻¹. The measured APC production is 28–50% less than predicted by the simple scaling arguments presented in Section 2, which demonstrates the limitation of using these calculations. Discrepancies may arise from assuming a constant bulk concentration (C_s) along the entire length of the flow chamber. It is likely that the substrates are depleted in the bulk as the boundary layer thickness approaches one-third to one-half of the channel height. This also suggests that surface-mediated anticoagulation mechanisms will have a greater effect in small vessels than large vessels. Indeed, the inhibition of thrombin generation by thrombomodulin under flow is greatly enhanced at high surface area to volume ratios.³⁷

The studies presented in this section use immobilized lipid bilayers functionalized with co-factors (TF, FVa, TM) in tubes or channels to measure the influence of flow on binding and enzymatic reactions. These examples show how the scaling arguments presented in Section 2 can be applied to experiments to predict transport-limited and reaction-limited regimes based on the scaling of substrate consumption or enzyme production as a function of flow velocity. Thus far, we have focused on a small set of reactions occurring in a very long tube. Long here means the reaction surface is much larger than the channel diameter. In Section 4, we will examine other biophysical phenomena that regulate the entire extrinsic pathway confined to small injuries, or those that are on the scale of the channel diameter.

4. Threshold response of thrombin formation to tissue factor surface concentration and injury size

In the previous section we reviewed how mass transfer regulates binding and enzymatic reactions in the production of FXa by the extrinsic tenase complex and thrombin by prothrombinase complex under flow on immobilized lipid bilayers. When both complexes are present, we saw that the problem becomes significantly more complicated given the competition for binding sites. As we consider the entire extrinsic pathway, the availability of surface binding sites and the size of an injury become significant regulators of coagulation under flow.

Biochemical networks with several positive feedback loops like coagulation are often characterized by a threshold activation response to stimuli.³⁸ Weak stimulation gives little to no thrombin generation due to inhibition by endogenous inhibitors, but above a threshold level there is a rapid burst in thrombin that overcomes these inhibitors.³⁹ Under static conditions, a burst of thrombin marks the propagation phase of coagulation where procoagulant products are generated at a rate that exceeds the ability of anticoagulant pathways to inhibit them.² Under flow, the same balance of pro- and anticoagulant pathways are at work with the added inhibition of dilution of products by blood flow as described in the purified systems in Section 3.

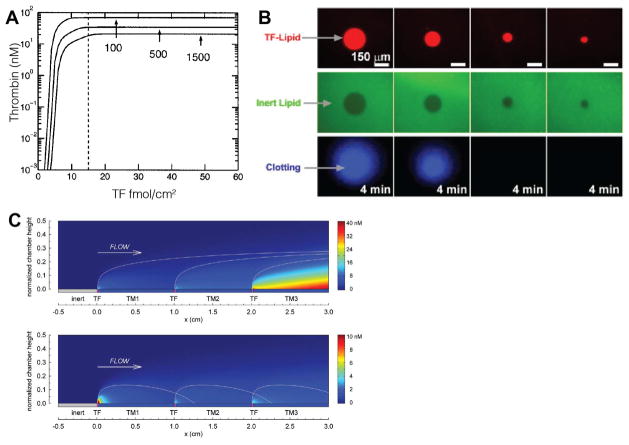
Due to the experimental limitations of tracking the concentration of all of the individual species in coagulation, mathematical models have proven valuable tools for revealing biochemical and biophysical mechanisms that regulate coagulation and thrombus formation.⁴⁰ Kuharsky and Fogelson developed a model of thrombus formation under flow on a small patch of TF on a wall.⁴¹ Mass transfer coefficients are used to model the transport of zymogens, enzymes, inhibitors, and platelets to and from the wall. Platelets are treated as chemical species that adhere to, and importantly, can physically inhibit access to wall-bound TF. The model predicts a threshold response in thrombin generation to TF surface concentration (Fig. 3A). These results have been confirmed experimentally in whole blood flow assays over collagen-TF microspots where both the qualitative threshold behavior and the quantitative TF surface concentrations needed to induce coagulation were in good agreement with model predictions.⁴² In the experiments, fibrin deposition is used as a marker for coagulation and similarly sharp thresholds to TF surface concentration are observed. A three-fold higher TF concentration is needed to promote fibrin deposition for a ten-fold increase in wall shear rate.

Figure 3. Threshold response to TF surface concentration and injury size.

Experiments and simulations show that TF surface concentration or injury size must exceed a threshold value to yield a burst in thrombin generation characteristic of the propagation phase of coagulation. A. A computational models of thrombus formation under flow predict a threshold response in thrombin generation to surface TF concentrations that is a function of wall shear rate (100, 500, 1500 s⁻¹). Note that above ~15 fmol/cm² of TF that thrombin generation saturates suggesting reaction-limited behavior. B. Under static conditions, a threshold TF spots size is necessary to initiate coagulation from plasma.⁴⁸ Below the threshold size coagulation products diffuse away from the spot before they can initiate robust thrombin generation. C. A computational model of plasma flowing over TF spots separated by TM coated walls. At low TM surface concentrations (top panel), thrombin generation is additive between adjacent TF sites because there is not enough APC to quench coagulation products between site. At high TM concentrations (bottom panel), the interaction between sites can be repressed.⁵¹

Thrombin generation in the Kuharsky and Fogelson model is mediated by platelets in two ways. First, the number of binding sites for zymogens and enzymes on the platelets modulates the thrombin burst, demonstrating the procoagulant function of platelets. Second, platelets serve an anticoagulant role by blocking access to TF. The model shows that dilution by flow and blocking access to wall-bound TF by adherent platelets are the primary mechanisms that inhibit coagulation and are more potent than TFPI and APC pathways, at least for small injuries.⁴³ This physical inhibition of TF was necessary to recreate the reduction in thrombin generation expected for severe FVIII and FIX deficiencies. In the absence of platelets, there was little difference in thrombin generation at low levels of FVIII and FIX. These predictions are supported by experiments showing severe FVIII deficiencies reduce fibrin formation in whole blood, but not in plasma, at high TF surface concentrations.^44,45

Presumably vessel walls are often subject to some degree of disruption, and thus TF exposure. Size thresholds likely exist to ensure that coagulation is initiated only on injuries that are sufficiently large or deep to expose high densities of TF. A mathematical model of coagulation that accounts for binding sites and surface diffusion predicts that at least a 5 μm patch of TF is necessary to initiate coagulation under static conditions, but that larger patches are necessary under flow.⁴⁶. Ismagilov and colleagues conducted a series of studies on the regulation of coagulation by injury size under both static and flow conditions.^47–50 In the experiments, photopatterning of lipid bilayers is used to define spots of TF-rich lipids surrounded by neutral lipids or thrombomodulin-rich lipids in microfluidic channels or capillary tubes. For a given TF surface concentration, a threshold TF patch size is necessary to initiate thrombin generation (Fig. 2B).⁴⁸ Under flow, this threshold size increases with increasing wall shear rate.⁴⁹ We can understand the relationship between the concentrations of coagulation products, shear rate (or velocity), and injury size by examining Eq. 15. Product concentration, C_P, is proportional to the size of the injury, L^2/3, and inversely proportional to the velocity, U^−2/3. Thus, to maintain the same product concentration at an increased shear rate requires a larger injury.

The size of an injury and the space between injuries, in the case of systemic endothelial dysfunction, coupled to blood flow, regulates the distribution of thrombin downstream of an injury and the effectiveness of the APC pathway. There is significant cross-talk between adjacent injuries in whole blood flow assay on collagen-TF in the absence of TM.⁴² Jordan and Chaikof developed a mathematical model to predict the effectiveness of TM-mediated APC generation in localizing thrombin to an injury site and eliminating cross-talk.⁵¹ At low TM concentrations, thrombin produced at an upstream injury can lead to higher thrombin concentrations at a downstream injury (Fig. 3C). However, sufficient levels of TM contain thrombin near the injury site, and similar to initiation of coagulation by TF, can completely inhibit thrombin generation above a threshold level.

5. Fibrin polymerization and deposition under flow

Fibrin fiber polymerization is a multi-step process that requires fibrin monomers to polymerize into oligomers; oligomers to form protofibrils; and protofibrils to laterally aggregate into fibers.⁵² Fibrin formed under flow is morphologically distinct from fibrin formed under static conditions. The highly porous and voluminous gels that characterize fibrin formed under static conditions are in stark contrast to the dense, mat-like structure of fibrin formed under flow.⁵³ Fibrin polymerization reactions are subject to the same transport- and reaction-limited arguments as coagulation reactions.

Since fibrin polymerization proceeds thrombin generation, the dilution effects of flow are even greater than those for the extrinsic pathway. Weiss and colleagues reported that fibrin deposition and fibrinopeptide A generation was inversely correlated with shear rate over the range of 50 – 2600 s⁻¹ in nonanticoagulated whole blood over animal derived subendothelium.^8,9 Maximum fibrin deposition was observed at a shear rate of 50 s⁻¹ followed by a sharp decrease at shear rates greater than 650 s⁻¹. Using blood from patients with low platelet counts showed that at low shear rates (<100 s⁻¹) platelet deposition was not necessary for fibrin deposition; however, at intermediate shear rate (650 s⁻¹), platelet adhesion was necessary. This reinforces the importance of platelet surfaces on propagating coagulation under flow. There is also a positive correlation between platelet count and fibrin deposition, while fibrinopeptide A generation was not correlated to platelet count.⁸ Tijburg and colleagues found similar trends in reduced fibrin deposition with increasing shear rate using whole blood treated with trace amount of low molecular weight heparin perfused over an extracellular matrix derived from activated endothelial cells.⁵⁴ However, fibrinopeptide A generation was independent of shear rate in contrast with the Weiss studies. Differences in prothrombotic substrate, flow chamber dimensions, and anticoagulant may account for this disagreement. Nevertheless, these studies suggest that while thrombin was being generated at sufficient quantities to cleave fibrinogen and activate platelets, flow dilutes fibrin monomers and oligomers before they can polymerize into fibers at arterial shear rates.

Fibrin accumulates in areas of disturbed or low flow in more complex geometries such as arterial branching models and indwelling catheter.^55–57 The presence of recirculation flow regions leads to low flow niches with prolonged residence times that yield fibrin fiber deposition. Additional evidence comes from whole blood flow assays at arterial shear rates on homogenized atherosclerotic plaque material containing collagen and TF.⁵⁸ The primary and secondary hemostasis occurred in sequence—in the first 5 to 6 minutes only platelet adhesion and aggregation took place followed by fibrin formation in the flow niches offered by the platelet aggregates and fostered by their activated membrane surfaces and the TF from the plaque. In the absence of flow, or in areas of low flow like recirculation zones, thrombin can propagate far from TF initiation sites.³⁷

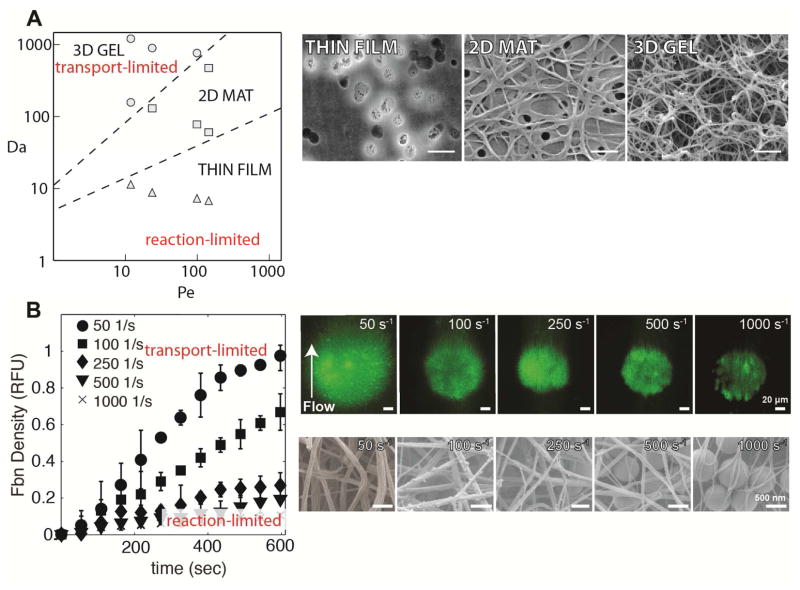
In a purified system containing thrombin introduced through a porous membrane into a flowing solution of fibrinogen, thrombin generation and shear rate dictate fibrin fiber morphology.⁵³ At normal thrombin generation, as shear rate increases, fiber diameter decreases and eventually distinct fibers cannot be visualized at shear rates greater than 100 s⁻¹. Computer simulations suggest that fibrinogen is converted to fibrin monomer at all shear rates, but that flow dilutes fibrin oligomers before they can polymerize to form protofibrils. Using Pe and Da calculated from fibrinogen consumption, a state diagram was proposed to map the conditions required for fibrin formation (Fig. 4A). There are three fibrin morphologies observed depending on the Pe and Da; (1) three-dimensional fibrin gels for Pe < 100 and Da > 900, (2) two-dimensional mats of fibrin fibers at 10 < Da < 900, and (3) thin films only a few fibers thick at Da < 10 (Fig. 4A–B). Notably, in this system there was no fibrin deposition at shear rates greater than 100 s⁻¹, even at very high thrombin fluxes, suggesting that it is unlikely for fibrin to form on flat surfaces at moderate to high shear rates. In vivo observations of arterial thrombi show significant fibrin content.^6,59 One hypothesis that reconciles these observations is that platelets and platelet aggregates protect coagulation and fibrin polymerization reactions from dilution by flow.

Figure 4. Mass transfer limitations of fibrin deposition.

The mass transfer limitations on fibrin deposition are more stringent than thrombin owing to the multistep polymerization process. A. A state diagram (left) for fibrin morphology as a function of Pe (Eq. 6) and Da (Eq. 12) demonstrates regimes of transport-limited and reaction-limited fibrin deposition. The different morphologies are shown in electron micrographs (right) thin films, two-dimensional mats of fibers, and three dimensional gels.⁵³ Scale bar = 1 μm. B. Fibrin deposition on TF coated silica beads during plasma perfusions at different shear rates (left).⁴⁴ There is a transition from a transport-limited regime that supports three dimensional fibrin gel formation and a reaction-limited regime where fibrin fibers are limited to the interstitial spaces between the beads. Panels on the right show fluorescent images and electron micrographs of fibrin deposition at different shear rates.

To test the hypothesis that fibrin polymerization needs protection from flow at arterial shear rates, 800 nm TF-coated silica beads were patterned into 10–100 μm spots.⁴⁴ Here, the beads act as physical analogs for platelets or other TF-bearing cells. For the same TF surface concentration, the TF-coated beads support coagulation and fibrin formation, while planar TF spots cannot. Shear rate and TF surface concentration dependent transport- and reaction-limited regimes are evident in the transient fibrin deposition data (Fig. 4B). The interstitial space between beads provides a low flow area that provides a reaction limited-regime where fibrin fibers can form and dilutional effects are reduced. At sufficiently high TF surface concentrations, three-dimensional fibrin gels would form with heights of 10–15 μm, but gel height is reduced with increasing shear rate.

The ultimate height of fibrin gels formed in parallel, laminar flow in straight channels is possibly limited by the transport of zymogens through the fibrin gel to the underlying wall-bound TF. A kinetic model of fibrin gel formation predicts two regimes of growth depending on the shear rate and gel permeability.⁶⁰ At high shear rates, growth is limited by dilution of fibrin polymers before they can reach a gelation concentration. At low shear rates, mass transfer of thrombin from the procoagulant surface to the surface of the gel limits growth where it can further cleave fibrinogen. The rate of thrombin transport is determined by the hydraulic permeability, a physical property of porous materials that determines fluid velocity for a given pressure gradient.⁶¹ The hydraulic permeability of fibrin gels varies over three orders-of-magnitude for fiber volume fractions of 0.02–0.54, which is representative of the range of fibrin content in retrieved thrombi from humans.⁶²

The morphology and orientation of fibrin fibers is strongly influenced by flow. On collagen activated platelets, an increase in shear rate from 5 s⁻¹ to 20 s⁻¹ results in a dramatic increase in fiber orientation with flow⁶³. Similarly, on TF-bearing fibroblasts, flow of plasma on a 30° incline results in increased orientation and fiber diameter compared to static conditions ⁶⁴. Fibers align with the direction of flow on TF-coated silica beads over the shear rates from 50–1000 s^−1.44 The mechanism(s) by which flow causes fibers to assembly in an anisotropic manner is unknown.

6. Interstitial transport

In Section 4, we introduced the concept that platelets limit thrombi growth by impeding the access of zymogens to TF:FVIIa and enzymes out of the thrombi.^41,65 In Section 5, we introduced this concept of self-limiting fibrin gel growth based on the rate of transport of thrombin from a procoagulant wall through a fibrin gel.^44,60 These studies suggest interstitial transport,⁶⁶ that is solute transport in the interstitial spaces between fibrin fibers and platelets may be a key regulator in thrombus growth. Here, we extend that concept to recent experimental and computational studies that provide finer grain spatial and temporal details of interstitial transport and its role in shaping thrombus architecture.

A core-shell structure of thrombi has emerged from the intravital imaging in the laser injury model in the cremaster arterioles of mice.⁶⁷ The core region is adjacent to the injured vessel and is characterized by densely packed P-selectin positive platelets. Thrombin and contact dependent signaling stabilize the core region. Fibrin is concentrated near the vessel wall and in the extravascular space (in the case of a puncture wound). The shell region is characterized by relatively loosely packed P-selectin negative platelets. The growth of the shell seems to stem from the ability of unactivated, discoid platelets to form tethers with other platelets in areas with gradient in shear stress.⁶⁸ However, the mechanical stabilization of the shell is ADP dependent, which is congruent with finds in a puncture wound model.⁶⁹ This architecture influences the transport of platelet agonists into and out of the thrombus.⁷⁰ The low porosity, core region impedes the escape to thrombin from the near-wall region, leading to highly activated platelets. Retraction and outside-in signaling through the α_2bβ3 integrin appears to regulate the formation of the core region.⁷¹ Thrombin moves more easily through the shell, which could limit thrombin accumulation, and ultimately thrombus growth. Computation simulations of interstitial transport based on intravital imaging estimate gap sizes between platelets of 10–200 nm, and Pe less than unity, suggesting diffusion-dominated transport within the thrombus core.⁷² Similar gap sizes were measured by focused ion bead-scanning electron microscopy of thrombi formed under flow in vitro.⁷³

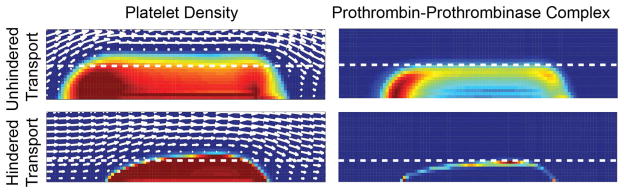
In a spatial-temporal computational model of thrombus formation, Leiderman and Fogelson found that hindered transport of coagulation zymogens and enzymes in the interstitial space results in smaller, more dense clots (Fig. 5).⁷⁴ The term hindered transport is used to describe the hindrance in diffusive and convective transport by steric and hydrodynamic factors in fibrous and porous media relative to transport in their solvent.^75,76 Close analysis of the distribution of coagulation factors reveals that in cases when transport is hindered, the access of a substrate to its enzyme can be limited, thus retarding thrombus development. For example, prothrombinase is restricted to the core and less prothrombin can reach it relative to the unhindered case (Fig. 5). This results in lower thrombin generation, and consequently less activated platelets and slowed growth.

Figure 5. Regulation of thrombus growth by interstitial transport.

The access of zymogens to their enzymes in a growing thrombus can limit growth. Here, computational simulations of thrombus formation on a TF surface for cases of unhindered and hindered transport.⁷⁴ In the left-hand column, colors indicate the platelet density from plasma concentration (blue) to dense packing (red). In the right-hand column, colors indicate the concentration of prothrombin bound to prothrombinase from low (blue) to high (red). Coagulation factor transport that is hindered due to reduced interstitial space between platelets that limits the ability of prothrombin to penetrate into the thrombus and reach platelet-bound prothrombinase. Note that hindered transport leads to a denser, smaller thrombi compared to unhindered transport.

Theories of hindered transport in dense media such as thrombi with high volume fractions of fibers and cells are lacking, making interpretation of experimental data and development of computational models challenging. Experimental measurements of fluid and solute transport in thrombi formed at a range of fibrin and platelet concentrations provide lookup tables of physical properties such as hydraulic permeability and diffusivity and insight into how these properties change with thrombus composition.^62,73 Thrombi elasticity is correlated to these transport properties, at least at low strains.⁷⁷ This link between measurements of clot mechanics through methods, such as ultrasound or thromboelastography, and interstitial transport, could guide therapeutic choices with respect to fibrinolytic agents and mechanical retrieval of thrombi.

7. Summary

Blood flow and mass transfer, in addition to the biochemical mechanisms we typically associate with coagulation, regulate the initiation and propagation of coagulation. The mass transfer mechanisms of diffusion and convection determine the local concentrations of zymogens, cofactors, enzymes, and inhibitors at the site of injury. The rates of these processes relative to biochemical reactions rates tells us whether the rate-limiting step is mass transfer or reaction. For the extrinsic pathway under flow, the initiation of coagulation shows threshold dependence on the surface density of co-factors (e.g., TF), binding sites, and injury size. Fibrin polymerization reactions are subject to even more stringent mass transfer regulation due to their multistep assembly. In order to form fibrin fibers, these reactions need protection from the dilutional effects of blood flow at moderate to high shear rates by geometric features of the vessel wall or blood cells. Mass transfer limitations also appear to play a role in the propagation of coagulation within a growing thrombi. The interstitial space between platelets regulates the transport of coagulation proteins and platelet agonists into and out of thrombi, ultimately determining its architecture and arrest.

Practice Points.

• Effectiveness of anticoagulation, replacement, and bypass therapies are coupled to blood flow velocity, vessel size, and injury size and composition.

Research Agenda.

• Transport and kinetic limitations of endogenous and therapeutic anticoagulants over range of blood flow conditions and injury compositions

• Measurements and models of coagulation in complex, non-parallel flows characteristic of arterial stenosis, venous valves, and aneurysms

• Role of erythrocytes and leukocytes in promoting and inhibiting coagulation under flow

Appendix ADefinition of variables and their units

Variable	Definition	SI Units
A	vessel cross-sectional area	m2
a	radius of interaction	m
CP	product concentration	mol/m3
CS	substrate concentration	mol/m3
Cs,wall	substrate concentration near wall	mol/m3
cs,o	number of surface binding sites	1/m2
cs	surface concentration	mol/m2
𝒟	diffusion coefficient	m2/s
𝒟2D	two-dimensional diffusion coefficient
Da	Dahmkohler number
Da2D	two-dimensional Dahmkohler number
d	vessel diameter	m
jC	convective flux	mol/m2 s
jD	diffusive flux	mol/m2 s
jD,max	maximum diffusive flux	mol/m2 s
jm	overall mass transfer flux	mol/m2 s
jR	reaction flux	mol/m2 s
KM	Michaelis constant	mol/m3
KM,app	apparent Michaelis constant	mol/m3
ka	1st order rate constant	1/s
kc	mass transfer coefficient	m/s
koff	dissociation rate constant	1/s
kon	association rate constant	m3/mol s
L	length along wall, injury size	m
Pe	Peclet number
Q	flow rate	m3/s
t	time	s
tlag	lag time to equilibrium	s
U	average velocity	m/s
Vmax	maximum reaction rate	mol/m2 s
δ	concentration boundary layer thickness	m
γ	wall shear rate	1/s