Prediction of Coronary Artery Disease Risk Based on Multiple Longitudinal Biomarkers

Abstract

In the last decade, few topics in the area of cardiovascular disease (CVD) research have received as much attention as risk prediction. One of the well documented risk factors for CVD is high blood pressure (BP). Traditional CVD risk prediction models consider BP levels measured at a single time and such models form the basis for current clinical guidelines for CVD prevention. However, in clinical practice, BP levels are often observed and recorded in a longitudinal fashion. Information on BP trajectories can be powerful predictors for CVD events. We consider joint modeling of time to coronary artery disease and individual longitudinal measures of systolic and diastolic BPs in a primary care cohort with up to 20 years of follow-up. We applied novel prediction metrics to assess the predictive performance of joint models. Predictive performances of proposed joint models and other models were assessed via simulations and illustrated using the primary care cohort.

1. Introduction

Cardiovascular disease (CVD) is the leading cause of death in the United States and the world. Primary prevention by identifying and treating at-risk individuals remains a major public health challenge. Although many traditional risk factors such as hypertension, diabetes, and hyperlipidemia have been found to be associated with increased CVD risk, predictive accuracy of these traditional risk factors for CVD remains modest and diminishes with the increase in age [1, 2, 3]. Numerous attempts to improve the prediction of CVD risk by using new biomarkers have only improved the risk prediction by a modest margin [3, 4, 5].

In many cohort studies and in usual clinical practice, longitudinal blood pressure (BP) measurements were often collected and BP trajectories can be powerful predictors for CVD risk [6, 7, 8]. Many current studies focus on systolic BP (SBP) based on the findings from the Framingham Heart Study in 1971 that SBP was a superior predictor of CVD risk than diastolic BP (DBP) [9]. Recently, however, DBP has also been recognized as an important independent risk factor for CVD [10]. In a recent article in the Journal of the American Medical Association [11], the authors focused on mid-BP (defined as the mean of SBP and DBP) trajectories demonstrating that DBP was a more important contributor to CVD risk in younger adults. In addition, it is also known that measurement error is usually different for DBP than for SBP because of the greater variability in the auscultatory end point [12].

The most widely used method to incorporate longitudinal measures into a predictive model for time to event is perhaps the Cox model with time-dependent covariates. However, such a model usually assumes that the longitudinal outcomes are continuously measured without errors, which may be unrealistic when the longitudinal measures are collected intermittently and measurement errors of SBP and DBP are known to be substantial. Furthermore, it is difficult to explore the association between trends in the longitudinal outcomes, other than current values, and time to event. Joint models for longitudinal and survival data have therefore been proposed to appropriately deal with these issues. Comprehensive reviews of joint models have been published [13, 14, 15] and survival prediction using a single longitudinal biomarker has been studied in the joint modeling framework [16, 17, 18, 19].

When multiple longitudinal measures are available, extension to the joint model framework needs to appropriately account for potential correlations among the longitudinal measures. Simultaneous modeling of multiple longitudinal outcomes in joint models offers a number of advantages over separate modeling of each longitudinal outcome [20, 21, 22, 23]. First, for correlated longitudinal outcomes it is more relevant to estimate the adjusted association of each longitudinal outcome with event risk [20]. Second, Fieuws et al. (2008) showed that accounting for the correlation between longitudinal measures may substantially enhance the predictive ability of joint models [24]. In addition, two papers found that joint models of multiple longitudinal outcomes are more efficient compared with separate modeling of each outcome in some settings [25, 26]. In many primary care clinics, SBP and DBP were repeatedly measured and recorded over time during routine visits to physician offices. To utilize the correlation between longitudinal SBP and DBP measures, and account for BP measurement errors, we cast the prediction of CAD risk into a joint model framework that simultaneously models time to CAD and bivariate longitudinal outcomes of SBP and DBP. The Expectation Maximization (EM) approach was used for the parameter estimation of joint models. For the prediction of survival probability in the joint model framework, we adopted the Monte Carlo (MC) simulation approach proposed by Rizopoulos (2011) [19].

In this article, we explored the predictive accuracy of different models using area under curve (AUC) and two other recently proposed prediction metrics, including above average risk difference (AARD) and mean risk difference (MRD) [27]. The AUC (for ROC) is a well-developed summary criterion for evaluating the performance of prediction models for binary outcomes and has also been extended to survival endpoints. Pencina et al. (2012) provided a thorough review of existing AUCs for time-to-event outcomes [28]. Rizopoulos (2011) studied the AUC in the joint model with a single longitudinal outcome [19]. However, several studies showed that the AUC may have low sensitivity for model comparison when new biomarkers are added, and the difference in AUC measures has no intuitive interpretation because AUC is a function of rank, not of predicted probabilities [29, 30]. In the past few years, more sensitive criteria have been proposed for the purpose of model comparison. Cook (2007) proposed a “reclassification table” to show how many subjects will be reclassified if a new biomarker is added to the existing model [29]. Pencina et al. (2008) extended the idea of reclassification table and proposed two new criteria: the Net Reclassification Improvement (NRI) and integrated discrimination improvement (IDI), a measure that integrates net reclassification over all possible cut-offs of the probability of the outcome [31]. The IDI is equivalent to the difference in discrimination slopes of two models [32], the difference in Pearson R² measures [33], or the difference in scaled Brier scores [34]. Similar criteria were extended to time-to-event outcomes by [35]. Recently Pepe and Janes defined AARD and MRD based on previous work of NRI and IDI [27]. AARD and MRD have been used to evaluate the improvement in prediction accuracy by adding new predictor to an existing Cox model. In this work, we apply AARD and MRD to the joint model framework and assess the predictive accuracy of multiple longitudinal biomarkers.

The remainder of this paper is organized as follows: Section 2 describes the motivating example of the primary care cohort. Section 3 introduces the joint models and estimation method. Section 4 presents the method to calculate conditional survival probabilities from the fitted joint model. Section 5 describes definitions and estimators of the AUC, AARD and MRD in the joint modeling framework. Sections 6 and 7 report simulation results and data application, respectively. Finally the paper is concluded with a discussion in Section 8.

2. A Primary Care Patient Cohort

This primary care patient cohort was assembled in 1991 as part of a depression screening study in Wishard Health Service. From 1991 to 1993, patients age 60 years or older were consented for depression screening during their regular clinical visits to their primary care physicians. A total of 4,413 primary care patients were initially contacted, of whom 115 refused; 57 were ineligible due to severe cognitive impairment; 284 were not eligible because they were non-English speakers, in prison, in a nursing home, or had a hearing impairment; 3,957 patients were enrolled in the study. Details about the study have been published in [36, 37, 38]. Electronic medical records (EMR) data data are available from all enrolled patients and the information include diagnosis of medical conditions, BP measures, laboratory test measures and medications order and dispensing.

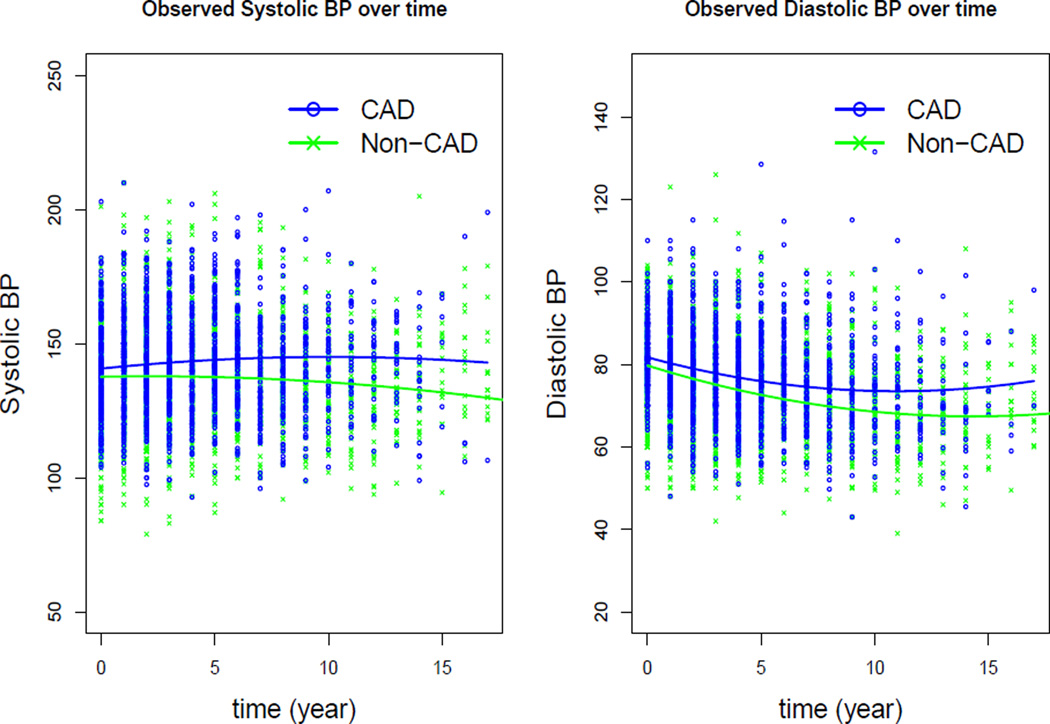
Among the 3,957 patients, 2,654 (797 males and 1857 females) were free of CAD at enrollment. For patients with an incident CAD event, the date of diagnosis was used as the event time; otherwise the last outpatient clinic visit prior to December 31, 2010 was used as the right censoring time. SBP and DBP measured in sitting position from outpatient clinic visits were collected. Since it has been shown that males have significantly increased CAD risk than females [39, 40], we focused this analysis to the 797 male patients in the cohort, of whom 28% had incident CAD during the follow-up period. Mean baseline age of patients in the analysis sample was 68 years; 65.1% were black, 31.9% were smokers, and 33.6% had history of diabetes at baseline. We found that the frequency of BP measure varied from patient to patient with a mean frequency of 20.5. For computational convenience, annualized SBP and DBP measures during the study period were derived for each participant. On average, there were about 5.3 BP measures per subject. Figure 1 plots the annualized longitudinal SBP and DBP measures over time by CAD status. The blue and green curves represent fitted population mean profiles for the CAD and non-CAD group respectively, using quadratic linear mixed-effects models. It can be seen that the population mean SBP and DBP were higher over time for the CAD group than the non-CAD group, indicating a potential association between the risk of CAD and longitudinal SBP and DBP measures.

Figure 1.

Observed annualized longitudinal SBP and DBP measures over time and fitted population mean curves for the CAD and non-CAD group.

3. Joint Models and Estimation Method

3.1. Longitudinal Models

Let y_l(t_ij) denote the observed measurement of the l-th longitudinal outcome for the i-th subject at the j-th time point, t_ij, where i = 1, …, n, j = 1, …, n_i, l = 1, …, L. The observed longitudinal trajectory for the i-th subject is modeled as

$${\mathbf{y}}_l({\mathbf{t}}_i)={\mathbf{y}}_l^{*}({\mathbf{t}}_i)+{\mathit{\epsilon }}_{il}={\mathbf{X}}_l^T({\mathbf{t}}_i){\mathit{\beta }}_l+{\mathbf{Z}}_l^T({\mathbf{t}}_i){\mathbf{b}}_{il}+{\mathit{\epsilon }}_{il}$$

where ${\mathbf{y}}_l^{*}({\mathbf{t}}_i)$ is the true underlying longitudinal measures of the l-th biomarker for the i-th subject; ${\mathbf{X}}_l^T({\mathbf{t}}_i)$ is the design matrix of fixed effects, including time effects and baseline covariates; β_l is the corresponding vector of the fixed effects; ${\mathbf{Z}}_l^T({\mathbf{t}}_i)$ is the design matrix for the random effects, b_il, distributed as b_i = (b_i1, b_i2, …, b_iL)^T ~ N(0, D); ε_il is the corresponding measurement error term, which is assumed to be normally distributed as ${\mathit{\epsilon }}_{il}{~}^{iid}N(0,{\sigma }_l^2{I}_{n_i})$. It is worth noting that the correlations among the multiple longitudinal processes and within-subject correlation for each longitudinal biomarker are represented in the variance-covariance matrix of random effects D. We assume that the measurement errors of different longitudinal outcomes are independent of each other, and they are also independent of the random effects b_i.

3.2. The Survival Model

For the i-th subject, let $T_i^{*}$ and C_i denote the true event time and censoring time respectively. Define the observed event time $T_i=\text{min}(T_i^{*},C_i)$ and the event indicator ${\delta }_i=I(T_i^{*}\le C_i)$. Let h₀(t) denote the baseline hazard function. Assuming that the hazard function depends on some functions of the true longitudinal measures at event time point, $ℱ({\mathbf{y}}_{il}^{*}(t))$, and the baseline covariates, w_i, then the hazard function can be written as

$$h_i(t)=h_0(t)\text{ exp }({\mathit{\gamma }}^T{\mathbf{w}}_{\mathbf{i}}+\sum _{l-1}^L{\alpha }_lℱ({\mathbf{y}}_{il}^{*}(t))),$$

where α_l represents the association between the function of the true longitudinal measures of the lth biomarker at event time and the time-to-event outcome; γ is the coefficient vector for the baseline risk factors. In this work, α_l, l = 1, 2, …, L, are of primary interest. The correlation between the multiple longitudinal biomarkers and the time-to-event outcome is induced by the common random effects shared in the longitudinal and survival models. We assume the censoring time and the event time are independent given the true longitudinal biomarker measures.

The function ℱ(·) can be chosen to explore different functional forms depending on the interest of the study. For example, if the focus is the association between longitudinal values and event risk, ℱ(·) can be an identity function; if the change in the longitudinal measures is of interest, ℱ(·) can be chosen as derivative functions with respect to time t; for studies interested in the cumulative history of the longitudinal measures over time and event risk, ℱ(·) can be an integration function of ${\mathbf{y}}_{il}^{*}(t)$ over time t. Depending on the choice of the ℱ(·) random effects b_i can enter the exponential term in the hazard function in a non-linear fashion. This is in contrast with the frailty type of joint models where the random effects were part of a linear function in the hazard exponential term.

3.3. Joint Likelihood Function and Estimation Method

Under the conditional independence assumption between b_i and ε_i, the kernel of the joint likelihood function can be factored into three components as

$$L(\mathit{\theta })=\prod _{i=1}^n\int p(T_i,{\delta }_i|\mathit{\theta },{\mathbf{b}}_i)p({\mathbf{y}}_{i1}|\mathit{\theta },{\mathbf{b}}_i)\cdots p({\mathbf{y}}_{iL}|\mathit{\theta },{\mathbf{b}}_i)p({\mathbf{b}}_i|\mathit{\theta })d{\mathbf{b}}_i,$$ (1)

where θ = (γ, α, h₀, β, σ, D)^T is the vector containing all parameters in the models. Under the assumed models for the longitudinal and survival outcomes, the components in (1) are:

$$p({\mathbf{b}}_i|\mathit{\theta })\propto {|\mathbf{D}|}^{-1/2}\text{ exp }(-\frac{1}{2}{\mathbf{b}}_i^T{\mathbf{D}}^{-1}{\mathbf{b}}_i),$$

$$p({\mathbf{y}}_{ij}|\mathit{\theta },{\mathbf{b}}_i)\propto {\text{exp}}^{-\frac{1}{2{\sigma }_l^2}{\sum }_{j=1}^{n_i}{[{\mathbf{y}}_l(t_{ij})-({\mathbf{X}}_l^T(t_{ij}){\mathit{\beta }}_l+{\mathbf{Z}}_l^T(t_{ij}){\mathbf{b}}_{il})]}^2}.$$

$$p(T_i,{\delta }_i|\mathit{\theta },b_i)={\{h_0(T_i)\text{ exp }[{\mathbf{w}}_i^T\gamma +\sum _{l=1}^L{\alpha }_lℱ({\mathbf{X}}_l^T(T_i){\mathit{\beta }}_l+{\mathbf{Z}}_l^T(T_i){\mathbf{b}}_{il})\left]\right\}}^{{\delta }_i}\text{exp }\{-{\int }_0^{T_i}{h}_0(u)\text{ exp }[{\mathbf{w}}_i^T\gamma +\sum _{l=1}^L{\alpha }_lℱ({\mathbf{X}}_l^T(u){\mathit{\beta }}_l+{\mathbf{Z}}_l^T(u){\mathbf{b}}_{il})]du\},$$

In the literature of joint models there are three general types of estimation methods: a two-stage approach, Bayesian Markov Chain Monte Carlo (MCMC) method, and maximum-likelihood approach. In the two-stage approach, parameter estimation is conducted separately for the longitudinal model and the survival model separately. Although the two-stage approach is computationally simple, it can introduce bias and loss of efficiency since it ignores the time-to-event information when modeling the longitudinal process [41, 42] as the survival process in this setting essentially produces non-ignorable missing data for the longitudinal outcomes. The two-stage approach has been discussed by many authors [43, 42]. Alternatively, both the Bayesian MCMC approach and the maximum-likelihood approach incorporate both types of outcomes into a joint likelihood function and simultaneously estimates model parameters. The Bayesian MCMC approach has been used for joint models of multiple longitudinal outcomes and time-to-event variable [21, 20]. The maximum-likelihood method using EM algorithm has also been applied to the joint models for time-to-event outcome and a single longitudinal outcome [13, 44, 45, 46, 47]. In this work, the maximum-likelihood method using EM algorithm is used to obtain parameter estimation of joint models for multiple longitudinal processes and time-to-event outcome. For computation of the expected likelihood function, pseudo-adoptive Gaussian-Hermit quadrature rule was used to approximate the integrals [47]. The parameter estimation using EM algorithm was implemented in R [48].

4. Predictive Accuracy

The focus on predictive accuracy of a survival model can be different varying from calibration, discrimination to reclassification. Calibration focuses on quantifying how close the predicted outcomes are to the observed outcomes, while discrimination quantifies how well a model distinguishes subjects with events from those who do not experience events. Reclassification, on the other hand, evaluates the incremental values resulting from adding new predictors in the model. In this work we focus on reclassification to evaluate the predictive accuracy of new longitudinal biomarker in the joint modeling framework.

We assume that the maximum-likelihood estimates of the joint models have been obtained from a training sample 𝒟_n = {T_i, δ_i, y_i1, …, y_iL; i = 1, 2, …, n}. Based on the multiple longitudinal measurements up to time t of a given new subject from a testing sample similar to the training sample, one can predict the survival probability at any time point t. We propose to define true positive rate (TPR) and false positive rate (FPR) using a subject’s current risk at time t, i.e.,

$$r_i(t)=P(T_i\le t|{𝒴}_i^{*}(t,{\mathbf{b}}_i,\mathit{\theta }),{𝒟}_n;\mathit{\theta })=1-S_i(t|{𝒴}^{*}(t,{\mathbf{b}}_i,\mathit{\theta });\mathit{\theta }),$$

where the current risk at time t, r_i(t), depends on the predicted longitudinal biomarker measures up to time t, ${𝒴}^{*}(t,{\mathbf{b}}_i,\mathit{\theta })\equiv \{y_l^{*}(s):l=1,\dots ,L,0<s<t\}$, and the fitted joint models.

In this work we concentrate on assessing predictive accuracy using the current risk function. If the interest is to assess predictive accuracy at a future time point, t + Δt, based on the longitudinal biomarker measures up to time t, one can utilize the conditional risk function in defining TPR and FPR,

$$r_i(t+\mathrm{\Delta }t|t)=P(T_i\le t+\mathrm{\Delta }t|T_i>t,{𝒴}_i^{*}(t,{\mathbf{b}}_i,\mathit{\theta }),{𝒟}_n;\mathit{\theta })=1-S_i(t+\mathrm{\Delta }t|T_i>t,{𝒴}^{*}(t,{\mathbf{b}}_i,\mathit{\theta });\mathit{\theta }).$$

The risk function r_i(t) is equivalent to r_i(t + Δt | t) when Δt is equal to 0, thus the concept of using conditional risk function of r_i(t + Δt|t) in predictive accuracy is similar to using the current risk function of r_i(t).

For the prediction of survival probability, we explored two methods discussed in [19]: the empirical Bayes method and Monte Carlo (MC) simulation approach. The empirical Bayes method is essentially the first order approximation of the survival probability function

$$\widehat{s_i}(t)=S_i(t|{𝒴}^{*}(t,\widehat{{\mathbf{b}}_{\mathbf{i}}},\hat{\mathit{\theta }});\hat{\mathit{\theta }})+O(n_i^{-1}),$$

where the subject-specific random effect prediction, b_i, is calculated by ${\text{argmax}}_{\mathbf{b}}\{\text{log}p(T_i^{*}>t,{𝒴}_i(t),\mathbf{b};\hat{\mathit{\theta }})\})$ using the observed data from the testing sample; the maximum-likelihood parameter estimates (θ̂) of the joint models are based on the training sample. The empirical Bayes approach has the advantage of computational simplicity, but the derivation of its standard error is not straightforward. The MC simulation approach was proposed to predict conditional survival probabilities [19]. Instead of directly calculating the survival probability, the predicted survival probability is summarized from a series of posterior expectation of the survival function. In the simulation section, we assessed the performance of these two methods in survival probability prediction.

For a given threshold p, we define TPR_t(p) = P(r(t) ≥ p | T ≤ t) and FPR_t(p) = P(r(t) ≥ p | T > t). Based on Zheng et al. (2013) [49], the estimators of TPR and FPR are written as follows

$${\widehat{\mathrm{T}\mathrm{P}\mathrm{R}}}_t(p)=\frac{{\sum }_{i=1}^n\widehat{r_i}(t)I(\widehat{r_i}(t)\ge p)}{{\sum }_{i=1}^n\widehat{r_i}(t)},$$ (2)

$${\widehat{\mathrm{F}\mathrm{P}\mathrm{R}}}_t(p)=\frac{{\sum }_{i=1}^n(1-\widehat{r_i}(t))I(\widehat{r_i}(t)\ge p)}{{\sum }_{i=1}^n(1-\widehat{r_i}(t))}.$$ (3)

Note that (2) and (3) use data from all subjects including those censored for the risk prediction.

AUC is a commonly used criterion for discrimination in prediction. However, researches showed that the AUC may have low sensitivity for risk model comparison, and the difference in AUC measures has no intuitive interpretation [29, 30]. AUC at time t can be written as $\mathrm{A}\mathrm{U}{\mathrm{C}}_t=\int \mathrm{T}\mathrm{P}{\mathrm{R}}_t\mathrm{F}\mathrm{P}{\mathrm{R}}_t^{-1}(u)du$ and estimated by

$${\widehat{\mathrm{A}\mathrm{U}\mathrm{C}}}_t=\int {\widehat{\mathrm{T}\mathrm{P}\mathrm{R}}}_t{\widehat{\mathrm{F}\mathrm{P}\mathrm{R}}}_t^{-1}(u)du.$$

Pepe et al. (2008) and Pepe and Janes (2013) proposed two new measures, Above Average Risk Difference (AARD) and Difference in Mean Risk (MRD), which may be more sensitive in comparing models with different risk predictors and have more meaningful interpretations [50, 27]. AARD and MRD are defined as following:

$$\mathrm{A}\mathrm{A}\mathrm{R}\mathrm{D}=P(\mathbf{r}(t)>{\rho }_t|\mathbf{T}\le t)-P(\mathbf{r}(t)>{\rho }_t|\mathbf{T}>t),$$

$$\mathrm{M}\mathrm{R}\mathrm{D}=E(\mathbf{r}(t)|\mathbf{T}\le t)-E(\mathbf{r}(t)|\mathbf{T}>t),$$

where ρ_t = P(T ≤ t). Similarly, the estimation of AARD and MRD are written as follows:

$${\widehat{\mathrm{A}\mathrm{A}\mathrm{R}\mathrm{D}}}_t={\widehat{\mathrm{T}\mathrm{P}\mathrm{R}}}_t(\hat{\rho })-{\widehat{\mathrm{F}\mathrm{P}\mathrm{R}}}_t(\hat{\rho }),$$

$${\widehat{\mathrm{M}\mathrm{R}\mathrm{D}}}_t={\int }_p{\widehat{\mathrm{T}\mathrm{P}\mathrm{R}}}_t(p)dp-{\int }_p{\widehat{\mathrm{F}\mathrm{P}\mathrm{R}}}_t(p)dp,$$

where ρ̂ is the average risk in the population. AARD can be interpreted as the difference in the proportions of events and non-events at the average risk in the population while MRD measures the area between TPRt(p) and FPRt(p) across the risk scale.

5. Simulation Study

We first assessed the performance of the empirical Bayes and the MC simulation approaches in predicting conditional survival probabilities in joint modeling framework with two longitudinal biomarkers and a time-to-event outcome. We then applied the 3 criteria of AUC, AARD and MRD to assess the predictive accuracy of various prediction models.

We adopted a split sample design where one sample is used to build the prognostic model and the other sample is used to validate the model and make predictions. We first simulated 200 training data sets from joint models with two correlated normally distributed longitudinal outcome variables and one time-to-event outcome variable. Additional 200 testing data sets were simulated using the same covariate values and random effects as in training data sets. Longitudinal data were simulated for 500 subjects each with 11 equally spaced bivariate longitudinal evaluations over a 5-year period. We considered the similar fixed and random model structures for the two longitudinal outcomes, where the fixed effects included intercept, time effect, and one binary baseline covariate, and the random effects included random intercept and random slope. The correlation between the two longitudinal outcomes is represented by the correlation between the random variables. The longitudinal models are then written as follows:

$$y_1(t_{ij})=y_1^{*}(t_{ij})+{\epsilon }_1(t_{ij})={\beta }_{01}+{\beta }_{11}{t}_{ij}+{\beta }_{21}{w}_i+b_{01i}+b_{11i}{t}_i+{\epsilon }_1(t_{ij}),$$

$$y_2(t_{ij})=y_2^{*}(t_{ij})+{\epsilon }_2(t_{ij})={\beta }_{02}+{\beta }_{12}{t}_{ij}+{\beta }_{22}{w}_i+b_{02i}+b_{12i}{t}_i+{\epsilon }_2(t_{ij}),$$

where ${\epsilon }_1(t_{ij})~N(0,{\sigma }_1^2),{\epsilon }_2(t_{ij})~N(0,{\sigma }_2^2)$. The random effects (b_01i, b_11i, b_02i, b_12i) are normally distributed with mean 0 and standard deviation σ₀₁, σ₁₁, σ₀₂, and σ₁₂ respectively. They are pairwise independent except that b_01i and b_02i are correlated with correlation coefficient ρ.

The time-to-event endpoint was simulated from a proportional hazard model with a Weibull baseline hazard function, h₀(t) = abt^b−1, where a and b are the corresponding shape and scale parameters respectively. The proportional hazard model is assumed to depend on the current values of the two longitudinal outcomes at the event time point. Particularly, the proportional hazard model is written as $h(t)=ab{t}^{b-1}\text{exp}({\alpha }_1{y}_1^{*}(t)+{\alpha }_2{y}_2^{*}(t))$. Overall, the censoring percentage is about 30% and on average there are about 6 repeated bivariate measurements for each subject. In the actual model fitting, we used a more flexible piecewise constant baseline hazard function instead of the parametric Weibull baseline risk function. Three simulation scenarios were considered by varying variances of residual errors and variance-covariance matrix of random effects:

• Scenario 1 : σ₁ = σ₂ = 0.2, σ₀₁ = σ₀₂ = 0.2, σ₁₁ = σ₁₂ = 0.05;

• Scenario 2 : σ₁ = σ₂ = 0.5, σ₀₁ = σ₀₂ = 0.5, σ₁₁ = σ₁₂ = 0.2;

• Scenario 3 : σ₁ = σ₂ = 0.2, σ₀₁ = σ₀₂ = 0.5, σ₁₁ = σ₁₂ = 0.2.

Other parameters are set as β₀₁ = 0.2, β₁₁ = 0.5, β₂₁ = 0.2, β₀₂ = 1, β₁₂ = 0.2, β₂₂ = 0.5, ρ = 0.5, a = 0.005, b = 1.1, α₁ = 1, and α₂ = 1.

5.1. MC Simulation vs. Empirical Bayes for Predicting Conditional Survival Probabilities

Let 𝒴_i(t) = {y_i1(s), y_i2(s), …, y_Li(s); 0 ≤ s ≤ t} denote the ith new subject’s longitudinal biomarker measures up to time t for L different biomarkers, the conditional survival probability at time t + Δt given the survival up to time t can be written as

$$s_i(t+\mathrm{\Delta }t|t)=P(T_i\ge t+\mathrm{\Delta }t|T_i>t,{𝒴}_i(t),{𝒟}_n;\mathit{\theta }).$$

We fitted joint models to each training data set and estimated parameters using the EM algorithm. For each testing data set, data from the first 2 years was used to predict subject specific random effects. Twenty subjects were randomly selected from each testing data set. Selected subjects’ conditional survival probabilities at different time points t (t > 2) and Δt were predicted with the empirical Bayes approach and the MC simulation approach separately, using parameter estimates from the training data set and predicted random effects using the first 2 years of the testing data. In the MC simulation approach, the median based on 200 MC replicates was used as the predicted conditional survival probability. Predicted conditional survival probabilities obtained from the two approaches were compared to predictions based on random effects and parameter values used in generating the longitudinal and survival outcomes. We reported the average biases between the true and predicted conditional survival probabilities for the selected subjects over the 200 testing data sets.

Results are presented in the supporting web materials. It is evident that the MC simulation approach generally performs better in predicting conditional survival probabilities than the empirical Bayes approach - smaller biases are observed for the MC simulation approach. In addition, the results show that for fixed Δt, biases increase as time t increases. This may be explained by the fact that more subjects drop out as time t increases leading to less accurate random effect predictions. On the other hand, the results also indicate that for fixed time t, biases generally increase as the prediction window Δt increases. In other words, conditioning on the same number of longitudinal biomarker measures, the performance of the prediction gets worse when the window for prediction is longer.

5.2. Predictive Accuracy

The formulation in the prediction of conditional survival outcomes can also readily extended to the prediction of survival outcome by specifying Δt = 0. In this section, we present additional simulations to examine the performance of AUC, AARD and MRD in evaluating the predictive performance of various models based on parameter estimates from training data sets. Our main interest is in comparing AUC, AARD and MRD of joint models using only the first longitudinal biomarker (JM1), and joint models using both longitudinal biomarkers (JM2). However, as the Cox’s models were also commonly used in analyzing this type of data, we included the Cox model using only baseline biomarker measures as time-independent covariates (Cox baseline), Cox model with longitudinal biomarker measures as time-dependent covariate (Cox time-dependent) in the simulation comparisons.

For JM1 and JM2 models, individual survival probabilities at time t (t > 2) for subjects from testing data set were obtained using similar procedures as described for predicting conditional survival probabilities in the previous section. For the Cox’s baseline model, individual survival probabilities were calculated using estimated parameters from the training data set and longitudinal measures at baseline from the testing data. The same technique was applied for the Cox’s time-dependent model, except for using the longitudinal measures up to time t from the testing data. Based on predicted survival probabilities, TPR and FPR can be readily calculated for different models. Accordingly, AUC, AARD and MRD were derived from TPR and FPR values.

The sample means and empirical standard errors of AUC, AARD, and MRD for the four models were summarized over the 200 testing data sets in Tables 1, 2 and 3. It was shown that JM2 model had notable better predictive performance compared to JM1 model. The predictive measures under the true models using pre-specified parameter values and random effects provided the upper ceiling of these criteria. Considering the differences in the numeric ranges for the three measures, we included percentage gains in the prediction accuracy criteria from adding a second longitudinal marker. In particular, we presented two quantities: true percentage gain and estimated percentage gain. In terms of AUC, they were calculated as (AUC_JM2 − AUC_JM1)/AUC_true and (AUC_JM2 − AUC_JM1)/AUC_JM2 respectively. These quantities were calculated similarly for AARD and MRD. The estimated prediction gain can be used in data applications when the true measures are unknown. Both AARD and MRD showed much higher true and estimated percentage gains from the addition of the new longitudinal marker than AUC, with MRD showing the greatest gain among the three measures. We also observe that JM2 has better predictive performance on AUC, AARD and MRD than the two Cox models as expected. From the results of JM2 we observe that the predictive performance improves as time t increases which can be explained by the increased numbers of both longitudinal measures and events.

Table 1.

Simulation results for comparison of AUC, AARD, and MRD from JM2 to the other 3 models under simulation Scenario 1. Percent gain and estimated percent gain are calculated as (JM2−JM1)/True and (JM2−JM1)/JM2 respectively.

		Cox (baseline)		Cox (time-dependent)		JM1		JM2		% gain (JM2 vs JM1)
t	True	Mean	ESD	Mean	ESD	Mean	ESD	Mean	ESD	True	Estimated
AUC
3	0.659	0.634	0.028	0.501	0.031	0.624	0.029	0.649	0.028	0.038	0.039
3.5	0.673	0.643	0.026	0.497	0.029	0.634	0.028	0.662	0.027	0.042	0.042
4	0.692	0.657	0.026	0.497	0.028	0.644	0.027	0.679	0.027	0.051	0.052
4.5	0.715	0.672	0.026	0.496	0.029	0.657	0.025	0.699	0.025	0.059	0.06
5	0.745	0.691	0.027	0.499	0.032	0.676	0.026	0.725	0.025	0.066	0.068
AARD
3	0.230	0.198	0.048	0.013	0.054	0.180	0.051	0.219	0.048	0.17	0.178
3.5	0.252	0.210	0.045	−0.002	0.050	0.194	0.051	0.237	0.048	0.171	0.181
4	0.281	0.232	0.045	−0.018	0.049	0.211	0.047	0.262	0.048	0.181	0.195
4.5	0.316	0.255	0.043	−0.036	0.052	0.226	0.047	0.293	0.048	0.212	0.229
5	0.363	0.283	0.048	−0.043	0.055	0.254	0.047	0.331	0.044	0.212	0.233
MRD
3	0.065	0.044	0.015	0.003	0.013	0.028	0.009	0.055	0.014	0.415	0.491
3.5	0.088	0.058	0.018	0.000	0.016	0.040	0.011	0.075	0.017	0.398	0.467
4	0.113	0.073	0.020	−0.002	0.018	0.052	0.013	0.096	0.020	0.389	0.458
4.5	0.134	0.084	0.022	−0.004	0.019	0.062	0.014	0.114	0.021	0.388	0.456
5	0.147	0.088	0.022	−0.002	0.020	0.069	0.014	0.125	0.021	0.381	0.448

Table 2.

Simulation results for comparison of AUC, AARD, and MRD from JM2 to the other 3 models under simulation Scenario 2. Percent gain and estimated percent gain are calculated as (JM2−JM1)/True and (JM2−JM1)/JM2 respectively.

		Cox’s(Baseline)		Cox’s(time-dependent)		JM1		JM2		% gain (JM2 vs JM1)
t	True	Mean	ESD	Mean	ESD	Mean	ESD	Mean	ESD	True	Estimated
AUC
3	0.791	0.696	0.027	0.659	0.028	0.696	0.025	0.749	0.024	0.067	0.071
3.5	0.811	0.696	0.025	0.663	0.025	0.704	0.023	0.763	0.021	0.073	0.077
4	0.830	0.694	0.022	0.665	0.024	0.709	0.022	0.775	0.019	0.08	0.085
4.5	0.851	0.693	0.023	0.669	0.023	0.713	0.023	0.786	0.019	0.086	0.093
5	0.871	0.694	0.024	0.675	0.024	0.717	0.022	0.798	0.019	0.093	0.102
AARD
3	0.434	0.288	0.048	0.231	0.048	0.288	0.045	0.368	0.050	0.184	0.217
3.5	0.465	0.285	0.044	0.233	0.044	0.299	0.043	0.388	0.041	0.191	0.229
4	0.502	0.281	0.042	0.229	0.043	0.303	0.045	0.405	0.038	0.203	0.252
4.5	0.540	0.278	0.042	0.231	0.044	0.308	0.046	0.420	0.039	0.207	0.267
5	0.582	0.279	0.043	0.233	0.045	0.311	0.042	0.436	0.038	0.215	0.287
MRD
3	0.258	0.084	0.022	0.112	0.024	0.071	0.016	0.154	0.021	0.322	0.539
3.5	0.303	0.097	0.023	0.127	0.024	0.089	0.019	0.186	0.022	0.32	0.522
4	0.337	0.103	0.023	0.127	0.023	0.103	0.020	0.211	0.022	0.32	0.512
4.5	0.362	0.104	0.023	0.119	0.022	0.114	0.021	0.230	0.022	0.32	0.504
5	0.379	0.102	0.022	0.108	0.022	0.121	0.021	0.244	0.022	0.325	0.504

Table 3.

Simulation results for comparison of AUC, AARD, and MRD from JM2 to the other 3 models under scenario 3. Percent gain and estimated percent gain are calculated as (JM2−JM1)/True and (JM2−JM1)/JM2 respectively.

		Cox’s(Baseline)		Cox’s(time-dependent)		JM1		JM2		% gain (JM2 vs JM1)
t	True	Mean	ESD	Mean	ESD	Mean	ESD	Mean	ESD	True	Estimated
AUC
3	0.791	0.738	0.026	0.683	0.027	0.720	0.025	0.774	0.023	0.068	0.07
3.5	0.811	0.737	0.023	0.686	0.024	0.728	0.023	0.790	0.021	0.076	0.078
4	0.830	0.736	0.022	0.688	0.023	0.733	0.022	0.805	0.019	0.087	0.089
4.5	0.851	0.734	0.022	0.692	0.022	0.738	0.023	0.819	0.018	0.095	0.099
5	0.871	0.735	0.022	0.697	0.023	0.745	0.023	0.834	0.017	0.102	0.107
AARD
3	0.434	0.348	0.048	0.263	0.04	0.323	0.047	0.407	0.046	0.194	0.206
3.5	0.465	0.345	0.043	0.267	0.042	0.335	0.043	0.433	0.041	0.211	0.226
4	0.502	0.343	0.042	0.264	0.042	0.342	0.043	0.454	0.039	0.223	0.247
4.5	0.540	0.341	0.042	0.267	0.042	0.347	0.042	0.478	0.039	0.243	0.274
5	0.582	0.343	0.044	0.270	0.044	0.355	0.042	0.503	0.038	0.254	0.294
MRD
3	0.258	0.130	0.026	0.161	0.028	0.088	0.018	0.203	0.025	0.446	0.567
3.5	0.303	0.146	0.027	0.175	0.027	0.108	0.021	0.241	0.025	0.439	0.552
4	0.337	0.153	0.026	0.173	0.026	0.125	0.023	0.270	0.025	0.43	0.537
4.5	0.362	0.154	0.026	0.164	0.026	0.136	0.023	0.292	0.024	0.431	0.534
5	0.379	0.149	0.025	0.155	0.026	0.145	0.024	0.306	0.024	0.425	0.526

For the Cox baseline model, as expected, the predictive performance does not improve as t increases because only the baseline measurements are used in the survival probability prediction. However, it’s interesting that the Cox time-dependent model has even worse predictive performance than the Cox baseline model despite that more longitudinal measures were used in survival probability prediction. It’s worth noting that parameter estimation of Cox time-dependent model is based on the training dataset, and the repeated measurements up to time t were used in the survival probability prediction. In particular, parameter estimates in Cox time-dependent model heavily rely on the observed longitudinal outcomes in the training dataset which contributes to the biases in survival probability predictions in the testing dataset. When further simulations using the same datasets as training and testing data were conducted, we found that Cox time-dependent model had satisfactory predictive performance, thus confirming that predictive accuracy of Cox time-dependent models were sensitive to variations between the training and testing data (results not presented).

Additional simulations were conducted to assess how the prediction of random effect predictions and (fixed) parameter estimates in the joint models influence prediction accuracy. These simulation results were presented in the supporting web materials. We observe that the accuracy of random effect predictions had significant impact on prediction accuracy.

6. Data Application

We applied joint models to the aforementioned primary care patient cohort data of 797 male patients. Out of the 797 subjects, we randomly selected 597 subjects to create the training data set and used the remaining 200 subjects as the testing data set. For convenience we centered patients’ baseline age at 60 years. In order to explore different longitudinal trajectories over time and various functions of longitudinal outcomes in the survival model, we fitted four different sets of joint models to the training data set using the proposed EM algorithm. The best set of models were determined using the Akaike Information Criterion (AIC). Based on Figure 1, the annualized longitudinal SBP and DBP measures over time by CAD status, there seems no clear nonlinear pattern thus the linear mixed-effects model with quadratic fixed effect terms is able to capture the underlying longitudinal trajectory in blood pressure measures. The 4 sets of joint models differing in the longitudinal model or hazard function are as follows.

Joint models 1 consider the following models

$$y_l(t_{ij})={\beta }_{0l}+{\beta }_{1l}{t}_{ij}+{\beta }_{2l}{\text{age}}_i+{\beta }_{3l}{\text{race}}_i+b_{0li}+b_{1li}{t}_{ij}+{\epsilon }_{ijl},l=1,2$$ (4)

for the observed longitudinal SBP and DBP measures respectively. The random effect vector b_i = (b_01i, b_11i, b_02i, b_12i)^T is normally distributed with mean zero and an unstructured variance-covariance matrix of D; ε_ij1 and ε_ij2 and are independently distributed as $N(0,{\sigma }_1^2)$ and $N(0,{\sigma }_2^2)$ respectively. The hazard function satisfies

$$h(t)=h_0(t)\text{ exp }\{{\gamma }_1{\text{age}}_i+{\gamma }_2{\text{smoke}}_i+{\gamma }_3{\text{race}}_i+{\gamma }_4{\text{diabetes}}_i+{\alpha }_1{y}_{i1}^{*}(t)+{\alpha }_2{y}_{i2}^{*}(t)\},$$ (5)

where the piecewise constant function h₀(t) consists of 7 equally spaced intervals with 6 interior knots based on percentiles of the observed event time points. The above hazard function depends on the current values of SBP and DBP measures and some baseline risk factors.

Joint models 2 assume the same longitudinal models (4) as in the joint models 1, but use the slopes of SBP and DBP measures in the hazard function instead,

$$h(t)=h_0(t)\text{ exp }\{{\gamma }_1{\text{age}}_i+{\gamma }_2{\text{smoke}}_i+{\gamma }_3{\text{race}}_i+{\gamma }_4{\text{diabetes}}_i+{\alpha }_1{y}_{i1}^{*\prime }(t)+{\alpha }_2{y}_{i2}^{*\prime }(t)\}.$$ (6)

Joint models 3 assume the same hazard model (5) in the joint model 1, but include a quadratic fixed time effect for both SBP and DBP measures,

$$y_l(t_{ij})={\beta }_{0l}+{\beta }_{1l}{t}_{ij}+\underset{¯}{{\beta }_{2l}{t}_{ij}^2}+{\beta }_{3l}{\text{age}}_i+{\beta }_{4l}{\text{race}}_i+b_{0li}+b_{1li}{t}_{ij}+{\epsilon }_{ijl},l=1,2.$$ (7)

Joint models 4 assumes (6) and (7).

In the implementation of the EM algorithm, we used 3 pseudo-adaptive Gaussian-Hermite quadrature points for numerical integration over the random effects and 7 Gaussian-Kronrod quadrature points for the integration in the survival function. Models were compared according to AIC: smaller AIC indicates better model fit. Among the 4 joint models considered, Joint models 3 was the best fitting (AIC=49464) followed by Joint models 4 (AIC=49475), Joint models 1 (AIC=49537) and Joint models 2 (AIC=49548). Here we present parameter estimates from Joint models 3 in Table 4.

Table 4.

Parameter estimates, standard errors and 95%CI using the training data set. α₁ and α₂ are the association estimates between the risk of CAD and current value of SBP and DBP at event time point, respectively. λ_i i = 1, …, 7 denote the baseline hazards of the 7 piecewise constant intervals.

Parameter	Estimate	StdErr	lower 95 %CI	upper 95 %CI
Longitudinal SBP
Intercept	135.20	0.96	133.31	137.08
time	0.33	0.18	−0.03	0.69
time2	−0.04	0.01	−0.07	−0.02
Age	−0.04	0.06	−0.17	0.08
Race	5.33	0.98	3.41	7.25
log(σ1)	2.49	0.01	2.46	2.52
Longitudinal DBP
Intercept	79.19	0.40	78.41	79.97
time	−1.64	0.11	−1.85	−1.43
time2	0.05	0.01	0.04	0.07
Age	−0.13	0.03	−0.18	−0.08
Race	3.18	0.37	2.45	3.90
log(σ1)	1.94	0.01	1.91	1.97
Time-to-CAD
Age	0.06	0.01	0.04	0.08
Smoking History	0.36	0.18	0.01	0.71
Race	−0.53	0.19	−0.90	−0.17
Diabetes	0.06	0.17	−0.27	0.40
α1	0.021	0.010	0.001	0.041
α2	0.018	0.017	−0.015	0.050
log(λ1)	−8.41	1.00	−10.38	−6.45
log(λ2)	−8.79	1.00	−10.75	−6.83
log(λ3)	−8.43	1.00	−10.38	−6.47
log(λ4)	−7.70	0.98	−9.62	−5.79
log(λ5)	−6.96	0.96	−8.85	−5.07
log(λ6)	−7.09	0.95	−8.96	−5.22
log(λ7)	−6.51	0.92	−8.32	−4.70

We then used data from the first 5 years in the testing data set to estimate patients’ subject-specific random effects. Based on parameter estimates from the training data set and the random effect estimates from the first 5 year testing data, predicted conditional survival probabilities given t (t > 5) were further computed using the MC simulation approach.

6.1. Predicting Conditional Survival Probabilities

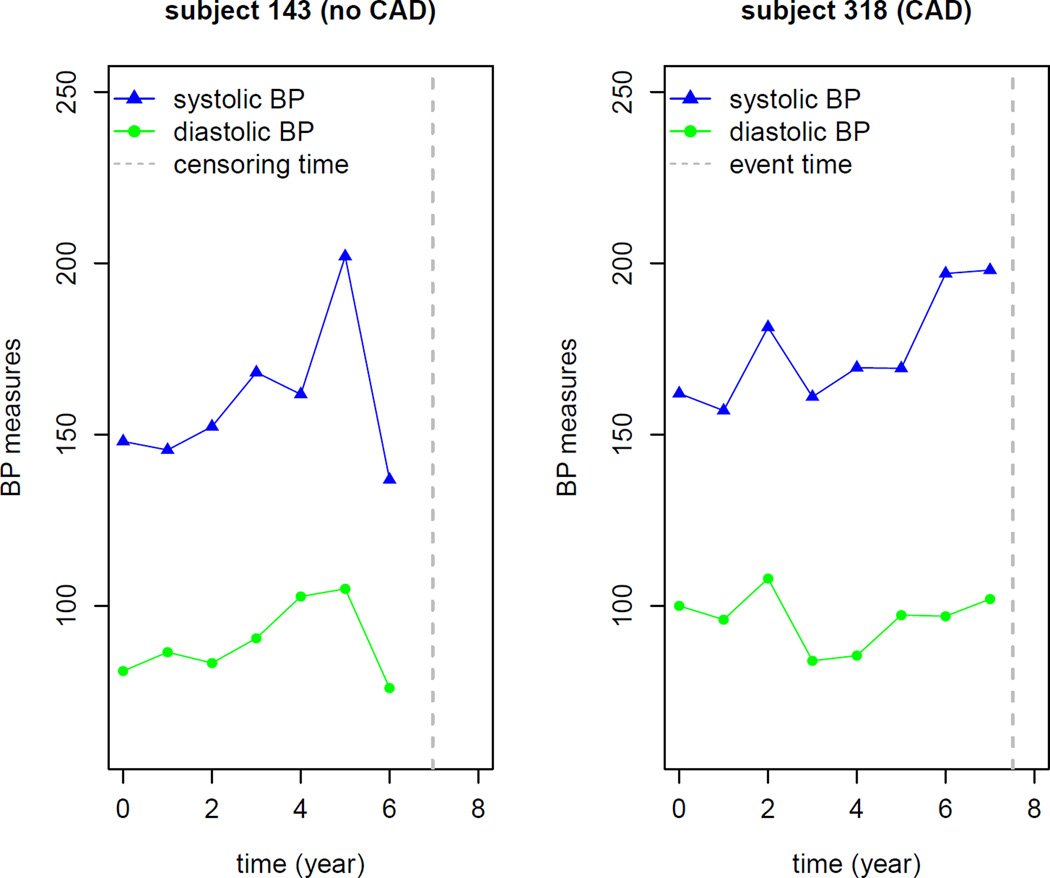
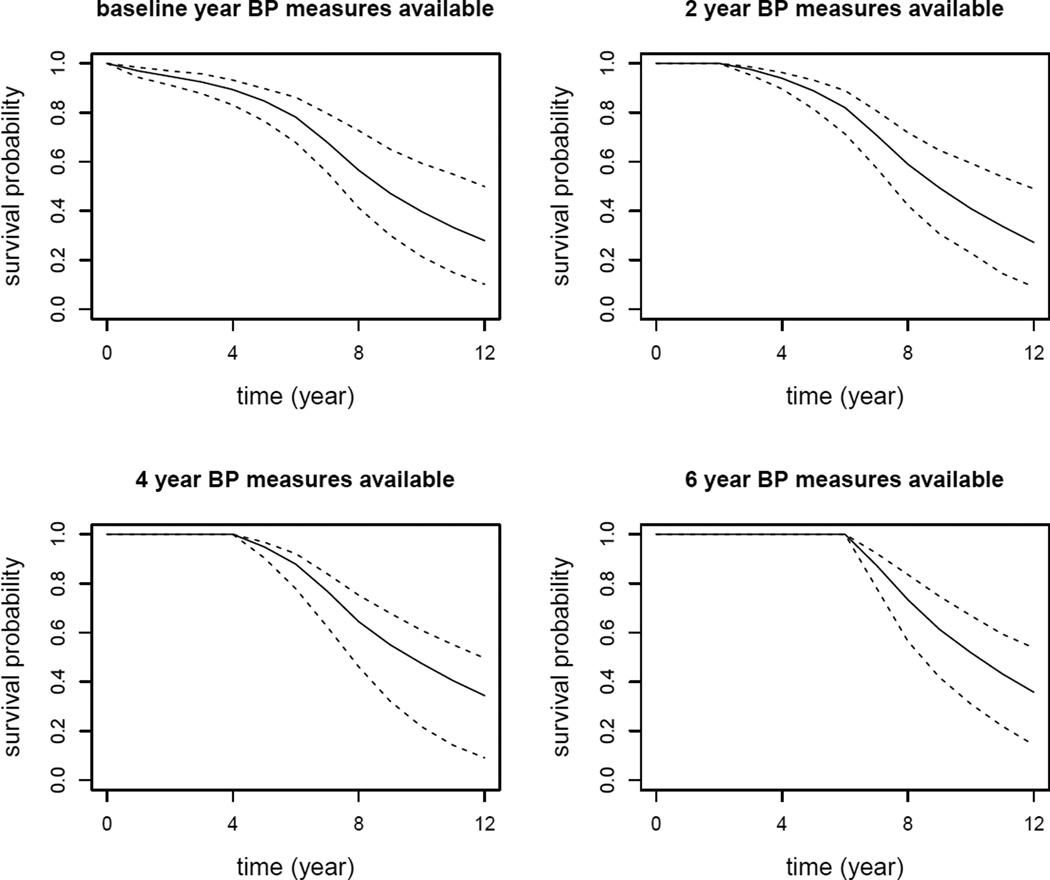
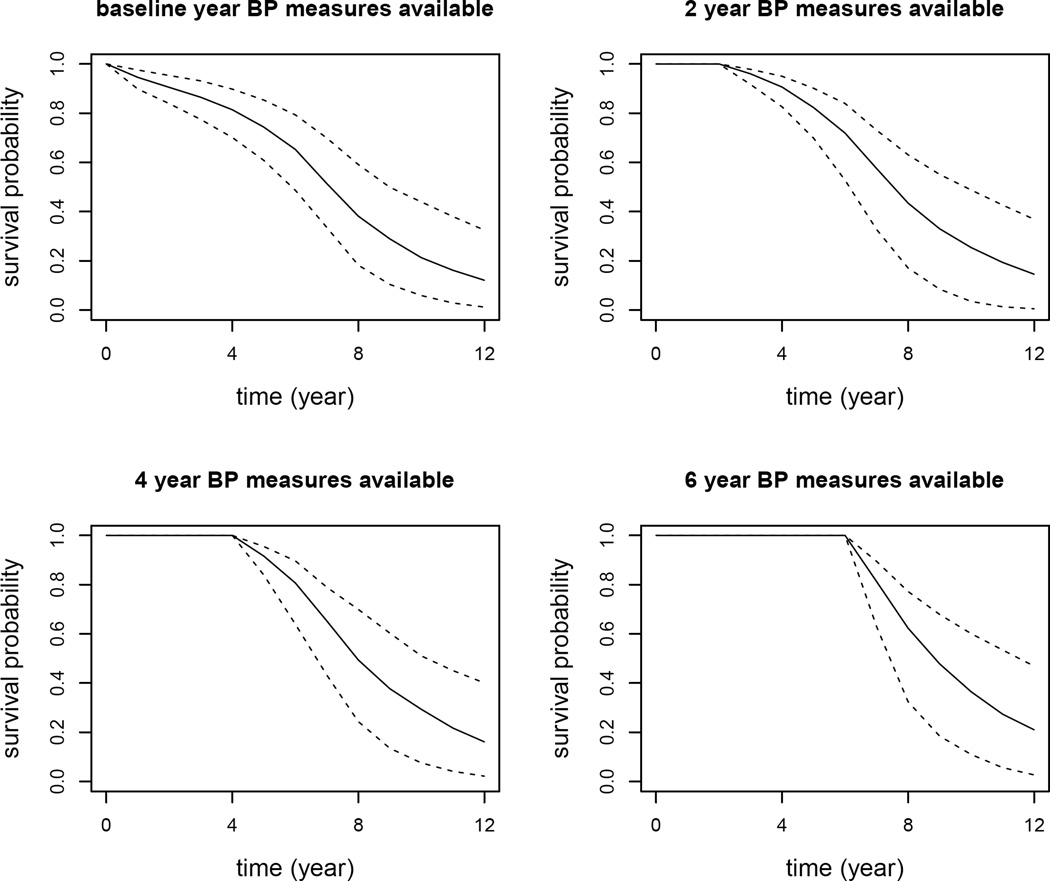
As an example, we chose two subjects from the testing data set to illustrate how the longitudinal BP measures over time influence the conditional survival probability predictions. We selected subjects 143 and 318 with the same baseline risk covariates. Subject 143 is a 66 years old black male with a history of smoking and diabetes, and was lost to follow up 6.97 years after baseline. Subject 318 has the same demographics as subject 143, except that a CAD event was observed at year 7.5. The two selected subjects have the same characteristics allowing us to study the effect of longitudinal BP measures over time on the risk of developing CAD. The plot of longitudinal BP measures over time for the two subjects is plotted in Figure 2. It is observed that, in general, longitudinal BP measures of subject 143 increase and then decrease over time, while subject 318 has an increasing and then decreasing trend in BP measures over time. The two subjects’ predicted conditional survival probabilities were plotted in Figures 3 and 4. In Figures 3 and 4, the upper left panel is the conditional survival probability plot when t = 0 and Δt varies from 0 to 12 years; the upper right panel is the conditional survival probability plot when t = 2 and Δt varies from 0 to 10 years; the lower left panel is the conditional survival probability plot when t = 4 and Δt varies from 0 to 8 years; the lower right is the conditional survival probability plot when t = 6 and Δt varies from 0 to 6 years. From the two plots, we clearly observed how the longitudinal BP measures impacted on the risk of developing CAD. Overall, subject 318 had larger risk in developing CAD than subject 143.

Figure 2.

Longitudinal blood pressure profiles for two selected patients.

Figure 3.

Conditional survival probability predictions for subject 143. The solid line denotes the median of predicted conditional survival probabilities over the 200 MC samples. The two dashed lines represent the 95% point-wise confidence intervals.

Figure 4.

Conditional survival probability predictions for subject 318. The solid line denotes the median of predicted conditional survival probabilities over the 200 MC samples. The two dashed lines represent the 95% point-wise confidence intervals.

6.2. Predictive Accuracy

We evaluated the predictive performance of Joint models 3 using the testing data set. Predictive results of joint models with both longitudinal SBP and DBP (JM2) were also compared to the other commonly used models, including the Cox model with baseline SBP and DBP as fixed covariates, the Cox model with observed longitudinal SBP and DBP as time-dependent covariates, joint models with only longitudinal SBP (JM1), and joint models with only longitudinal DBP (JM1). Predictive results using different models and criteria at various time points were presented in Table 5. From these results, we observe that JM2 model has the best predictive performance: AUC, AARD and MRD of JM2 are higher than those of all the other models. Particularly, JM2 model has better prediction performance than either of the two JM1 models, indicating that the joint models incorporating both longitudinal SBP and DBP can enhance the predictive ability of CAD than using either SBP or DBP. It is worth to noticing that in joint models 3, we observed that SBP and DBP is highly correlated through the random intercepts, 0.78 (95% CI [0.72, 0.85]). The strong correlation between SBP and DBP may substantially enhance the predictive ability of joint models, which is consistent with the findings in Fieuws et al [24].

Table 5.

Data application results for comparing predictive accuracy criteria of different models using the testing dataset.

t (year)	Cox’s Baseline	Cox’s Time-dep	JM1 (SBP)	JM1 (DBP)	JM2	Estimated % Gain
						JM2 vs JM1(SBP)	JM2 vs JM1(DBP)
AUC
8	0.637	0.662	0.646	0.656	0.673	0.042	0.026
10	0.647	0.664	0.654	0.659	0.678	0.037	0.029
12	0.652	0.678	0.653	0.674	0.683	0.046	0.013
15	0.670	0.694	0.670	0.679	0.703	0.049	0.035
AARD
8	0.197	0.234	0.213	0.221	0.249	0.169	0.127
10	0.210	0.234	0.221	0.222	0.256	0.158	0.153
12	0.218	0.253	0.217	0.244	0.264	0.217	0.082
15	0.245	0.280	0.245	0.252	0.296	0.208	0.175
MRD
8	0.052	0.072	0.057	0.066	0.083	0.456	0.258
10	0.067	0.087	0.073	0.077	0.099	0.356	0.286
12	0.073	0.102	0.074	0.097	0.108	0.459	0.113
15	0.085	0.114	0.088	0.099	0.127	0.443	0.283

AARD and MRD provide summary measures of the distance between the events and non-events risk distributions. For example, AARD of JM2 (SBP and DBP) at year 15 is approximately 0.30 which means that 30% more people in the CAD group than patients in the non-CAD group are above the population average risk. Compared to prediction models using only SBP or DBP, joint models using both SBP and DBP (JM2) can provide about 20.8% estimated gains in prediction when compared to models using SBP only, and 17.5% gains in prediction compared to using DBP only. Similarly, MRD of JM2 model at year 15 is 0.127 implying the mean CAD risk in the CAD group is 13% higher that in the non-CAD group. Joint model using both SBP and DBP also shows 44% estimated gains in MRD than the model using SBP only and 28% estimated gains than the model using DBP only. Both AARD and MRD shows greater gains of the joint models with two biomarkers over the single biomarker models than the estimated gains using AUC.

7. Discussion

When multiple longitudinal outcomes are collected along with the primary endpoint of time-to-event variable in biomedical studies, it’s of practical need and scientific interest to assess how these longitudinal measurements can be used to predict the survival probability and how much the longitudinal measurements can contribute to prediction. In this work we studied the predictive performance of multiple longitudinal measurements for a time-to-event outcome in a joint modeling framework. Especially, we applied various prediction metrics including AARD and MRD to evaluate the predictive accuracy of various models. Extensive cross-validation based simulations were conducted to assess the predictive performance of various models using different predictive criteria.

Joint models of multiple longitudinal outcomes and time-to-event outcome can find many applications in practical use. The joint modeling framework offers a powerful tool for data collected in routine clinical practice where biomarkers such as BP, lipids, glucose level and other markers are collected as part of routine clinical care. The use of joint modeling approach can offer prospective prediction of patients’ risk for various diseases based on the collective longitudinal measures of these marker values and give clinicians a better tool to utilize these repeatedly measured marker values. In health care system with comprehensive electronic medical record data, the modeling and prediction approach can be incorporated into the computer system to offer real-time modeling and prediction results for individual patient, providing on-going decision support to clinicians and leading ultimately to better patient care and health outcomes.

Parameter estimation for this work was implemented using the EM algorithm in R. When the number of longitudinal outcomes are highly increased, to avoid potential slow computation using the EM algorithm, alternatively, one can apply a Bayesian MCMC approach. The Bayesian MCMC approach has been applied previously in joint models of multiple longitudinal and time-to-event outcomes [51, 22, 21, 20, 52].

The predictive accuracy measures proposed in this work are model-based, hence their validity depends on the correct specification of both the longitudinal and the survival models. Our simulation results demonstrated the potential impact of omitting a longitudinal variable from the models. Further research will be needed to fully determine the robustness of these predictive accuracy measures with mis-specified models.

In this work, we didn’t construct any formal statistics to test the prediction improvement in joint models with multiple longitudinal outcomes compared to other models. This remains an interesting research extension in computing the standard errors of predictive criteria by performing Bootstrap techniques, for example. In simulations, it is also observed that random effect prediction has some impact on the predictive accuracy of joint models. It is therefore of interest to propose new approaches to improve the accuracy of random effect prediction in the joint modeling framework.