Large conditional single-photon cross-phase modulation

Significance

Strong, coherent interactions between individual photons can revolutionize communication and computation technology. An interaction between two photons that changes their relative phase by 180° could serve as the basis for universal quantum logic. Realizing such interaction, however, has been a grand experimental challenge. We use atoms trapped between high-reflectivity mirrors to make two individual photons interact strongly with each other. We demonstrate that the phase of a light wave can be changed by up to 60° by a single light quanta. With today’s technology, this approach may enable the realization of deterministic quantum gates.

Abstract

Deterministic optical quantum logic requires a nonlinear quantum process that alters the phase of a quantum optical state by π through interaction with only one photon. Here, we demonstrate a large conditional cross-phase modulation between a signal field, stored inside an atomic quantum memory, and a control photon that traverses a high-finesse optical cavity containing the atomic memory. This approach avoids fundamental limitations associated with multimode effects for traveling optical photons. We measure a conditional cross-phase shift of $\pi /6$ (and up to $\pi /3$ by postselection on photons that remain in the system longer than average) between the retrieved signal and control photons, and confirm deterministic entanglement between the signal and control modes by extracting a positive concurrence. By upgrading to a state-of-the-art cavity, our system can reach a coherent phase shift of π at low loss, enabling deterministic and universal photonic quantum logic.

Universal quantum gates (1, 2) can be implemented with an interaction that produces a conditional π-phase shift by one qubit on another (3). For photonic qubits, this requires an as-of-yet–unrealized strong cross-phase nonlinear interaction at the single-photon level. Photons do not directly interact with each other, and hence must be interfaced in a medium with a giant nonlinearity while preserving optical coherence (4, 5). The strong nonlinearities introduced by interacting Rydberg atoms (6–9) and cavity quantum electrodynamic (cQED) systems (10–12) have led to the observation of up to π-phase shifts between two propagating photons in the same mode. This type of quantum phase switch can be used to sort photons and implement a Bell state analyzer (13). The realization of a deterministic and universal optical gate, however, requires cross-phase modulation between distinct optical modes. Using a photon–atom gate in a cQED system, photon–photon entanglement (14) has been demonstrated. However, large conditional photon–photon phase shift remains an experimental challenge. For light pulses propagating in nonlinear fibers (15) and nonlinear slow-light media (16, 17), cross-phase modulation on the order of microradians per photon has been observed. In a pioneering cQED experiment two decades ago, Turchette et al. (18) measured the average polarization rotation of a weak continuous probe beam by another beam copropagating in the same cavity, and extrapolated a nonlinear phase shift of 0.28 rad per photon. However, the characteristic time of the nonlinearity (the cavity lifetime) in that experiment was much shorter than the photon wavepacket duration necessary to spectrally separate the two modes, which precludes the modulation of the entire wavepacket (19). Very recently, a much smaller but conditional cross-phase modulation of 18 μrad by a single postselected photon was measured in a nonlinear slow-light system using electromagnetically induced transparency (EIT) (20). However, as shown by Shapiro (21), and in an extension to EIT by Gea-Banacloche (22), locality and causality prohibit high-fidelity π-phase shifting operations between traveling photons.

To realize a giant optical Kerr effect that is not subject to Shapiro’s no-go theorem, we coherently store a weak signal pulse in an atomic quantum memory as a collective spin excitation via EIT (23). A control photon traveling through a high-finesse cavity containing the EIT medium interacts with the entire collective atomic excitation simultaneously, and the stored signal light is retrieved after detecting the control photon (Fig. 1). A similar setup was previously used to implement an optical transistor whose transmission depended on the stored photon number in the quantum memory (24). That work demonstrated that one stored photon can block the transmission of many cavity photons resonant with the atomic transition. The current experiment instead investigates the dispersive regime of atom-cavity coupling: a control photon induces a differential light shift on the two atomic states in the collective excitation, thus shifting the optical phase of the signal light retrieved later. Conversely, a stored signal photon changes the center frequency of the cavity and shifts the phase of a weak control pulse. We measure this cross-Kerr modulation on both signal and control light, conditioned on the detection of a photon in the other mode, while maintaining high fringe visibility.

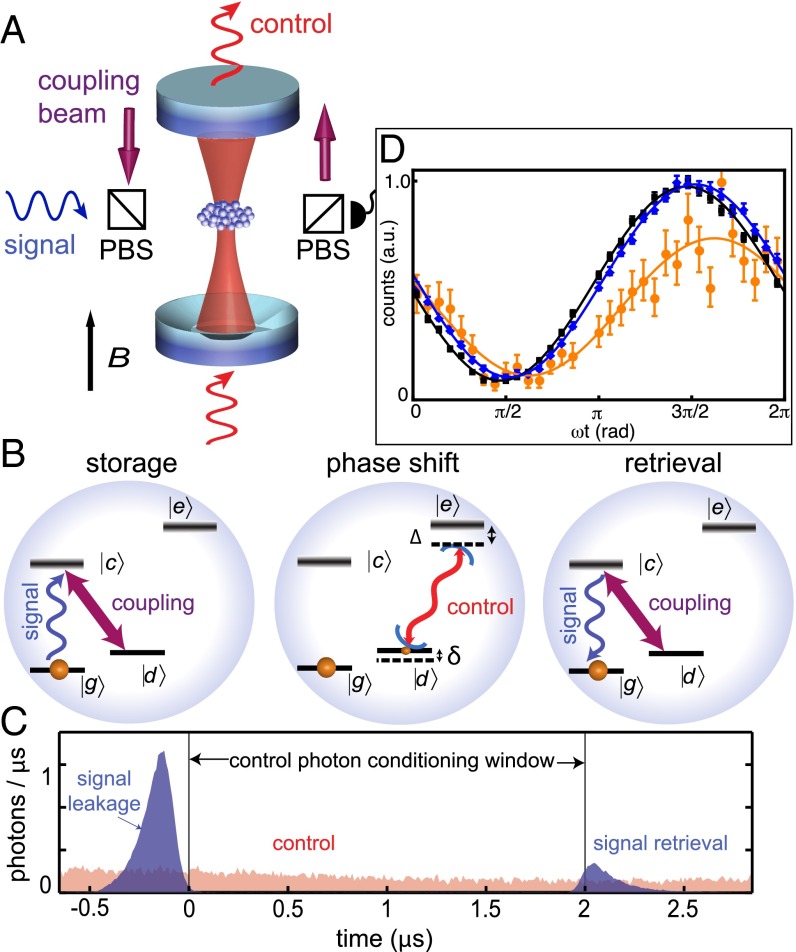
Fig. 1.

Scheme for imprinting large single-photon phase shift onto stored light. (A and B) A signal photon traveling orthogonal to the cavity axis is stored as an atomic coherence between states $|g\rangle =|S_{1/2},F=3,m_F=3\rangle$ and $|d\rangle =|S_{1/2},\mathrm{4,4}\rangle$ via the EIT process created by coupling light resonant with the $|d\rangle \leftrightarrow |c\rangle =|P_{3/2},\mathrm{3,3}\rangle$ transition. A control photon resonant with the optical cavity, and detuned by $\mathrm{\Delta }$ from the $|d\rangle$ to $|e\rangle =|P_{3/2},\mathrm{5,5}\rangle$ transition, is sent through the cavity during the storage time. The signal photon is retrieved after the control photon leaves the cavity. (C) The experimental signal leakage and retrieval (blue), and control (red) light pulses are shown as a function of time. (D) The phase of the retrieved signal light is measured without control light (black), conditioned on not detecting a transmitted control photon (blue), and conditioned on the detection of a transmitted control photon (red) by its interference with a copropagating reference beam (not shown). In this and the following figures, the error bars represent $\pm 1$ SD of statistical error.

Methods

Our system consists of an ensemble of laser-cooled ¹³³Cs atoms trapped in a dipole trap tightly focused at the center of a high-finesse optical cavity (Fig. 1A). Initially, the atoms are optically pumped into the state $|g\rangle$. We then make use of the resonant $\mathrm{\Lambda }$-type energy-level structure, $|g\rangle \leftrightarrow |c\rangle \leftrightarrow |d\rangle$, to induce EIT. Signal light resonant with the $|g\rangle \leftrightarrow |c\rangle$ transition slowly propagates through the atomic medium while its group velocity is controlled by a strong copropagating coupling beam resonant with the $|d\rangle \leftrightarrow |c\rangle$ transition (Fig. 1B). By adiabatically switching off this coupling beam (Fig. 1C), the signal photon is stored in the ensemble as an atomic coherence between the $|g\rangle$ and $|d\rangle$ states. In the absence of control photons, we typically store and retrieve more than 10% of the input signal pulse when we switch on the coupling laser again after 2 μs of storage. This retrieval efficiency depends on the ensemble optical depth (OD) and decoherence rate (${\gamma }_0$) of the atomic coherence, measured to be $\mathrm{OD}=7$ and ${\gamma }_0/2\pi =50$ kHz, respectively.

To measure the conditional phase shift ϕ imprinted by one control photon on the stored signal field, control light (a weak coherent state with less than one photon on average during the storage time) impinges on the optical cavity, and light-shifts the atomic levels. The resulting phase shift of the atomic excitation is mapped onto the signal light upon retrieval, and is measured by comparison with a 30-MHz detuned reference pulse that travels along the signal path, and matches the temporal shape and amplitude of the retrieved signal light. (The detuning was chosen to limit atomic heating by absorption of the reference beam while ensuring that the resulting 33-ns beat note could be resolved by our detection system.) The reference and retrieved signal light mix on a photodetector and are detected as photon clicks. These arrival times are binned by phase into a single fringe after correcting for the drift of the path length difference between signal and reference beams, which is separately measured during each 0.5-s-long experimental cycle. The conditional nonlinear phase shift is the difference between the measured signal phase when we detect one transmitted control photon in the conditioning window, compared with the signal phase when no control light is applied (Fig. 1D). To construct such a curve, data were typically accumulated for 600 experimental cycles, or ∼250,000 individual storage–retrieval sequences.

Results

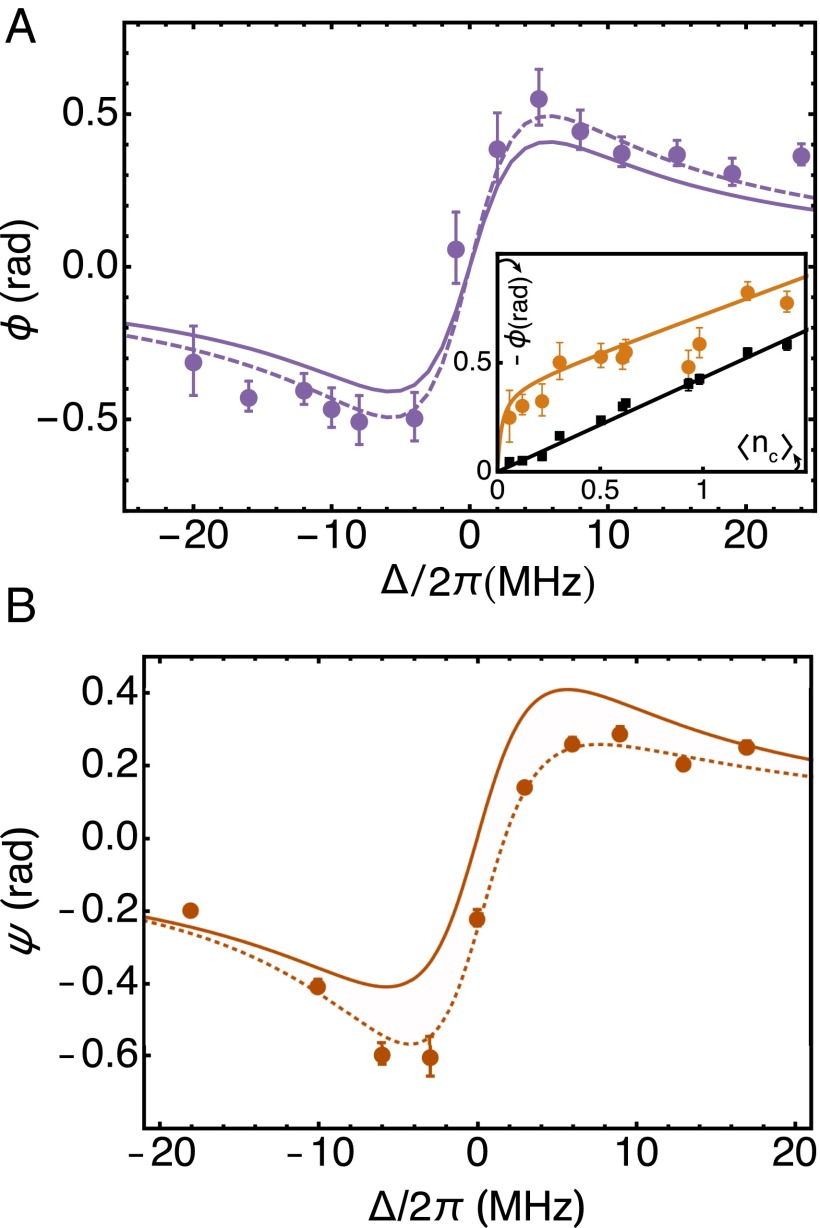
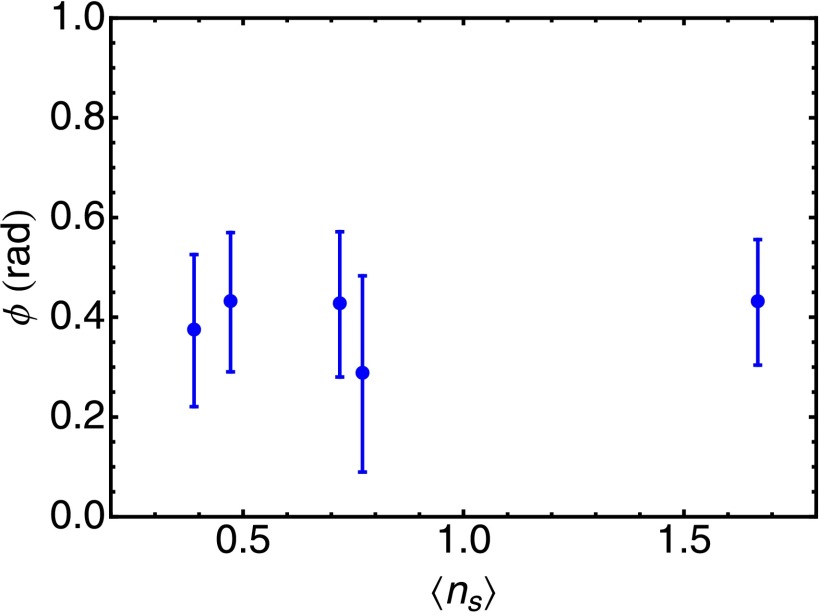
Fig. 2A shows the measured conditional signal phase shift as a function of the detuning $\mathrm{\Delta }$ between the input control light and the atomic transition $|d\rangle \leftrightarrow |e\rangle$. The phase shift results from the light shift $\delta =\eta \hspace{0.17em}{\kappa }_0\hspace{0.17em}\text{Re}\left[\chi \right]/2$ of the control photon on the atomic state $|d\rangle$. Here, $\chi =\left(\left(2\mathrm{\Delta }/\mathrm{\Gamma }\right)+i\right)/\left(1+{\left(2\mathrm{\Delta }/\mathrm{\Gamma }\right)}^2\right)$, $\eta =4g^2/{\kappa }_0\mathrm{\Gamma }=3.8$ is the spatially averaged cavity cooperativity (ref. 25 and Supporting Information), ${\kappa }_0=2\pi \times 150$ kHz is the measured empty-cavity linewidth, $2g=2\pi \times 1.7$ MHz is the effective single-photon Rabi frequency, and $\mathrm{\Gamma }=2\pi \times 5.2$ MHz is the excited-state decay rate. The control-induced nonlinear atomic phase shift is then approximately $\varphi =\delta \cdot \tau$, where $\tau =1/\kappa$ is the mean interaction time, and $\kappa ={\kappa }_0\left(1+\eta \text{Im}\left[\chi \right]\right)$ (25) is the increased cavity linewidth in the presence of a signal photon. We measure a conditional single-photon phase shift of $\left|\varphi \right|=0.4\left(1\right)$ rad at $\left|\mathrm{\Delta }\right|=$ 8 MHz, in good agreement with the theoretical prediction of $\varphi =\left(1/2\right)\eta \text{Re}\left[\chi \right]/\left(1+\eta \text{Im}\left[\chi \right]\right)$, valid for moderate $\eta \lesssim 6$ (see Supporting Information for full model). The average shift (not conditioned on detecting a control photon) is linear with $\langle n_c\rangle$, the mean input control photon number in the 2-μs conditioning window (Inset to Fig. 2A), and is, in principle, independent of the stored signal photon number $n_s$ (Fig. S1). The linear slope of 0.43(1) rad per photon is close to the expected phase shift per cavity photon of 0.39 rad per photon, and to the conditional phase shift of 0.4(1) rad depicted in Fig. 2A. For $\langle n_c\rangle \ll 1$, background counts reduce the measured conditional phase. For $\langle n_c\rangle \gtrsim 1$, the contribution from undetected photons increases the measured conditional phase. Throughout this paper, we operate at mean photon numbers $\langle n_c\rangle \le 0.5$.

Fig. 2.

Conditional phase shift induced by a single photon. (A) The phase shift of the stored signal field, conditioned on detecting a control photon, is plotted as a function of control-atom detuning $\mathrm{\Delta }$. The solid line is the model prediction for a single control photon in a cavity with cooperativity $\eta =3.8$; the dashed line is this same prediction including corrections for multiple control photons (mean recovered signal photon number $\langle n_s\rangle$ = 0.3, mean control photon number $\langle n_c\rangle$ = 0.4). The Inset plots the measured average phase shift (black circles) and conditional phase shift (red circles) as a function of $\langle n_c\rangle$ at $\mathrm{\Delta }/2\pi =-8$ MHz and $\langle n_s\rangle =0.3$. The average phase shift fits to a line (black) with slope of 0.43(1) rad per photon that agrees with the expected phase shift per cavity photon of 0.38 rad per photon. The red line is the model’s prediction for the conditional phase shift that accounts for contributions from multiple photons, as well as false conditioning on background counts that reduces the measured conditional phase at very small $\langle n_c\rangle$. (B) The control phase shift ψ, inferred from polarization rotation, conditioned on the detection of a signal photon. The deviation of the experimental data from the theoretical model (solid line) can be explained by a small light-cavity detuning of ${\delta }_c/2\pi =$25 kHz that is included in the model shown as the dotted line (Supporting Information).

Fig. S1.

Conditional phase shift of the signal light as a function of mean stored signal photon number. The phase shift is independent of the stored signal photon number.

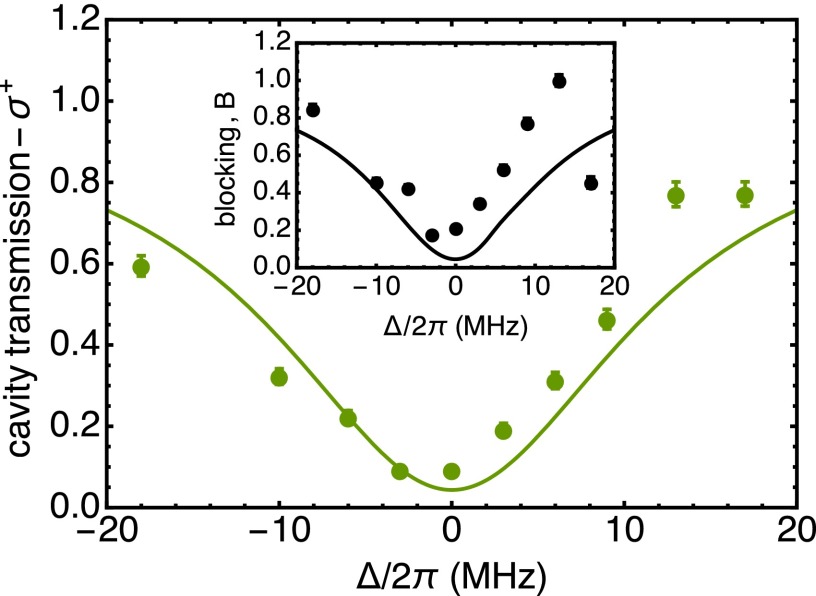
While the control photon shifts the phase of the retrieved signal light, the signal light also acts back on the control light. The cavity resonance is shifted by the stored signal light (26), which in turn changes the phase of the transmitted control light. We measure the conditional control phase ψ by using linearly polarized input light on the cavity path, and measuring its polarization change conditioned on detecting one retrieved signal photon. The weakly interacting ${\sigma }^{-}$-polarized component thus serves as a phase reference for the strongly interacting ${\sigma }^{+}$-polarized control light (Fig. S2). This conditional control phase shift ψ is plotted as a function of control-atom detuning in Fig. 2B.

Fig. S2.

Cavity transmission for right-circularly polarized light conditioned on detecting one retrieved signal photons is plotted as a function of light-atom detuning. The solid line represents the theoretical expectation. Inset shows the blocking factor, B, of the linearly polarized control light plotted conditioned on detecting a signal photon. The solid line represents the theoretical expectation. The deviation of the data from the theory in the Inset can be explained by the interaction of ${\sigma }^{-}$-polarized light with excited states other than $|F\prime =5,m_f=3\rangle$ not taken into consideration in the model.

In fact, the combined control-signal optical state can be ideally described as a two-mode entangled state $|\mathrm{\Psi }\rangle =p_{00}|0_s{0}_c\rangle +p_{01}|0_s{1}_c\rangle +p_{10}|1_s{0}_c\rangle +p_{11}{e}^{i\theta }|1_s{1}_c\rangle$, where $0_s$ ($1_s$) refers to zero (one) signal photon, whereas $0_c$ ($1_c$) represents a ${\sigma }^{-}$ (${\sigma }^{+}$)-polarized control photon, $p_{ij}$ is the probability amplitude of being in state $|i_s{j}_c\rangle$, and θ is the nonlinear interaction phase. (Note that we are using a single-rail representation, i.e., photon number basis for the signal light, whereas we are using a dual-rail representation, i.e., polarization basis for the cavity light.) Thus, in the ideal system, we expect $\varphi =\psi =\theta$. In the presence of decoherence and loss, the two-mode system must be described by a density matrix. We reconstruct the reduced density matrix, ${\rho }_{ij}\left(i,j\mathit{ϵ}\left\{\mathrm{0,1}\right\}\right)$, of the outgoing signal and control modes by measuring coincidences between these two paths (Supporting Information and Table S1). We extract a nonlinear phase shift of $\theta =0.45\left(2\right)$ rad, and a concurrence (27) of $C=0.082\pm 0.005$ (statistical) $\pm 0.016$ (systematic) $>$ 0, after correcting for detection efficiencies and propagation losses (see Table S2 for error analysis). The positive concurrence demonstrates deterministic photon number-polarization entanglement between the outgoing signal and control light, and is comparable to the maximal expected concurrence of $C=0.11$ for states with the same coherent amplitudes and conditional phase shift as measured in our experiment. In practice, this number-polarization entanglement is difficult to use for quantum computing because single-qubit rotations require nonlinear interactions. A dual-rail (polarization) representation for both signal and control modes will be preferable in future experiments.

Table S1.

The 16 measurements needed to reconstruct the density matrix in the photon-number basis of signal mode and polarization basis of the control mode

ν	Signal	Control	${\theta }_s$	${\theta }_h$	${\theta }_q$
1	$|0_s\rangle$	$|0_c\rangle$	NA	0	$\pi /4$
2	$|0_s\rangle$	$|1_c\rangle$	NA	0	−$\pi /4$
3	$|1_s\rangle$	$|1_c\rangle$	NA	0	−$\pi /4$
4	$|1_s\rangle$	$|0_c\rangle$	NA	0	$\pi /4$
5	$|0_s\rangle -i|1_s\rangle$	$|0_c\rangle$	$3\pi /2$	0	$\pi /4$
6	$|0_s\rangle -i|1_s\rangle$	$|1_c\rangle$	$3\pi /2$	0	−$\pi /4$
7	$|0_s\rangle +|1_s\rangle$	$|1_c\rangle$	0	0	−$\pi /4$
8	$|0_s\rangle +|1_s\rangle$	$|0_c\rangle$	0	0	$\pi /4$
9	$|0_s\rangle +|1_s\rangle$	$|0_c\rangle -i|1_c\rangle$	0	−$\pi /8$	0
10	$|0_s\rangle +|1_s\rangle$	$|0_c\rangle +|1_c\rangle$	0	0	0
11	$|0_s\rangle -i|1_s\rangle$	$|0_c\rangle +|1_c\rangle$	$3\pi /2$	0	0
12	$|0_s\rangle$	$|0_c\rangle +|1_c\rangle$	NA	0	0
13	$|1_s\rangle$	$|0_c\rangle +|1_c\rangle$	NA	0	0
14	$|1_s\rangle$	$|0_c\rangle +i|1_c\rangle$	NA	$\pi /8$	0
15	$|0_s\rangle$	$|0_c\rangle +i|1_c\rangle$	NA	$\pi /8$	0
16	$|0_s\rangle -i|1_s\rangle$	$|0_c\rangle +i|1_c\rangle$	$3\pi /2$	$\pi /8$	0

The measurement phase angle is listed as NA when there is no phase reference on the signal path. ${\theta }_h$ and ${\theta }_q$ represent angles of the HWP and QWP placed after the cavity.

Table S2.

Main sources of uncertainty in reconstructing the density matrix of the two-photon state, indicating the resulting maximum systematic error in the concurrence estimate

Variable	Source	Maximum relative uncertainty, %	Maximum concurrence uncertainty
Quantum efficiency	Fiber coupling, detector efficiency, frequency filter transmission	15	0.01
Control polarization	Atom number fluctuation, atom loss	4	0.007
Signal reference phase estimation	Reference fast phase fluctuation, shot noise	5	0.009
Signal power fluctuation	Fiber optics, shot noise	4	0.002
Signal fringe normalization	Power fluctuation, shot noise	5	0.005
Total error	All of the above		0.016

The total systematic error should be compared with the statistical error of 0.005.

Discussion

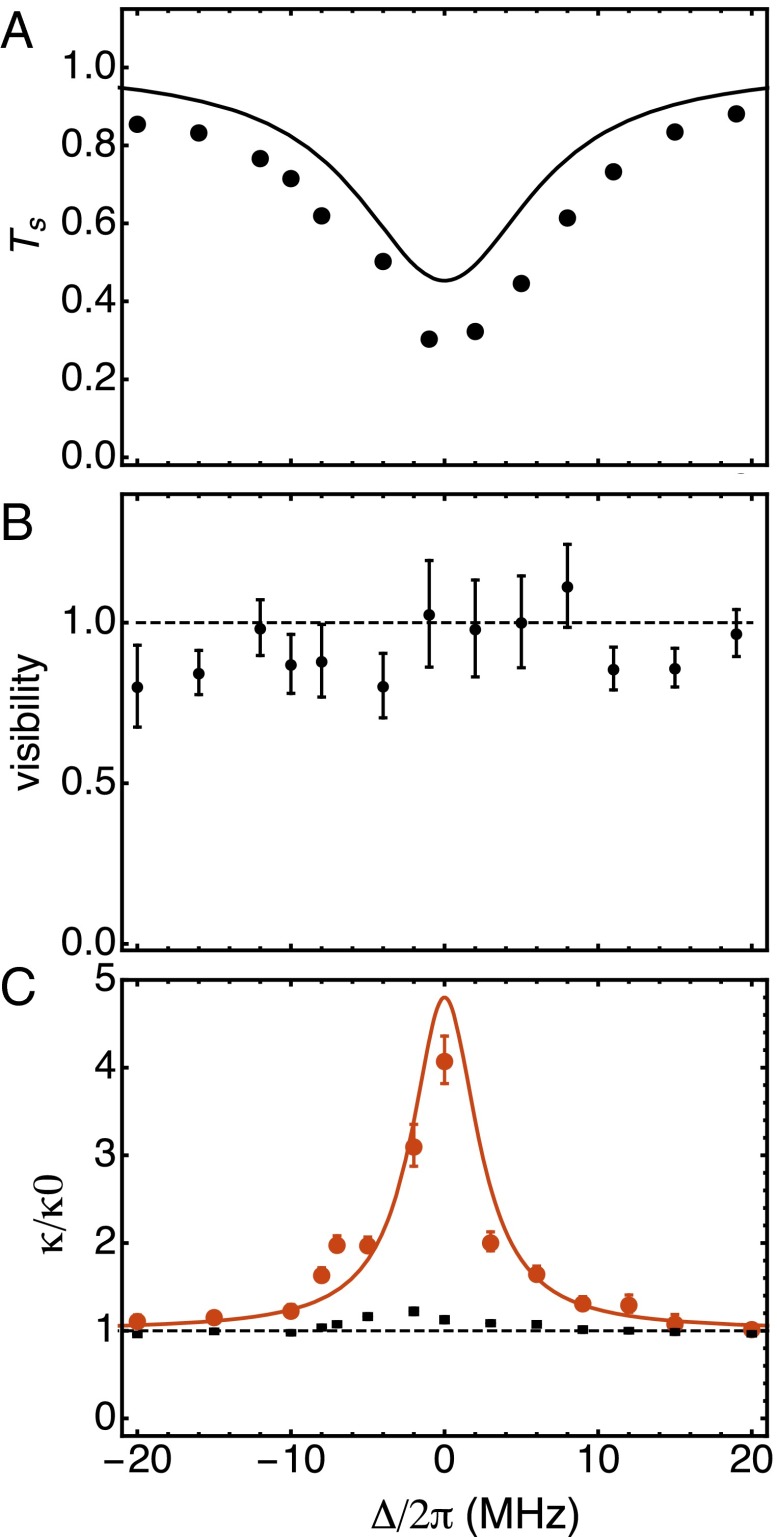
At a given moderate cooperativity η ($\eta \lesssim 6$), the nonlinear phase shift takes on its maximum value $\varphi \simeq \eta /\left(4\sqrt{1+\eta }\right)$ at a cavity-atom detuning of $\mathrm{\Delta }/\mathrm{\Gamma }=\sqrt{1+\eta }/2$, and is accompanied by reduced signal transmission $T_s/T_0=e^{-\eta /2\left(1+\eta \right)}=0.67$ for $\eta =3.8$. Here, $T_0$ is the signal transmission without control light, and $T_s$ is the (reduced) signal transmission due to light scattering out of the cavity mode by an atom in state $|d\rangle$. Scattering photons into free space destroys the collective spin excitation associated with the stored signal photon. Fig. 3A shows this signal recovery efficiency conditioned on the detection of a control photon. The solid curve is the theoretical expectation for transmission, taking into account the signal loss due to the scattering of the control photon, given by $T_s/T_0=\exp \left(-\eta \text{Im}\left[\chi \right]{\kappa }_0/\kappa \right)$. Additional cavity-induced losses, not included in the theory, are responsible for the remaining deviation between the experimental data and this curve. Although the primary recovery loss is due to scattering of cavity photons, two other factors reduce the signal recovery. Because the atomic cloud extends beyond the cavity waist and also extends over several periods of the cavity standing wave, there is recovery loss due the inhomogeneous phase shift imprinted by the cavity photon along the cavity and signal axes, a result of the spatially inhomogeneous cavity coupling. These effects are described in more detail in the supplemental material of ref. 28. Moreover, the occasional presence of more than one cavity photon reduces further the signal photon’s survival probability beyond the expected conditional transmission (shown in Fig. 3A).

Fig. 3.

Signal transmission, signal visibility, and cavity linewidth. (A) The fractional signal transmission conditioned on detecting a control photon (black circles), measured at $\langle n_c\rangle =0.4$ and $\langle n_s\rangle =0.3$. The solid line is the theoretical expectation accounting only for scattering of control light. The discrepancy is discussed in the text. (B) Fringe visibility of recovered signal light after correction for the signal loss shown in A, which is the dominant contrast loss mechanism. The data are consistent with no contrast loss from other effects (dashed line). (C) The cavity linewidth conditioned on detecting a signal photon (red circles) and averaged cavity linewidth (black squares), normalized to the bare linewidth ${\kappa }_0=2\pi \times 150$ kHz, measured for $\langle n_s\rangle =0.2$.

As there is uncertainly on the timescale ${\kappa }^{-1}$ when a control photon enters or exits the cavity, we expect a randomization $\delta \varphi$ of the nonlinear phase (19) at the level of $\delta \varphi /\varphi ={\left(\kappa {\tau }_p\right)}^{-1}\sim 0.25$, where ${\tau }_p=2$ μs is the input control pulse length. This would limit the visibility of the recovered phase to about 0.99 at $\varphi =0.4$ rad. The visibility of our phase beat note after correcting for the transmission loss is shown in Fig. 3B. This measurement yields an average visibility of 0.9(1) at $\mathrm{\Delta }=-8$ MHz that is consistent with expected visibility reduction and appears to be independent of $\mathrm{\Delta }$.

The lifetime of the cavity photon, $1/\kappa$, decreases in the presence of the atomic excitation (stored signal photon) that can scatter light out of the cavity. To confirm this aspect of our model, we excite the cavity with a short pulse (200 ns) and measure the cavity decay time conditioned on detecting a stored signal photon. In Fig. 3C, we plot the conditional cavity linewidth κ as a function of the control-atom detuning $\mathrm{\Delta }$. A single atom in state $|d\rangle$ increases the cavity linewidth by $\kappa /{\kappa }_0=1+\eta \text{Im}\left[\chi \right]$ (25), which is plotted as the theoretical curve in Fig. 3A. The observed increase of the cavity linewidth agrees with the theory. Remarkably, the cavity lifetime is shortened even in those instances when the signal photon is detected, that is, the scattering of the cavity photon into free space did not actually occur. The mere presence of the additional decay path shortens the cavity lifetime, akin to the situation of a two-sided optical cavity whose linewidth depends on both mirrors even for those photons that are measured to exit on one particular side.

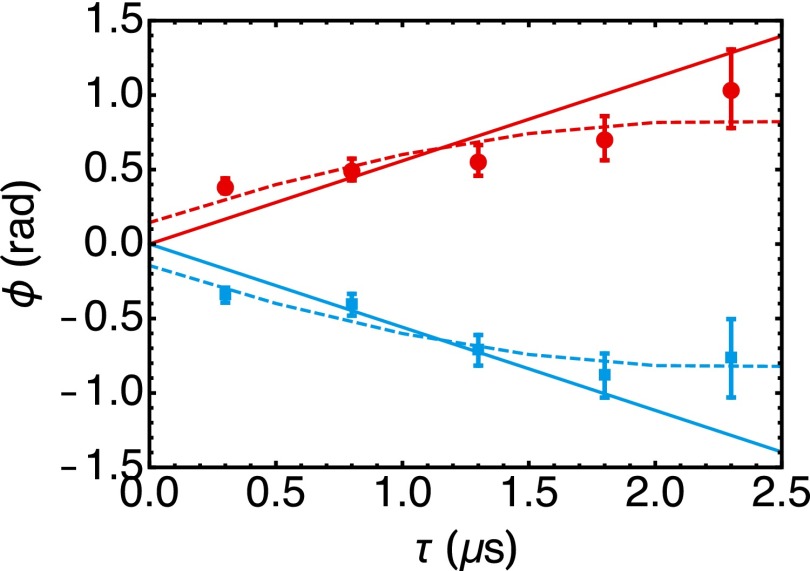
In this short-pulse excitation (${\tau }_p\ll {\kappa }^{-1}$) limit, we can directly measure the change in the imprinted phase shift with control photon dwell time. The imprinted phase shift on the signal light should be proportional to the time the control photon spends in the cavity, exerting a light shift on the spin wave. Therefore, we can increase the phase shift by postselecting on control photons that exit the cavity later than average. In Fig. 4, we plot the resulting phase shift as a function of the conditioning time for control-atom detunings $\mathrm{\Delta }/2\pi =\pm 8$ MHz. The observed conditional phase shift increases for long control photon dwell times. The largest phase shift we observe is 1.0(4) rad, 2.5 times larger than the phase shift observed with a continuous control field and ${\tau }_p>{\kappa }^{-1}$.

Fig. 4.

Signal phase shift conditioned on control photon dwell time. The conditional phase shift from short control pulses for $\mathrm{\Delta }/2\pi =\pm 8$ MHz is plotted as a function of conditioning time τ for signal pulses stored for 3 μs, $\langle n_c\rangle =0.8$, and $\langle n_s\rangle =0.6$. The conditioning window is 0.5 μs. The solid lines model the phase as linear in control photon dwell time; the dashed lines are the complete model predictions and include the effect of multiple control photons (important at early conditioning times) and background counts (important at long conditioning times) (Supporting Information).

Our current implementation has a limited maximal phase shift, noise from timing uncertainty on the phase shift, and low signal transmission. Using a single-sided cavity with $\eta =10$ would enable us to reach phase shifts of π on atomic resonance, as was recently measured between a photon and an atom (14), with signal photon survival probability exceeding 85%. Alternatively, increasing the cavity cooperativity in the present geometry to $\eta =100$, compatible with current state of the art (29), enables phase shifts approaching π close to resonance: by storing a signal photon in the $\left\{{\sigma }^{+},{\sigma }^{-}\right\}$ logical basis in an ensemble prepared in a 2-G magnetic field with secondary ground states $|d\rangle =|S_{1/2},\mathrm{4,4}\rangle$ and $|d\prime \rangle =|S_{1/2},\mathrm{4,2}\rangle$ and using matched detunings $\mathrm{\Delta }=\pm 0.7$ MHz, each state near maximizes its phase shift of $\pi /2$ resulting in a phase change of $0.87\pi$. This scheme also would allow us to use a polarization, instead of the single-rail, logical basis to describe the signal photon’s logical state.

Two separate effects reduce the signal transmission. First, control light can be scattered by atoms into free space. At large detuning, scattering is inversely proportional to the detuning $\mathrm{\Delta }$. By working with a larger-cooperativity system, we can choose to work at a greater light-atom detuning to simultaneously achieve high phase shift and high transmission. With a cooperativity $\eta =100$, we expect a phase shift of π with 98% signal transmission in a single-sided setup on atomic resonance ($\mathrm{\Delta }=0$), and a phase shift of $0.33\pi$ with 90% transmission at $\mathrm{\Delta }=2\pi \times 80$ MHz in a double-sided setup. Spatially inhomogeneous cavity coupling further reduces transmission, which can be eliminated by trapping the atoms in an intracavity dipole trap at twice the control wavelength (30).

The phase noise resulting from timing randomization can be circumvented by storing the signal photon longer and applying a long control pulse (i.e., one much narrower than the cavity bandwidth) that enters and exits the system during the storage time. Our maximum storage time is governed by the decoherence rate ${\gamma }_0$, which is dominated by effective magnetic field variations from the spatially varying polarization in our tightly focused dipole trap, and Doppler decoherence from atomic motion.

In conclusion, we have measured a conditional phase shift of 0.4(1) rad imparted onto a weak coherent state by a single photon using quasi-monochromatic light, and up to 1.0(4) rad by using a short control pulse and postselecting on photons that remain in the system for longer than average. The underlying interaction entangles the outgoing signal and cavity modes as verified by a positive concurrence, and can be extended to π-phase shift with high signal transmission with today’s technology. Such large and efficient conditional phase modulation at the single-photon level would enable deterministic optical quantum logic (31), the engineering of cluster states (32, 33), and entanglement concentration (34).

SI Materials and Methods

The Cs atoms in our experiment are held in a far off-resonant dipole trap that is focused at the cavity waist. This trap is formed by 32 mW of 937-nm light focused through an in-vacuum lens to give an expected transverse waist of 2.5 μm at the atoms. The corresponding calculated trap frequencies are ${\omega }_{\text{radial}}/2\pi =46$ kHz and ${\omega }_{\text{axial}}/2\pi =4$ kHz. From absorption images of the atomic cloud, we measure the atoms to have a transverse rms radius of 2(1) μm and an axial rms radius of 17(1) μm.

The atom-cavity coupling g, and thus the cooperativity $\eta =4g^2/\kappa \mathrm{\Gamma }$, varies along the standing wave of the cavity axis and with the radial extent of the cavity mode. The extent of the atomic cloud and its placement determine the effective cooperativity we realize in the experiment. The maximal cooperativity ${\eta }_0=\left(24\mathrm{ℱ}/\pi \right)/\left(k^2{w}_c^2\right)=8.6\left(1\right)$ is determined by the wavevector $k=2\pi /\lambda$, where $\lambda =852.347$ nm, the cavity waist $w_c=35.5\left(2\right)$ μm, and the cavity finesse $\mathrm{ℱ}=77.1\left(5\right)\mathrm{\times }{10}^3$. The maximal value is realized on the cavity axis at an antinode of the cavity standing wave. The effective cooperativity is the value averaged over all possible atomic positions:

$$\eta ={\eta }_0{\displaystyle \iiint \rho \left(x,y,z\right){\cos }^2\left(kz\right)e^{-\frac{x^2+y^2}{2w_c^2}}dx\hspace{0.17em}dy\hspace{0.17em}dz},$$ [S1]

where $\rho \left(x,y,z\right)$ is the normalized atomic density. From the above atomic distribution, we predict an effective cooperativity $\eta =3.8\left(1\right)$. This number is used to plot the expected theory curves in all of the figures in the main text.

Phase Reconstruction.

We record 410 storage-and-retrieval attempts with phase measurement every experimental cycle, and typically combine data from 600 experimental cycles (about 5 min of data). In these, we collect about 150 coincidences, which we use to reconstruct the phase. The photon arrival times (modulo the signal-reference beat note period) are then binned and fit with a sine wave to extract the phase.

An additional detail in our implementation is that we did not actively stabilize the path length difference between the signal and reference light, which are produced by two separate acoustooptic modulators (AOMs) whose input light comes from a single laser. The AOMs are modulated with different frequencies so that the output beams have a frequency difference of 30 MHz. We recalibrate the phase difference between the two paths each 0.5-s experimental cycle to account for thermal and mechanical drifts. This phase difference is removed from data taken in that cycle so that all data are effectively compared with the same time origin.

We additionally reconstruct the phase for the data without cavity light measured in 410 additional storage-and-retrieval attempts in each experimental cycle in the same way, and measure the signal transmission without the reference in a third set. These sets are interleaved in the data.

Input Control Photon Number.

To calculate the input control photon number $\langle n_c\rangle$, we measure the mean photon number transmitted through the cavity and divide it by the detection efficiency (0.45), fiber collection efficiency (0.7), cavity outcoupling efficiency (0.66), and atom-induced cavity transmission (25):

$$T_c=\frac{1}{{\left(1+\langle n_s\rangle \eta \text{Im}\left[\chi \right]\right)}^2+{\left(\frac{2{\delta }_{\text{c}}}{\kappa }+\langle {\text{n}}_{\text{s}}\rangle \eta \text{Re}\left[\chi \right]\right)}^2},$$ [S2]

taking into account the mean stored signal photon number $\langle n_s\rangle <1$. [$\chi =\left(\left(2\mathrm{\Delta }/\mathrm{\Gamma }\right)+i\right)/\left(1+{\left(2\mathrm{\Delta }/\mathrm{\Gamma }\right)}^2\right)$, as defined in the main text.] The calculated $\langle n_c\rangle$ is equivalent to the mean input control photon number at the input of a fully impedance-matched cavity during the 2-μs storage time.

Stored Signal Photon Number.

The stored signal photon number $\langle n_s\rangle$ is similarly derived from the mean detected signal photon number, corrected for the detection efficiency (0.45), fiber collection efficiency (0.7), and filter etalon transmission (0.8). The measured signal phase is independent of the stored signal photon number, as shown in Fig. S1.

Conditional Phase Shift from a Coherent State

The equally weighted total conditional signal phase shift is given by the following:

$$\varphi \left(t\right)=\text{Arg}\left[{\displaystyle \sum _{m}P\left(m|n\right)e^{m\varphi }}\right],$$ [S3]

where ϕ is the phase shift of a single cavity photon induced on the signal light and $P\left(m|n\right)$ is probability of having m photons conditioning on detecting n photons given by the following (20):

$$P\left(m|n_c\right)=\left(\begin{array}{c}m+n_{bg}\\ n\end{array}\right){\mathit{ϵ}}_d^n{\left(1-{\mathit{ϵ}}_d\right)}^{n_{bg}+m-n}P\left(m\right),$$ [S4]

where the background counts $n_{bg}=R_{b}t$ with detected background rate $R_b$ and conditioning time window t, ${\mathit{ϵ}}_d$ is the detection efficiency of the conditioning path, and $P\left(m\right)$ is the probability for m photons to be observed in a given coherent state.

Conditional Cross-Phase Modulation

To calculate the conditional phase shift, we diagonalize the system Hamiltonian approximately given by the following:

$$\frac{\widehat{H}}{\hslash }={\omega }_a\widehat{S}+{\omega }_c{\widehat{c}}^{\mathrm{†}}\widehat{c}+\mathrm{\Omega }{\widehat{c}}^{\mathrm{†}}\widehat{c}\widehat{S}+{\displaystyle \int d\omega \hspace{0.17em}\omega \left({\widehat{b}}_{\omega }^{\mathrm{†}}{\widehat{b}}_{\omega }+{\widehat{d}}_{\omega }^{\mathrm{†}}{\widehat{d}}_{\omega }\right)}+i\sqrt{\frac{{\kappa }_0}{4\pi }}{\displaystyle \int d\omega \left\{\left[{\widehat{b}}_{\omega }^{\mathrm{†}}\widehat{c}-{\widehat{c}}^{\mathrm{†}}{\widehat{b}}_{\omega }\right]+\left[{\widehat{d}}_{\omega }^{\mathrm{†}}\widehat{c}-{\widehat{c}}^{\mathrm{†}}{\widehat{d}}_{\omega }\right]\right\}},$$ [S5]

where ${\omega }_a$ and ${\omega }_c$ are frequencies of the atomic spin ($\widehat{S}=|d\rangle \langle d|-|g\rangle \langle g|$) and intracavity optical field ($\widehat{c}$), respectively. By adiabatically eliminating the excited state, we define the effective atom-light coupling strength, $\mathrm{\Omega }=g^2\mathrm{\Delta }/\left({\mathrm{\Delta }}^2+{\left(\mathrm{\Gamma }/2\right)}^2\right)$, with one-photon detuning $\mathrm{\Delta }$, single-photon Rabi frequency $2g$, and excited-state decay rate of $\mathrm{\Gamma }$. The last two terms of the Hamiltonian account for energy and multimode coupling of input (or reflected) and transmitted light represented by modes ${\widehat{b}}_{\omega }$ and ${\widehat{d}}_{\omega }$, respectively. To diagonalize the Hamiltonian, we follow ref. 35 and define the following operators:

$${\widehat{a}}_{\omega }=\frac{1}{{\left(\omega -{\omega }_c-\mathrm{\Omega }\widehat{S}\right)}^2+{\left({\kappa }_0/2\right)}^2}[i\sqrt{\frac{{\kappa }_0}{2\pi }}{\widehat{c}}^{\mathrm{†}}+\frac{{\kappa }_0}{2\sqrt{2\pi }}{\widehat{c}}^{\mathrm{†}}{\displaystyle \int \widehat{d}\omega \prime \frac{{\widehat{b}}_{\omega }^{\mathrm{†}}+{\widehat{d}}_{\omega }^{\mathrm{†}}}{\omega -\omega \prime }+\frac{1}{\sqrt{2}}\left(\omega -{\omega }_c-\mathrm{\Omega }\widehat{S}\right)\left({\widehat{b}}_{\omega }^{\mathrm{†}}+{\widehat{d}}_{\omega }^{\mathrm{†}}\right)]},$$ [S6]

$${\widehat{\overline{a}}}_{\omega }=\frac{1}{\sqrt{2}}\left(-{\widehat{b}}_{\omega }^{\mathrm{†}}+{\widehat{d}}_{\omega }^{\mathrm{†}}\right),$$ [S7]

to rewrite the Hamiltonian as follows:

$$\frac{\widehat{H}}{\hslash }={\omega }_a\widehat{S}+{\displaystyle \int d\omega \hspace{0.17em}\omega \left({\widehat{a}}_{\omega }^{\mathrm{†}}{\widehat{a}}_{\omega }+{\widehat{\overline{a}}}_{\omega }^{\mathrm{†}}{\widehat{\overline{a}}}_{\omega }\right)}.$$ [S8]

Note that these operators have the following commutation relation:

$$\left[{\widehat{a}}_{\omega },{\widehat{a}}_{\omega \prime }^{\mathrm{†}}\right]=\delta \left(\omega -\omega \prime \right),$$ [S9]

$$\left[{\widehat{\overline{a}}}_{\omega },{\widehat{\overline{a}}}_{\omega \prime }^{\mathrm{†}}\right]=\delta \left(\omega -\omega \prime \right),$$ [S10]

$$\left[{\widehat{a}}_{\omega },{\widehat{\overline{a}}}_{\omega \prime }^{\mathrm{†}}\right]=0.$$ [S11]

For transmitted cavity light, the final state of the system after an interaction time of t:

$$|\mathrm{\Psi }\rangle =e^{-i(m\mathrm{\Phi }+{\omega }_{a}t\widehat{S})}|{\mathrm{\Psi }}_a\rangle \otimes \frac{1}{\sqrt{m!}}{\left[{\displaystyle \int d\omega B\left(\omega \right){\widehat{d}}_{\omega }^{\mathrm{†}}}\right]}^m|0\rangle ,$$ [S12]

where $|{\mathrm{\Psi }}_a\rangle$ and $|0\rangle$ are field eigenstates, $B\left(\mathit{\omega }\right)$ is the pulse amplitude spectrum, and m is the photon number. The phase $\mathrm{\Phi }=\text{arctan}\left(\left(2{\delta }_c/\kappa \right)+\mathit{\varphi }\right)$ and

$$\mathit{\varphi }\mathrm{=}\frac{\eta }{2}\text{Re}\left[\chi \right]\frac{{\kappa }_0}{\kappa },$$ [S13]

$$\mathit{\kappa }={\kappa }_0\left(1+\eta \text{Im}\left[\chi \right]\right),$$ [S14]

$$\mathit{\chi }=\left(\frac{2\mathrm{\Delta }}{\mathrm{\Gamma }}+i\right)/\left(1+{\left(\frac{2\mathrm{\Delta }}{\mathrm{\Gamma }}\right)}^2\right).$$ [S15]

Here, ${\kappa }_0\mathrm{=}2\pi \times 150$ kHz is the measured empty-cavity linewidth, $2g=2\pi \times 1.6$ MHz is the single-photon Rabi frequency, and $\mathrm{\Gamma }=2\pi \times 5.2$ MHz is the excited-state decay rate. Using Eq. S13, the conditional phase shift between a single cavity photon and one stored atomic excitation can then be written as follows:

$$\mathrm{\Phi }=\text{arctan}\left(\frac{2{\delta }_c}{\kappa }+\frac{\eta }{2}\frac{\text{Re}\left[\chi \right]}{1+\eta \text{Im}\left[\chi \right]}\right)-\text{arctan}\left(\frac{2{\delta }_c}{{\kappa }_0}\right),$$ [S16]

where ${\delta }_c=\omega -{\omega }_c$ is detuning of light from empty cavity resonance. In the limit of small detuning ${\delta }_c/\kappa \ll 1$, the conditional phase shift is approximately given by the following:

$$\mathrm{\Phi }\simeq \mathit{\varphi }=\frac{\eta }{2}\frac{\text{Re}\left[\chi \right]}{1+\eta \text{Im}\left[\chi \right]}.$$ [S17]

Conditional Control Phase Shift

In the main text, we focus on the phase shift measurement of the stored atomic excitation due to its interaction with a control photon. The control light also undergoes a phase shift. This phase shift is the result of shift in cavity resonance frequency imposed by atoms in the cavity mode. To measure the phase shift on the control light, we linearly polarize the input control light and measure its conditional polarization rotation.

The effective cooperativity of the ${\sigma }^{-}$-polarized light is reduced by a factor of 45 compared with ${\sigma }^{+}$-polarized light and detuned by 8 MHz from $|F=4,m_f=4\rangle \to |F\prime =5,m_f=3\rangle$ transition when ${\sigma }^{+}$ light is resonant with $|F=4,m_f=4\rangle \to |F\prime =5,m_f=5\rangle$ transition. The interaction of linearly polarized light then predominantly the interaction of the ${\sigma }^{+}$ polarization component. Therefore, we can measure the phase shift on ${\sigma }^{+}$ light as a polarization rotation on the outgoing control light. This polarization rotation is measured using two photon counters placed at the two ports of a polarizing beam splitter (PBS) after the cavity. By rotating the polarization before the PBS by 45° and subtracting the two photon-count rates, $d_1$ and $d_2$, a signal proportional to $\sin \left(\psi \right)$ is obtained as $\left(d_1-d_2\right)/\left(d_1+d_2\right)=\left(2\sqrt{B}/\left(1+B\right)\right)\sin \left(\psi \right)$. Here, B is the blocking factor that accounts for different transmission of ${\sigma }^{+}$ and ${\sigma }^{-}$ components of light. In presence of a stored signal photon, the transmission on cavity resonance for ${\sigma }^{+}$-polarized light is reduced by this factor $B\simeq {\left(1+\eta \text{Im}\left[\chi \right]\right)}^2+{\left(\eta \text{Re}\left[\chi \right]\right)}^2$ compared with the ${\sigma }^{-}$ transmission. We separately measure B (Fig. S2, Inset) by detecting the cavity transmission for each circular polarization conditioned on retrieving a signal photon. This measured blocking factor allows us to extract the cavity phase shift (Fig. S2). We attribute the asymmetry in the shape of the phase shift as a function of detuning plotted in Fig. 2B to nonzero detuning of light from the cavity. The solid line is the theoretical expectation (Eq. S16) assuming a light-cavity detuning ${\delta }_c=0$ kHz. As the sign of the frequency shift in the cavity resonance conditioned on detecting one recovered signal photon changes with the sign of light-atom detuning $\mathrm{\Delta }$, having a nonzero ${\delta }_c$ results in total shift of the cavity resonance that is different in magnitude for positive and negative detuning $\mathrm{\Delta }$. This causes an asymmetry in the phase shift as a function of $\mathrm{\Delta }$ (Fig. 2B). This change with light-atom detuning can be understood as a different interaction time: the lifetime of cavity photons effectively reduces with detuning of light from the cavity resonance.

Reconstruction of Density Matrix

Based on the density matrix reconstruction provided by James et al. (36) for polarization-entangled photons, we developed a method to reconstruct the full density matrix of a number-polarization entangled state $|\mathrm{\Psi }\rangle$ by measuring coincidences in the $|0_s\rangle$ and $|1_s\rangle$ signal photon basis and the $|0_c\rangle$ and $|1_c\rangle$ control polarization basis, where we use the 0 and 1 number representation for zero and one signal photon, and $0_c$ and $1_c$ to indicate different circularly polarized control photons, that is, $0_c\leftrightarrow {\sigma }^{-}$ and $1_c\leftrightarrow {\sigma }^{+}$. Coherently interfering the signal state with a phase reference allows us to measure the signal state in an arbitrary superposition $|0_s\rangle +e^{i{\theta }_s}|1_s\rangle$. To project the control light into the desired state, $|0_c\rangle +e^{i{\theta }_c}|1_c\rangle$, we use a half-wave plate (HWP) and quarter-wave plate (QWP) after the cavity followed by a PBS. The phases ${\theta }_s$ and ${\theta }_c$ can be chosen for each measurement by changing phase of the signal reference light and polarization of the control light after the cavity, respectively. However, the auxiliary optical phase reference adds a complication: as this reference light is not part of the signal photon state and adds photons to the detected field, we need to normalize out its contribution to the measured coincidences to ensure the reconstructed density matrix is independent of the reference light intensity.

Coincidence Measurements.

In total, 16 coincidence measurements are required to reconstruct the complete density matrix. To arrive at the derived coincidences for the output number-polarization state, we measure the raw coincidences, normalize, and then reconstruct coincidences for $|\mathrm{\Psi }\rangle$.

Measure raw coincidences.

The tomographic states equivalent to ref. 36 for coincidences $n_{\nu }\left(\nu =\mathrm{1,2},\mathrm{..16}\right)$ are listed for signal and control modes in Table S1.

In our experiment, these tomographic states are obtained through interference measurements of the signal with an optical phase reference and polarization measurement of the control light. For the signal path, the phase reference light is a frequency-shifted beam copropagating with the signal. This light mixes on the detector to form a beat note with a period of about 33 ns. All relative phase angles ${\theta }_s$ are measured in a single dataset. For the control path, we linearly polarize the input cavity light so that the phase between control light (the ${\sigma }^{+}$-polarized component) and its reference (${\sigma }^{-}$-polarized component) appears as a polarization rotation at the cavity output. We use a HWP, QWP, and a polarizing beam splitter to analyze the output at different projection angles ${\theta }_c$.

We measure the raw coincidences $n_{\nu }\left(\nu =\mathrm{1,2},\mathrm{..16}\right)$ on a pair of single-photon counters. Measuring in four configurations, we measure all 16 tomographic states as follows:

• • Coincidences for $\nu =1-4$ are measured without signal phase reference, whereas control light is measured in ${\sigma }^{+}$ or ${\sigma }^{-}$ polarization. The coincidences are then extracted from these measurements. For example, $n_3$ is the number of times that a signal photon (without reference) and a ${\sigma }^{+}$-polarized control photon are simultaneously detected, and $n_1$ is number of coincidences where no signal photon (without reference) and a ${\sigma }^{-}$-polarized control photon are detected.

• • Coincidences for $\nu =5-8$ are measured with a phase reference light in the signal mode. To reconstruct interference fringes, signal photons are conditioned on the detection of a ${\sigma }^{-}$ or ${\sigma }^{+}$ control photon. The resulting coincidence counts form a beat note. The coincidence counts $n_{\nu }$ are then the number of coincidences at the phase ${\theta }_s$, which we extract from a fit to the counts at all phases. Detector counts on the signal path at ${\theta }_s=0\hspace{0.17em}\left(3\pi /2\right)$ corresponds to projecting the $|\mathrm{\Psi }\rangle$ to $|0_s\rangle +|1_s\rangle$ ($|0_s\rangle -i|1_s\rangle$). To be concrete, $n_6$ is the number of coincidences with a ${\sigma }^{+}$ photons detected on the control at ${\theta }_s=3\pi /2$ and corresponds to a tomographic measurement onto signal state $|0_s\rangle -i|1_s\rangle$ and control state $|1_c\rangle$.

• • Coincidences for $\nu =12-15$ are measured with no signal reference, whereas the control light is projected into different superposition state of ${\sigma }^{-}$ and ${\sigma }^{+}$-polarized light. The HWP and QWP placed after the cavity and before a PBS followed by a single-photon detector, set the measurement basis and thus the relative phase angle ${\theta }_c$. The coincidence count $n_{14}$, for example, is the number of times one photon is detected in the signal path and one photon is detected on the control path with the analysis HWP at $\pi /8$, which corresponds to a relative phase ${\theta }_c=\pi /2$ between ${\sigma }^{-}$ and ${\sigma }^{+}$-polarized light. This is a tomographic measurement onto the signal state $|1_s\rangle$ and control state $|0_c\rangle +i|1_c\rangle$.

• • Coincidences for $\nu =9-11$ and $\nu =16$ are measured with signal phase reference, whereas control light is projected into different superposition state of ${\sigma }^{-}$ and ${\sigma }^{+}$-polarized light. These elements are determined as for $\nu =5-8$: detected signal photons are conditioned on detecting one control photon (now at a relative phase angle ${\theta }_c$), and the coincidence counts $n_{\nu }$ are the number of coincidences at phase ${\theta }_s$.

Normalizing coincidences.

The coincidences for $\nu =\mathrm{5,6},\mathrm{\dots },16$ are measured using signal phase reference that needs to be normalized out. To do this, we calculate the interference parameter ${\mathrm{ℐ}}_{\nu }$ which takes on values between −1 and 1. On the signal path, the interference parameter is just $\vartheta \cos \theta$, that is, the value of a zero-centered interference fringe with contrast ϑ and a phase difference of θ.

To obtain ${\mathrm{ℐ}}_{\nu }$, we make two additional measurements. We measure the signal and signal phase reference beat note with input light on the signal path only (no control light), as well as the linearly polarized control without signal light at different HWP angles to reconstruct a complete fringe. This measures the contrast in the absence of interactions. We then calculate $\mathrm{ℐ}$ as follows:

• 1. We subtract the averaged value of the raw coincidences (coincidence number averaged over all signal phases or angles of the HWP in the control path) from $n_{\nu }$ ($\nu =5,\mathrm{\dots },16$).

• 2. We divide the coincidence number by the total number of detected counts in the conditioning port.

• 3. We finally divide through by the fringe amplitude measured in our additional measurements without interaction to correct for nonunity contrast without interactions, for example, due to power imbalance between the signal and phase reference.

Reconstruct coincidences.

The values of ${\mathrm{ℐ}}_{\nu }$ together with $n_{\nu }\left(\nu =\mathrm{1,2,3,4}\right)$ are used to reconstruct the coincidence numbers for $|\mathrm{\Psi }\rangle$ alone for all 16 tomographic measurements. We first rescale coincidences $n_{\nu }\left(\nu =\mathrm{1,2,3,4}\right)$ to correct for detection losses, ${\mathit{ϵ}}_d$. The efficiency ${\mathit{ϵ}}_d\simeq 0.2$ for both signal and control modes. Projecting the general output state $|\mathrm{\Psi }\rangle =p_{00}|0_s{0}_c\rangle +p_{01}{e}^{i{\varphi }_{01}}|0_s{1}_c\rangle +p_{10}{e}^{i{\varphi }_{10}}|1_s{0}_c\rangle +p_{11}{e}^{i{\varphi }_{11}}|1_s{1}_c\rangle$ (with probability amplitudes $p_{ij}$ and phase shift ${\varphi }_{ij}$) to the relevant tomographic state for each $\nu =5,\mathrm{\dots },16$ allows us to evaluate coincidences in terms of $\mathrm{ℐ}$ and $n_{\nu }\left(\nu =\mathrm{1,2,3,4}\right)$. For example, to reconstruct $n_5$, we project $|\mathrm{\Psi }\rangle$ onto $\left(|0_s\rangle +e^{i{\theta }_s}|1_s\rangle \right)|0_c\rangle$. The expectation value for this parameter is then as follows:

$$\begin{array}{c}\langle n_5\rangle ={\left|\langle \psi |\mathrm{\Psi }\rangle \right|}^2=p_{00}^2+p_{10}^2+2p_{00}{p}_{10}{ℐ}_5,\end{array}$$ [S18]

where ${\mathrm{ℐ}}_5$ is the corresponding interference parameter which accounts for the visibility ϑ, the relative phase angle θ_s=3π/2 and ϕ₁₀. Repeating this for each $n_{\nu }\left(\nu =5,\mathrm{\dots },16\right)$, and expressing total coincidences in terms of $\mathrm{ℐ}$ and $n_{\nu }\left(\nu =\mathrm{1,2,3,4}\right)$, we find the following:

$$n_5=\frac{n_1+n_4}{2}+\sqrt{n_1{n}_4}{\mathrm{ℐ}}_5,$$ [S19]

$$n_6=\frac{n_2+n_3}{2}+\sqrt{n_2{n}_3}{\mathrm{ℐ}}_6,$$ [S20]

$$n_6=\frac{n_2+n_3}{2}+\sqrt{n_2{n}_3}{\mathrm{ℐ}}_7,$$ [S21]

$$n_8=\frac{n_1+n_4}{2}+\sqrt{n_1{n}_4}{\mathrm{ℐ}}_8,$$ [S22]

$$\begin{array}{c}{n}_9=\frac{n_1+n_2+n_3+n_4}{4}+\\ \frac{1}{2}\sqrt{{\left(\sqrt{n_1{n}_4}+\sqrt{n_2{n}_3}\right)}^2+{\left(\sqrt{n_2{n}_4}-\sqrt{n_1{n}_3}\right)}^2}{\mathrm{ℐ}}_9,\end{array}$$ [S23]

$$\begin{array}{c}{n}_{10}=\frac{n_1+n_2+n_3+n_4+2\sqrt{n_1{n}_2}+2\sqrt{n_3{n}_4}}{4}+\frac{1}{2}\left(\sqrt{n_1}+\sqrt{n_2}\right)\left(\sqrt{n_3}+\sqrt{n_4}\right){\mathrm{ℐ}}_{10},\end{array}$$ [S24]

$$\begin{array}{c}{n}_{11}=\frac{n_1+n_2+n_3+n_4+2\sqrt{n_1{n}_2}+2\sqrt{n_3{n}_4}}{4}+\frac{1}{2}\left(\sqrt{n_1}+\sqrt{n_2}\right)\left(\sqrt{n_3}+\sqrt{n_4}\right){\mathrm{ℐ}}_{11},\end{array}$$ [S25]

$$n_{12}=\frac{n_1+n_2}{2}+\sqrt{n_1{n}_2}{\mathrm{ℐ}}_{12},$$ [S26]

$$n_{13}=\frac{n_3+n_4}{2}+\sqrt{n_3{n}_4}{\mathrm{ℐ}}_{13},$$ [S27]

$$n_{14}=\frac{n_3+n_4}{2}+\sqrt{n_3{n}_4}{\mathrm{ℐ}}_{14},$$ [S28]

$$n_{15}=\frac{n_1+n_2}{2}+\sqrt{n_1{n}_2}{\mathrm{ℐ}}_{15},$$ [S29]

$$\begin{array}{c}{n}_{16}=\frac{n_1+n_2+n_3+n_4}{4}+\frac{1}{2}\sqrt{{\left(\sqrt{n_1{n}_4}+\sqrt{n_2{n}_3}\right)}^2+{\left(\sqrt{n_2{n}_4}-\sqrt{n_1{n}_3}\right)}^2}{\mathrm{ℐ}}_{16}.\end{array}$$ [S30]

Experimental Density Matrix.

The final coincidences can then be used to reconstruct the experimental density matrix following ref. 36:

$${\widehat{\rho }}_{ex}=\frac{{\displaystyle {\sum }_{\nu =1}^{16}{M}_{\nu }{n}_{\nu }}}{{\displaystyle {\sum }_{\nu =1}^4{n}_{\nu }}},$$ [S31]

where matrices ${\mathit{M}}_{\nu }$ in these bases are provided below. By doing so, we arrive at the following measured experimental density matrix:

$${\widehat{\rho }}_{ex}=\left(\begin{array}{cccc}0.6358& 0.4319-0.07635i& 0.1337-0.00026i& 0.00154-0.0222i\\ 0.4319+0.07635i& 0.3205& 0.1292-0.07199i& 0.0593-0.01282i\\ 0.1337+0.00026i& 0.1292+0.07199i& 0.02899& 0.0184-0.0084i\\ 0.00154+0.0222i& 0.0593+0.01282i& 0.0184+0.0084i& 0.0146\end{array}\right).$$

Reconstruction of the Physical Density Matrix.

To reconstruct the physical density matrix that most probably describes the measurement results, we use the maximum-likelihood (Maxlik) method as outlined in ref. 36. This requires finding minimum of the following function:

$$\begin{array}{l}\mathrm{ℒ}\left(t_1,t_2,\mathrm{\dots },t_{16}\right)={\displaystyle \sum _{\nu =1}^{16}\frac{{\left(\mathcal{N}\langle {\psi }_{\nu }|{\widehat{\rho }}_p\left(t_1,t_2,\mathrm{\dots },t_{16}\right)|{\psi }_{\nu }\rangle -n_{\nu }\right)}^2}{2\mathcal{N}{\sigma }_{\nu }^2}},\end{array}$$ [S32]

where

$${\widehat{\rho }}_p\left(t\right)=\frac{{\widehat{T}}^{\mathrm{†}}\widehat{T}}{\text{Tr}\left[{\widehat{\text{T}}}^{\mathrm{†}}\widehat{\text{T}}\right]},$$ [S33]

$$\widehat{T}=\left(\begin{array}{cccc}{t}_1& 0& 0& 0\\ t_5+i{t}_6& t_2& 0& 0\\ t_{11}+i{t}_{12}& t_7+i{t}_8& t_3& 0\\ t_{15}+i{t}_{16}& t_{13}+i{t}_{14}& t_9+i{t}_{10}& t_4\end{array}\right),$$ [S34]

$$\mathcal{N}={\displaystyle \sum _{n=1}^4{n}_{\nu }},$$ [S35]

and ${\sigma }_{\nu }$ is the SD for the νth coincidence measurement given approximately by $\sqrt{n_{\nu }}$ (Poisson noise). The initial estimation of $t_1,\mathrm{\dots }{t}_{16}$ is obtained using the inverse relationship by which elements of $\widehat{T}$ can be expressed in terms of elements of ${\widehat{\rho }}_{exp}$ (36). After the Maxlik reconstruction of the density matrix and subtracting the global phases, we obtain the following matrix:

$${\widehat{\rho }}_p=\left(\begin{array}{cccc}0.6315& 0.4174& 0.1375& 0.0495-0.0239i\\ 0.4174& 0.321224& 0.0996-0.0035i& 0.0527-0.0248i\\ 0.1375& 0.0996+0.0035i& 0.0319& 0.0153-0.0054i\\ 0.0495+0.0239i& 0.0527+0.0248i& 0.0153+0.0054i& 0.0154\end{array}\right),$$

where we calculate Tr$\left[{\rho }^2\right]=0.92$ as a measure of purity. The concurrence is evaluated as $C\left(\rho \right)=\text{max}\left(0,{\lambda }_1-{\lambda }_2-{\lambda }_3-{\lambda }_4\right)$, where ${\lambda }_i$ values are the square roots of the eigenvalues of $\rho \rho \prime$ in descending order, $\rho \prime =\left({\sigma }_y\otimes {\sigma }_y\right){\rho }^{\mathrm{\ast }}\left({\sigma }_y\otimes {\sigma }_y\right)$, and ${\sigma }_y$ is Pauli y matrix. We obtain a concurrence of $C=0.082\pm 0.005$ (statistical) $\pm 0.016$ (systematic) and nonlinear phase shift measured as ${\varphi }_{nl}=\text{Arg}\left({\rho }_p\left[\mathrm{1,4}\right]\right)=0.45\left(2\right)$ that agrees with the measured conditional phase shift. To estimate the statistical error in determining concurrence and phase, we randomly sample one-half of the data 100 times and reconstruct the density matrix each time and find the SD of the concurrence and phase calculations. Table S2 summarizes the various systematic uncertainties that go into our estimate of the concurrence.

Note that the maximum concurrence at this phase shift using the same coherent states as in our experiment is 0.11. In the case where input states are equal superposition of $|0_s\rangle$ and $|1_s\rangle$, a concurrence on the order of $\left|\sin \left(\varphi /2\right)\right|$ is ideally achievable (37).

The $M_{\nu }$ Matrices.

The $M_{\nu }$ matrices defined below are from ref. 36 with corrected typos in $M_2$ and $M_{14}$:

$$M_1=\frac{1}{2}\left(\begin{array}{cccc}\mathrm{2}& -\left(1-i\right)& -\left(1+i\right)& 1\\ -\left(1+i\right)& 0& i& 0\\ -\left(1-i\right)& -i& 0& 0\\ 1& 0& 0& 0\end{array}\right),$$

$$M_2=\frac{1}{2}\left(\begin{array}{cccc}0& -\left(1-i\right)& 0& 1\\ -\left(1+i\right)& 2& i& -\left(1+i\right)\\ 0& -i& 0& 0\\ 1& -\left(1-i\right)& 0& 0\end{array}\right),$$

$$M_3=\frac{1}{2}\left(\begin{array}{cccc}0& 0& 0& 1\\ 0& 0& i& -\left(1+i\right)\\ 0& -i& 0& -\left(1-i\right)\\ 1& -\left(1-i\right)& -\left(1+i\right)& 2\end{array}\right),$$

$$M_4=\frac{1}{2}\left(\begin{array}{cccc}0& 0& -\left(1+i\right)& 1\\ 0& 0& i& 0\\ -\left(1-i\right)& -i& 2& -\left(1-i\right)\\ 1& 0& -\left(1+i\right)& 0\end{array}\right),$$

$$M_5=\frac{1}{2}\left(\begin{array}{cccc}0& 0& 2i& -\left(1+i\right)\\ 0& 0& \left(1-i\right)& 0\\ -2i& \left(1+i\right)& 0& 0\\ -\left(1-i\right)& 0& 0& 0\end{array}\right),$$

$$M_6=\frac{1}{2}\left(\begin{array}{cccc}0& 0& 0& -\left(1+i\right)\\ 0& 0& \left(1-i\right)& 2i\\ 0& \left(1+i\right)& 0& 0\\ -\left(1-i\right)& -2i& 0& 0\end{array}\right),$$

$$M_7=\frac{1}{2}\left(\begin{array}{cccc}0& 0& 0& -\left(1+i\right)\\ 0& 0& -\left(1-i\right)& 2\\ 0& -\left(1+i\right)& 0& 0\\ -\left(1-i\right)& 2& 0& 0\end{array}\right),$$

$$M_8=\frac{1}{2}\left(\begin{array}{cccc}0& 0& 2& -\left(1+i\right)\\ 0& 0& -\left(1-i\right)& 0\\ 2& -\left(1+i\right)& 0& 0\\ -\left(1-i\right)& 0& 0& 0\end{array}\right),$$

$$M_9=\left(\begin{array}{cccc}0& 0& 0& i\\ 0& 0& -i& 0\\ 0& i& 0& 0\\ -i& 0& 0& 0\end{array}\right),$$

$$M_{10}=\left(\begin{array}{cccc}0& 0& 0& 1\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 1& 0& 0& 0\end{array}\right),$$

$$M_{11}=\left(\begin{array}{cccc}0& 0& 0& i\\ 0& 0& i& 0\\ 0& -i& 0& 0\\ -i& 0& 0& 0\end{array}\right),$$

$$M_{12}=\frac{1}{2}\left(\begin{array}{cccc}0& 2& 0& -\left(1+i\right)\\ 2& 0& -\left(1+i\right)& 0\\ 0& -\left(1-i\right)& 0& 0\\ -\left(1-i\right)& 0& 0& 0\end{array}\right),$$

$$M_{13}=\frac{1}{2}\left(\begin{array}{cccc}0& 0& 0& -\left(1+i\right)\\ 0& 0& -\left(1+i\right)& 0\\ 0& -\left(1-i\right)& 0& 2\\ -\left(1-i\right)& 0& 2& 0\end{array}\right),$$

$$M_{14}=\frac{1}{2}\left(\begin{array}{cccc}0& 0& 0& -\left(1-i\right)\\ 0& 0& \left(1-i\right)& 0\\ 0& \left(1+i\right)& 0& -2i\\ -\left(1+i\right)& 0& 2i& 0\end{array}\right),$$

$$M_{15}=\frac{1}{2}\left(\begin{array}{cccc}0& -2i& 0& -\left(1-i\right)\\ 2i& 0& \left(1-i\right)& 0\\ 0& \left(1+i\right)& 0& 0\\ -\left(1+i\right)& 0& 0& 0\end{array}\right),$$

$$M_{16}=\left(\begin{array}{cccc}0& 0& 0& 1\\ 0& 0& -1& 0\\ 0& -1& 0& 0\\ 1& 0& 0& 0\end{array}\right).$$ [S36]