Ultrasound (in)accuracy: it's in the formulae not in the technique – assessment of accuracy of abdominal circumference measurement in term pregnancies

Abstract

Introduction: Fetal abdominal circumference (AC) is utilised in calculations for the estimation of fetal weight (EFW) and has been proposed as a method of monitoring diabetic pregnancies. We evaluated true ultrasound accuracy by comparing fetal AC biometry with neonatal anthropometry and compared this with standard ultrasound estimations of fetal weight.

Methods: A prospective observational study was performed at a tertiary referral centre. Women who were having their confinement of a term, singleton gestation either by induction of labour or elective caesarean section from 2009–2011 were approached to participate. An ultrasound was performed within 24 hours of delivery measuring the biometric parameters of AC, head circumference (HC), biparietal diameter and femur length. Following delivery the AC, HC and birthweight were measured on the neonate.

Results: Fifty‐two patients were enrolled in the study with data collected from 50. Mean AC measurement was 35.1 ± 2.1 cm and birth weight was 3596 ± 517 g. A Bland‐Altman plot was used to compare the two AC measurements with the 95% limits of agreement ranging from −2.33–4.69 cm around a mean difference of 1.2 cm. Mean percentage error was 5.0% and 6.2% for the AC and HC measurements respectively, in comparison with percentage errors of 7.0–13.8% for estimation of fetal weight (EFW) from 27 formulae.

Conclusions: Sonographic AC measurement is accurate in term pregnancies, with a percentage error less than HC or EFW. Perceptions of ultrasound inaccuracy may relate to the application of formulae rather than the ultrasound technique itself. Fetal surveillance using serial AC measurement has been proposed, in particular monitoring of diabetic pregnancies and in such a group AC may be easier and faster to obtain and more meaningful than EFW.

Introduction

Fetal abdominal circumference (AC) is a measurement widely used in obstetric antenatal care. The AC measurement was described in 1975 and is taken at the level of the widest part of the fetal abdomen, across the liver. ¹ The transverse section includes the fetal stomach, spine and deep portion of the umbilical vein. It is a major component of the formulae used to estimate fetal weight antenatally. ¹ The measurement also provides important information for growth restriction (the fetal liver is one of the first organs to be affected), ² and for macrosomia in diabetes (where the AC measurement is proportionally larger when compared to the other measurements of growth). ^{3 – 5} In twin pregnancies the AC has been used to determine fetal growth discordance at a range of gestations. ⁶

Proposed applications for sonographic AC measurement include surveillance in diabetic pregnancies to identify those patients who require close diabetic control. ⁷ It has also been shown that fetal asymmetry (abdominal vs. biparietal diameter) can be used in the prediction of shoulder dystocia ⁸ which may be helpful in planning mode of delivery and intrapartum management.

Despite identifying 238 papers over the last 30 years correlating estimated fetal with actual neonatal weight, we could identify no paper in this time period that compared fetal ultrasound biometry with actual anthropometry. This true measure of accuracy has thus been ignored in the recent literature. This study aimed to show that sonographic measurement of fetal AC was accurate when compared to the neonatal AC measurement.

Methods

A prospective observational study was conducted at the Royal Hospital for Women, Sydney, Australia between 2009 and 2011. The study received approval from the institutional scientific and ethics committees (HREC ref 08/218).

Women were invited to participate in the study at the time of admission for induction of labour or routine elective caesarean section. Eligibility criteria included adult women at term gestation (≥ 37 weeks) with a singleton pregnancy. Women of any parity were included. Study participants were consented following the receipt of written information and had the opportunity to ask study‐related questions of the investigator.

Exclusion criteria included preterm gestation, complications of intrauterine growth restriction (known EFW < 10th centile), oligohydramnios, multiple gestation, known fetal anomalies, spontaneous rupture of membranes, or if the subjects were in active labour. Women who were unable to comprehend written and spoken English were also excluded.

Participating women had brief interview and antenatal history taken and their antenatal file consulted to ensure compliance with the eligibility criteria. An ultrasound was performed by the study investigator within 24 hours prior to delivery or after commencement of cervical ripening for induction of labour. The ultrasound measurements included AC, head circumference (HC), biparietal diameter (BPD), and femur length (FL). The results of these measurements were blinded to the patient and the other members of the research team. The AC measurement was taken using the standard ultrasound criteria at the level of the widest part of the fetal abdomen, across the liver, including the fetal stomach, spine and deep portion of the umbilical vein in transverse section as described by Campbell. ¹ (Figure 1).

Figure 1.

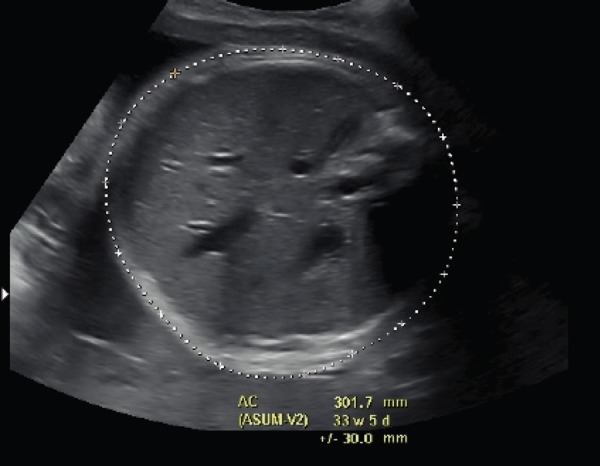
AC measurement including the fetal spine, stomach and umbilical vein.

Measurements were taken in the absence of active breathing movement. Three sequential measurements were recorded for each variable. The AC measurement was performed using the tracing rather than the elliptical method, due to the irregularities created by fetal limbs in the third trimester. The ultrasound was performed using a single machine (Voluson 730E, GE Medical Systems Zipf, Austria) and operator (ENH) to ensure consistency between subjects.

Within 24 hours of delivery, measurements of the neonatal AC were performed by a second investigator, who was blinded to the ultrasound results. The measurement was performed at the level of the liver, approximately 2–2.5 cm above the umbilicus using a measuring tape. Three individual measurements were taken and the results averaged. The time of birth, birth weight and HC taken at the time of delivery were also recorded for each baby.

Statistical analyses were performed using SPSS 20.0 (SPSS Inc, Chicago, IL, USA). Data were presented in mean and standard deviation, median and range or interquartile range as appropriate. The difference between the ultrasound measurement of AC and the neonatal measurements were calculated using the following formula for percentage error where percentage error = (ultrasound AC – neonatal AC)/neonatal AC × 100. This calculation was also applied to the pre‐ and post‐natal measurement of HC and the actual birth weight and each of 27 estimated fetal weight formulae (Table 1). ^{1 , 9 – 21} Paired t‐tests were used to compare the percentage error for each measurement. Intra‐class correlations were performed on the ultrasound measurements to ensure reliability of data. A Bland‐Altman assessment of agreement was used to compare the two measurements. A range of agreement was defined as mean bias ± 1.96SD. ²² In order to show agreement with a 95% CI of 0.5s (where s is the standard deviation of the differences between the measurements) a sample size of 48 was calculated.

Table 1.

Ultrasonic fetal biometric formulae for estimating fetal weight.

Formula	Year	Regression equation
Hadlock 1 16	1985	Log10EFW = 1.3596 − 0.00386 AC × FL + 0.0064 HC + 0.00061 BPD × AC + 0.0424 AC ൻ 0.174 FL
Hadlock 2 16	1985	Log10EFW = 1.304 + 0.05281 AC + 0.1938 FL − 0.004 AC × FL
Hadlock 3 16	1985	Log10EFW = 1.335 − 0.0034 AC × FL + 0.0316 BPD + 0.0457 AC + 0.1623 FL
Hadlock 4 16	1985	Log10EFW = 1.325 − 0.00326 AC × FL + 0.0107 HC + 0.0438 AC + 0.158 FL
Hadlock 5 15	1984	Log10EFW = 1.5662 − 0.0108 HC + 0.0468 AC + 0.171 FL + 0.00034 HC2 − 0.003685 AC × FL
Hadlock 6 15	1984	LogeEFW = 2.695 + 0.253 AC − 0.00275 AC2
Hadlock 7 15	1984	Log10EFW = 1.1134 + 0.05845 AC − 0.000604 AC2 − 0.007365 BPD2 + 0.000595 BPD × AC + 0.1694 BPD
Hadlock 8 15	1984	Log10EFW = 1.182 + 0.0273 HC + 0.07057 AC − 0.00063 AC2 − 0.0002184 HC × AC
Merz 10	1988	EFW = −3200.40479 + 157.07186 AC + 15.90391 BPD2
Warsof 1 20	1977	Log10EFW = −1.599 + 0.144 BPD + 0.032 AC − 0.111(BPD2 × AC)/1000
Warsof 2 20	1977	Log10EFW = −1.8367 + 0.092 AC − 0.000019 AC3
Shephard 19	1982	Log10EFW = −1.7492 + 0.166 BPD + 0.046 AC − 2.646(AC × BPD)/1000
Campbell 1	1975	LogeEFW = −4.564 + 0.282 AC − 0.00331 AC2
Higginbottom 9	1975	EFW = 0.0816 AC3
Jordaan 1 11	1983	Log10EFW = 0.6328 + 0.1881 AC − 0.0043 AC2 + 0.000036239 AC3
Jordaan 2 11	1983	Log10EFW = −1.1683 + 0.0377 AC + 0.0950 BPD − 0.0015 BPD × AC
Jordaan 3 11	1983	Log10EFW = 0.9119 + 0.0488 HC + 0.0824 AC − 0.001599 HC × AC
Jordaan 4 11	1983	Log10EFW = 2.3231 + 0.02904 AC + 0.0079 HC − 0.0058 BPD
Woo 1 12	1985	Log10EFW = 0.59 + 0.08 AC + 0.28 FL − 0.00716 AC × FL
Woo 2 12	1985	Log10EFW = 1.63 + 0.16 BPD + 0.00111 AC2 − 0.0000859 BPD AC2
Woo 3 12	1985	Log10EFW = 1.54 + 0.15 BPD + 0.00111 AC2 − 0.0000764 BPD × AC2 + 0.05 FL − 0.000992 FL × AC
Vintzelios 14	1987	Log10EFW = 1.879 + 0.084 BPD + 0.026 AC
Hsieh 1 18	1987	Log10EFW = 2.1315 + 0.0056541 AC × BPD − 0.00015515 BPD AC2 + 0.000019782 AC3 + 0.052594
Hsieh 2 18	1987	Log10EFW = 2.7193 + 0.0094962 AC × BPD − 0.1432 FL − 0.00076742 AC × BPD2 + 0.001745 FL × BPD2
Shinozuka 17	1987	Log10EFW = 0.23966 AC2 × FL + 1.6230 BPD3
Ott 13	1986	Log10EFW = −2.0661 + 0.04355 HC + 0.05394 AC − 0.0008582 HC × AC + 1.2594 FL/AC
Combs 21	1993	EFW = 0.23718 AC2 × FL + 0.03312 HC3

Results

Fifty‐two women, aged 19 to 49 were recruited to the study. Neonatal data was incomplete for two study participants who were not present for or did not agree to AC measurement post‐natally. These participants were excluded and data was collected from 50 patients. Patient demographics are outlined in Table 2. Presence or absence of diabetes and the type of diabetes was recorded. Of the 50 participants, nine women had gestational diabetes. There were no cases of pre‐existing diabetes in the cohort. The mean AC measurement was 35.1 ± 2.1 cm, mean HC was 33.1 ± 1.5 cm, BPD 9.3 ± 0.4 cm and FL 7.3 ± 0.3 cm. The mean birth weight was 3596 ± 517 g.

Table 2.

Demographic data.

	Participants (n = 52)
Age (y)	32 (26–38)
Parity	1 (0–2)
Gestation (weeks)	39.5 (38.2–40.6)
Height (cm)	163 (155–171)
Weight (kg)	65 (51–79)
BMI (kg/m2)	24 (19–29)
Gestational diabetes	9 (17%)

Intraclass correlation coefficients (ICC) were performed for each of the three measurements for each ultrasound study variable. The results for all measurements showed high reliability with AC ICC 0.94 (95% CI 0.90–0.96), HC ICC 0.90 (95% CI 0.85–0.94), BPD ICC 0.89 (95% CI 0.84–0.93) and FL 0.83 (95% CI 0.75–.089).

Percentage error was determined for the ultrasound versus neonatal measurements of AC and HC. Mean percentage error was 5.0% (± 3.2%) for AC and 6.2% (± 3.7%) for HC. The mean percentage errors for the EFW formulae are shown in Figure 2 and Table 3 and range from 7.1 to 13.8%. When compared with birth weight, 12/27 EFW formulae were not significantly different (Table 3). The most commonly used formula for EFW (Hadlock 5) ¹⁵ showed a percentage error of 9.2% (± 7.2%). Interestingly, it was one of the formulae that was found to be significantly different to the birth weight on paired t‐test.

Figure 2.

Percentage accuracy and standard deviation of each of 27 EFW formulae compared with AC and HC measurements.

Table 3.

Percentage differences of EFW formulae vs. actual birth weight.

	Formula	Percentage difference	Regression	T‐test
		Mean SD	Min‐Max	R	P value
1	Hadlock 1	7.6 6.3	0.0–31.4	.802	.011∗
2	Hadlock 2	7.9 6.5	0.0–24.7	.764	.192
3	Hadlock 3	7.2 6.1	0.1–30.7	.798	.141
4	Hadlock 4	8.3 6.7	0.0–29.0	.793	.001∗
5	Hadlock 5	9.2 7.2	0.4–31.5	.789	< .001∗
6	Hadlock 6	7.7 6.3	0.2–24.8	.745	.597
7	Hadlock 7	7.2 6.1	0.7–36.0	.782	.630
8	Hadlock 8	9.0 7.2	0.1–32.9	.767	< .001∗
9	Merz	7.0 5.7	0.0–27.0	.785	.049∗
10	Warsof 1	9.5 8.5	0.2–48.7	.779	< .001∗
11	Warsof 2	7.8 5.9	0.1–20.0	.729	.216
12	Shephard	7.6 7.0	0.3–42.0	.779	.234
13	Campbell	8.3 6.7	0.1–27.1	.741	.013∗
14	Higginbottom	9.4 8.4	0.2–30.5	.741	.536
15	Jordaan 1	13.8 9.4	0.0–39.4	.746	< .001∗
16	Jordaan 2	7.4 6.2	0.2–34.8	.778	.477
17	Jordaan 3	8.7 6.4	0.9–24.6	.683	.349
18	Jordaan 4	8.1 6.7	0.0–26.7	.757	.808
19	Woo 1	12.3 7.1	0.7–27.2	.755	< .001∗
20	Woo 2	13.8 9.7	1.1–53.2	.786	< .001∗
21	Woo 3	7.6 6.9	0.1–40.2	.795	.007∗
22	Vintzelios	8.9 7.4	0.2–36.0	.770	.003∗
23	Hsieh 1	7.7 7.0	0.0–40.4	.788	.292
24	Hsieh 2	7.4 7.3	0.2–43.9	.795	.074
25	Shinozuka	7.1 6.4	0.3–36.4	.813	.004∗
26	Ott	8.3 6.6	0.3–30.4	.796	< .001∗
27	Combs	9.7 7.4	0.3–34.2	.795	< .001∗

On comparison of the mean percentage errors for the ultrasound AC and the EFW formulae, the mean error of the AC measurement on ultrasound was significantly closer to zero than all but two of the EFW formulae, the latter (Hsieh 2 ¹⁸ and Shinozuka ¹⁷ ) being rarely used in clinical practice (Figure 2).

The Bland‐Altman analysis indicates that the 95% limit of agreement of the pre‐ and post‐natal AC measurements ranged from −2.33 to 4.69 around the mean of 1.18cm (Figure 3).

Figure 3.

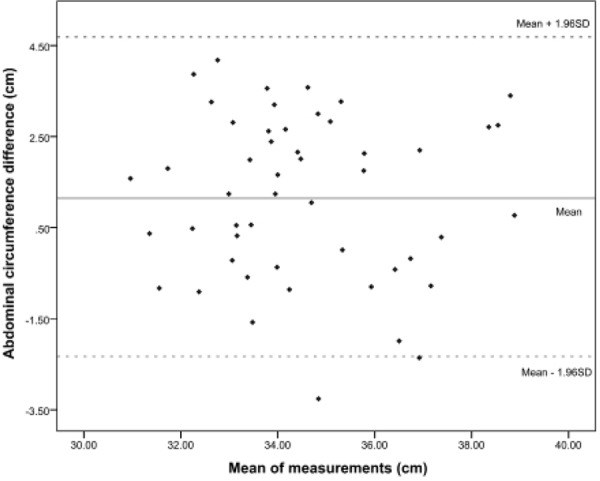
Bland‐Altman plot.

Discussion

Since the introduction of diagnostic ultrasound for the estimation of fetal biometry in the 1970s, the AC measurement has been recognised as a major predictor of the EFW and is therefore one of the main components in most calculations. ^{1 , 23 , 24} This has lead to the suggestion of the AC as a standalone predictor of EFW, especially for the determination of macrosomia. ^{5 , 25} A systematic review of the data has compared AC with EFW for the prediction of macrosomia and found both measures equally effective. ²⁶ Despite this, and unlike the data for HC, the AC has never been tested to ensure accuracy in the measurement itself. True ultrasound accuracy should be taken to be the correlation between an ultrasound measurement and the actual structure being measured. Our study has shown that this measurement is indeed reliable in the term singleton pregnancy.

A limitation of this study is that the reliability of the AC measurement has only been established in term pregnancies. However prenatal AC measurements are accurate at earlier gestations, therefore this technique can be reliably used to monitor fetal wellbeing, especially in large for gestational age (LGA) babies.

The AC measurement was found to be closer in accuracy when compared with the neonatal measurements than the 27 formulae of EFW that were also applied to the measurements taken. Ultrasound measurements of EFW are described as having a margin of error of ± 15%. ²⁷ Given the accuracy of ± 5.0% demonstrated for the AC measurement in this study, the error margin of EFW most likely reflects the formulae that are applied to the individual measurements rather than the measurements themselves. This is possibly unsurprising as each formula assumes a standard density and proportion to all fetuses and thus is likely to generate inaccuracies. Pregnancies with known intrauterine growth restriction were excluded from the current study as this would have artificially exaggerated the differences between AC anthropometry and ultrasound formulae for the reasons above.

The EFW formula of Hadlock including the AC, HC and FL, ¹⁵ which is commonly used in clinical practice was one of the 12 formulae that were found to be statistically different to the birth weight on t‐testing. An explanation for this could relate to the reliance of this measurement of the fetal HC, which is very technically difficult to perform at such a late stage of pregnancy due to fetal head engagement in the maternal pelvis. The formulae that concentrated on the AC were more likely to be statistically similar to the birth weights.

The scanning and measurements in this study were performed by an accredited trainee (Erin Nesbitt‐Hawes (ENH)) in obstetrics and gynaecology, not a qualified sonographer. ENH undertook a course in ultrasound prior to commencing the study and performed the first 10 scans in the presence of a sonographer. Reliability was confirmed within 7.5% for the measurements taken by the sonographer compared with ENH. Recent work has compared the inter‐observer reliability when performing fetal biometry with 95% limits of agreement for AC ± 8.8%. ²⁸ Although it was possible that the results would be affected by the relative inexperience of ENH and the fact that that AC measurement is difficult to measure reliably, particularly in the third trimester, ^{29 , 30} the data showing accuracy for the AC measurement are reassuring. This indicates that with appropriate training the AC measurement can be relied upon when performed by clinicians in situations when a sonographer is not easily accessible, for example in the labour ward of the hospital. Quality regulation in assessing the fetal AC is important though, with the AC shown to be the measurement where sonographers were most likely to be missing the quality criteria. ³¹ Tracing measurement of the fetal AC has been shown to more accurately fit the abdominal outline than elliptical measurement, particularly in term pregnancies where the fetal limbs often indent the smooth contour of the AC. ³¹ Due to this, the tracing method was utilised in this study.

Since the early 1990s the AC measurement has been proposed as an adjunct in the treatment of women with diabetes in pregnancy. Growth patterns of the AC throughout pregnancy have been shown to be altered for women with diabetes compared with normal controls ³² with AC measurements showing increased growth rate in large for gestational age (LGA) infants. ^{4 , 33 , 34} Symmetry of the AC and HC measurements is also important with fetuses of diabetic mothers having an increased AC/HC ratio. ³² LGA infants with increased AC/HC ratio have a higher risk of neonatal morbidity and should be identified prior to delivery. ³⁴ Rather than relying on the EFW as a standalone result, the AC and its ratio to the HC can provide extra information to women when counselling regarding delivery and risks of adverse outcomes such as shoulder dystocia. Other work has shown that LGA offspring of gestational diabetic mothers have increased rates of obesity compared with those born at a normal weight. ³⁵ This has led to the proposal of ultrasound monitoring of the AC to identify those fetuses at high risk and tailoring a stricter diabetic regime, with relaxed control for those at low risk. ⁷ Four randomised controlled trials have been performed, with three out of four showing a significant reduction in LGA infants at birth when a modified diabetic treatment regime was used in high risk pregnancies (defined as AC > 70 or 75th percentile). ^{36 – 39}

The data are clear that poor control of gestational diabetes is associated with higher rates of macrosomia, LGA and shoulder dysto cia. ^{4 , 40} Monitoring of the fetus is vital given these correlations. Given the association between altered growth patterns and AC/HC ratios in women with diabetes, the AC measurement is fundamental in the management of these women. The sample size of this study was sufficient to show a correlation between the two measurements in the whole group, however with only 17% of patients with gestational diabetes there were not enough participants to test its reliability in this subset of the population. Further research is underway to confirm the accuracy in this group of patients, in order to apply the measurement to monitor the effects of the diabetic treatment regime, or to aid in decisions regarding labour and delivery.

Proposed applications for the AC measurement include the monitoring of compliance with diabetic control during pregnancy complicated by gestational diabetes with AC growth charts to track the change over time. Charts of this nature could allow clinicians to detect acceleration in growth at an earlier timeframe and therefore allow earlier interventions and an opportunity to prevent associated complications. The utilisation of the AC measurement for this purpose would allow a low cost monitoring technique within the scope of the diabetic clinic, with associated resource implications.

Although the AC requires more quality assurance to ensure accurate level of measurement compared with the HC and BPD in the third trimester, the fetal abdomen is more accessible to scan than the head, particularly late in the pregnancy. ^{29 – 31} As such, the AC measurement is faster and easier to obtain than the EFW in a term pregnancy, where the engaged head can make the HC and BPD measurements technically difficult and less reliable. It is also one of the measurements which appears to be more achievable in the obese population, with equivalence of image quality compared with patients of average BMI. ⁴¹ This may be an important factor in the gestational diabetic population, who are more likely to be obese and therefore more difficult to scan.

Conclusion

Since the advent of ultrasound in the 1970's and the introduction of EFW formulae soon after, the ultrasound literature has focused on the accuracy of these formulae at the expense of research into the anthropometric measurements themselves. The EFW formulae are only as good as the measurements from which they are derived. In a term pregnancy, HC is technically difficult to obtain and AC represents a feasible measurement, with a low percentage error. This study has gone back to basics to demonstrate the accuracy of AC as a standalone measurement.