Allometry of the Tendon Enthesis: Mechanisms of Load Transfer Between Tendon and Bone

Abstract

Several features of the tendon-to-bone attachment were examined allometrically to determine load transfer mechanisms. The humeral head diameter increased geometrically with animal mass. Area of the attachment site exhibited a near isometric increase with muscle physiological cross section. In contrast, the interfacial roughness as well as the mineral gradient width demonstrated a hypoallometric relationship with physiologic cross-sectional area (PCSA). The isometric increase in attachment area indicates that as muscle forces increase, the attachment area increases accordingly, thus maintaining a constant interfacial stress. Due to the presence of constant stresses at the attachment, the micrometer-scale features may not need to vary with increasing load.

Introduction

Tendon attaches to bone across a specialized tissue called the enthesis. This tissue serves to connect two materials with a 2 order-of-magnitude mismatch in modulus: stiff bone and compliant tendon. A number of mechanisms exist at multiple length scales at this interface to alleviate stress concentrations and allow for effective load transfer (Fig. 1) [1–3]. At the millimeter length scale, the tendon attaches to the bone with a splayed geometry that dissipates stresses that would otherwise arise at the corners [4]. As a result of this splayed morphology, the tendon attachment to the bone has a millimeter-scale footprint. Distribution of the load across this attachment area may serve to decrease the stress applied at the interface. At the micrometer level, the collagen fibers from the unmineralized region interdigitate into the mineralized fibrocartilage forming a wavy or interdigitating interface (Fig. 1). In silico studies examining interdigitating interfaces indicated that the waviness of an interface affects both its strength and toughness [5]. Uniformly increasing amplitude and frequency of the interfacial waviness results in a decrease in interfacial strength due to an increase in stress concentrations. However, increased variation in the peak amplitude and frequency leads to an increase in the interfacial toughness by enabling continued interfacial integrity following the onset of injury. As a result, a tradeoff arises between increased interfacial toughness and decreased interfacial strength. For physiologic interfaces, the interdigitation geometry exhibits high toughness for a relatively small loss in strength. At the same length scale, the collagen fibers also exhibit a gradient in orientation from the mineralized to the unmineralized region of the attachment. This gradient allows for the formation of an interfacial compliant zone that mitigates stress concentrations [1]. Additionally, the tendon-to-bone attachment also displays a gradient in mineral content from the mineralized to the unmineralized zones at this length scale leading to graded increases in stiffness. At the nanometer length scale, the arrangement of mineral on collagen fibrils, whether extrafibrillar or intrafibrillar, leads to specific trends of stiffening with respect to volume fraction of mineral [2]. The functional grading across the transitional tissue between tendon and bone results in smooth load transfer without compliance mismatches, thereby minimizing the formation of stress concentrations [6]. Together, these mechanisms across multiple hierarchies combine to create a strong and tough tendon-to-bone attachment.

Fig. 1.

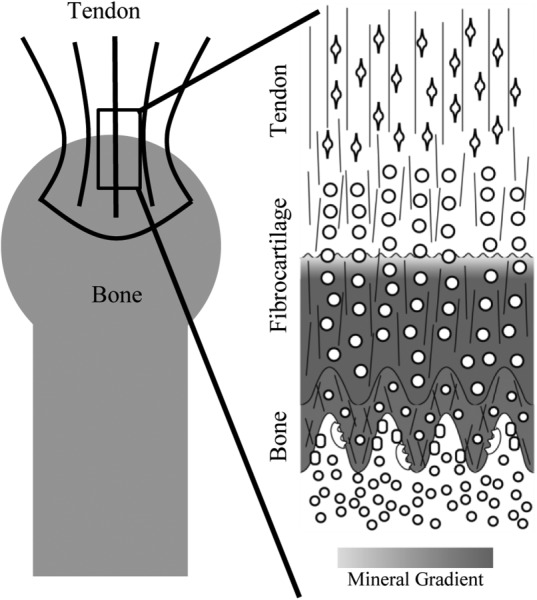
Multiscale structures of the tendon-to-bone enthesis. At the macroscale (left), the tendon attaches to the bone with a splayed geometry leading to a large insertion area. The microscale interface (right) is characterized by gradients in cell geometry (open circles, ovals, and diamonds), mineralization (high mineralization is gray and unmineralized is white), collagen orientation (thin lines) and composition. Of interest to this study is the gradient in mineralization between the mineralized and unmineralized fibrocartilage as well as the waviness of this interface.

Surgical protocols for repair of tendon to bone, as required in the repair of rotator cuff tears and reconstruction of the anterior cruciate ligament, include no effort to promote the reformation of this hierarchy of structural features. As a result, repaired attachment sites are prone to stress concentrations and increased risk of failure. For example, failure rates of rotator cuff repairs range from 20% in young, healthy patients with partial tears, to 94% for massive tears in the elderly [7,8]. To decrease this high failure rate, it is necessary to better understand the mechanisms of tendon-to-bone load transfer at different length scales and their stress dissipating capacity. By investigating how changes in attachment area, interfacial roughness, and mineral gradient affect tissue attachment mechanics, surgical and tissue engineering design criteria can be established to improve the quality of tendon-to-bone repair.

Most research on the repair and regeneration of the tendon-to-bone attachment has relied on small animal models such as the rat rotator cuff. The proper scaling of these findings from small animals, however, to the attachments of larger animals such as humans is unknown. When designing scaffolds for human tendon-to-bone repair, for example, does the ∼20 μm long mineral gradient found in the rat tendon-to-bone attachment [9] translate to ∼120 μm in humans, whose mass is ∼250 times that of rats? Allometry provides a way to study the relationship between the shapes and sizes of stress-mitigating structures at the interface and increasing animal mass and applied loads [10]. The concept of allometry was first suggested by Galileo in 1638, who found that bones became larger and more robust with increasing animal size [11]. However, the term and field of study were not fully established until Huxley and Teissier in 1936, who are credited with discovering the power-law relationship typically seen between the size of a feature and the size of an organism [12]. Since the time of Galileo, allometry has been used to examine the relationships between brain growth and head size, claw and horn size as a function of body size in lobsters and beetles, fossil and animal size in extinct species, and more recently, the relationship between body size, metabolic rate, and locomotion [13–17].

Allometry is a field of study that correlates anatomical characteristics of animals with size. These relationships are often described by a power law: the value of a characteristic (y) is related to a size (x) according to the equation y = bx^α. The scaling factor α provides information about the rate at which a characteristic changes as a function of size. Any relationship that follows this power law can be defined as allometric; however, there are specific forms of allometry that are of particular interest. Isometry, also known as geometric scaling, describes the situation where the proportionality of characteristics remains the same with changes in size. For example, the ratio of humerus length (l) to humerus width (w) remains constant for quadrupeds of all sizes [18]. Since $l\propto w$, the relationship is isometric and the scaling factor is equal to 1. Isometry follows the square-cube law. If $l\propto w$, then the cross-sectional area of the bone (A), with units of length squared, must be proportional to l or w with a scaling factor of α = 0.5, i.e., $l\propto A^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$. Equivalently, volume, with units of length cubed, will scale with l according to $l\propto V^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}$. If the scaling factor is smaller than the expected isometric value, the relationship is considered hypoallometric. A hypoallometric relationship indicates that the characteristic of interest changes at a slower rate than the independent characteristic. For example, the human brain grows more slowly than the human skeleton, indicative of a hypoallometric relationship [19]. On the other hand, hyperallometry indicates that the characteristic of interest changes at a faster rate than the independent characteristic.

In the current study, allometry was employed to compare animal size, and therefore increased applied load, with four specific stress-mitigating features of the tendon-to-bone attachment: the size of the humeral head, the tendon-to-bone attachment area, the roughness of interfacial interdigitation, and the width of the mineral gradient. Understanding of how these features from a range of length scales are modified to dissipate increasing applied loads will help to clarify the role and importance of these structures for load transfer between tendon and bone.

Methods

Animal Models.

Supraspinatus tendon–humeral head constructs were collected from 56-day-old CD1 mice (average mass approximated at 0.03 kg, N = 3), 6-month-old Sprague-Dawley rats (0.29 ± 0.01 kg, N = 3), 7-month-old New Zealand white rabbits (4.24 ± 0.22 kg, N = 2), adult canines (21.7 ± 2.3 kg, N = 3), and 10-month-old Yucatan minipigs (45.3 ± 2.3 kg, N = 3) (Fig. 2). Special attention was directed to maintaining the integrity of the tendon-to-bone attachment. Samples were fresh-frozen at −20 °C and stored until the analyses described below were performed.

Fig. 2.

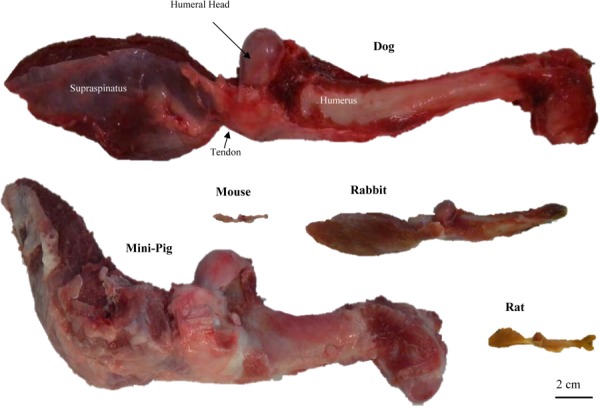
Posterior view of representative supraspinatus–humerus complexes for all of the species studied. Shown is the supraspinatus muscle attaching to the humerus via the supraspinatus tendon and humeral head.

Millimeter-Scale Measurements.

The humeral head diameter was measured for each sample using digital calipers. The right humeral head was measured three times at it widest point in the anterior–posterior direction and the average of the three measurements was used. To determine the bony attachment area for the tendon, the left humeral heads of each animal were cut using a low-speed bone saw such that the region of interest, the supraspinatus attachment, fit fully into the 38.9 mm diameter sampling volume of the microcomputed tomography (μCT) instrument (Scanco VivaCT40). The samples were imaged at 70 kVp, 114 μA, and 8 W with a nominal voxel size of 38 μm. Two regions of interest were selected to calculate the surface area of the tendon attachment. The first region represents the surface of the bone, contoured using the manufacturer's semi-automated implementation of a snake contouring algorithm (Scanco, Zurich, Switzerland). The second region represents a volume that intersects the surface of the bone along the outer edge of the tendon attachment. The edge of this region was visually determined by an experienced operator as the location where the soft tissue thinned to the thickness of the periosteum. The outer surfaces of the bone and outer volume were then meshed using an implementation of the cgalsurf library in matlab [20]. The triangles on the surface of the bone contained within the volume were considered as the attachment area as shown in Fig. 3(a).

Fig. 3.

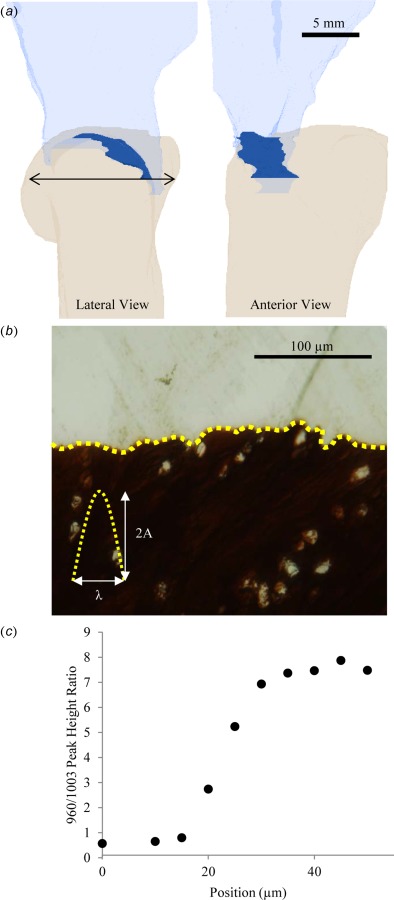
(a) μCT of the humeral head and supraspinatus tendon of a rabbit. The attachment area is highlighted in the dark opaque region. Thearrow indicates the measured humeral head diameter. (b) von Kossa stained histological section of the tendon-to-bone attachment. The interfacial roughness, which is highlighted by the dashed line, is measured by the peak height, 2A, and peak width, λ. (c) Plot of the 960/1003 Raman peak height ratio (representing relative concentration of mineral to collagen) as a function of position from the interface between mineralized and unmineralized fibrocartilage in a rat. The gradient in mineralization is approximately 30 μm long.

Micrometer-Scale Measurements.

In order to determine the interdigitation geometry of the attachments, supraspinatus tendon-to-humeral head specimens from each animal were prepared for histology. The specimens were initially fixed in paraformaldehyde overnight. Next, they were dehydrated in increasing concentrations of ethanol. The dehydrated samples were then infiltrated and mounted in polymethyl methacrylate. They subsequently were microtomed into 2-μm thick sections. The sections were stained according to von Kossa's method to highlight the interface between mineralized and unmineralized regions of the interface. Photomicrographs of the attachment sites were then analyzed by direct measurement (Fig. 3(b)). The tendon-to-bone interface was divided into segments, each containing a single protrusion of the mineralized fibrocartilage into the unmineralized tissue. For each protrusion, a baseline was drawn between the two minima of the protrusion using imagej, the length of which was defined as the width (λ). A line starting at and perpendicular to the baseline was drawn up to the maxima of the protrusion and defined as the height (2A). The means and standard deviations of these measurements were calculated for each animal.

In order to characterize the mineral at the attachment, supraspinatus tendon-to-humeral head specimens from each animal were sectioned along the coronal oblique plane to expose the tendon-to-bone attachment. The samples were flushed of marrow by centrifuging for 20 min at 4000 rpm, then washed three times in phosphate buffered saline solution, and refrozen at −20 °C until immediately before analysis. Spectra were collected using a laser Raman microprobe (HoloLab Series 5000 fiberoptically coupled Raman Microscope, Kaiser Optical Systems, Inc., Ann Arbor, MI) and techniques described previously [9]. Spectra were acquired using 10 mW of a 532-nm laser focused using an 80× objective (N.A. = 0.85) to a ∼1-μm beam spot on the surface of the sample. The scattered light was collected as 30 4-s acquisitions in a backscattered configuration through the objective lens and transmitted fiberoptically to a 2048-channel CCD detector. Use of the detector in 2D allowed for concurrent detection in the range of 100–4000 Δcm⁻¹ at 2.5 cm⁻¹ spectral resolution. Raman spectra were collected across the attachment from the unmineralized to the fully mineralized region at intervals of 3–5 μm. The Raman signal was optimized at each spot via manual focusing and care was taken to avoid cells and vascular tissue that might affect the spectral signal.

Spectra were analyzed as previously described [1,9,21,22]. Briefly, spectra were background corrected to eliminate the effects of fluorescence, and peaks within the spectral range of 700–1200 Δcm⁻¹ were deconvolved with a mixed Gaussian–Lorentzian peak-fitting algorithm in the Grams32^® software package (Galactic, Salem, NH). The relative mineral concentration at each measurement location was inferred from the ratio of the peak intensities for the ν₁ P–O stretching band of hydroxylapatite (∼960 Δcm⁻¹) and the aromatic ring stretching band of phenylalanine residues in collagen (∼1003 Δcm⁻¹). This measure does not indicate the absolute amount of either mineral or matrix present, but does provide useful information about their relative concentrations, which can be compared between samples. Effects of collagen orientation on the matrix signal were negligible (Fig. S1). The width of the mineral gradient between mineralized and unmineralized fibrocartilage was determined from the maximum spectral mineral-to-matrix ratio divided by the slope of the gradient. The slope of the mineral gradient was calculated for each animal by plotting the Raman-measured mineral-to-matrix ratio versus position across the attachment (Fig. 3(c)) and performing a linear regression using a window of at least five sequential points. The slope was then defined as the first-order term calculated from the window of points that resulted in the greatest R² statistic.

Physiologic Cross-Sectional Area.

Muscle volumes for each sample were measured via the Archimedes method. Briefly, the supraspinatus–humerus complex was held such that the bone- and muscle-free tendon was suspended above the water while the muscle was completely submerged. The volume of water displaced by the submerged muscle is equivalent to the muscle volume. From the muscle volume, the physiological cross-sectional area of the muscle was determined according to the equation

$$\text{PCSA}=\frac{V\hspace{0.17em}\text{cos}\hspace{0.17em}\theta }{L_{\mathrm{f}}}$$

where V is the muscle volume, θ is the pennation angle of the muscle fibers, and L_f is the muscle fiber length. Values of pennation angle and fiber length for the supraspinatus muscle of each animal were taken from Mathewson et al. [23]. The value of PCSA for a particular muscle is directly proportional to the force generated by that muscle [24–26].

Scaling Factor.

Measured values of humeral head diameter, attachment area, interdigitation geometry, and gradient width were plotted against animal mass or muscle PCSA on a log–log plot. In all cases, the data exhibited linear relationships. The data were fit via a power function, $y=C{x}^a$, where C is a constant that accounts for the units of y and x. A scaling factor with a value below that expected for isometry implies hypoallometry, indicating that the measure changes at a slower rate than animal mass or muscle PCSA. An absolute value of α greater than that expected for isometry implies hyperallometry, indicating that the measure changes at a faster rate than animal mass or muscle PCSA. Isometry, also known as geometric scaling, implies that the relationship between two characteristics of equal units, length and length, for example, has a scaling factor of 1. For characteristics of unequal units, length and area, the square-cube law is applied, and in this case α = 0.5 for isometry.

Results and Discussion

Humeral Head Diameter Scales Geometrically With Mass, Leading to Increased Stress With Increased Mass.

In the current study, the humeral head diameter scaled to body mass with a scaling factor of 0.38 ± 0.02 (α ± 95% confidence interval, R²= 0.99), i.e., similar to the geometric factor of 0.33 (Fig. 4(a)). This value is consistent with data indicating the humeral head diameter scales almost isometrically (α = 1.01) with midshaft diameter [27]. It also points to nearly geometric scaling between the humeral head and body mass. A number of studies have examined the relationships between bone geometry and animal body size [27–30]. However, few have examined the epiphyses of those bones (i.e., near the joints), where muscle forces are transferred. For the humerus, it has been shown that the midshaft diameter and the humeral mass scale to body mass with scaling factors of 0.35 and 1.083, respectively [29,31,32]. These results indicate that the relationships between these values and body mass are nearly isometric; the geometry of the bone is maintained with increasing body size. The bone diameter (d) grows proportionally to the bone length (l), $\propto l$. As a result, the animal mass (M), which is assumed to be proportional to the volume, is proportional to $l\cdot d^2\propto l^3$. The mass of the bone is therefore isometrically proportional to the body mass and $d\propto M^{\frac{1}{3}}$ [18].

Fig. 4.

Millimeter-scale features: (a) plot of humeral head diameter as a function of animal mass. The scaling factor was 0.38, indicating a near isometric relationship. Isometry of α = 0.33 is shown as a dotted line. (b) Plot of insertion area as a function of PCSA. The scaling factor was 0.84, indicating near isometric behavior. Isometry of α = 1 is shown as a dotted line. Ninety-five percent of confidence intervals are shown as dashed lines.

Geometric scaling between the bone size and body mass suggests that the humeral head will experience relatively elevated stresses with increased body size. Although the applied force increases isometrically with animal mass ($F\propto M)$, the area over which the force is distributed (d²) is proportional to M^2/3. As a result, the applied stress (σ), defined as force relative to the cross-sectional area it is applied across, is proportional to M^1/3. To accommodate the increased stresses, larger animals must adjust joint structures and/or mechanics, e.g., by increasing tissue strength or transferring the load more efficiently. Structurally, this can be achieved by improving trabecular bone architecture. However, allometric studies have shown that the scaling factor of trabecular thickness and numbers, although variable among species, always exhibit hypoallometry with animal size [33–36]. These values indicate that as body mass increases, the trabecular architecture becomes relatively sparser, with relatively thinner trabeculae. Therefore, trabecular bone architecture does not appear to change to accommodate increased stresses. The driving force for this mechanically deficient trabecular structure in large animals is thought to be physiologic, with a need to maintain adequate surface area for calcium homeostasis [35]. Therefore, other structures around the joint must evolve to dissipate increased stresses before they are transferred to the bone epiphysis.

Tendon-to-Bone Attachment Area Scales Isometrically With PCSA to Maintain a Constant Stress.

Mechanically, tendons behave viscoelastically. They are able to stretch during muscle loading and recoil upon release. The elastic behavior of tendon allows it to store and return strain energy during movement, thereby reducing expenditure of metabolic energy [37,38]. Allometric optimization studies have found an ideal tendon-to-muscle cross section ratio of 1:34 that allows the tendon to act elastically without failing [39,40]. Although these relatively slender tendons are ideal for storing and releasing energy, the small cross sections result in a large stresses. To alleviate this potentially damaging stress, the supraspinatus tendon attaches to the humeral head with a splayed morphology. This results in a large bony attachment area relative to the tendon cross section. The attachment areas measured in this study via μCT varied from 1.2 to 300.3 mm² across the animals studied. When plotted as a function of animal mass, a scaling factor of 0.76 ± 0.08 (R²= 0.98) was obtained. This is higher than the isometric value of 0.67 and the experimental value of 0.60–0.68 usually obtained for the tendon midsubstance cross-sectional area [41], indicating that the attachment area increases faster that the tendon cross-sectional area with increasing mass.

In order to obtain a more accurate measure of the applied muscle loads for each animal, the PCSA of the supraspinatus muscle was determined and plotted against attachment area. The attachment area increased with PCSA with a scaling factor of 0.84 ± 0.12 (R²= 0.94), indicating an allometric relationship nearing isometry (Fig. 4(b)). An approximately isometric relationship suggests that the millimeter length scale attachment area increases at nearly the same rate as the applied force. Taking stress as the ratio of force to the initial area over which it is distributed, this result demonstrates that as the applied load increases, the attachment area increases accordingly to maintain a near constant interfacial stress. In other words, although the applied load on the tendon increases by a factor of 1000 with animal size, the force is redistributed over the increased attachment area to produce a local stress that increases by less than a factor of 2 on the attachment.

Interfacial Roughness and Mineral Gradient Width Scale Hypoallometrically With PCSA.

At the micrometer length scale, the interface between the mineralized and unmineralized tissues exhibits a waviness or interfacial roughness. In silico models have shown that a wavy interface between two dissimilar materials can serve to increase interfacial toughness at the cost of interfacial strength [42]. An increase in peak height (A) versus peak width (λ), as measured by the A/λ ratio, increases the magnitude of stress concentrations, leading to a decrease in strength. For the animals in this study, the ratio of peak height to peak width varied from 0.11 to 0.14. When plotted as a function of PCSA, the A/λ ratio had a scaling factor of −0.003 ± 0.04 (R²= 0.006) (Fig. 5(a)). Since A/λ is a dimensionless value, this result could indicate that the size of the protrusions increased isometrically (i.e., both A and λ increase isometrically), or that the size of the protrusions did not change at all (i.e., both A and λ remained constant). However, mean values of A varied from 1.6 to 3.5 μm and exhibited a scaling factor with PCSA of 0.025 ± 0.10. Similarly, mean values of λ varied from 13.0 to 38.0 μm, with a scaling factor with PCSA of 0.046 ± 0.14. Both of these values exhibited strong hypoallometry compared to the expected isometric value of α = 0.5 (Fig. 5(a), insets). These results suggest that, instead of having an isometric increase in the size of the protrusions, the protrusions did not change significantly with animal size. This indicates that the interfacial roughness was not affected by increasing the applied muscle load. In silico studies have also shown that high variability in A/λ at the interface (i.e., random interfacial roughness) increases the interfacial toughness. As a measure of this variability, the normalized standard deviation of the A/λ values was determined for each animal. The normalized standard deviation of A/λ ranged from 0.28 to 0.49. When plotted against PCSA, the standard deviation of A/λ had a scaling factor of −0.025 ± 0.28 (R²= 0.14) (Fig. 5(b)). To confirm that this was not an indication that the standard deviation increases isometrically but that the standard deviation does not change with increased load, the standard deviations of A and λ were plotted as a function of PCSA (Fig. 5(b), insets). The standard deviation of A varied from 0.2 to 7.1 μm and exhibited a scaling factor with PCSA of −0.069 ± 0.44. The standard deviation of λ ranged from 3.9 to 42.5 μm with a scaling factor of α = 0.049 ± 0.39. The standard deviations of A and λ both exhibited strong hypoallometric behavior compared to the expected isometric scaling factor of 0.5 (Fig. 5(b), insets). Therefore, the micrometer-scale histological analysis indicated that roughness at the interface between mineralized and unmineralized tissue does not vary with muscle load.

Fig. 5.

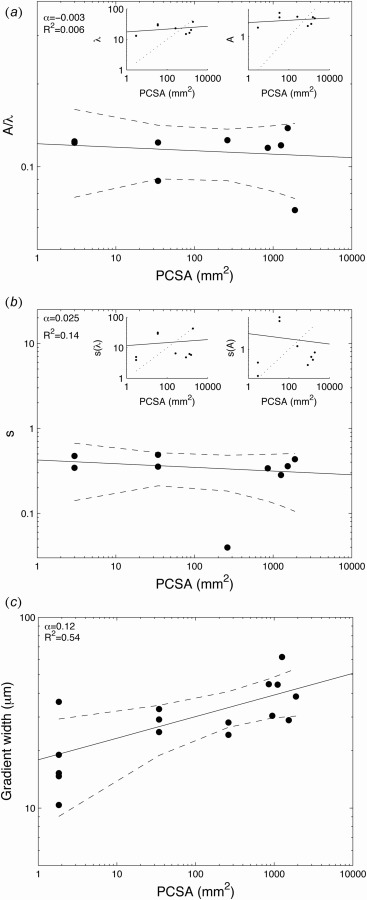
Micrometer-scale features: (a) plot of A/λ as a function of PCSA. The insets show A and λ independently as a function of PCSA. Isometry of α = 0.5 is shown as dotted lines in the inset. The small scaling factors for A, λ, and A/λ indicate hypoallometry of the roughness. (b) Plot of the standard deviation of A/λ as a function of PCSA. The insets show standard deviations of A and λ independently as a function of PCSA. Isometry of α = 0.5 is shown as dotted lined in the inset. The small scaling factors of the standard deviation of A, λ, and A/λ indicate a hypoallometric relationship. (c) Plot of width of the mineralization gradient as a function of PCSA. The scaling factor was 0.12, indicating a hypoallometric relationship compared to the isometry (dotted line) of α = 0.5. Ninety-five percent of confidence intervals are shown as dashed lines.

At the micrometer scale, the supraspinatus-to-humeral head attachment also exhibits a gradient in mineral between the mineralized and unmineralized tissue. Functional grading in mechanical properties across an interface between dissimilar materials decreases the stress concentrations that otherwise would occur at an abrupt change in mechanical properties and allows for more effective stress transfer [6]. In biological systems, graded structures can be found at many interfaces [43], including the beak-to-mouth interface in squids [44], the anchor-to-foot interface in mussels [45], and as discussed here, the soft tissue-to-bone interface in mammals [21,22,46–50]. The width of the supraspinatus tendon-to-bone mineral gradient has been previously examined in mice and found to span a distance of ∼20 μm [22]. However, this width was found not to change significantly during postnatal development in the mouse, even though the animal size increased by nearly tenfold [22]. In the current study, mineral gradient widths measured using Raman spectroscopy spanned distances of 10–60 μm. The scaling factor for the gradient width as a function of PCSA was 0.12 ± 0.07 (R²= 0.54) (Fig. 5(c)). This is a strongly hypoallometric relationship (isometry α = 0.5), indicating that there is minimal change in gradient width with increasing muscle loads. This result is consistent for growing mice as well as across species. Although the animal mass from mouse to pig increased by a factor of over 1000, the mineral gradient width increased only by a factor of 2.

The hypoallometric relationship between the mineral gradient width and PCSA suggests that this feature does not play a major role in mediating stress transfer at the tendon-to-bone attachment macroscopically. Instead, micrometer-scale features may be driven by cell-level stresses rather than tissue-level forces. Conversely, this result implies that the gradient is not optimized to affect the way the forces at the millimeter length scale influence cell behavior on the micrometer length scale. Considering that attachment area increases near isometrically with increasing force, stress at the cellular level does not exhibit large changes with increasing force at the tissue level. Therefore, the biophysical cues that the cell is exposed to are nearly the same, regardless of the animal or muscle size. Previous observations during postnatal mineralization of the tendon-to-bone attachment have shown that the mineral gradient forms in a polarized fashion by mineralizing chondrocytes. Mineral is deposited by cells in one direction, forming a scalloped edge [22]. In the current study, the gradient length increased from 10 to 60 μm between the smallest (mouse) and largest (minipig) animals studied. If this relatively small change in gradient length were indeed controlled locally by individual cells, an increase in cell size with increasing animal and muscle size would be expected. Due the large volume and highly mineralized nature of the samples used in this study, it was not possible to measure cell size in the histological sections. Other studies have shown that the cells of fly wings, eyes, and basitarus increase in size with an increase in body length [51,52]. Osteocyte size in birds also increases with body size, with a scaling coefficient of 0.128, similar to the scaling coefficient of the gradient width found here [53]. These studies imply that an increase in cell size may explain the relatively small change in gradient width; however, measurements by Breur et al. show that although hypertrophic chondrocyte size increases with longitudinal bone growth in individual rats and pigs, it does not vary between species [54]. Although the micrometer-scale features such as mineral gradient width are clearly not driven by millimeter-scale muscle forces, it remains unclear if they are driven by local cellular events.

Study Limitations.

In this study, only five different species were examined, which span a range of 3 orders of magnitude in weight. Larger animals such as bovids and equine mammals could have been investigated in an expanded study. However, it has been shown that large animals, specifically bovids and ceratomorphs, exhibit modified allometric scaling relative to bone size. These large animals tend to have relatively shorter and thicker bones compared to animals under 100 kg [38,55]. In order to avoid this shift in allometric behavior, minipigs were selected as the largest species of interest. Additionally, these specific species were selected due to their common use in the laboratory setting. For each species studied, approximately three animals were used. Such sample sizes are not uncommon for allometric studies in which the number of species is of greater importance than the number of individual animals [23,41]. The spread in the variables is quite small with an n = 3; therefore, this value was employed to minimize animal usage.

Conclusions

The humeral head diameter, attachment area, interfacial roughness, and mineralization gradient width were measured for the supraspinatus–humerus tendon-to-bone complex for a number of commonly studied animal species. These measures were plotted as a function of body mass and PCSA to determine how structures across multiple length scales of the tendon-to-bone complex varied with load. The humeral head diameter exhibited a nearly geometric scaling with body mass, as has been previously reported for other humeral parameters. The microscale structures, mineral gradient width and interfacial roughness, varied hypoallometrically with PCSA, suggesting that these features play minimal roles is dissipating stresses associated with loads at the macroscale. However, the tendon-to-bone attachment area increased nearly isometrically with PCSA. Therefore, increased loads are distributed across an increased attachment area in a way that results in constant stress at the humeral head regardless of animal or muscle size. If tendon-to-bone interfacial stress is maintained constant via millimeter-scale mechanisms such as attachment areas, the micrometer-scale features of mineral gradient and interfacial roughness do not need to adapt to the increasing loads. These micrometer-level structures may therefore be controlled by local cellular features (e.g., cell size and/or polarization) driven by stress rather than applied macroscopic loads. These results provide the design criteria for tissue engineered scaffolds for tendon-to-bone repair. Furthermore, they provide immediate guidance for surgical repair of tendon to bone, specifically indicating that repairs should focus on repair-site attachment strategies that distribute load across an appropriate footprint area.