Abstract
Clinical decisions are often based on the results of third trimester sonograms, particularly with small or large babies and so accuracy of estimating fetal weight (EFW) is essential. There are numerous EFW formula available and yet in Australia no one formula has been recommended for use due to the lack of clinical evidence as to their accuracy.
Objectives: 1 To assess inter/intra observer error for fetal parameter measurements with multiple observers. 2 To compare six of the most commonly used EFW formulae and analyse inter/intra formulae variations for different weight range.
Method: EFW of 121 pregnancies assessed within 7 days of birth by measuring the BPD, OFD, HC, AC, FL and comparing to actual birth weight.
Results: Inter‐observer error: 1.3 to 3.1%. Intra‐observer error: 1.1 to 1.9% depending on fetal parameter. Accuracy of each EFW formula changed with different weight ranges. For all formulae the highest random error occurred in the macrosomic group. The lowest random error in all weight groups was the Hadlock B formula incorporating the HC/AC/FL (7.7%).
Conclusion: Considering the possible problems of head moulding this study suggests the use of: Hadlock FP et al (1982) – Formula B – incorporating HC/AC/FL.
Keywords: estimation, fetal, weight
Background to the study
“No formula for estimating fetal weight has achieved an accuracy which enables us to recommend its use”.
This ASUM policy statement on normal ultrasonic fetal measurements was released in 1991 then updated in 1996 and again in 2002. 1 Antenatal ultrasound has become one of the clinicians' most important tools for assessing fetal age, growth and wellbeing. Compared with the physical examination of the pregnant uterus the most accurate method for assessing and tracking fetal size and growth is with the use of ultrasound imaging and measuring of the various fetal parameters. Estimating fetal weight (EFW) is an expected adjunct of the third trimester sonogram as clinical decisions to intervene in the timing of the delivery are often based on the ultrasound findings, especially with small or large for gestational age babies, and so any improvement in the reliability of EFW may help improve clinical outcomes.
There is a choice of over 20 EFW formulae on current ultrasound systems with most of these formulae being over 25 years old. The Altman group 2 advised the use of the EFW formula with lowest random error (standard deviation) across the weight ranges but literature reviews 3 have shown this to be difficult as the formulae best suited to identifying the under 1000 g fetus 4 is not the most suitable for predicting a macrosomic baby. The Hadlock group 5 – 7 developed at least seven regression models using different combinations of fetal parameters and found the mean deviation from actual birth weight to be a low 0.3 to 0.4% for all of their formulas but the standard deviations varied with the AC/HC being the least accurate at 9.1% compared with the AC/FL at ± 8.2%, BPD/AC/FL at ± 7.7%, HC/AC/FL at ± 7.6% and BPD/HC/AC/FL with a ± 7.5% standard deviation. When divided into weight ranges the accuracy for each formula within each group changed and this led Hadlock to advocate the use of the HC/ AC/FL formula. The accepted accuracy, or margin of error, between estimated and actual birth weight is ± 15%. 8 The accuracy of any ultrasonic fetal weight formula is dependent on its 95% confidence limit. For example, one of the more popular formulas is the Hadlock HC/AC/FL where the 95% confidence limit is ± 15% and so it is expected that 95% of actual birth weights will be within ± 15% of the predicted birth weight. It has been claimed 8 that the more parameters included in the weight formula, the more accurate they are but this is influenced by the accuracy of the measurements of the various parameters used in the equation. The best example of this is the use of one of the earliest fetal weight charts, that of Campbell and Wilkins, 9 which relied solely on the fetal abdominal circumference measurement in the equation. Apart from correct image plane another error factor was the reliance of a digital map measurer to trace the circumference from a polaroid image similar to the method used by other early researchers such as the Hadlock, Deter and Shepard groups. 5 , 10 , 11 The formula by Hadlock, et al. which used only the abdomen has a 95% confidence limit of ± 22%, which is too great for clinical use as compared with the other Hadlock group formulae of head and abdomen, resulting in ± 18%, abdomen and femur ±16% and head, abdomen and femur with a ± 15% confidence limit.
Most fetal weight formulae are based on the presumption of normal fetal growth and do not take into consideration the factors attributing to either a growth restricted or macrosomic (> 4000 g) fetus. This led many authors to question the accuracy of fetal weight estimations, particularly for prediction of macrosomia. 12 The differing abdominal circumference of a normal fetus and one affected by gestational diabetes is a prime example where it is claimed there is a distinction between weight prediction in diabetic and non diabetic pregnancies with the difference in the 95% confidence limit for formulas that utilise head, abdomen and femur being ± 24% for diabetic compared with ± 15% in normal pregnancies. A retrospective study by Parry, et al. 13 showed a 42% false positive rate for predicting macrosomia with ultrasound, as for birth weights between 3500 g and 4000 g only 24% of pregnancies were correctly identified as being non‐macrosomic. Another retrospective study by Rouse and Owen 14 showed that ultrasound of 100 pregnancies identified 16 macrosomic fetuses of which only seven were actually greater than 4000 g at birth.
As mentioned in the ASUM statement, in Australia no one formula has been recommended for use across the entire gestation / birth weight range due to the lack of clinical evidence as to their accuracy. 15 Analysing the possible reasoning for this it would appear that obtaining the correct imaging plane for measuring the various fetal parameters used in the EFW formula is one of the main problems. These fetal parameter measurements may impact on the outcome of a pregnancy and so it is therefore essential they be performed in a consistent and reproducible way. 16 The variations seen in fetal weight estimations on the same fetus could be due to intra/interobserver error. 17 Numerous studies have analysed inter/intraobserver variations in fetal parameter measurements 18 , 19 which highlight the importance of accuracy and reproducibility. The abdominal circumference has been described by many authors 16 , 20 , 21 as being the most difficult of all the fetal parameters, especially in the third trimester, as it is the measurement most likely to be inaccurate and yet is one of the most essential for inclusion in a fetal weight formula. From 30 weeks gestation the abdominal circumference expands from 262 mm by around 10 mm per week to be 362 mm at 40 weeks and so if suspecting either growth restriction or macrosomia an incorrect imaging plane combined with a measuring error can cause serious consequences and if these errors continue at subsequent examinations the errors may be compounded.
Northern Sydney Health statistics show that birthweights are increasing, and with this increase in weight comes a rise in intervention rates 22 and so best clinical outcomes will rely heavily on identification of the large or macrosomic baby with accurate estimation of fetal weight. The plethora of problems for assessing fetal size, growth and estimating birth weight was succinctly described in a review of Australian charts for assessing fetal growth by Hui 3 who commented that while different practices use different standards and charts to report on fetal size and growth, erroneous conclusions and inappropriate management decisions will be made.
Objectives
The objectives of this study were:
-
1
To assess inter/intra observer error for fetal parameters measurements used for estimating fetal weight in the third trimester
-
2
To compare the most commonly used EFW formulae and analyse inter/intra formulae variations for different weight ranges
-
3
To compare random error (standard deviation) and percentage mean birth weight deviation for each formula and birth weight range
-
4
To determine which EFW formula best reflects clinical outcomes.
Methodology
Approval and clearance for this study was obtained from relevant Area Health and hospital departments.
Fetal parameters – inter/intraobserver:
The imaging planes and fetal parameter measuring methods used in this study for estimating fetal weight are those recommended by ASUM. 1 , 23
- Three late third trimester pregnancies of 36, 38 and 40 week gestation were each scanned by three observers.
-
–images for measuring femur length, BPD, OFD, head and abdominal circumference were stored on a GE Voluson E8 by all operators
-
–All observers measured their own and other observers fetal parameters twice
-
–
A further two observers recalled images and measured all fetal parameters twice
Observer obstetric scanning experience ranged from 1–35 years (mean 19.4 years)
Inter/intra observer error was the mean deviation calculated as a percentage of the mean parameter measurement.
EFW Formulae
Graphed and compared the six most commonly used EFW formulae (Table 1) and compared against Australian birth weight graph of Roberts and Lancaster (1999).
- Data collection:
-
–121 pregnancies assessed by the same operator for fetal size within 7 days of birth (mean 5.1 days) by measuring the BPD, OFD, HC, AC, FL and calculating EFW
-
–Range of gestation: 36 weeks 1 day–41 weeks 3 days (Mean gestation: 38w 2d)
-
–Birth weight range: 2483 g to 4251 g (Mean birth weight: 3634 g ± 302 g)
-
–Birth weights grouped to < 3000 g (mean 2812 ± 156 g), 3000–3500 g (mean 3348 ± 183 g), 3500–4000 g (mean 3791 ± 201 g) and > 4000 g (mean 4073 ± 149 g)
-
–Using a variation of parameters and fetal weight regression formula, the resultant EFW was compared with the actual birth weight of 121 subjects
-
–Mean deviation between predicted/actual weight calculated for each formula in each birth weight group and expressed as a percentage of actual weight ± standard deviation (random error)
-
–The percentage deviation (predicted weight – actual weight/actual weight ∗∗∗× 100) and average random error calculated across entire weight range
-
–Analysed inter/intra formula for different weight ranges
-
–Compared results with 1984 study by Hadlock's group.
-
–
Table 1.
| Year | Author | Fetal parameters |
|---|---|---|
| 1982 | Shepard, et al. | BPD/AC |
| 1982 | Hadlock, et al. | HC/AC |
| 1982 | Hadlock, et al. – A | AC/FL |
| 1983 | Hadlock, et al. – B | HC/AC/FL |
| 1984 | Hadlock, et al. – C | BPD/HC/AC/FL |
| 1985 | Hadlock, et al. – D | BPD/AC/FL |
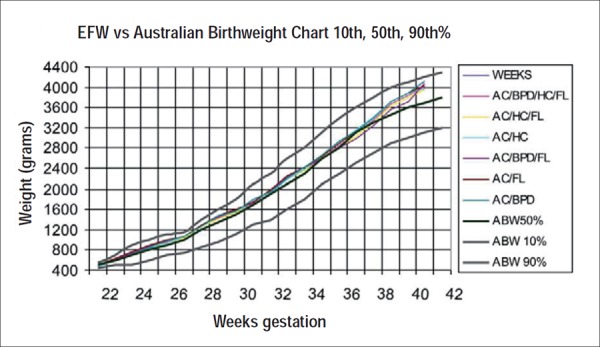
Graph 1.
Results
Fetal parameter imaging planes and measurements
In agreement with early researchers the imaging plane for the abdominal circumference was the fetal parameter most difficult to reproduce by operators. Due to the advanced gestation none of the operators obtained a complete abdominal outline on any of the fetuses due to fetal lie and shadowing from bones. Transducer pressure changed the shape of the abdomen thus varying the ease of measurement. The femur length measurement was more reproducible if the recommended imaging plane was used. Once the femur was at more than 30° to the horizontal the measurements became more variable. Measuring the 38‐week fetus was difficult due to a dolichocephalic head lying low in the maternal pelvis and highlighted the importance of the cephalic index when estimating fetal weight. The CI = (BPD/OFD) × 100% (normal range 73.9–82.7). If the CI is not within the normal range do not use an EFW formula that incorporates the BPD.
Fetal parameters – inter/intraobserver
The intra/interobserver error for each of the fetal parameters used for estimating fetal weight is shown in Table 2. There are two components to estimating fetal weight. The first involves scanning the subject to obtain the correct imaging plane for measuring the fetal parameters used in the EFW formula and the second is the actual measuring of the parameter. Three of the five observers imaged and measured the various fetal parameters while another two measured recalled images obtained by another observer. It was evident that edge perception was more difficult when the operator had not actually obtained the image as this was reflected in the measurements, particularly the abdominal circumference. The comparison studies in Table 2 involved a single fetus in the mid trimester while this study required the measuring of three late pregnancies with the results averaged for both inter and intra observer.
Table 2.
| Fetal Parameter | Intra‐observer | Inter‐observer | Other studies |
|---|---|---|---|
| Head circumference | 1.2% | 2.1% | Hadlock ‘82 Inter 1.2% |
| BPD | 1.1% | 1.3% | Hadlock ‘82 Inter 1.5% |
| OFD | 1.7% | 2.8% | |
| Femur | 1.6% | 2.7% | Hadlock ‘82 Inter 2.8% |
| Abdominal circumference | 1.3% | 2.2% | Deter ‘82 Inter 2.4% |
| EFW BPD,HC,AC,FL | 1.9% | 3.1% | Gull ‘00 Intra 2% Inter 5.8% |
EFW formula comparison
Comparison of the six most popular EFW formulae (Table 1), displayed against the Australian birthweight percentiles of Roberts and Lancaster (Graph 1) showed:
To 30 weeks gestation there is less than 50 g difference between the graphs. By 34 weeks this difference had increased to 100 g (lowest AC/HC/FL, highest AC/BPD) with a steady increase to 200 g by 39 weeks (lowest AC/BPD/FL, highest AC/BPD). After 40 weeks the difference reduces to less than 150 g with integrity of three formulas questionable (AC/BPD/FL, AC/ BPD and AC/HC)
Highest EFW across gestation was AC/BPD formula of Shepard, et al.
Lowest EFW to 40 weeks: AC/BPD/FL Hadlock, et al.
Compared with the Australian birthweight percentiles there was a marked deviation seen after 37 weeks where the EFW was significantly higher than the actual mean birth weight.
Using a variation of parameters and fetal weight regression formula, the resultant estimated fetal weights from the 121 pregnancies were compared with the actual birth weight. The mean deviation between predicted and actual weight was calculated for each formula and expressed as a percentage of actual weight ± standard deviation (random error).
Table 3 shows how each EFW formula performed in the various weight ranges. The acuracy of each formula changed with different weight ranges. For all formulae the highest random error occurred in the macrosomic group. The lowest random error in all weight groups was the Hadlock B formula incorporating the head and abdominal circumference and femur length. This was followed by Hadlock C formula, which added the BPD to the HC, AC and femur. The least accurate formula was the AC/BPD of the Shepherd group, particularly for the low birth weight range.
Table 3.
| EFW Fetal parameters | Authors | < 3000 g Mean 2812 g n = 21 | 3000–3500 g Mean 3348 g n = 45 | 3500–4000 g Mean 3791 g n = 36 | > 4000 g Mean 4073 g n = 19 |
|---|---|---|---|---|---|
| AC/BPD | Shepherd, et al. | ‐2.1 ± 11.2 | ‐1.9 ± 8.3 | ‐0.5 ± 7.9 | ‐1.1 ±10.1 |
| HC/AC | Hadlock, et al. | ‐1.6 ± 8.3 | ‐0.6 ±7.8 | ‐2.7 ± 8.4 | ‐3.8 ±10.6 |
| AC/FL | Hadlock, et al. A | ‐0.5 ± 7.5 | 0.7 ± 7.1 | ‐4.1 ± 7.6 | ‐2.9 ± 9.8 |
| HC/AC/FL | Hadlock, et al. B | ‐0.8 ± 7.4 | ‐1.6 ±6.9 | ‐2.7 ± 7.2 | ‐2.6 ± 9.6 |
| BPD/HC/AC/FL | Hadlock, et al. C | 1.8 ± 8.0 | 0.9 ± 7.2 | ‐3.4 ± 7.3 | 3.7 ± 9.7 |
| BPD/AC/FL | Hadlock, et al. D | 1.4 ± 8.9 | ‐1.1 ±7.2 | ‐3.3 ± 7.2 | ‐4.3 ± 10.2 |
A comparison with the 1984 study of Hadlock, et al. (Table 4) shows the standard deviation to be higher in all but one formula. The standard deviations varied, with the Shepherd AC/BPD and Hadlock HC/AC being the least accurate in both studies with standard deviations of 9.1% and 9.3%. The margin of error (95% confidence limit) is drawn from the literature. 5 , 11
Table 4.
| EFW formula | Authors | 95% Confidence Limit – % | %Mean BW deviation∗ Hadlock ‘84 | Standard deviation % of EFW # Hadlock ‘84 | Standard deviation % of EFW # Westerway |
|---|---|---|---|---|---|
| AC/BPD | Shepherd | 18 | 0.4 | 9.1 | 9.3 |
| HC/AC | Hadlock | 16 | 0.4 | 9.1 | 9.3 |
| AC/FL | Hadlock A | 16 | 0.3 | 8.2 | 8.1 |
| HC/AC/FL | Hadlock B | 15 | 0.3 | 7.6 | 7.7 |
| BPD/HC/AC/FL | Hadlock C | 15 | 0.3 | 7.5 | 7.9 |
| BPD/AC/FL | Hadlock D | 16 | 0.3 | 7.7 | 8.5 |
∗ % deviation = predicted weight‐actual weight/actual weight × 100. # average standard deviation across weight range
Discussion
All of the formulae used in this study assume normal fetal growth and do not make allowances for the growth restricted/ diabetes affected fetus. As mentioned by Doubilet 13 in pregnancies affected by diabetes the confidence limit increases in formulae incorporating abdominal circumference due to possible asymmetric growth. With the higher incidence of gestational diabetes mellitus seen in our ethnic population (15% for Asians versus 4% for Caucasians) it is important to look at the various fetal parameter ratios, in particular the AC/HC ratio. The integrity of EFW formula incorporating a BPD but no HC are at risk of inaccuracy due to variations of head shape such as doliocephaly. This is especially seen in the third trimester and while head volume will not change, head moulding may distort the BPD and therefore the EFW so it is suggested that measuring the OFD and assessing the cephalic index be added to all practice protocols.
Another important factor is ethnicity. It has been shown 22 that the abdominal circumference of a Chinese fetus for instance is smaller than a Caucasian fetus after 32 weeks gestation. Measuring the fundal height in late pregnancy may prompt scan requests querying small for gestational age. The problems associated with macrosomia (> 4000 g) in a Caucasian woman may appear in a Chinese pregnancy at a lower birth weight. When incorporated into an EFW formula the Chinese fetus may be wrongly classified as small for gestational age even though it is the correct size for its ethnicity.
Quality control in medical ultrasound begins in the individual practice with the implementation of protocols and ensuring ongoing operator training. This quality control in clinical practice will help improve clinical out comes. Hui 3 stressed the importance of report consistency with the same biometry and weight charts used on all systems, reporting the percentile band for each fetal parameter and plotting fetal growth. Current model ultrasound systems usually give the option of adding various parameter ratios and percentiles to report pages, which will assist in supplying more information if planning pregnancy intervention.
There are two reliable EFW formulas, both giving low deviations from actual birth weight and with low random error of 7.7 and 7.9% across the weight ranges. The Hadlock group formula B with HC, AC and FL and the Hadlock C formula with BPD, HC, AC and FL both fit the criteria of Altman, et al. 2 for choosing an EFW formula. Considering the possible problems of head moulding and BPD measuring this study suggests the use of:
Hadlock FP, Harrist RB, Deter RL, Park SK (1982) – Formula B – incorporating HC/AC/FL:
Log 10 BW = 1.5662 − 0.0108 (HC) + 0.0468(AC) + 0.171 (FL) + 0.00034 (HC)10 − 0.003685 (AC × FL)
Conclusion
Based on the results of this study the following are recommendations to assist in achieving best outcomes:
Standardisation of obstetric scanning protocols and imaging planes for measuring to help reduce EFW errors
All systems within a group practice have the same default EFW formula and biometry charts
Biometry measurements done accurately
Incorporate cephalic index and other ratios into routine reports
Report all fetal parameters and percentiles to put EFW into perspective
Be aware of ethnic variance in fetal size
Estimated fetal weight is only as accurate as the accuracy of the individual fetal parameter measurements used in the selected formula
Errors in individual parameter measurements compound to an under/over estimation of weight
Estimated fetal weight should be treated as such – an estimation.
References
- 1. Australasian Society for Ultrasound in Medicine . Statement on normal ultrasonic fetal measurements. ASUM Bulletin 2001; 4: 28–31. [Google Scholar]
- 2. Altman DG, Chitty L. Charts of fetal size: Methodology. Br J Obstet Gynaecol 1994; 101: 29–34. [DOI] [PubMed] [Google Scholar]
- 3. Hui L. Australian charts for assessing fetal growth: a review. Ultrasound Bulletin 2008; 11: 12–18. [Google Scholar]
- 4. Scott F, Beeby P, Abbott J, Edelman D, Boogert A. New formula for estimating fetal weight below 1000g: comparison with existing formulas. J Ultrasound Med 1996; 15: 669–72. [DOI] [PubMed] [Google Scholar]
- 5. Hadlock FP, Harrist R, Carpenter R, Deter R, Park S. Sonographic estimation of fetal weight. Radiology 1984; 150: 535–40. [DOI] [PubMed] [Google Scholar]
- 6. Hadlock FP, Harrist R, Sharman R, Deter R. Estimation of fetal weight with the use of head, body and femur measurements – a prospective study. Am J Obstet Gynecol 1985; 151: 333–37. [DOI] [PubMed] [Google Scholar]
- 7. Hadlock FP, Harrist R, Martinez‐Poyer J. In utero analysis of fetal growth: a sonographic weight standard. Radiology 1991; 181: 129–33. [DOI] [PubMed] [Google Scholar]
- 8. Benson CB, Doubilet PM. Sonographic prediction of gestational age: Accuracy of second and third trimester fetal measurements. AJR Am J Roentgenol 1991; 157: 1275–7. [DOI] [PubMed] [Google Scholar]
- 9. Campbell S, Wilkins D. Ultrasonic measurement of fetal abdominal circumference in the estimation of fetal weight. Br J Obstet Gynaecol 1975; 82: 689–97. [DOI] [PubMed] [Google Scholar]
- 10. Deter RL, Harrist R, Hadlock F. Fetal head and abdominal circumference 1: Evaluation of measurement errors. J Clin Ultrasound 1982; 10: 357–63. [DOI] [PubMed] [Google Scholar]
- 11. Shepard MJ, Richards V, Berkowitz R, Warsof S, Hobbins J. An evaluation of two equations for predicting fetal weight by ultrasound. Am J Obstet Gynecol 1982; 142 (1): 47–54. [DOI] [PubMed] [Google Scholar]
- 12. Doubilet PM, Benson CB. Fetal growth disturbances. Semin Roentgenol 1990; 25: 309–16. [DOI] [PubMed] [Google Scholar]
- 13. Parry S, Severs CP, Sehdev HM, Macones GA, White LM, Morgan MA. Ultrasonic prediction of fetal macrosomia: association with cesarian delivery. J Reprod Med 2000; 45 (1): 17–22. [PubMed] [Google Scholar]
- 14. Rouse DJ, Owen J. Prophylactic cesarean delivery for fetal macrosomia diagnosed by means of ultrasonography – A Faustian bargain? Am J Obstet Gynecol 1999; 181 (2): 332–38. [DOI] [PubMed] [Google Scholar]
- 15. Edwards A. In the balance: the accuracy of sonographic estimation of fetal weight. ASUM Bulletin 2001; 4: 3–6. [Google Scholar]
- 16. Dudley NJ, Chapman E. The importance of quality management in fetal measurement. Ultrasound Obstet Gynecol 2002; 19 (2): 190–6. [DOI] [PubMed] [Google Scholar]
- 17. Gull I, Fait G, Har‐Toov J, Kupferminc M, Lessing J, Jaffa A. Prediction of fetal weight by ultrasound: the contribution of additional examiners. Ultrasound Obstet Gynecol 2000; 20 (1): 57–60. [DOI] [PubMed] [Google Scholar]
- 18. Sarmandal P, Bailey SM, Grant JM. A comparison of three methods of assessing inter‐observer variation applied to ultrasonic fetal measurements in the third trimester. Br J Obstet Gynaecol 1989; 96: 1261–65. [DOI] [PubMed] [Google Scholar]
- 19. Chang TC, Robson S, Spencer J, Gallivan S. Ultrasonic fetal weight estimation: analysis of inter and intra‐observer variability. J Clin Ultrasound 1993; 21: 515–19. [DOI] [PubMed] [Google Scholar]
- 20. Rossavik IK, Deter R. The effect of abdominal profile shape changes on the estimation of fetal weight. J Clin Ultrasound 1984; 12: 57–9. [DOI] [PubMed] [Google Scholar]
- 21. Jeanty P, Cantraine F, Romero R. A longitudinal study of fetal weight growth. J Ultrasound Med 1984; 3: 321–8. [DOI] [PubMed] [Google Scholar]
- 22. Westerway SC, Keogh J, Heard R, Morris J. The incidence of fetal macrosomia and birth complications in Chinese immigrant women. Aust N Z J Obstet Gynaecol 2003; 43 (1): 46–49. [DOI] [PubMed] [Google Scholar]
- 23. Westerway SC. Ultrasonic fetal measurements: new Australian standards for the new millennium. Aust N Z J Obstet Gynaecol 2000; 40 (3): 297–302. [DOI] [PubMed] [Google Scholar]
- 24. Anderson NG, Jolley IJ, Wells JE. Sonographic estimation of fetal weight: comparison of bias, precision and consistency using 12 different formulae. Ultrasound Obstet Gynecol 2007; 30 (2): 173–9. [DOI] [PubMed] [Google Scholar]


