High-accuracy reference standards for two-photon absorption in the 680–1050 nm wavelength range

Abstract

Degenerate two-photon absorption (2PA) of a series of organic fluorophores is measured using femtosecond fluorescence excitation method in the wavelength range, λ_2PA = 680–1050 nm, and ~100 MHz pulse repetition rate. The function of relative 2PA spectral shape is obtained with estimated accuracy 5%, and the absolute 2PA cross section is measured at selected wavelengths with the accuracy 8%. Significant improvement of the accuracy is achieved by means of rigorous evaluation of the quadratic dependence of the fluorescence signal on the incident photon flux in the whole wavelength range, by comparing results obtained from two independent experiments, as well as due to meticulous evaluation of critical experimental parameters, including the excitation spatial- and temporal pulse shape, laser power and sample geometry. Application of the reference standards in nonlinear transmittance measurements is discussed.

1. Introduction

Spectroscopic reference standards facilitate carrying out measurements of molecular absorption- and scattering cross sections, quantum yields, etc. under circumstances, where absolute methods are overly involved or inapplicable [1]. Reference standards are even more vital in nonlinear-optical spectroscopy [2], where accurate absolute determination of the nonlinear molecular parameters requires knowledge on the instantaneous photon flux, i.e. the number of photons incident on the sample per unit time and per unit area. For this, one would need to perform equally accurate measurements of the spatial- and temporal properties of the excitation beam in a broad range of wavelengths, which, given the notorious inconsistency of tunable lasers, may pose a challenging task.

Degenerate 2-photon absorption (2PA) is a process where two photons of the same wavelength (frequency) and polarization are absorbed simultaneously [3]. The concept of reference standards in the 2PA spectroscopy is well established in the literature [4–7], and consists in calibrating the measurements performed with the sample under study with respect to the measurements performed with a suitable reference under identical conditions. In a generic 2-photon excited fluorescence (2PEF) experiment, one uses a reference standards whose 2PA spectral shape is known to find the so-called 2PA spectral shape correction function, which adjusts for the relative variation of the excitation photon flux in the wavelength range under study. In the second step, the absolute 2PA cross section value, σ_2PA, is determined at select wavelengths using a reference standard, whose absolute σ_2PA is known, and whose emission spectrum overlaps with that of the system under investigation. The final 2PA spectrum is found by scaling the shape function according to the 2PA cross section. Reference standards are also increasingly used in nonlinear transmittance (NLT) experiments [8], including z-scan [9].

In [7] a set of 2PA fluorophores were characterized using a femtosecond optical parametric amplifier (OPA) operating at 1 kHz pulse repetition rate. However, because the OPA wavelength tuning was inherently discontinuous, and the excitation pulse parameters changed abruptly between the different tuning ranges, especially at the degeneracy point around 800 nm, this previous data may contain sizable uncertainties. Experimental errors may also occur when multi-photon absorption exhibits dependence on the excitation pulse repetition rate. Since many applications use mode-locked femtosecond oscillators operating at, ~100 MHz, it is advisable that applicability of the 2PA values obtained at 1 kHz [7] is independently ascertained at higher pulse rates. Most importantly, using up to 5 orders of magnitude higher pulse repetition rates is usually accompanied by much lower peak photon flux, which, in turn, means that the relative magnitude one-photon excited fluorescence increases relative to 2PEF signal. This issue becomes most critical in case of potential overlap between the 1PA and 2PA spectra [10]. Nevertheless, due to lack of better alternatives, the data presented in [7] continues to be used under many different conditions, even if the consistency and reliability of the standards is not yet fully verified.

In this work, we strive to substantially improve the accuracy of the reference standards, both in terms of the relative 2PA spectral shape as well as regarding the absolute cross section values. Augmented accuracy is most critical for calibration and optimization of fluorophores used in multi-photon microscopy [11–13], as well as in the emerging area of quantitative 2PA spectroscopy for measuring the strength of intra- and intermolecular electric fields [14] For this purpose, we have constructed two independent experimental setups, using different 76 – 80 MHz pulse repetition rate femtosecond lasers, where one setup is optimized for the measurement of 2PA spectral shapes and the other is optimized for the absolute cross section measurement, and where we have increased the accuracy of characterization of all critical temporal-, spatial- and spectral parameters of the excitation beam. For the 2PA shape measurement, we use a ~80 MHz pulse repetition rate laser that is continuously tunable without gaps over the wavelength range of commonly-used mode-locked femtosecond sources, 680 – 1050 nm. The quadratic dependence is measured with high fidelity for each wavelength, thus minimizing potential artifacts. The new reference fluorophores set comprises both commercial organic dyes such as Prodan, Coumarin 153 (C153), Fluorescein and Rhodamine 590 (Rh 6G), but also two custom-synthesized compounds 4,4’-Bis-(diphenylamino)-stilbene (BDPAS) and 7,7',7”-(1,3,5-triazine-2,4,6-triyl)tris[9,9-didecyl-N,N-diphenyl 9H-Fluoren-2-amine CAS Registry Number, 517874-02-13 (AF455), were the latter two possess a superior peak 2PA value compared to the commercial counterparts. Perylene, Lucifer yellow and chloroanthracenes show relatively low peak 2PA cross section, σ_2PA < 10 GM (1 GM = 10⁻⁵⁰ cm⁴ s photon⁻¹), and were therefore not considered in the present set. Solutions of Rhodamine 610 (Rhodamine B), on the other hand, even though showing a relative large peak σ_2PA, exhibit undesired dependence of the absorbance on the concentration and temperature, most likely due to the presence of different equilibrium forms (protonated cation, zwitterion and lactone) [15,16], and were therefore excluded from current measurements. The fluorescence emission spectral range, 375 - 600 nm, is chosen to match the emission wavelengths of common fluorescent microscopy probes such as green fluorescent proteins. Finally, in order to cover a sufficiently broad wavelength range, we take advantage of large solvatochromic and fluorosolvatochromic shifts of the 1PA and 2PA spectra of some of the chromophores.

2. Theoretical considerations

When a monochromatic beam of light propagates through a thin slab of 2-photon absorbing medium, then the difference between the input- and output photon flux (in photon cm⁻² s⁻¹) may be expressed as:

$$\Delta I_{2PA}=-{\sigma }_{2PA}{N}_c\Delta z{I}_{2PA}^2,$$ (1)

where the σ_2PA is in cm⁴ s photon⁻¹, N_c is the 2-photon fluorophore concentration (in cm⁻³), Δz is the thickness (in cm) and I_2PA is the incident photon flux. In most cases, the flux changes only by a relatively small amount, ΔI_2PA << I_2PA, which makes measurement of ΔI_2PA, and, accordingly, accurate determination σ_2PA difficult. Alternatively, one can use the relation between the 2PA cross section and the corresponding 2-photon excitation rate,

$${\dot{n}}_{2PA}=\frac{1}{2}{\sigma }_{2PA}{I}_{2PA}^2,$$ (2)

where the latter is determined from experiment by detecting 2PEF emitted by the chromophores, whereas some other detection schemes involving e.g. phosphorescence [17], generation of heat [18] or acoustic waves [19], have also been demonstrated.

Suppose that the 2PEF medium is excited by a periodic train of ultrashort pulses at the rate g (in Hz), and the wavelength, λ_2PA. Then the average fluorescence signal may be expressed as:

$$F_{2PA}({\lambda }_{2PA})=\Delta t_{2PA}\left[g{N}_c\frac{1}{2}{\sigma }_{2PA}({\lambda }_{2PA})\Delta z{\displaystyle \iiint I_{2PA}^2}(t,x,y;{\lambda }_{2PA})dxdydt\right]\left[{\displaystyle \underset{{\lambda }_{\min }}{\overset{{\lambda }_{\max }}{\int }}\eta ({\lambda }_{em})\varphi ({\lambda }_{em})d{\lambda }_{em}}\right],$$ (3)

where Δt_2PA is the fluorescence detector integration time, φ(λ_em) is the differential quantum efficiency of fluorescence emission at the emission wavelength, λ_em, and η(λ_em) is the aggregate detection efficiency that accounts for the efficiency of fluorescence collection, spectrometer/diffraction grating through-put, efficiency of the detector, etc. The differential quantum efficiency is defined as,

$${\displaystyle \underset{0}{\overset{\infty }{\int }}\phi ({\lambda }^{\prime })d{\lambda }^{\prime }}=Q,$$ (4)

where Q is the standard quantum yield, equal to the ratio of the radiative decay rate to the total decay rate of the S₁ state. The quantity enclosed in the first square brackets in Eq. (3) stands for the average number of molecules excited per second, while the quantity inside the second square brackets accounts for the fluorescence signal that is detected within a finite wavelength interval. If the photon flux, I_2PA(t, x, y;λ_em), and the parameters, η(λ_em) and φ(λ_em), were known, then the relation Eq. (3) could be immediately used to evaluate the cross section, σ_2PA(λ_2PA). As was pointed out above, this information is, however, rarely available. At this point it is convenient to present the photon flux as a product of four factors:

$$I_{2PA}(t,x,y;{\lambda }_{2PA})=\frac{P_{2PA}({\lambda }_{2PA})}{t_{ave}{S}_{ave}}{f}_{time}(t)f_{area}(x,y)f_{corr}({\lambda }_{2PA}),$$ (5)

where P_2PA is the total number of photons in the excitation pulse, t_ave is the average pulse duration, S_ave is the average beam area, f_time and f_area are the normalized functions describing, respectively, the temporal pulse shape and spatial beam profile and f_corr is the so-called wavelength-dependent correction function that quantifies the deviation of the pulse parameters from the average value as a function of λ_2PA.

If the Kasha-Vavilov rule is obeyed, then we are allowed to assume that the differential quantum efficiency is independent of the excitation wavelength, and the relative 2-photon absorption spectrum may be obtained then measuring F_2PA as function of λ_2PA:

$${\sigma }_{2PA}^{rel}({\lambda }_{2PA})=c_{norm}\frac{F_{2PA}({\lambda }_{2PA})}{P_{2PA}^2({\lambda }_{2PA})f_{corr}^2({\lambda }_{2PA})}.$$ (6)

Since we are dealing here only with the 2PA spectral shape, we can set the empirical normalization factor, c_norm, such that the peak value equals unity, max(σ_2PA^rel) = 1.

To obtain the absolute 2-photon cross section, we need to know the value of the quantity enclosed in the second square bracket in Eq. (3). If we excite the fluorescence by 1-photon absorption in the same sample, using exact same experimental geometry and same fluorescence detection as in the 2-photon measurement, then the corresponding 1-photon excited fluorescence signal may be expressed as:

$$F_{1PA}=\Delta t_{1PA}\left[(1-{10}^{-OD}){\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{I}_{1PA}(x,y)dxdy}\right]\left[{\displaystyle \underset{{\lambda }_{\min }}{\overset{{\lambda }_{\max }}{\int }}\eta ({\lambda }_{em})\varphi ({\lambda }_{em})d{\lambda }_{em}}\right],$$ (7)

where I_1PA is the time-average photon flux, Δt_1PA is the fluorescence signal integration time and OD = N_cσ_1PAΔz is the optical density of the sample and σ_1PA is the 1-photon absorption cross section at the 1-photon excitation wavelength. Here the quantity in the first square brackets represents the number of molecules excited per second, whereas the second term is the same as in Eq. (3). Note that the one-photon excitation rate depends neither on the beam spatial profile nor on its temporal structure. By combining Eqs. (3) and (7), we can express the absolute 2PA cross section as:

$$\begin{array}{l}{\sigma }_{2PA}({\lambda }_{2PA})=\frac{F_{2PA}({\lambda }_{ex})}{F_{1PA}({\lambda }_{1PA})}\frac{\Delta t_{1PA}}{\Delta t_{2PA}}\frac{2(1-{10}^{-OD}){\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{I}_{1PA}(x,y)dxdy}}{g{N}_c\Delta z{\left[\frac{P_{2PA}({\lambda }_{2PA})f_{corr}({\lambda }_{2PA})}{t_{time}{S}_{area}}\right]}^2{\displaystyle \iiint f_{time}^2(t)f_{area}^2(x,y)dxdydt}}.\\ \end{array}$$ (8)

3. Experimental

3.1 Materials, linear spectroscopy and sample preparation

Prodan, C153, Fluorescein and Rh 6G were obtained from Aldrich and were used as received. BDPAS was custom-synthesized by K. Schanze group (U of Florida) as described in [8]. AF455 was provided by Dr. S. Tan from the Air Force Research Laboratory. The synthesis of AF455 is described in [20, 21]. All solvents were purchased from Sigma-Aldrich and were used without further purification. Stock solutions were prepared by mixing the solvent with 1 − 3 mg of dry dye, where the latter was weighed using Mettler-Toledo Model AT2611 analytical balance. Linear absorption spectra were obtained with Shimadzu UV-3600Plus spectrophotometer and corrected fluorescence spectra were measured with Perkin-Elmer Fluorimeter LS55. Extinction coefficients were determined by the dilution method, where a set of daughter solutions with maximum absorbance in the range OD = 0.5 - 1.5 were prepared from the stock solution. The samples were contained 1 cm quartz cuvettes. The chromophore concentration used in the 2PA and 1 PA measurements was in the range 10⁻⁶ - 10⁻³ M.

3.2 Measurement of relative 2PA spectral shape function

Schematic of the 2PA spectral shape measurement setup is shown in Fig. 1(a) . In this part of the experiment, we use 80-MHz repetition rate femtosecond laser (Spectra-Physics InSight DeepSee) continuously tunable in the 680-1300 nm wavelength range with average output power 0.6 – 1.5 W. The laser output was spatially-filtered by focusing the beam through a 50 μm diameter pinhole. To avoid thermal lensing effects in the sample the average laser power was reduced by factor 10 using a 100 Hz chopper wheel. The collimated beam was focused with f = 400 mm achromatic lens (Thorlabs) and passed through a motorized variable transmittance circular neutral density filter (OD = 0.1 – 2.0). Beam reflected from a flat glass plate positioned in front of the sample was detected with a pyroelectric pulse energy probe (Molectron) and was used as reference. The variation of the responsivity of the reference detector at different wavelengths was calibrated relative to a thermoelectric probe (Ophir P1) and did not exceed +/− 2% in the 680 −1100 nm range. The focused beam intensity profile at the sample was measured using a microscope objective and CCD camera (Allied Stingray) in the 680 −990 nm range and InGaAs SWIR camera (Xenics Bobcat 320) in the 970 – 1100 nm range. The measured spot size varied in the range 0.2 – 0.4 mm depending on the wavelength. The pulse duration was measured with custom-adapted auto-correlator using a scanning delay line (ODL-150, Clark MXR) and 0.1 mm thick BBO crystal set up for non-collinear SHG with computer-controlled phase matching angle adjustment. The laser spectrum was measured with a diffraction grating spectrometer (OceanOptics USB4000). The fluorescence from the sample was collected at 90° angle with respect to the propagation direction and vertical linear polarization of the excitation beam. The fluorescence was directed through a stack of short-pass filters to a photomultiplier (Hamamatsu R777) working in current detection mode. The output voltage from the photomultiplier and the reference detector were directed to respective A/D converters (National Instruments USB6009). The sample solutions were contained in 1-2 mm path length spectroscopic cuvettes to minimize effect of absorption by the solvent. Iris diaphragms were used to monitor alignment of the laser beam.

Fig. 1.

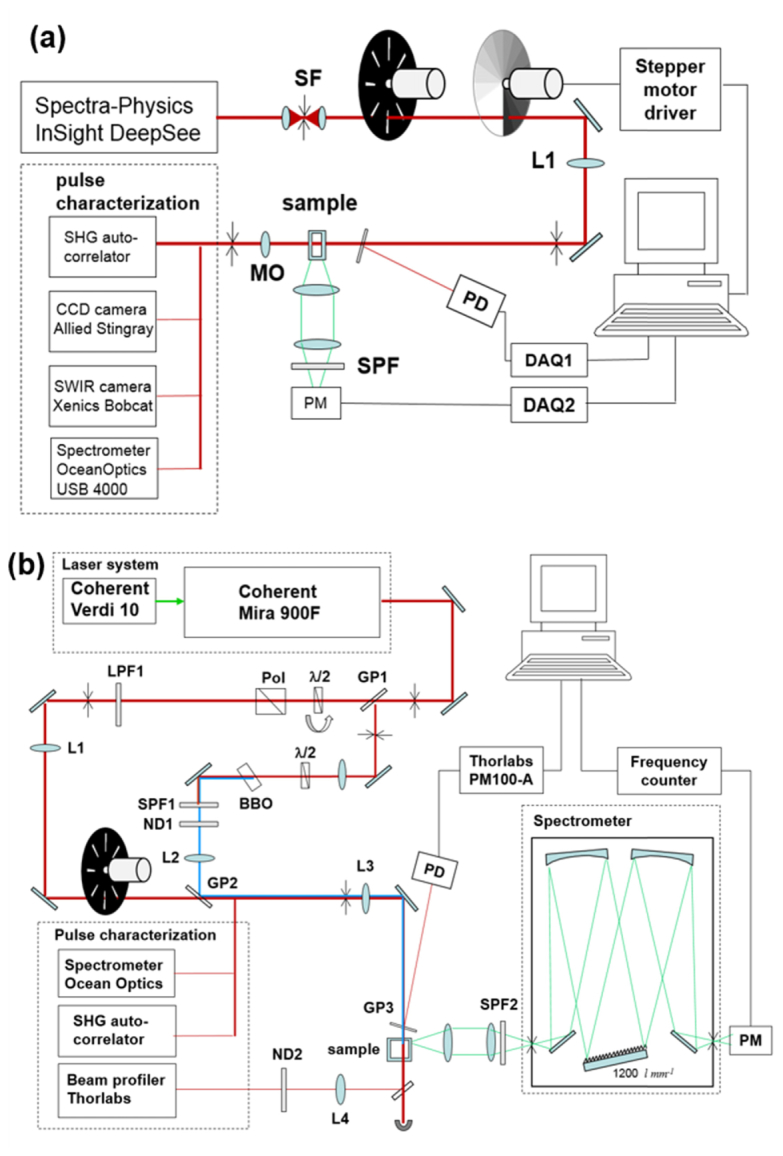
Schematics of experimental set-ups; (a) Measurement of relative 2PA spectra; (b) Measurement of absolute 2PA cross section. SF – spatial filter; L1, L2, L3, L4 – focusing lenses; MO – microscope objective; ND – neutral density filter wheel; SPF – short-pass glass filter; LPF – long-pass glass filter; GP – glass plate; PM – photomultiplier; DAQ – data acquisition, A/D converters; Pol - Glan-Taylor polarizer; PD – photodetector.

The relative 2PA cross section spectra were measured by varying the laser wavelength with 2nm steps in the 680 – 1100 nm range and by measuring at each wavelength the dependence of the fluorescence signal on the incident photon flux by varying the transmittance through the OD filter in 20 discrete steps. The control of the laser wavelength, setting of the OD filter wheel and acquisition of the fluorescence- and reference signals was accomplished using PC via LabView program. The average time for tuning the laser and collecting the data was about 40 - 60 s per one wavelength step.

3.3 Measurement of absolute 2PA cross sections

Schematic of the setup is shown in Fig. 1(b). Here we used a 76-MHz pulse repetition rate mode-locked Ti:Sapphire femtosecond oscillator (Coherent Mira 900) pumped by 10 W cw frequency-doubled Nd:YVO₄ laser (Coherent Verdi V-10). The femtosecond laser wavelength was tuned manually in the range 690 - 960 nm with the average output power varying in the range 0.5 – 1.5 W.

The fundamental laser spectrum was measured with diffraction grating spectrometer (OceanOptics USB4000). The pulse temporal shape was measured with a modified optical auto-correlator (INRAD 5-14A), where the variable delay was produced by rotating glass plates (glass thickness 1 mm) and non-collinear second harmonic generation was produced in 0.1 mm BBO crystal. The spatial beam profile at the sample location was measured with the CCD-camera based beam profiler (Thorlabs BC106-VIS) (the sample was removed for these measurements).

To minimize detrimental effect of thermal lensing in the optical elements and in the sample, the average fundamental laser power was reduced by factor 10 using a 100 Hz optical chopper (Thorlabs MC2000). The fundamental power reaching the sample was further varied by manually rotating a λ/2 plate that was positioned in front of a Glan-Taylor polarizer (GL10-B Thorlabs) (Pol). The relative average power of the fundamental beam at the sample was monitored by reflecting a portion of the incident beam to integrating sphere silicon photodetector (Thorlabs S140C) coupled to optical power meter (Thorlabs PM100A). Absolute fundamental power was measured with optical power meter (Coherent FieldMate) with thermoelectric probe (Coherent Powermax PM10) placed directly in front of the sample. Single reflection (~4%) off a glass plate (GP1) was focused on a Type I phase matched BBO crystal that generated second harmonic (blue) light, which was then recombined with the main fundamental wavelength beam using the second glass plate (GP2). At short wavelengths, ~700 nm, the glass plate was replaced by a flipping mirror to compensate for drop in laser output power. A λ/2 plate in front of the SHG crystal rotated the pump beam polarization to the horizontal direction in order to assure that the second harmonic beam had the same (vertical) polarization as the fundamental beam, After GP2 the two beams followed the same path and were incident on the same spot at sample. The blue beam power was adjusted by using continuously variable metallic-coated filter wheel (ND1), and the corresponding power was measured with integrating sphere silicon photodetector (Thorlabs S140C) or with standard silicon photodetector (Thorlabs S120VC) placed directly in front of the sample.

A combination of focusing and collimating lenses (L1 - L3) were used to shape both beams so that they have approximately the same spot size, ~0.3 mm. A color glass long-pass filter (LPF1) was used to cut off residual short-wavelength pump laser light and a glass short-pass filter (SPF1) was used to cut off residual fundamental wavelength after the SHG crystal.

Fluorescence signal was collected in 90° geometry and focused on the entrance slit of a scanning diffraction grating spectrometer (LOMO MDR-12). Scattered laser light was additionally suppressed by a stack of short-pass color glass filters (SPF2). The fluorescence signal was detected with a photon counting module (Hamamatsu H6240-01) coupled to a frequency counter with PC readout.

The absolute cross-section was determined at a fixed wavelength by measuring the fluorescence signal on the incident photon flux in both 1PA and 2PA successively and all the laser characterization, e.g. spectral profile, beam profile and temporal profile. Average time needed to evaluate absolute 2PA cross section at 1 wavelength, including stabilizing the laser mode-locking, setting the laser wavelengths and performing the beam characterization measurements, was about 4 h.

4. Results

The normalized fluorescence spectra are shown in Fig. 2 . The corresponding peak- and min/max fluorescence wavelengths are listed in Table 1 .

Fig. 2.

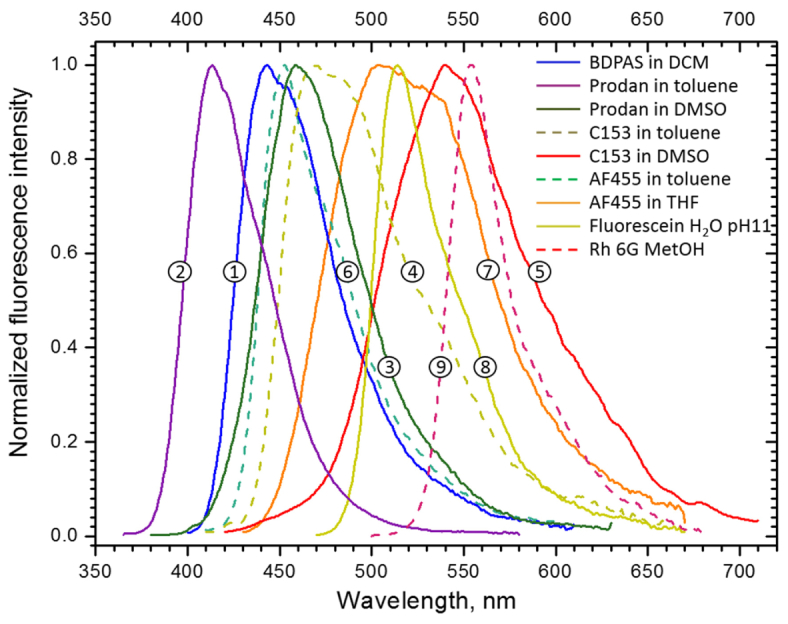
Corrected fluorescence spectra of (1) BDPAS in methylene chloride; (2) Prodan in toluene; (3) Prodan in DMSO; (4) C153 in toluene; (5) C153 in DMSO; (6) AF455 in toluene; (7) AF455 in THF; (8) Fluorescein in H₂O pH11 buffer; (9) Rh 6G in Methanol.

Table 1. 1-photon and 2-photon photophysical properties of the systems studied. The σ_2PA and Δσ_2PA values are obtained by averaging over all measurements performed.

	Comp.	Solvent	ε (λ1PA)	min λem–max λ em (peakλem)	σ2PA(λ2PA)	Δσ2PA
			M-1 cm-1 (nm)	nm	GM (nm)	±%
1	BDPAS	DCM	52.6x103 (388)	415 – 540 (443)	175 (690) 138 (700)	8 8
2	Prodan	toluene	19.8x103 (349)	390 – 480 (414)	19 (700)	6
3	Prodan	DMSO	17.5x103 (358)	420 – 550 (459)	20 (723)	8
4	C153	toluene	20.5x103 (408)	440 – 600 (468)	17 (816)	5
5	C153	DMSO	18.5x103 (427)	480 – 650 (540)	17 (851)	7
6	AF455	toluene	117x103 (419)	430 – 550 (453)	404 (784)	7
7	AF455	THF	106x103 (415)	450 – 630 (504)	392 (784)	6
8	Fluorescein	H2O pH11	88.6x103 (491) 8.7x103 (322)	490 – 580 (514)	26 (785) 6.5(860)	5 8
9	Rh 6G	MetOH	122x103 (528) 12.1x103 (347)	580 – 630 (554)	79 (812) 202 (692)	8 8

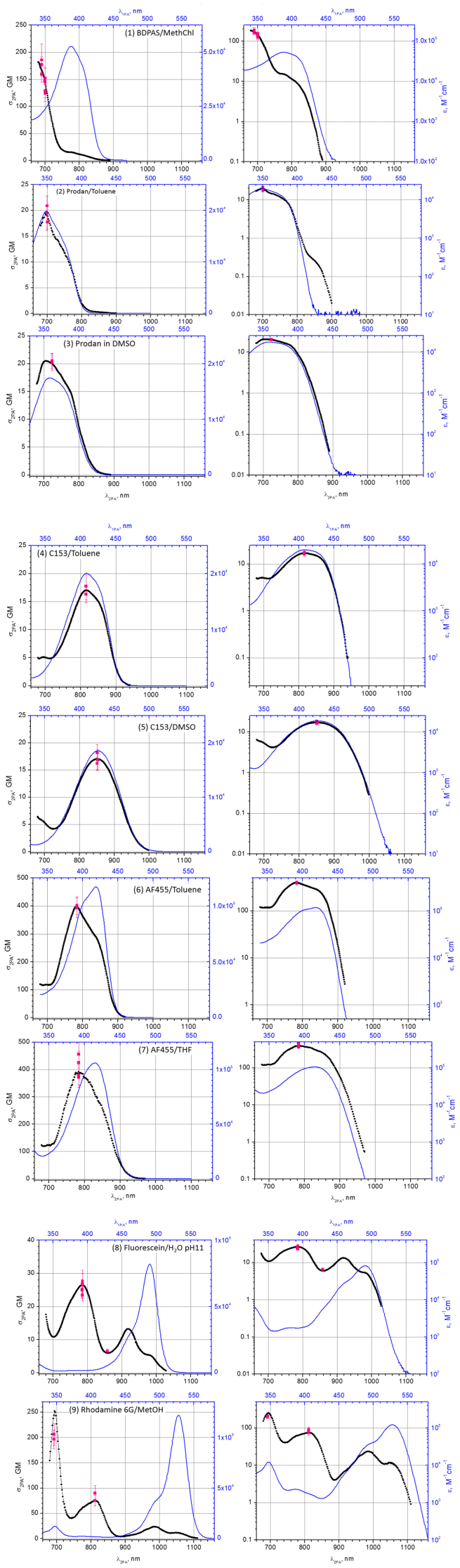
The 2PA spectral shapes are presented in Fig. 3 by black symbols, and the corresponding absolute cross section measurements are shown as red squares. The shape functions are scaled to give the best match with average absolute cross sections at the select wavelengths. The linear extinction spectra are shown by blue solid line. The two panels (left and right) present the same data in the linear and logarithmic vertical scales. The lower horizontal axis of the plots is calibrated in the wavelength of the 2-photon excitation (λ_2PA), while the upper axis is calibrated in 1-photon absorption wavelength (λ_1PA). The same data is presented in Table 2 in the Appendix.

Fig. 3.

2PA spectra of (1) BDPAS in methylene chloride; (2) Prodan in toluene; (3) Prodan in DMSO; (4) C153 in toluene; (5) C153 in DMSO; (6) AF455 in toluene; (7) AF455 in THF; (8) Fluorescein in H₂O pH11 buffer; (9) Rh 6G in methanol.

Table 2. 2-photon cross sections (GM) of the dyes at selected wavelengths (nm). The maximum relative error of the numbers shown here is given in Table 1. Please note that the values in Table 1 are obtained directly from measuring the absolute cross section at few select wavelengths, and as shown in Fig. 3, whereas the values shown here are the best fit by scaling the experimentally measured shape function according to the absolute cross section data.

λ2PA (nm)	σ2PA (GM)
	BDPAS MethCl	Prodan toluene	Prodan DMSO	C153 toluene	C153 DMSO	AF455 toluene	AF455 THF	Fluor. H2O pH11	Rh6G MetOH
680	179	17	16	4.9	6.4	122	123	17	162
690	166	19	19	5.0	5.8	119	120	12	248
700	146	19	20	5.0	5.3	120	123	11	237
710	108	17	20	4.8	4.6	120	126	11	145
720	74	15	20	4.9	4.2	137	144	13	76
730	46	14	20	5.4	4.2	177	186	16	51
740	28	13	19	6.4	4.5	231	240	19	43
750	20	12	18	7.6	5.2	284	288	21	44
760	16	10	17	9.1	6.3	331	327	23	50
770	15	8.9	16	11	7.7	374	366	24	60
780	15	6.6	14	13	9.3	403	390	26	65
790	13	4.0	12	14	11	396	388	26	70
800	11	2.1	8.7	16	13	372	374	24	73
810	10	1.1	6.4	17	14	350	361	21	78
820	8.3	0.62	4.3	17	15	330	341	16	76
830	6.3	0.39	2.6	16	16	309	310	11	62
840	4.4	0.31	1.5	16	17	290	285	7.8	44
850	2.6	0.26	0.83	15	17	260	260	6.2	26
860	1.3	0.21	0.42	14	17	210	223	5.8	14
870	0.64	0.15	0.20	12	16	148	180	6.2	7.5
880	0.24	0.08	0.09	8.6	15	83	131	7.0	4.7
890		0.04	0.04	5.7	14	42	89	8.3	4.3
900			0.02	3.3	13	20	59	10	5.1
910				1.7	11	7.6	36	12	6.3
920				0.75	9.0	2.8	20	13	7.5
930				0.31	7.0		11	12	8.9
940				0.10	5.2		4.9	9.8	11
950					3.7		2.3	7.3	14
960					2.5		1.1	6.1	18
970					1.6		0.54	5.4	21
980					0.94			5.2	24
990					0.51			4.6	24
1000								3.3	21
1010								2.1	17
1020								1.2	13
1030									11
1040									11
1050									12

Key 2-photon data for all 9 standards, along with the peak molecular extinction coefficient, and estimated maximum fluorophore concentration and the solution stability assessment, is collected in Table 1. The peak cross section value for BDPAS in methylene chloride (1), σ_2PA = 175 ± 14 GM, is less than was reported earlier [7], which we attribute to relatively rapid photo-degradation and low dark stability of the solution [8]. In our current measurements all precautions were taken by continuously monitoring the sample for signs of potential degradation. Note that BDPAS is especially useful in case of blue-emitting fluorophores, and in the wavelength range, λ_2PA = 680 – 860 nm. At longer wavelengths, the cross section drops below 1 GM. Prodan in toluene (2) and in DMSO (3) have also relatively short wavelength fluorescence emission. These solutions showed no measurable degradation over a period of several months, even though their peak cross section is also lower, σ_2PA ~17 GM. Remarkable feature of C153 in DMSO is that its 2PA and 1PA profiles practically coincide in the range λ_2PA = 740 - 1000 nm. Physical background of this phenomenon was recently discussed in [14]. The peak cross section of Fluorescein (aqueous, pH11) (8) is σ_2PA = 26 ± 1.2 GM at 780 nm. This is again about factor 2 less than the earlier reported value [7], most likely because this wavelength coincides with degeneracy of the OPA, where the beam parameters may deteriorate. In our current measurement this issue did not occur. We should note that relative 2-photon cross sections reported for Prodan and C153 in [14] were measured using the Fluorescein data from [7], which may have led to over-estimation of σ_2PA. Rh 6G in methanol (9) absorbs and emits at the longest wavelengths,compared to other fluorophores in the current set. The absolute cross section at 810 nm is, σ_2PA = 79 ± 6 GM, and correlates well with the value reported in [5]. However, both the absolute value and the shape function are higher at 690 nm. This discrepancy is most likely caused by the narrow spectral band at, λ_2PA = 680 - 710 nm. The spectral FWHM of the excitation pulses in that particular wavelength range was measured to be Δλ_2PA = 3 - 4 nm, i.e. is comparable to the half-width of the named band. For comparison, in the earlier measurements the pulses were spectrally about factor of two broader [5], which may explain why the spectral feature appears more pronounced in the current data. We must underline that,contrary to 1-photon spectroscopy, where spectral retrieval via deconvolution can be quite effective, inherent nonlinear nature of the 2PA precludes application of such straightforward techniques [22].

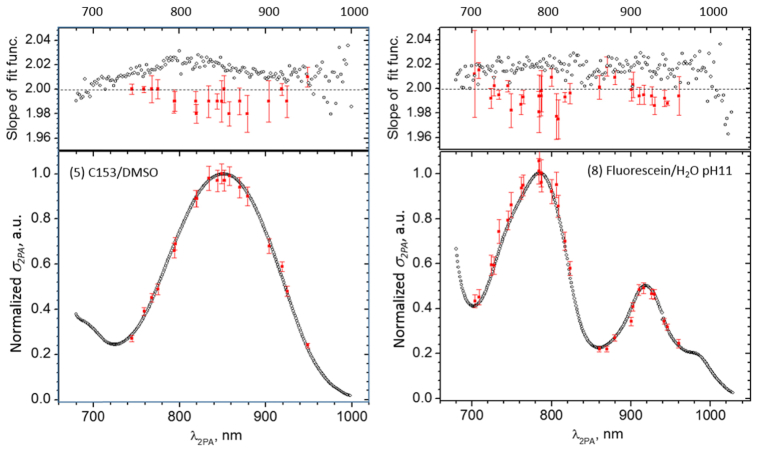
5. Evaluation of experimental uncertainty

Main causes of experimental uncertainty in the relative spectral shape measurement are due to (a) deviation from the quadratic dependence of the 2PEF signal on the photon flux and (b) errors in the determination of the temporal- and spatial shape of the laser beam. The quadratic power dependence was ascertained at each wavelength by varying the average incident power over ~2 orders of magnitude, and by fitting the resulting 2PEF signal vs. power data, presented in double-logarithmic scale, with a linear function. The measurements accepted have a power law coefficient in the 1.96-2.04 range. Upper panels in Fig. 4 shows the power law coefficient in C153 in DMSO (left) and in Fluorescein (right) obtained in the relative 2PA spectral shape experiment (empty symbols). The power dependence measurement was performed also on the absolute 2PA experimental systems (filled rectangles), and showed very similar behavior. Even though different measurement systems behave slightly differently, the maximum deviation from the exact quadratic dependence does not exceed 3%. In order to further verify the measured spectral shape functions, we performed a relative 2PA shape measurement for a few select standards using the absolute 2PA measurement setup. Lower panels in Fig. 4 show the corresponding normalized shape functions for C153 in DMSO (left) and in Fluorescein (right), measured by the two complementary experiments. The discrepancy between the two measurements does not exceed 4%. This allows us to estimate that the overall uncertainty of the 2-photon shape functions presented here is about 5%. Since the two experiments were truly independent, we conclude that the relative accuracy of measuring the photon flux and, accordingly, the relative beam spatial- and temporal profiles, was also about5% or less. In the case of the absolute cross section measurement, there is an additional uncertainty due to the measurement of the 1-photon excited fluorescence. Firstly, for this measurement, the 1-photon excitation beam should be aligned to illuminate the exact same sample volume as the 2PEF excitation beam. If the beams are even slightly misaligned, then the two fluorescence signals may no longer be collected from the exact same sample volume. Secondly, because the maxima of the 2-photon and 1-photon spectra do not always coincide, when we tune the 2-photon excitation wavelength near the peak of the 2PA spectrum, then the corresponding 1-photon excitation wavelength may be located where the linear absorbance is very low or changes abruptly, thus making it difficult to accurately determine how many photons are absorbed in the sample When combined with the above 5% error due to the characterization of the excitation beam, we arrived at the estimated maximum uncertainty of the 2-photon cross section value of about 8%.

Fig. 4.

. Comparison between independent 2PEF measurement techniques in two reference samples: C153 in DMSO (left) and Fluorescein in aqueous, pH11 (right). Upper panel: Experimentally determined power law coefficient as a function of laser wavelength measured using the scanning laser setup (empty symbols) and manually-tuned laser setup (filled symbols). Lower panel: 2PA shape functions measured by the scanning laser setup (empty symbols) and manually tuned laser setup (filled symbols). The maximum value of the shape functions is normalized to unity. The manually-tuned data is averaged over 9 measurements in C153 and 3 measurements in Fluorescein.

6. Application notes

How to apply reference standards in the 2PEF-based measurements was described previously in [7]. Here, we would like to briefly discuss the utilization of the reference standards for augmenting nonlinear transmittance-type experiments [2, 9, 24, 25]. According to the Eq. (1), the photon flux passing through a thin layer of 2-photon absorbers decreases in proportion to the number density of the absorbers. In case of finite thickness, it is useful to introduce the effective NLT strength,

$${\kappa }_{2PA}={\sigma }_{2PA}{N}_{c}d,$$ (9)

where d is the sample thickness. If d is expressed in cm, the chromophore concentration N_c is given in mM (10⁻³ M) and σ_2PA is expressed in GM, then the maximum effective NLT strength would be typically in the range, κ_2PA = 1 - 10². The chromophores described here have been selected to exhibit good solubility in their respective solvents, with the maximum concentration, ~5 – 10 mM. By using d = 1 cm and selecting the standards that have σ_2PA > 10 GM, an sufficiently large value, κ_2PA > 10, may be achieved in the whole wavelength range 680 - 1050 nm. Also, because the reference samples are often exposed to intense laser light, the solutions were evaluated for photo-stability as well as for dark storage stability over a period of about 1 month. Out of the samples tested, only BDPAS in DCM showed an increased photo-induced decomposition [8], which was accompanied by relatively short dark stability of less than ~1 week. One might assume that larger κ_2PA would allow larger maximum absolute change of the transmittance, |ΔT_max|, which, in turn, would facilitate more accurate determination of σ_2PA values. However, depending on the beam parameters, the nonlinear transmittance may exhibit a quite complicated dependence on the incident photon flux [25]. For this reason, special care should be taken not to use excessively large κ_2PA values, especially if the sample and the reference have very different NLT signals. Based on practical experience, if the maximum transmittance change of both the sample and the reference is, |ΔT_max| < 10%, then one can obtain the 2PA spectrum of the sample under study by using the relation,

$${\sigma }_{2PA}({\lambda }_{2PA})={\sigma }_{2PA}^{ref}({\lambda }_{2PA})\frac{B_{NLT}({\lambda }_{2PA})}{B_{NLT}^{ref}({\lambda }_{2PA})}\frac{N_c^{ref}{d}^{ref}}{N_{c}d},$$ (10)

where σ_2PA^ref is the 2PA spectrum of the reference standard, N_c^ref and d^ref are, respectively, the concentration and the thickness of the reference sample and the coefficients B_NLT and B^ref_NLT are obtained from fitting the measured nonlinear transmittance as a function of the number of incident photons with the linear function,

$$f_{lin}=1-B_{NLT}{\displaystyle \iiint I_{2PA}}(t,x,y;{\lambda }_{2PA})dxdydt.$$ (11)

Still another potential issue in the NLT measurements stems from near-IR absorption of common solvents. For example, at the wavelengths > 900 nm both toluene and DMSO show peak absorbance, A_max~0.1, in 1 cm cuvette. One way to minimize the uncertainty caused by solvent absorption would be to either use the same solvent for the reference as for the system under study, or if that is not feasible, then to subtract from the 2PA spectrum given by the Eq. (10) the artifacts that may be present when the measurement is performed with the neat solvent.

7. Conclusions

We presented absolute two-photon absorption spectra of a series of organic fluorophores in the excitation wavelength range, 680 - 1050 nm, By using stable femtosecond lasers and by cross-checking independently performed measurements, we have achieved accuracy of at least 5% for the shape of the 2PA spectra and 8% for in the absolute 2PA cross section values. This constitutes at least a factor of 4 - 5 improvement compared to the previously established 2-photon reference standards. The chromophores were selected to provide improved solubility and stability and are therefore well suited not only for the 2PEF-based experiments, but also for calibration of nonlinear transmission measurement, which often require higher sample concentration. The new data further alleviates the need for tedious characterization of the excitation laser parameters and allows for quantitative comparison and optimization of molecular probes used in multiphoton microscopy and imaging, for quantifying the multiphoton absorption efficiency of chromophores in different environments, as well as many other applications of nonlinear optics and -spectroscopy.