Abstract
Interest in time resolved flow cytometry is growing. In this paper, we collect time-resolved flow cytometry data and use it to create polar plots showing distributions that are a function of measured fluorescence decay rates from individual fluorescently-labeled cells and fluorescent microspheres. Phasor, or polar, graphics are commonly used in fluorescence lifetime imaging microscopy (FLIM). In FLIM measurements, the plotted points on a phasor graph represent the phase-shift and demodulation of the frequency-domain fluorescence signal collected by the imaging system for each image pixel. Here, we take a flow cytometry cell counting system, introduce into it frequency-domain optoelectronics, and process the data so that each point on a phasor plot represents the phase shift and demodulation of an individual cell or particle. In order to demonstrate the value of this technique, we show that phasor graphs can be used to discriminate among populations of (i) fluorescent microspheres, which are labeled with one fluorophore type; (ii) Chinese hamster ovary (CHO) cells labeled with one and two different fluorophore types; and (iii) Saccharomyces cerevisiae cells that express combinations of fluorescent proteins with different fluorescence lifetimes. The resulting phasor plots reveal differences in the fluorescence lifetimes within each sample and provide a distribution from which we can infer the number of cells expressing unique single or dual fluorescence lifetimes. These methods should facilitate analysis time resolved flow cytometry data to reveal complex fluorescence decay kinetics.
OCIS codes: (170.1420) Biology; (170.3650) Lifetime-based sensing; (170.6280) Spectroscopy, fluorescence and luminescence; (300.2530) Fluorescence, laser-induced
1. Introduction
Flow cytometry is a powerful means for analysis of single cells. It has been exploited for many decades mainly because it provides knowledge about the distribution and heterogeneity of phenotypes of individual cells within cell populations. Flow cytometers collect data on the number of cells that have a particular phenotype (or genotype and shape), often with the help of fluorescent agents bound to receptors, proteins, nucleic acids, organelles, or other places within or on the surface of the cell. Flow cytometers can be configured in different ways to collect different kinds of data. For example, an instrument can detect (i) multiple fluorescence emission colors from every single cell; (ii) a full spectrum of fluorescence emission from individual cells; (iii) light scattered by individual cells in different directions; and (iv) fluorescence decay times, represented as the average fluorescence lifetime. The first three approaches are consistently used and available on commercial cytometers. The last, the measurement of time-resolved signals [1–5], is not so widely used.
We have recently worked to advance time-resolved flow cytometry by building and modifying cytometers to measure fluorescence lifetimes. We have demonstrated instruments that use digital laser modulation or pulsation, high speed data acquisition, and digital signal processing to provide fluorescence lifetime-based values for cell counting or sorting that operate at rates of thousands of cells per second [6–9]. These approaches for measuring fluorescence lifetimes with flow cytometers have involved both frequency-domain as well as time-domain methods.
We and others have demonstrated different versions of time-resolved flow cytometry [3, 7–14], and the main objective for augmenting flow cytometers to detect fluorescence lifetimes is to enhance cytometric data with a quantitative parameter that is independent of the measured fluorescence intensity [11, 15–17]. As a parameter, fluorescence lifetime can be used to discriminate among spectrally overlapping fluorescence signals as well as to validate the fluorescence intensity changes that arise from quenched fluorophores such as during Förster resonance energy transfer (FRET) events like those arising from changes in association state of tagged cytoplasmic proteins. A variety of cellular applications might include use of fluorescence lifetimes to discriminate among multiple exogenous fluorophores labeled to cell surface receptors (i.e. immunofluorescence), to correlate the fluorescent protein intracellular location with fluorescence decay kinetics, to sort cells that express fluorescent proteins with high quantum yields (because QY is proportional to the fluorescence lifetime), or to detect shifts in cellular metabolism for large populations of cell using autofluorescence lifetime shifts of the bound state of NADH [15, 18–21]. These listed applications are but a few among many reasons to measure the decay kinetics of fluorescent species in order to understand intracellular biochemistry and molecular events, or to detect protein conformational changes.
Among the various time-resolved flow cytometry systems described in the literature, none measure the presence of multiple fluorescence lifetime components in a single color channel. We have sought to address this gap by developing laser-pulsed systems [8] and by exploiting square-wave modulation [9], an extension of work on double-frequency modulation systems [22]. Issues in getting these systems to work include low signal to noise and modulation depth in the fluorescence signals collected at high frequencies, frequency aliasing, required high frequency bandwidth in the detection and data acquisition hardware, and time-consuming data analysis steps. Here, we describe another approach, phasor plotting. This approach can be used with existing systems to measure two independent fluorescence decay-dependent values from individual cells, obtained at a single frequency, and can indicate whether or not the measured signal can be attributed to a single or dual-lifetime component.
In this letter we show how to take cytometry data and generate phasor plots to determine independent fluorescence lifetime components in a measured signal from a single cell. A phasor plot combines the phase shift, ϕ, and demodulation, m, parameters from a frequency-domain fluorescence measurement. Within a phasor plot, points on a graph are at a radial distance from the pole, which is equal to the measured demodulation, m. The angle between the phasor axis (x-axis) and the radius is called the phasor angle, which is equal to the angle of phase shift, ϕ, as shown in Fig. 3. Presenting data in this fashion provides a visual tool to reveal differences in fluorescence lifetimes as a result of the phase shift and demodulation values.
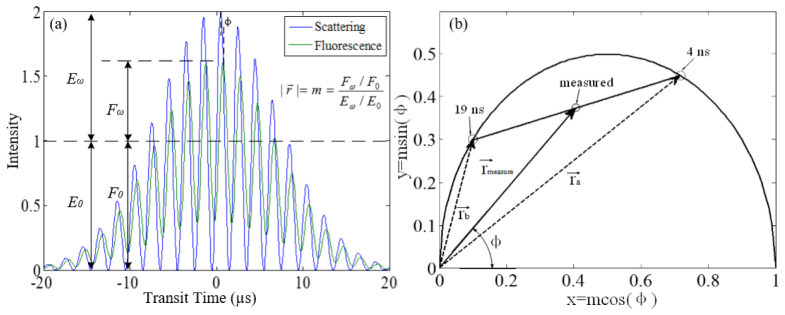
Fig. 3.
The transfer from a raw data of an event (a) to one dot in the phasor plot where the dots located on semicircle indicate single lifetimes (b). The location [1, 0] represents 0 ns, and the location of origin [0, 0] represents an infinite lifetime. Fluorescence lifetimes along the semicircle increase counter-clockwise to the left. In this coordinate system the measured value is the intensity-weighted average of the lifetime components. The magnitude of the vector equals the demodulation of the measured event m, and the angle between x-axis and vector equals the phase shift ϕ. The line joining the lifetime components notes the location of the measured event. In this example, the measured event is located in the middle of the line joining single lifetimes of 4 ns and 19 ns. The plot reveals the event consists of an equivalent fraction of 4 ns and 19 ns components. The solid lines represent the phase shift and demodulation vector for the dual-lifetime simulation, and the dashed lines represent single lifetime component vectors thereof.
The fluorescence lifetime imaging microscopy (FLIM) and fluorimetry communities have been implementing phasor plots for several years [19, 23–27] because of the ease with which one can visualize distributions of multiple lifetime components taken from the different pixels comprising images of groups of cells. The use of phasor plots can aid evaluation of intracellular release of therapeutics from nanoparticles that are taken up by cells [20], detect changes in the metabolism (i.e. metabolic mapping) of single cancer cells, neurons, and other tissue types [21], fingerprint photo-activatable fluorescent proteins [28], and quantify FRET events in cells. In these examples the use of microscopy allows relatively small numbers of cells to be evaluated, and use of flow cytometry offers the potential to collect data from a significantly larger cell population at a rapid rate and to use the data as a basis of cell sorting.
As a step toward demonstrating the use of full phasor plots, we have previously adopted a method that constructs pseudo-phasor plots for fluorescence activated cell sorting [14]. This approach provided a means to perform real-time analysis of ϕ, and m dependent values. Herein we extend this analysis to the construction of full phasor plots. We use these to visualize multiple lifetime components for single cells during a cytometry run. We demonstrate the utility of these methods with measurements of fluorescence microspheres, Chinese hamster ovary (CHO-K1) cells labeled with one or two fluorophores, and Saccharomyces cerevisiae cells expressing two spectrally overlapping fluorescent proteins.
2. Materials and methods
2.1 Single lifetime component experiment
For proof of concept studies, we first took fluorophores that decay (on average) following single exponential fluorescence kinetics. We used fluorescently labeled microspheres (fluorescein, Catalog Code: 891; and propidium iodide, Catalog Code: 892, Bangs Laboratories Inc., Fishers, IN). When excited at 488nm both fluorophores are highly quantum efficient with known fluorescence lifetimes (4 ns +/− 0.2 ns for fluorescein, and 16 ns +/− 0.5 ns for propidium iodide, respectively [29, 30]). We suspended the microspheres (7 to 9 µm) in DI water to a concentration of 1 × 106 /mL, and measured them using 496-nm long pass and 488-nm band pass filter for fluorescence and side scatter detection, respectively.
2.2 Dual-lifetime component experiment
To examine the use of phasor plots for samples with dual lifetimes, viable mammalian cells were fixed and stained with two different fluorophores. CHO-K1 cells were fluorescently labeled with ethidium bromide (EB) and fluorescein isothiocyanate (FITC). Standard cell culture techniques were applied (i.e. cell growth in DMEM/F12 media, Life technologies, Grand Island, NY; supplemented with 10% fetal bovine serum; and incubated at 80% relative humidity, with 5% CO2 at 37 °C). At slightly under full confluence, cells were collected, centrifuged, and re-suspended in phosphate buffered saline to obtain three treatment samples each having a concentration of ~106 cells/mL. Each population was fixed and prepared for fluorescent labeling (95% ethanol solution + RNase at 30 µL of 1 µg/mL). The following treatments were prepared for the three groups, respectively: (1) ethidium bromide at a concentration of 20 mg/L, (2) FITC at a concentration of 10 mg/L, (3) EB and FITC at concentrations of 20 mg/L and 10 mg/L, respectively. Prior reports indicate that FITC and EB have approximate fluorescence lifetimes of 4 ns +/− 0.2 ns and 19 ns +/− 0.2 [31, 32].
2.3 Yeast cell experiment
Saccharomyces cerevisiae cells constitutively expressing fluorescent protein variants were cultured and measured. We cultured a yeast strain that expressed teal fluorescence protein, TFP, as well as a strain that expressed a tandem, TFP, which is linked to dark-state converted citrine fluorescence protein, TFP-dCit. We described development of these fluorescent protein constructs previously [14]. The benefit of these variants are that they emit in similar spectral ranges yet have different fluorescence lifetimes. TFP has an average lifetime of 2.85 ns +/− 0.2, while TFP is linked to dCit, it has an average fluorescence lifetime of 1.6 ns +/− 0.2 [14].
2.4 Time-resolved flow cytometer and data acquisition system
All cells and microspheres were counted using a time-resolved FACSVantageTM SE flow cytometer (Becton Dickinson, CA). Unless otherwise noted the basic cytometry components (i.e. fluidics, photodetectors, CellQuestTM Pro analysis software) were not modified. The components of the flow cytometer we did modify for time-resolved analysis are illustrated in Fig. 1 . The instrument was aligned with a 488-nm laser (150 mW solid state OBIS, Coherent, Inc., Santa Clara, CA) for microsphere and CHO-K1 cell measurements. Yeast samples were measured with an aligned 445-nm laser (150 mW solid state OBIS, Coherent, Inc., Santa Clara, CA). For time-resolved measurements, the laser sources (488-nm and 445-nm) were digitally modulated (25 MHz) with an arbitrary function generator (Tektronix Inc., Beaverton, model AFG3120) and focused to an approximate spot size of 20 µm. The fluorescence signals and side scattered optical signals were detected using photomultiplier tubes (PMTs, R1477-04, Hamamatsu Photonics, CA), and the resulting outputs were amplified (60 dB, DC-100, Advanced Research Instruments, CO) then digitized with a 250 mega samples per second data acquisition system (Innovative Integration, X5-210M, Simi Valley, CA). The data system was controlled by a graphical interface for gating and analysis (Kytos software, DarklingX, Los Alamos, NM).
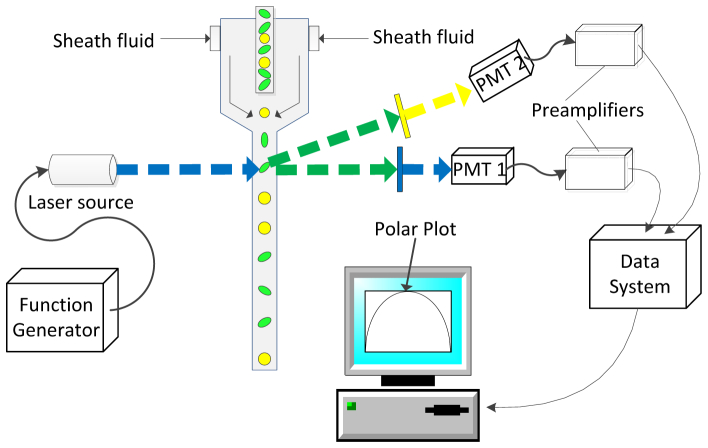
Fig. 1.
Frequency-domain flow cytometry system used for the generation of phasor plots. A laser-excited sample is driven by pressurized fluidics. The samples (depicted by circles and ovals) transit the laser beam (represented by blue dashed line), which is modulated by a function generator. Fluorescence (yellow dashed line directed to PMT2) and side scattering signals (blue dashed line before PMT1) are focused onto the side of two similar PMTs (Hamamatsu, San Diego, model R1477-04). The full cytometry waveforms are collected with a 250 MSPS high-speed Innovative data acquisition system. After collection of the full waveforms, MATLAB was used to build phasor plots for analyses of multiple lifetime components.
2.5 Phasor plot analysis
We generated phasor plots by collecting the modulated fluorescence emission signals and calculating the phase shift, ϕ, and reduction in the amplitude, m, relative to the excitation signal. Our work can be described by the following theory (proved by G. I. Redford and R. M. Clegg [23]). Firstly, the excitation laser beam is mathematically represented by:
| (1) |
where ω is the angular frequency of the excitation modulation, E0 and Eɷ are the DC (average signal) and AC intensity (amplitude of the modulation), and ϕE is the phase of the excitation. Eω/E0 is the depth of the excitation modulation, ME. Similarly, the modulated fluorescence emission signal is:
| (2) |
where ϕF is the fluorescence phase, and the depth of fluorescence modulation is MF = Fω/F0. The relative phase shift, ϕ = ϕF - ϕE, and relative depth of modulation, m = MF/ME, are correlated to fluorescence lifetime by Eqs. (3) and (4), which are:
| (3) |
| (4) |
where τϕ and τm are known as phase and demodulation lifetimes. The phase and demodulation lifetimes are equal for single exponentially decaying fluorophores [23].
We create a phasor plot with Eq. (5) by setting τϕ of Eq. (3) equivalent to τm of Eq. (4). Representing these data in a graph also involves coordinate transformation (Eq. (6) and (7)) and then translation (Eq. (8)) and simplification (Eq. (9)). Finally, we graph the function represented by Eq. (9) is graphed with a radius of 0.5 centered at the coordinate [0.5, 0] in the first quadrant. The origin [0, 0] is the pole of the phasor plot.
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
Applying the above methods to experimental data is straightforward. The demodulation and phase values are calculated directly from flow cytometry fluorescence and side scatter measurements, which become digitized waveforms subsequent to PMT detection and signal amplification. Therefore, two waveforms, or a ‘correlated set’ is collected, where one set represents the passage of a single cell or particle through the excitation source. These discrete waveform sets (see Fig. 2(a) as an example of one waveform) are compiled into a digital .csv file by the data acquisition system. Next, a MATLAB algorithm imports the data file and applies a discrete Fourier transform (DFT) on each set of correlated (side scatter and fluorescence) waveforms. The output of the DFT is a frequency spectrum with an obvious dominant frequency. See Fig. 2(b) as an example of the frequency spectrum result where a 1MHz simulated waveform was processed resulting with a spectrum output with a dominant 1MHz frequency.
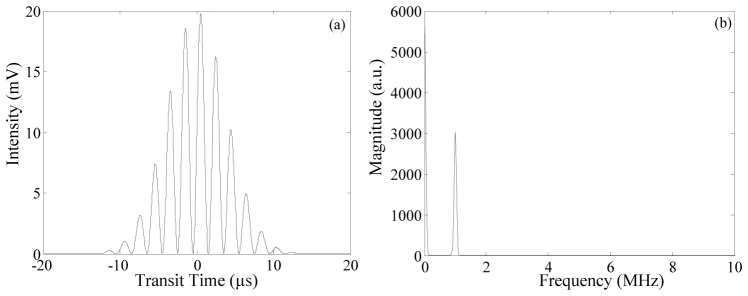
Fig. 2.
Modulated flow cytometry waveform (a) and the resulting frequency spectrum output (b) after applying a discrete Fourier transform to the data. In this example the modulation frequency was 1 MHz.
Processing the correlated data sets into a single phasor plot is then finalized by calculating two values subsequent to the DFT: the signal phase and demodulation. For the resultant dominant frequency the phase of the side scattered and fluorescence signals are calculated. That is, the phase angles of the complex DFT output at the fundamental frequency are calculated. The final phase shift for each correlated set is then obtained by subtracting the two phase values, ϕ = ϕfluorescence - ϕscattering. This assumes that the phase of the side scattered signal has a “zero” fluorescence lifetime value, as it is the best representation of the excitation signal phase. The demodulation, m, is derived by taking the ratio of the peak alternate current (AC) intensity and total direct current (DC) intensity from the DFT frequency spectrum output. A constant modulation depth of the excitation is assumed. These calculations are possible by calibrating the instrumentation and finding the phase shift and demodulation for samples with a known single exponential fluorescence lifetime. We chose to use fluorescein microspheres because fluorescein is known to have a single lifetime component of 4 ns [33].
After collecting the phase shift ϕ and demodulation m, we are able to plot a semicircle as a reference line, (see again Eq. (9)), and then add all calculated phase shifts, ϕ, and demodulation, m, values, where each dot on the phasor plot represents one event (i.e. microsphere or cell’s passage through the laser). The method for generating a phasor plot is also illustrated in Fig. 3 . Figure 3(a) is a plot of two correlated cytometric waveforms, or digitized signals from fluorescence and side scatter PMTs taken during frequency domain measurements. For every event, or cell, both waveforms are collected by our data acquisition system. Subsequent conversion into a phasor plot is straightforward; the ϕ is located at its appropriate angle between the x-axis and the radius, and m is located at its respective distance from the pole (i.e. radius length). Figure 3(b) is an example phasor plot of a simulated fluorescence signal consisting of 50% of a 4-ns lifetime component and 50% of 19-ns fluorescence lifetime component. Note that the ‘dot’ location is in the middle of the line that joins the two lifetime components (4 ns and 19 ns). A difference in modulation lifetime and phase lifetime is immediately apparent by these plots; any point that deviates into the interior semicircle and does not lie on the line itself indicates the presence of multiple fluorescence lifetimes in the signal. Ultimately the intensity percentage of a two-lifetime component signal can be calculated based on vector addition represented by [23]:
| (10) |
where a and b are fractional factors of the lifetime components.
3. Results and discussion
3.1 Single lifetime component experiment
Phasor plotting results after cytometry measurements of microspheres labeled with fluorophores with single exponential decay are presented in Fig. 4 . The centroid of the distribution of single lifetime events is located, as expected on the semicircle of the phasor plot, indicating a single lifetime component.
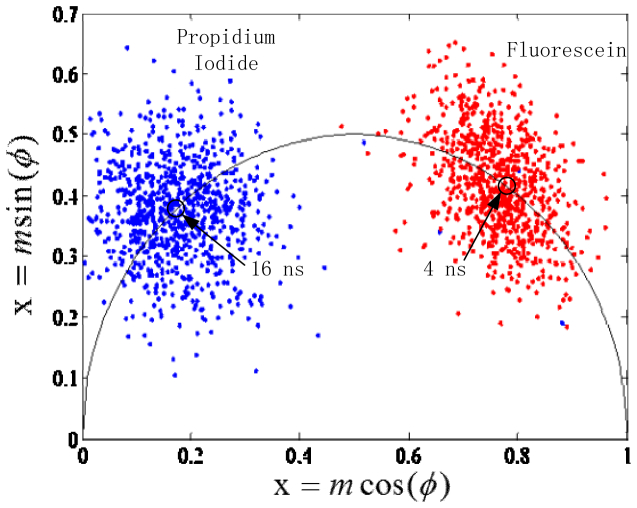
Fig. 4.
Phasor plot representations from fluorescence data on single fluorophore-labeled microspheres. The red population is data from fluorescein microspheres and the blue is of PI microspheres, with the calculated value of their respective fluorescent lifetimes shown by the open marker on the semicircle.
The red population in Fig. 4 shows data for fluorescein microsphere phase and modulation lifetimes, and the blue in Fig. 4 shows data for the PI-labeled microspheres. As can be seen in the phasor plot, the PI microsphere fluorescence lifetime is longer and shows on the plot represented by a larger phase shift and lower demodulation value. The fluorescein microspheres have shorter decay kinetics, and have a shorter phase shift and longer demodulation time. The fluorescence lifetime of fluorescein microspheres was calculated as 4.0 ns +/− 1.5 and 16 ns +/− 2 for the PI microspheres. These average fluorescence lifetimes match published values. Also seen in Fig. 4 is a large variation in the microsphere data. A substantial distribution in the values is present due to the fact that each fluorescent particle passes through the laser in under 10 µs, which limits the amount of light collected, as opposed to FLIM where the detector exposure time is one to three orders of magnitude longer. Moreover, these commercially available fluorescent microspheres containing a single fluorophore are made with a relatively low fluorophore concentration so that they can be used for referencing, cytometry alignment, and calibration. As a consequence our flow cytometric measurements had an overall lower signal to noise ratio (SNR) leading to broad scatter distribution of events in the phasor plots.
3.2 Dual-lifetime component experiment
Phasor plot results that represent the distributions of cells labeled with one and/or two unique fluorochromes are presented in Fig. 5 . From Fig. 5 it is apparent that the FITC (red dots) and EB (blue dots) stained cells are located on the semicircle in the phasor plot, indicating single exponential decay of these fluorophores. Likewise, the dual-stained cell data points (brown dots) are located along a dashed line that joins the central location of the FITC and EB data points. Based on the location of dual-stained cells, about 65% of the contribution to the intensity signal is owing to EB and 35% owing to FITC. The figure shows how these plots can resolve signals from species with two different lifetimes and estimate the proportion of each species in labeled cells.
Fig. 5.
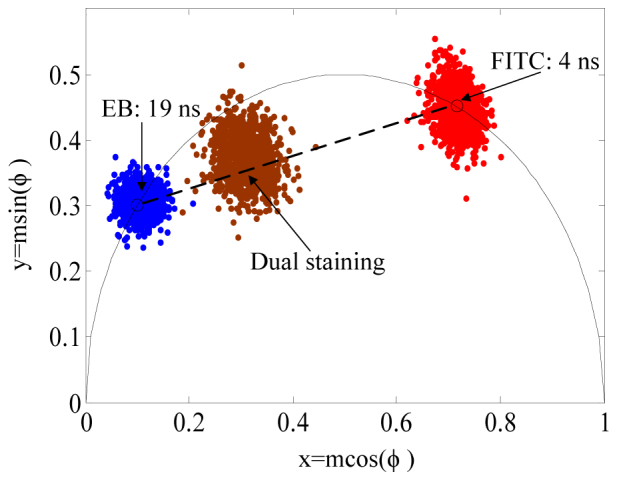
Phasor plot representation of cells labeled with FITC (red dots), EB (blue dots), and a combination of FITC and EB (brown dots), with the open markers being the calculated values of the fluorescent lifetimes of FITC and EB on the phasor semicircle.
3.3 Dual-lifetime yeast cell experiment
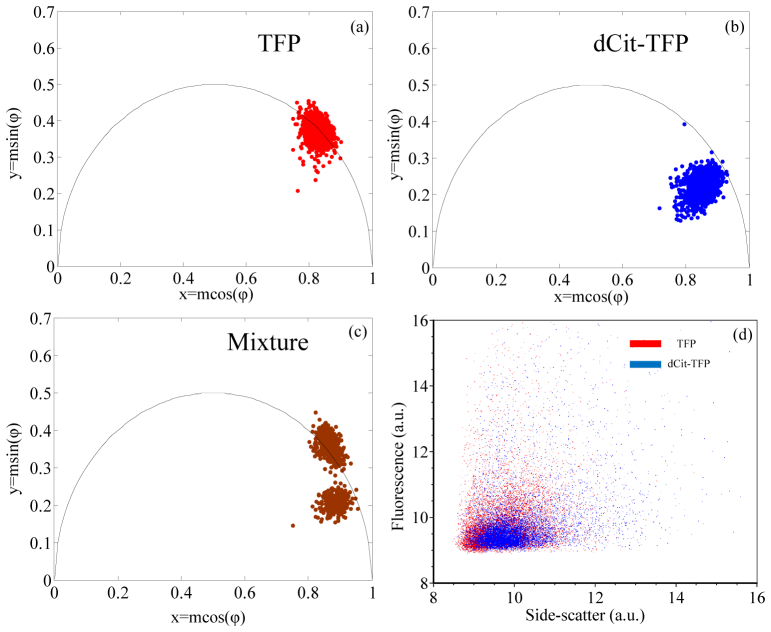
Phasor plot results from measured fluorescence from Saccharomyces cerevisiae cells are presented in Fig. 6 . The red population in Fig. 6(a) represents TFP expressing yeast cells, and the blue population in Fig. 6(b) represents TFP-dCit expressing yeast cells. As shown in Fig. 6(a), the centroid distribution of TFP measurements is on the semicircle, indicating single exponential decay, consistent with our previous work [14]. The center of the TFP-dCit distribution in Fig. 6(b) is not on the semicircle, indicating that these cells show multi-exponential decay. Figure 6(c) is a phasor plot created after time-resolved cytometry measurements of a mixture of TFP and TFP-dCit yeast cells. There are two cell populations in this phasor plot (TFP and TFP-dCit yeast) are distinguishable by their fluorescence lifetime values. But from Fig. 5(d), we noticed the populations are not distinguishable by fluorescence intensity alone, because both cell types express proteins that emit in the same spectral wavelength bandwidth.
Fig. 6.
Phasor plot representations of yeast cells expressing different fluorescent protein constructs. (a), (b), and (c) are the phasor plots of cells producing TFP, TFP linked to dark citrine fluorescence protein, and an equal mixture of cells that express either TFP or TFP-dCit, respectively. (d) is a dot plot of two parameters (side scatter and fluorescence intensity) where the blue dots represent TFP-dCit expressing cells and the red dots represent the TFP expressing cells.
4. Conclusions
In this study, we have demonstrated the ability to make phasor plots from time resolved flow cytometry data. We present plots of fluorescence signals from microspheres, mammalian cells, and yeast cultures labeled with single and dual fluorescence lifetime components. This approach takes time-resolved flow cytometry measurements and transforms the data into phase and demodulation values. To-date, time-resolved flow cytometry data sets have been limited to single fluorescence lifetime measurements mainly owing to the limitations in data acquisition speeds and digitization rates as well as the need to perform real-time signal processing at cell sorting event rates. However, with the increases in data system sampling rates we are able to show significant advances toward measuring multi-lifetime data from single cells. With a flow cytometry based polar plot, we are able to visualize when and if data from a single cell or particle in each data set includes more than one fluorescence lifetime value. The ability to perform this calculation in real-time is only limited by time required to perform the digital signal processing, and we demonstrated the feasibility of real time processing for batches of 1000 microspheres and cells. However, as an ‘off-line’ measurement, the number of events counted is essentially limitless.
When phasor plots are used in FLIM microscopy, each point on the plot represents the fluorescence lifetime and demodulation for a single image pixel. In these plots we describe here, each point represents the same values for an individual cell or particle in the cytometry run. Such plots display more information than the fluorescent lifetime alone. In such plots, points from cells with single lifetime values lie on a semicircle (“the universal semicircle”), while points from cells with complex decays or multiple lifetime values lie inside the semicircle. The locations of the points therefore indicate whether the population distribution is of single, double, or multiple lifetimes within the population. Additionally, the vector representation of the phasor plot allows calculation of the relative amount of a given fluorophore that may be present within cells/microspheres that have more than one components.
There are advantages of phasor plotting with flow cytometry over traditional time-resolved flow cytometry; these are related to the ease with which the ϕ and m alone can be graphed, observed, and used for analysis as individual measurements as compared to the usual measurement of the fluorescence lifetime, τ. In order to graph a fluorescence lifetime cytometry histogram, the values of ϕ and m are first calculated then translated into fluorescence lifetime values using Eqs. (3) and (4) and subsequently turned into list-mode data. Thus the phasor plot simplifies the computational steps. Moreover, a phasor plot will reveal not only differences in fluorescence lifetimes among measured cells and particles, but also indicate if the signal is composed of one or more fluorescence lifetime component, which simple plots of τ do not. In fact, if more than one fluorescence lifetime component is to be determined with frequency-domain flow cytometry approaches without phasor analysis, then multiple modulation frequencies are required. In flow, the ability to shift laser modulation frequencies to carry out multiple measurements on a cell or particle is limited because cells pass the detector very quickly, on the order of microseconds. Finally, compared to traditional, or intensity-based flow cytometry, plots of ϕ and m, show distributions of data that are independent of a spectral emission wavelength range. This means that the future flow cytometers might gather data without a need to separate emission based on color, allowing a simplified flow cytometry configuration and the ability to collect more light due to the fact that spectral spillover is no longer important
As the instrumentation has become more common, the use of fluorescence lifetime measurements in cytometry assays has increased, and with it the desire to interpret fluorescence signals that contain multiple fluorescence lifetime values. The brief demonstration we provide here builds upon our prior work using pseudo-phasor plots for cell sorting [14]. Additionally, it builds on prior work from Redford and Clegg over a decade ago [23], and on work by modern FLIM communities who now embrace phasor plots to analyze bulk fluorescence decay signals that may contain more than one fluorescence lifetime component. Future work will involve analysis of more complex lifetime systems with cells with three or more fluorescence lifetime components. Such plots would contain data points that form three vertices of a triangle on the phasor plot, which can be mapped to three different individual single lifetime components. Other improvements will include using these plots in real-time analysis in cytometry systems capable of cell sorting based on the fluorescence decay kinetic parameters. These improvements will allow phasor plots to be used to their full advantage, for example for counting and sorting populations of cells based on differences in Förster resonance energy transfer, differences in fluorescent protein expression, or differences in cell metabolism to facilitate metabolic mapping [34].
Acknowledgments
This work was supported by U54 CA132383 and NSF CAREER DBI 1150202 to JPH and U54 CA132383 and NIH R01 GM097479 to RB
RC and PJ prepared the samples, performed measurements with the flow cytometer and made the calculations for the phasor plots. WP worked with RC and provided guidance on the phasor analysis. BS developed the fluorescent protein fusions for insertion into the yeast cells. MN provided the data acquisition system used to collect the cytometry data offline. JPH and RB directed the work and its interpretation, wrote the paper, and guarantee the integrity of its results.
References and links
- 1.Deka C., Steinkamp J. A., “Time-resolved fluorescence decay measurements for flowing particles,” (Google Patents, 1999). [Google Scholar]
- 2.Steinkamp J. A., Crissman H. A., “Resolution of fluorescence signals from cells labeled with fluorochromes having different lifetimes by phase-sensitive flow cytometry,” Cytometry 14(2), 210–216 (1993). 10.1002/cyto.990140214 [DOI] [PubMed] [Google Scholar]
- 3.Houston J. P., Naivar M. A., Freyer J. P., “Digital analysis and sorting of fluorescence lifetime by flow cytometry,” Cytometry A 77(9), 861–872 (2010). 10.1002/cyto.a.20930 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Pinsky B. G., Ladasky J. J., Lakowicz J. R., Berndt K., Hoffman R. A., “Phase-resolved fluorescence lifetime measurements for flow cytometry,” Cytometry 14(2), 123–135 (1993). 10.1002/cyto.990140204 [DOI] [PubMed] [Google Scholar]
- 5.Steinkamp J. A., Keij J. F., “Fluorescence intensity and lifetime measurement of free and particle-bound fluorophore in a sample stream by phase-sensitive flow cytometry,” Rev. Sci. Instrum. 70(12), 4682–4688 (1999). 10.1063/1.1150143 [DOI] [Google Scholar]
- 6.J. P. Houston, M. A. Naivar, P. Jenkins, and J. P. Freyer, “Capture of fluorescence decay times by flow cytometry,” Current Protocols in Cytometry, 1–21 (2012). 10.1002/0471142956.cy0125s59 [DOI] [PMC free article] [PubMed]
- 7.Cao R., Naivar M. A., Wilder M., Houston J. P., “Expanding the potential of standard flow cytometry by extracting fluorescence lifetimes from cytometric pulse shifts,” Cytometry A 85(12), 999–1010 (2014). 10.1002/cyto.a.22574 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Li W., Vacca G., Castillo M., Houston K. D., Houston J. P., “Fluorescence lifetime excitation cytometry by kinetic dithering,” Electrophoresis 35(12-13), 1846–1854 (2014). 10.1002/elps.201300618 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jenkins P., Naivar M. A., Houston J. P., “Toward the measurement of multiple fluorescence lifetimes in flow cytometry: maximizing multi-harmonic content from cells and microspheres,” J. Biophotonics 8(11-12), 908–917 (2015). 10.1002/jbio.201400115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Cao R., Pankayatselvan V., Houston J. P., “Cytometric sorting based on the fluorescence lifetime of spectrally overlapping signals,” Opt. Express 21(12), 14816–14831 (2013). 10.1364/OE.21.014816 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Nedbal J., Visitkul V., Ortiz-Zapater E., Weitsman G., Chana P., Matthews D. R., Ng T., Ameer-Beg S. M., “Time-domain microfluidic fluorescence lifetime flow cytometry for high-throughput Förster resonance energy transfer screening,” Cytometry A 87(2), 104–118 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dean K. M., Davis L. M., Lubbeck J. L., Manna P., Friis P., Palmer A. E., Jimenez R., “High-speed multiparameter photophysical analyses of fluorophore libraries,” Anal. Chem. 87(10), 5026–5030 (2015). 10.1021/acs.analchem.5b00607 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lu Y., Lu J., Zhao J., Cusido J., Raymo F. M., Yuan J., Yang S., Leif R. C., Huo Y., Piper J. A., Paul Robinson J., Goldys E. M., Jin D., “On-the-fly decoding luminescence lifetimes in the microsecond region for lanthanide-encoded suspension arrays,” Nat. Commun. 5, 3741 (2014). 10.1038/ncomms4741 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sands B., Jenkins P., Peria W. J., Naivar M., Houston J. P., Brent R., “Measuring and sorting cell populations expressing isospectral fluorescent proteins with different fluorescence lifetimes,” PLoS One 9(10), e109940 (2014). 10.1371/journal.pone.0109940 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gohar A. V., Cao R., Jenkins P., Li W., Houston J. P., Houston K. D., “Subcellular localization-dependent changes in EGFP fluorescence lifetime measured by time-resolved flow cytometry,” Biomed. Opt. Express 4(8), 1390–1400 (2013). 10.1364/BOE.4.001390 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cui H. H., Valdez J. G., Steinkamp J. A., Crissman H. A., “Fluorescence lifetime-based discrimination and quantification of cellular DNA and RNA with phase-sensitive flow cytometry,” Cytometry A 52(1), 46–55 (2003). 10.1002/cyto.a.10022 [DOI] [PubMed] [Google Scholar]
- 17.Steinkamp J. A., Lehnert B. E., Lehnert N. M., “Discrimination of damaged/dead cells by propidium iodide uptake in immunofluorescently labeled populations analyzed by phase-sensitive flow cytometry,” J. Immunol. Methods 226(1-2), 59–70 (1999). 10.1016/S0022-1759(99)00053-8 [DOI] [PubMed] [Google Scholar]
- 18.Stringari C., Cinquin A., Cinquin O., Digman M. A., Donovan P. J., Gratton E., “Phasor approach to fluorescence lifetime microscopy distinguishes different metabolic states of germ cells in a live tissue,” Proc. Natl. Acad. Sci. U.S.A. 108(33), 13582–13587 (2011). 10.1073/pnas.1108161108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cutrale F., Salih A., Gratton E., “Spectral Phasor approach for fingerprinting of photo-activatable fluorescent proteins Dronpa, Kaede and KikGR,” Methods Appl. Fluoresc. 1(3), 035001 (2013). 10.1088/2050-6120/1/3/035001 [DOI] [PubMed] [Google Scholar]
- 20.Basuki J. S., Duong H. T., Macmillan A., Erlich R. B., Esser L., Akerfeldt M. C., Whan R. M., Kavallaris M., Boyer C., Davis T. P., “Using fluorescence lifetime imaging microscopy to monitor theranostic nanoparticle uptake and intracellular doxorubicin release,” ACS Nano 7(11), 10175–10189 (2013). 10.1021/nn404407g [DOI] [PubMed] [Google Scholar]
- 21.Schweitzer D., Schenke S., Hammer M., Schweitzer F., Jentsch S., Birckner E., Becker W., Bergmann A., “Towards metabolic mapping of the human retina,” Microsc. Res. Tech. 70(5), 410–419 (2007). 10.1002/jemt.20427 [DOI] [PubMed] [Google Scholar]
- 22.Deka C., Cram L. S., Habbersett R., Martin J. C., Sklar L. A., Steinkamp J. A., “Simultaneous dual-frequency phase-sensitive flow cytometric measurements for rapid identification of heterogeneous fluorescence decays in fluorochrome-labeled cells and particles,” Cytometry 21(4), 318–328 (1995). 10.1002/cyto.990210403 [DOI] [PubMed] [Google Scholar]
- 23.Redford G. I., Clegg R. M., “Polar plot representation for frequency-domain analysis of fluorescence lifetimes,” J. Fluoresc. 15(5), 805–815 (2005). 10.1007/s10895-005-2990-8 [DOI] [PubMed] [Google Scholar]
- 24.Digman M. A., Caiolfa V. R., Zamai M., Gratton E., “The phasor approach to fluorescence lifetime imaging analysis,” Biophys. J. 94(2), L14–L16 (2008). 10.1529/biophysj.107.120154 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Stringari C., Cinquin A., Cinquin O., Digman M. A., Donovan P. J., Gratton E., “Phasor approach to fluorescence lifetime microscopy distinguishes different metabolic states of germ cells in a live tissue,” Proc. Natl. Acad. Sci. U.S.A. 108(33), 13582–13587 (2011). 10.1073/pnas.1108161108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Campos-Delgado D. U., Navarro O. G., Arce-Santana E. R., Jo J. A., “Extended output phasor representation of multi-spectral fluorescence lifetime imaging microscopy,” Biomed. Opt. Express 6(6), 2088–2105 (2015). 10.1364/BOE.6.002088 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Szmacinski H., Toshchakov V., Lakowicz J. R., “Application of phasor plot and autofluorescence correction for study of heterogeneous cell population,” J. Biomed. Opt. 19(4), 046017 (2014). 10.1117/1.JBO.19.4.046017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Pepperkok R., Squire A., Geley S., Bastiaens P. I., “Simultaneous detection of multiple green fluorescent proteins in live cells by fluorescence lifetime imaging microscopy,” Curr. Biol. 9(5), 269–274 (1999). 10.1016/S0960-9822(99)80117-1 [DOI] [PubMed] [Google Scholar]
- 29.Hammer M., Schweitzer D., Richter S., Königsdörffer E., “Sodium fluorescein as a retinal pH indicator?” Physiol. Meas. 26(4), N9–N12 (2005). 10.1088/0967-3334/26/4/N01 [DOI] [PubMed] [Google Scholar]
- 30.Verveer P. J., Squire A., Bastiaens P. I., “Global analysis of fluorescence lifetime imaging microscopy data,” Biophys. J. 78(4), 2127–2137 (2000). 10.1016/S0006-3495(00)76759-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Deka C., Lehnert B. E., Lehnert N. M., Jones G. M., Sklar L. A., Steinkamp J. A., “Analysis of fluorescence lifetime and quenching of FITC-conjugated antibodies on cells by phase-sensitive flow cytometry,” Cytometry 25(3), 271–279 (1996). [DOI] [PubMed] [Google Scholar]
- 32.Heller D. P., Greenstock C. L., “Fluorescence lifetime analysis of DNA intercalated ethidium bromide and quenching by free dye,” Biophys. Chem. 50(3), 305–312 (1994). 10.1016/0301-4622(93)E0101-A [DOI] [PubMed] [Google Scholar]
- 33.Boens N., Qin W., Basarić N., Hofkens J., Ameloot M., Pouget J., Lefèvre J.-P., Valeur B., Gratton E., vandeVen M., Silva N. D., Jr, Engelborghs Y., Willaert K., Sillen A., Rumbles G., Phillips D., Visser A. J., van Hoek A., Lakowicz J. R., Malak H., Gryczynski I., Szabo A. G., Krajcarski D. T., Tamai N., Miura A., “Fluorescence lifetime standards for time and frequency domain fluorescence spectroscopy,” Anal. Chem. 79(5), 2137–2149 (2007). 10.1021/ac062160k [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Stringari C., Edwards R. A., Pate K. T., Waterman M. L., Donovan P. J., Gratton E., “Metabolic trajectory of cellular differentiation in small intestine by Phasor Fluorescence Lifetime Microscopy of NADH,” Sci. Rep. 2, 568 (2012). 10.1038/srep00568 [DOI] [PMC free article] [PubMed] [Google Scholar]