Abstract
Photoacoustic spectrum analysis (PASA) has been demonstrated as a new method for quantitative tissue imaging and characterization. The ability of PASA in evaluating micro-size tissue features was limited by the bandwidth of detectors for photoacoustic (PA) signal acquisition. We improve upon such a limit, and report on developments of PASA facilitated by an optical ultrasonic detector based on micro-ring resonator. The detector’s broad and flat frequency response significantly improves the performance of PASA and extents its characterization capability from the tissue level to cellular level. The performance of the system in characterizing cellular level (a few microns) stochastic objects was first shown via a study on size-controlled optically absorbing phantoms. As a further demonstration of PASA’s potential clinical application, it was employed to characterize the morphological changes of red blood cells (RBCs) from a biconcave shape to a spherical shape as a result of aging. This work demonstrates that PASA equipped with the micro-ring ultrasonic detectors is an effective technique in characterizing cellular-level micro-features of biological samples.
OCIS codes: (170.0170) Medical optics and biotechnology, (170.5120) Photoacoustic imaging, (170.6935) Tissue characterization
1. Introduction
Photoacoustic Imaging (PAI) is a hybrid medical imaging modality based on laser-induced thermo-acoustic effect in biological tissues. PAI combines the advantages of both optical and ultrasound imaging as it is able to present optical contrast in subsurface tissues with an excellent spatial resolution. A majority of previous studies on PAI were focused on measurements of photoacoustic (PA) signal amplitude which is related to the overall optical absorption of the target tissue. Recent studies have demonstrated that the power spectrum of the broadband radio frequency (RF) PA signal contains the micro-structural information of the tissue [1–9]. Aiming at quantitative imaging and tissue characterization, a technique termed ‘photoacoustic spectral analysis (PASA)’ has been developed. Similar to ultrasound spectral analysis (USSA), PASA uses the slope, mid-band fit, and intercept of the linear regression model to characterize the main features of the signal power spectrum [4]. PASA is based on the fact that the frequency components of the PA signals are closely correlated to the morphological properties of optically absorbing objects in tissues, including their sizes, shapes, and densities [4, 10]. For example, smaller objects generate shorter PA signals in the time domain, which leads to broader power spectra containing more high frequency components than the PA signals from larger objects. Quantitative analysis of the PA signals in the frequency domain would enable an objective evaluation of the morphologies of optically absorbing objects stochastically distributed in biological tissues [3, 11]. PASA offers solutions to a number of practical issues faced by conventional PAI. First, the averaged power spectrum provides a robust method of quickly characterizing the stochastic nature of tissue microstructures, and can lead to measurements that are more repeatable. Second, PASA also minimizes the contributions of system components, and leads to measurements that are more objective and quantitative.
Previous PASA was based on conventional piezoelectric transducers, which usually had limited detection bandwidth. For example, by using commercially available or home-fabricated piezoelectric transducers, PASA has been explored for applications in diagnosis of prostate cancer [6, 12, 13] and evaluation of liver conditions [7, 8, 14]. In these studies, PASA was performed on the tissue level, and the targeted biological tissues (e.g., small vessels, cellular groups, and lipid clusters) have features on the scale of over 100 microns. In order to achieve more sensitive and accurate evaluation of cells with sizes on the order of a few microns, the detector(s) for PA signal acquisition should have a bandwidth of a few hundreds of MHz. Photoacoustic microscopy systems with specially-designed high-frequency piezoelectric transducers have been used to study the morphology of single red blood cells [9, 15–17]. Detecting high-frequency ultrasound signals (e.g., ~hundreds of MHz) usually requires carefully manufactured transducers with thin and fragile piezoelectric elements. Besides, due to the resonance effect in the piezoelectric part, these transducers usually have maximum responses at a high frequency, and therefore, a reduced response at the low frequency regime [18–20].
In this work, we demonstrate, for the first time to the best of our knowledge, an all-optical PASA system using a polystyrene (PS) micro-ring resonator as the ultrasonic detector [21]. Micro-ring resonator has been demonstrated as a high-performance ultrasound detector with both broad bandwidth and great detection sensitivity. Our previous studies have shown that the micro-ring detector has an intrinsic acoustic response from nearly DC up to 350MHz at −3dB [22], and a noise equivalent detectable pressure over this bandwidth as low as 105 Pa. This sensitivity is comparable to or even better than those of conventional piezoelectric transducers. PA signals from biological samples contain information of both micro- and macro-size structures, and are broadband in nature. Micro-ring ultrasonic detectors can largely improve the performance of PASA for tissue characterizations by extending its scope from the tissue level to cellular level. With such a system, we can achieve size characterization of PS microspheres below 20 µm, and can differentiate cells with different morphologies.
2. Methods and Principles
2.1. Experimental setup and phantoms preparation
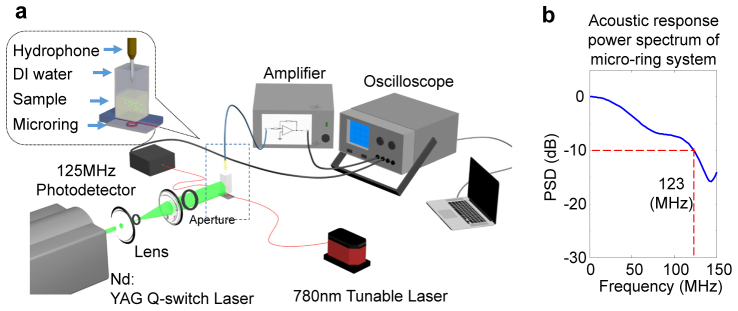
The setup for our PASA system for tissue characterization is shown in Fig. 1(a) . Laser pulses from an optical parametric oscillator (OPO) pumped by a Nd: YAG laser (Vibrant B, Opotek) were used to illuminate the sample and generate PA signals. The pulses had a wavelength of 532 nm, pulse duration of 5 ns, and repetition rate of 10Hz. To achieve a relative uniform light illumination (laser fluence in the range of 15-20 mJ/cm2), the light beam from the laser was first focused by a lens with shorter focal length. At the focal point, a small aperture (a pinhole) was used to filter the high spectral frequency component. Then the light beam was expanded by the second lens with longer focal length. A second larger aperture was added to further reduce the noise at the edge of the beam. Each sample held in a plastic container was made from 10% porcine gel. The samples contained stochastically distributed polystyrene-based latex microspheres or red blood cells (RBCs). The container had openings at top and bottom. The PA signals propagated downward to the ring and upwards to the hydrophone. The micro-ring placed underneath the sample was covered by a thin light-blocking film (silver Mylar balloon) to protect from being damaged by the scattered laser light. DI water was injected between the micro-ring and the film for better coupling of acoustic signal. To compare the performance of the micro-ring to conventional piezoelectric transducers, a calibrated needle hydrophone (HNC-1500, Onda) with a detection band from 0 to 37 MHz (−10dB) was placed on the top of the sample for measurement of PA signals. The distances from the center of the laser beam to the two ultrasonic detectors (i.e., the micro-ring and the hydrophone) were kept the same (3 mm). The PA signals received by the micro-ring and the hydrophone were recorded at the same time by a digital oscilloscope (TDS 540B, Tektronics, sampling frequency 500MHz) and averaged 300 times to increase the signal to noise ratio (SNR).
Fig. 1.
(a) Schematic of the PASA system equipped with a micro-ring detector beneath the sample. For comparison of performance, a calibrated needle hydrophone was positioned above the sample. (b) The power spectral density (PSD) of the PA signal received by a micro-ring produced by illuminating 5-ns laser pulses on a 200-nm thick Cr film. This PSD demonstrates a −10 dB bandwidth of 123 MHz.
To explore the ability of PASA equipped with a micro-ring, experiments on phantom and biology samples were conducted. The phantom samples we used were microsphere particles (Fluoresbrite plain YG micro-spheres, Polysciences) with sizes of 3 µm, 6 µm, 10 µm, 20 µm, and 45 µm. With these phantoms, we explored the capability of PASA in characterizing the size information of the optically absorbing objects. The biological samples we used were two groups (fresh and aged) of red blood cell samples, one using fresh human blood specimens (< 2 weeks in storage) and the other using aged human blood specimens (3 months in storage). Healthy RBCs are biconcave, disc-shaped, and are ~7-8 microns in diameter, 1-2 microns in height, and 80-100 femtoliters (fl) in volume [23]; while aged RBCs are spherical shaped.
To prepare the phantoms with stochastically distributed microspheres or blood cells, we mixed the samples in porcine gel. The densities were controlled so that the generated PA signals had similar signal noise ratios. No aggregation of either microspheres or RBCs happened, as confirmed by checking the samples under a microscopy. The properly controlled density also allowed light beam to pass through the entire phantom without significant attenuation, so that the illumination intensity is relatively uniform over the whole phantom. The microspheres were diluted by the porcine gel directly. The blood samples were diluted 1:100 in phosphate buffered saline (PBS) and then mixed 1:30 with 10% porcine gel. The microspheres were added at 46°C and the blood cells were added a temperature below 37°C and the gel was stirred using a magnetic stirring bar to achieve stochastic distribution of optical absorbers. After the gel was cooled and solidified, a phantom containing randomly distributed objects were ready for use. The densities of microsphere particles in the gel were 1.7 × 106, 2.1 × 105, 4.6 × 104, 1.9 × 104, and 1.7 × 103 particles/mL, respectively, for sizes of 3 µm, 6 µm, 10 µm, 20 µm, and 45 µm. The densities of RBCs in the gel were 1.2-1.8 × 106 cells/mL.
2.2. Principles
The details of the micro-ring based ultrasonic detectors have been discussed in our previous publications [24, 25]. A micro-ring resonator consists of a ring-shaped waveguide coupled with a straight bus waveguide and there is light coupling in and out of the ring in the gap region. The output intensity spectrum shows dips occurred at specific wavelengths when the corresponding round trip phase accumulation in the ring waveguide equals to multiples of 2π radians. This round trip phase accumulation depends on many parameters, such as the ring radius, cross-section size, and refractive index of the polymer waveguide core/cladding, all of which can affect the effective index of the propagating mode. For polymer micro-rings in contact with ultrasound waves, the intrinsic refractive index will be modulated through the elastic-optic effect [26]. At the same time, the ring is deformed by the ultrasound waves, affecting the effective index of the propagating waveguide mode. These two effects altogether shift the ring resonant wavelength. By setting the probe laser (TLB 6700, Velocity Tunable Laser) wavelength at the slope of the ring transmission dip, the incident ultrasound waves could be recorded by the varying output intensity detected by a high speed photodetector (125MHz, Model 1801, Newport) from the device. Micro-ring has been utilized in high-resolution PA imaging [27, 28], as well as real-time THz pulse detection [29]. The device has demonstrated an ultra-broadband intrinsic frequency response from nearly DC to 350 MHz at −3dB [22]. However, the whole system response bandwidth is not only limited by the bandwidth of the photodetector but also by the duration of the laser pulses. To evaluate the impulse response of the PASA system equipped with the micro-ring, the 5-ns laser pulse was illuminated on a super-thin Cr film (200-nm thick), and then the generated PA signals were detected by the micro-ring placed at 3 mm from the Cr film. The PSD of the PA signal from the Cr film is shown in Fig. 1(b) which illustrates a system bandwidth of 123 MHz at −10dB.
The working principle of PASA is based on a linear regression on the power spectrum of PA signal from a target sample. The power spectrum represents the distribution of power along the ultrasound frequency, which is calculated as the square of the fast fourier transform of the time-domain PA signal magnitude. PA signals from spherical objects have been derived analytically and the power spectrum of those time-domain bipolar signals show periodic dip pattern at certain frequencies [30]. A general approach to differentiate two spheres with different sizes is to identify the locations of the minima in power spectrum. This method will become invalid when sample the concentration of optically absorbing objects goes up and then the details in the spectrum such as the minima in the spectrum becomes less obvious to observe, leaving only a contour of the curve. In most cases, the power spectrum over frequency show an overall linear descending trend, and a simple and robust linear regression can be used to evaluate this trend when a broad enough spectrum is fitted. The linear fitting is sensitive to the ratio between the high frequency and the low frequency components which is directly related to the morphologies of the microstructures in the tissue. In order to make this linear fitting accurate, the bandwidth of the ultrasound detector must be broad enough so that the descending contour of the PSD can be captured. In addition, to reduce the impact of individual measurement system to the quantified results, the system impulse response needs to be removed from the PSD before linear regression is conducted. Among the three spectral parameters quantified from the linear fitting, the slope of the fitting line is the one most sensitive to the size and the shape of the optically absorbing objects in the sample, and is less susceptible to their concentration.
2.3 Simulation
For individual microspheres and RBCs experiments, we compared the measured spectrum with the spectrum simulated by the k-wave toolbox in Matlab described in [30].
For individual microspheres, we simulated the PA spectrums of the microspheres of sizes 20 μm, 45 μm and 100 μm. For RBCs samples, the biconcave shape used to describe healthy RBCs has a diameter of 7.82 μm, a minimum height of 0.81 μm, a maximum height of 2.58 μm, and a volume of 94 μm3 [23]. When RBCs are aged, their shapes are changed to spheroid, while their volumes are kept the same [31]. Both samples contained stochastically distributed RBCs with a concentration of 1.7 × 106 cells/mL. The concentration of RBC here is consistent with the concentration in the experiment. Due to the gravity and the bi-concave shape of the RBCs, their orientations in the space were not uniform. As observed under the microscope, more RBCs had their long axis oriented along the horizontal plane, and fewer oriented along the vertical direction. Compared to uniform distribution, Gaussian distribution better describes the orientations of the RBCs. This was considered in the simulation. The density, the speed of sound (SOS), and the ultrasound attenuation of the sample were set as 1000 kg/m3, 1540 m/s, 0.2 dB/(MHz·cm), respectively. For each group (i.e., biconcave and spheroid), 100 samples (N = 100) were studied for statistical analysis.
3. Results
3.1. PASA of individual microspheres
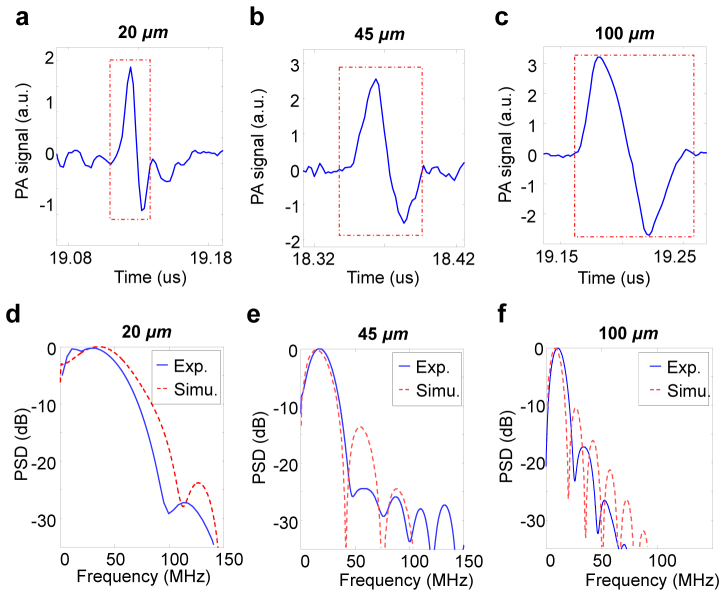
The performance of the PASA system was first evaluated by recording the PA signals from individual microspheres (Fluoresbrite plain YG micro-spheres, Polysciences) of different sizes (i.e., 20 µm, 45 µm, and 100 µm in diameter, respectively). Example PA signals from the individual microspheres with different sizes are shown in Figs. 2(a)-2(c) . Each one shows a characteristic bipolar shape. The normalized PSD for microspheres with three different sizes are shown in Figs. 2(d)-2(f) with the solid curves. In this study, facilitated by the ultra-broad detection band of the micro-ring, the PSD from 20 µm, 45 µm and 100 µm microspheres were in reasonably good agreement with the results from simulation, as shown by the dashed curves in Figs. 2(d)-2(f). Experimental results show the first “dips” in the PSD profiles at 113 MHz, 48 MHz, and 26 MHz for 20-μm, 45-μm, and 100-μm microspheres, respectively, which are relative close to the numbers from the simulation (i.e., 100 MHz, 50 MHz, and 23 MHz, respectively). The mild disagreement between the results from simulation and experiment is at least in part due to the difference between the claimed size and the actual size of the microspheres. For example, according to the information from the manufacture, the microspheres with a mean size of 45 μm have a coefficient of variation of up to 20%, meaning the actual size can be anywhere between 36 and 54 μm.
Fig. 2.
PA signal power spectrum of individual microspheres. (a)-(c) Time domain PA signals from the microspheres with different sizes (i.e., 20 μm, 45 μm and 100 μm). (d)- (f) Normalized PSD curve from each individual microsphere measured by the PASA system equipped with the micro-ring (solid line). Simulated PSD curves from the individual microspheres with sizes same as the ones in the experiment (dashed line).
3.2. PASA of stochastically distributed microspheres
The phantoms were prepared using the methods described in section 2.1. For each size, a group of 4 phantoms were measured. PA signals from each phantom were recorded by the micro-ring and the needle hydrophone simultaneously. The linear regression was conducted within the −10 dB spectral range of each system (micro-ring vs. hydrophone). In addition, The PSD below 2MHz was excluded in the linear regression in order to remove the interference from the low frequency noise. This low frequency noise was from the PA signals generated by the light illumination on the the gel. Therefore, the frequency range of linear regression fitting was 2-123MHz for the micro-ring based system, and was 2-37 MHz for the hydrophone based system. Before performing the linear fitting, the impulse response of each system was removed from the PSD. The spectral parameter slope of each fitting line was quantified, and the measures from 4 phantoms in each group were averaged.
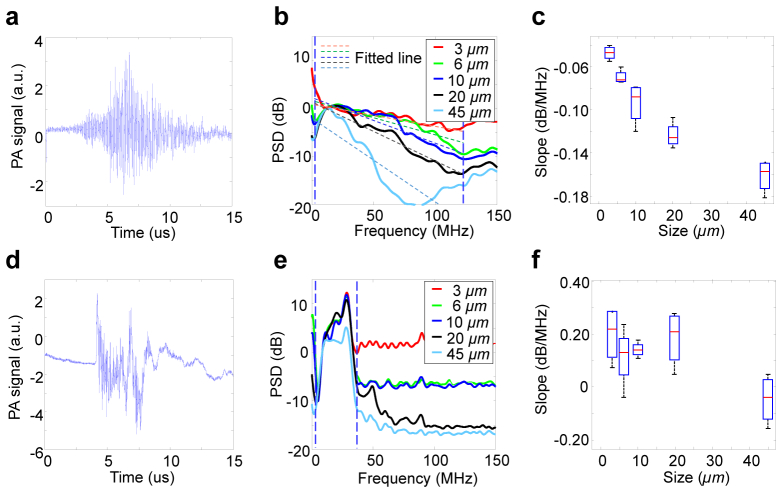
Example PA signals from a phantom containing 20 µm microspheres as measured by micro-ring and hydrophone are shown in Figs. 3(a) and 3(d) , respectively. The normalized and averaged PSD curves of the PA signals from the phantoms with different sizes of microspheres are plotted in Figs. 3(b) and 3(e). The difference in the descending rate of PSD curve corresponding to the difference in object size from 3 to 45 µm is well demonstrated by the measurements using the micro-ring detector. In contrast, the measurements from the hydrophone which has a narrower detection bandwidth are not able to differentiate the phantoms containing microspheres with such small sizes. The qualified spectral parameter slopes for the results from the micro-ring and the hydrophone are compared in Figs. 3(c) and 3(f). It can be seen that PASA using the hydrophone can hardly distinguish the phantoms containing microspheres smaller than 20 μm. In contrast, PASA using micro-ring shows an excellent capability in differentiating the phantoms with microsphere sizes ranging from 3 to 45 µm. This study on phantoms with well-controlled particle sizes indicates that micro-ring’s ultra-broadband response facilitates reliable PA characterization of stochastically distributed micron-size objects.
Fig. 3.
PASA of phantoms containing different sizes of microspheres (including 3 μm, 6 μm, 10 μm, 20 μm, and 45 μm). Each size group contains 4 phantoms. (a) An example PA signal from a 20 μm microspheres measured by the micro-ring. (b) Normalized and averaged PSD curve for each group as measured by the micro-ring. The fitting line was made for each PSD in the range of 2-123MHz (R2 = 0.85, 0.84, 0.80, 0.89 and 0.74, respectively, for 3 μm, 6 μm, 10 μm, 20 μm, and 45 μm). (c) The qualified PA spectral parameter slope for each group as measured by the micro-ring. (d) An example PA signal from a 20 μm microspheres measured by the hydrophone. (e) Normalized and averaged PSD curve for each group as measured by the hydrophone. (f) The qualified PA spectral parameter slope for each group as measured by the hydrophone.
3.3. PASA of ex vivo human blood specimens
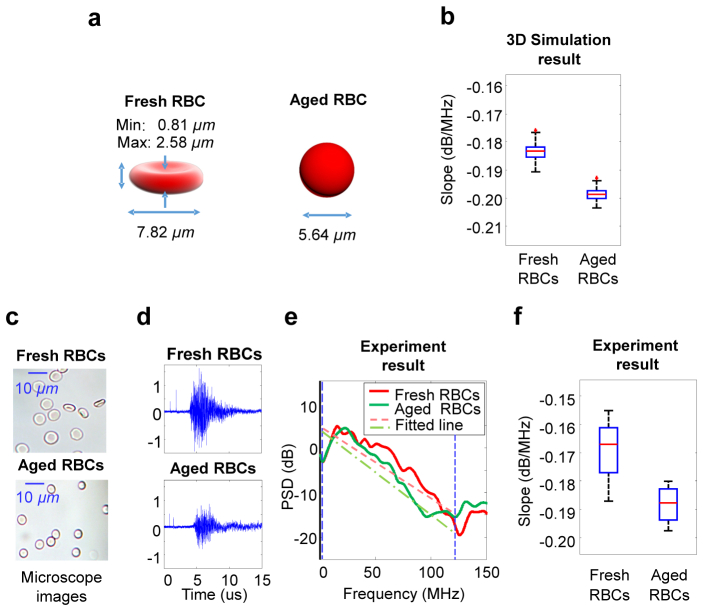
In this study, we explored the feasibility of PASA in evaluating the morphological change of RBCs as a function of the blood storage time. The procedure of PASA was the same as that in the experiments on microspheres. Healthy RBCs have biconcave, disc-shape and therefore have larger surface area to volume ratio. Previous studies have shown that the geometry of RBCs becomes more spherical with storage, and therefore have a smaller surface area to volume ratio [32]. This morphology change can be reflected in the power spectrum of the PA signals. Before the experiment, we performed simulation using the toolbox mentioned in section 2.3. Two groups of samples each containing different shapes of RBCs (biconcave and spheroid) reflecting different levels of freshness (fresh and aged) were studied. The detailed geometries of biconcave and spheroid RBCs are shown in Fig. 4(a) and simulation details are discussed in 2.3. Similarly, the impulse response of each system was removed from the measured PSD before doing the linear fitting. The PA spectral parameter slopes for the two groups, as quantified in the simulation, are compared in Fig. 4(b). For the fresh RBCs, most of them sit flat in each sample. For these RBCs, what measured by the micro-ring located at the bottom of the sample were their small vertical thicknesses which produced large high frequency components. For the aged RBCs, even though their diameters appear smaller in Fig. 4(c), their vertical thicknesses were actually larger than those of the fresh ones. This difference in shapes explains why the aged RBCs, although appearing smaller under the microscope, produced weaker high frequency components and, therefore, smaller spectral parameter slope.
Fig. 4.
PASA of ex vivo human blood specimens. (a) The geometries and dimensions of biconcave (fresh) and spheroid (aged) RBCs used for simulation. (b) PA spectral parameter slopes for the two groups of blood samples (i.e. fresh blood and aged blood), as quantified in the simulation (N = 100). The fitting line was made for each PSD in the range of 2-123 MHz. (c) Microscopy images of the fresh and the aged blood specimens used in the experiment, showing the morphological changes in RBCs as a result of storage. (d) PA signal and (e) PSD curves from the samples containing fresh RBCs and aged RBCs, as measured in experiment. The fitting line was made for each PSD in the range of 2-123MHz (R2 = 0.81, 0.90, respectively, for fresh and aged RBCs). (f) Spectral parameter slope qualified for the two groups of samples (fresh vs. aged) measured in the experiment (N = 4). The two groups can be differentiated with a p<0.05.
In the experiment, two groups of samples each containing different shapes of RBCs (biconcave and spheroid for fresh and aged blood) were studied. The RBCs in both specimens were photographed under a microscope (FMA050, Amscope), as the example pictures shown in Fig. 4(c). The sample preparation was described in section 2.1. Figs. 4(d) and 4(e) shows an example PA signal and PSD curve from each group. As expected, aged RBC sample has high frequency component in the PSD. By performing the linear regression fit of the power spectrum in the range of 2-123 MHz, the quantified spectral parameter slopes from the two groups were obtained, as compared in Fig. 4(f), where aged RBC sample showed reduced slope. This experimental result matches with the finding from the simulation.
4. Discussion
The attenuation of the ultrasound and light could affect this linear fitting model’s accuracy by modifying the slope, especially for dense medium. However, in our experiments, we controlled the concentrations of the optical absorbers (either microspheres or RBCs) low. This ensured that all the samples were highly optically transparent. Also, we controlled the uniformity of light illumination on the sample. Therefore, we don’t expect the small optical attenuation will affect the results. To achieve similar ultrasound attenuation for all measurements, we measured all the samples at a same distance, and the gel concentration in the samples was the same. Since the microspheres occupied <0.01% of the sample volume, they would not strongly affect the ultrasound attenuation. As a result, all samples had the same attenuation with that of the gel itself.
The findings from this study on well-controlled phantoms and ex vivo biological tissues suggest that PASA based on micro-ring ultrasonic detectors, which have an ultra-broad and flat detection band, has the ability of characterizing morphological features including both size and shape in biological samples on the micron-size level. Besides, compared to extremely high-frequency piezoelectric transducers that usually involve sophisticated fabrication and, hence, are usually expensive, PS micro-ring is fabricated with much lower cost and better repeatability using nano-imprinting technology [25, 33]. The micro-ring based PASA technique holds potential to detect morphological abnormalities of cells and relate them with corresponding pathological conditions. Unlike existing technologies such as flow cytometry and peripheral blood smear examination, which are based on the analysis of individual cells, PASA is essentially a statistical method and, hence, may better deal with the stochastic nature of biological samples. Moreover, PASA technique could be further developed into a fast-speed cell morphology analysis system for clinical use, and could provide quantitative diagnostic information that is not accessible by the current qualitative imaging methods. For example, certain diseases, infections, or exposure to toxic chemicals can alter the morphological features of RBCs, impairing their functionalities. Since various morphological abnormalities of RBCs are closely correlated with specific disease states, previous studies have been focused on developing techniques that can characterize the morphological changes in RBCs in vivo or ex vivo [30, 34–36]. Therefore, one potential application of PASA, as explored initially in this study, is the in vivo diagnosis of RBC-related diseases or ex vivo characterization of donated blood. Besides RBCs, other cells with strong intrinsic optical absorption contrast, such as melanoma cells, could also be evaluated with PASA working at proper optical wavelengths.
In the future, employment of a PA light source providing a shorter pulse duration and a photodetector with a larger bandwidth could further increase the bandwidth of the micro-ring based PASA system up to 350 MHz. Working at such a high frequency, however, the penetration depth in biological tissues is limited due to the large acoustic attenuation in tissues. Therefore, the applications of cellular-level PASA should be either focused on superficial tissues, such as illness detection of mucous membrane in the gastrointestinal track, or realized via a miniaturized PA device that can be placed in deep tissue in a minimally invasive manner. For example, when a PA probe can be miniaturized and integrated into a biopsy needle, early detection and characterization of cancer cells may be achieved. All of these potential applications could benefit from the all-optical design facilitated by the micro-ring detector.
Acknowledgements
This research was supported by National Institute of Health under grant numbers R01AR060350 and R01CA186769, and R21AR061594. National Science Foundation DBI1256001. National Natural Science Foundation of China under grant numbers 11574231, and 61201425, Natural Science Foundation of Jiangsu Province under grants number BK20131280, and the Priority Academic Program Development of Jiangsu Higher Education Institutions. The authors acknowledge the technical support from Lurie Nanofabrication Facility at the University of Michigan.
References and links
- 1.Kumon R. E., Deng C. X., Wang X., “Frequency-domain analysis of photoacoustic imaging data from prostate adenocarcinoma tumors in a murine model,” Ultrasound Med. Biol. 37(5), 834–839 (2011). 10.1016/j.ultrasmedbio.2011.01.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Yang Y., Wang S., Tao C., Wang X., Liu X., “Photoacoustic tomography of tissue subwavelength microstructure with a narrowband and low frequency system,” Appl. Phys. Lett. 101(3), 034105 (2012). 10.1063/1.4736994 [DOI] [Google Scholar]
- 3.Wang S., Tao C., Wang X., Liu X., “Quantitative detection of stochastic microstructure in turbid media by photoacoustic spectral matching,” Appl. Phys. Lett. 102(11), 114102 (2013). 10.1063/1.4798272 [DOI] [Google Scholar]
- 4.Xu G., Dar I. A., Tao C., Liu X., Deng C. X., Wang X., “Photoacoustic spectrum analysis for microstructure characterization in biological tissue: A feasibility study,” Appl. Phys. Lett. 101(22), 221102 (2012). 10.1063/1.4768703 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Strohm E. M., Gorelikov I., Matsuura N., Kolios M. C., “Modeling photoacoustic spectral features of micron-sized particles,” Phys. Med. Biol. 59(19), 5795–5810 (2014). 10.1088/0031-9155/59/19/5795 [DOI] [PubMed] [Google Scholar]
- 6.Kumon R. E., Deng C. X., Wang X., “Frequency-domain analysis of photoacoustic imaging data from prostate adenocarcinoma tumors in a murine model,” Ultrasound Med. Biol. 37(5), 834–839 (2011). 10.1016/j.ultrasmedbio.2011.01.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Xu G., Meng Z. X., Lin J. D., Deng C. X., Carson P. L., Fowlkes J. B., Tao C., Liu X., Wang X., “High resolution physio-chemical tissue analysis: towards non-invasive in vivo biopsy,” Sci. Rep. 6, 16937 (2016). 10.1038/srep16937 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Patterson M. P., Riley C. B., Kolios M. C., Whelan W. M., “Optoacoustic signal amplitude and frequency spectrum analysis laser heated bovine liver ex vivo,” in 2011 IEEE International Ultrasonics Symposium (IUS) (IEEE, 2011), pp. 300–303. 10.1109/ULTSYM.2011.0072 [DOI] [Google Scholar]
- 9.Saha R. K., Kolios M. C., “A simulation study on photoacoustic signals from red blood cells,” J. Acoust. Soc. Am. 129(5), 2935–2943 (2011). 10.1121/1.3570946 [DOI] [PubMed] [Google Scholar]
- 10.Diebold G. J., Sun T., Khan M. I., “Photoacoustic monopole radiation in one, two, and three dimensions,” Phys. Rev. Lett. 67(24), 3384–3387 (1991). 10.1103/PhysRevLett.67.3384 [DOI] [PubMed] [Google Scholar]
- 11.Wang S., Tao C., Yang Y., Wang X., Liu X., “Theoretical and experimental study of spectral characteristics of the photoacoustic signal from stochastically distributed particles,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 62(7), 1245–1255 (2015). 10.1109/TUFFC.2014.006806 [DOI] [PubMed] [Google Scholar]
- 12.Patterson M. P., Riley C. B., Kolios M. C., Whelan W. M., “Optoacoustic characterization of prostate cancer in an in vivo transgenic murine model,” J. Biomed. Opt. 19(5), 056008 (2014). 10.1117/1.JBO.19.5.056008 [DOI] [PubMed] [Google Scholar]
- 13.Xu G., Davis M. C., Siddiqui J., Tomlins S. A., Huang S., Kunju L. P., Wei J. T., Wang X., “Quantifying Gleason scores with photoacoustic spectral analysis: feasibility study with human tissues,” Biomed. Opt. Express 6(12), 4781–4789 (2015). 10.1364/BOE.6.004781 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Xu G., Meng Z.-X., Lin J. D., Yuan J., Carson P. L., Joshi B., Wang X., “The functional pitch of an organ: quantification of tissue texture with photoacoustic spectrum analysis,” Radiology 271(1), 248–254 (2014). 10.1148/radiol.13130777 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Strohm E. M., Berndl E. S., Kolios M. C., “Probing red blood cell morphology using high-frequency photoacoustics,” Biophys. J. 105(1), 59–67 (2013). 10.1016/j.bpj.2013.05.037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Strohm E. M., Berndl E. S., Kolios M. C., “High frequency label-free photoacoustic microscopy of single cells,” Photoacoustics 1(3-4), 49–53 (2013). 10.1016/j.pacs.2013.08.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Strohm E. M., Moore M. J., Kolios M. C., “Single cell photoacoustic microscopy: a review,” IEEE J. Sel. Top. Quantum Electron. 22(3), 1–15 (2016). 10.1109/JSTQE.2015.2497323 [DOI] [Google Scholar]
- 18.Hunt J. W., Arditi M., Foster F. S., “Ultrasound transducers for pulse-echo medical imaging,” IEEE Trans. Biomed. Eng. 30(8), 453–481 (1983). 10.1109/TBME.1983.325150 [DOI] [PubMed] [Google Scholar]
- 19.Davidsen R. E., Smith S. W., “Two-dimensional arrays for medical ultrasound using multilayer flexible circuit interconnection,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 45(2), 338–348 (1998). 10.1109/58.660144 [DOI] [PubMed] [Google Scholar]
- 20.Foster F. S., Harasiewicz K. A., Sherar M. D., “A history of medical and biological imaging with polyvinylidene fluoride (PVDF) transducers,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 47(6), 1363–1371 (2000). 10.1109/58.883525 [DOI] [PubMed] [Google Scholar]
- 21.Zhang C., Chen S.-L., Ling T., Guo L., “Review of imprinted polymer microring as ultrasound detector: fabrication, characterization and applications,” IEEE Sens. J. 15, 3241–3248 (2015). 10.1109/JSEN.2015.2421519 [DOI] [Google Scholar]
- 22.Zhang C., Ling T., Chen S.-L., Guo L. J., “Ultrabroad bandwidth and highly sensitive optical ultrasonic detector for photoacoustic imaging,” ACS Photonics 1(11), 1093–1098 (2014). 10.1021/ph500159g [DOI] [Google Scholar]
- 23.Evans E., Fung Y.-C., “Improved measurements of the erythrocyte geometry,” Microvasc. Res. 4(4), 335–347 (1972). 10.1016/0026-2862(72)90069-6 [DOI] [PubMed] [Google Scholar]
- 24.Zhang C., Chen S.-L., Ling T., Guo L. J., “Imprinted Polymer Microrings as High-Performance Ultrasound Detectors in Photoacoustic Imaging,” J. Lightwave Technol. 33(20), 4318–4328 (2015). 10.1109/JLT.2015.2466661 [DOI] [Google Scholar]
- 25.Ling T., Chen S.-L., Guo L. J., “Fabrication and characterization of high Q polymer micro-ring resonator and its application as a sensitive ultrasonic detector,” Opt. Express 19(2), 861–869 (2011). 10.1364/OE.19.000861 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Saleh B. E., Teich M. C., Saleh B. E., Fundamentals of Photonics (Wiley; New York, 1991), Chap. 20. [Google Scholar]
- 27.Xie Z., Chen S.-L., Ling T., Guo L. J., Carson P. L., Wang X., “Pure optical photoacoustic microscopy,” Opt. Express 19(10), 9027–9034 (2011). 10.1364/OE.19.009027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hsieh B.-Y., Chen S.-L., Ling T., Guo L. J., Li P.-C., “All-optical scanhead for ultrasound and photoacoustic dual-modality imaging,” Opt. Express 20(2), 1588–1596 (2012). 10.1364/OE.20.001588 [DOI] [PubMed] [Google Scholar]
- 29.Chen S.-L., Chang Y.-C., Zhang C., Ok J. G., Ling T., Mihnev M. T., Norris T. B., Guo L. J., “Efficient real-time detection of terahertz pulse radiation based on photoacoustic conversion by carbon nanotube nanocomposite,” Nat. Photonics 8(7), 537–542 (2014). 10.1038/nphoton.2014.96 [DOI] [Google Scholar]
- 30.Gandjbakhche A. H., Mills P., Snabre P., “Light-scattering technique for the study of orientation and deformation of red blood cells in a concentrated suspension,” Appl. Opt. 33(6), 1070–1078 (1994). 10.1364/AO.33.001070 [DOI] [PubMed] [Google Scholar]
- 31.Strohm E. M., Hysi E., Kolios M. C., “Photoacoustic measurements of single red blood cells,” in 2012 IEEE International Ultrasonics Symposium (IUS) (IEEE, 2012), pp. 1406–1409. 10.1109/ULTSYM.2012.0351 [DOI] [Google Scholar]
- 32.Nakao M., Nakao T., Yamazoe S., “Adenosine triphosphate and maintenance of shape of the human red cells,” Nature 187(4741), 945–946 (1960). 10.1038/187945a0 [DOI] [PubMed] [Google Scholar]
- 33.Zhang C., Subbaraman H., Li Q., Pan Z., Ok J. G., Ling T., Chung C.-J., Zhang X., Lin X., Chen R. T., Guo L. J., “Printed photonic elements: nanoimprinting and beyond,” J. Mater. Chem. C Mater. Opt. Electron. Devices 4(23), 5133–5153 (2016). 10.1039/C6TC01237J [DOI] [Google Scholar]
- 34.Musielak M., “Red blood cell-deformability measurement: review of techniques,” Clin. Hemorheol. Microcirc. 42(1), 47–64 (2009). [DOI] [PubMed] [Google Scholar]
- 35.Park Y., Best C. A., Badizadegan K., Dasari R. R., Feld M. S., Kuriabova T., Henle M. L., Levine A. J., Popescu G., “Measurement of red blood cell mechanics during morphological changes,” Proc. Natl. Acad. Sci. U.S.A. 107(15), 6731–6736 (2010). 10.1073/pnas.0909533107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Brandão M. M., Fontes A., Barjas-Castro M. L., Barbosa L. C., Costa F. F., Cesar C. L., Saad S. T., “Optical tweezers for measuring red blood cell elasticity: application to the study of drug response in sickle cell disease,” Eur. J. Haematol. 70(4), 207–211 (2003). 10.1034/j.1600-0609.2003.00027.x [DOI] [PubMed] [Google Scholar]