Epsin N-terminal Homology Domain (ENTH) Activity as a Function of Membrane Tension

Abstract

The epsin N-terminal homology domain (ENTH) is a major player in clathrin-mediated endocytosis. To investigate the influence of initial membrane tension on ENTH binding and activity, we established a bilayer system based on adhered giant unilamellar vesicles (GUVs) to be able to control and adjust the membrane tension σ covering a broad regime. The shape of each individual adhered GUV as well as its adhesion area was monitored by spinning disc confocal laser microscopy. Control of σ in a range of 0.08-1.02 mN/m was achieved by altering the Mg²⁺ concentration in solution, which changes the surface adhesion energy per unit area of the GUVs. Specific binding of ENTH to phosphatidylinositol 4,5-bisphosphate leads to a substantial increase in adhesion area of the sessile GUV. At low tension (<0.1 mN/m) binding of ENTH can induce tubular structures, whereas at higher membrane tension the ENTH interaction deflates the sessile GUV and thereby increases the adhesion area. The increase in adhesion area is mainly attributed to a decrease in the area compressibility modulus K_A. We propose that the insertion of the ENTH helix-0 into the membrane is largely responsible for the observed decrease in K_A, which is supported by the observation that the mutant ENTH L6E shows a reduced increase in adhesion area. These results demonstrate that even in the absence of tubule formation, the area compressibility modulus and, as such, the bending rigidity of the membrane is considerably reduced upon ENTH binding. This renders membrane bending and tubule formation energetically less costly.

Introduction

Clathrin-mediated endocytosis is one of the key metabolic pathways for the uptake of macromolecules into eukaryotic cells (1–4). Driven by a chain of remodeling events and an elaborate set of proteins acting in an orchestrated manner, an almost flat patch of plasma membrane is transformed into a closed, cargo-containing vesicle. As plasma membrane shape transformation is associated with significant local bending of the membrane, the process is highly sensitive to lateral membrane tension. Plasma membrane tension originates from two primary sources; that is, hydrostatic pressure across the lipid bilayer and cytoskeleton-membrane adhesion (5). Depending on the cell type, plasma membrane tensions span a range of roughly 0.003–0.45 mN/m (5–8). Even though it had become clear already in the late 1990s that tension plays a role in exo- and endocytosis (9, 10), only in recent years has significant evidence been accumulated that membrane tension is of utmost importance for processes that rely on membrane remodeling (11–14). Cells actively maintain and regulate their membrane tension and use it to control exo- and endocytosis (15). In K562 cells it has been reported that endocytosis is completely suppressed under hypoosmotic conditions (16). Generally, high lateral membrane tension suppresses membrane deformation as both stretching the lipid bilayer and opening bonds between the cytoskeleton and the plasma membrane requires a large amount of energy (17).

One protein domain that is involved in endocytosis is the epsin N-terminal homology domain (ENTH) (18, 19). It is known that ENTH of epsin-1 binds specifically to the receptor lipid PtdIns(4,5)P₂ (20–22), resulting in tubulation or even vesiculation (23, 24) as a result of membrane bending. Upon binding to PtdIns(4,5)P₂ an additional α-helix, referred to as helix-0 (amino acids 3–15) at the N terminus of ENTH, is formed. This newly formed helix-0 inserts into the inner monolayer of the plasma membrane resulting in an asymmetry that produces membrane curvature (25, 26). By means of protruded pore-spanning membranes exhibiting a lateral tension of ∼2 mN/m, we recently showed that specific ENTH binding to PtdIns(4,5)P₂-containing membranes reduces membrane tension (27). However, ENTH-induced tubulation was never observed. We thus asked the question, whether the initial lateral membrane tension influences the process that is initiated by ENTH- PtdIns(4,5)P₂ interaction.

To control lateral membrane tension in an artificial well defined membrane system, we made use of giant unilamellar vesicles (GUVs) that adhere to an avidin-coated glass substrate. By adjusting the Mg²⁺ concentration in solution, we were able to control and tune the lateral membrane tension of these GUVs in a range of 0.08–1.02 mN/m. These values are well below the tension value of 2 mN/m reported in the previous study (27) and might allow monitoring ENTH-induced membrane changes including tubulation or vesiculation. We show that with this system in hand, binding and helix-0 insertion of ENTH can be monitored in a label-free fashion by determining the increase in adhesion area of the GUV. From our observations, we conclude that ENTH binding results in a substantial softening of the lipid bilayer, which can eventually result in tubule formation at low initial lateral tension.

Results and Discussion

Tuning the Adhesion of GUVs by Mg²⁺

Fluorescently labeled GUVs composed of DOPC/DOPE/Atto488 DPPE³ were doped with N-(cap-biotinyl)-DOPE to attach them onto the avidin-coated glass surface (28). For specific binding of ENTH to GUVs, the natural receptor lipid PtdIns(4,5)P₂ with a concentration of 0.8 mol% was supplemented. To obtain the shape of the vesicles, they were imaged by spinning disc confocal laser microscopy (SDCLM) (Fig. 1, bottom images). Attractive forces between the GUV and the avidin-coated surface change its shape from a sphere with a radius R_v to a spherical cap with a slightly increased radius of the cap denoted as R_ad (Fig. 1, top images). The spherical cap geometry is indicative of the strong adhesion regime (29, 30). In the limit of strong adhesion the bending energy associated with changes in the shape of the vesicle can be ignored, and the vesicle can be described as a spherical cap usually parameterized solely by the contact angle ϴ with the surface (30, 31). The adhered GUV forms a circular contact area with the functionalized glass substrate with a radius R_i (Fig. 1, top image) (32). This adhesion area increases until the free energy of the vesicle is minimized. The elastic energy encompasses stretching energy, bending energy, and the entropic cost of suppressing thermal fluctuations of the contact area between the GUV and the substrate (33). Adhesion energy is obtained from the surface energy times the contact area. In the strong adhesion limit, we can safely assume that the free energy F_v comprises only an elastic stretching term and an adhesion term (Equation 1),

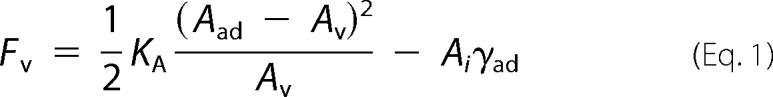where K_A is the area compressibility modulus of the bilayer, A_ad is the area of the adhered vesicle, A_v is the area of the free vesicle, A_i is the contact area, and γ_ad is the adhesion energy per unit area mainly originating from bond formation between a GUV and the substrate. Minimization of the free energy assuming constant volume requires the shell to be laterally dilated to allow generation of a finite-sized adhesion zone (31). Naturally, stretching of the bilayer inevitably generates lateral tension. Therefore, controlling the adhesion area permits to adjust membrane tension.

FIGURE 1.

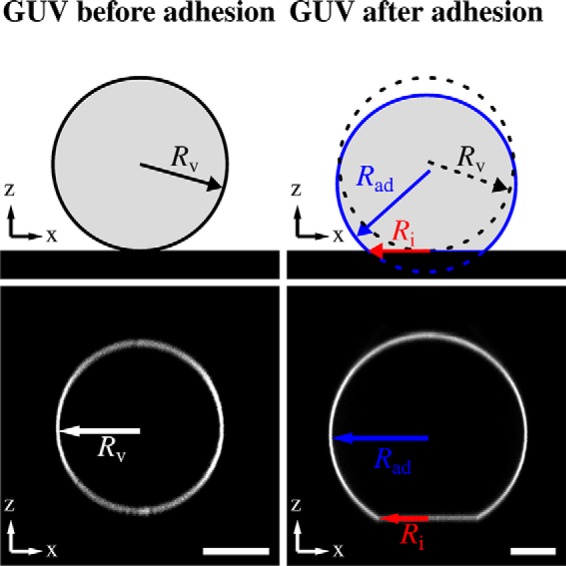
Scheme of an adhered GUV. Shown is a schematic drawing (top images) and corresponding SDCLM images (bottom images) of a GUV on an avidin-coated surface before and after adhesion. Without adhesion, the GUV geometry can be approximated as a sphere (radius R_v). After adhesion, a spherical cap with a radius of R_ad and a circular contact area (with a radius of R_i) is formed. Scale bars: 10 μm.

To modify the contact area of a GUV, we made use of the fact that divalent cations increase the membrane-surface interaction, i.e. it was found that a strong interaction between phosphatidylcholine and Mg²⁺ promotes spreading of vesicles to planar supported bilayers (34–36). To adjust the Mg²⁺ concentration, GUVs formed in sucrose solution (298 mosmol/kg) were added to a sucrose-containing buffer solution (2 mm HEPES, sucrose, pH 7.4, 298 mosmol/kg) doped with different MgCl₂ concentrations. Isoosmolar conditions are required as the size of the contact area is also a function of the GUV excess area, which depends on the osmolality gradient. GUVs were allowed to bind to the avidin-coated surface and were imaged by SDCLM. Fig. 2 illustrates the increase in contact area of GUVs doped with 0.8 mol% PtdIns(4,5)P₂ as a function of Mg²⁺ concentration. To compare GUVs of different sizes, the radius R_i of the contact area was related to the radius R_ad of the adhered GUV (Fig. 2). This allowed us to normalize the adhesion area to the size of the GUV and compare different ensembles. The increase of R_i/R_ad with Mg²⁺ concentration (Fig. 3) suggests that Mg²⁺ promotes the adhesion of the GUVs by interaction of the lipid head groups of the membrane with the functionalized glass surface (34, 37). In addition to this interaction, it is also conceivable that Mg²⁺ influences the biotin-avidin-interaction itself. Holmberg et al. (38) showed that the dissociation of a biotin-streptavidin bond strongly depends on the ionic strength and is almost fully prevented in the presence of Mg²⁺. In essence, both effects result in a larger contact area with increasing Mg²⁺ concentration.

FIGURE 2.

Vesicle contact area as a function of Mg²⁺ concentration. Representative three-dimensional reconstructions of SDCLM images of GUVs (DOPC/DOPE/cap-biotin-PE/Atto488-DPPE/PtdIns(4,5)P₂, 66.2:30:2:1:0.8) adhering on an avidin-coated glass surface. Adhesion strength is modulated by different Mg²⁺ concentrations. The ratio of the contact area (red) to the equatorial plane (blue) of a GUV is a function of the Mg²⁺ concentration. Scale bars: 10 μm.

FIGURE 3.

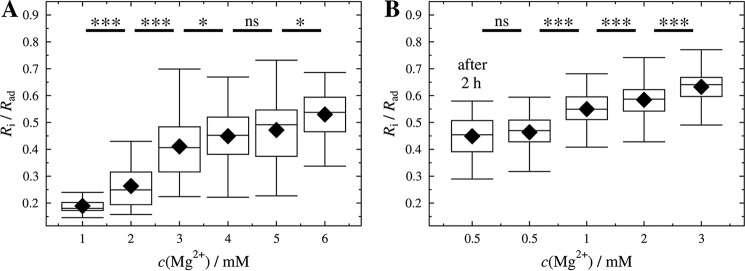
Ratios R_i/R_ad as a function of Mg²⁺ concentration. Ratios of contact radius to initial vesicle radius R_i/R_ad of GUVs composed of DOPC/DOPE/cap-biotin-PE/Atto488-DPPE (67:30:2:1) (A) and DOPC/DOPE/cap-biotin-PE/Atto488-DPPE/PtdIns(4,5)P₂ (66.2:30:2:1:0.8) (B) adhered to an avidin-coated glass surface measured at different Mg²⁺ concentrations. For each condition 31–101 GUVs (n_total = 413, A) and 79–117 GUVs (n_total = 467, B) were measured obtained from at least two independent preparations for each condition. After 2 h of incubation the same values were obtained (see in B, after 2 h). Black diamonds represent the mean. ***, p < 0.001; *, p < 0.05; ns, not significant.

Estimating Lateral Membrane Tension from the Contact Area

The observed contact area of the GUV with the glass surface provides information about the lateral tension of the GUV membrane. Assuming constant volume of the GUV during the course of the experiment due to the low water permeability of the membrane (39) and isoosmolar conditions, lateral tension can be computed from the area dilatation generated by adhesion. In equilibrium, larger adhesion forces generate larger area dilatation. To calculate the lateral membrane tension from the normalized area increase, one has to consider two contributions, one from ironing out membrane undulations and one from dilating a flat membrane laterally in a two-dimensional Hookean fashion (40). Excess area stored in thermally excited membrane undulations is sacrificed first followed by lateral expansion of lipids. Equation 2 relates area dilatation to membrane tension σ of an adhered GUV (41),

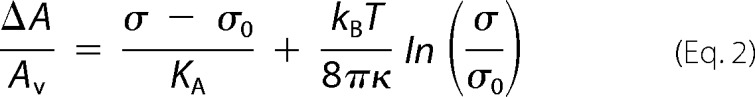The bending rigidity κ of a DOPC membrane is assumed to be 21 k_BT, and the area compressibility modulus K_A = 265 mN/m accordingly (42). As a reference state, we choose the free vesicle with tension σ₀, which depends on the size of the vesicle and the osmotic pressure between inside and outside of the vesicle. Equation 2 holds, if σ₀ ≪ σ, and allows the estimation of the lateral membrane tension σ of an adhered GUV numerically. Because it is impossible to determine σ₀ for all vesicles used here independently, we determined σ₀ for a few representative GUVs by parallel plate compression in conjunction with optical microscopy (43). We found σ₀ to be in the range of 10⁻⁶-10⁻⁴ N/m in accordance with typical values for weakly adhering GUVs on a glass substrate as obtained by reflectometric interference microscopy (44).

To calculate the tension σ, we need to determine the relative area dilatation after adhesion of the vesicle. A free GUV forms a sphere with an area A_v. It changes its geometry upon adhesion and forms a spherical cap with an increased surface area A_ad. Note that a spherical cap geometry corresponds to the limit of strong adhesion with respect to membrane undulations (29). The normalized change in surface area ΔA/A_v can be calculated from the shape change (Equation 3),

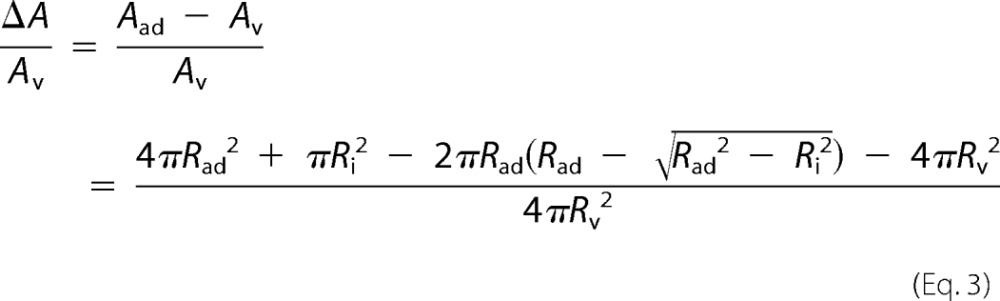with the condition of constant volume,

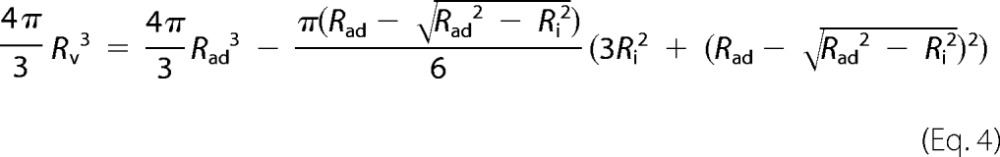ΔA/A_v is only a function of R_i/R_ad, which is related to the contact angle between a sessile vesicle and the substrate by ϴ = sin⁻¹(R_i/R_ad).

Fig. 3 shows the R_i/R_ad values (n_total = 467) of adhered PtdIns(4,5)P₂ containing GUVs with an average radius of R_v = 18 ± 5 μm for different Mg²⁺ concentrations. The mean ratios of R_i/R_ad increased from 0.46 at a Mg²⁺ concentration of 0.5 mm to 0.63 at 3.0 mm. For GUVs lacking PtdIns(4,5)P₂ (n_total = 413) with an average radius of R_v = 18 ± 5 μm, R_i/R_ad increased from 0.19 at a Mg²⁺ concentration of 1 mm to 0.53 at 6.0 mm. Fig. 4 shows how area dilatation and lateral tension change as a function of R_i/R_ad according to Equations 2, 3 and 4.

FIGURE 4.

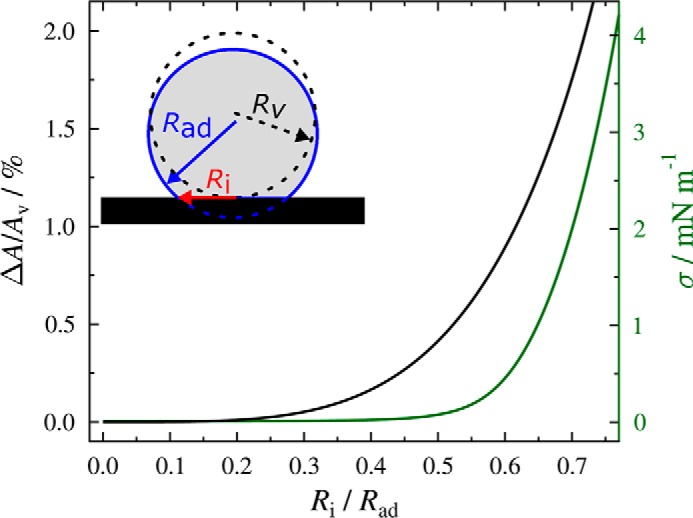
Normalized area dilatation ΔA/A_v as a function of R_i/R_ad. The theoretically calculated relationship of the normalized area dilatation (ΔA/A_v) as a function of R_i/R_ad according to Equations 1 and 2 is shown as a solid black line. The lateral tension resulting from the area dilatation was calculated using Equation 3 and 4 with K_A = 265 mN/m, κ = 21 k_BT and σ₀ = 10⁻⁵ N/m (green line).

Based on this theoretical framework, the lateral tension of GUVs composed of DOPC/DOPE/cap-biotin-PE/Atto488-DPPE/PtdIns(4,5)P₂ (66.2:30:2:1:0.8) adhering to an avidin-coated glass surface using different Mg²⁺ concentrations can be calculated (Fig. 5). The mean tensions cover a range of 0.08–1.02 mN/m assuming σ₀ = 10⁻⁵ N/m. The upper value is slightly larger than values found for cell membranes, which range between 0.003 and 0.45 mN/m (5–8).

FIGURE 5.

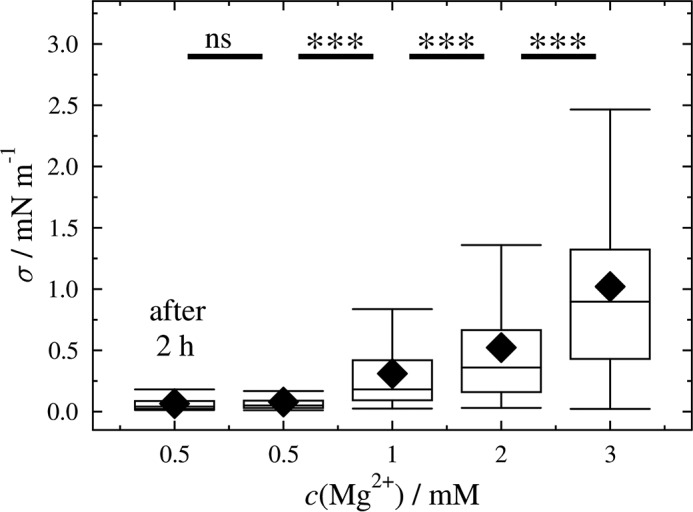
Calculated membrane tension as a function of Mg²⁺ concentration. Lateral membrane tension of GUVs (DOPC/DOPE/cap-biotin-PE/Atto488-DPPE/PtdIns(4,5)P₂, 66.2:30:2:1:0.8) adhering on an avidin-coated glass surface obtained at different Mg²⁺ concentrations. The mean tensions at different Mg²⁺ concentrations are: 0.08 mN/m (0.5 mm), 0.31 mN/m (1 mm), 0.52 mN/m (2 mm), and 1.02 mN/m (3 mm). For each condition 79–117 GUVs were measured (n_total = 467). After 2 h of incubation the same values were obtained (after 2 h). Black diamonds represent the mean. ***, p < 0.001; ns, not significant.

A small change in R_i/R_ad can result in a rather large change in lateral membrane tension (Fig. 4). At low R_i/R_ad, the excess area of the GUV stored in undulations compensates for the area dilation caused by adhesion on the surface (R_i/R_ad = 0.46, σ = 0.08 mN/m), whereas for larger R_i/R_ad undulations are ironed out, and the lateral membrane tension increases significantly due to the first term in Equation 2 (R_i/R_ad = 0.63, σ = 1.02 mN/m). The results clearly demonstrate that the lateral membrane tension of adhered GUVs can be readily adjusted within a certain regime making use of different Mg²⁺ concentrations to control γ_ad, the adhesion energy per unit area. This system thus enables us to study the influence of the specific binding of ENTH to PtdIns(4,5)P₂ containing GUVs as a function of a given initial lateral membrane tension.

ENTH Binding to PtdIns(4,5)P₂-doped GUVs

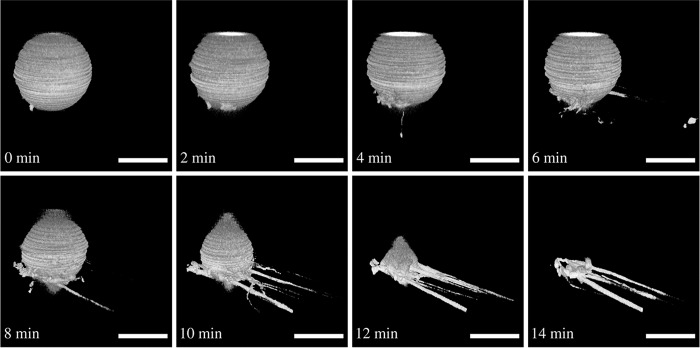
ENTH can induce membrane tubulation (22, 25). Recently we showed that binding of ENTH to PtdIns(4,5)P₂-doped and slightly curved pore-spanning membranes results in a reduction of the lateral membrane tension (27). However, the initial tension of the bilayer was rather high, and it is well conceivable that tubulation is suppressed at elevated tension. To answer the question of how ENTH binding to PtdIns(4,5)P₂ containing adhered GUVs alters their shape dependent on the preadjusted lateral membrane tension, we prepared GUVs composed of DOPC/DOPE/cap-biotin-PE/Atto488-DPPE/PtdIns(4,5)P₂, (66.2:30:2:1:0.8) in the presence of 0.5 mm and 2 mm Mg²⁺. The resulting mean membrane tensions were 0.08 mN/m and 0.52 mN/m, respectively. To these adhered GUVs, ENTH was added at a final concentration of c_ENTH = 1 μm. Interestingly, dependent on the preadjusted lateral membrane tension, two different behaviors were observed after protein addition. At a low lateral membrane tension (σ = 0.08 mN/m), the addition of ENTH can indeed result in the formation of tubules, eventually leading to the disappearance of the GUV (Fig. 6). Because of the stirring of the solution, tubules appear preferentially on one side of the GUV and also elongated along this direction. Of note, even at this low lateral membrane tension, only part of the GUVs show tubulation, whereas others display an increase in adhesion area indicative of transient reduction in lateral membrane tension (see below).

FIGURE 6.

Tubulation after ENTH binding to a GUV with low membrane tension. Time series of three-dimensional reconstructions of SDCLM images of a GUV (DOPC/DOPE/cap-biotin-PE/Atto488-DPPE/PtdIns(4,5)P₂, 66.2:30:2:1:0.8) adhering on an avidin-coated glass surface at low membrane tension (c(Mg²⁺) = 0.5 mm). The GUV starts to tubulate after ENTH addition (c_ENTH = 1 μm) and forms tethers until all lipid material is dissipated. Tubulation starts at t = 0 min. Scale bars: 10 μm.

It has been shown that upon binding of ENTH to PtdIns(4,5)P₂, the protein experiences a change in structure in which helix-0 inserts into the lipid bilayer as demonstrated by EPR spectroscopy (22). This increases the surface area of the outer leaflet of the GUV membrane and induces an asymmetry in the two bilayer leaflets facilitating membrane bending by generating spontaneous curvature (26, 45). In agreement with our observations of tubule formation upon ENTH binding, association of full-length epsin and ENTH to non-adhered tension-free GUVs also resulted in the formation of irregular structures such as vesicles and tubules (23, 25, 46, 47) dependent on the experimental conditions and on the surface density of bound protein (48, 49). Recently, Shi and Baumgart (49) provided experimental evidence for a mechanism whereby local membrane tension reduction mediated by endocytic proteins reduces the elastic energy required for membrane deformation and thus facilitates membrane budding and tubulation. Molecular dynamics simulations predicted that the formation of tubules requires a lower protein coverage on the membrane than the formation of vesicles (48). To calculate the protein surface coverage in this study, we determined the dissociation constant of ENTH to PtdIns(4,5)P₂-doped planar POPC membranes (9:1) by reflectometric interference spectroscopy, which resulted in a K_D = 0.8 μm. This in turn means that at an ENTH concentration of 1 μm, 56% of the receptor lipids are occupied. The GUVs used in this study contain 0.8% of the receptor lipid PtdIns(4,5)P₂. Taking the protein's footprint of 16 nm² (50) into account and assuming a 1:1 binding of ENTH to PtdIns(4,5)P₂ results in a protein surface coverage on the membrane of 10%. This rather low protein coverage agrees with the observation that only tubules are formed and no vesicles (50, 51).

However, if GUVs with a larger membrane tension of σ = 0.52 mN/m was incubated with ENTH, in none of the cases was tubulation observed. Instead, the adhered vesicles started to flatten, and their contact area increased after ENTH binding (Fig. 7), i.e. the distance between the equatorial plane of the GUV (Fig. 7, blue line) and its contact area (Fig. 7, red line) was reduced as a function of time. The size of the adhesion area is a result of the newly established equilibrium between adhesion force and membrane tension (33). When the new equilibrium was adjusted after ENTH binding, the membrane tension again reached its previous value of σ = 0.52 mN/m, which essentially prevents tubule formation as any deformation would require further dilation of the membrane as long as the volume is conserved.

FIGURE 7.

Flattening of a GUV with elevated membrane tension after ENTH binding. Time series of three-dimensional reconstructions of SDCLM images of a GUV (DOPC/DOPE/cap-biotin-PE/Atto488-DPPE/PtdIns(4,5)P₂, 66.2:30:2:1:0.8) adhering on an avidin-coated glass surface generating high membrane tension (c(Mg²⁺) = 2 mm). The GUV starts to flatten after ENTH addition (c_ENTH = 1 μm), and R_i/R_ad increases. Flattening starts at t = 0 min. Scale bars: 20 μm.

This unique experimental approach allowed us to obtain statistically meaningful data by imaging 10s of GUVs before and after protein addition as a function of membrane tension. Normalized contact radii R_i/R_ad of GUVs adhered to an avidin-coated substrate at three different Mg²⁺ concentrations were imaged by SDCLM before and after incubation with ENTH for 1 h to ensure equilibrium conditions. Fig. 8 clearly shows that for each Mg²⁺ concentration the ratio of R_i/R_ad is significantly larger after ENTH addition (Fig. 8, gray boxes) than before (Fig. 8, white boxes). For low membrane tension, where also tubulation can occur, only those GUVs with no indication of tubulation were used for statistical analysis.

FIGURE 8.

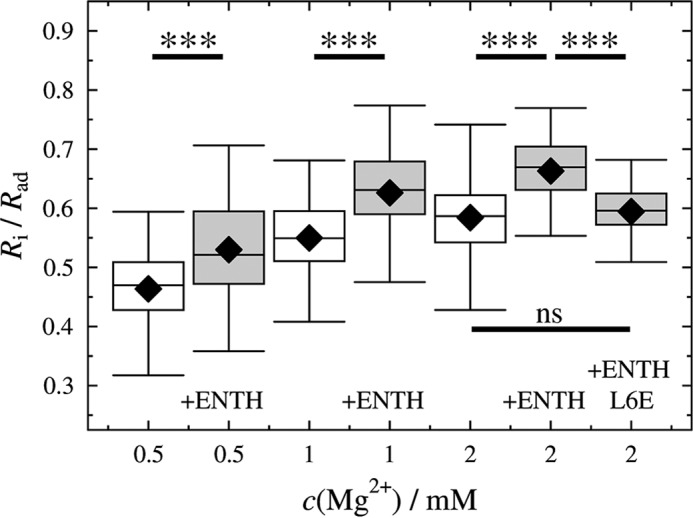
Changes in R_i/R_ad in response to ENTH binding as a function of initial membrane tensions. R_i/R_ad of GUVs adhering on an avidin-coated glass surface measured at different Mg²⁺ concentrations before and after ENTH addition (c_ENTH = 1 μm). For each condition 52–117 GUVs were measured obtained from at least two independent preparations; black diamonds represent the mean; n_total = 556. ***, p < 0.001; ns, not significant.

Under the assumptions that the adhesion energy per unit area remains the same and the initial tension is restored after insertion of the proteins' helix-0, an increase in R_i/R_ad can only be explained by an area increase δA_ENTH upon helix-0 insertion or by a decrease of the area compressibility modulus K_A,ENTH (for details see “Appendix”). First, we estimate the expected increase in area δA_ENTH due to helix insertion. Therefore, we take the area of helix-0 of ENTH into account, which is ∼10–30% (= 1.6–4.8 nm²) of the ENTH surface projection. Employing the determined dissociation constant K_D and the known PtdIns(4,5)P₂ concentration assuming a PtdIns(4,5)P₂ area of 0.7 nm² (52) in the GUVs, this translates into a maximal expected relative area increase of 1–3%. Next, we compare this estimate with the experimentally obtained relative area change deduced from the measured changes in R_i/R_ad before and after ENTH binding. Under the assumption that the adhesion energy per unit area of the GUV and its volume remain constant, a relative area increase of 83% is calculated (see “Appendix“). The computed relative area increase is independent of the initial tension. Such a tremendous area increase is unrealistic and contradicts the theoretically expected relative area increase. Thus, we conclude that δA_ENTH does not explain the significant change in R_i/R_ad. Instead, a substantially reduced area compressibility modulus K_A might explain the observation. Neglecting in this case the area increase of δA_ENTH due to insertion alone and calculating the altered K_A values, one finds that K_A reduces from the initial value of K_A = 265 mN/m to 145 mN/m independent of the initial lateral membrane tension.

We speculate that the insertion of helix-0 of ENTH into one leaflet of the membrane is responsible for the observed reduction in K_A. To confirm this hypothesis, we performed the same GUV experiments at 2 mm Mg²⁺ but replaced wild type ENTH with the mutant ENTH L6E. This mutant binds Ins(1,4,5)P₃ with the same affinity constant as the wild type but has a reduced binding affinity to short chain diC8PtdIns(4,5)P₂ and does not induce tubules in vesicles (23, 25). The result depicted in Fig. 8 demonstrates that the change in R_i/R_ad is significantly smaller than that observed for wild type ENTH, suggesting that helix-0 is largely responsible for the observed change in K_A. A reduction in K_A directly translates into a reduction of the bending rigidity κ, i.e. ENTH binding accompanied by helix-0 insertion reduces the energetic cost for bending and thus tubule formation.

Membrane softening has been shown to occur upon interaction of several small peptides with membranes and has been ascribed to perturbations on the membrane organization and to a direct modulation of κ by membrane thinning (53–55). Settles et al. (53) showed that Sar1p, a protein involved in vesicle trafficking, dramatically lowers the rigidity of lipid bilayer membranes. This membrane softening does not rely on the imposition of strong local curvature and is a profoundly different mode of action than those typically ascribed to intracellular curvature-associated proteins. For ENTH, elasticity theory predicts curvature generation based on membrane insertion of helix-0 (56), which can occur on the local scale. In our setup, membrane softening due to helix-0 coupled to the local curvature of the membrane led either to tubule formation, if this process is faster than the adjustment of the new equilibrium state of the GUVs, or to an increase in R_i/R_ad if tubule formation is slower. In contrast, GUVs with a larger initial tension do not become floppy enough so that local curvature did not lead to tubule formation. Instead, the GUVs reached the new equilibrium state upon membrane softening, observable as an increased R_i/R_ad. It is conceivable that this is a kinetic effect, i.e. the GUV spreads faster regaining its initial tension than tubules can be formed. As the amount of bound ENTH is largely given by the mole fraction of the receptor lipid PtdIns(4,5)P₂, the reduction in K_A, κ is independent of the initial lateral membrane tension as expected. Fig. 9 proposes a model based on our findings. Insertion of helix-0 into a prestressed vesicle (1) relaxes tension until either tubulation sets in at low initial tension (2′) or a new equilibrium state is adopted (3) by generating a larger adhesion area to maintain tension.

FIGURE 9.

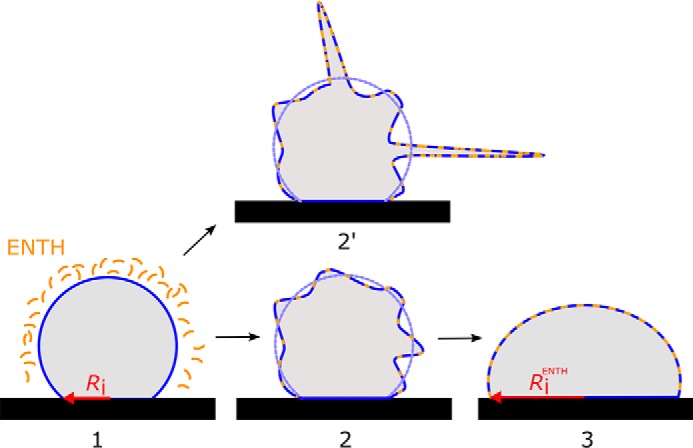
Model of ENTH action. Insertion of helix-0 into a sessile vesicle (1) relaxes its tension until either tubulation sets in at low initial tension (2′) or a new equilibrium state is established (3) that requires to produce a larger adhesion area.

Our results are in line with a recent study of Shi and Baumgart (49). They have shown by micropipette aspiration experiments on single GUVs that a larger membrane tension of 0.25 mN/m strongly inhibits N-BAR-induced shape instability, which is required for the formation of tubules (49). N-BAR domains are found in endocytic proteins and are one of the best studied examples of proteins that sense and induce membrane curvature and whose binding involves also the insertion of parts of the protein into the membrane (57). Molecular dynamics simulations support the findings of Baumgart and coworkers (58) showing that a membrane tension in the range of 0.2 mN/m and larger increases the free energy barrier for the formation of tubules from a planar membrane and inhibits polymerization of N-BAR domains (59). Our results as well as those of others are also in line with the notion that exo- and endocytic pathways are regulated by lateral membrane tension in vivo. Hypoosmotic conditions resulted in a membrane tension of 4.2 mN/m and completely suppressed endocytosis in K562 cells (16). The endocytic activity in 2H3 cells decreased after increasing the membrane tension by osmotic swelling, whereas membrane tension dropped if the cells were stimulated to secrete (10).

Conclusions

We have shown that it is possible to adjust the lateral membrane tension of GUVs adhered to an avidin-coated glass surface by varying the Mg²⁺ concentration in solution. In contrast to micropipette aspiration, where the lateral tension can be precisely adjusted, the presented method has the advantage that 10s of GUVs can be imaged simultaneously allowing for high statistics to be obtained. The influence of protein binding on the morphology of the adhered GUVs as well as on the membrane's mechanical properties can be easily inspected by confocal microscopy without the need for protein labeling. Based on our results, we propose that the insertion of helix-0 of ENTH into the membrane is largely responsible for tubule formation at low lateral tension, whereas it mainly softens the membrane at higher membrane tensions. Our findings contribute to the overall discussion about how helix-0 insertion modulates membrane curvature and mechanical properties of the membranes. We suggest that the reduction of bending rigidity of membranes plays a pivotal role in all forms of endocytosis.

Experimental Procedures

Preparation of GUVs

Lipids (Avanti Polar Lipids, Alabaster, AL) were dissolved in CHCl₃ in the desired ratio and deposited on indium tin oxide-coated cover slips (V = 50 μl, c = 0.8 mg/ml). After solvent removal under reduced pressure for 3 h at room temperature, GUVs were formed by electroformation (AC, 3 V, 5 Hz, 2 h) in sucrose solution (298 mosmol/kg). GUVs were composed of either DOPC/DOPE/N-(cap biotinyl)-DOPE/Atto488 DPPE (67:30:2:1), or DOPC/DOPE/N-(cap biotinyl)-DOPE/PtdIns(4,5)P₂/Atto488 DPPE (66.2:30:2:1:0.8).

Preparation of Avidin-coated Glass Slides

Glass slides (Ibidi GmbH, Planegg, Germany) were treated with a mixture of H₂O/NH₃/H₂O₂ (5:1:1, v/v/v) for 20 min at 70 °C before incubation with an avidin solution (c = 10 μm) dissolved in phosphate-buffered saline (PBS, 137 mm NaCl, 2.7 mm KCl, 10 mm Na₂HPO₄, 1.8 mm KH₂PO₄, pH 7.4) for 30 min at room temperature, and the glass slides were thoroughly rinsed with ultrapure H₂O. After adsorption of avidin and rinsing with buffer, the avidin-coated glass surface was passivated by incubation with bovine serum albumin (10 mg/ml) for 30 min. Afterward, the glass slides were transferred into sucrose-containing buffer (2 mm HEPES, sucrose, pH 7.4, O_final = 298 mosmol/kg) with the desired Mg²⁺ concentration.

ENTH Expression

ENTH (wild type and L6E mutant) was expressed and purified as described previously (27). ENTH of rat epsin1 (residues 1–164) fused with a glutathione S-transferase tag was cloned into the vector pGEX-6P-1. After protein expression in BL21 cells for 3 h at 37 °C, the cells were lysed using Emulsiflex C3 and spun at 140,000 × g for 30 min at 4 °C in a Beckman Ti45 rotor. The supernatant was bound to glutathione beads for 30 min. Afterward, the beads were washed 6 times with 20 mm HEPES, 150 mm NaCl, 2 mm dithiothreitol, 2 mm EDTA, pH 7.4, with 2 washes at 700 mm NaCl in between. After cleavage of the glutathione S-transferase tag using PreScission proteases, the cleaved proteins were further purified by gel filtration (Superdex 200). The protein was transferred into sucrose-containing buffer with the corresponding Mg²⁺ concentration using Amicon® Ultra 4 ml Filters (NMGG10000, Merck, 3 × 30 min, 4000 × g, 4 °C; Allegra™ X-22R, Rotor SX4250, Beckman Coulter, Krefeld, Germany).

Spinning Disk Confocal Fluorescence Setup

Fluorescence images were obtained using a spinning disc confocal microscope (spinning disc unit: Yokogawa CSU-X, Rota Yokogawa GmbH & Co. KG, Wehr, Germany; stand: Olympus custom-made, Olympus Deutschland GmbH, Hamburg, Germany; piezo nanofocusing z-drive: P-721-CDQ, Physik Instrumente GmbH & Co. KG, Karlsruhe/Palmbach, Germany; camera: iXON 897Ultra, Andor Technology Ltd., Belfast, UK) equipped with a water immersion objective CFI Plan 100XW 100 ×/1.1 (Nikon GmbH, Düsseldorf, Germany) and a custom-made humidity chamber. The humidity chamber minimized water evaporation and ensured isoosmolarity for at least 2 h. Atto 488 DPPE was excited at λ = 488 nm, and the fluorescence light was selected with a 496/LP emission filter (AHF Analysentechnik AG, Tübingen, Germany). Fluorescence microscopy images were visualized by the program IMARIS (version 8.1.2, Bitplane AG, Zürich, Switzerland). A median filter (3 × 3 × 3) was used for smoothing.

GUV Data Evaluation

To automatically determine the z-position of the contact area of the GUV, a custom-written Matlab-script was used. An intensity profile was measured at the GUV center, and the center positions were determined by fitting Gaussian functions to the profile. The two maxima define the positions of the GUV contact area and the upper membrane of the GUV. The contact radius R_i was calculated from the circular contact area that was measured by threshold analysis. To determine the radius R_ad of the spherical cap after adhesion, the circular equatorial plane of each adhered GUV was determined.

Reflectometric Interference Spectroscopy

Reflectometric interference spectroscopy measurements were performed using a custom-built setup equipped with a NanoCalc-2000 spectrometer (OceanOptics Germany GmbH, Ostfildern, Germany) (60). SiO₂ wafers with an oxide layer of 5 μm were incubated in a solution of NH₃ and H₂O₂ (H₂O/NH₃/H₂O₂, 5:1:1) for 20 min at 70 °C. The time course of bilayer formation after the addition of small unilamellar vesicles obtained by sonication (61) was monitored until a stable optical thickness was reached. After rinsing with buffer, the resulting membrane was treated with a bovine serum albumin solution (1 mg/ml) to prevent nonspecific protein adsorption. After again rinsing with buffer, ENTH was added, and spectra were recorded every 2 s and the optical thickness determined (60).

Author Contributions

M. G. performed the GUV experiments and analyzed the data. C. F. and N. T. performed the reflectometric interference spectroscopy experiments. B. K. and M. M. expressed and purified the proteins. T.-T. K. established the GUV adhesion mediated by Mg²⁺. A. J. devised the theoretical model. C. S. and M. M. designed the experiments and wrote the manuscript. All authors reviewed the results and approved the final version of the manuscript.

Appendix

The free energy F_v of a vesicle adhering to a surface in the strong adhesion limits is given by Equation 1. Minimizing the free energy F_v leads to the following equilibrium condition,

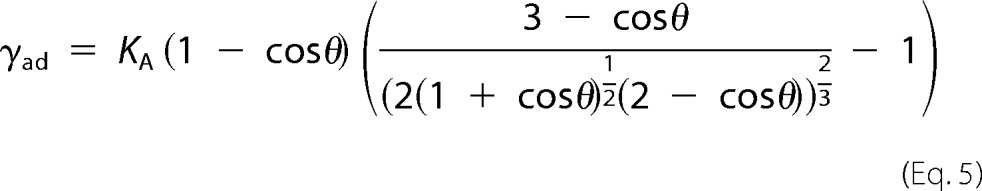with θ = sin⁻¹ (R_i/R_ad) (31). Adhesion energies larger than 10⁻⁴ J/m² were calculated for vesicles adhering to an avidin-coated glass surface based on the vesicle geometry using Equation 5 and K_A = 0.265 N/m (30, 42). Adhesion energies of 1.25·10⁻⁴ J/m², 3.32·10⁻⁴ J/m², 4.78·10⁻⁴ J/m², and 7.70·10⁻⁴ J/m² at Mg²⁺ concentrations of 0.5, 1, 2, and 3 mm, respectively, were determined in accordance with the assumption of the limit of strong adhesion.

An increase in R_i was measured as a result of ENTH binding, and we assume that helix-0 insertion into the bilayer enlarges the vesicle's surface area by δA_ENTH. Equation 1 can then be rewritten to,

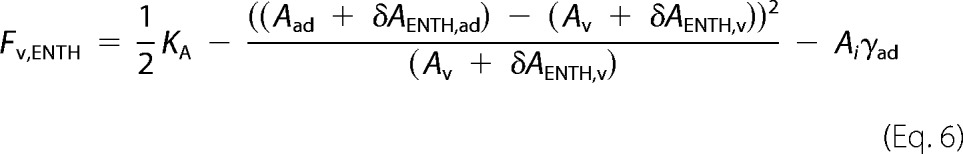δA_ENTH,ad denotes the area change of an adhered vesicle due to ENTH helix-0 insertion, whereas δA_ENTH,v is the corresponding change in area of a free vesicle. Rearranging Equation 6 assuming δA_ENTH,ad ≅ δA_ENTH,v ≅ δA_ENTH yields,

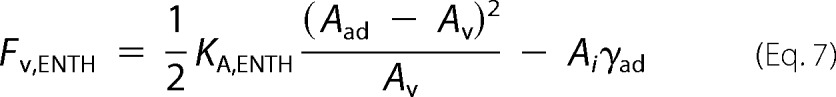with an apparent area compressibility modulus K_A,ENTH after ENTH binding of,

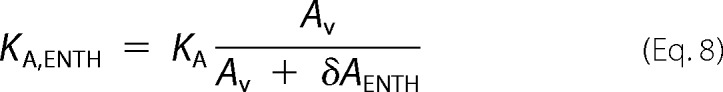Assuming a constant adhesion energy γ_ad before and after ENTH addition, K_A,ENTH can be obtained from,

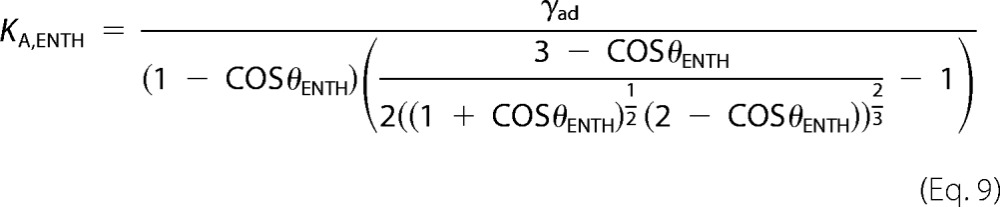where θ_ENTH is the equilibrium contact angle after ENTH addition. A mean apparent area compressibility modulus of K_A,ENTH = 0.145 ± 0.009 N/m after ENTH addition was calculated for 3 initial lateral membrane tensions. The necessary change in vesicle area caused by binding of ENTH (δA_ENTH) required for a reduction of K_A = 0.265 N/m to the apparent area compressibility modulus K_A,ENTH = 0.145 N/m was then calculated using Equation 9. An area increase caused by helix-0 insertion of ENTH of 83% would be required to explain the observed reduction in the apparent area compressibility modulus while keeping K_A constant. This is unrealistic, as the relative area increase caused by the insertion of the ENTH helix was approximated to be 1–3% based on the protein's crystal structure. Therefore, the insertion of the ENTH helix is believed to cause the observed change of the area compressibility modulus neglecting the small change in area as a result of helix-0 insertion. The decrease in K_A translates into a reduction of the bending rigidity, i.e. a softening of the membrane as observed after insertion of helical peptides into lipid bilayers (53–55).