Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Sep 16;6:33397. doi: 10.1038/srep33397

Direct theoretical evidence for weaker correlations in electron-doped and Hg-based hole-doped cuprates

Seung Woo Jang 1, Hirofumi Sakakibara 2,3, Hiori Kino 4, Takao Kotani 2, Kazuhiko Kuroki 5, Myung Joon Han 1,6,a
PMCID: PMC5025755  PMID: 27633802

Abstract

Many important questions for high-Tc cuprates are closely related to the insulating nature of parent compounds. While there has been intensive discussion on this issue, all arguments rely strongly on, or are closely related to, the correlation strength of the materials. Clear understanding has been seriously hampered by the absence of a direct measure of this interaction, traditionally denoted by U. Here, we report a first-principles estimation of U for several different types of cuprates. The U values clearly increase as a function of the inverse bond distance between apical oxygen and copper. Our results show that the electron-doped cuprates are less correlated than their hole-doped counterparts, which supports the Slater picture rather than the Mott picture. Further, the U values significantly vary even among the hole-doped families. The correlation strengths of the Hg-cuprates are noticeably weaker than that of La2CuO4. Our results suggest that the strong correlation enough to induce Mott gap may not be a prerequisite for the high-Tc superconductivity.

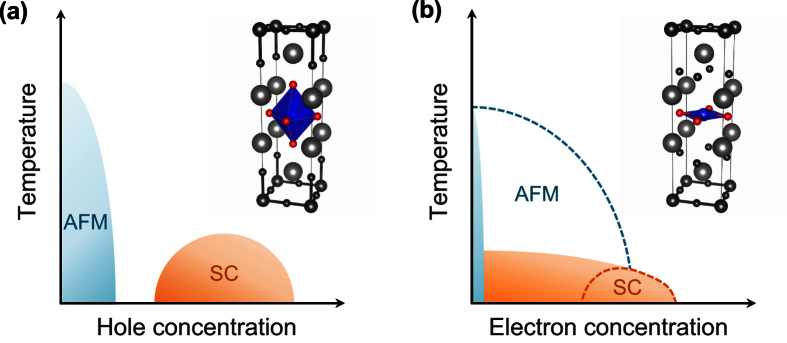
Due to extensive efforts over the last 30 years1, significant progress has been made in the understanding of high-temperature superconducting materials. Although the pairing mechanism and the intriguing interplay between competing orders still remain elusive, many aspects of this series of copper-oxides have now been well established. Basically, all cuprates share common phase diagram features, and each phase has been a subject of intensive study. The ‘dome’-shaped region of superconductivity, which only appears after the long-range magnetic order is suppressed (see Fig. 1), is possibly the key to understanding the pairing principle of cuprates. These features are also found in other families of superconducting materials, such as Fe-based and heavy Fermion compounds, and have been well recognized, likely suggesting that the same superconducting mechanism exists in the different families2.

Figure 1.

Figure 1

Open in a new tab

Schematic phase diagram of superconducting (SC) and antiferromagnetic (AFM) states for the (a) hole-doped and (b) electron-doped region. The insets show the representative crystal structure for each region: (a) La2CuO4 and (b) RE2CuO4 where the large, medium, and small spheres represent La/RE (grey), Cu (black or blue), and O (black or red), respectively. The octahedral CuO6 and planar CuO4 unit are shaded blue.

The superconducting dome has been considered to be particularly important in the framework of some outstanding theoretical models or ‘pictures’ that assume or predict its existence3,4. Therefore, it is striking that a series of recent experiments for electron-doped cuprates have reported data that contradicts this feature. According to a systematic re-investigation of electron-doped samples, RE2CuO4 (RE = rare-earth: Nd, Pr, Sm, etc.), the superconducting region does not cease to exist as the carrier concentration decreases, but this region extends to very low doping, quite close to zero5,6,7,8,9,10,11,12,13,14,15,16,17,18. Further, as the doping approaches zero, the superconducting transition temperature (Tc) seems to keep increasing with no indication of the dome (see Fig. 1(b)). While further study needs to be performed to clarify this issue, it seems indicative that the undoped parent compounds of RE2CuO4 are a Slater-type insulator rather than a Mott-type insulator. Therefore, the ‘doped Mott insulator’ picture may not be appropriate, at least for the electron-doped family.

Some theoretical suggestions are supportive of this conclusion. According to Weber et al.19,20, for example, an electron-doped material, Nd2CuO4, is less correlated and should be identified as a Slater insulator, while the hole-doped La2CuO4 should be considered as a Mott insulator. The LDA + DMFT (local density approximation plus the dynamical mean field theory) calculation by Das and Saha-Dasgupta21 showed that the T-structured La2CuO4 is insulating while the T′-structured La2CuO4 is metallic at U = 4.5 eV. Comanac et al.22 also concluded that the correlation strengths in cuprates are not strong enough to be identified as Mott insulators.

In spite of its crucial importance, however, this issue is quite challenging because of the difficulty in quantifying the ‘Mott-ness’ or in estimating the correlation strengths. Here, we also note that while Comanac et al. concluded that all the cuprates are Slater insulators22, Weber et al., as well as Das and Saha-Dasgupta, made a sharp distinction between the electron-doped and the hole-doped families19,20,21. One clear and well-defined way for resolving this issue is to calculate or ‘measure’ the material dependence of the correlation strength, which is traditionally denoted by the parameter U (on-site Coulomb repulsion within the single-band Hubbard model). Further, calculating the material dependent U values can illuminate other important issues such as pairing principle. Because electron-doped cuprates generally have lower Tc (≤30 K) than hole-doped materials, whose Tc sometimes exceeds 100 K (e.g., the triple-layered Hg-cuprates), it is important to determine if there is a notable difference in the correlation strengths of these two different families.

Here, we try to provide a clear answer to this long standing question by performing the direct estimation of U for several different types of cuprates. Our first-principles calculations show that both of the previous conclusions are not quite correct. On one hand, our result provides the first direct confirmation that the correlation strength of electron-doped materials is weaker than that of hole-doped counterparts. On the other, we significantly revise the previous conclusion: Not all of the hole-doped cuprates have stronger correlation compared to the electron doped ones. In fact, one representative hole-doped family, namely Hg-cuprates (and presumably many other multi-layered cuprates), has weaker electron correlation strength comparable to the electron-doped materials. Our result has a profound implication for the pairing principle: The correlation effects, strong enough to produce the Mott insulating state, may not be a prerequisite for high Tc superconductivity.

Results

The results are summarized in Fig. 2. We clearly see that T’-structures (or, the parent compounds of electron-doped materials) have significantly smaller U values than the hole-doped materials (parent phases), especially La2CuO4. The calculated U for RE2CuO4 (RE: Nd, Pr, Sm) is 1.24–1.34 eV, which is considerably smaller than the La2CuO4 value of 3.15 eV. The material dependent U/t was also estimated (see Fig. 2; the data in green color and the right vertical axis), where the nearest-neighbor hopping parameter, t, was calculated with the standard Wannier-function technique23,24 (see Supplementary Information). The calculated U/t for La2CuO4 is ~7 which compares reasonably well with the widely used values for the model Hamiltonian studies25. The U/t value for the RE2CuO4 series is ~3, which is significantly smaller (~43% of the La2CuO4 value).

Figure 2. Calculated U and U/t for cuprate parent compounds.

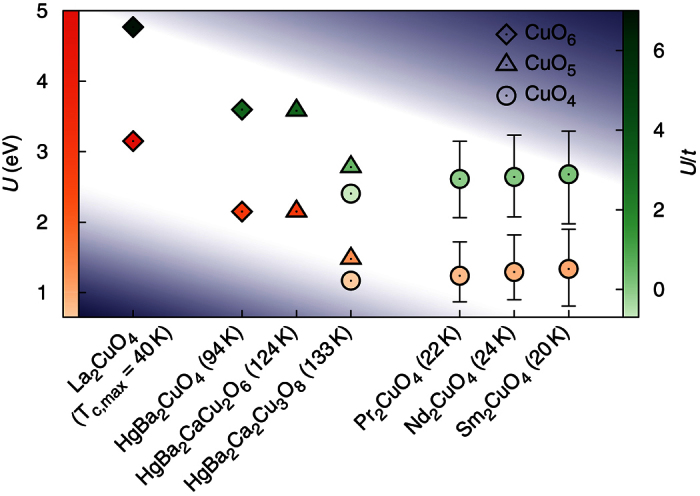
Figure 2

Open in a new tab

The left (orange) and the right (green) vertical axis correspond to U and U/t, respectively. A total of seven different materials have been calculated: La2CuO4 (single layered, hole doped), HgBa2CuO4 (single layered, hole doped), HgBa2CaCu2O6 (double layered, hole doped), HgBa2Ca2Cu3O8 (triple layered, hole doped), Pr2CuO4 (single layered, electron doped), Nd2CuO4 (single layered, electron doped), and Sm2CuO4 (single layered, electron doped). For the electron-doped materials, RE2CuO4, three different techniques have been used to treat the RE-4f electrons (see the text for more details). The average values are presented and the error bars indicate the largest and smallest values. The symbols represent the local CuOn structures: diamonds, triangles, and circles correspond to CuO6, CuO5, and CuO4, respectively. The numbers in parentheses are the optimal superconducting Tc,max of each material.

The 4f electrons in RE2CuO4 located around the Fermi level must be considered carefully. Because there is no well-established method to treat these states, first-principles calculations of rare-earth compounds has been challenging. One widely-used method is to treat the 4f electrons as part of the core electrons, as was done in refs 19 and 20. To minimize the ambiguity caused by this technical difficulty, we used three different methods; Method 1, 2, and 3 (see the Supplementary Information). For presentation, we took the average of these three values as the main data, and the error bars represent the largest and smallest values obtained by Methods 1–3 in Fig. 2. Importantly, our conclusions were the same regardless of which values are considered. In fact, if we consider the previously-used technique, Method 1, the U/t difference between the RE2CuO4 and La2CuO4 is enlarged (see the Supplementary Information).

Arguably, our calculation is the most direct way to determine the correlation strengths. For the estimation of correlation strength the previous theoretical approaches analyzed either the mass renormalization factor or the optical conductivity19,20,21,22 with U as a parameter. In the present study, we directly calculated U from first-principles without any adjustable parameter (see Methods and Supplementary Information). Therefore, our results, which show a smaller U value in electron-doped materials, can be regarded as direct evidence that materials with the T′-type lattice structure are less correlated.

A characteristic feature that determines the material dependence of the correlation strength can be represented by a single parameter. Figure 3(a) shows the calculated U/t as a function of the inverse of the apical oxygen height (1/hO) (i.e., the average of the inverse bond distance between apical oxygen and copper). As 1/hO increases, the increasing trend of U/t from the electron-doped materials, RE2CuO4, to the hole-doped HgBa2CuO4, and to La2CuO4 is obvious. For the case of RE2CuO4 with no apical oxygen, 1/hO can be regarded as zero. While both (hole-doped) La2CuO4 and HgBa2CuO4 have well-defined octahedral oxygen cages around the Cu ions (i.e., CuO6), no apical oxygen is found in RE2CuO4, and CuO4 is formed instead of CuO6 (see Fig. 1, inset). The absence of two apical oxygen atoms can cause a significant difference in electronic properties and effectively reduce the correlation strengths. This relationship between U/t (or U) and hO can be used as a good rule of thumb to measure the correlation strength.

Figure 3.

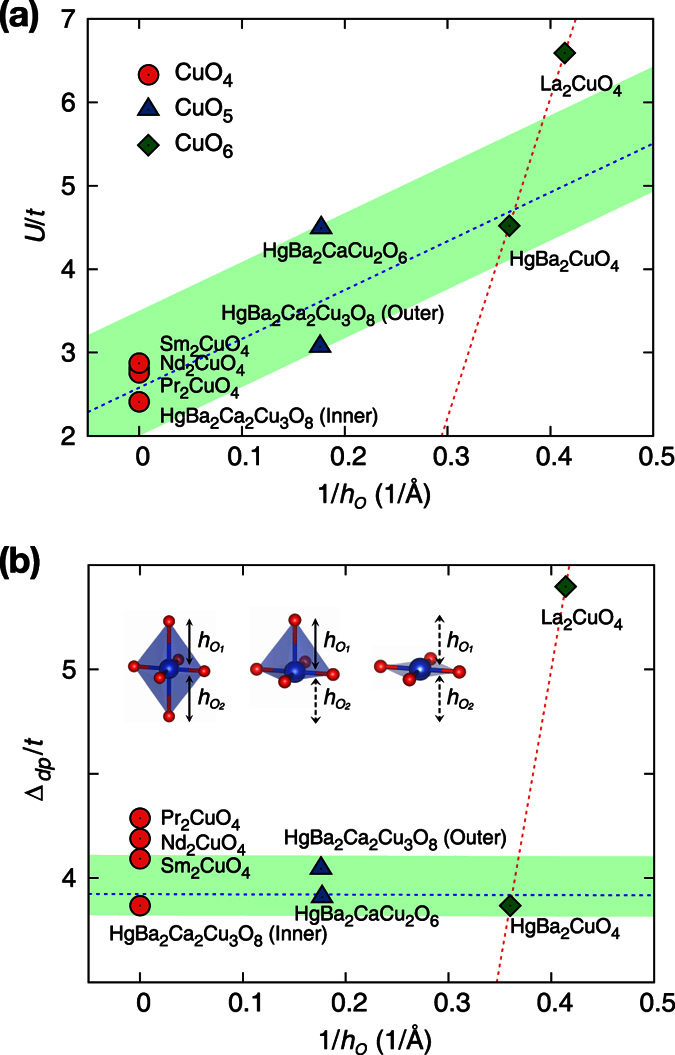
Figure 3

Open in a new tab

The calculated U/t (a) and Δdp/t (b) as a function of the inverse apical oxygen height, 1/hO. The color and shape of each point represent the local structure of materials: CuO6 (green diamonds), CuO5 (blue triangles), and CuO4 (red circles) having two, one, and no apical oxygen, respectively. The local structures are presented in the inset of (b). 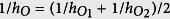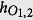The effective bond length between Cu and the apical oxygen, hO, is defined as Inline graphic where Inline graphic indicates the Cu to apical oxygen bond distance and the distance can be defined to be ∞ when there is no apical oxygen. For the case with no apical oxygen (CuO4), 1/hO can be regarded as zero. For CuO5 which has one apical oxygen, 1/hO is defined as half of the inverse of the bond distance between Cu and apical O. The red line shows the fitting from two data points of single-layer hole-doped compounds, La2CuO4 and HgBa2CuO4. The blue line shows the fitting from the four data points of the Hg-compounds. The shaded green blocks provide a guide for the eyes.

It is noteworthy that the hole-doped family can also have copper-oxygen layers with no apical oxygen. For example, the inner-layer of HgBa2Ca2Cu3O8 has the same local structure as RE2CuO4 (i.e., no apical oxygens; CuO4). Figures 2 and 3(a) clearly show that the inner-layer Cu in triple-layered HgBa2Ca2Cu3O8 has a similar value of U and U/t to RE2CuO4.

It is a remarkable new finding that some of the hole-doped cuprates have correlation strengths comparable to the electron-doped materials. It raises a question about the simple classification that categorizes all hole-doped cuprates as Mott insulators. As shown in Figs 2 and 3(a), the calculated U and U/t values of the Hg-cuprates are located in between those of RE2CuO4 and La2CuO4. Note that the single-layer HgBa2CuO4 has a well-defined CuO6 local unit as in La2CuO4, and its correlation strength is noticeably weaker than that of La2CuO4. According to our calculations, the difference of U (U/t) between HgBa2CuO4 and La2CuO4 is 1.0 eV (2.1). That difference is larger than the difference between HgBa2CuO4 and RE2CuO4, which is ~0.9 eV (~1.7). In the case of the triple-layer Hg-compounds, the correlation strengths decrease to be even closer to the values of electron-doped materials. We emphasize its significant implication for the pairing principle: Considering that the Hg-based cuprates exhibit quite high Tc ≥ 100 K, the correlation effects strong enough to produce the Mott insulating mother compound may not be a prerequisite for high Tc superconductivity.

It is instructive to see how these features are related to the charge transfer energy, Δdp = Ed (Cu-3d energy level) − Ep (O-2p energy level), which is another key parameter in many of the transition-metal oxides26. While Δdp is a quantity for the d-p model (not the single-band model), one can examine the behavior of Δdp/t in comparison to U/t. Figure 3(b) shows the calculated Δdp/t as a function of 1/hO. We note that the charge transfer energies of the Hg-compounds are more similar to the values of RE2CuO4 than those of La2CuO4. The overall behavior of U and Δdp is not quite different nor entirely similar. the same when plotted as a function of 1/hO. The similarity is likely due to that a large Δdp results in a smaller d-p hybridization, making Wannier orbital more localized. At the same time, the details of the band structure play some role in determining the correlation strength.

Importantly, the results of both U and Δdp indicate that Hg-compounds are significantly less correlated than La2CuO4, and their correlation strengths are comparable to those of electron-doped materials. Therefore, a simple classification of the parent compounds in terms of the carrier types is not pertinent, and the previous studies that regarded La2CuO4 as a prototype hole-doped cuprate should be re-interpreted. It may be more desirable to classify some of the hole-doped materials as Slater-type insulators.

Discussion

Comparison of our result with experiments is not at all straightforward and any direct quantitative argument may not be possible. The determination of U based on any experimental data is eventually to fit onto a certain type of model. Within such an obvious limitation, it may be instructive to see the optical conductivity data as a possible consistency check. The previous experiments on the hole-doped materials, for example, seem basically consistent with our results: Charge transfer gap of La2CuO4 is larger than that of Nd2CuO4, and the integrated Drude weight of (doped) T’-materials is larger than La2CuO4. The trend of other materials is also compatible with our calculations while the data from the undoped parent compounds is not always available22,27,28,29,30,31,32.

Our results can provide natural explanations for recent experiments7,8,9,10,11,12,13,14,15,16 in which the phase diagram of the electron-doped cuprates exhibits monotonically increasing Tc toward zero doping (see Fig. 1(b)). This behavior has been observed in the carefully-annealed samples of both thin film and single crystal forms7,8,9,10,11,12,13,14,15,16. If it is indeed the case, the implication can be profound and the electron-doped side of the phase diagram should be re-drawn (Fig. 1(b)). According to our calculations, this behavior is a result of the relatively weak correlation in the electron-doped materials. In this context, it is instructive to recall a recent numerical result by variational Monte Carlo calculations. Yokoyama et al. showed in their one-band Hubbard model study that a small value of U/t ≤ 6 produces an increasing Tc region of superconductivity whereas a larger U/t value always gives the dome-shape33.

The Hg-cuprates are of interest in this regard. Being a hole-doped family, their correlation strength is significantly weaker than that of La2CuO4 and close to the electron-doped cuprates, especially in the triple-layer compound. Nevertheless, the dome-like doping dependence of Tc has been observed in both single-layer34 and multilayer35 Hg-cuprates. Therefore, the dome-shaped Tc may not necessarily be a consequence of strong electron correlation. In fact, a mechanism that can induce the dome-shaped Tc without Mott-ness has recently been proposed36. In this theory, the intrinsic electron-hole asymmetry of the hybridized Cu3d–O2p electronic structure plays an essential role. Regarding the absence or presence of antiferromagnetic ordering, it is important to note that the low doping regime (<5%) has not been experimentally reached for the single-layer Hg-compound due to the presence of excess oxygen34. Hence, considering the moderate value of U/t in single-layer Hg-cuprates, the presence of antiferromagnetism as well as the Mott-insulating state in the non-doping limit may still be an open issue. We expect the Tl-based cuprate, which also has a large hO value, have similar behavior37. For multilayer Hg-compounds, antiferromagnetism has been reported in the underdoped regime35. Our result suggests that this insulating state can be of the Slater-type rather than the Mott-type. The robust presence of antiferromagnetism in these multilayer cases (compared to the electron-doped cases) might be due to the interlayer coupling.

Summary and Conclusion

We performed the first direct calculation of the material dependent correlation strengths in cuprates. A clear increasing trend of U is found as a function of 1/hO. Our result strongly supports the Slater picture for electron-doped cuprates. It is the first direct evidence of weaker correlations in electron-doped materials, and can be regarded as a (theoretical) confirmation. On the other hand, we significantly revise the current understanding of this issue. Contrary to the previous conclusion, some of the hole-doped cuprates (e.g., the Hg-compounds) have considerably weaker correlations which are comparable to those in electron-doped materials. Our results indicate that the electron correlation strong enough to induce the Mott gap may not be a prerequisite for high Tc superconductivity.

Methods

Computation details

We used so-called ‘constrained random phase approximation (cRPA)’ method to estimate the correlation strength. This recently-established technique38,39,40,41,42,43,44,45,46 has been proven to be reliable in many different types of materials40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56, including 3d, 4d, 5d transition-metal oxides47,48,49,50,51,52 and Fe-based superconductors53,54,55,56, while it has never been systematically applied to cuprates. Early calculations of La2CuO4 based on constrained LDA (cLDA) predict too large U value of ~7–10 eV57,58,59,60,61. It is a typical feature of cLDA due to the limitation for describing the electronic screening41. Our implementation of cRPA into our own software package ‘ecalj’62 follows one of the most recent standard formalisms by Şaşιoğlu et al.44,45 (see the Supplementary Information). We have checked that the previously reported data for many different materials were well reproduced by our implementation (see the Supplementary Information).

In order to avoid the ambiguity related to the 4f electrons in RE2CuO4, we used three different methods. Method 1 treats the RE-4f orbitals as the core as in the previous studies19,20. This method removes some screening channels (but not the on-site d-d transitions) around the Fermi energy and can cause some deviation in the U estimation. Method 2 replaces RE ions with La while maintaining the experimental lattice parameters. The resulting effect is expected to be similar to Method 1. We emphasize, however, that the whole procedure is determined in a self-consistent way, and the position and the width of the Cu-3d band is adjusted accordingly. Therefore, the naive guess for the final U value might not be correct. Method 3 keeps the RE-4f states around the Fermi energy as described by LDA. Within LDA, these less-renormalized and uncorrelated 4f-bands are located closer to the Fermi level and contribute to the screening. In spite of the complexity of the LDA band structure, the Cu-eg bands are well identified by the standard Wannier fitting, and therefore, Method 3 works as well as the other two approaches (see the Supplementary Information). The average of these three values is presented as the main data while the error bars represent the largest and smallest values obtained by Methods 1–3 (Fig. 2).

The LDA band structure was calculated by an all-electron full-potential method with the PMT basis (augmented plane wave + muffin-tin orbital)63. The polarization function is expanded by the mixed product basis in which the imaginary part along the real axis is accumulated with the tetrahedron method and the real part is obtained by a Hilbert transformation. Our approach has a clear advantage in terms of its accuracy compared to other methods, such as simple k-point sampling, Matsubara-frequency sampling, and the pseudopotential method. We have carefully verified the k-point dependency and found that our conclusions are robust against the computation details (see the Supplementary Information). The calculated U value of 3.15 eV for La2CuO4 is in good agreement with the only available data of 3.65 eV49. For further details, see the Supplementary Information.

Additional Information

How to cite this article: Jang, S. W. et al. Direct theoretical evidence for weaker correlations in electron-doped and Hg-based hole-doped cuprates. Sci. Rep. 6, 33397; doi: 10.1038/srep33397 (2016).

Supplementary Material

Supplementary Information
srep33397-s1.pdf (1.3MB, pdf)

Acknowledgments

We thank Dr. Takashi Miyake for providing us the the maximally localized Wannier function code implemented on top of ‘ecalj’ package. S.W.J. and M.J.H. were supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2014R1A1A2057202). The computing resource is supported by National Institute of Supercomputing and Networking/Korea Institute of Science and Technology Information with supercomputing resources including technical support (KSC-2014-C2-015) and by Computing System for Research in Kyushu University. T.K. was supported by the Advanced Low Carbon Technology Research and Development Program (ALCA), the “High-efficiency Energy Conversion by Spinodal Nano-decomposition” program of the Japan Science and Technology Agency (JST), and the JSPS Core-to-Core Program Advanced Research Networks (“Computational Nano-materials Design on Green Energy”). H.S. was supported by JSPS KAKENHI (Grant-in-Aid for Young Scientists B, Grant No. 16J21175). Computational calculations was partly done at the supercomputer (HOKUSAI) at RIKEN, the supercomputing system of the ISSP.

Footnotes

The authors declare no competing financial interests.

Author Contributions T.K. and H.K. developed the LDA and cRPA code. S.W.J. performed cRPA calculations. S.W.J. and H.S. calculated Δdp. All authors contributed to analyzing the results and writing the manuscript.

References

  1. Bednorz J. G. & Müller K. A. Possible high Tc superconductivity in the Ba-La-Cu-O system. Z. Phys. B: Condens. Matter 64, 189–193 (1986). [Google Scholar]
  2. Scalapino D. J. A common thread: The pairing interaction for unconventional superconductors. Rev. Mod. Phys. 84, 1383–1417 (2012). [Google Scholar]
  3. Lee P. A., Nagaosa N. & Wen X.-G. Doping a Mott insulator: Physics of high-temperature superconductivity. Rev. Mod. Phys. 78, 17–85 (2006). [Google Scholar]
  4. Ogata M. & Fukuyama H. The t-J model for the oxide high-Tc superconductors. Rep. Prog. Phys. 71, 036501 (2008). [Google Scholar]
  5. Armitage N. P., Fournier P. & Greene R. L. Progress and perspectives on electron-doped cuprates. Rev. Mod. Phys. 82, 2421–2487 (2010). [Google Scholar]
  6. Fournier P. T′ and infinite-layer electron-doped cuprates. Physica C 514, 314–338 (2015). [Google Scholar]
  7. Brinkmann M., Rex T., Bach H. & Westerholt K. Extended superconducting concentration range observed in Pr2−xCexCuO4. Phys. Rev. Lett. 74, 4927–4930 (1995). [DOI] [PubMed] [Google Scholar]
  8. Matsumoto O. et al. Superconductivity in undoped T′-RE2CuO4 with Tc over 30 K. Physica C 468, 1148–1151 (2008). [Google Scholar]
  9. Matsumoto O. et al. Synthesis and properties of superconducting T′-R2CuO4 (R = Pr, Nd, Sm, Eu, Gd). Phys. Rev. B 79, 100508(R) (2009). [Google Scholar]
  10. Matsumoto O. et al. Generic phase diagram of “electron-doped” T′ cuprates. Physica C 469, 924–927 (2009). [Google Scholar]
  11. Matsumoto O. et al. Reduction dependence of superconductivity in the end-member T′ cuprates. Physica C 469, 940–943 (2009). [Google Scholar]
  12. Matsumoto O., Tsukada A., Yamamoto H., Manabe T. & Naito M. Generic phase diagram of Nd2−xCexCuO4. Physica C 470, S101–S103 (2010). [Google Scholar]
  13. Yamamoto H., Matsumoto O., Krockenberger Y., Yamagami K. & Naito M. Molecular beam epitaxy of superconducting Pr2CuO4 films. Solid State Commun. 151, 771–774 (2011). [Google Scholar]
  14. Krockenberger Y., Yamamoto H., Tsukada A., Mitsuhashi M. & Naito M. Unconventional transport and superconducting properties in electron-doped cuprates. Phys. Rev. B 85, 184502 (2012). [Google Scholar]
  15. Krockenberger Y. et al. Emerging superconductivity hidden beneath charge-transfer insulators. Sci. Rep. 3, 2235 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Chanda G. et al. Optical study of superconducting Pr2CuOx with Inline graphic. Phys. Rev. B 90, 024503 (2014). [Google Scholar]
  17. Tsukada A. et al. New class of T′-structure cuprate superconductors. Solid State Commun. 133, 427–431 (2005). [Google Scholar]
  18. Adachi T. et al. Evolution of the electronic state through the reduction annealing in electron-doped Pr1.3−xLa0.7CexCuO4+δ (x = 0.10) Single Crystals: Antiferromagnetism, Kondo Effect, and Superconductivity. J. Phys. Soc. Jpn. 82, 063713 (2013). [Google Scholar]
  19. Weber C., Haule K. & Kotliar G. Strength of correlations in electron- and hole-doped cuprates. Nature Phys. 6, 574–578 (2010). [Google Scholar]
  20. Weber C., Haule K. & Kotliar G. Apical oxygens and correlation strength in electron- and hole-doped copper oxides. Phys. Rev. B 82, 125107 (2010). [Google Scholar]
  21. Das H. & Saha-Dasgupta T. Electronic structure of La2CuO4 in the T and T′ crystal structures using dynamical mean field theory. Phys. Rev. B 79, 134522 (2009). [Google Scholar]
  22. Comanac A., de’ Medici L., Capone M. & Millis A. J. Optical conductivity and the correlation strength of high-temperature copper-oxide superconductors. Nature Phys. 4, 287–290 (2008). [Google Scholar]
  23. Marzari N. & Vanderbilt D. Maximally localized generalized Wannier functions for composite energy bands. Phys. Rev. B 56, 12847–12865 (1997). [Google Scholar]
  24. Souza I., Marzari N. & Vanderbilt D. Maximally localized Wannier functions for entangled energy bands. Phys. Rev. B 65, 035109 (2001). [Google Scholar]
  25. Araújo M. A. N., Carmelo J. M. P., Sampaio M. J. & White S. R. Spin-spectral-weight distribution and energy range of the parent compound La2CuO4. Eur. Phys. Lett. 98, 67004 (2012). [Google Scholar]
  26. Zaanen J., Sawatzky G. A. & Allen J. W. Band gaps and electronic structure of transition-metal compounds. Phys. Rev. Lett. 55, 418 (1985). [DOI] [PubMed] [Google Scholar]
  27. Lucarelli A. et al. Phase diagram of La2−xSrxCuO4 probed in the infrared: Imprints of charge stripe excitations. Phys. Rev. Lett. 90, 037002 (2003). [DOI] [PubMed] [Google Scholar]
  28. Onose Y., Taguchi Y., Ishizaka K. & Tokura Y. Charge dynamics in underdoped Nd2−xCexCuO4: Pseudogap and related phenomena. Phys. Rev. B 69, 024504 (2004). [DOI] [PubMed] [Google Scholar]
  29. Cooper S. L. et al. Optical studies of the a-, b-, and c-axis charge dynamics in Yba2Cu3O6+x. Phys. Rev. B 47, 8233–8248 (1993). [DOI] [PubMed] [Google Scholar]
  30. Hwang J., Timusk T. & Gu G. D. J. Doping dependent optical properties of Bi2Sr2CaCu2O8+δ. Phys. Condens. Matter 19, 125208 (2007). [Google Scholar]
  31. Tokura Y. et al. Cu-O network dependence of optical charge-transfer gaps and spin-pair excitations in single-CuO2-layer compounds. Phys. Rev. B 41, 11657(R) (1990). [DOI] [PubMed] [Google Scholar]
  32. Uchida S. et al. Optical spectra of La2−xSrxCuO4: Effect of carrier doping on the electronic structure of the CuO2 plane. Phys. Rev. B 43, 7942 (1991). [DOI] [PubMed] [Google Scholar]
  33. Yokoyama H., Ogata M., Tanaka Y., Kobayashi K. & Tsuchiura H. Crossover between BCS Superconductor and Doped Mott Insulator of d-Wave Pairing State in Two-Dimensional Hubbard Model. J. Phys. Soc. Jpn. 82, 014707 (2013). [Google Scholar]
  34. Yamamoto A., Hu W.-Z. & Tajima S. Thermoelectric power and resistivity of HgBa2CuO4+δ over a wide doping range. Phys. Rev. B 63, 024504 (2000). [Google Scholar]
  35. Mukuda H., Shimizu S., Iyo A. & Kitaoka Y. High-Tc superconductivity and antiferromagnetism in multilayered copper oxides –A new paradigm of superconducting mechanism–. J. Phys. Soc. Jpn. 81, 011008 (2012). [Google Scholar]
  36. Ogura D. & Kuroki K. Asymmetry of superconductivity in hole- and electron-doped cuprates: explanation within two-particle self-consistent analsys for the three band model. arXiv: 1505.04017.
  37. Shimakawa Y., Kubo Y., Manako T. & Igarashi H. Variation in TC and carrier concentration in Tl based sperconductors. Phys. Rev. B 40, 11400(R) (1989). [PubMed] [Google Scholar]
  38. Springer M. & Aryasetiawan F. Frequency-dependent screened interaction in Ni within the random-phase approximation. Phys. Rev. B 57, 4364–4368 (1998). [Google Scholar]
  39. Kotani T. Ab initio random-phase-approximation calculation of the frequency-dependent effective interaction between 3d electrons: Ni, Fe, and MnO. J. Phys.: Condens. Matter 12, 2413–2422 (2000). [Google Scholar]
  40. Aryasetiawan F. et al. Frequency-dependent local interactions and low-energy effective models from electronic structure calculations. Phys. Rev. B 70, 195104 (2004). [Google Scholar]
  41. Aryasetiawan F., Karlsson K., Jepsen O. & Schönberger U. Calculations of Hubbard U from first-principles. Phys. Rev. B 74, 125106 (2006). [Google Scholar]
  42. Miyake T. & Aryasetiawan F. Screened Coulomb interaction in the maximally localized Wannier basis. Phys. Rev. B 77, 085122 (2008). [Google Scholar]
  43. Miyake T., Aryasetiawan F. & Imada M. Ab initio procedure for constructing effective models of correlated materials with entangled band structure. Phys. Rev. B 80, 155134 (2009). [Google Scholar]
  44. Şaşιoğlu E., Friedrich C. & Blügel S. Effective Coulomb interaction in transition metals from constrained random-phase approximation. Phys. Rev. B 83, 121101(R) (2011). [Google Scholar]
  45. Şaşιoğlu E., Galanakis I., Friedrich C. & Blügel S. Ab initio calculation of the effective on-site Coulomb interaction parameters for half-metallic magnets. Phys. Rev. B 88, 134402 (2013). [Google Scholar]
  46. Amadon B., Applencourt T. & Bruneval F. Screened Coulomb interaction calculations: cRPA implementation and applications to dynamical screening and self-consistency in uranium dioxide and cerium. Phys. Rev. B 89, 125110 (2014). [Google Scholar]
  47. Vaugier L., Jiang H. & Biermann S. Hubbard U and Hund exchange J in transition metal oxides: Screening versus localization trends from constrained random phase approximation. Phys. Rev. B 86, 165105 (2012). [Google Scholar]
  48. Sakuma R. & Aryasetiawan F. First-principles calculations of dynamical screened interactions for the transition metal oxides MO (M = Mn, Fe, Co, Ni). Phys. Rev. B 87, 165118 (2013). [Google Scholar]
  49. Werner P., Sakuma R., Nilsson F. & Aryasetiawan F. Dynamical screening in La2CuO4. Phys. Rev. B 91, 125142 (2015). [Google Scholar]
  50. Mravlje J. et al. Coherence-incoherence crossover and the mass-renormalization puzzles in Sr2RuO4. Phys. Rev. Lett. 106, 096401 (2011). [DOI] [PubMed] [Google Scholar]
  51. Martins C., Aichhorn M., Vaugier L. & Biermann S. Reduced effective spin-orbital degeneracy and spin-orbital ordering in paramagnetic transition-metal oxides: Sr2IrO4 versus Sr2RhO4. Phys. Rev. Lett. 107, 266404 (2011). [DOI] [PubMed] [Google Scholar]
  52. Arita R., Kuneš J., Kozhevnikov V., Aichhorn M., Eguiluz A. G. & Imada M. Ab initio studies on the interplay between spin-orbit interaction and Coulomb correlation in Sr2IrO4 and Ba2IrO4. Phys. Rev. Lett. 108, 086403 (2012). [DOI] [PubMed] [Google Scholar]
  53. Miyake T., Pourovskii L., Vildosola V., Biermann S. & Georges A. d- and f-orbital correlations in the REFeAsO compounds. J. Phys. Soc. Jpn. 77, 99–102 (2008). [Google Scholar]
  54. Nakamura K., Arita R. & Imada M. Ab initio derivation of low-energy model for iron-based superconductors LaFeAsO and LaFePO. J. Phys. Soc. Jpn. 77, 093711 (2008). [Google Scholar]
  55. Miyake T., Nakamura K., Arita R. & Imada M. Comparison of Ab initio low-energy models for LaFePO, LaFeAsO, BaFe2As2, LiFeAs, FeSe, and FeTe: electron correlation and covalency. J. Phys. Soc. Jpn. 79, 044705 (2010). [Google Scholar]
  56. Werner P. et al. Satellites and large doping and temperature dependence of electronic properties in hole-doped BaFe2As2. Nature Phys. 8, 331–337 (2012). [Google Scholar]
  57. McMahan A. K., Martin R. M. & Satpathy S. Calculated effective Hamiltonian for La2CuO4 and solution in the impurity Anderson approximation. Phys. Rev. B 38, 6650 (1988). [DOI] [PubMed] [Google Scholar]
  58. Hybertsen M. S., Schlüter M. & Christensen N. E. Calculation of Coulomb-interaction parameters for La2CuO4 using a constrained-density-functional approach. Phys. Rev. B 39, 9028 (1989). [DOI] [PubMed] [Google Scholar]
  59. McMahan A. K., Annett J. F. & Martin R. M. Cuprate parameters from numerical Wannier functions. Phys. Rev. B 42, 6268 (1990). [DOI] [PubMed] [Google Scholar]
  60. Grant J. B. & McMahan A. K. Spin bags and quasiparticles in doped La2CuO4. Phys. Rev. B 46, 8440 (1992). [DOI] [PubMed] [Google Scholar]
  61. Anisimov V. I., Korotin M. A., Nekrasov I. A., Pchelkina Z. V. & Sorella S. First principles electronic model for high-temperature superconductivity. Phys. Rev. B 66, 100502(R) (1990). [Google Scholar]
  62. Kotani T. ecalj package. Available at: https://github.com/tkotani/ecalj (2009).
  63. Kotani T., Kino H. & Akai H. Formulation of the augmented plane-wave and muffin-tin orbital method. J. Phys. Soc. Jpn. 84, 034702 (2015). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep33397-s1.pdf (1.3MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES