Abstract
Characterizing the nanoscale dynamic organization within lipid bilayer membranes is central to our understanding of cell membranes at a molecular level. We investigate phase separation and communication across leaflets in ternary lipid bilayers, including saturated lipids with between 12 and 20 carbons per tail. Coarse-grained molecular dynamics simulations reveal a novel two-step kinetics due to hydrophobic mismatch, in which the initial response of the apposed leaflets upon quenching is to increase local asymmetry (antiregistration), followed by dominance of symmetry (registration) as the bilayer equilibrates. Antiregistration can become thermodynamically preferred if domain size is restricted below ∼20 nm, with implications for the symmetry of rafts and nanoclusters in cell membranes, which have similar reported sizes. We relate our findings to theory derived from a semimicroscopic model in which the leaflets experience a “direct” area-dependent coupling, and an “indirect” coupling that arises from hydrophobic mismatch and is most important at domain boundaries. Registered phases differ in composition from antiregistered phases, consistent with a direct coupling between the leaflets. Increased hydrophobic mismatch purifies the phases, suggesting that it contributes to the molecule-level lipid immiscibility. Our results demonstrate an interplay of competing interleaflet couplings that affect phase compositions and kinetics, and lead to a length scale that can influence lateral and transverse bilayer organization within cells.
Introduction
Cell membranes contain dynamic, nanoscale sterol- and/or sphingolipid-enriched ordered assemblies containing specific proteins,1 sometimes called lipid rafts.2 Much of the evidence for rafts is indirect.3 Simplified ternary mixtures of lipids phase-separate in vitro into liquid-disordered Ld and ordered Lo regions,4 but these conditions are far from those in cells. More convincingly, recent work shows that vesicles derived from the plasma membrane of living cells5,6 do spontaneously phase separate upon cooling below physiological temperatures. Critical fluctuations of this underlying miscibility transition could provide thermodynamically easy modes for domain assembly at physiological temperatures, under the additional influence of the cytoskeleton and membrane proteins.7
Ordered domains in cell membranes are typically tens of nanometers in size.8−11 The fact that rafts in vivo do not coarsen to larger size has sparked a variety of theoretical explanations, including the critical fluctuation hypothesis,12 elastic repulsion,13 hybrid lipids,14 or a microemulsion-like state.15 We do not adjudicate on these explanations here, though we will closely study the consequences of such limited raft size for transbilayer organization.
Interleaflet interactions are a key aspect of domain formation and are potentially crucial in cell membrane biology. Communication between domains in apposed leaflets is implicated in protein clustering and signaling,16,17 while work on model lipid systems shows that the phase behavior of leaflets is coupled.18−21 Moreover, inter- and intraleaflet interactions are inextricably linked. For example, interleaflet dimerization of cholesterol can cause cholesterol precipitation in bilayers, whereas similarly prepared monolayers remain uniform.22 Hydrophobic lipid tail length mismatch implicitly couples the leaflets21,23 as well as affecting lateral phase separation.
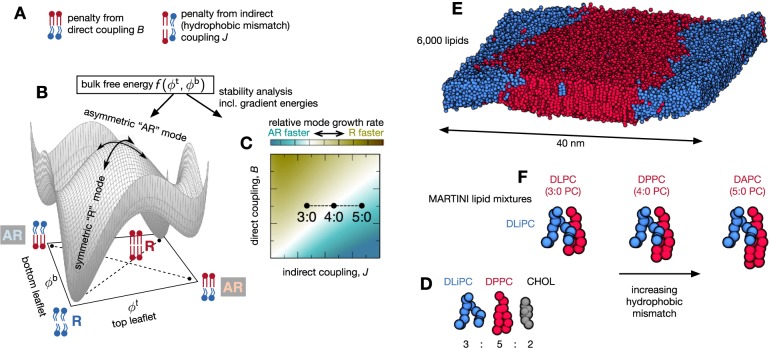
Traditional phase diagrams of model ternary bilayers (typically saturated and unsaturated lipids plus cholesterol) employ a Gibbs triangle to map coexisting phases in ternary composition space, while ignoring the distinct leaflets. To address this, phase separation can instead be described in “leaflet–leaflet” space18−21 with a free-energy landscape f(ϕt, ϕb) (see Figure 1B). The top (bottom) leaflet is described by a composition variable ϕt(b) for the area fraction of, e.g., saturated lipid—this amounts to a pseudobinary mapping20,24 of the ternary mixture within each leaflet.
Figure 1.
Bilayers may separate into registered R or antiregistered AR phases, in which the two leaflets are locally approximately symmetric, or strongly asymmetric, respectively. (A) A semimicroscopic theoretical model includes competing direct (B) and indirect (J, hydrophobic mismatch) interleaflet couplings,21 which respectively favor transbilayer symmetry and asymmetry. (B) A schematic “leaflet–leaflet” free-energy landscape f(ϕt, ϕb) with an axis for each leaflet’s composition,18−21 which determines phase coexistences through the common tangent plane construction.21 Tie-lines (dashed) for R–R and AR–AR coexistences are sketched beneath the landscape. For the overall leaflet compositions simulated here R–R has the lowest bulk free energy, while AR–AR is metastable. Both R and AR demixing modes exist (curved arrows). (C) Schematic map of linear instability growth rates for R versus AR demixing modes, obtained from f(ϕt, ϕb) plus gradient terms for thickness or composition boundaries between domains.21 For a longer saturated lipid (5:0 PC) we expect the AR mode to grow fastest, leading to initial demixing into an AR–AR state. (D) The overall composition is a mixture of 3:5:2 molar ratios DLiPC:DnPC:cholesterol. (E) A snapshot after 10 μs of simulation showing how the lipids have separated into registered ordered and disordered phases (water is not shown). (F) Altering the number of beads in the tail of the saturated lipid relative to DPPC tunes the tail length mismatch with the unsaturated lipid, DLiPC.
Two- or three-phase coexistences are then derived by drawing common tangent planes touching the surface f(ϕt, ϕb). For instance, the conventional coexistence of two symmetric phases in a bilayer of symmetric overall compositions corresponds to an R–R tie-line linking the two registered (“R”) minima of f(ϕt, ϕb) in Figure 1B. AR–AR tie-lines allow coexistence of two antiregistered (“AR”) phases.25 The three-phase state observed in ref. (18) for asymmetric overall leaflet compositions was explained as a triangle of R–R–AR coexistence in which one phase is strongly asymmetric and two are approximately symmetric.18,20
In this paper, we use molecular simulations to explore phase separation upon quenching ternary lipid bilayers whose overall leaflet compositions are symmetric. We link our simulation observations to a recent theory in which the free energy f(ϕt, ϕb) and associated phase-transition kinetics were derived from a semimicroscopic model of coupled leaflets,21 in order to infer the underlying intra- and interleaflet interactions which, in turn, could have biological implications.
Our simulations use a chemically realistic coarse-graining scheme, MARTINI.26,27 MARTINI and its predecessors can accurately model the insertion of proteins into membranes,28,29 the bending rigidity of simple bilayers,30 the diffusion of membrane proteins,31 and multicomponent asymmetric representations of the plasma membrane.32,33
Our results verify a prediction that large hydrophobic tail length mismatch between the lipids induces a two-step or nonmonotonic kinetics.21 Upon a quench, metastable antiregistered phases can initially grow fastest, before the equilibrium registered phases take over and dominate. By systematically varying simulation size we find evidence of competing area- and line-dependent energies; we obtain a quantitative estimate of a length scale below which antiregistration can be thermodynamically preferable due to restricted domain size, ∼20 nm for the strongest hydrophobic mismatch studied. This implies a length scale dependence characterizing competing contributions to transbilayer communication in cell membranes. In addition, we measure the bulk phase compositions within the leaflets, and show how they exhibit the influence of interleaflet coupling and hydrophobic mismatch.
Theory
Leaflets may be coupled by several mechanisms. There is evidence for a “direct” coupling acting over the area of the bilayer to favor domain registration.18,34−42 This has been incorporated into phenomenological theories,18−20 wherein separate effective free-energies for each leaflet are augmented with a term proportional to (ϕt – ϕb)2, thereby coupling one leaflet composition to the other. Such an area-dependent coupling may in general comprise both enthalpic and entropic contributions37 and has been attributed to, e.g., the properties of lipid tails,37 cholesterol flip-flop or chain interdigitation.36,40 Recent molecular simulations suggest that chloroform (a small hydrophobic molecule) can induce an entropic contribution to direct coupling by rapidly flipping between leaflets.41 Other proposed sources of direct coupling include undulations43 or curvature44 of the leaflets.
In contrast, hydrophobic thickness mismatch (e.g., thick Lo phases versus thinner Ld) may encourage antiregistration, in order to maintain uniform bilayer thickness (Figure 1A).21,25,36,41,45 This is an “indirect” coupling in the sense that lipids in apposed leaflets interact via the bilayer hydrophobic thickness of their surroundings. In some regimes, hydrophobic mismatch is predicted to promote registration instead,46 though this is not general.47
Williamson and Olmsted have recently proposed a semimicroscopic theory of coupled leaflets.21,24,48 The theoretical model employs a two-layer lattice to represent the two leaflets. The lattice contains S and U species, where S (“saturated”) is taken to have a larger preferred hydrophobic length than the U (“unsaturated”) lipid. There are three key ingredients (cf. Figure 1A). (1) Microscopically, each lipid apposes a lipid of the same or different species in the other leaflet. (2) A direct coupling B encourages like species to appose (analogously to the phenomenological coupling term used previously18−20). (3) A multibody indirect coupling J encourages unlike species to appose to minimize hydrophobic mismatch with their surroundings. Explanation of the model’s Hamiltonian appears in the Supporting Information, while detailed calculations and discussion appear in ref. (21). A similar model23 has successfully captured experimental measurements of “complementarity,” a preference for short lipids in one leaflet to appose long ones in the other, at the single-lipid level.45
The coupled lattice model yields a free-energy landscape f(ϕt, ϕb) (Figure 1B) playing the same role as the simpler phenomenological free energies used in previous approaches.18−20 Once this landscape is found, common tangent planes (analogous to the common tangent line construction) are used to determine two- or three-phase coexistences.21 Consider, as in the molecular simulations presented below, roughly equal overall leaflet compositions and area fractions of Lo and Ld-forming lipids in each leaflet, i.e., the center (ϕt ≈ 0.5, ϕb ≈ 0.5) of the free-energy landscape in Figure 1B. The equilibrium (lowest bulk free energy) tangent plane for this composition corresponds to a tie-line of R–R coexistence, but (ϕt ≈ 0.5, ϕb ≈ 0.5) can also access an AR–AR tie-line describing a metastable state of two coexisting antiregistered phases. For general overall compositions a variety of metastable and equilibrium states exist (e.g., AR-AR-R and R-R-AR), in which the degree of local transbilayer asymmetry is either greater or lesser than if the leaflets were completely uncorrelated.24
Upon a quench, a bilayer may experience instabilities to the two competing demixing modes indicated by curved arrows on Figure 1B. This competition can be studied by linear stability analysis as a function of the semimicroscopic model’s parameters (Figure 1C). The analysis compares the free energy gain of demixing (downward curvature of the bulk free energy in Figure 1B) with penalties for creating interfaces between domains of differing composition and/or thickness.21 For large enough hydrophobic mismatch, the asymmetric AR mode can grow faster than the symmetric R mode (Figure 1C). A key prediction of the theoretical model is thus the possibility of “two-step” kinetics in which, after a quench, a bilayer first responds by preferentially forming AR phases before later reaching its equilibrium R–R state.24
This picture of competing area- and line-dependent energies further implies that domains restricted to sufficiently small size may thermodynamically prefer the AR–AR state, such that compositional perturbations in one leaflet colocalize with asymmetric perturbations in the apposed leaflet.48 This nucleation-like scenario was proposed theoretically36,49 and invoked to explain molecular simulations showing antiregistered phases.25,41 However, neither the existence of this crossover behavior nor the relevant length scale have yet been determined explicitly. Ref. (36) estimated 2 nm for a single parameter set, while in ref. (48) the predicted critical size depended sensitively on the direct and indirect coupling strengths.
Results
We now present the results of our MARTINI molecular simulations (see Methods). We first study a ternary mixture of an unsaturated lipid (DLiPC), a saturated lipid (DPPC), and cholesterol in the ratio 3:5:2 (Figure 1D). This has a moderate degree of hydrophobic mismatch and has been previously shown50,51 to rapidly phase-separate into registered ordered and disordered regions (Figure 1E). We study varying numbers of beads in the saturated lipids’ hydrophobic tails. MARTINI replaces every four heavy atoms in the lipid tail by a single coarse-grained bead. Therefore, the 16 carbon atoms in each tail of DPPC are represented by four beads in the coarse-grained simulations (Figure 1F), so that this lipid can also be described as 4:0 PC. Removing one coarse-grained bead from each tail of DPPC gives DLPC (or 3:0 PC), which has minimal hydrophobic mismatch with the unsaturated lipid DLiPC. Conversely, adding one bead to each tail yields DAPC (or 5:0 PC), which has the largest amount of hydrophobic mismatch. Hereafter we shall use the notations 4:0 PC and DPPC (etc.) interchangeably.
All Mixtures Reach a Registered R–R Equilibrium State; But Strong Hydrophobic Mismatch Leads to Two-Step Kinetics via a Metastable AR–AR State
Three bilayers of 6000 lipids were simulated for each of the three lipid mixtures (Table S1) and analyzed as described in the Methods. In analogy with the semimicroscopic model,21 we define four categories of transbilayer phospholipid arrangement: saturated lipids aligned with saturated lipids in the apposed leaflet (SS), unsaturated lipids apposing unsaturated (UU); or saturated apposing unsaturated (SU or US).21,23 Thus, at the local scale lipids are considered pairwise registered (SS, UU) or pairwise antiregistered (SU, US), cf. Figure 1A,B.21,23,45 We use this fine-grained description to simply and directly inspect the degree of local symmetry, i.e., the proportion of bilayer area where lipids appose one of the same species.24,41 One should not describe, e.g., an isolated saturated lipid as an Lo phase. Rather, we will define S-enriched and U-enriched regions as Lo and Ld phases only at the scale of at least a few lipids, which becomes necessary when measuring the bulk phase compositions.
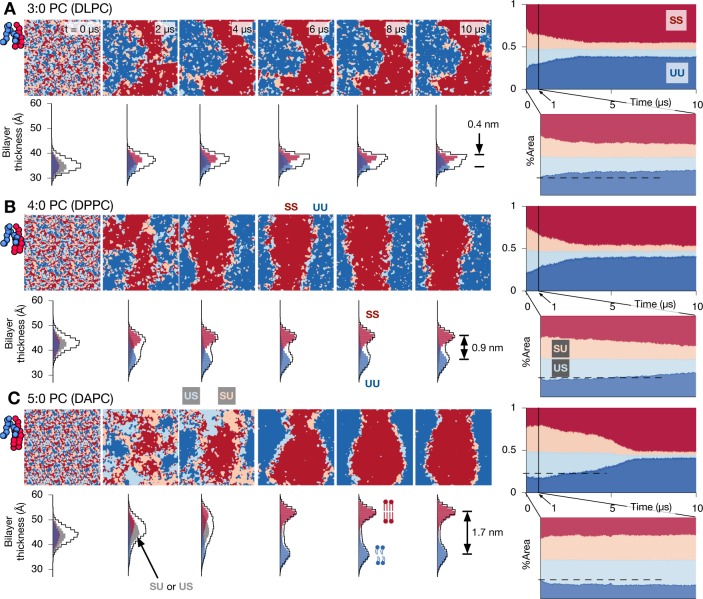
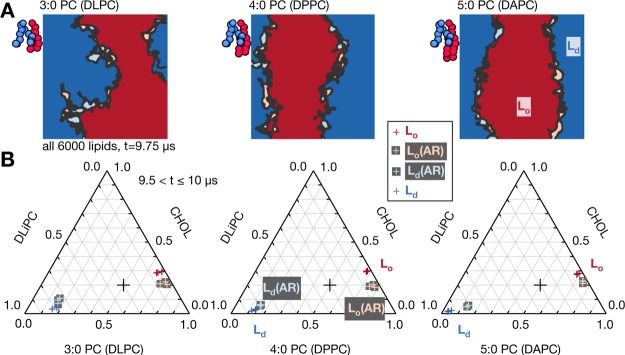
Plane views of all three different mixtures (Figure 2) reveal separation into two contiguous registered domains after 10 μs, which can be identified as the bulk, registered Lo and Ld phases. For most physical parameter regimes in the semimicroscopic model,21 and as in Figure 1B, this R–R coexistence is predicted to be the equilibrium state in bulk. For the smallest hydrophobic tail length mismatch (Figure 2A), the equilibrium R–R state exhibits significant compositional impurities within the bulk phases, which become less apparent as hydrophobic mismatch increases, indicating stronger segregation. We address this quantitatively later. In terms of kinetics, we observe that significant antiregistered domains form in the first few μs of the simulation with the largest hydrophobic mismatch (Figure 2C).
Figure 2.
Increasing hydrophobic mismatch leads to two-step kinetics, but a registered equilibrium state is always reached. The equilibrium separated phases appear purer for stronger hydrophobic mismatch. (A) Images mapping evolution of the local lipid compositions in both leaflets for the DLPC (3:0 PC) mixture. There are four categories of transbilayer arrangements: both leaflets saturated (SS, red), both unsaturated (UU, blue) and asymmetric arrangements (SU, pink or US, light blue). The hydrophobic mismatch is small and the bilayer separates directly into registered ordered and disordered phases. The images on the far right show how the area of each local arrangement varies with time. Also shown are the corresponding distributions of the thickness of the bilayer, showing a final thickness difference of 0.4 nm between the registered ordered and disordered phases. (B) Increasing the tail length of the saturated lipid by one bead (DPPC) leads to a larger hydrophobic mismatch between the disordered and ordered phases. There is a small initial increase in the area of antiregistration (SU and US) until t ≃ 0.05 μs. (C) Increasing the number of beads in each tail of the saturated lipid to five (DAPC) further increases the degree of hydrophobic mismatch, leading to a final thickness difference of 1.7 nm between the registered ordered and disordered phases. Initial demixing is dominated by antiregistered domains causing an increase in the area of SU and US up to t ≃ 1.1 μs, after which registration takes over to complete the two-step kinetics. As expected, the bilayer thickness of the antiregistered phases is intermediate between the registered ordered and disordered phases. Repeat simulations with different initial conditions appear in the Supporting Information.
To examine the kinetics in more detail we plot the time dependence of the area fraction of each transbilayer arrangement (SS, UU, SU, or US), along with snapshots of the distribution of bilayer thickness measured by the distance between the phosphate beads of the phospholipids (Figure 2). Because the lipids are initially randomly mixed and the area fractions in each leaflet are roughly equal, there are initially approximately equal areas of SS, UU, SU, US.
For the DLPC (3:0 PC) mixture, the amount of antiregistration (SU and US) decreases monotonically throughout the simulation. This signifies dominance of the R demixing mode leading to a continuous evolution toward the equilibrium R–R state (Figure 2A). The overall thickness distribution does not change significantly during the simulation, and the saturated SS and unsaturated UU registered regions have only a small (≃0.4 nm) mismatch in thickness. The Lo phase of all three simulations of this mixture converted to the gel phase after the registered phases became established; a simulation at a higher temperature (323 K) did not become gel-like but otherwise showed similar kinetics (Figure S4).
Increasing the tail length of the saturated lipid to 4:0 (DPPC) results in a larger thickness difference ≃0.9 nm between saturated SS and unsaturated UU registered regions (Figure 2B), indicating significant hydrophobic mismatch. This system again exhibits a decrease in antiregistration over the simulation time, albeit with slightly different kinetics. There is, however, a very brief initial increase in the proportion of antiregistration in the first tens of nanoseconds which was absent in the 3:0 PC case.
Finally, DAPC (5:0 PC) induces a large hydrophobic mismatch (≃1.7 nm) between the registered saturated SS and unsaturated UU regions (Figure 2C). The kinetics is now markedly nonmonotonic, or “two-step”. AR phases initially dominate demixing, leading to a clear increase in the proportion of antiregistered (SU and US) regions. Then R regions coalesce into nuclei and grow to form the equilibrium R–R state. This behavior is robust across the repeat simulations (Figure S6).
The schematic dashed line superimposed on the instability analysis (Figure 1C) illustrates our explanation for the emergence of two-step kinetics. A greater tail length mismatch should predominantly affect the indirect coupling J, and for the 5:0 PC system this is sufficient to render the AR demixing mode fastest. These results therefore verify quantitative estimates that appropriate model parameters for typical phospholipids straddle the line between dominant R or AR demixing modes,21 so that small changes to molecular properties can tip the balance one way or the other.
In the final equilibrium states (especially for 5:0 PC) there are significant regions of SU and US antiregistered lipids confined to the interfaces between the large SS and UU-dominated (registered Lo and Ld) domains. These are not true phases but “slip regions” that spread the cost of hydrophobic mismatch.46 Hence, we conclude that at late times the expected thermodynamic equilibrium of two bulk registered phases (R–R) has been reached, even with the largest hydrophobic mismatch studied.
We have verified that the two-step kinetics of the 5:0 PC mixture is also exhibited when compositions with smaller or larger fractions of cholesterol (Figure S7B,C) are used. With less cholesterol (Figure S7B) it appears that the transition to registration occurs more slowly. It is tempting to attribute this to the smaller cholesterol fraction. Cholesterol has been suggested as a contributor to direct coupling36 so a smaller fraction could decrease the direct coupling and lead to a weaker and slower transition to registration. However, extensive further studies would be needed to confirm whether the difference suggested in Figure S7B is statistically valid and to explain it. The role of cholesterol is highly complex, including effects on the position in the phase diagram and hence on the properties of the Lo and Ld phases.
Reducing the Size of the System Destabilizes the Registered Phases
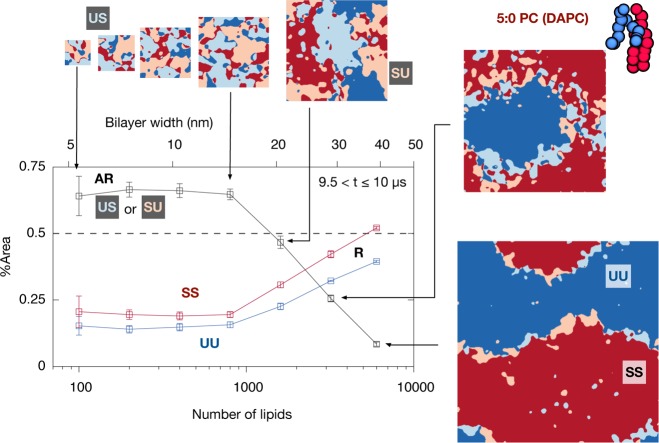
The nucleation of equilibrium R phases from a metastable AR–AR background is expected to involve a line-dependent hydrophobic mismatch cost and an area-dependent energy gain for registration.48 This implies restricting the domains to below a critical size could favor the AR–AR state. To test this we ran a series of smaller simulations of the mixture with the largest degree of hydrophobic mismatch (DAPC, DLiPC, cholesterol), with between 100 and 6000 lipids (Figure S8). Each simulation was run for 10 μs, which had been long enough to form equilibrium registered states in all the main 6000-lipid simulations (Figure 2C, S6).
With an equal area fraction Lo–Ld mixture in each leaflet, the expected area fraction of AR lipids if the leaflets were completely uncorrelated (the “high-temperature limit”24) is ≈50%. Values lower than this benchmark indicate that interleaflet correlations associated with phase separation favor registration, while higher values indicate a preference for antiregistration. In marked contrast to the large main simulations, bilayers with 800 or fewer lipids strongly exhibited >50% AR area after 10 μs (Figure 3). For the 1600-lipid simulation, neither registered nor antiregistered phases dominated, perhaps indicating disruption of nucleation energetics by the small system size to create a complex free-energy landscape. The ratio of registered to antiregistered area was the same for times between t = 8 μs and t = 10 μs (Figure 3, S9).
Figure 3.
Decreasing the size of the simulation unit cell favors antiregistered phases. A series of simulations with the 5:0 saturated lipid (3:5:2 DLiPC:DAPC:cholesterol) of decreasing size, from 6000 to 100 lipids/bilayer. Restricting the domains to smaller length scales in this manner should increase the importance of line energies. After 10 μs, simulations with ≤800 lipids (size ≤ 14.9 nm) show a preference for antiregistration indicated by >50% AR area. In contrast the simulation within 6000 lipids (size = 39.6 nm) became fully registered. (This is the same simulation as in Figure 2C). For the simulation with 1600 lipids significant registered regions have appeared but not dominated. Areas are averaged over the last 0.5 μs of each simulation.
Supporting Information Figures S10, S11 show corresponding results for the 4:0 PC and 3:0 PC systems. Unlike the clear behavior in Figure 3, 4:0 PC required significantly smaller system sizes to show an effect, as would be expected for smaller hydrophobic mismatch.48 The attainment of >50% AR area was in fact barely resolvable with the available statistics. The 3:0 PC system tended toward 50% AR area but showed no sign of exceeding 50%. This may indicate that increased compositional impurity due to weak phase segregation for 3:0 PC (cf. Figure 2A) tends to bring the measurement toward its high-temperature limit of 50%, as opposed to a preference for AR that should push the measurement above 50%. That a restricted domain size induces a weak AR preference (4:0 PC) or none at all (3:0 PC) is compatible with the kinetics discussed in the previous section, where 4:0 PC showed weak initial growth of AR and 3:0 PC showed none (Figure 2).
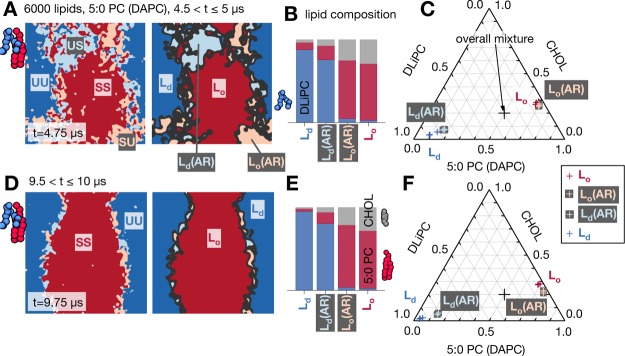
Figure 4.
Analysis of bulk phase leaflet compositions in the DAPC (5:0 PC) system at intermediate (A,B,C) and late (D,E,F) time. At intermediate time the leaflet compositions in the bulk antiregistered phases are less pure than in the registered. At late time the interfacial regions comprise antiregistered slip regions46 which also exhibit reduced purity. (A) Snapshot at t = 4.75 μs. As described in the Methods, the main interfaces are identified (black) and ignored in the analysis, while each contiguous region they enclose is assigned to a bulk phase: registered Lo, Ld, or antiregistered, either Lo that apposes Ld, denoted Lo(AR), or vice versa Ld(AR). (B) Compositions averaged over t = 4.5–5 μs in one representative simulation. (C) Information from (B) plotted as crosses on a Gibbs triangle, with a separate data point for each of the three simulations of this mixture. The fixed overall composition is marked as a large black cross. (D,E,F) At late time the contiguous antiregistered regions are confined to slip regions at the interfaces between the equilibrium registered phases.46
Figure 3 supports the idea that competing area- and line-dependent interleaflet couplings36,49 lead to a crossover length scale, below which the thermodynamic preference can be for one leaflet to organize asymmetrically to the pattern of local composition within the other. Figure 3 suggests the crossover for this system occurs around ∼20 nm. Intriguingly, this is approximately the size of some previous MARTINI simulations with DAPC that, instead of evolving toward registration, found stable antiregistration.25,41 Further, it falls within the putative size range of lipid rafts in vivo. The biophysical ramifications of a length scale set by competing interleaflet couplings are explored further in the Discussion.
Phase Compositions Are Coupled Across Leaflets and Influenced by Hydrophobic Mismatch
To measure the leaflet compositions within the different phases, we first identified the bulk phases as described in the Methods and illustrated in Figure 4A. Each contiguous region enclosed by the main interfaces, including its small fluctuating impurities, was assigned to a bulk phase.
We begin with the DAPC (5:0 PC) system and consider intermediate time (Figure 4A–C) at which there are significant contiguous bulk regions of both R and AR phases. Figure 4B shows that the registered Ld phase predominantly comprises the unsaturated lipid DLiPC, with a small proportion of DAPC and a tiny amount of cholesterol. The registered Lo phase contains DAPC enriched in cholesterol with negligible unsaturated lipid. The leaflet compositions within the bulk antiregistered phases, either Lo that apposes Ld (denoted Lo(AR)), or vice versa (Ld(AR)), are qualitatively similar to their respective registered compositions but are quantitatively less pure.
These leaflet phase compositions can be plotted on a standard Gibbs triangle (Figure 4C). The measured tie-lines are roughly consistent with a previous MARTINI study also using the doubly unsaturated lipid DLiPC.52 From our comparative measurements of bulk R and AR compositions, we infer the influence of an area-dependent direct interleaflet coupling, which would tend to make the AR minima of Figure 1B less well-separated than the R minima,19−21 and therefore make the AR phases less pure. This agrees with previous studies of overall asymmetric bilayers in experiment18 and simulation.25 For instance, in ref. (18) the AR phase in a state of R–R–AR coexistence was found to have less pure leaflet compositions than the R phases, which was explained by phenomenological theories18,20 similarly invoking a direct interleaflet composition coupling term.
At late times (Figure 4D–F) contiguous AR regions are only present at interfaces, and again exhibit reduced purity relative to the R phases. This implies that, as well as forming slip regions,46 the equilibrium R–R interfaces further reduce their energy via interfacial mixing. This was suggested, though not quantitatively included, in theoretical work.46,48
We next compare the systems with shorter saturated lipids to determine the effect of hydrophobic mismatch on composition, focusing on the bulk registered phase compositions at late times (Figure 5). The phases become significantly less pure for smaller hydrophobic mismatch. The composition of the Lo phase changes slightly, while the proportion of saturated lipid in the Ld phase increases strongly from 4.8% to 14.7% as the number of MARTINI beads in the tail is reduced from 5 to 3. This points to a role for hydrophobic mismatch in driving phase separation, which we consider in the Discussion along with related experiments.53,54
Figure 5.
Equilibrium Lo and Ld phases become purer with increasing hydrophobic tail length mismatch (3:0 PC, 4:0 PC, and 5:0 PC saturated lipids). The bulk compositions are measured as for Figure 4, outlined in the Methods. (A) Representative snapshots at t = 9.75 μs for each mixture (compare those in Figure 2). (B) The compositions of the phases are identified as in Figure 4 and averaged over the final 0.5 μs, and points for the three separate simulations of each mixture plotted on Gibbs triangles. The overall composition is shown as a black cross.
Discussion
The nature of interleaflet coupling,17,18,20,36,37,41 and the role of hydrophobic tail length mismatch21,23,25,41,45,46,53−56 are key to the fundamental interactions and thermodynamics of mixed bilayers, which biological membranes may exploit or resist in a given physiological context. We have investigated these via a molecular dynamics study of the kinetics and compositions of registered (R, approximately symmetric) and antiregistered (AR, strongly asymmetric) phases, using model ternary mixtures in which the overall composition of each leaflet is the same, comprising roughly equal area fractions of Lo and Ld -forming lipids. We used the coarse-grained MARTINI force field,26,27 which has been repeatedly shown to reproduce both physical chemical properties of bilayers and biological phenomena. We studied ternary mixtures comprising of DLiPC, cholesterol, and one of three saturated lipids exhibiting increasing hydrophobic mismatch with DLiPC: 3:0 PC, 4:0 PC and 5:0 PC (MARTINI representations of DLPC, DPPC and DAPC).
We have the following principal findings:
-
1.
Novel two-step phase-transition kinetics occurs for bilayers with significant hydrophobic mismatch, observable clearly in the 5:0 PC mixture and slightly in the 4:0 PC mixture. The bilayer first becomes locally more asymmetric, developing antiregistration, before the registered equilibrium state takes over. This behavior is predicted for estimated physical parameters in a semimicroscopic theory,21 and exhibited in simple lattice simulations.24 The early stages of kinetics, i.e., a bilayer’s initial response to a change in external conditions, may be important for cell membrane domains which form transiently and are small.
-
2.
Smaller simulations for the 5:0 PC system (Figure 3) show that restricting domains below a certain length scale ca. 20 nm may favor antiregistration.36,49 Along with the two-step kinetics, this behavior further evidences the competing line- and area-dependent interleaflet couplings. A recent theory claimed that registration can be explained by line tensions alone.46 However, that study did not properly calculate the total line energy, and when this is accounted for one finds that a bulk (i.e., area-dependent) free-energy difference between R and AR phases is needed to explain registration in general.47
The estimated crossover length scale is ∼20 nm for the largest hydrophobic mismatch studied, consistent with theoretical predictions,48 though expected to be dependent on parameters such as tail length or structure mismatch. It is comparable to the simulation size of previous MARTINI studies,25,41 perhaps contributing to their observing stable antiregistration with DAPC rather than the registration that was reached in all large simulations here. However, in ref. (41) even a control DAPC simulation with increased size apparently failed to reach registration, which may indicate that the lower temperature (295 K versus 310 K) of ref. (41) plays a role in determining the crossover length scale. It would be interesting to systematically study the role of parameters such as temperature or pressure57 on the interplay of interleaflet couplings.
In complex biological membranes, domain size is not restricted by a simulation box but by a variety of proposed mechanisms,12−15,58−61 so that true “stability” of antiregistration in practice depends on the independent mechanism(s) restricting the domain size. We have not addressed these, instead focusing on the consequences of restricted domain size for the associated transbilayer organization. More generally, the complexity of biomembranes and inherently nonequilibrium features like turnover62 preclude the wholesale transfer of findings from equilibrium model systems. Nevertheless, the stable antiregistration simulated here and in refs. (25,41) manifests a thermodynamic preference for local asymmetry given domains of a certain size, and the fundamental interactions responsible have clear biological implications.
For a cell membrane, the direct interleaflet coupling alone would imply that local composition perturbations in one leaflet (e.g., a cluster of longer-than-average lipids and proteins) can colocalize similar perturbations in the other (perhaps similar tail structure and/or cholesterol content19,36,37). Conversely, our study reveals a lateral length scale below which asymmetric organization of the leaflets’ perturbations can be thermodynamically preferable (e.g., a complementary domain of shorter-than-average bilayer constituents). That is, the equilibrium thermodynamic contribution to transbilayer organization in cells is predicted to be length scale dependent.
-
3.
Measurements of bulk phase composition reveal direct (area-dependent) interleaflet coupling. At intermediate times in the 5:0 PC system (Figure 4A–C) bulk regions of AR phases are present, but with leaflet compositions of reduced purity (Figure 4C) relative to those in the R phases. This can be attributed to a direct compositional coupling between the leaflets, which penalises the difference between apposed leaflets’ compositions within an AR phase, causing shorter AR–AR tie-lines and hence less pure leaflet compositions. This agrees with previous experiments18 and simulations,25 which were explained by a direct interleaflet coupling.18−20
The eventual formation of equilibrium registered phases in all of the large simulations here may be contrasted to a particular calculation in ref. (46) that was performed specifically for periodic boundaries. The authors predicted that, without an area-dependent coupling, antiregistration would be equilibrium in silico (though not, they argued, in a real system—but see ref. (47)). In our 5:0 PC simulations, significant AR phases form but give way to registration instead of persisting, as would have been expected if AR were equilibrium in silico. This suggests that area-dependent coupling should be accounted for in the calculation as well. Which enthalpic or entropic effects contribute most to such a direct coupling remains to be determined.36,37,40,41,43,44
-
4.
Increasing hydrophobic tail length mismatch increased the purity of the phases, seen qualitatively in Figure 2 and measured in the tie-lines of Figure 5. This agrees with previous simulation measurements showing more intense phase separation as hydrophobic mismatch was increased.25,41 We propose that hydrophobic mismatch increases the immiscibility of the lipids at the microscopic scale, and therefore the separation of the minima in the free-energy landscape Figure 1B, resulting in purer phases. (One would expect an analogous effect on immiscibility by increasing the unsaturation in the unsaturated lipids, which was similarly found to lengthen the tie-lines between separated phases.52) Such a role for hydrophobic mismatch arises naturally from our semimicroscopic theoretical model (see Supporting Information and ref. (21)), while in phenomenological approaches it would be incorporated into an effective (Flory-like) parameter for the intraleaflet lipid immiscibility.19,20 The simultaneous influence of hydrophobic mismatch on both lateral phase separation and transbilayer organization underlines the intimate link between intra- and interleaflet interactions.21
Thus, hydrophobic tail length mismatch appears to “drive” phase separation, as argued for on the basis of experiments that showed increased mixing temperatures for greater hydrophobic mismatch.53 In theories of phase separation,19,20 higher mixing temperature at given overall composition (as in ref. (53)) and greater phase purity at a given temperature/composition (as found here) typically share common dependence on an effective immiscibility parameter. Though this relationship need not always hold in real systems, our results can thus be considered in accord with ref. (53).
Refs. (54,56) raise important caveats to this picture. First, the mixing temperature depends on the entire phase boundary for the given system and on the chosen overall composition, so there cannot be a unique relationship between mixing temperature and hydrophobic mismatch.56 Second, using a variety of unsaturated and saturated lipids (including noncanonical cases where the pure saturated lipids had shorter carbon chains than the unsaturated ones), ref. (54) found no general trend between the highest mixing temperature of a given mixture and any single parameter such as hydrophobic mismatch or number of carbons. Nonetheless, in the case most comparable to ours, a monotonic trend was found; increasing the saturated chain length for fixed other components led to an increase in the highest mixing temperature.54
Our study reveals generic interactions and thermodynamics that can be expected to contribute to the lateral and transbilayer organization in complex biological membranes. Membrane proteins will certainly perturb the behaviour relative to lipid-only model systems, leading to a variety of possible additional effects. For example, an integral membrane protein matching the hydrophobic thickness at the interface between registered phases could behave as a linactant14 to reduce the interface energy between registered phases. A similar effect was observed for a peripheral cell signalling protein.51 Alternatively, other membrane proteins could promote antiregistered regions, leading to changes in both the organisation and types of domains in the membrane and potentially also the sorting of proteins. Indeed, the generic interactions studied here should apply quite directly to membrane proteins themselves. Experiments have shown that protein-membrane hydrophobic mismatch induces protein clustering,68 and simulations suggest that both symmetric and asymmetric modes of aggregation are possible for non-transmembrane proteins, determined by their hydrophobic length.69
Whilst the coarse-grained forcefield MARTINI is well-established for the study of the lipid bilayers, it requires the doubly-unsaturated lipid DLiPC in order to display phase separation on simulation timescales. This degree of unsaturation is not unusual in biology,63,64 but does lead to the relatively long tie-lines measured here, and in the MARTINI simulations of Ackerman and Feigenson52. These authors found that reducing the average degree of unsaturation by adding a fraction of PUPC lipids progressively shortened the simulation tie-lines into a range more typical of experimental model systems that employ singly-unsaturated lipids.
Methods
Simulation Protocols
Identical patches of 6000 coarse-grained lipids comprising an unsaturated lipid dilinoleyl-phosphatidylcholine (DLiPC), cholesterol, and one of three saturated lipids—dilauroyl-phosphatidylcholine (DLPC), dipalmitoyl-phosphatidylcholine (DPPC) or diarachidoyl-phosphatidylcholine (DAPC) (Figure 1F)—were prepared by mutating lipids65 as described elsewhere.51 Version 2.2 of the MARTINI force field was used.26,27 The membranes have a molar ratio of 3:5:2 DLiPC:DnPC:cholesterol. Three separate patches of 6000 lipids were prepared for each of the three mixtures and solvated using coarse-grained water and sodium and chloride ions as described in Table S1. The total number of beads ranged from 137 000 to 167 000. In addition, two small patches of 100 and 200 lipids, with the same composition as above, were prepared. These were tessellated to yield a series of patches where the number of lipids doubled with each step: 100, 200, 400, 800, 1600 and 3200 lipids. Finally, lipids were deleted from the 3200 lipid 3:5:2 DLiPC:DAPC:cholesterol patch to create two further patches with altered compositions. First half the cholesterol was deleted, yielding a patch of 2880 lipids with a 3:5:1 composition. Then some of the saturated and unsaturated lipids were deleted, producing a patch of 2560 lipids with a 2:4:2 composition. A complete list of simulations can be found in Table S1.
The energy of each patch was minimized for 5000 steps using the steepest descent algorithm of GROMACS 4.5.566 before 10 μs of dynamics was simulated using an integration time step of 20 fs. The exception was the three 6000 lipid simulations containing DPPC for which corresponding 5 μs simulations from a previous paper51 were simply extended. Electrostatic forces were calculated using a reaction-field scheme in conjunction with periodic boundary conditions, a switching distance of 1.2 nm, and a dielectric constant of 15. van der Waals interactions were cut off at 1.2 nm and switched from 0.9 nm. A Berendsen thermostat with a relaxation time of 1 ps applied separately to the lipids and the solute was used to maintain the temperature at 310 K. The pressure was kept at 1 atm by a Berendsen barostat that was applied semi-isotropically with a relaxation time of 2 ps and a compressibility of 3 × 10–4 bar–1. Coordinates were written to disc every 2 ns.
Simulation Analysis
To measure bilayer symmetry and determine the bulk phases and interfaces we treated each bilayer as an image (Figure S1) and applied image-processing techniques.51 Each leaflet was described by three separate arrays of pixels, one for each lipid species. The pixels are 0.1 × 0.1 nm square and represent the (x, y) plane of the bilayer. A pixel was set if it coincides with the (x, y) Cartesian coordinates of the center of the phosphate bead (or the hydroxyl bead for cholesterol) of the relevant lipid species. These arrays were then convolved with a Gaussian of width 0.8 nm and the density of the species at each pixel was determined by cubic interpolation (Figure S1A). The width of the Gaussian was chosen to mimic the average area per lipid.
Subtracting the saturated density from the unsaturated density yields an array of the difference in densities for each leaflet. If this is greater than zero then locally there are more unsaturated lipids (and vice versa). Applying a threshold at zero defined regions either with more saturated lipids (drawn throughout in red) or with more unsaturated lipids (drawn in blue): we call this the region_mask. Cholesterol is ignored when defining these regions. Using the scikit-image python module we applied the Canny edge detection algorithm67 with a smoothing Gaussian of 0.2 nm to this image to identify the interfaces between the regions. These were also convolved with a Gaussian of width 0.8 nm. A routine from the same module that identifies contiguous regions was then used and only the main interfaces that were larger than 1% of the total area were kept. In addition, the z-values of the phosphate beads were cubically interpolated onto a grid to create an array of the height of each leaflet (Figure S1B).
These arrays from each leaflet can be then combined to analyze the entire bilayer (Figure S2). Adding 2× the regions [upper] to the regions [lower] arrays (Figure S2A) yields the regions [overlap] array which distinguishes saturated lipids apposing saturated lipids (SS regions) along with the other three combinations (UU, SU, US). Simple masks can be extracted from these to calculate properties of each region type. Summing the number of pixels of each mask array gives, for example, the proportion of the total area taken up by unsaturated lipids apposing unsaturated lipids (UU regions).
To define the compositions of bulk phases, small fluctuations of the “wrong” species within a contiguous bulk region (e.g., a small droplet of SU within a surrounding UU domain) should be included as part of the bulk phase in question. Such impurities arise from the equilibrium solubility of, e.g., saturated lipids in the Ld phase. (Strictly, such droplets can be defined as fluctuations within a parent phase if their size is of order or less than the correlation length for composition fluctuations.) To achieve this we multiplied the interface_masks of each leaflet together (Figure S2B) and identified contiguous regions, as before. Each region was defined according to the dominant lipid arrangement, which yielded a “bulk” array in which the fine interfaces are masked out, and small regions of impurity have been reassigned as members of the surrounding contiguous phase in which they are solvated. Thereafter, masks can be extracted from this array which can then be multiplied by, for example, the density of a specific lipid to calculate the lipid fractions present in that bulk phase. Lastly, the difference between the two surface arrays simply yields the variation in thickness across the patch of bilayer.
Acknowledgments
PWF was funded by the Wellcome Trust (092970/Z/10/Z). We are grateful to the University of Oxford Advanced Research Computing (ARC) facility for providing computing resource. PDO and JJW thank Georgetown University and the Ives Endowment for funding, as well as the CAPITALS project (EPSRC EP/J017566/1) in the earliest stages of this work.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.6b04880.
Supplementary tables and figures (PDF)
Author Present Address
‡ Nuffield Department of Medicine, John Radcliffe Hospital, University of Oxford, Headley Way, Oxford, OX3 9DU, U.K.
Author Present Address
§ The Francis Crick Institute, Lincoln’s Inn Fields Laboratories, 44 Lincoln’s Inn Fields, London WC2A 3LY, U.K.
The authors declare no competing financial interest.
Supplementary Material
References
- Lingwood D.; Simons K. Science 2010, 327, 46. 10.1126/science.1174621. [DOI] [PubMed] [Google Scholar]
- Simons K.; Ikonen E. Nature 1997, 387, 569. 10.1038/42408. [DOI] [PubMed] [Google Scholar]
- Munro S. Cell 2003, 115, 377. 10.1016/S0092-8674(03)00882-1. [DOI] [PubMed] [Google Scholar]
- Veatch S. L.; Keller S. L. Biophys. J. 2003, 85, 3074. 10.1016/S0006-3495(03)74726-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veatch S. L.; Cicuta P.; Sengupta P.; Honerkamp-Smith A.; Holowka D.; Baird B. ACS Chem. Biol. 2008, 3, 287. 10.1021/cb800012x. [DOI] [PubMed] [Google Scholar]
- Sezgin E.; Kaiser H.-J.; Baumgart T.; Schwille P.; Simons K.; Levental I. Nat. Protoc. 2012, 7, 1042. 10.1038/nprot.2012.059. [DOI] [PubMed] [Google Scholar]
- Gómez-Llobregat J.; Buceta J.; Reigada R. Sci. Rep. 2013, 3, 2608. 10.1038/srep02608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eggeling C.; Ringemann C.; Medda R.; Schwarzmann G.; Sandhoff K.; Polyakova S.; Belov V. N.; Hein B.; von Middendorff C.; Schönle A.; Hell S. W. Nature 2009, 457, 1159. 10.1038/nature07596. [DOI] [PubMed] [Google Scholar]
- Frisz J. F.; Lou K.; Klitzing H. A.; Hanafin W. P.; Lizunov V.; Wilson R. L.; Carpenter K. J.; Kim R.; Hutcheon I. D.; Zimmerberg J.; Weber P. K.; Kraft M. L. Proc. Natl. Acad. Sci. U. S. A. 2013, 110, E613. 10.1073/pnas.1216585110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frisz J. F.; Klitzing H. A.; Lous K.; Hutcheon I. D.; Weber P. K.; Zimmerberg J.; Kraft M. L. J. Biol. Chem. 2013, 288, 16855. 10.1074/jbc.M113.473207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraft M. L. Mol. Biol. Cell 2013, 24, 2765. 10.1091/mbc.E13-03-0165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veatch S. L.; Soubias O.; Keller S. L.; Gawrisch K. Proc. Natl. Acad. Sci. U. S. A. 2007, 104, 17650. 10.1073/pnas.0703513104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meinhardt S.; Vink R. L. C.; Schmid F. Proc. Natl. Acad. Sci. U. S. A. 2013, 110, 4476. 10.1073/pnas.1221075110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmieri B.; Yamamoto T.; Brewster R. C.; Safran S. A. Adv. Colloid Interface Sci. 2014, 208, 58. 10.1016/j.cis.2014.02.007. [DOI] [PubMed] [Google Scholar]; Special issue in honour of Wolfgang Helfrich.
- Shlomovitz R.; Maibaum L.; Schick M. Biophys. J. 2014, 106, 1979. 10.1016/j.bpj.2014.03.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raghupathy R.; Anilkumar A. A.; Polley A.; Singh P. P.; Yadav M.; Johnson C.; Suryawanshi S.; Saikam V.; Sawant S. D.; Panda A.; Guo Z.; Vishwakarma R. A.; Rao M.; Mayor S. Cell 2015, 161, 581. 10.1016/j.cell.2015.03.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kusumi A.; Koyama-Honda I.; Suzuki K. Traffic 2004, 5, 213. 10.1111/j.1600-0854.2004.0178.x. [DOI] [PubMed] [Google Scholar]
- Collins M. D.; Keller S. L. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 124. 10.1073/pnas.0702970105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner A. J.; Loew S.; May S. Biophys. J. 2007, 93, 4268. 10.1529/biophysj.107.115675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garbès Putzel G.; Schick M. Biophys. J. 2008, 94, 869. 10.1529/biophysj.107.116251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williamson J. J.; Olmsted P. D. Biophys. J. 2015, 108, 1963. 10.1016/j.bpj.2015.03.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamamoto T.; Safran S. A. Soft Matter 2012, 8, 5439. 10.1039/c2sm25343g. [DOI] [Google Scholar]
- Bossa G. V.; Roth J.; May S. Langmuir 2015, 31, 9924. 10.1021/acs.langmuir.5b01719. [DOI] [PubMed] [Google Scholar]
- Williamson J. J.; Olmsted P. D. Phys. Rev. E 2015, 92, 052721. 10.1103/PhysRevE.92.052721. [DOI] [PubMed] [Google Scholar]
- Perlmutter J. D.; Sachs J. N. J. Am. Chem. Soc. 2011, 133, 6563. 10.1021/ja106626r. [DOI] [PubMed] [Google Scholar]
- Marrink S. J.; Risselada H. J.; Yefimov S.; Tieleman D. P.; de Vries A. H. J. Phys. Chem. B 2007, 111, 7812. 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- Periole X.; Marrink S.-J. In Biomolecular Simulations: Methods and Protocols; Monticelli L., Salonen E., Eds.; Humana Press: Totowa, NJ, 2013; p 533. [Google Scholar]
- Bond P. J.; Sansom M. S. P. J. Am. Chem. Soc. 2006, 128, 2697. 10.1021/ja0569104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stansfeld P. J.; Goose J. E.; Caffrey M.; Carpenter E. P.; Parker J. L.; Newstead S.; Sansom M. S. P. Structure 2015, 23, 1. 10.1016/j.str.2015.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watson M. C.; Brandt E. G.; Welch P. M.; Brown F. L. H. Phys. Rev. Lett. 2012, 109, 1. 10.1103/PhysRevLett.109.028102. [DOI] [PubMed] [Google Scholar]
- Rassam P.; Copeland N. A.; Birkholz O.; Tóth C.; Chavent M.; Duncan A. L.; Cross S. J.; Housden N. G.; Kaminska R.; Seger U.; Quinn D. M.; Garrod T. J.; Sansom M. S. P.; Piehler J.; Baumann C. G.; Kleanthous C. Nature 2015, 523, 333. 10.1038/nature14461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koldsø H.; Sansom M. S. P. J. Am. Chem. Soc. 2015, 137, 14694. 10.1021/jacs.5b08048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ingólfsson H. I.; Melo M. N.; van Eerden F. J.; Arnarez C.; López C. A.; Wassenaar T. A.; Periole X.; De Vries A. H.; Tieleman D. P.; Marrink S. J. J. Am. Chem. Soc. 2014, 136, 14554. 10.1021/ja507832e. [DOI] [PubMed] [Google Scholar]
- Korlach J.; Schwille P.; Webb W. W.; Feigenson G. W. Proc. Natl. Acad. Sci. U. S. A. 1999, 96, 8461. 10.1073/pnas.96.15.8461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dietrich C.; Bagatolli L.; Volovyk Z.; Thompson N.; Levi M.; Jacobson K.; Gratton E. Biophys. J. 2001, 80, 1417. 10.1016/S0006-3495(01)76114-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- May S. Soft Matter 2009, 5, 3148. 10.1039/b901647c. [DOI] [Google Scholar]
- Garbès Putzel G.; Uline M. J.; Szleifer I.; Schick M. Biophys. J. 2011, 100, 996. 10.1016/j.bpj.2011.01.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Risselada H. J.; Marrink S. J. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 17367. 10.1073/pnas.0807527105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polley A.; Mayor S.; Rao M. J. Chem. Phys. 2014, 141, 064903. 10.1063/1.4892087. [DOI] [PubMed] [Google Scholar]
- Lin Q.; London E. Biophys. J. 2015, 108, 2212. 10.1016/j.bpj.2015.03.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reigada R.; Sagués F. J. R. Soc., Interface 2015, 12, 20150197. 10.1098/rsif.2015.0197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blosser M. C.; Honerkamp-Smith A. R.; Han T.; Haataja M.; Keller S. Biophys. J. 2015, 109, 2317. 10.1016/j.bpj.2015.10.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horner A.; Antonenko Y. N.; Pohl P. Biophys. J. 2009, 96, 2689. 10.1016/j.bpj.2008.12.3931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pantano D. A.; Moore P. B.; Klein M. L.; Discher D. E. Soft Matter 2011, 7, 8182. 10.1039/c1sm05490b. [DOI] [Google Scholar]
- Zhang J.; Jing B.; Tokutake N.; Regen S. L. J. Am. Chem. Soc. 2004, 126, 10856. 10.1021/ja046892a. [DOI] [PubMed] [Google Scholar]
- Galimzyanov T. R.; Molotkovsky R. J.; Bozdaganyan M. E.; Cohen F. S.; Pohl P.; Akimov S. A. Phys. Rev. Lett. 2015, 115, 088101. 10.1103/PhysRevLett.115.088101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williamson J. J.; Olmsted P. D. Phys. Rev. Lett. 2016, 116, 079801. 10.1103/PhysRevLett.116.079801. [DOI] [PubMed] [Google Scholar]
- Williamson J. J.; Olmsted P. D. Soft Matter 2015, 11, 8948. 10.1039/C5SM01328C. [DOI] [PubMed] [Google Scholar]
- Wallace E. J.; Hooper N. M.; Olmsted P. D. Biophys. J. 2006, 90, 4104. 10.1529/biophysj.105.062778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Domanski J.; Marrink S. J.; Schäfer L. V. Biochim. Biophys. Acta, Biomembr. 2012, 1818, 984. 10.1016/j.bbamem.2011.08.021. [DOI] [PubMed] [Google Scholar]
- Jefferys E.; Sansom M. S. P.; Fowler P. W. Faraday Discuss. 2014, 169, 209. 10.1039/C3FD00131H. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ackerman D. G.; Feigenson G. W. J. Phys. Chem. B 2015, 119, 4240. 10.1021/jp511083z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- García-Sáez A. J.; Chiantia S.; Schwille P. J. Biol. Chem. 2007, 282, 33537. 10.1074/jbc.M706162200. [DOI] [PubMed] [Google Scholar]
- Bleecker J. V.; Cox P. A.; Foster R. N.; Litz J. P.; Blosser M. C.; Castner D. G.; Keller S. L. J. Phys. Chem. B 2016, 120, 2761. 10.1021/acs.jpcb.5b10165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simons K.; Gerl M. J. Nat. Rev. Mol. Cell Biol. 2010, 11, 688. 10.1038/nrm2977. [DOI] [PubMed] [Google Scholar]
- Bleecker J.; Cox P.; Keller S. Biophys. J. 2016, 110, 2305. 10.1016/j.bpj.2016.03.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Machta B.; Gray E.; Nouri M.; McCarthy N.; Gray E.; Miller A.; Brooks N.; Veatch S. Biophys. J. 2016, 111, 537. 10.1016/j.bpj.2016.06.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ritchie K.; Kusumi A. In Membrane Dynamics and Domains: Subcellular Biochemistry; Quinn P. J., Ed.; Springer US: Boston, MA, 2004; p 233. [Google Scholar]
- Smith A. W.; Huang H. H.; Endres N. F.; Rhodes C.; Groves J. T. J. Phys. Chem. B 2016, 120, 867. 10.1021/acs.jpcb.5b08887. [DOI] [PubMed] [Google Scholar]
- Koldsø H.; Reddy T.; Fowler P. W.; Duncan A. L.; Sansom M. S. P. J. J. Phys. Chem. B 2016, 10.1021/acs.jpcb.6b05846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kusumi A.; Suzuki K. G. N.; Kasai R. S.; Ritchie K.; Fujiwara T. K. Trends Biochem. Sci. 2011, 36, 604. 10.1016/j.tibs.2011.08.001. [DOI] [PubMed] [Google Scholar]
- Turner M. S.; Sens P.; Socci N. D. Phys. Rev. Lett. 2005, 95, 168301. 10.1103/PhysRevLett.95.168301. [DOI] [PubMed] [Google Scholar]
- Milovanovic D.; Honigmann A.; Koike S.; Göttfert F.; Pähler G.; Junius M.; Müllar S.; Diederichsen U.; Janshoff A.; Grubmüller H.; Risselada H. J.; Eggeling C.; Hell S. W.; van den Bogaart G.; Jahn R. Nature Communications 2015, 6, 5984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morozova D.; Guigas G.; Weiss M. PLoS Comput. Biol. 2011, 7, e1002067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valentine R. C.; Valentine D. L. Prog. Lipid Res. 2004, 43, 383. 10.1016/j.plipres.2004.05.004. [DOI] [PubMed] [Google Scholar]
- Levental K. R.; Lorent J. H.; Lin X.; Skinkle A. D.; Surma M. A.; Stockenbojer E. A.; Gorfe A. A.; Levental I. Biophys. J. 2016, 110, 1800. 10.1016/j.bpj.2016.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koldsø H.; Shorthouse D.; Hélie J.; Sansom M. S. P. PLoS Comput. Biol. 2014, 10, e1003911. 10.1371/journal.pcbi.1003911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pronk S.; Páll S.; Schulz R.; Larsson P.; Bjelkmar P.; Apostolov R.; Shirts M. R.; Smith J. C.; Kasson P. M.; van der Spoel D.; Hess B.; Lindahl E. Bioinformatics 2013, 29, 845. 10.1093/bioinformatics/btt055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Canny J. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679. 10.1109/TPAMI.1986.4767851. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.