Estimating the Aqueous Solubility of Pharmaceutical Hydrates

Abstract

Estimation of crystalline solute solubility is well documented throughout the literature. However, the anhydrous crystal form is typically considered with these models, which is not always the most stable crystal form in water. In this study an equation which predicts the aqueous solubility of a hydrate is presented. This research attempts to extend the utility of the ideal solubility equation by incorporating desolvation energetics of the hydrated crystal. Similar to the ideal solubility equation, which accounts for the energetics of melting, this model approximates the energy of dehydration to the entropy of vaporization for water. Aqueous solubilities, dehydration and melting temperatures, and log P values were collected experimentally and from the literature. The data set includes different hydrate types and a range of log P values. Three models are evaluated, the most accurate model approximates the entropy of dehydration (ΔS_d) by the entropy of vaporization (ΔS_vap) for water, and utilizes onset dehydration and melting temperatures in combination with log P. With this model, the average absolute error for the prediction of solubility of 14 compounds was 0.32 log units.

Introduction

The estimation of solubility for a drug or drug candidate is an important aspect to the drug development process for both academic and industrial research. Predictive models for the estimation of solubility provide the researcher with vital information of the compound to aid in experimental design and minimize expenses. As such, the development of models to predict solute solubility in both aqueous and organic solvents, as well as the effects cosolvents, surfactants, and pH have on solubility have been investigated for decades.^1–11 Computational models for solubility based on lipophilicity, solvation interactions, and substructure components can be found throughout the literature.^12–18 The advantages and disadvantages of different prediction models have been discussed in review articles.^19–22 Importantly, the impact of different crystal forms on solubility should be taken into consideration when evaluating solubility and the preparation of stable dosage forms.^23–25 Moreover, a specific crystal may affect the adsorption of the active drug from its dosage form.²⁶

Crystalline hydrates are a pharmaceutically important type of crystal form. An estimated one-third of active pharmaceutical substances are capable of forming a hydrate.²⁷ The addition of the water molecule(s) in the crystal lattice alters the physical structure and properties of the drug substance including changes to the dimensions, shape, symmetry, and the unit cell.²⁸ These changes lead to differences in pharmaceutical properties such as solubility and chemical stability.²⁸ The alteration of the physical structure and the properties that occur when a hydrate is formed should be considered for a solubility predictive model; however, the majority of solubility estimation methods either assume the most stable anhydrous crystal form, or do not address the impact of different crystal forms, including hydrates. This can be problematic considering that the meta-stable anhydrous form has been shown to be 2x, 3x, and even 22× more soluble than its hydrate.^29–30 As a result, it would be theoretically expected that aqueous solubility estimations, based on the anhydrous crystal form alone, would tend to over-predict the solubility of a drug that forms a more stable hydrate in water.

A theoretical model has been developed to predict the solubility ratio of polymorphs.³¹ However, there are no models that take into consideration additional energies present with hydrates, nor how those energies would affect the overall solubility. Therefore, the aim of this study is to describe a mathematical model based on an extension of the ideal solubility equation, which reasonably estimates the solubility of a hydrate. This model investigates the concept of accounting for the dehydration energetics of the hydrated solute in addition to the anhydrous melting energy. This model will lend itself to the appreciation of the solubility differences that can exist between hydrate and anhydrous drug forms.

Theoretical Background

The solubility of a solid solute is related to the energy necessary to break up the crystal and the mixing with a solvent. The contribution of the crystal term can be derived as a function of the melting point, whereas the mixing term is considered for non-ideal conditions and is dependent on the chemical structure of the solute and how it interacts with the solvent (activity coefficient). For aqueous conditions, the mixing term is often accounted for by the solute’s octanol-water partition coefficient (K_ow or P).

Ideal Solubility of Crystalline Anhydrous Solutes

The influence of the crystal on solubility can be related to how much energy it takes to convert the crystal into a hypothetical supercooled liquid (HSL) at a given temperature. Kirchoff’s law states that the energy of an irreversible process is equal to the energy of a series of reversible processes between the same end points.³² As such, the energy of melting at temperature T (converting the solid to a HSL), can be described by the sum of the enthalpies of the following processes: heating the solid to its melting point, melting the solid at its melting point, and cooling the liquid back down to temperature T. Based on these processes, the crystalline contribution to the ideal solubility of a solid solute can be determined from its solid-state properties via:

$${\mathit{RlnX}}_u^{\mathit{ideal}}=-\mathrm{\Delta }{H}_m\left(\frac{T_m-T}{T_{m}T}\right)+\mathrm{\Delta }{C}_p\left[\left(\frac{T_m-T}{T_m}\right)-ln\left(\frac{T_m}{T}\right)\right]$$ (1)

where X_u, ΔH_m, T_m, T, ΔC_p, and R correspond to the mole fraction solubility, heat of melting, melting point of the solid (K), reference temperature (K), heat capacity change on melting, and the gas constant, respectively.³³ It has been demonstrated that when calculating the ideal solubility, the ΔC_p term results in a small impact on the ideal solubility (especially for lower melting point compounds) and can be assumed to be equal to zero.³⁴ However, it is important to note that for compounds with a higher melting point the term can become significant³⁴ and it has been reported that in instances of increased molecular flexibility, ΔC_p is better approximated by using the value for the entropy of melting (ΔS_m).³⁵

Utilizing the assumption that the ΔC_p term is equal to zero, and recalling that at the melting point the Gibbs free energy (ΔG) is equal to zero (so that ΔH = TΔS) Eq. 1 can be rearranged to the following:

$${\mathit{lnX}}_u^{\mathit{ideal}}=-\mathrm{\Delta }{S}_m\frac{(T_m-T)}{RT}$$ (2)

OR

$${\mathit{logX}}_u^{\mathit{ideal}}=-\mathrm{\Delta }{S}_m\frac{(T_m-T)}{2.303RT}$$ (3)

To further simplify, it is convenient to apply Walden’s rule,³⁶ which states the ΔS_m of polycyclic aromatic derivatives can be approximated at 13.5 cal/K*mol, and evaluate the solubility at room temperature (298 K). This rendering provides a convenient model (Eq. 4) to describe the anhydrous crystal contribution to the ideal solubility of non-electrolytes.³³

$${\mathit{logX}}_u^{\mathit{ideal}}\approx -0.01(T_m-298)$$ (4)

Aqueous Solubility of Crystalline Hydrates

The focus of this research is to develop a method for estimating the solubility of crystalline hydrates by extending the theoretical constructs of the anhydrous ideal solubility theory to include the additional energetics of a hydrated solute. Specifically, it is postulated that the ideal mole fraction solubility for a hydrate can be estimated by considering both the energy necessary to break up the crystal (melting) and the energy of transition from hydrate to anhydrous (dehydration). Experimentally these energies can be observed from differential scanning calorimetry (DSC), which is commonly used to characterize pharmaceuticals.³⁷ By way of example, Figure 1 shows the DSC profiles of the anhydrous (top) and monohydrate (bottom) forms of beclomethasone dipropionate. Both profiles show the melting of the solid (209°C), however, the hydrate has an additional energy event for dehydration (onset of 82°C).

Figure 1.

DSC profiles of anhydrous (top) and monohydrate (bottom) forms of beclomethasone dipropionate.

Taking into consideration this additional energy, the energy of melting at temperature T can be described by the sum of the enthalpies of the following processes: heating the solid to its dehydration temperature, dehydrating the solid at its dehydration temperature, heating the solid to its melting point, melting the solid at its melting point, and cooling the liquid back down to temperature T. As discussed above, the last three steps in this sequence can be estimated by Eq. 4. Thus, an additional term must be considered to account for the transition from hydrate to dehydrate (anhydrous). By analogy to the derivation of Eq. 4, this energy can be described by Eq. 5 where ΔS_d and T_d correspond to the entropy of dehydration and the onset dehydration temperature (K), respectively.

$${\mathit{logX}}_u^{\mathit{dehydration}}=-\mathrm{\Delta }{S}_d\frac{(T_d-T)}{2.303RT}$$ (5)

Adding the hydrate term (Eq. 5) to Eq. 4 yields:

$${\mathit{logX}}_u^{\mathit{ideal}}=-\mathrm{\Delta }{S}_d\frac{(T_d-T)}{2.303RT}-0.01(T_m-298)$$ (6)

which can be considered the ideal mole fraction solubility of a hydrated crystal.

In order to estimate the aqueous solubility, it is necessary to account for the aqueous activity coefficient (deviation from ideality) of the solute in water. A convenient approach which utilizes the octanol-water partition coefficient (log P) to estimate the aqueous activity coefficient of a solute has previously been reported.³⁸ As a means of practicality, it is beneficial to convert the units of Eq. 6 from mole fraction to molarity. To do so, the mole fraction solubility is multiplied by 55.5 (the molarity of water).³⁸ This mathematically corresponds to the addition of 1.74 (log 55.5) to the log mole fraction solubility. Thus, by adding a constant to convert to molarity, and incorporating the log P term into Eq. 6, an expression to calculate the aqueous solubility of a hydrate can be defined by Eq. 7.

$$\mathit{log}{S}_w^{\mathit{hydrate}}\approx -\mathrm{\Delta }{S}_d\frac{(T_d-T)}{2.303RT}-0.01(T_m-298)-\mathit{logP}+1.74$$ (7)

Material and Methods

Myricetin (MYR) monohydrate, monobasic potassium phosphate, and dibasic sodium phosphate were purchased from Sigma-Aldrich (St. Louis, MO). Amoxicillin trihydrate and mercaptopurine monohydrate were acquired from Research Products International (Mount Prospect, IL). Acetic acid was bought from Fisher Scientific (Waltham, MA). Methanol was obtained from Spectrum Chemical Company (New Brunswick, NJ). Acetonitrile was purchased from EMD (Gibbstown, NJ). Syringe filters (0.2 μm) were acquired from Pall Life Sciences (Port Washington, NY). Millipore water purification system with a 0.22μm filter was used for water.

Methods

High performance liquid chromatography (HPLC)

Reverse-phase high performance liquid chromatography (HPLC) was used to analyze drug concentration from experimental conditions. Samples were analyzed with a Waters system consisting of an Alliance 2695 separation module, coupled with a 2487 dual absorbance detector (Waters Corporation, Milford, MA). Separation was achieved using a 150 mm × 3.9 mm Apollo C18 5.0 μm column. Isocratic methods were used throughout the investigations and drug concentrations were based on peak area.

To analyze amoxicillin trihydrate, UV detection was conducted at 230 nm. A 96:4 mobile phase of potassium phosphate (pH 5):acetonitrile (ACN) with a run time of 8 min was utilized. Standards were prepared from roughly 1000 μg/ml stock solution of amoxicillin trihydrate in 100% methanol (MeOH) and ranged from 50–500 μg/ml. The retention time was approximately 3.5 min. Samples were run with a constant flow rate of 1.2 ml/min and an injection volume of 5 μl. Mercaptopurine monohydrate samples were detected at 325 nm. A 90:10 mobile phase MeOH:H₂O with a run time of 8 min was utilized. Standards were prepared from roughly 500 μg/ml stock solution of mercaptopurine monohydrate in 100% MeOH and ranged from 25–200 μg/ml. The retention time was approximately 3 min. Samples were run with a constant flow rate of 1.0 ml/min and an injection volume of 25 μl. HPLC analysis for myricetin monohydrate was conducted at 373 nm. A method developed for the detection of the flavonol quercetin³⁹ was adapted for MYR analysis. A 50:50 mobile phase of MeOH:acetic acid (3%) with a run time of 10 min was utilized. Standards were prepared from a roughly 500 μg/ml stock solution of MYR in 100% MeOH and ranged from 0.5–200 μg/ml. The retention time for MYR was approximately 4.5 min. Samples were run with a constant flow rate of 1 ml/min and an injection volume of 10 μl.

Differential scanning calorimetry (DSC)

Dehydration and melting analysis were performed via a Q1000 differential scanning calorimeter (DSC) with an auto sampler (TA Instruments, New Castle, DE) and calibrated with indium. Drug samples were weighed (3–4 mg) and placed into an aluminum hermetic pan with a pin-hole lid. The effect of DSC pan configuration was evaluated by comparing profiles using an aluminum hermetic pan (with and without a pin-hole lid) and a standard closed aluminum pan. No differences in thermal profiles were noted. A nitrogen purge of 40 ml/min was used throughout. Samples were allowed to equilibrate at 30°C for five minutes, followed by a heat ramp of 10°C/min up to 50°C past the estimated melting point (MP).

Solubility Determination

Solubility values were determined in duplicate by adding excess drug to scintillation vials containing 20 ml of solvent (water) and then agitated with a rocking shaker. Samples were collected at multiple time points to ensure equilibrium, which typically occurred within 48 hrs. Drug concentration was analyzed by the HPLC methods described above.

Results and Discussion

Aqueous solubilities were determined at room temperature for amoxicillin trihydrate, mercaptopurine monohydrate, and myricetin (MYR) monohydrate. Dehydration temperatures, melting temperatures, and the entropies of dehydration were acquired experimentally from the DSC, while log P values were gathered from the literature. Furthermore, aqueous solubilities, dehydration and melting temperatures, and log P values for an additional eleven hydrates were compiled from the literature. Of these eleven, only four entropies of dehydration were available. The entire sample set includes a variety of hydrate types (mono, di, tri) with solubilities (log mg/ml) between −3.19 and 1.96, which represents a five-fold difference between the least and most soluble drug. Log P for the compounds ranges between −1.30 to 2.94. Table 1 provides a summary of the experimental and literature data collected for this study.

Table 1.

Experimental solubility, log P values, and thermal data for the compounds used in this study.

Drug	Hydrate Type	log P	DT (°C)	MP (°C)	ΔSd (cal/K*mol)	log Sw (mg/ml)
Alprazolam41,42	Di	2.33	68	226		−1.00
Amoxicillin	Tri	0.87	104	178	33.61	0.39
Ampicillin43,44	Tri	1.35	80	205		0.89
Caffeine45	0.8	−0.07	58	235		1.34
Carbamazepine46,47	Di	2.45	60	185	33.25	−0.90
Doxycycline48,49	Mono	−0.02	155	205		0.26
Fluconazole50	Mono	0.50	98	132	21.94	0.55
Lamivudine51	0.2	−1.30	135	160		1.93
Mercaptopurine	Mono	0.01	142	316	28.15	−0.93
Myricetin52	Mono	2.94	66	361	35.90	−3.19
Phenobarbital53	Mono	1.47	55	174		0.08
Piroxicam54	Mono	1.68	158	198	14.59	−1.91
Stavudine55	0.33	−0.80	142	171		1.96
Theophylline56	Mono	−0.17	71	271	33.61	0.83

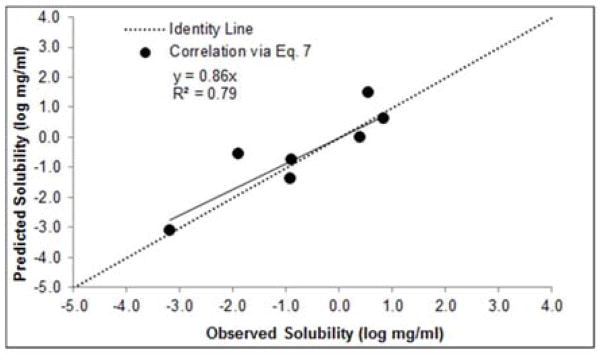
The experimental solubility values were compared to predicted solubility values generated from Eq. 7 (then converted to log mg/ml for convenience), for hydrates with available ΔS_d data (n=7). The onset endotherm temperatures were used for the dehydration (T_d) and melting (T_m) temperatures. Correlation of the predicted versus experimental solubilities for this subset resulted in an R² = 0.79 and an average absolute error of 0.51 log units (Figure 2). Although the results from Eq. 7 represent a decent prediction, the scarcity of experimental ΔS_d data limits its applicability. As a result, further investigations were made to improve the functionality of Eq. 7.

Figure 2.

Predicted (Eq. 7) vs. experimental hydrate solubility (n=7).

Analysis of the data set revealed that the average value for the experimental entropy of dehydrations (ΔS_d) is 28.9 cal/K*mol, which is comparable to the entropy of vaporization (ΔS_vap) of water (≈ 26 cal/K*mol).⁴⁰ Therefore, similar to the entropy of melting (ΔS_m) being estimated by Walden’s Rule, it was posited that the entropy of dehydration (ΔS_d) could be approximated by the entropy of vaporization for water. Thus, for room temperature calculations, Eq. 5 can be simplified to Eq. 8.

$${\mathit{logX}}_u^{\mathit{dehydration}}=-0.02(T_d-298)$$ (8)

Further assessment of the data showed that when the experimental solubility values were converted from log mole fraction to log molar, the average difference was approximately 1.7 log units. Therefore, 1.7 can be used for the molar conversion. Additionally, it was considered practical to express temperature in Celsius. As a result of the above observations, Eq. 8 can be substituted into the first term of Eq. 7 (the dehydration term) and the entire expression simplifies to:

$$\mathit{log}{S}_w^{\mathit{hydrate}}\approx -0.02(DT-25)-0.01(MP-25)-\mathit{log}P+1.7$$ (9)

where DT is the onset dehydration temperature in Celsius and MP is the onset temperature of melting in Celsius.

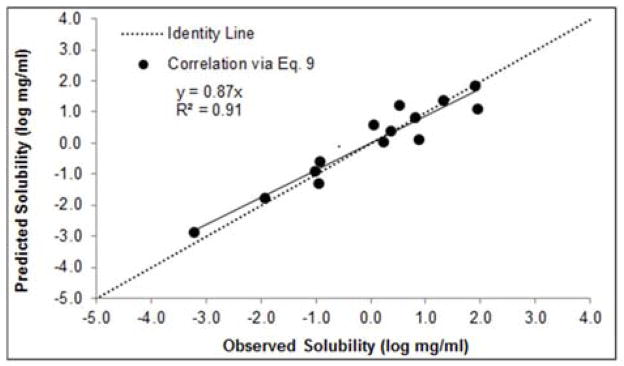
The data generated from Eq. 9 was converted to log mg/ml. The correlation of predicted solubilities using Eq. 9 versus experimental solubility for each hydrate in the data set can be seen in Figure 3. The immediate advantage of Eq. 9 vs. Eq. 7 is the fact that the solubility for all compounds in Table 1 could be estimated since experimental entropies of dehydration are not required. As seen from Figure 3 there is a very good correlation (R² = 0.91, y = 0.87x) between Eq. 9 and the experimental data.

Figure 3.

Predicted (Eq. 9) vs. experimental hydrate solubility (n=14).

A summary of experimental solubility, predicted solubility (Eq. 9), error, and absolute error can be seen in Table 2. The average error for the presented model using Eq. 9 is −0.06 log units, suggesting no systematic bias with this equation. Additionally, the average absolute error using Eq. 9 is 0.32 log units, which equates to a factor of two. No discernible pattern can be determined from the data set with respect to a relationship between hydrate type, log P, and the absolute error. In fact, the three drugs with the greatest absolute error include a mono, tri, and 0.33 hydrate with log P values of 0.5, 1.35, and −0.8, respectively. These compounds cover the full range of the data set and further strengthens the observation of no inherent bias with the model. However, further evaluation of the model with different hydrate stoichiometries is warranted.

Table 2.

Experimental vs. predicted (Eq. 9) S_w values.

Drug	Sw, mg/ml (log) Experimental	Sw, mg/ml (log) Predicted	Error (log)	Absolute Error (log)
Alprazolam	0.10 (−1.00)	0.11 (−0.96)	0.04	0.04
Amoxicillin	2.47 (0.39)	2.15 (0.33)	−0.06	0.06
Ampicillin	7.85 (0.89)	1.14 (0.06)	−0.84	0.84
Caffeine	22.0 (1.34)	21.3 (1.33)	−0.01	0.01
Carbamazepine	0.13 (−0.90)	0.24 (−0.62)	0.29	0.29
Doxycycline	1.80 (0.26)	0.97 (−0.01)	−0.27	0.27
Fluconazole	3.56 (0.55)	15.2 (1.18)	0.63	0.63
Lamivudine	84.9 (1.93)	65.6 (1.82)	−0.11	0.11
Mercaptopurine	0.12 (−0.93)	0.05 (−1.33)	−0.40	0.40
Myricetin	0.00 (−3.19)	0.00 (−2.89)	0.30	0.30
Phenobarbital	1.21 (0.08)	3.45 (0.54)	0.46	0.46
Piroxicam	0.01 (−1.91)	0.01 (−1.83)	0.08	0.08
Stavudine	90.6 (1.96)	11.5 (1.06)	−0.90	0.90
Theophylline	6.75 (0.83)	6.14 (0.79)	−0.04	0.04
Average			−0.06	0.32

To instill further applicability, an equation was developed that uses a fixed dehydration onset temperature of 100°C. This was done to provide a model should dehydration temperature be unknown or unattainable. By substituting 100°C into Eq. 9, the expression simplifies to Eq. 10.

$$\mathit{log}{S}_w^{\mathit{hydrate}}\approx -0.01(MP-25)-\mathit{log}P+0.2$$ (10)

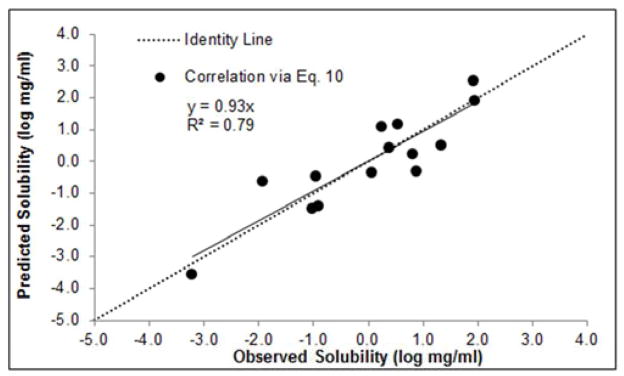
The data generated from Eq. 10 was converted to log mg/ml. The correlation of predicted versus experimental solubility for each hydrate using Eq. 10 can be seen in Figure 4. There is a reasonable correlation (R² = 0.79, y = 0.93x) between predicted solubility and experimental data when using Eq. 10. However, despite the nominal slope of the data in Figure 4, there is noticeably more scatter amongst the data as compared to Eq. 9 (see Figure 3). The average absolute error of the data given in Figure 4 is 0.59 log units. Thus, Eq. 9 should be utilized for the prediction of hydrate solubility if the dehydration temperature is known.

Figure 4.

Predicted (Eq. 10) vs. experimental hydrate solubility (n=14).

Conclusion

Extensions of the ideal solubility theory is provided to predict the solubility of pharmaceutical hydrates. The models account for both the melting and dehydration energies of the hydrated solute and result in an accurate solubility prediction. The data set includes compounds with different hydrate types and log P values that vary from −1.30 to 2.94. Most notably, experimental solubility values (log mg/ml) ranged as low as −3.19 and as high as 1.96. Three different models were developed and all provide a strong correlation between predicted solubility and experimental data. Amongst these three models, the most accurate model approximated the entropy of dehydration (ΔS_d) by the entropy of vaporization (ΔS_vap) for water and utilized onset dehydration and melting temperatures in combination with log P. With this model, the average absolute error for the prediction of solubility of 14 compounds was 0.32 log units.