Abstract
There is a growing concern that risks of disease outbreak and pandemics are increasing over time. We consider optimal investments in prevention before an outbreak using an endogenous risk approach within an optimal control setting. Using the threat of pandemic influenza as an illustrative example, we demonstrate that prevention expenditures are relatively small in comparison to the potential losses facing the USA, and these expenditures need to be flexible and responsive to changes in background risk. Failure to adjust these expenditures to changes in background risk poses a significant threat to social welfare into the future.
Keywords: endogenous risk, prevention schedule, optimal control, infectious disease
1. Introduction
The natural science community has warned policymakers of the increased health risks from disease outbreaks for both emerging and extant pathogens (e.g., Cohen, 2000, Morens et al., 2004; Weis and McMichael, 2004; Jones et al., 2008; Morse et al, 2012). Many factors drive the threat of emerging infectious disease (EID) including increased urbanization in developing countries that brings humans into new contact with diverse species in “hot spots” (Cohen, 2000; Weiss and McMichael, 2004; Jones et al, 2008). EID gain a foothold in these “hot spots” where poverty, poor sanitation and inadequate healthcare increase the risks to people vulnerable to an outbreak (Weiss and McMichael, 2004; Jones et al, 2008). Increased mobility from air travel and globalization allows pathogens to spread across the globe, implying that local risks are now global and exogenous to other nations (Cohen, 2000). In response policymakers have been encouraged to intervene to prevent new outbreaks (Cohen, 2000; Morse et al, 2012). Both the World Health Organization (WHO) and CDC track emerging diseases and focus on developing and implementing strategies for prevention and control (Cohen, 2000; Smith et al, 2003). This increasing threat from pathogens and improvements in epidemiological understanding has made prevention a vital strategy to counter these exogenous changes in risk. Investment in prevention is a costly strategy with uncertain benefits, and the trade-offs involved in combating an EID are important considerations for policymakers.
Herein we examine the optimal prevention for an EID with increasing exogenous risk for which there is no immunity, consistent with most emerging infectious diseases being zoonotic viruses (Taylor et al, 2001). We follow the approach of Reed and Heras (1992) (c.f., Kamien and Schwartz 1971) to reformulate a stochastic optimal control problem involving the random outbreak of a pathogen as a deterministic, infinite horizon problem1. We include a hazard rate for the introduction of an EID, which is increasing because of exogenous factors and can be mitigated by investment in prevention. We then provide both a formal analysis and phase plane analysis. We include a numerical example where an influenza pandemic threatens to cause lasting damages of .6% of GDP2 and can have lasting impacts due to changes in population characteristics (Meltzer et al, 1999; Almond, 2006; McKibbin and Sidorenko, 2007). Our phase plane analysis includes solving numerically for the path of prevention. We also perform a comparative dynamic analysis.
In doing so our approach extends the previous literature, which has assumed constant background risk over time. The only prior work to examine the random introduction of a pathogen is Horan and Fenichel (2007)3, who examine a wildlife-livestock system and implicitly assume constant background risk. Tsur and Withagen (2013) include an exogenously changing background risk when considering how a country or region responds to climate change. They focus on the decision to invest in adaptation capital that reduces ex post damages, but exclude investment in prevention because it is assumed impossible in the context of their problem. The problem of sudden stochastic regime change due to environmental degradation has also received a lot of attention4. This prior literature has assumed a constant background risk. This is due to the nature of the problems they examine. In these models the hazard rate is driven by stocks of pollution or environmental degradation which are controlled by policymakers. The hazard rate when considering EID is driven by changes in a wide subset of climatic, ecological, and human factors over which policy makers have little influence, but that drive disease emergence and spread (Cohen, 2000; Jones et al, 2008).
A key contribution in our paper is that we allow these exogenous changes in background risk to increase the risk of pandemic over time when exploring the endogenous management of infection risk. Our results suggest that prevention expenditures are relatively small in comparison to the potential losses, and these expenditures need to be flexible and responsive to changes in background risk. We focus on “prevention capital” which in this context consists of investments in surveillance, monitoring, research and infrastructure that can be used to prevent a pandemic. These investments could include surveillance to prevent the spread of an EID. Early detection allows quarantine measures and travel restrictions to be employed to prevent further spread, and time to prepare vaccinations that prevent endemic levels of the disease. These actions require infrastructure and knowledge that can be considered a capital stock, and depend on background risk. The stock requires investment over time as it depreciates due to the evolution of pathogens and vectors of spread. Investments overtime may also be required to identify new disease threats and to maintain capacity in hotspots where EIDs are the most likely to emerge. Failing to respond to increases in risk would leave society under protected and lower the expected value of future benefits as background risk increases. We find that an exogenous increase in risk makes it optimal to make large investments in prevention capital to build up a stock of prevention, similar to Tsur and Withagen's (2013) analysis of investments in adaptation. The build up of the prevention stock makes capital more effective at reducing the hazard rate, endogenizing the risk. We derive conditions for the schedule—not just the steady state—when it is optimal to invest in prevention. Because we solve for our paths numerically we provide estimates of the savings due to investing in prevention and estimates of the required investments in prevention.
2. Economic-Epidemiological Model of a Disease Outbreak
Consider a benevolent resource manager charged with managing the risk of a major disease outbreak. Here we simplify matters and partition time by the date of the outbreak at time τ, which is a random variable. The manager's investments in prevention can delay the outbreak by lowering the hazard faced by the system. Pre-outbreak, when t < τ, there are no damages although costly investments in prevention help avoid or delay future damages. Following an outbreak, when t ≥τ, realized damages have known intensity and duration, and are taken as given.
The probability of an outbreak at τ is represented using Reed and Heras (1992)'s method, following Barbier (2013). If G(t) is the probability that an outbreak has already occurred, then the probability an outbreak has not occurred is given by the survivor function S(t) = 1 – G(t) where S(t) = Pr (τ ≥ t). The risk of an outbreak has exogenous and endogenous components. Exogenous background risk drives the natural probability of outbreak, and is given by R(t). Investments made to a stock of prevention capital, N(t), counteract the background risk and make the hazard rate, Ψ(N(t), R(t)) endogenous. The hazard is (technically) the probability of an outbreak at any time t, given that there has not been an outbreak prior to t
| (1) |
where g(·) is the pdf of G(t). We assume Ψ (N(t), 0) = 0. The greater the background risk the greater the hazard or ΨR > 0 (where subscripts involving variables indicate partial derivatives). Increases in the stock of prevention reduce the hazard, or ΨN < 0, and also the marginal impact of background risk, ΨNR < 0. Barbier (2013) shows that the hazard can be equivalently expressed by (suppressing notation)
| (2) |
The relationship between the survivor function and the integrated hazard is
| (3) |
which allows the transformation
| (4) |
Denoting the integrated hazard as , the probability an outbreak has been avoided until time t is S(t) = e−y(t) where .
Prior to a disease outbreak (t < τ), a revenue generating activity (i.e. trade) generates a (constant) flow of social benefits in each period equal to B. These benefits are reduced by expenditures on prevention investments, z(t), so that net benefits at instant t are given by
| (5) |
If an outbreak occurs (at τ) it causes social damages that may arise with mortality, morbidity and any associated public health expenditures on treatment. Together we denote these social costs D(t). We abstract from any kind of additional optimization problem and assume the damages have known intensity and duration, such that the present value of ex post net benefits are e−rtJX, where
| (6) |
D(t) is a known damage function with non-negative range, and r is the discount rate. A full derivation of JX in a similar problem can be found in Clarke and Reed (1994). Given the expression in (6), the expected present value of net benefits is written as
| (7) |
where the expectations operator E reflects the uncertainty of outbreak time τ.
Following a transformation, as shown in De Zeeuw and Zemel (2012) and in greater detail in Tsur and Zemel (1997), and in an appendix available on request, equation (7) becomes
| (8) |
Using (8), we can write our maximization problem as
| (9) |
where δ is the depreciation rate of the prevention stock and σ(R(t)) indicates how background risk changes over time as a function of its current state. We make no assumptions about the properties of σ analytically.
Problem (9) is a deterministic, infinite-horizon problem (Reed and Heras, 1992) that can be solved by applying Pontryagin's maximum principle (Pontryagin and Boltyanskii, 1962; Kamien and Schwartz, 1991). The objective function accounts for the fact that economic risk is endogenous. Specifically, each period's net benefits are calculated as the current flow of ex ante net benefits plus the expected return from transitioning to the infected state, Ψ (N(t), R(t))JX, where the hazard rate associated with the transition depends on the prevention stock and background risk. These net benefits are then discounted and multiplied by the survival probability e−y(t), with y(t) being a risk-adjusted discount rate that depends dynamically on the prevention stock.
Reed and Heras (1992) derive the optimality conditions for this class of problems. First, define the current value Hamiltonian as (omitting time notation henceforth for brevity)
| (10) |
where μi are the current value costate variables. Next, define the conditional current value Hamiltonian (or simply the conditional Hamiltonian) by multiplying H by ey
| (11) |
Where ρi = μiey are the conditional current value costate variables, with ρ1 > 0, and ρ2, ρ3 < 0. The term conditional is used here to indicate that all values are conditional on the system surviving to time t.
Applying the maximum principle to (11) requires the optimal investment expenditure to follow the rules
| (12) |
Equation (12) relates the choice of investment expenditure to a comparison of the marginal cost of prevention (one dollar) with the marginal benefit of prevention, as given by the costate (shadow value) associated with the stock of prevention. If the marginal cost is larger than the shadow value, it is optimal to not prevent at all. If the marginal cost is less than the shadow value, an impulse investment in prevention is optimal. The singular solution, denoted z*, occurs when the marginal cost of prevention is exactly equal to the shadow value of prevention. In that case, condition (12) indicates ρ1 = 1 so that ρ1 = 1.
The adjoint conditions are (see Reed and Heras, 1992)
| (13) |
| (14) |
| (15) |
The dynamics of the system are completed with the equations of motion for the three states.
To better understand the role of risk in the optimality conditions, we first note that the adjoint condition (15) has the solution
| (16) |
where v is a dummy of integration and J* represents the optimized value of J at time t. Relation (16) indicates –ρ3 > 0 is the expected present value of net benefits from the current time onwards, or the ex ante value of an optimally managed system facing the threat of an outbreak.
Define γ = – ρ3 –JX to be the expected economic cost of the outbreak, i.e., the value by which ex ante net benefits are reduced when the system transitions to the ex post infected state. If γ > 0, then there is value associated with trying to prevent an outbreak. If γ < 0, then society is better off by allowing the outbreak to occur. The conditional Hamiltonian can be rewritten in terms of : H̄ = B – z – Ψ(N, R) γ + ρ1(z – δN) + ρ2 σ(R), as can the following adjoint conditions (13)-(15), the first two of which have been modified by dividing through by the co-states:
| (17) |
| (18) |
| (19) |
Equations (17)-(19) are “portfolio balance” equations that guide decision making to keep each stock or “asset” a competitive investment. Equation (17) requires the capital gains (or losses) of prevention capital, ρ̇1/ ρ1, to equal the difference in the (risk- and depreciation-adjusted) required rate of return to investment in prevention capital, r + δ + Ψ(N, R), and the rate of return to prevention in terms of reducing expected losses, (which is positive when γ > 0). The required rate of return to investment is opportunity cost of funds, r, adjusted for depreciation and the risk that the investment may be worthless (the hazard rate). Along the singular path with ρ̇1 = 0, marginal costs of prevention capital are required to perfectly balance marginal benefits and hold the value of ρ1 constant. If marginal costs exceed marginal benefits, then the portfolio balance condition along with condition (12) requires larger capital gains in the value of prevention capital, and investment should be zero. If marginal costs are less than marginal benefits, the portfolio balance condition along with condition (12) dictates that the value of prevention capital is excessive and investment should be as high as possible, driving down the value.
Equation (18) has a somewhat different interpretation since ρ2 < 0. The left hand side (LHS) of equation (18), ρ̇2(–ρ2), represents beneficial capital gains (when positive) or costly capital losses (when negative) due to changes in background risk. The right hand side (RHS) of (18) indicates these capital gains must adjust to cover the difference between the rate at which background risk increases expected losses, (which are positive when γ > 0), and the rate at which the value of background risk grows, r + Ψ(N, R) – σR(R). This growth rate consists of the discount rate, the hazard rate, and the marginal growth in background risk.
The final portfolio balance condition, equation (19), indicates how expected losses change over time. As indicated above, the solution is γ = – ρ3 –JX, where – ρ3 is defined in expression (16).
Although ρ2 and γ, and hence conditions (18) and (19), do not appear to trigger a behavioral response via condition (12), it can be shown that these variables do in fact influence the optimal choice of z via a series of feedback relations. We illustrate this result for the singular solution where , which implies ρ̇1 = 0. Condition (17) can then be solved for
| (20) |
Take the time derivative of condition (20) and set it equal to adjoint condition (19) to yield
| (21) |
Expression (21) defines a feedback relation for investment, z. However, the intuition and implications of this relation are better understood if we manipulate (21) somewhat. First, we apply Tahvonen and Salo's (1996) insights about the optimized Hamiltonian, as shown in the Appendix, to derive
| (22) |
The LHS of expression (22) is the value of changes in background risk. The second line of the RHS of expression (22) consists of two terms. The bracketed term represents the stationary equivalent of welfare (i.e., the optimized Hamiltonian; see Weitzman 1976) when there are no further changes in background risk (i.e., when σ(R) = 0). The second RHS term represents the flow value of net benefits along an optimal path. When R is at its steady state value R** so that σ(r**) = 0, expression (22) indicates that N should be at a steady state value N(R**) such that the two RHS terms are equivalent (note that such an outcome also satisfies (21) with a steady state value z = δN(R**)). Otherwise, when σ(R) ≠0, the value of the difference in the two RHS terms is captured by – ρ2, which can be rewritten as
| (23) |
Substituting expression (23) into (21), we can obtain the following singular feedback expression
| (24) |
Where .Whether investments in the prevention stock are made to exceed depreciation depend on the sign of the second RHS term in expression (24). In the Appendix we argue that 1 > γN. Hence, if background risk is increasing, then net investments will be increasing if the bracketed term in (24) is positive. The first term in brackets, the shadow value of background risk, is clearly positive: the greater the value of background risk, the greater the required net investment in prevention.
Consider the second term in brackets on the RHS of (24). The coefficient of the parenthetical term is the rate of substitution of N for R in managing the hazard rate, which is positive. The term in parentheses may be positive or negative. In particular, the elasticity εψR,N measures the relative endogeneity of risk, or the degree to which the impacts of background risk on the hazard can be managed via the stock of prevention, N. The larger this elasticity, the more effective is the prevention stock and the smaller the investment z needed to manage the hazard (given that ∂z/∂εψR,N < 0). The smaller this elasticity, the less effective the prevention stock and the greater the investment z needed to manage the hazard. In our numerical example in section 3, the elasticity increases linearly with the prevention stock. The implications are that increases in the stock of prevention increase the relative endogeneity of risk. For example, larger surveillance programs or early detection capacity will lead to increasingly effective risk reductions.
Together, the two terms in the brackets of (24) lay out how investment adjusts, through economic responses to risk (through the shadow value of risk) and through technological responses to risk, given by the relative endogeneity of risk. The feedback expression captures the net of these two forces, and provides the key component for our analysis. We use the feedback expression for prevention to construct and analyze a phase plane in (R, N) space so that we may investigate the system dynamics.
3. Dynamics of optimal solutions
We examine the dynamics of the optimal solution through the use of a numerical example of the U.S. economy facing a pandemic outbreak. The functional forms and parameters used for the example are described here and presented in Table 1. The benefit flow B=13593.2 reflects 2012 US GDP in billions of chained 2005 US dollars. For simplicity this flow is assumed constant over time. Depending on the severity of a pandemic, McKibbin and Sidorenko (2007) estimate it would cause a 0.6% to 3% loss in US GDP. The losses are due to a decrease in the labor force, increased cost of doing business, shifts in consumer preferences and changes in investment risk. McKibbin and Sidorenko (2007) include adaptation and control efforts by including a “health policy index” that estimates the ability of healthcare systems in different nations to deal with a pandemic. There is also the possibility the effects of a pandemic persist through lasting impacts on human health and population characteristics (Almond, 2006). Because of this, a small initial impact on the economy may persist for a long time while the system slowly returns to equilibrium. Together, we assume JX, or the value of the system after an outbreak is equal to $450,388 billion in 2005 US dollars. The value reflects the infinite sum of U.S. GDP that suffers a sustained 0.6% reduction. It is likely that this reduction would be sustained for an extended period of time as the system recovered, but our assumption is for clarity in results.
Table 1. Parameter values and sources for numerical example.
| Parameter | Functional Form / Value | Source | |
|---|---|---|---|
| Exogenous background risk, σ(t) |
|
Arbitrary | |
| Steady state background risk, R** | .1 | Calibrated to 3 pandemics over 100 years (Meltzer et al., 1999) | |
| Hazard rate, ψ(N(t), R(t)) | R(t)e−cN(t) | Arbitrary | |
| Effectiveness of the prevention stock, c | .5 | Arbitrary | |
| Depreciation rate δ | .05 | Arbitrary | |
| Discount rate r | .03 | Arbitrary | |
| Ex ante value of an optimally managed system facing threat of outbreak, JX | $450,388.0267 | McKibbin and Sidorenko (2007) | |
| Flow of benefits, B | $13,593.2 (billion) | US GDP in chained 2005 US dollars |
Background risk, R, is assumed to evolve logistically over time, increasing or decreasing over time to a long-run level, R**, where . R** is chosen to be 0.1, consistent with the historical 3 pandemics over 100 years (Meltzer et al., 1999). Finally, the hazard rate is taken to be ψ(N, R) = Re−cN where c is the effectiveness of the prevention stock in controlling the hazard. In the absence of any information we arbitrarily chose c = 0.5 and take the discount rate to be r = 0.03. A comprehensive comparative dynamics analysis is presented in section 3.5 to examine how sensitive the model results are to changes in the parameters just described. All simulations were performed in Mathematica.
3.1 Partitions of the phase plane
We begin by focusing on the singular solution, with the associated singular phase plane presented in Figure 1a. First, we partition the phase plane into isosectors using the Ṅ = 0 and Ṙ = 0 isoclines. The Ṅ = 0 isocline follows from the equation of motion after substitution of the relation z(R,N). The Ṙ = 0 isocline is the equilibrium level of background risk, R**. The R directions of movement are simple given the logistic form of the changes in background risk. The N directionals were found numerically.
Figure 1.
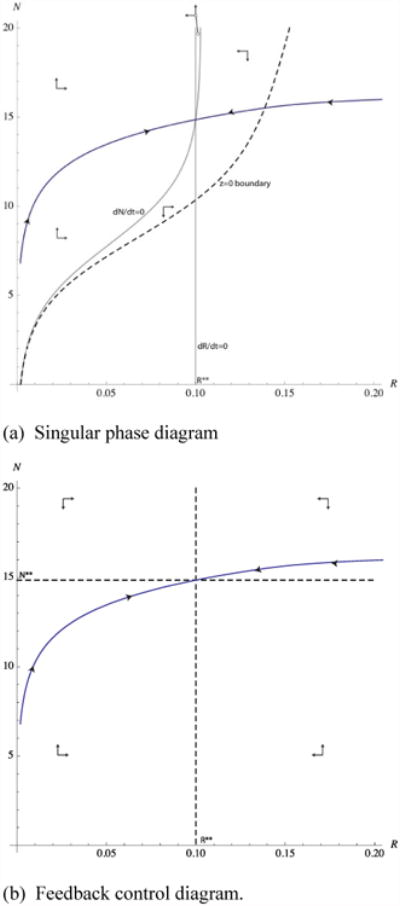
In both panels, background risk is on the horizontal axis and prevention stock (in billions of US dollars) on the vertical axis. In Panel (a), the plane is partitioned by the dashed line (z(R,N)=0) into a positive prevention area above the dashed line, and the area where no prevention is optimal, below the dashed line. The two grey lines trace out the singular isoclines. The singular path is blue and shown with arrows indicating the direction of movement along the path. Arrows indicate directions of movement for the singular path. Panel (b) illustrates the MRAP directions of movement and the singular path.
Additionally, the behavioral rules in condition (12) are used to partition the phase plane into regions where z* > 0 and z* = 0. We do this by solving for the boundary where the singular value just vanishes, z(R,N) = 0. This boundary splits the phase plane into two regions: (i) z(R,N) > 0 above the boundary, and (ii) z(R,N) = 0 below the boundary.
3.2 Optimal trajectories
Optimal trajectories depend on the behavioral rules (conditions (12) and (24)) and the joint dynamics Ṅ and Ṙ. First, consider the dynamics associated with the singular solution. The exogenous dynamics for R lead to the steady state value, R**, which we demonstrated above results in a steady state value for N at the intersection of the isoclines. Numerically, we have evaluated the eigenvalues of the linearized system to determine this steady state is a saddle point, which is consistent with the phase arrows in Figure 1a. The separatrices were then computed using the procedure outlined in Conrad and Clark (1987). The portion of the separatrix to the right of the z = 0 boundary represents the adjustment path with z = 0 that becomes singular as the boundary is crossed.
We should emphasize that the phase arrows, as well as the z = 0 boundary, are only relevant for the singular solution. However, as the singular solution only exists on the separatrices, the phase arrows and the boundary are not relevant off the separatrices. Instead, starting at any point off the separatrices, condition (12) indicates a most rapid approach path (MRAP) to the singular solution is optimal. The full solution, involving both singular and non-singular controls, is illustrated using the feedback control diagram in Figure 1b.
We have assumed Ṙ evolves exogenously over time. The direction of change in R depends on the initial value R0 relative to R**. We therefore use the following sections to describe optimal investment strategies for two cases: (a) R0 < R**, so that R increases to its long-run equilibrium, or (b) R0 > R**, so that R decreases to its long-run equilibrium.
3.3 Case a. Increasing background risk
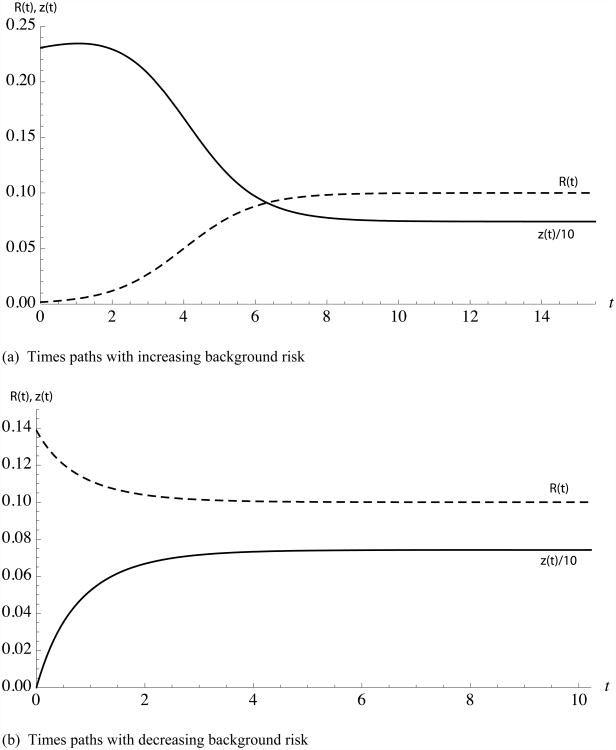
Suppose R0 < R**, so that the singular path is given by the left separatrix in Figure 1. If N0 < N*, then an impulse investment in z will be required to instantaneously build up the prevention stock to the singular value N*. The singular value N* is increasing in R, but at a decreasing rate. This indicates z* is, at least eventually, declining in R and N prior to attaining a steady state. The investment schedule is illustrated in Figure 2a: investments in prevention initially increase in response to higher background risk, but later decline in R. This can be explained, in part, by the fact that the relatively endogeneity of risk increases as N increases: εψR,N = cN along the singular path. Investments are made in the prevention stock so that it becomes highly effective at reducing risk, after which fewer additional investments are required. From expression (24), the impact of this effect diminishes as σ(R)→0 and so investment levels optimally converge to the steady state value δN**.
Figure 2.
Panel (a) shows the singular path of investment in prevention for the increasing background risk case, scaled in (billions of US dollars)/10 (solid line), and the background risk as it increases to R** (dashed line. Panel (b) shows the same three variables for the decreasing risk case in the interval when z(t)>0.
The consequences of increasing background risk on the economic cost of outbreak, γ, are enumerated in the model. As background risk grows, the economic cost of the outbreak grows from $2,682 billion to $2,688 billion, in much the same pattern as the stock of prevention. As ρ3 represents the expected present value of net benefits from the current time onwards from (16), we know that the ex ante value of the system falls from $453,079 billion to $453,077 billion.
3.4 Case b. Decreasing background risk
Suppose R0 < R**, so that the singular path is given by the left separatrix in Figure 1. As above: if N0 < N*, then an impulse investment in z will be required to instantaneously build up the prevention stock to the singular value N*. However, immediately after this investment z(R,N)=0 may be optimal for a time (i.e., if, given R0, the singular value N* lies to the right of the z = 0 boundary. In this case, there will be an interval of no investment and depreciation of the stock as background risk declines. This is similar to Tsur and Withagen (2013) where the probability of a regime shift is exogenous, yet investment in their model is in adaptation capital (capital that helps society adapt to the regime shift, ex post). They also show when the level of capital is above the steady state it is optimal to not invest and allow the capital stock to depreciate over time. Here, it is only optimal to not invest beyond the z(R, N) = 0 boundary.
As R declines, so does the singular value N*, and at an increasing rate. This suggests that, after possibly some period of zero investment, z* should rise begin to increase prior to attaining a steady state. The investment schedule is illustrated in Figure 2b: investments in prevention initially increase in response to higher background risk, before leveling off at a steady state value. As above, the initial increase in investment can be explained, in part, by the fact that the relative endogeneity of risk decreases as N depreciates: the smaller prevention stock becomes less effective at countering background risk, spurring additional investment z to slow the depreciation. However, from expression (24), the impact of this effect diminishes as σ(R)→ 0 and so investment levels optimally converge to the steady state value δN**.
Along the right separatrix, the economic cost of the outbreak declines from $2,689 billion to $2,688 billion. The net decline follows from the fall in the background risk of outbreak, and overwhelms the increased investments in prevention. The ex ante value of the system also increases from $453,070 billion to $453,077 billion.
3.5 Comparative dynamics
The effect of variations in different parameters on the results was examined. The parameters of interest included the value of the system following an outbreak, which can also be considered the impact of the disease, the discount rate, the stream of benefits, the depreciation rate of prevention capital, the effectiveness of prevention, and the rate at which the background risk approaches the steady state. The results are summarized in Table 2. We also search for threshold levels of each parameter when it becomes optimal not to invest and to have no prevention capital stock, all else constant. These values provide limits where, ceteris paribus, it is optimal to not invest in prevention. In order to find these values, we consider a situation with no investment in prevention capital, no existing capital stock, and where background risk is at its steady state level. We also assume the decision maker is indifferent between investing or not. This ensures it is just optimal to not invest in the long run. The results are included in Table 3.
Table 2.
Results from the comparative dynamics analysis in section 3.5.
| Comparative Dynamics Results (increase in given parameter) | |||||
|---|---|---|---|---|---|
| Parameter | Description | Increasing Risk | Decreasing Risk | ||
| Effect of an increase on investment in prevention | Effect of an increase on steady state stock of prevention capital | Effect of an increase on investment in prevention | Effect of an increase on steady state stock of prevention capital | ||
| JX | Value of an optimally managed ex post system | Lower investment | Lower steady state stock | Lower investment | Lower steady state stock |
| r | Discount rate | Less investment | Lower steady state stock | Less investment | Lower steady state stock |
| B | The flow of benefits the system | More investment in prevention | Higher steady state stock | Higher investment | Higher steady state stock |
| δ | Depreciation rate of prevention capital stock | Higher investment | Lower steady state stock | Higher investment | Lower steady state stock |
| c | Effectiveness of prevention | Lower investment | lower steady state stock | Lower investment | Lower steady state stock |
| χ | This scales the rate of approach to the steady state. A higher value approaches the steady state faster.6 | Faster increase in prevention | Unchanged | Faster decrease in investment | Unchanged |
Table 3.
Boundary values of parameters for investment in prevention to be optimal, holding all others constant.
| Parameter | Threshold |
|---|---|
| R** | A risk of pandemic of .006% |
| JX | Damages of .003% |
| r | A discount rate of 3.018% |
| B | Benefits of $13,512 |
| δ | N/A |
| C | .003 |
On the singular path, a more valuable system after an outbreak, or less damaging disease (a higher JX) leads to lower prevention. The comparative dynamic results are shown in detail in Figure 3. The potential benefits of prevention are lower because the difference between an infected and uninfected system is smaller. The flow of investment into the stock and the stock are both lower. In this case, it is optimal to invest less at each point in time because the marginal benefit is lower, so the stock builds at a slower rate to a lower steady state. The threshold for investment (Table 3) is found as damages approach 0.003% of GDP (JX=453090). Damages less than this value (all else constant) become too negligible for investment in prevention to be optimal. The boundary for investment in prevention to be optimal increases when the disease is more damaging. The steady state level of prevention is also higher. This is because a more damaging disease is more valuable to avoid.
Figure 3.
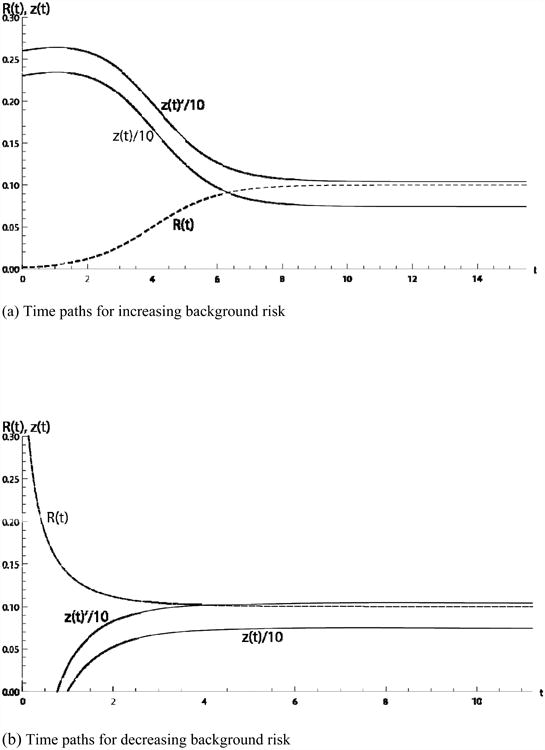
The comparative dynamic results for an increase in JX are shown above, where JX is greater along the z(t)′ curves. Panel (a) shows the comparative dynamic results for the path of investment in prevention for the increasing background risk case, scaled in (billions of US dollars)/10 (solid line), and the background risk as it increases to R** (dashed line) Panel (b) shows the same variables for the decreasing risk case in the interval when z(t)>0. Only investment in prevention shifts, upward from z(t) to z′(t) as the value of JX falls and the disease becomes more damaging.
Increases in the discount rate r, lower the present value of benefits delivered by prevention in the future. This leads to less investment in prevention and a lower stock of prevention on the singular path. When the background risk is increasing, a higher discount rate implies lower levels of investment initially to build up a (eventually lower) prevention stock. When the background risk is decreasing, at first the stock is allowed to fall without any investment. Eventually investment in prevention is turned on, and a higher discount rate implies less investment at every point in time, leading to a lower steady state stock of prevention.
The threshold in r, above which it is not optimal to invest in prevention, in the current parameterization is 3.018%5. At higher discount rates the value of ρ1 is too low to satisfy the first-order condition for a singular solution in the steady state. A higher flow of benefits compared to JX, or a lower JX compared to the flow of benefits increases the threshold discount rate. A higher depreciation rate or hazard rate lowers the threshold discount rate because both act as additional discount rates. A more effective prevention capital stock increases the threshold discount rate.
Greater levels of benefits provided by a system effect both the flow of benefits ex ante, and the value of an ex post system. A higher flow of benefits leads to higher investment in prevention when the background risk is increasing. In this case there is a higher flow of prevention at every point, and a higher steady state stock of prevention. In the inverse, when there is a higher flow of benefits and the risk is decreasing, investment in prevention increases to a higher steady state stock of prevention. If the flow of benefits is lower, it is possible that investment in prevention is not turned on until later than our base case reflecting the higher steady state. Lower benefits lead to a lower steady state level of prevention capital. If we increase the flow of benefits, B, while holding the value of the ex post system constant (increase only B) then our result is clearer. In this case we also find that it is optimal to increase investment in prevention at every point and to maintain a higher stock of prevention capital. This reflects the importance of the flow of ex ante benefits relative to the value of a system after an outbreak occurs. In this case the ex post system declines relative to our ex ante benefits leading to the increased flow of prevention and larger stock both when risk is increasing and decreasing. If the flow of benefits decreases while holding the ex post value of an infected system constant, it is possible that it is never optimal to invest in prevention. If the flow of benefits is equal to only $13,512 billion, or just .6% lower, then it is never optimal to invest in prevention.
Changes in the depreciation rate of capital, δ, lead to intuitive impacts on investment and the stock of prevention stock. A larger depreciation rate leads to a smaller steady state level of prevention capital. A higher depreciation rate implies a higher level of investment at every point when the background risk is increasing. More investment is required to counter faster depreciation. A larger depreciation rate also implies that there will be a positive level of investment earlier when the risk is decreasing. This is because, all else equal, a larger depreciation rate will cause the stock of prevention capital to reach the steady state faster when we are lowering the capital stock as risk falls. There is no reasonable threshold level of depreciation where it is optimal to not invest in prevention.
A greater effectiveness of prevention, c, leads to smaller levels of investment in prevention at every point. It also leads to a smaller steady state stock of prevention. These results are consistent with our interpretation of the relative endogeneity of risk, which is proportional to c, i.e., εψR,N = cN. It is also consistent with related work. For instance, Kim et al (2006) and Finnoff et al (2012) both find that if the marginal cost of early prevention is significantly high it is not efficient to expend a larger share of resources on prevention. This result holds in our example when the effectiveness of prevention approaches zero. Less effective prevention implies a higher steady state level of prevention capital. The threshold level for the effectiveness of prevention is .003, compared to the assumed rate of .5.
The final parameter we investigate governs the shape of the background hazard function. When the background risk increases to the steady state at a slower rate, investment in prevention is reduced along the singular path. This is because initially the risk is too low to invest much in prevention, and there is more time to build up the stock of prevention. If the background risk is decreasing, investment in prevention falls along the singular path. This slows the depreciation of the prevention stock in response to the lingering risk.
4. Discussion
This paper examines the optimal investment in prevention of a pandemic given the reality of increasing levels of background risk over time. Focusing on emerging infectious diseases (EID) as our motivating example, our main result is that the planner should invest immediately in a significant level of prevention capital. This is due to the relatively endogeneity of risk, whereby large initial investments are made in the prevention stock so that it becomes more effective at countering the background risk. After this, fewer additional investments are required to maintain the relative endogenity of risk. Then as the expected net present value of benefits falls as the background risk rises, investment in prevention will decrease as the steady state level of the prevention capital stock is reached. This result is illustrated in our US influenza pandemic example with background risk that increases from 0.2% to 10%. Here we estimate that the stock of prevention capital increases rapidly to $15 billion from $7 billion, and the optimal level of investment declines to $700 million from $2.3 billion. This decreases the expected present value of future GDP to $453,077 billion from $453,079 billion (2005 US dollars). This setting is in line with arguments made concerned with the threats of globalization, climate change or changes to the influenza virus that make it more infectious to humans (Cohen, 2000; McKibbin and Sidorenko,2007). The sensitivity of optimal paths to variations in key parameters is illustrated in a comprehensive comparative dynamic analysis.
We have demonstrated the importance of including the increasing background drivers of risk in analysis concerning the risk of introduction of an emerging infectious disease. It is vital that investments in prevention are responsive to increases in the background risk. The threat of repeated introduction would be a valuable extension to our model, and would increase the value of prevention. We leave this extension to future work. A more direct investigation of trade-offs between prevention and other control strategies would also be a valuable addition to the literature. While our results are dependent on our choices of parameters, we expect our results to provide significant guidance to policy makers charged with managing the endogenous risk of disease outbreaks.
Acknowledgments
We gratefully acknowledge funding from NOAA CSCOR Grant No. NA09NOS4780192, the National Institute of General Medical Sciences (NIGMS) at the National Institutes of Health, grant #1R01GM100471-01, and USDA National Institute of Food and Agriculture, Grant #2011-67023-30872. The contents of the paper are solely the responsibility of the authors and do not necessarily represent the official views of NOAA CSCOR, NIGMS, or USDA.
Appendix
Singular Solution
Consider the singular solution where ρ1 = 1, which implies ρ̇1 = 0 and
| (A.1) |
Taking the time derivative of (A.1) and setting it equal to the adjoint condition (Equation 19 in the main text)
| (A.2) |
The intuition and implications of expression (A.2) are better understood if we first derive a relation between the optimized Hamiltonian and γ(N,R).
The optimized conditional Hamiltonian can be written in open loop form as .The time derivative of the present value of H̄* can be written
| (A.3) |
Suppose a singular solution is being pursued with respect to z (for the case of a non-singular interval of the optimal solution, examining the Lagrangian that accounts for upper and lower bounds on n produces identical results). Then, following Tahvonnen and Salo (1996), the necessary conditions can be used to write (A.3) as
| (A.4) |
Integrating both sides from any time τ onward yields
| (A.5) |
where . Assuming H̄* (∞) is finite, expression (A.5) becomes
| (A.6) |
where J*(τ) represents the present value of expected optimized net benefits from time τ onwards, discounted to time 0. Using (Equation 16 in the main text), expression (A.6) can be rewritten as
| (A.7) |
where the final RHS expression stems from the definition of γ. Equation (A.7) can be maintained by an appropriate value of ρ2 given we can re-write (A.7)
| (A.8) |
where the condition ρ1 = 1 has been imposed. Solving equation (A.8) yields
| (A.9) |
The time derivative of (A.9) satisfies adjoint condition (Equation 18 of the main text). Note that expression (A.9) only holds when σ(R) ≠ 0. When σ(R) = 0, so that R is at its steady state value R**, then expression (A.9) yields the relation
| (A.10) |
which implies the constant value N(R**) and is consistent with condition (A.2).
The final necessary condition to satisfy is condition (A.2). Using (A.10), condition (A.2) is written as
| (A.11) |
Let N(R) | γN=1 be the solution to γN(N, R) = 1, and let N(R) |γR= ρ2(N,R) be the solution to ρ2(N,R) = γR. As N(R)|γN=1 generally does not equal N(R)|γR = ρ2(N,R), except for possibly at a discrete number of values of R, condition (A.11) implies that γN(N, R) ≠1 and ρ2(N, R) ≠ γR. This means there will be a deviation between the co-states and the marginal impacts of the states on the costs of infection. This is expected, since relation (Equation 16 of the main text) implies γi = –∂ρ3 (N,R)/ ∂i = ∂[ert+y*J*]/∂i = ert+y* J*(∂y*/∂i) + ert+y*∂J*/ ∂i. Léonard's (1987) results indicate that ρ1 = ert+y*∂J* /∂N and ρ2 = ert+y*∂J* /∂R. Using these results along with the previous relation, we derive
| (A.12) |
The signs of the RHS expressions in (A.12) are generally ambiguous.7 Recall that is the integrative effective hazard. Starting at time 0 (or any other time prior to t), an expected increase in the future value of N(t) or R(t) will alter the entire path of N*(τ) for τ ≤ t. It is perhaps reasonable to assume ∂y*(t)/ ∂N(t) > 0, since more investments will need to be made earlier if N(t) is to increase. It is less clear whether the trajectory of prior preventative investments will yield ∂y*(t)/ ∂R(t) < 0 or ∂y*(t)/ ∂R(t) > 0 in preparation for an increase in future background risk, R(t). Roughly speaking, the case of ∂y*(t)/ ∂R(t) < 0 arises when the behavioral response to increased background risk (indirect effect, which reduces y) dominates the direct effect of increased background risk on the integrative hazard. The opposite is consistent with ∂y*(t)/ ∂R(t) > 0.
Given our prior result that γN(N, R) ≠ 1, we can divide (A.11) by [1 – γN] to obtain a feedback expression for n. Noting that [∂y*(t)/ ∂R(t)]/[∂y*(t)/ ∂N(t)] = [∂S*(t)/ ∂R(t)]/ [∂S*(t)/ ∂N(t)], we can write the feedback expression as
| (A.13) |
Suppose background risk is increasing. Then net investment in prevention will increase when the rate at which the stock of prevention can be technically substituted for background risk is positive. This occurs when the indirect effect dominates the direct effect.
Greater insight into the substitution possibilities can be seen by using the middle expression of (A.13), along with the definitions of ρ2(N,R) and γ(N,R), to rewrite expression (A.13) as
| (A.14) |
Note that:
Hence, (A.14) becomes
| (A.15) |
Footnotes
This approach has been applied to managing forests at risk of fire (Reed, 1984; Reed, 1987a; Reed, 1987b), fisheries at risk of collapse and other environmental applications (Reed and Heras, 1992), resources subject to a regime shift (Polasky et al, 2011), and resource collapse due to land conversion (Barbier, 2013).
Depending on the severity of a pandemic, McKibbin and Sidorenko (2007) estimate it would cause a .6% to 3% loss in GDP for the US. These estimates include investment in control and adaptation with estimates of how effective different countries would be able to deal with a pandemic. The losses are due to a decrease in the labor force, increased cost of doing business, shifts in consumer preferences and changes in investment risk.
The ex post problem has received significant attention, see Geoffard and Philipson (1997), Goldman and Lightwood (2002), Gersovitz and Hammer (2003), Gersovitz and Hammer (2005), Fenichel et al. (2010), Aadland et al. (2011), and Rowthorn and Toxvaerd (2012).
The impact of endogenous versus exogenous risk on the optimal choice of prevention has been examined in detail (Tsur and Zemel, 2007; Polasky et al., 2011). Tsur and Zemel (2009) examine how the social discount rate is made endogenous by the threat of catastrophic climate change and the implications for control. Tsur and Zemel (2008) explore costate variables and derive Pigouvain taxes to reduce the hazard rate when the endogenous risk of a shift is related to a stock of an environmental bad. Kagan (2012) examines the impacts of climate change skepticism and finds that even when agents are nonresponsive to their impact on the probability of a regime shift, they will react to the risk if they expect some future change in benefits. The endogeneity of risk has been shown to matter when considering the tradeoff between prevention and adaptation in managing the risks of climate change (De Zeeuw and Zemel, 2012; Van der Ploeg and de Zeeuw 2013).
It is interesting to note that at the current parameterization, a planner employing a discount rate of 1.4% (consistent with the Stern report, 2007), would optimally employ prevention, leading to an optimal stock of prevention at the steady state of $26 billion, compared to $15 billion in the base case. Yet, if the planner were to employ the mean discount rate of Weitzman's (2001) survey of 3.96%, they would not prevent at all (taking the other parameters as given).
For this comparative dynamic, our background hazard function is changed to so that it is possible to scale the speed in which it moves towards the steady state.
Explicit expressions for the derivatives of y with respect to the states at time t are not easy to derive since y is defined as an integral (over the interval 0 to t) over a function of one state (N) that optimally responds to expected changes in future states (Léonard 1987). However, signing the derivative is less difficult.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Kevin Berry, Email: kberry@uwyo.edu.
David Finnoff, Email: finnoff@uwyo.edu.
Richard D. Horan, Email: horan@msu.edu.
Jason F. Shogren, Email: Jramses@uwyo.edu.
References
- Aadland D, Finnoff D, Huang K. The dynamics of economic epidemiology equilibria. Working Paper (2011) 2011 [Google Scholar]
- Almond D. Is the 1918 Influenza pandemic over? Long-term effects of in utero Influenza exposure in the post-1940 US population. Journal of Political Economy. 2006;114(4):672–712. [Google Scholar]
- Barbier EB. Wealth accounting, ecological capital and ecosystem services. Environment and Development Economics. 2013;18(02):133–161. [Google Scholar]
- Clarke HR, Reed WJ. Consumption/pollution tradeoffs in an environment vulnerable to pollution-related catastrophic collapse. Journal of Economic Dynamics and Control. 1994;18(5):991–1010. [Google Scholar]
- Cohen ML. Changing patterns of infectious disease. Nature. 2000;406(6797):762–767. doi: 10.1038/35021206. [DOI] [PubMed] [Google Scholar]
- Conrad JM, Clark CW. Natural Resource Economics Notes and Problems. New York: Cambridge University Press; 1987. [Google Scholar]
- De Zeeuw A, Zemel A. Regime shifts and uncertainty in pollution control. Journal of Economic Dynamics and Control. 2012;36(7):939–950. [Google Scholar]
- Fenichel EP, Horan RD, Hickling GJ. Management of infectious wildlife diseases: bridging conventional and bioeconomic approaches. Ecological Applications. 2010;20(4):903–914. doi: 10.1890/09-0446.1. [DOI] [PubMed] [Google Scholar]
- Finnoff D, Horan RD, McDermott SM, Sims C, Shogren JF. Economic Control of Invasive Species. In: Levin S, editor. Encyclopedia of Biodiversity. 2nd. San Diego: Cambridge University Press; 2012. [Google Scholar]
- Geoffard P, Philipson T. Disease eradication: private versus public vaccination. American Economic Review. 1997;87(1):222–230. [Google Scholar]
- Gersovitz M, Hammer JS. Infectious diseases, public policy, and the marriage of economics and epidemiology. The world bank research observer. 2003;18(2):129–157. [Google Scholar]
- Gersovitz M, Hammer JS. Tax/subsidy policies toward vector-borne infectious diseases. Journal of Public Economics. 2005;89(4):647–674. [Google Scholar]
- Goldman SM, Lightwood J. Cost optimization in the SIS model of infectious disease with treatment. Topics in Economic Analysis & Policy. 2002;2(1) [Google Scholar]
- Horan RD, Fenichel EP. Economics and ecology of managing emerging infectious animal diseases. American Journal of Agricultural Economics. 2007;89(5):1232–1238. [Google Scholar]
- Jones KE, Patel NG, Levy MA, Storeygard A, Balk D, Gittleman JL, Daszak P. Global trends in emerging infectious diseases. Nature. 2008;451(7181):990–993. doi: 10.1038/nature06536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kagan M. Climate Change Skepticism in the Face of Catastrophe. Tinbergen Institute Discussion Paper No 12-112/VIII 2012 [Google Scholar]
- Kamien MI, Schwartz NL. Optimal maintenance and sale age for a machine subject to failure. Management Science. 1971;17(8):B-495–B-504. [Google Scholar]
- Kamien MI, Schwartz NL. Dynamic Optimization: The Calculus of Variations and Optimal Control in Economics and Management. Amsterdam: Advanced Textbooks in Economics; 1991. [Google Scholar]
- Kim CS, Lubowski RN, Lewandrowski J, Eiswerth ME. Prevention or control: optimal government policies for invasive species management. Agricultural and Resource Economics Review. 2006;35(1):29–40. [Google Scholar]
- Léonard D. Co-state variables correctly value stocks at each instant A proof. Journal of Economic Dynamics and Control. 1987;11(1):117–122. [Google Scholar]
- McKibbin W, Sidorenko A. The Global Costs of an Influenza Pandemic. The Milken Institute Review of Economic Policy, third quarter. 2007:18–27. [Google Scholar]
- Meltzer MI, Cox NJ, Fukuda K. The economic impact of pandemic influenza in the United States: priorities for intervention. Emerging infectious diseases. 1999;5:659–671. doi: 10.3201/eid0505.990507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morens DM, Folkers GK, Fauci AS. The challenge of emerging and re-emerging infectious diseases. Nature. 2004;430(6996):242–249. doi: 10.1038/nature02759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morse SS, Mazet JA, Woolhouse M, Parrish CR, Carroll D, Karesh WB, Zambrana-Torrelio C, Lipkin WI, Daszak P. Prediction and prevention of the next pandemic zoonosis. The Lancet. 2012;380(9857):1956–1965. doi: 10.1016/S0140-6736(12)61684-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polasky S, De Zeeuw A, Wagener F. Optimal management with potential regime shifts. Journal of Environmental Economics and Management. 2011;62(2):229–240. [Google Scholar]
- Pontryagin LS, Boltyanskii VG. Mathematical Theory of Optimal Processes. New York: John Wiley & Sons Inc; 1962. [Google Scholar]
- Reed WJ. The effects of the risk of fire on the optimal rotation of a forest. Journal of Environmental Economics and Management. 1984;11(2):180–190. [Google Scholar]
- Reed WJ. Optimal preventive maintenance, protection, and replacement of a revenue-earning asset. Applied mathematics and computation. 1987a;24(3):241–261. [Google Scholar]
- Reed WJ. Protecting a forest against fire: optimal protection patterns and harvest policies. Natural Resource Modeling. 1987b;2(1):23–52. [Google Scholar]
- Reed WJ, Heras HE. The conservation and exploitation of vulnerable resources. Bulletin of Mathematical Biology. 1992;54(2):185–207. [Google Scholar]
- Rowthorn BRE, Toxvaerd F. The optimal control of infectious diseases via prevention and treatment. Working paper 2012 [Google Scholar]
- Smith DL, Johnson JA, Harris AD, Furuno JP, Perencevich EN, Morris JG., Jr Assessing risks for a pre-emergent pathogen: virginiamycin use and the emergence of streptogramin resistance in Enterococcus faecium. The Lancet infectious diseases. 2003;3(4):241–249. doi: 10.1016/s1473-3099(03)00581-4. [DOI] [PubMed] [Google Scholar]
- Stern N. The economics of climate change: the Stern review. Cambridge: Cambridge University press; 2007. [Google Scholar]
- Tahvonen O, Salo S. Nonconvexities in optimal pollution accumulation. Journal of Environmental Economics and Management. 1996;31(2):160–177. [Google Scholar]
- Taylor LH, Latham SM, Mark EJ. Risk factors for human disease emergence. Philosophical Transactions of the Royal Society of London, Series B: Biological Sciences. 2001;356(1411):983–989. doi: 10.1098/rstb.2001.0888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsur Y, Zemel A. Decentralization and Coordination of Water Resource Management. Springer; US: 1997. On event uncertainty and renewable resource management; pp. 283–298. [Google Scholar]
- Tsur Y, Zemel A. Sustainability and Diversity of Forest Ecosystems. Springer; Japan: 2007. Bio-economic resource management under threats of environmental catastrophes; pp. 431–438. [Google Scholar]
- Tsur Y, Zemel A. Regulating environmental threats. Environmental & Resource Economics. 2008;39(3):297–310. [Google Scholar]
- Tsur Y, Zemel A. Endogenous discounting and climate policy. Environmental and Resource Economics. 2009;44(4):507–520. [Google Scholar]
- Tsur Y, Withagen C. Preparing for catastrophic climate change. Journal of Economics. 2013;110(3):225–239. [Google Scholar]
- van der Ploeg F, de Zeeuw A. Oxcarre working papers. Oxford Centre for the Analysis of Resource Rich Economies; University of Oxford: 2013. Climate policy and catastrophic change: Be prepared and avert risk. [Google Scholar]
- Weiss RA, McMichael AJ. Social and environmental risk factors in the emergence of infectious diseases. Nature medicine. 2004;10:S70–S76. doi: 10.1038/nm1150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weitzman ML. On the Welfare Significance of National Product in a Dynamic Economy. Quarterly Journal of Economics. 1976;90:156–162. [Google Scholar]
- Weitzman ML. Gamma discounting. American Economic Review. 2001;91:260–271. [Google Scholar]