How to Distinguish Conformational Selection and Induced Fit Based on Chemical Relaxation Rates

Abstract

Protein binding often involves conformational changes. Important questions are whether a conformational change occurs prior to a binding event (‘conformational selection’) or after a binding event (‘induced fit’), and how conformational transition rates can be obtained from experiments. In this article, we present general results for the chemical relaxation rates of conformational-selection and induced-fit binding processes that hold for all concentrations of proteins and ligands and, thus, go beyond the standard pseudo-first-order approximation of large ligand concentration. These results allow to distinguish conformational-selection from induced-fit processes—also in cases in which such a distinction is not possible under pseudo-first-order conditions—and to extract conformational transition rates of proteins from chemical relaxation data.

Author Summary

The function of proteins is affected by their conformational dynamics, i.e. by transitions between lower-energy ground-state conformations and higher-energy excited-state conformations of the proteins. Advanced NMR and single-molecule experiments indicate that higher-energy conformations in the unbound state of proteins can be similar to ground-state conformations in the bound state, and vice versa. These experiments illustrate that the conformational change of a protein during binding may occur before a binding event, rather than being induced by this binding event. However, determining the temporal order of conformational transitions and binding events typically requires additional information from chemical relaxation experiments that probe the relaxation kinetics of a mixture of proteins and ligands into binding equilibrium. These chemical relaxation experiments are usually performed and analysed at ligand concentrations that are much larger than the protein concentrations. At such high ligand concentrations, the temporal order of conformational transitions and binding events can only be inferred in special cases. In this article, we present general equations that describe the dominant chemical relaxation kinetics for all protein and ligand concentrations. Our general equations allow to clearly infer from relaxation data whether a conformational transition occurs prior to a binding event, or after the binding event.

Introduction

Protein function often involves conformational changes during the binding to ligand molecules [1]. Advanced NMR experiments [2–7] and single-molecule spectroscopy [8–10] indicate that these conformational changes can occur without ligand, or with bound ligand and thus point to an intrinsic conformational dynamics of the proteins. An important question is how the conformational dynamics is coupled to the binding events. Two mechanisms for this coupling are ‘conformational selection’ [11] and ‘induced fit’ [12] (see Fig 1(a) and 1(b)). In conformational-selection binding, a conformational change occurs prior to the binding of a ligand molecule, as a conformational excitation from the unbound-ground state conformation of the protein. In this mechanism, the ligand seems to ‘select’ and stabilize a higher-energy conformation for binding. In induced-fit binding, the conformational change occurs after ligand binding and is a conformational relaxation into the bound ground-state conformation that is apparently ‘induced’ by the ligand. These two mechanisms are in particular plausible for small ligand molecules that can quickly ‘hop’ in and out of the protein binding pocket, i.e. that can enter and exit this binding pocket within transition times that are significantly smaller than the residence or dwell times of the proteins in the different conformations [13].

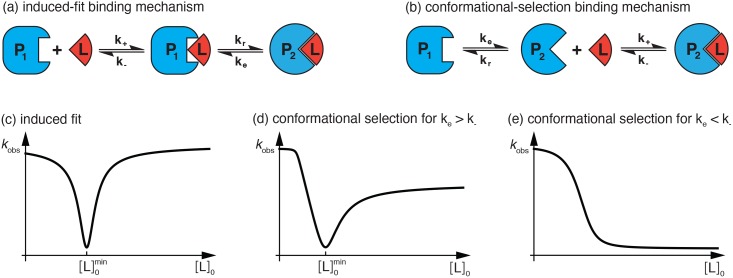
Fig 1. Characteristic chemical relaxation of induced-fit and conformational-selection binding.

(a) In induced-fit binding, the change between the conformations P₁ and P₂ of the protein occurs after binding of the ligand L. The intermediate state P₁L relaxes into the bound ground state P₂L with rate k_r, and is excited from the ground state with rate k_e. (b) In conformational-selection binding, the conformational change of the protein occurs prior to ligand binding. The intermediate state P₂ is excited from the unbound ground state P₁ with rate k_e, and relaxes back into the ground state with rate k_r. (c) The dominant, smallest relaxation rate k_obs of induced-fit binding is minimal at the total ligand concentration ${\left[\text{L}\right]}_0^{\text{min}}={\left[\text{P}\right]}_0-K_d$ where [P]₀ is the total protein concentration and K_d the overall dissociation constant. As a function of [L]₀, the dominant rate k_obs is symmetric with respect to this minimum. (d) The dominant, smallest relaxation rate k_obs of conformational-selection binding has a characteristic minimum as a function of [L]₀ for k_e > k₋, but is not symmetric with respect to this minimum. (e) The dominant rate k_obs of conformational-selection binding decreases monotonically with [L]₀ for k_e < k₋.

A central problem is to identify protein binding mechanisms based on experimental data [13–24]. Advanced NMR experiments and single-molecule spectroscopy can reveal higher-energy conformations that are necessary for conformational-selection or induced-fit binding, but do not directly indicate the binding mechanism because such higher-energy conformations may exist both in the bound and unbound state of the protein [4, 8]. In principle, both conformational-selection or induced-fit binding then are possible. Standard mixing or temperature-jump experiments that probe the chemical relaxation into the binding equilibrium can provide additional information that allows to identify the binding mechanism [22, 25–28]. Of particular interest is the dominant, slowest relaxation rate k_obs observed in the experiments, and how this rate depends on the total ligand concentration [L]₀ [22, 25, 28]. The chemical relaxation experiments are often performed and analysed under pseudo-first-oder conditions, i.e. at ligand concentrations that greatly exceed the protein concentrations [22, 25, 29–36]. In the case of induced-fit binding, the dominant relaxation rate k_obs increases monotonically with the ligand concentration [L]₀ under pseudo-first-oder conditions. In the case of conformational-selection binding, k_obs decreases monotonically with increasing [L]₀ for conformational excitation rates k_e < k₋, and increases monotonically with [L]₀ for k_e > k₋ where k₋ is the unbinding rate of the ligand from the bound ground-state conformation of the protein (see Fig 1(b)). A decrease of the dominant relaxation rate k_obs with increasing ligand concentration [L]₀ thus indicates conformational-selection binding [25]. However, an increase of k_obs with [L]₀ under pseudo-first-order conditions is possible both for induced-fit binding and conformational-selection binding and does not uniquely point towards a binding mechanism [22].

In this article, we present general analytical results for the dominant relaxation rate k_obs of induced-fit binding and conformational-selection binding processes that hold for all ligand and protein concentrations. Our general results are based on an expansion of the rate equations for these binding processes around the equilibrium concentrations of ligands and proteins, and include the pseudo-first-order results in the limit of large ligand concentrations. In the case of induced-fit binding, we find that k_obs exhibits a minimum at the total ligand concentration ${\left[\text{L}\right]}_0^{\text{min}}={\left[\text{P}\right]}_0-K_d$ for total protein concentrations [P]₀ that are larger than the overall dissociation constant K_d of the binding process. As a characteristic feature, the function k_obs([L]₀) for induced-fit binding is symmetric with respect to this minimum. At sufficiently large protein concentrations [P]₀, the function k_obs([L]₀) tends to identical values for small ligand concentrations [L]₀ ≪ [P]₀ and for large ligand concentrations [L]₀ ≫ [P]₀ because of its symmetry (see Fig 1(c)). In the case of conformational-selection binding, we find that k_obs exhibits a minimum for conformational excitation rates k_e > k₋ and sufficiently large protein concentrations [P]₀ (see Fig 1(d)). The location ${\left[\text{L}\right]}_0^{\text{min}}$ of this minimum depends on [P]₀, K_d, and the rates k_e and k₋ (see Eq (10) below). In contrast to induced-fit binding, the function k_obs([L]₀) for conformational-selection binding is not symmetric with respect to this minimum. At sufficiently large protein concentrations [P]₀, the function k_obs([L]₀) attains values for small ligand concentrations [L]₀ ≪ [P]₀ that can greatly exceed the values for large ligand concentrations [L]₀ ≫ [P]₀ (see Fig 1(d)). For excitation rates k_e < k₋ of conformational-selection binding processes, the dominant relaxation rate k_obs decreases monotonically with increasing ligand concentration [L]₀ (see Fig 1(e)). Our general results for the dominant relaxation rate k_obs of induced-fit and conformational-selection binding processes allow to clearly distinguish between these two binding mechanisms for sufficiently large protein concentrations [P]₀ (see Figs 2 and 3 below for numerical examples).

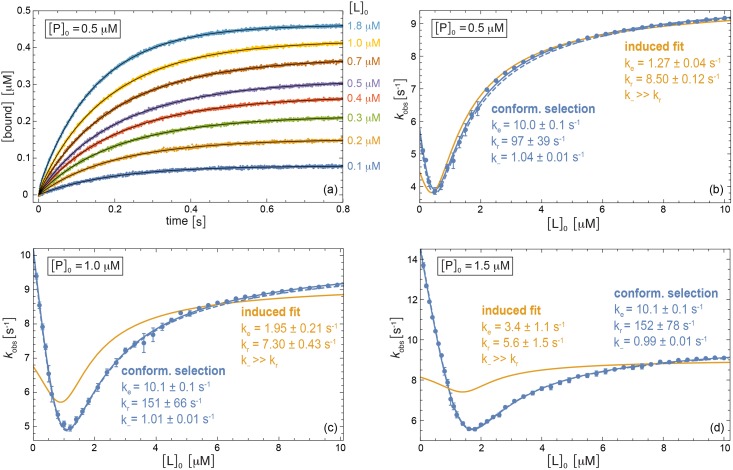
Fig 2. Numerical example for conformational-selection binding with the rate constants k_e = 10 s⁻¹, k_r = 100 s⁻¹, k₊ = 100 μM⁻¹s⁻¹, and k₋ = 1 s⁻¹.

(a) Relaxation data for the bound complex obtained by numerical integration of the rate equations and subsequent addition of Gaussian noise with amplitude 0.002 μM at the total protein concentration [P]₀ = 0.5 μM and exemplary total ligand concentrations [L]₀. The black lines represent multi-exponential fits of the data points. (b) to (d) Comparison of k_obs values obtained from multi-exponential fits of numerical relaxation data (points) to our theoretical results for k_obs (lines) at the three different total protein concentrations [P]₀ = 0.5 μM, 1.0 μM, and 1.5 μM and total ligand concentrations [L]₀ between 0.1 μM and 10 μM. The full lines represent fits of Eq (6) for conformational-selection binding (blue) and of Eq (1) for induced-fit binding (orange), with fit parameter values specified in the figure. In these fits, the dissociation constant K_d = 0.11 μM is assumed to be known from equilibrium data. The dashed blue lines are obtained from Eq (6) for the ‘true’ rate constants of the numerical example.

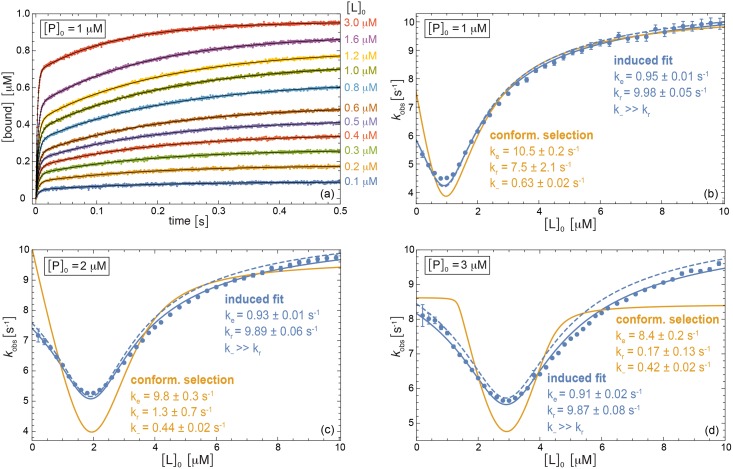
Fig 3. Numerical example for induced-fit binding with the rate constants k₊ = 100 μM⁻¹s⁻¹, k₋ = 100 s⁻¹, k_e = 1 s⁻¹, and k_r = 10 s⁻¹.

(a) Relaxation data for the bound complex obtained by numerical integration of the rate equations and subsequent addition of Gaussian noise with amplitude 0.004 μM at the total protein concentration [P]₀ = 1 μM and exemplary total ligand concentrations [L]₀. The black lines represent multi-exponential fits of the data points. (b) to (d) Comparison of k_obs values obtained from multi-exponential fits of numerical relaxation data (points) to our theoretical results for k_obs (lines) at the three different total protein concentrations [P]₀ = 1 μM, 2 μM, and 3 μM and total ligand concentrations [L]₀ between 0.1 μM and 10 μM. The full lines represent fits of Eq (1) for induced-fit binding (blue) and of Eq (6) for conformational-selection binding (orange), with fit parameter values specified in the figure. In these fits, the dissociation constant K_d = 1/11 μM is assumed to be known from equilibrium data. The dashed blue lines are obtained from Eq (1) for the ‘true’ rate constants of the numerical example.

Results

Solving the rate equations of the induced-fit and conformational-selection binding models shown in Fig 1(a) and 1(b) is complicated by the fact that the binding steps in these models are second-order reactions that depend on the product of the time-dependent concentrations of unbound proteins and unbound ligands. In the standard pseudo-first-order approximation, the rate equations are simplified by assuming that the total ligand concentration greatly exceeds the total protein concentration, so that the amount of ligand consumed during binding is negligible compared to the total amount of ligand. The concentration of the unbound ligand then can be taken to be constant, and the rate equations only contain terms that are linear in the time-dependent concentration of the protein, which makes them solvable. In our more general approach, a linearization of the rate equations is achieved by expanding around the equilibrium concentrations of the bound and unbound proteins and ligands (see Methods). This expansion captures the final relaxation into equilibrium, which is governed by the smallest, dominant relaxation rate k_obs, for all concentrations of proteins and ligands, and leads to general results for k_obs that include the results from the pseudo-first-order approximation in the limit of large ligand concentrations.

Dominant relaxation rate of induced-fit binding

Expanding the rate equations of the induced-fit binding mechanism shown in Fig 1(a) around the equilibrium concentrations of proteins and ligands leads to the dominant, smallest relaxation rate (see Methods)

$$k_{\text{obs}}=k_e+k_r+\frac{1}{2}\gamma -\frac{1}{2}\sqrt{{\gamma }^2+4k_{-}{k}_r}$$ (1)

with

$$\gamma =-k_e-k_r+k_{-}+k_{+}\left(\delta -K_d\right)$$ (2)

$$\delta =\sqrt{{\left({\left[\text{L}\right]}_0-{\left[\text{P}\right]}_0+K_d\right)}^2+4{\left[\text{P}\right]}_0{K}_d}$$ (3)

and with the overall dissociation constant

$$K_d=\frac{k_{-}{k}_e}{k_{+}(k_e+k_r)}$$ (4)

of induced-fit binding. This general result for k_obs holds for all total ligand concentrations [L]₀ and protein concentrations [P]₀. In the limit of large ligand concentrations [L]₀ ≫ [P]₀, we obtain δ ≃ [L]₀ + K_d and γ ≃ − k_e − k_r + k₋ + k₊[L]₀ from Eqs (2) and (3), which agrees with results derived in pseudo-first-order approximation [21, 22].

As a function of the total ligand concentration [L]₀, the dominant relaxation rate k_obs exhibits a minimum at

$${\left[\text{L}\right]}_0^{\text{min}}={\left[P\right]}_0-K_d$$ (5)

for total protein concentrations [P]₀ > K_d. The function k_obs([L]₀) is symmetric with respect to ${\left[\text{L}\right]}_0^{\text{min}}$ (see (Fig 1(c)). This symmetry and the location ${\left[\text{L}\right]}_0^{\text{min}}$ of the minimum result from the fact that k_obs depends on [L]₀ only via the term δ, which is minimal at ${\left[\text{L}\right]}_0^{\text{min}}$ and symmetric with respect to ${\left[\text{L}\right]}_0^{\text{min}}$. The dominant relaxation rate k_obs is minimal when δ is minimal. For large ligand concentrations [L]₀, k_obs tends towards the maximum value k_e + k_r as in pseudo-first-order approximation. The location ${\left[\text{L}\right]}_0^{\text{min}}$ of the minimum and the symmetry of the function k_obs([L]₀) with respect to this minimum are properties that the induced-fit binding model appears to ‘inherit’ from the elementary binding model P + L ⇌ PL (see Eq (46) in Methods section). However, the function k_obs([L]₀) of the elementary binding model is V-shaped and does not tend to a constant maximum value for large ligand concentrations [L]₀.

Dominant relaxation rate of conformational-selection binding

For the conformational-selection binding mechanism shown in Fig 1(b), an expansion of the rate equations around the equilibrium concentrations of proteins and ligands leads to the dominant, smallest relaxation rate (see Methods)

$$k_{\text{obs}}=k_e+\frac{1}{2}\alpha -\frac{1}{2}\sqrt{{\alpha }^2+\beta }$$ (6)

with

$$\alpha =k_r-k_e+\frac{k_{-}\left((2k_e+k_r)\delta +k_r\left({\left[L\right]}_0-{\left[P\right]}_0-K_d\right)\right)}{2k_e{K}_d}$$ (7)

$$\beta =2k_r\left(2k_e-k_{-}-\frac{k_{-}\left(\delta -{\left[L\right]}_0+{\left[P\right]}_0\right)}{K_d}\right)$$ (8)

and δ as in Eq (3), and with the overall dissociation constant

$$K_d=\frac{k_{-}(k_e+k_r)}{k_{+}{k}_e}$$ (9)

of conformational-selection binding. This general result for k_obs holds for all total ligand concentrations [L]₀ and protein concentrations [P]₀. In the limit of large ligand concentrations [L]₀ ≫ [P]₀, we obtain α ≃ − k_e + k_r + k₋ + k₊[L]₀ and β ≃ 4k_r(k_e − k₋) from Eqs (3), (7) and (8), in agreement with results derived in pseudo-first-order approximation [21, 22].

For conformational-selection binding, the shape of the function k_obs([L]₀) depends on the values of the conformational excitation rate k_e and the unbinding rate k₋ (see Fig 1(d) and 1(e)). For k_e < k₋, the dominant relaxation rate k_obs decreases monotonically with increasing total ligand concentration [L]₀. For k_e > k₋, the dominant relaxation rate k_obs exhibits a minimum as a function of [L]₀ at sufficiently large total protein concentrations [P]₀. The minimum is located at (see Methods)

$${\left[\text{L}\right]}_0^{min}\simeq \frac{k_e+k_{-}}{k_e-k_{-}}{\left[\text{P}\right]}_0-K_d$$ (10)

if the conformational relaxation rate k_r is much larger than the excitation rate k_e, which typically holds for the conformational exchange between ground-state and excited-state conformations of proteins. In contrast to induced-fit binding, the function k_obs([L]₀) is not symmetric with respect to this minimum. For large ligand concentrations, the limiting value of the dominant relaxation rate is k_obs(∞) = k_e as in pseudo-first-order approximation. For vanishing ligand concentrations [L]₀ → 0, the limiting value is k_obs(0) = k_e + k_r for total protein concentrations [P]₀ > K_d(k_e + k_r − k₋)/k₋ and k_obs(0) = k₋([P]₀ + K_d)/K_d for [P]₀ < K_d(k_e + k_r − k₋)/k₋.

Distinguishing induced fit and conformational selection

The general results for the dominant relaxation rate k_obs presented in the previous sections allow to clearly distinguish induced-fit from conformational-selection binding processes. In Fig 2, we consider a conformational-selection binding process with the rate constants k_e = 10 s⁻¹, k_r = 100 s⁻¹, k₊ = 100 μM⁻¹s⁻¹, and k₋ = 1 s⁻¹ as a numerical example. The data points in Fig 2(a) represent relaxation curves for the bound complex that have been generated by numerical integration of the rate equations and subsequent addition of Gaussian noise to mimic measurement errors. The black lines in Fig 2(a) are multi-exponential fits of the data points. The number of exponentials in these fits has been determined with the Akaike information criterion (AIC), which is a standard criterion for the trade-off between quality of fit and number of fit parameters, and ranges from 2 to 4. The data points in Fig 2(b) to 2(d) represent the dominant relaxation rates k_obs that are obtained from multi-exponential fits of relaxation curves for different total ligand concentrations [L]₀ and total protein concentrations [P]₀. The dominant relaxation rate k_obs here is identified as the smallest relaxation rate of a multi-exponential fit. The full blue lines in Fig 2(b) to 2(d) result from fitting our general result Eq (6) for conformational-selection binding to the k_obs data points. The full orange lines represent fits of our general result Eq (1) for induced-fit binding. For all fits, we assume that the dissociation constant K_d = 0.11 μM is known from equilibrium data, and use k_e, k_r, and k₋ as fit parameters. Finally, the blue dashed lines in Fig 2(b) to 2(d) are the k_obs curves obtained from Eq (6) for the ‘true’ rate constants of the conformational-selection binding process given above. These dashed lines agree with the data points, which indicates that the k_obs values from multi-exponential fits as in Fig 2(a) are identical to the values obtained from Eq (6) within the statistical errors of the numerical example.

The fits in Fig 2(b) to 2(d) clearly identify conformational selection as the correct binding mechanism in this example. The blue fit curves for conformational selection agree with the data points within statistical errors, while the orange fit curves for induced fit deviate from the data. For conformational-selection binding, the fit values of the conformational transition rates k_e and k_r and of the unbinding rate k₋ specified in the figure agree with the correct values k_e = 10 s⁻¹, k_r = 100 s⁻¹, and k₋ = 1 s⁻¹ of the numerical example within statistical errors.

In Fig 3, we consider an induced-fit binding process with rate constants k₊ = 100 μM⁻¹s⁻¹, k₋ = 100 s⁻¹, k_e = 1 s⁻¹, and k_r = 10 s⁻¹ as a second numerical example. The k_obs data points in Fig 3(b) to 3(d) are again obtained from multi-exponential fits of relaxation curves that have been generated by numerical integration of the rate equations and subsequent addition of Gaussian noise (see Fig 3(a)). The fits in Fig 3(b) to 3(d) clearly identify induced-fit binding as the correct mechanism in this example. The full blue curves that represent fits of Eq (1) for induced-fit binding are in overall agreement with the k_obs points, while the orange fit curves of Eq (6) for conformational-selection binding deviate from the data. The fit values of the conformational transition rates k_e and k_r for the induced-fit binding model are in good agreement with the correct values k_e = 1 s⁻¹, and k_r = 10 s⁻¹ of the example. The dashed blue curves in Fig 3(b) to 3(d), which are obtained from Eq (1) for the ‘true’ rate constants of the induced-fit binding process, are in overall agreement with the data points. Slight deviations result from the fact that the amplitude of the slow relaxation mode with rate k_obs is rather small compared to the amplitude of the fast modes (see Fig 3(a)), which can lead to numerical inaccuracies.

In both numerical examples of Figs 2 and 3, the correct binding mechanism cannot be identified under pseudo-first-order conditions because k_obs is monotonically increasing with [L]₀ for ligand concentrations that greatly exceed the protein concentration [P]₀ [22].

Analysis of chemical relaxation rates for recoverin binding

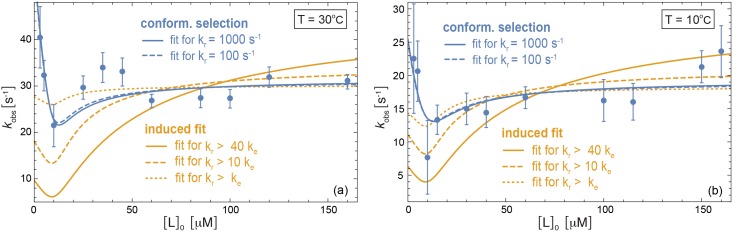
Chakrabarti et al. [28] have recently investigated the conformational dynamics and binding kinetics of the protein recoverin with chemical relaxation and advanced NMR experiments. Recoverin exhibits a conformational change during binding of its ligand, which is a rhodopsin kinase peptide fused to the B1 domain of immunoglobulin protein G in the experiments of Chakrabarti et al. [28]. The data points in Fig 4 represent the dominant relaxation rates k_obs obtained by Chakrabarti et al. from relaxation experiments at the temperatures 30°C and 10°C for a recoverin concentration of 10 μM. The lines in Fig 4 result from fitting our general results Eqs (1) and (6) for the dominant relaxation rate k_obs of induced-fit and conformational-selection binding processes. In these fits, we have used the values K_d = 1.0 ± 0.2 μM and K_d = 1.8 ± 0.2 μM obtained by Chakrabarti et al. from isothermal titration calometry experiments at 30°C and 10°C, which reduces the parameters to k_e, k_r, and k₋. The fits of our general result Eq (6) for conformational-selection binding are rather insensitive to the relaxation rate k_r, which is illustrated in Fig 4 by nearly identical fits for k_r = 100 s⁻¹ and k_r = 1000 s⁻¹ (see dashed and full blue lines). Our fit values for the conformational excitation rate k_e specified in the figure caption agree with the values k_e = 33 ± 5 s⁻¹ and k_e = 23 ± 5 s⁻¹ obtained by Chakrabarti et al. from advanced NMR experiments at 30°C and 10°C, respectively. From these experiments, Chakrabarti et al. obtain the values k_r = 990 ± 100 s⁻¹ and k_r = 920 ± 200 s⁻¹ at 30°C and 10°C, which cannot be deduced from our fits of the k_obs data because these fits are insensitive to k_r. The NMR experiments indicate that the higher-energy conformation of unbound recoverin resembles the ground-state conformation of bound recoverin [28] as required for the conformational-selection binding mechanism illustrated in Fig 1(b), and that the excited-state conformation of unbound recoverin has the equilibrium occupancy P_e = k_e/(k_r + k_e) = 3.2% ± 0.5% at 30°C and P_e = 2.4% ± 0.7% at 10°C, relative to the ground-state conformation.

Fig 4. Analysis of experimentally determined relaxation rates k_obs for the binding of recoverin to a rhodopsin kinase peptide ligand.

The data points represent results of Chakrabarti et al. [28] obtained from chemical relaxation experiments at the temperatures 30°C and 10°C for a recoverin concentration of 10 μM. The blue lines result from fits of Eq (6) for conformational-selection binding with the values k_r = 1000 s⁻¹ (full) and k_r = 100 s⁻¹ (dashed) of the conformational relaxation rate. At 30°C, the parameter values obtained from fitting are k_e = 31.5 ± 0.8 s⁻¹ and k₋ = 5.1 ± 0.4 s⁻¹ for k_r = 1000 s⁻¹, and k_e = 31.1 ± 0.8 s⁻¹ and k₋ = 5.0 ± 0.4 s⁻¹ for k_r = 100 s⁻¹. At 10°C, the fit parameter values are k_e = 19.3 ± 1.4 s⁻¹ and k₋ = 3.9 ± 0.7 s⁻¹ for k_r = 1000 s⁻¹, and k_e = 19.0 ± 1.3 s⁻¹ and k₋ = 3.8 ± 0.7 s⁻¹ for k_r = 100s⁻¹. The yellow lines represent fits of Eq (1) for induced-fit binding with constraints on the conformational excitation and relaxation rates k_e and k_r. At 30°C, the obtained fit values for the conformational exchange rates are k_e = k_r = 15 ± 10 s⁻¹ for the constraint k_r > k_e, k_e = 3.1 ± 1.9 s⁻¹ and k_r = 31 ± 4s⁻¹ for the constraint k_r > 10k_e, and k_e = 1.1 ± 0.8 s⁻¹ and k_r = 44 ± 8 s⁻¹ for k_r > 40k_e. At 10°C, the fit values are k_e = 4.5 ± 4.0 s⁻¹ and k_r = 14 ± 10 s⁻¹ for the constraint k_r > k_e, k_e = 1.9 ± 1.5 s⁻¹ and k_r = 19 ± 5 s⁻¹ for k_r > 10k_e, and k_e = 0.7 ± 0.5 s⁻¹ and k_r = 28 ± 11 s⁻¹ for k_r > 40k_e. In all fits of Eq (1) for induced-fit binding, we obtain k₋ ≫ k_r, i.e. the fit values of the unbinding rate k₋ are much larger than the conformational relaxation rate k_r and cannot be specified.

Fits of our general result Eq (1) for the dominant relaxation rate k_obs of induced-fit binding with unconstrained parameters k_e, k_r, and k₋ lead to fit values for the conformational exchange rates k_e and k_r with k_e ≫ k_r. For such values of k_e and k_r, the conformation 1 of the induced-fit binding model illustrated in Fig 1(a) is the ground-state conformation both for the unbound state and the bound state of recoverin, which contradicts the experimental observation that recoverin changes its conformation during binding [28]. Distinct ground-state conformations for the unbound and bound state of recoverin can be enforced by constraining k_r to values larger than k_e. The yellow lines in Fig 4 result from fits with the constraints k_r > k_e, k_r > 10k_e, and k_r > 40k_e. These constraints correspond to equilibrium occupancies P_e of the excited-state conformation of bound recoverin with P_e < 50%, P_e < 9.1%, and P_e < 2.4%, respectively. The fits of Eq (1) for induced-fit binding with the constraints k_r > 10k_e and k_r > 40k_e deviate rather strongly from the two data points with the smallest ligand concentrations [L]₀ = 3 μM and 5 μM, in contrast to fits of Eq (6) for conformational-selection binding (blue lines). A Bayesian model comparison of conformational-selection binding and induced-fit binding based on Eqs (1) and (6) leads to Bayes factors of 9.8 ⋅ 10¹³ and 1.5 ⋅ 10²³ at 30°C for the constraints k_r > 10k_e and k_r > 40k_e, and to Bayes factors of 4.2 ⋅ 10³ and 9.6 ⋅ 10⁹ at 10°C for k_r > 10k_e, and k_r > 40k_e, respectively (see Methods for details). These Bayes factors indicate that the k_obs data of Fig 4 strongly point towards conformational-selection binding. Bayes factors larger than 10² are generally considered to be decisive [37]. For the bound recoverin complex, Chakrabarti et al. did not observe an excited-state conformation in NMR experiments, which limits the excited-state occupancy P_e to undetectable values smaller than 1% for a conformational exchange that is fast compared to the NMR timescale as in the case of unbound recoverin. The analysis of the experimental data for the dominant relaxation rate k_obs of recoverin binding based on our general results Eqs (1) and (6) thus indicates a conformational-selection binding mechanism, in agreement with a numerical analysis of Chakrabarti et al. [28]. In this numerical analysis, Chakrabarti et al. include the chemical relaxation data for recoverin binding, additional relaxation data from dilution experiments, the values for the conformational exchange rates k_e and k_r obtained from NMR experiments, and the K_d values deduced from isothermal titration calometry [28]. In contrast, our analysis of the k_obs data in Fig 4 from the chemical relaxation experiments of recoverin binding only includes the K_d values from isothermal titration calometry as additional input.

Discussion

We have shown here that the dominant rate k_obs of chemical relaxation experiments with total protein and ligand concentrations of comparable magnitude conveys information on the binding mechanism and conformational transition rates of proteins. For sufficiently large protein concentrations [P]₀, the function k_obs([L]₀) obtained from such experiments has characteristic features that are clearly distinct for induced-fit binding and conformational-selection binding. The function k_obs([L]₀) of induced-fit binding exhibits a characteristic symmetry around a minimum and tends to identical values for small and large ligand concentrations [L]₀ as in Fig 1(c) if the protein concentration [P]₀, which determines the location of the minimum, is sufficiently large. In contrast, the function k_obs([L]₀) of conformational-selection binding is either monotonically decreasing for k_e < k₋, or asymmetric around a minimum for k_e > k₋. In both cases, k_obs([L]₀) tends for small ligand concentrations [L]₀ to values that exceed the values for large ligand concentrations as in Fig 1(d) and 1(e) if the protein concentration [P]₀ is sufficiently large.

Our general results for the dominant rate k_obs of chemical relaxation experiments thus provide a transparent route to distinguish induced-fit binding from conformational-selection binding based on the shape of the function k_obs([L]₀), and to infer conformational transition rates from fitting. Alternatively, these binding mechanisms can be identified from a numerical analysis of time-dependent relaxation curves [26–28], based on steric effects that may prohibit ligand entry and exit in the bound ground-state conformation of the protein and, thus, rule out conformational-selection binding [15], from a comparison of conformational excitation rates to overall, effective binding and unbinding rates [4, 13], or from the effect of distal mutations that mainly affect the conformational exchange, but not the binding kinetics in different protein conformations [13, 16, 21, 38]. Of particular interest is how such mutations change the overall binding and unbinding rates. If both conformational-selection and induced-fit binding are viable, increasing the ligand concentration may shift the binding mechanism from conformational selection to induced fit [16, 18, 26, 39, 40].

Methods

Near-equilibrium relaxation of induced-fit binding

The induced-fit binding model of Fig 1(a) leads to the four rate equations

$$\frac{\mathrm{d}}{\mathrm{d}t}\left[{\mathrm{P}}_1\right]=-k_{+}\left[{\mathrm{P}}_1\right]\left[\mathrm{L}\right]+k_{-}\left[{\mathrm{P}}_1\mathrm{L}\right]$$ (11)

$$\frac{\mathrm{d}}{\mathrm{d}t}\left[\mathrm{L}\right]=-k_{+}\left[{\mathrm{P}}_1\right]\left[\mathrm{L}\right]+k_{-}\left[{\mathrm{P}}_1\mathrm{L}\right]$$ (12)

$$\frac{\mathrm{d}}{\mathrm{d}t}\left[{\mathrm{P}}_1\mathrm{L}\right]=k_{+}\left[{\mathrm{P}}_1\right]\left[\mathrm{L}\right]-k_{-}\left[{\mathrm{P}}_1\mathrm{L}\right]+k_e\left[{\mathrm{P}}_2\mathrm{L}\right]-k_r\left[{\mathrm{P}}_1\mathrm{L}\right]$$ (13)

$$\frac{\mathrm{d}}{\mathrm{d}t}\left[{\mathrm{P}}_2\mathrm{L}\right]=k_r\left[{\mathrm{P}}_1\mathrm{L}\right]-k_e\left[{\mathrm{P}}_2\mathrm{L}\right]$$ (14)

that describe the time-dependent evolution of the concentration [P₁] of the unbound protein, the concentration [L] of the unbound ligand, and the concentrations [P₁L] and [P₂L] of the bound complexes. These four rate equations are redundant because the total concentrations [P]₀ and [L]₀ of proteins and ligands are conserved:

$$\left[{\mathrm{P}}_1\mathrm{L}\right]+\left[{\mathrm{P}}_2\mathrm{L}\right]+\left[{\mathrm{P}}_1\right]={\left[\mathrm{P}\right]}_0$$ (15)

$$\left[\mathrm{L}\right]+\left[{\mathrm{P}}_1\mathrm{L}\right]+\left[{\mathrm{P}}_2\mathrm{L}\right]={\left[\mathrm{L}\right]}_0$$ (16)

With Eqs (15) and (16), the concentrations [P₁] and [P₁L] can be expressed in terms of [L] and [P₂L], which results in the two non-redundant rate equations

$$\frac{\mathrm{d}}{\mathrm{d}t}\left[\mathrm{L}\right]=-k_{+}(\left[\mathrm{L}\right]-{\left[\mathrm{L}\right]}_0+{\left[\mathrm{P}\right]}_0)\left[\mathrm{L}\right]+k_{-}({\left[\mathrm{L}\right]}_0-\left[\mathrm{L}\right]-\left[{\mathrm{P}}_2\mathrm{L}\right])$$ (17)

$$\frac{\mathrm{d}}{\mathrm{d}t}\left[{\mathrm{P}}_2\mathrm{L}\right]=k_r({\left[\mathrm{L}\right]}_0-\left[\mathrm{L}\right]-\left[{\mathrm{P}}_2\mathrm{L}\right])-k_e\left[{\mathrm{P}}_2\mathrm{L}\right]$$ (18)

These rate equations can be written in the vectorial form

$$\frac{\mathrm{d}}{\mathrm{d}t}\mathbf{c}=\mathbf{F}\left(\mathbf{c}\right)$$ (19)

with

$$\mathbf{c}\left(t\right)\equiv \left(\begin{array}{c}\left[\mathrm{L}\right]\left(t\right)\\ [{\mathrm{P}}_2\mathrm{L}]\left(t\right)\end{array}\right)$$ (20)

The two components of the vector F(c) in Eq (19) are the right-hand sides of the Eqs (17) and (18). The rate equations describe the temporal evolution of the concentrations [L] and [P₂L] towards equilibrium, and are nonlinear because of the quadratic term in [L] on the right-hand side of Eq (17).

To obtain linearized versions of the rate equations that describe the slow processes corresponding to the final relaxation into equilibrium, we expand the vector F(c) in Eq (19) around the equilibrium concentrations c_eq:

$$\mathbf{F}\left(\mathbf{c}\right)=\mathbf{F}({\mathbf{c}}_{\text{eq}}+\Delta \mathbf{c})\simeq \mathbf{F}\left({\mathbf{c}}_{\text{eq}}\right)+J\left({\mathbf{c}}_{\text{eq}}\right)\Delta \mathbf{c}=J\left({\mathbf{c}}_{\text{eq}}\right)\Delta \mathbf{c}$$ (21)

Here, J is the Jacobian matrix of F with elements J_ij = ∂F_i/∂c_j. The right-hand side of Eq (21) follows from F(c_eq) = 0. Inserting the expansion (21) into Eq (19) and making use of $\frac{\mathrm{d}}{\mathrm{d}t}\mathbf{c}=\frac{\mathrm{d}}{\mathrm{d}t}({\mathbf{c}}_{\text{eq}}+\Delta \mathbf{c})=\frac{\mathrm{d}}{\mathrm{d}t}\Delta \mathbf{c}$ leads to the linearized rate equations

$$\frac{\mathrm{d}}{\mathrm{d}t}\Delta \mathbf{c}=J\left({\mathbf{c}}_{\text{eq}}\right)\Delta \mathbf{c}$$ (22)

with

$$J\left({\mathbf{c}}_{\text{eq}}\right)=\left(\begin{array}{cc}{k}_{+}\left({\left[\mathrm{L}\right]}_0-2{\left[\mathrm{L}\right]}_{\text{eq}}-{\left[\mathrm{P}\right]}_0\right)-k_{-}& -k_{-}\\ -k_r& -k_e-k_r\end{array}\right)$$ (23)

and the equilibrium concentration of the unbound ligand

$${\left[\mathrm{L}\right]}_{\text{eq}}=\frac{1}{2}\left({\left[\mathrm{L}\right]}_0-{\left[\mathrm{P}\right]}_0-K_d+\sqrt{{\left({\left[\mathrm{L}\right]}_0-{\left[\mathrm{P}\right]}_0+K_d\right)}^2+4{\left[\mathrm{P}\right]}_0{K}_d}\right)$$ (24)

The overall dissociation constant K_d of the induced-fit binding process is given in Eq (4). The relaxation rates of the linearized rate Eq (22) are the two eigenvalues of the matrix −J(c_eq). These eigenvalues are k_obs given in Eq (1) and

$$k_2=k_e+k_r+\frac{1}{2}\gamma +\frac{1}{2}\sqrt{{\gamma }^2+4k_{-}{k}_r}$$ (25)

with γ and δ given in Eqs (2) and (3). The relaxation rate k_obs is smaller than k₂ and, thus, dominates the final relaxation into equilibrium.

Near-equilibrium relaxation of conformational-selection binding

The four rate equations of the conformational-selection binding model of Fig 1(b) are

$$\frac{\mathrm{d}}{\mathrm{d}t}\left[{\mathrm{P}}_1\right]=-k_e\left[{\mathrm{P}}_1\right]+k_r\left[{\mathrm{P}}_2\right]$$ (26)

$$\frac{\mathrm{d}}{\mathrm{d}t}\left[{\mathrm{P}}_2\right]=k_e\left[{\mathrm{P}}_1\right]-k_r\left[{\mathrm{P}}_2\right]+k_{-}\left[{\mathrm{P}}_2\mathrm{L}\right]-k_{+}\left[{\mathrm{P}}_2\right]\left[\mathrm{L}\right]$$ (27)

$$\frac{\mathrm{d}}{\mathrm{d}t}\left[\mathrm{L}\right]=k_{-}\left[{\mathrm{P}}_2\mathrm{L}\right]-k_{+}\left[{\mathrm{P}}_2\right]\left[\mathrm{L}\right]$$ (28)

$$\frac{\mathrm{d}}{\mathrm{d}t}\left[{\mathrm{P}}_2\mathrm{L}\right]=-k_{-}\left[{\mathrm{P}}_2\mathrm{L}\right]+k_{+}\left[{\mathrm{P}}_2\right]\left[\mathrm{L}\right]$$ (29)

The total concentrations [L]₀ and [P]₀ of the ligands and proteins are conserved:

$$\left[\mathrm{L}\right]+\left[{\mathrm{P}}_2\mathrm{L}\right]={\left[\mathrm{L}\right]}_0$$ (30)

$$\left[{\mathrm{P}}_1\right]+\left[{\mathrm{P}}_2\right]+\left[{\mathrm{P}}_2\mathrm{L}\right]={\left[\mathrm{P}\right]}_0$$ (31)

With these equations, the concentrations [P₁] and [P₂L] can be expressed in terms of [L] and [P₂], which leads to the two rate equations

$$\frac{\mathrm{d}}{\mathrm{d}t}\left[{\mathrm{P}}_2\right]=k_e\left({\left[\text{P}\right]}_0-\left[{\text{P}}_2\right]\right)-(k_r+k_{+}\left[\mathrm{L}\right])\left[{\text{P}}_2\right]+(k_{-}-k_e)({\left[\mathrm{L}\right]}_0-\left[\mathrm{L}\right])$$ (32)

$$\frac{\mathrm{d}}{\mathrm{d}t}\left[\mathrm{L}\right]=k_{-}({\left[\mathrm{L}\right]}_0-\left[\mathrm{L}\right])-k_{+}\left[{\mathrm{P}}_2\right]\left[\mathrm{L}\right]$$ (33)

These rate equations can be written in the vectorial form of Eq (19) with

$$\mathbf{c}\left(t\right)\equiv \left(\begin{array}{c}\left[{\mathrm{P}}_2\right]\left(t\right)\\ \left[\mathrm{L}\right]\left(t\right)\end{array}\right)$$ (34)

and with a vector F(c) that contains the right-hand sides of the Eqs (32) and (33) as components. An expansion of the vector F(c) around the equilibrium concentrations c_eq leads to Eq (22) with the Jacobian matrix

$$J\left({\mathbf{c}}_{\text{eq}}\right)=-\left(\begin{array}{cc}{k}_r+k_e+k_{+}{\left[\mathrm{L}\right]}_{\text{eq}}& -k_e+k_{-}+k_{+}{\left[{\mathrm{P}}_2\right]}_{\text{eq}}\\ k_{+}{\left[\mathrm{L}\right]}_{\text{eq}}& k_{-}+k_{+}{\left[{\mathrm{P}}_2\right]}_{\text{eq}}\end{array}\right)$$ (35)

and the equilibrium concentrations

$${\left[{\mathrm{P}}_2\right]}_{\text{eq}}=\frac{1}{2K_d}\frac{k_{-}}{k_{+}}\left({\left[\mathrm{P}\right]}_0-{\left[\mathrm{L}\right]}_0-K_d+\sqrt{{({\left[\mathrm{P}\right]}_0-{\left[\mathrm{L}\right]}_0-K_d)}^2+4K_d{\left[\mathrm{P}\right]}_0}\right)$$ (36)

$${\left[\mathrm{L}\right]}_{\text{eq}}=\frac{1}{2}\left({\left[\mathrm{L}\right]}_0-{\left[\mathrm{P}\right]}_0-K_d+\sqrt{{({\left[\mathrm{P}\right]}_0-{\left[\mathrm{L}\right]}_0-K_d)}^2+4K_d{\left[\mathrm{P}\right]}_0}\right)$$ (37)

The overall dissociation constant K_d of the conformational-selection binding process is given in Eq (9). The relaxation rates of the linearized rate equations are the two eigenvalues of the matrix −J(c_eq). These eigenvalues are k_obs given in Eq (6) and

$$k_2=k_e+\frac{1}{2}\alpha +\frac{1}{2}\sqrt{{\alpha }^2+\beta }$$ (38)

with α and β given in Eqs (7) and (8). The relaxation rate k_obs is smaller than k₂ and therefore dominates the final relaxation into equilibrium.

To derive Eq (10) for the location of the minimum of k_obs as a function of the total ligand concentration [L]₀, we now consider the near-equilibrium relaxation of the conformational-selection model in quasi-steady-state approximation (qssa), which assumes that the concentration of the intermediate [P₂] does not change in time. The left-hand side of Eq (32) then is equal to zero, and the two Eqs (32) and (33) reduce to the single equation

$$\frac{\mathrm{d}}{\mathrm{d}t}\left[\mathrm{L}\right]=-k_e{k}_{-}\frac{\left(\left[\mathrm{L}\right]+K_d\right)\left(\left[\mathrm{L}\right]-{\left[\mathrm{L}\right]}_0\right)+\left[\mathrm{L}\right]{\left[\mathrm{P}\right]}_0}{k_{-}\left[\mathrm{L}\right]+k_e{K}_d}=f\left(\left[\mathrm{L}\right]\right)$$ (39)

An expansion of the function f([L]) around the equilibrium concentration [L]_eq leads to the linear equation $\mathrm{d}\left[\mathrm{L}\right]/\mathrm{d}t\simeq -k_{\text{obs}}^{\text{(qssa)}}(\left[\mathrm{L}\right]-{\left[\mathrm{L}\right]}_{\text{eq}})$ with

$$k_{\text{obs}}^{\text{(qssa)}}=-\frac{\mathrm{d}f\left(\right[\mathrm{L}\left]\right)}{\mathrm{d}\left[\mathrm{L}\right]}{|}_{\left[\mathrm{L}\right]={\left[\mathrm{L}\right]}_{\text{eq}}}=\frac{k_{-}{k}_e\delta }{k_e{K}_d+k_{-}{\left[\mathrm{L}\right]}_{\text{eq}}}$$ (40)

and δ and [L]_eq given in Eqs (3) and (37). The derivative of $k_{\text{obs}}^{\text{(qssa)}}$ is zero at ${\left[\mathrm{L}\right]}_0={\left[\mathrm{L}\right]}_0^{\text{min}}$ with ${\left[\mathrm{L}\right]}_0^{\text{min}}$ given in Eq (10). In general, the quasi-steady-state result $k_{\text{obs}}^{\text{(qssa)}}$ is a good approximation of k_obs if the rates for the transitions out of the intermediate state P₂ of conformational-selection binding are much larger than the rates for the transitions to P₂. A numerical analysis shows that the location ${\left[\mathrm{L}\right]}_0^{\text{min}}$ of the minimum of $k_{\text{obs}}^{\text{(qssa)}}\left(\left[\mathrm{L}\right]\right)$ is in good agreement with the location of the minimum of k_obs([L]) for conformational transitions rates with k_r ≫ k_e.

Multi-exponential relaxation

In the numerical examples illustrated in Figs 2 and 3, chemical relaxation curves for conformational-selection and induced-fit binding are fitted with a multi-exponential model. Such multi-exponential models are an adequate description for the time evolution of concentrations in first-order chemical reactions. However, the binding steps of the induced-fit and conformational-selection models of Fig 1(a) and 1(b) are of second order. To justify that multi-exponential models can also be used to approximate the chemical relaxation of second-order reactions, we consider here the elementary binding model

$$\text{P}+\text{L}\underset{k_{-}}{\overset{k_{+}[\text{P}][\text{L}]}{\rightleftharpoons }}\text{PL}$$ (41)

of a protein P and ligand L. For the initial condition [PL](0) = 0, the rate equation of the elementary binding model can be written as

$$\frac{\mathrm{d}}{\mathrm{d}t}\left[\text{PL}\right]=k_{+}\left({\left[\mathrm{P}\right]}_0-\left[\text{PL}\right]\right)\left({\left[\mathrm{L}\right]}_0-\left[\text{PL}\right]\right)-k_{-}\left[\text{PL}\right]$$ (42)

and has the analytical solution [38]

$$\left[\text{PL}\right]\left(t\right)=-\frac{{\lambda }_1\left({\mathrm{e}}^{({\lambda }_1-{\lambda }_2)t}-1\right)}{k_{\text{+}}\left({\mathrm{e}}^{({\lambda }_1-{\lambda }_2)t}-{\lambda }_1/{\lambda }_2\right)}$$ (43)

with

$${\lambda }_{1,2}=-\frac{1}{2}{k}_{+}\left({\left[\mathrm{P}\right]}_0+{\left[\mathrm{L}\right]}_0+K_d\pm \sqrt{{\left({\left[\mathrm{P}\right]}_0+{\left[\mathrm{L}\right]}_0+K_d\right)}^2-4{\left[\mathrm{P}\right]}_0{\left[\mathrm{L}\right]}_0}\right)$$ (44)

where K_d = k₋/k₊ is the dissociation constant of the elementary binding model.

We first show that λ₂ − λ₁ is identical to the dominant relaxation rate k_obs obtained from a linear expansion around equilibrium. An expansion of the right-hand side of Eq (42) around the equilibrium concentration

$${\left[\text{PL}\right]}_{\text{eq}}=\frac{1}{2}\left({\left[\mathrm{P}\right]}_0+{\left[\mathrm{L}\right]}_0+K_d-\sqrt{{({\left[\mathrm{L}\right]}_0-{\left[P\right]}_0+K_d)}^2+4K_d{\left[P\right]}_0}\right)$$ (45)

leads to the linear equation d[PL]/dt ≃ −k_obs([PL] − [PL]_eq) with

$$k_{\text{obs}}=k_{+}\sqrt{{({\left[\mathrm{L}\right]}_0-{\left[P\right]}_0+K_d)}^2+4K_d{\left[P\right]}_0}$$ (46)

This dominant relaxation rate k_obs is identical to λ₂ − λ₁. As a function of [L]₀, the dominant rate k_obs of the elementary binding model exhibits a minimum at ${\left[\mathrm{L}\right]}_0^{\text{min}}={\left[P\right]}_0-K_d$ and is symmetric with respect to this minimum.

We next use the limit of the geometric series ${\sum }_{n=0}^{\infty }{q}^n=1/(1-q)$ with q = e^−k_obst λ₂/λ₁ to rewrite Eq (43) as

$$\left[\text{PL}\right]\left(t\right)\propto {\lambda }_2+\left({\lambda }_2-{\lambda }_1\right)\sum _{n=1}^{\infty }\frac{{\mathrm{e}}^{-n{k}_{\text{obs}}t}}{{\left({\lambda }_1/{\lambda }_2\right)}^n}$$ (47)

which shows that the chemical relaxation of the elementary binding model can be described as an infinite sum of exponential functions. The exponents of these functions are integer multiples of k_obs, which is reminiscent of the higher harmonics in oscillatory phenomena. The prefactors (λ₂/λ₁)ⁿ in Eq (47) decay exponentially with the order n of the harmonic because of λ₂/λ₁ < 1. The infinite sum of Eq (47) therefore can be truncated in practical situations. Under pseudo-first-order conditions, Eq (47) reduces to a single-exponential relaxation.

In analogy to the elementary binding model, we propose that the time evolution of the concentrations in the induced-fit and conformational-selection models can be represented as a sum of exponentials where the exponents are integer combinations −ik_obs − jk₂ with i, j = 0, 1, 2, 3, … of the relaxation rates k_obs and k₂ obtained from a linear expansion around the equilibrium concentrations. Under pseudo-first-order conditions, the chemical relaxation reduces to a double-exponential relaxation [16, 21, 22].

In the numerical examples of Figs 2 and 3, the chemical relaxation of the bound complexes is fitted with a multi-exponential model

$$\left[\text{bound}\right]\left(t\right)=A_0+\sum _{n=1}^N{A}_n{e}^{-k_{n}t}$$ (48)

with k_n > 0 for all n. We have used the routine NonlinearModelFit of the software Mathematica [41] with the differential evolution algorithm [42], which was repeatedly run with different values of its F parameter ranging from 0.1 to 1 for a given number of exponentials N. Among different runs, we have selected fit results based on the residual sum of squares, after discarding fits with singular results in which two rates k_n coincide within 95% confidence intervals, or in which one or more rates k_n are identical to 0 within 95% confidence intervals. We have then determined the number of exponentials N based on the small-sample-size corrected version of Akaike’s information criterion (AIC) [43].

Bayes factors

The Bayes factor K is as measure for how plausible one model is relatively to an alternative model, given experimental data [44]. The Bayes factor for the plausibility of the conformational-selection binding model relative to induced-fit binding model is

$$K=\frac{\int p(\text{data}\mid \text{conformational-selection}\text{binding},\theta )p\left(\theta \right)\mathrm{d}\theta }{\int p(\text{data}\mid \text{induced-fit}\text{binding},\theta )p\left(\theta \right)\mathrm{d}\theta }$$ (49)

Here, p(data ∣ M, θ) is the probability that the data were produced by the model M with given parameters θ, where M either stands for conformational-selection binding or induced-fit binding, and p(θ) is the prior distribution on the parameter values, which encodes any prior knowledge that we have about the parameters. The integrals of Eq (49) are taken over all parameter values and result in the probability p(data ∣ M) that the data were produced by the model, regardless of specific parameter values. The data here consist of the slowest relaxation rates $k_{\text{obs}}^{\left(i\right)}$ with i = 1, 2, …, N obtained from multi-exponential fits of the N time series with ligand concentrations ${\left[L\right]}_0^{\left(i\right)}$, and the errors σ_i of these rates. Following standard approaches [44], the probability that the data were generated by the model M with parameters θ = (k_e, k_r, k₋, K_d, [P]₀) is

$$p(\text{data}\mid M,\theta )\propto \prod _{i=1}^{N}exp\left[-\frac{{\left(k_{\text{obs}}^{\left(i\right)}-k_{\text{obs}}^M\left(\theta ,{\left[L\right]}_0^{\left(i\right)}\right)\right)}^2}{2{\sigma }_i^2}\right]$$ (50)

for k_r > nk_e, and 0 otherwise. The inequality k_r > nk_e reflects constraints on the conformational relaxation rate k_r and excitation rate k_e of the models (see section “Analysis of chemical relaxation rates for recoverin binding”). Eq (50) implies that the errors $k_{\text{obs}}^{\left(i\right)}-k_{\text{obs}}^M(\theta ,{\left[L\right]}_0^{\left(i\right)})$ are independently and normally distributed random variables with standard deviations σ_i. Depending on the model M, we either use Eqs (1) or (6) to determine $k_{\text{obs}}^M(\theta ,{\left[L\right]}_0^{\left(i\right)})$. For simplicity, K_d and [P]₀ are kept fixed at the experimentally measured values. We choose a prior p(θ) that is uniform in the logarithm of the rates k_e, k_r, k₋. Taking the logarithm of the rates is not crucial, as a uniform prior on the rates gives similar results in the analysis of recoverin binding and, thus, leads to the same conclusions. The prior p(θ) here can be chosen to be uniform because it is identical for both the induced-fit and conformational-selection binding models due to the equivalent parameters of the models [45].

Data Availability

All relevant data are within the paper.

Funding Statement

This work was supported by Deusche Forschungsgemeinschaft http://www.dfg.de/en/ collective grant SFB 1114 http://gepris.dfg.de/gepris/projekt/235221301?language=en (to FP TRW). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.