Control of colloidal placement by modulated molecular orientation in nematic cells

Control of colloidal placement is achieved in nematic cells with photopatterned, spatially modulated molecular orientation.

Abstract

Colloids self-assemble into various organized superstructures determined by particle interactions. There is tremendous progress in both the scientific understanding and the applications of self-assemblies of single-type identical particles. Forming superstructures in which the colloidal particles occupy predesigned sites and remain in these sites despite thermal fluctuations represents a major challenge of the current state of the art. We propose a versatile approach to directing placement of colloids using nematic liquid crystals with spatially varying molecular orientation preimposed by substrate photoalignment. Colloidal particles in a nematic environment are subject to the long-range elastic forces originating in the orientational order of the nematic. Gradients of the orientational order create an elastic energy landscape that drives the colloids into locations with preferred type of deformations. As an example, we demonstrate that colloidal spheres with perpendicular surface anchoring are driven into the regions of maximum splay, whereas spheres with tangential surface anchoring settle into the regions of bend. Elastic forces responsible for preferential placement are measured by exploring overdamped dynamics of the colloids. Control of colloidal self-assembly through patterned molecular orientation opens new opportunities for designing materials and devices in which particles should be placed in predesigned locations.

INTRODUCTION

Self-assembled colloidal structures are formed by small particles that interact in a predefined manner to create complex patterns (1). Self-assembly in isotropic solutions such as water already demonstrated a great potential to design materials for various scientific and technological purposes (2). Colloidal interactions and thus complexity of superstructures can be markedly enriched by using liquid crystals (LCs) as a dispersion medium (3). Long-range orientational order of LCs leads to anisotropic colloidal interactions that control assembly into clusters (4–13); mediate interactions of particles with flat (14), curved (15), and templated interfaces (16, 17); and cause trapping at topological defects (18–23). The spectrum of possible design pathways of colloidal self-assembly through LC dispersions is further expanded by sensitivity of the liquid crystalline order to external electromagnetic fields, temperature, or confinement.

Colloidal self-assembly in both isotropic and anisotropic media is currently well explored for the case when the particles are of the same type and occupy locations determined by interactions with other particles and bounding surfaces. The challenge is to develop robust approaches to placing particles into predesigned locations. Current methods of heterogeneous design are based on lock-and-key colloidal interactions of nonspherical particles (24), programmable interactions of DNA molecules attached to the surface of particles (25), and use of substrates with patterned magnetic (26) or hydrophobic properties (27). Here, we propose a new approach to the placement of colloidal particles that is based on LCs with predesigned molecular orientation, achieved through the substrate photopatterning.

We use the simplest type of LC, the so-called nematic, in which elongated molecules are oriented along a single direction called the director $\widehat{\mathbf{n}}$, with the properties $\widehat{\mathbf{n}}\equiv -\widehat{\mathbf{n}}$ and ${\widehat{\mathbf{n}}}^2=1$. The flat nematic cells bounded by two glass plates are designed in such a way that the director field experiences periodic one-dimensional (1D) distortions with alternating stripes of splay and bend. These deformations are preimposed by the substrate photoalignment technique developed recently (28, 29). Spherical particles demonstrate a marked selectivity in spatial locations within the preimposed landscape of director deformations, depending on their surface-anchoring properties, that is, the preferred direction of the local $\widehat{\mathbf{n}}$. Namely, spheres with tangential surface alignment of $\widehat{\mathbf{n}}$ are attracted to the regions of bend, whereas spheres with perpendicular alignment are attracted to the regions of splay. Analysis of the colloidal dynamics allows us to determine the interaction potential of the particles with the underlying director landscape.

RESULTS

We explore a stripe pattern with periodic splay $\mathrm{d}\mathrm{i}\mathrm{v}\widehat{\mathbf{n}}\ne 0$ and bend $\widehat{\mathbf{n}}\times \text{curl}\widehat{\mathbf{n}}\ne 0$ modulated along the y axis. The director is everywhere, parallel to the bounding plates; therefore, there is no z component, n_z = 0. The director field imposed by the surface photoalignment layer is of the form

$$\widehat{\mathbf{n}}=({\mathit{n}}_{\mathit{x}},{\mathit{n}}_{\mathit{y}},{\mathit{n}}_{\mathit{z}})=(\text{cos}\mathrm{\alpha }, \text{sin}\mathrm{\alpha },0)$$ (1)

where α = πy/l and l = 80 μm is the period (Fig. 1). An experimental cell represents a thin (with a thickness of h = 20 μm) flat layer of a nematic sandwiched between two glass plates with identical photo-induced alignment patterns at the top (z = h) and bottom (z = 0) surfaces. Splay and bend contribute to the Oseen-Frank free-energy density of the distorted nematic

$$\mathit{f}=\frac{1}{2}{\mathit{K}}_1{(\mathrm{d}\mathrm{i}\mathrm{v}\widehat{\mathbf{n}})}^2+\frac{1}{2}{\mathit{K}}_2{(\widehat{\mathbf{n}}\cdot \text{curl}\widehat{\mathbf{n}})}^2+\frac{1}{2}{\mathit{K}}_3{(\widehat{\mathbf{n}}\times \text{curl}\widehat{\mathbf{n}})}^2$$ (2)

with the elastic constants of splay (K₁), twist (K₂), and bend (K₃). For the director patterns (Eq. 1) used in this work, twist (as well as saddle-splay) deformations vanish because the director does not change along the z axis. Figure 1B shows the spatial distribution of the dimensionless splay energy density ${(\mathit{l}/\mathrm{\pi })}^2{(\mathrm{d}\mathrm{i}\mathrm{v}\widehat{\mathbf{n}})}^2={\text{cos}}^2(\mathrm{\pi }\mathit{y}/\mathit{l})$ corresponding to Eq. 1. As detailed by the experiments below, the alternating regions of splay and bend attract colloidal spheres with different surface anchoring: spheres with normal anchoring are attracted to the splay regions (Fig. 1), and spheres with tangential anchoring are attracted to the bend regions, as discussed later.

Fig. 1. Elasticity-directed placement and assembly of normally anchored polystyrene spheres in regions with splay deformations of the patterned director.

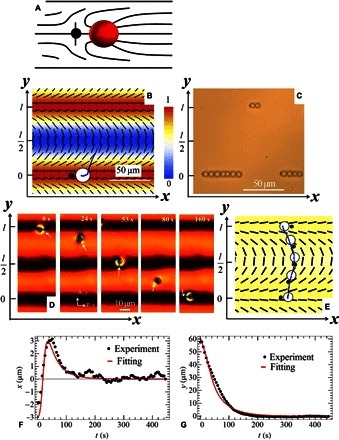
(A) A sphere with perpendicular surface anchoring placed in a uniform nematic causes an appearance of a hyperbolic hedgehog that can be located on either the left- or right-hand side; the resulting director deformations are of a dipolar type. (B) Periodic splay-bend stripe pattern; the normalized splay energy density is labeled by colors according to the scale on the right-hand side. A sphere is placed in the bend region by optical tweezers and released there, and migrates toward the splay region. The dark blue curve is the typical experimental trajectory of the sphere’s center. (C) Self-assembly of spheres into linear chains in the regions of maximum splay with p > 0 [bright-field microscope with unpolarized light, and nematic liquid crystal pentylcyanobiphenyl (5CB)]. (D) Polarizing microscopy images of a sphere moving from one splay region to the next splay region, with concomitant reorientation of the structural dipole from p < 0 to p > 0; the white arrows point toward the hyperbolic hedgehog. (E) Typical experimental trajectory of the sphere within the director configuration mapped in the PolScope mode of observation of the experimental cell. (F) Experimentally measured x(t) dependence for a sphere moving from y = l to y = 0 and its theoretical fit by Eq. 5. (G) Experimentally measured y(t) dependence for a sphere moving from y = l to y = 0 and its theoretical fit by Eq. 6. All spheres have a radius of R = 2.5 μm; the period of the patterned director is l = 80 μm. The nematic material corresponding to parts (D) to (G) is MLC6815.

Spheres with normal anchoring

Polystyrene spheres with a radius of R = 2.5 μm were covered with a thin layer of a surfactant to produce perpendicular (also called homeotropic or normal) alignment of the director at their surfaces. When such a sphere is placed in a nematic with a uniform director field ${\widehat{\mathbf{n}}}_0=(1,0,0)$, the radial-like director around the sphere is topologically compensated by a point defect, the so-called hyperbolic hedgehog located on either the right- or left-hand side of the sphere (3, 30). The resulting director structure is in the form of a dipole (Fig. 1A). We direct the unit vector $\widehat{\mathbf{p}}$ of the dipole from the hedgehog toward the sphere. Note that once the direction of the dipole is randomly selected to be either parallel or antiparallel to the x axis of the uniform cell with ${\widehat{\mathbf{n}}}_0=(1,0,0)$, it cannot be reversed into the opposite orientation because the energy barrier for such a realignment, on the order of KR ≈ (10⁻¹⁶ to 10⁻¹⁷) J, is much larger than the thermal energy k_BT = 4.2 × 10⁻²¹ J, with the typical value of the Frank elastic constant K being a few tens of piconewton. In principle, in very shallow cells (with a thickness comparable to the colloid diameter), the dipolar structure can transform into a Saturn ring configuration (31); however, in all our experiments, the dipolar structure remained stable (32, 33). This implies that the homeotropic anchoring is strong, with the anchoring coefficient being larger than K/R ≈ 10⁻⁵ J/m².

Individual spheres with normal anchoring placed in the cell with a periodic splay and bend migrate toward the regions with the maximum splay, y = 0, ± l, ± 2l, … (Fig. 1B). When the concentration of spheres is high enough, they form linear chains along the x axis, located at the same ordinate of the maximum splay, y = 0, ± l, ± 2l, … (Fig. 1C and fig. S1).

It is important to note a polar character of colloidal assemblies in the splay regions. In a uniform nematic, the “left” and “right” orientations of $\widehat{\mathbf{p}}$ are equally probable. In the described splay-bend pattern, which lacks the left-right mirror symmetry, all the dipoles align themselves along the same direction, forming a ferroelectric type of order. For the chosen geometry of the splay-bend pattern (Eq. 1 and Fig. 1B), the dipoles $\widehat{\mathbf{p}}$ of the spheres trapped at the splay locations y = 0, ± l, ± 2l, … are always parallel to the x axis. If we use optical tweezers and place a sphere in any location within the pattern specified by Eq. 1, then the sphere orients its dipole $\widehat{\mathbf{p}}$ parallel or antiparallel to the local director. If the sphere is released from the optical tweezers, it moves toward the regions y = 0, ± l, ± 2l, … while simultaneously rotating the dipole in accordance with the rotating local director orientation (Fig. 1B). In particular, the tweezers can place a sphere in the splay region in such a way that the dipole $\widehat{\mathbf{p}}$ is antiparallel to the x axis. This configuration is unstable because $\widehat{\mathbf{p}}$ prefers to be parallel to the x axis at equilibrium. The sphere with the “wrong” orientation of $\widehat{\mathbf{p}}$ moves across the stripe pattern, rotating $\widehat{\mathbf{p}}$ in accordance with the local director, until it reaches the neighboring splay region with $\widehat{\mathbf{p}}$ being parallel to the x axis, that is, completing a 180° rotation through a shift by |Δy| = l (Fig. 1, D and E, and movie S1). Note that the simple reorientation of $\widehat{\mathbf{p}}$ by 180° with the sphere keeping its y coordinate unchanged (|Δy| = 0) is never observed in our experiments; the reason is that this process is associated with a huge energy barrier KR >> k_BT, similar to the case of the uniform cell discussed above.

At moderate concentrations, colloidal particles with homeotropic anchoring gather into linear chains (Fig. 1C). Note that all the chains have the same direction of the individual dipole moments $\widehat{\mathbf{p}}$ and are separated by the same distance l along the y axis. By increasing the concentration of colloids, the length of the chains can be increased, but because we are primarily interested in the individual behavior, we limit the study by using relatively low concentrations, in which the number of particles in each chain is less than about 10.

The interaction potential between a colloidal sphere with a dipolar director and a distorted director has been derived by Pergamenshchik (34). We follow the study of Pergamenshchik (34) but use a modified expression that conforms to our definition of the dipole; for a sphere of radius R << l, the interaction potential writes

$${\mathit{U}}_{\mathrm{d}}=-8\mathrm{\pi }\mathrm{\beta }\mathit{K}{\mathit{R}}^2(\widehat{\mathbf{p}}\cdot \widehat{\mathbf{n}}\text{div}\widehat{\mathbf{n}}$$ (3)

where β is the amplitude of the dipole director distortions that depends on the strength of surface anchoring, anisotropy of elastic constants, accuracy of the dipolar approximation, etc., and K is the effective elastic constant in the so-called one-constant approximation. In the analysis below, we treat β as an unknown numerical coefficient, which we determine from the fitting of experimental data. In Eq. 3, we introduce the scalar product $(\widehat{\mathbf{p}}\cdot \widehat{\mathbf{n}})$ to account for the polar character of coupling between the splay $\mathrm{d}\mathrm{i}\mathrm{v}\widehat{\mathbf{n}}$ and $\widehat{\mathbf{p}}$ and also to preserve the nematic symmetry $\widehat{\mathbf{n}}\text{≡}-\widehat{\mathbf{n}}$. For the director field in Eq. 1, $\widehat{\mathbf{n}}=[\text{cos}(\mathrm{\pi }\mathit{y}/\mathit{l}),\text{sin}(\mathrm{\pi }\mathit{y}/\mathit{l}),0]$, the interaction potential for a given sphere that keeps $(\widehat{\mathbf{p}}\cdot \widehat{\mathbf{n}})=1$ [namely, U_d = −8π²βK(R²/l)cos(πy/l)] reaches its minimum U_d,min = −8π²βK(R²/l) at the locations y = 0, ± 2l, … and maximum U_d,max = 8π²βK(R²/l) at the locations y= ± l, ± 3l, …. That is, the normally anchored spheres are expected to gather in the regions with a maximum splay, being oriented in such a way that the dipole $\widehat{\mathbf{p}}$ fits the polarity of splay $\widehat{\mathbf{n}}\text{div}\widehat{\mathbf{n}}$.

The potential (Eq. 3) also explains the behavior of a sphere placed using the optical tweezers in a splay region with the wrong polarity. Such a sphere moves along the potential energy landscape from the maximum energy at y = l toward the minimum at y = 0 (Fig. 1, D and E). The dynamics of the sphere from y = l toward y = 0 can be used to extract the information about the energetics of elastic coupling between the colloids and the surrounding director distortions, as detailed below.

The particle’s dipole preserves its orientation parallel to the local director during migration. Then, the elastic force driving the sphere to the minimum energy location writes

$$\mathbf{F}=-(\partial {\mathit{U}}_{\mathrm{d}}/\partial \mathit{y}){\widehat{\mathbf{e}}}_{\mathit{y}}=-8{\mathrm{\pi }}^3\mathrm{\beta }\mathit{K}{(\frac{\mathit{R}}{\mathit{l}})}^2\text{sin}(\frac{\mathrm{\pi }\mathit{y}}{\mathit{l}}){\widehat{\mathbf{e}}}_{\mathit{y}}$$ (4)

where ê_y is the unit vector along the y axis. Because the Reynolds number in our experiments is small and because inertia contributions can be neglected, the driving force is balanced by the viscous drag force ${\mathbf{F}}_{\mathrm{d}}=-6\mathrm{\pi }\mathit{R}\overleftrightarrow{\mathrm{\eta }}\mathbf{v}$, where $\overleftrightarrow{\mathrm{\eta }}$ is the diagonal viscosity tensor with the components η_∥ and η_⊥, and v is the particle velocity vector with the components v_∥ and v_⊥; the subscripts ∥ and ⊥ refer to the components parallel and perpendicular to the director, respectively. The drag force can be rewritten in terms of the components of the viscosity tensor, F_d/6πR = η_∥v_∥(ê_x cos α + ê_y sin α) + η_⊥v_⊥(−ê_x sin α + ê_y cos α). By balancing the driving and drag forces in the laboratory coordinate system, we obtain the equations for the velocity components ${\mathit{v}}_{\mathit{x}}={\mathit{v}}_{\parallel }\text{cos}\frac{\mathrm{\pi }\mathit{y}}{\mathit{l}}-{\mathit{v}}_{\perp } \text{sin}\frac{\mathrm{\pi }\mathit{y}}{\mathit{l}}$ and ${\mathit{v}}_{\mathit{y}}={\mathit{v}}_{\parallel }\text{sin}(\frac{\mathrm{\pi }\mathit{y}}{\mathit{l}})+{\mathit{v}}_{\perp }\text{cos}(\frac{\mathrm{\pi }\mathit{y}}{\mathit{l}})$ in the following form

$$\frac{\partial \mathit{x}}{\partial \mathit{t}}=-\frac{4{\mathrm{\pi }}^2}{3}\frac{{\mathrm{\eta }}_{\perp }-{\mathrm{\eta }}_{\parallel }}{{\mathrm{\eta }}_{\parallel }{\mathrm{\eta }}_{\perp }}\mathrm{\beta }\frac{\mathit{K}\mathit{R}}{{\mathit{l}}^2}{\text{sin}}^2\frac{\mathrm{\pi }\mathit{y}}{\mathit{l}} \text{cos}\frac{\mathrm{\pi }\mathit{y}}{\mathit{l}}$$ (5)

$$\frac{\partial \mathit{y}}{\partial \mathit{t}}=-\frac{4{\mathrm{\pi }}^2}{3}\mathrm{\beta }\frac{\mathit{K}\mathit{R}}{{\mathit{l}}^2}\frac{{\mathrm{\eta }}_{\perp }{\text{sin}}^2\frac{\mathrm{\pi }\mathit{y}}{\mathit{l}}+{\mathrm{\eta }}_{\parallel }{\text{cos}}^2\frac{\mathrm{\pi }\mathit{y}}{\mathit{l}}}{{\mathrm{\eta }}_{\perp }{\mathrm{\eta }}_{\parallel }}\text{sin}\frac{\mathrm{\pi }\mathit{y}}{\mathit{l}}$$ (6)

Solutions of Eqs. 5 and 6 establish how the sphere’s coordinates, x and y, vary with time. These theoretical dependencies are used to fit the experimental trajectory in Fig. 1 (F and G) to verify the model and to deduce the unknown parameter β.

Fitting of the experimental dynamics of the colloids requires knowledge of the two components of the viscosity tensor, η_∥ and η_⊥. These two were experimentally determined for the same LC and normally anchored spheres by measuring the mean square displacements (MSDs) as a function of time for the Brownian diffusion parallel and perpendicular to the director in uniformly aligned cells, ${\widehat{\mathbf{n}}}_0=(1,0,0)$ (Fig. 2). The slopes of the MSDs versus time dependencies yield the diffusion coefficient D_∥ = (7.6 ± 0.2) × 10⁻¹⁵ m²/s for the direction parallel to ${\widehat{\mathbf{n}}}_0$ and D_⊥ = (4.1 ± 0.2) × 10⁻¹⁵ m²/s for the perpendicular direction. These values yield the corresponding components of the viscosity tensor, η_∥ = (12 ± 1) mPa ⋅ s and η_⊥ = (22 ± 1) mPa ⋅ s, which follow from the Stokes-Einstein formula η = k_BT/(6πRD).

Fig. 2. MSD of a dipolar colloid in uniformly aligned LC cell.

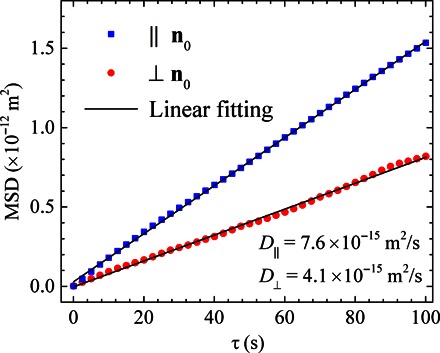
Homeotropically anchored sphere with a radius of 2.5 μm in a nematic MLC6815 cell with uniform alignment ${\widehat{\mathbf{n}}}_0$, which is achieved by unidirectional rubbing of the aligning layer of PI2555 deposited on the bounding plates.

As clearly seen from Fig. 1 (F and G), the experimental data are closely matched by the expected theoretical behavior, despite the fact that the model uses the so-called one-constant approximation. The only fitting parameter is β = 0.20 ± 0.02. Note that with this value and with K = 10⁻¹¹ N, the depth of the potential minimum [U_d,max − U_d,min = 16π²βK(R²/l)] is 2.2 × 10⁻¹⁷ J, that is, about four orders of magnitude higher than the thermal energy k_BT = 4.2 × 10⁻²¹ J. In other words, the elastic trapping is much stronger than the randomizing forces associated with thermal fluctuations. One can also estimate the stiffness of the potential trap that keeps the normally anchored spheres in the splay regions of a “correct” polarity. For y → 0, the stiffness of the elastic trap $\mathit{k}=\frac{{\partial }^2{\mathit{U}}_{\mathrm{d}}}{\partial {\mathit{y}}^2}=8{\mathrm{\pi }}^4\mathrm{\beta }\frac{{\mathit{R}}^2}{{\mathit{l}}^3}\mathit{K}$ is about 1.9 × 10⁻⁸ N/m.

Spheres with tangential anchoring

Polystyrene spheres without surfactant coatings produce spontaneous tangential (parallel to the interface and degenerate) anchoring. The director deformations around these spheres in a uniform nematic are of quadrupolar symmetry, with two point defects, called boojums, at the poles (Fig. 3A). Placing these spheres in the splay-bend stripe pattern (Eq. 1) produces behavior qualitatively different from the normally anchored spheres (Fig. 3). Figure 3B maps the dimensionless bend energy ${(\mathit{l}/\mathrm{\pi })}^2{(\widehat{\mathbf{n}}\times \text{curl}\widehat{\mathbf{n}})}^2={\text{sin}}^2(\mathrm{\pi }\mathit{y}/\mathit{l})$ stored in the stripe pattern. The tangentially anchored spheres migrate toward the regions with the maximum bend, that is, locations at y = ± l/2, ± 3l/2, … (Fig. 3, B and C). As the concentration of spheres increases, they assemble into chains with tilted arrangements of the neighboring spheres, similar to those described for uniform nematic cells in the work of Smalyukh et al. (5). Figure 3C shows only the short chains since we are primarily interested in the individual behavior of colloids in the patterned landscape. Longer chains form in more concentrated dispersions and can extend over a length of 50 to 70 μm across the region with bend distortions; they are disrupted when their ends become close to the regions with splay deformations.

Fig. 3. Elasticity-directed placement and assembly of tangentially anchored polystyrene spheres in regions with bend deformations of the patterned director.

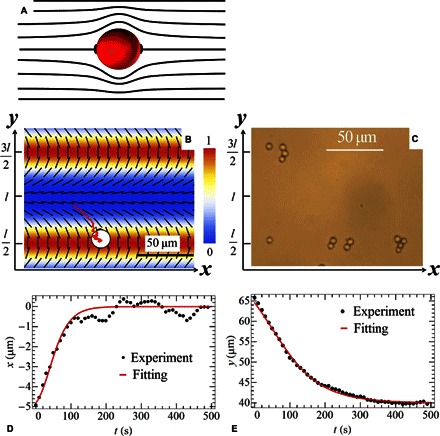
(A) Director deformations around a tangentially anchored sphere in a uniform nematic are of quadrupolar symmetry, with two point defects, called boojums, at the poles. (B) Periodic splay-bend stripe pattern; the normalized bend energy density is labeled by colors according to the scale on the right-hand side. A sphere placed and released in the splay region using optical tweezers migrates toward the bend region. The dark red curve is the typical experimental trajectory of the sphere’s center. (C) Self-assembly of spheres into chains in the regions of maximum bend (bright-field microscope and unpolarized light). (D) Experimentally measured x(t) dependence for a sphere moving from y = l to y = l/2 and its theoretical fit by Eq. 9. (E) Experimentally measured y(t) of a sphere moving from y = l to y = l/2 and its theoretical fit by Eq. 10. All spheres have radius of R = 2.5 μm; periodicity of the director pattern is l = 80 μm. The LCs used are 5CB (C) and MLC6815 (D and E).

The potential of interaction between a quadrupolar particle and the distorted director field reads, following Pergamenshchik (34), as

$${\mathit{U}}_{\mathrm{Q}}=-4\mathrm{\pi }\mathit{K}\mathrm{\chi }{\mathit{R}}^3(\widehat{\mathbf{n}}\cdot \nabla )\text{div}\widehat{\mathbf{n}}$$ (7)

where χ is the dimensionless coefficient of the quadrupolar moment, the value of which is unknown and depends on the surface anchoring. For the patterned director field (Eq. 1), this potential reduces to ${\mathit{U}}_{\mathrm{Q}}=4{\mathrm{\pi }}^3\mathrm{\chi }\mathit{K}\frac{{\mathit{R}}^3}{{\mathit{l}}^2}{\text{sin}}^2\frac{\mathrm{\pi }\mathit{y}}{\mathit{l}}$, thus predicting that the spheres with χ < 0 will minimize the potential by migrating toward the locations with bend (y = ± l/2, ± 3l/2, …), as observed in the experiments (Fig. 3C). The corresponding force driving the spheres to the equilibrium locations is

$${\mathit{F}}_{\mathrm{Q}}=-(\partial {\mathit{U}}_{\mathrm{Q}}/\partial \mathit{y})=-4{\mathrm{\pi }}^4\mathrm{\chi }\mathit{K}{\left(\frac{\mathit{R}}{\mathit{l}}\right)}^3 \text{sin}\frac{2\mathrm{\pi }\mathit{y}}{\mathit{l}}$$ (8)

If the sphere is placed in the splay region y = 0, ± l, …, using the optical tweezers, a fluctuative displacement from that location causes the sphere to move toward the bend stripe region at y = ± l/2, ± 3l/2 …, as shown by a trajectory in Fig. 3B. By balancing the driving and drag forces, one finds the x and y components of the velocity, similarly to the case of normally anchored spheres

$$\frac{\partial \mathit{x}}{\partial \mathit{t}}=-\frac{{\mathrm{\pi }}^3}{3}\frac{{\mathrm{\eta }}_{\perp }-{\mathrm{\eta }}_{\parallel }}{{\mathrm{\eta }}_{\parallel }{\mathrm{\eta }}_{\perp }}\mathrm{\chi }\frac{\mathit{K}{\mathit{R}}^2}{{\mathit{l}}^3}{\text{sin}}^2\frac{2\mathrm{\pi }\mathit{y}}{\mathit{l}}$$ (9)

$$\frac{\partial \mathit{y}}{\partial \mathit{t}}=-\frac{2{\mathrm{\pi }}^3}{3}\mathrm{\chi }\frac{\mathit{K}{\mathit{R}}^2}{{\mathit{l}}^3}\frac{{\mathrm{\eta }}_{\perp }{\text{sin}}^2\frac{\mathrm{\pi }\mathit{y}}{\mathit{l}}+{\mathrm{\eta }}_{\parallel }{\text{cos}}^2\frac{\mathrm{\pi }\mathit{y}}{\mathit{l}}}{{\mathrm{\eta }}_{\parallel }{\mathrm{\eta }}_{\perp }}\text{sin}\frac{2\mathrm{\pi }\mathit{y}}{\mathit{l}}$$ (10)

Proceeding as above, by solving Eqs. 9 and 10 and by finding the theoretical trajectory of the particle, we fit the experimental dependencies x(t) and y(t) (Fig. 3, D and E). The model describes the experimental behavior well and yields the value of quadrupolar parameter χ = −0.95 ± 0.10. With this value, the depth of the trapping potential ${\mathit{U}}_{\mathrm{Q},\text{max}}-{\mathit{U}}_{\mathrm{Q},\text{min}}=4{\mathrm{\pi }}^3|\mathrm{\chi }|\frac{\mathit{K}{\mathit{R}}^3}{{\mathit{l}}^2}$ can be estimated as 2.9 × 10⁻¹⁸ J, which is much larger than the thermal energy. Finally, we can estimate the stiffness $\mathit{k}={\frac{{\partial }^2{\mathit{U}}_{\mathrm{Q}}}{\partial {\mathit{y}}^2}|}_{\mathit{y}\to \mathit{l}/2}=8{\mathrm{\pi }}^5\mathit{K}|\mathrm{\chi }|\frac{{\mathit{R}}^3}{{\mathit{l}}^4}$ of the potential, which is 9 × 10⁻⁹ N/m, that is, about two times weaker than the stiffness of the splay trap acting on the normally anchored spheres.

Preferential placement of spheres with different surface anchoring

So far, we have discussed dispersions of single-type particles. When the cell is filled with a mixture of two types of particles, the surface-patterned director landscape leads to their preferential placement in different regions of the cell (Fig. 4). Namely, the normally anchored spheres migrate toward the splay (y = 0), and the tangentially anchored spheres migrate toward the bend (y = ± l/2) (Fig. 4). Depending on the overall concentration of the spheres, they can form larger or smaller aggregates. The normally anchored spheres produce linear chains parallel to the direction of stripes, whereas the tangentially anchored spheres form chains that are predominantly perpendicular to this direction, which is an expected behavior, as evidenced by previous studies of aggregation of both types of spheres in uniformly aligned nematic cells (Fig. 4) (3).

Fig. 4. Preferential placement of colloids with different surface properties in a cell with periodically patterned splay-bend director field.

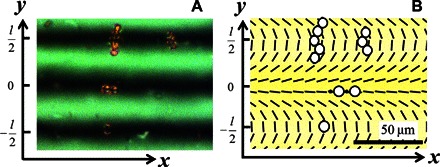
(A) Polarizing microscope texture of polystyrene colloids with homeotropic and tangential anchoring located in the alternating bands of splay and bend, respectively. (B) Scheme of preferential placement with the experimentally determined director pattern (PolScope observations). The homeotropically anchored spheres reside in the region of splay (y = 0), whereas tangentially anchored spheres localize in the regions of bend (y = ±l/2). Note the different orientations of chains formed by homeotropic spheres (along the x axis) and by the tangential spheres (perpendicular to the x axis). The colloids are placed in an LC mixture with zero dielectric anisotropy. Polarizer is parallel to the x axis and analyzer along the y axis.

DISCUSSION

Here, we demonstrate a new approach to controlling colloidal placement, by using the long-range elastic forces in spatially modulated nematic LC. The approach is based on the predesigned molecular orientation pattern at the bounding plates of the cell. The colloidal spheres interact with the underlying director distortions and migrate into the regions where the elastic energy of interactions is minimized. For spheres with normal anchoring, these regions correspond to the splay deformations; in contrast, tangentially anchored spheres are localized in the regions of bend.

The periodic splay-bend director pattern imposes strong limitations on the collective behavior of the colloids. For example, the spheres with normal anchoring form a ferroelectric type of macroscopic ordering, in which the structural dipole moment $\widehat{\mathbf{p}}$ of each and every particle points to the same direction. The system is very deterministic since we do not observe any “mistakes” made by the colloids, for example, wrong orientation of $\widehat{\mathbf{p}}$ or wrong placement of the sphere with the tangential anchoring (which would be in the regions of splay). Note here that we explored four different nematic materials, and all of them showed similar behavior, which underscores a general and robust character of the colloidal interactions mediated by surface anchoring and elasticity of the preimposed director patterns.

Because the period l of the splay-bend background is much bigger than the particle radius R, the interaction potential is adequately described by the lowest multipole deformation around the particles that grows as R²/l for the spheres with locally dipolar director configuration around them and as R³/l² for quadrupolar spheres with tangential anchoring. Thermal fluctuations do not affect the particle dynamics in our experiments. For the given strength of director gradients, defined by the period l = 80 μm, the smallest radius of the spheres that can be trapped at the desired location in space can be estimated by comparing the depth of the trapping potentials to the thermal energy. For the dipolar particles, the smallest radius estimated from the condition U_d,max − U_d,min = k_BT is 34 nm. The last estimate presumes that the surface-anchoring strength W is sufficiently strong to maintain the dipolar configuration, namely, K/W ~ 10 nm or so. For the quadrupolar particles, placed in a pattern with l = 80 μm, the minimum size is about 220 nm. The feature of a relatively large size limit follows from the additional factor R/l in the quadrupolar potential as compared to the dipolar potential. By making the pattern with a smaller period l, one can decrease the minimum size of the controllable particles below the estimates above. However, to accurately describe the case of smaller l, one needs to account for (i) the finite size of the particles and (ii) the finite surface-anchoring strength at the surface of the spheres and at the bounding plates.

The presented experimental data on dynamics and placement of the colloidal particles are well described by the elastic model based on the Frank-Oseen functional and the dipolar and quadrupolar type of director deformations around the particles. One of the reasons why the experiment and the theory match well is the relatively large size of the colloids (5 μm). For submicrometer particles and for high concentration of particles, the description might require a more elaborate approach that would, for example, account for the finite anchoring strength. Furthermore, the theoretical description might be supplemented by the consideration of thermal fluctuations. In the uniformly aligned LC environment, the displacement of particles caused by Brownian motion is both anisotropic (35) and, at time scales on the order of the relaxation time of the director, anomalous (36). It would be of interest to explore how the prepatterned director deformations might influence the regimes of colloidal Brownian motion.

CONCLUSIONS

To conclude, the photopatterning surface alignment offers a versatile method to control colloidal assemblies by directing particles into predesigned locations and trapping them in these locations with forces that exceed those of entropic nature. Besides the practical utility, the study clearly demonstrates and experimentally quantifies the mechanisms of selective interactions between the colloids and the surrounding landscape of a distorted director. Here, we demonstrated the principle using spheres and a relatively simple periodic director pattern with alternating splay and bend. However, it is obvious that the similar approach can be extended to particles of different shape or size and to more complex 2D and even 3D patterns of the director field. We also expect that the approach is not limited by just normal and tangential anchoring at the surface of the colloidal particles; tilted anchoring is also expected to show selectivity in equilibrium placement within a patterned director field. Colloidal placement in the photopatterned templates can be realized at practically any spatial scale without mechanical stimuli (for example, shearing, pressure gradients) or topographically modified surfaces (37). The described ability to deterministically predesign locations of colloidal particles of different types in self-assembled patterns can be of importance for the development of microfluidic, electrooptical, and sensing devices. One of the applications might be sorting of particles with different surface properties and chemical composition, which we currently explore.

MATERIALS AND METHODS

Materials

We used the nematic 5CB, MLC6815, and an LC mixture with zero dielectric anisotropy (|Δε| ≤ 10⁻³) formulated by MLC7026-000 and E7 (in weight proportion of 89.1:10.9) (all materials are purchased from EM Industries). The LCs were doped with 0.01 weight % of polystyrene colloids with a radius of 2.5 μm (Duke Scientific). Untreated colloids yielded tangential anchoring. The colloids treated with octadecyl-dimethyl-(3-trimethoxysilylpropyl) ammonium chloride (DMOAP) produced perpendicular director alignment and dipolar structures with a hyperbolic hedgehog on one side of the sphere. The colloidal dispersion in the LC was injected into the photopatterned cell with a thickness of h = 20 μm at room temperature (22°C).

Optical microscopy

We used the Nikon TE2000 inverted microscope with both immersion [100×; Fluor; numerical aperture (NA), 1.3] and dry (60×; M Plan ELWD; NA, 0.7) objectives. Immersion objective was used with the optical tweezers (Verdi V6 green laser; 532 nm, 10 mW) mounted with the microscope to move the particle off the equilibrium state. Polarizing microscopic images were captured using the Energent HR-20000 camera, and the dynamics images were taken by the monochromatic MotionBlitz EoSens mini2 camera with different frame rates (1 to 20 fps).

PolScope microscopy

The director fields produced by photopatterning were established with the help of a microscope (Nikon E600) equipped with the Cambridge Research Abrio LC-PolScope package. The PolScope uses a monochromatic illumination at 546 nm and maps optical retardance and orientation of the optical axis (38).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/9/e1600932/DC1

fig. S1. Self-assembly of colloids with homeotropic anchoring in the regions of photopatterned splay distortions during the filling of the LC into the cell.

movie S1. Colloidal sphere with dipolar director is transported from one splay region to the next splay distortion due to elastic interaction.