Skip to main content
PMC home page
Heredity logoLink to Heredity
. 2016 May 11;117(4):207–216. doi: 10.1038/hdy.2016.30

A method for detecting recent changes in contemporary effective population size from linkage disequilibrium at linked and unlinked loci

C M Hollenbeck 1,*, D S Portnoy 1, J R Gold 1
PMCID: PMC5026753  PMID: 27165767

Abstract

Estimation of contemporary effective population size (Ne) from linkage disequilibrium (LD) between unlinked pairs of genetic markers has become an important tool in the field of population and conservation genetics. If data pertaining to physical linkage or genomic position are available for genetic markers, estimates of recombination rate between loci can be combined with LD data to estimate contemporary Ne at various times in the past. We extend the well-known, LD-based method of estimating contemporary Ne to include linkage information and show via simulation that even relatively small, recent changes in Ne can be detected reliably with a modest number of single-nucleotide polymorphism (SNP) loci. We explore several issues important to interpretation of the results and quantify the bias in estimates of contemporary Ne associated with the assumption that all loci in a large SNP data set are unlinked. The approach is applied to an empirical data set of SNP genotypes from a population of a marine fish where a recent, temporary decline in Ne is known to have occurred.

Introduction

Measurement of linkage disequilibrium (LD) between pairs of unlinked genetic markers has become the most prevalent method to estimate contemporary effective population size (Ne) in the fields of population and conservation genetics. This is due largely to the relative ease with which the approach can be applied, as it only requires a single sample and ~20 polymorphic genetic markers (Waples, 2006). In addition, well-established analytical methods and software packages for application are available (Waples, 2006; Waples and Do, 2008; Do et al., 2014). Whereas microsatellite loci previously have been the most commonly used genetic markers for applying the LD method, genomics techniques now allow the generation of data sets with genotypes at thousands to tens of thousands of single-nucleotide polymorphisms (SNPs). This is beneficial for application of LD-based methods to estimate Ne as the ability to genotype hundreds or thousands of SNPs permits greatly improved precision (Waples and Do, 2010). However, the ability to generate genotypes at many loci distributed across the genome presents a problem in that many of the markers are likely to be linked physically, and if all loci are assumed to be unlinked, estimates of Ne may be downwardly biased because of excess LD caused by linkage rather than drift (Sved et al., 2013). A straightforward solution to this problem is to remove pairwise comparisons involving known linked loci (Larson et al., 2014). This approach, however, does not take full advantage of all information present in a large SNP data set. As noted by Hill (1981), although LD from unlinked loci reflects current contemporary Ne (hereafter current Ne), LD from physically linked loci reflects contemporary Ne in past generations (hereafter past Ne) because recombination takes relatively longer to break down LD between tightly linked loci. Thus, if information pertaining to physical linkage is available for large number of markers, for example in the form of a genome sequence (from which recombination rate can be estimated) or a genetic linkage map, LD can be evaluated across a spectrum of linkage values to remove the downward bias on current Ne caused by linked loci and, in addition, identify potential changes in Ne in prior generations.

Use of LD and linkage data to estimate past Ne largely has been limited to model species because of the need for linkage or genomic position data. Hayes et al. (2003) introduced a novel measure of LD, chromosome segment homozygosity, that was used in simulated data sets to track changes in Ne over time and, with empirical data, to infer demographic population histories in dairy cattle and humans. Using chromosome segment homozygosity, Hayes et al. (2003) also derived an approximate relationship between the degree of linkage (the recombination rate, c) and the number of generations in the past (t) to which an estimate of Ne would apply: 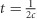Inline graphic. Tenesa et al. (2007) expanded upon this by instead using the LD statistic r2 that has the same expected relationship to Ne as chromosome segment homozygosity. The authors used r2 estimated from haplotypes of ~1 000 000 SNPs identified in the human HapMap project (Gibbs et al., 2003) to infer a recent increase in human Ne over the past 1000 years. Subsequently, several studies involving domesticated animals (Corbin et al., 2010; Flury et al., 2010; Qanbari et al., 2010; Alam et al., 2012; Herrero-Medrano et al., 2013) have shown that with extremely dense genotype and genome-sequence data, estimates of contemporary Ne can be obtained from roughly the previous generation to t generations in the past. However, these studies utilized haplotype-based methods to estimate LD that require that marker phase is either known or estimable from the data. Haplotype-based estimators require relatively rare, long haplotypes to estimate Ne in the very recent past (t⩽50), and because precision of the estimate is dependent upon the number of locus pairs used (Hill, 1981), estimates representing the recent past are less precise than estimates from the more distant past (Hayes et al., 2003).

There is potential to apply a linkage-based approach to nonmodel species for which large SNP data sets and linkage information (from linkage maps or whole genomes) are increasingly available. However, marker densities in these species may be relatively low and phased haplotypes cannot be computed with accuracy, meaning that the approach has limited utility for nonmodel species when investigating processes that act on evolutionary timescales. For example, a linkage map constructed with 100 individuals will only be able to resolve LD at loci separated by 0.01 Morgans (M). Assuming the approximate relationship between recombination rate and time derived by Hayes et al. (2003), this would reflect Ne ∼50 generations in the past. However, understanding changes in Ne in the recent past (⩽50 generations) is of great interest to conservation biologists because detecting recent declines (for example, because of anthropogenic effects) or expansions (because of recovery efforts) are important components of genetic monitoring programs (Luikart et al., 2010). Using a linkage-based approach would have an advantage over traditional LD- (Waples and Do, 2008) and variance-based (Nei and Tajima, 1981; Pollak, 1983) approaches to detect recent changes in Ne in that it requires only a single genetic sample rather than sampling over multiple years before and after a demographic change (Antao et al., 2011).

Here, we extend the LD-based approach of Waples and Do (2008) by including linkage information to estimate Ne over a range of time points in the past. The advantage of this approach (hereafter, the linkage approach) over haplotype-based methods is twofold: (1) a composite LD measure (that does not require distinction between coupling and repulsion double heterozygotes) is used, enabling calculation of pairwise LD from genotype data in the absence of phase information; and (2) because the vast majority of locus pairs in the genome are unlinked, high precision for estimating current Ne can be achieved without biases associated with inclusion of physically linked loci. We apply this approach to simulated data to assess the ability to detect demographic changes (changes in Ne) in past generations across a variety of demographic models, using a data set of 1000 SNP loci. We also explore issues important to interpretation of the results. These include the importance of correcting for bias caused by small sample size relative to the true Ne, the effect of rare alleles on estimates made at multiple points in time and the effect of time of sampling relative to a change in Ne. In addition, we compare estimates of current Ne in which physical linkage is taken into account with estimates, based on the same data, where all locus pairs are assumed to be unlinked, in order to quantify bias. Finally, to demonstrate the effectiveness of the method on an actual data set, we apply the linkage approach to an empirical data set of SNP genotypes from a sample of a marine fish where a recent, temporary reduction in Ne was known to have occurred.

Materials and methods

The method presented here requires genotype data from a diploid species and a matrix of pairwise recombination rates for all genotyped markers. The latter could be obtained from linkage mapping data or estimated from genome sequence data. The general strategy involves binning estimates of LD between pairs of loci based on similar observed recombination rates (c). Previous work (Hayes et al., 2003) showed that the time period to which an LD-based estimate of Ne applies is a function of c (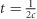Inline graphic). This equation suggests that time and recombination rate do not scale linearly and that most of the range of possible recombination rates (0–0.5 M) relates to generations in the recent past. Thus, bins were defined by generations rather than by recombination rate and calculated as 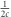Inline graphic. For these analyses, bins were defined from 1 to 3.33 generations in the past (c=0.5 to 0.15 M), 3.33 to 5 generations (c=0.15 to 0.1 M), 5 to 10 generations (c=0.1 to 0.05 M), and ⩾10 generations (c=0.05 to 0.0 M). We note that bins could be otherwise defined to suit particular research questions. For each bin, weighted estimates of total r2 (r2total) and r2 attributable to sampling variation (r2sample) for all pairs of loci were obtained, following Waples and Do (2008). The difference between r2total and r2sample, which is equal to the component of the total r2 attributable to genetic drift (r2drift), and the mean c value of pairs of loci in each bin (in Morgans) were then used to calculate Ne, following Hill (1981) and Waples (2006). A software program, LinkNe, was written in the Perl programming language to facilitate analyses and is available at https://github.com/chollenbeck/LinkNe. A detailed description of the program and calculations can be found in Supplementary Appendix 1.

Simulation

Precision and bias

Simulations were used to evaluate the effectiveness of the linkage approach to detect changes in Ne under a variety of demographic models and to explore important properties of the method. Simulations were written in Python, utilizing libraries from the program simuPOP (Peng and Kimmel, 2005). All simulations included a single, closed ‘constant' population with discrete generations, equal sex ratio and binomially distributed reproductive success, such that the census size (N) is approximately equal to Ne. Although Ne under the simulated conditions is actually slightly larger than N, that is, Ne=N+1/(2N)+0.5 (Balloux, 2004), the correction term 1/(2N)+0.5 was used for all calculations as the ‘true' Ne; for simplicity N and Ne will be treated as equivalent hereafter, following Waples (2006). Populations with an initial (starting) effective size of Ne=100, 250, 500 and 1000 were used in simulations, with each simulation replicated 100 times. The genome used in simulations consisted of 25 chromosomes, each 0.75 M in size; for each chromosome, map positions for 200 SNP loci were chosen randomly at the beginning of each simulation. Initial allele frequencies at each SNP locus were determined by a pseudorandom draw from a uniform distribution (0, 1). Consequently, each replicate began with loci near linkage equilibrium. Theoretical results (Sved, 1971) indicate that for populations with Ne⩽1000, loci separated by at least 0.01 M and starting in linkage equilibrium should reach steady-state levels of LD in ∼200 generations. Thus, all replicates were ‘burned-in' for 200 generations. The per locus mutation rate followed a SNP model, with the rate of forward mutation equal to 1 × 10−8 and the reverse mutation rate equal to 1 × 10−9. The probability of recombination between adjacent loci was proportional to the distance between them, that is, loci 0.01 M apart have a 1% chance of recombination in each individual in each generation. After 250 generations, 50 individuals were sampled from each simulated population and genotypes at 1000 randomly selected, polymorphic SNP loci were recorded into a single Genepop file. A square matrix of recombination rates for all pairs of loci also was generated for each simulated population. For each population, Ne was estimated by using pairs of loci binned as noted previously; loci with minor alleles at frequency <0.05 were excluded from the analysis. Initial runs revealed a downward bias in estimates of Ne in prior generations because of tightly linked loci that had not reached steady-state linkage disequilibrium; consequently, locus pairs separated by <0.015 M were excluded from estimations. Estimates of the coefficient of variation of Ne, calculated as in Hill (1981), were used to generate 95% confidence intervals for each bin, and harmonic means of estimates of Ne and their confidence intervals across replicates were plotted using the ggplot2 package (Wickham, 2009) in R (R Core Team, 2015). Bias of each estimate was computed as the distance of the harmonic mean of estimated Ne, across replicates, from the true Ne and expressed as a percentage of the true Ne. Precision was measured as the coefficient of variation of Ne (Hill, 1981).

Detection of changes in Ne

Five different demographic models were simulated in addition to the ‘constant' population described above. Three models involved declines in effective size (to 25, 50 and 75% of starting size), whereas two involved expansions (to 2 × and 5 × of starting size). All models were simulated as an instantaneous change in census size that occurred five generations before sampling; otherwise, all simulations were run in exactly the same manner as with the constant population. A sample (S) of 50 individuals was taken at the end of each simulation except when a model involved a reduction in census size to <50 individuals, in which case all remaining individuals were sampled. Detection of a change in Ne was assessed by observing whether confidence intervals overlapped between the estimate of Ne from the most recent bin (1 to 3.3 generations in the past) and the estimate from bin furthest in the past (⩾10 generations). Bias and precision of each estimate were evaluated as discussed at the end of the prior section.

Evaluation of sample-size bias correction

Because the linkage approach is intended to identify possible demographic changes by evaluating differences in Ne measured using pairs of markers that have various linkage relationships, it is important to determine whether estimates of Ne made from any single bin are more or less biased than estimates from other bins. If so, different levels of bias among bins could be incorrectly interpreted as demographic change. Waples (2006) and England et al. (2006) reported a bias in estimating Ne because of exclusion of second- and higher-order terms when accounting for the contribution of sampling error to LD measured in a finite sample. The bias is downward and is particularly large when S is small relative to the true Ne. To account for the bias, an empirically derived correction factor was proposed by Waples (2006). To explore the effect of the correction on estimates of Ne from prior generations, all simulations of the constant population model were evaluated with both the sample-size bias correction and using only 1/S to account for r2sample. Ne was again measured across 100 replicates and the harmonic mean of results across replicates recorded.

Allele-frequency cutoff

The presence of rare alleles also can bias LD-based estimates of Ne (Waples, 2006), and excluding rare alleles has been proposed (Waples and Do, 2008) as a means to reduce the bias. We explored the effect of this bias by testing a series of allele-frequency cutoff thresholds (0.10, 0.05, 0.02, 0.01 and 0) using the constant population model with N=250. Here, and in all subsequent analyses, the sample-size bias correction proposed by Waples (2006) was applied to estimations of Ne. As above, Ne was measured across 100 replicates and results averaged across replicates.

Effect of time between demographic change and sampling

Over time, drift and recombination reorganize patterns of LD, removing signatures of past Ne. In order to evaluate effectiveness of the linkage approach to detect past demographic change, the length of time that signatures of past Ne persist in the genome was assessed under two different models, a decline to 25% and an expansion to 2 ×, both with a starting Ne of 250. The simulation was modified to adjust the number of generations (1, 5, 10, 20 and 50) between the demographic change and the time at which sampling occurred. As above, results were averaged across 100 replicates.

Comparison with the LDNe method

More often than not, linkage relationships of marker pairs are not known and current Ne is estimated by LD under the assumption that all loci are unlinked. This assumption becomes compromised when genotypes at thousands of genetic markers are obtained, an increasingly common standard in genomics studies of nonmodel species (Allendorf et al., 2010). To evaluate the effect of this assumption, we used NeEstimator v.2.01 (Do et al., 2014) to estimate current Ne from the simulated data, using the constant population model for each ‘true' Ne (100, 250, 500 and 1000). Estimates of Ne and parametric confidence intervals were obtained by excluding alleles with frequency <0.05 and recording the harmonic mean from 100 replicates. The difference between estimates of Ne and the true Ne was estimated and compared with results when using only unlinked pairs of loci and LinkNe.

Empirical data

The linkage approach also was applied to genotype data from a single sample consisting of two consecutive cohorts of juvenile red drum (Sciaenops ocellatus) sampled from West Matagorda Bay, Texas, in 2008. West Matagorda Bay is one of several Texas bays and estuaries that are stocked annually with fingerling red drum as part of a state-wide stock enhancement program (Vega et al., 2003) and was one of several bays sampled over a period of years to monitor the relative contribution of stocked fish to wild populations, using genetic parentage assignment (Karlsson et al., 2008; Carson et al., 2014). The sample from West Matagorda Bay was selected for analysis because it contained an abnormally high proportion (>16%) of juvenile fish of hatchery origin (Carson et al., 2014). Because the hatchery-raised individuals likely originated from a limited number of breeders (Gold et al., 2008; Carson et al., 2014), the result was a relatively small Ne in the sample that contained both hatchery-raised and ‘wild' fish (Table 1). In addition, because the reduced Ne is a first-generation effect caused by the presence of a large proportion of hatchery-raised individuals in the sample, the reduction in Ne should not be detected in prior generations. Genotype data were obtained through double-digest restriction-site associated DNA sequencing, following standard protocols (Peterson et al., 2012). Pairwise recombination rates for SNP markers were estimated using genotype data from parents and F1 progeny from an outbred cross previously used to develop a linkage map for red drum (Hollenbeck et al., 2015). Illumina data were processed with the dDocent pipeline (Puritz et al., 2014); details are presented in Supplementary Appendix 2. Genotypic data and a matrix of pairwise recombination rates were used to generate estimates of Ne using LinkNe. The program was run as in the simulations except that no filter was applied to remove tightly linked locus pairs. Data were summarized using the ggplot2 package in R.

Table 1. Estimates of current effective population size (Ne) for: (1) all juvenile red drum sampled from West Matagorda Bay, Texas; (2) wild individuals only; and (3) hatchery-raised individuals only.

Sample Low Ne High
All (S=56) 206.9 208.3 209.7
Wild (S=42) 4753.5 5912.6 7817.1
Hatchery (S=14) 12.4 12.4 12.5
Open in a new tab

Estimates were generated using NeEstimator2 (Do et al., 2014); low/high refers to parametric 95% confidence intervals. Rare alleles were excluded below a threshold of 0.05. S refers to sample size.

Results

Simulations

Simulations involving populations of constant size were used to assess precision and bias associated with estimates of Ne at different points in the past. The strategy used to bin locus pairs resulted in four bins, each producing an estimate of Ne at a different time in the past. The exact time point used for each estimate (t) was dependent upon the distribution of loci in the genome that was randomly determined at the beginning of each simulation. Mean time estimates for the four bins, averaged across all starting values of Ne, were 1.01, 3.99, 6.65 and 14.35 generations in the past. Bias and precision of Ne estimates are presented in Table 2.

Table 2. Bias and precision for estimates of effective population size (Ne) at all time periods using simulated populations of constant size.

True Ne Time Percent bias CV
100 14.377 2.290 0.053
100 6.650 −2.425 0.055
100 3.994 −6.094 0.074
100 1.009 3.540 0.017
250 14.339 −0.350 0.069
250 6.649 −7.344 0.084
250 3.997 −8.002 0.130
250 1.009 3.151 0.039
500 14.340 −4.850 0.096
500 6.647 −3.509 0.140
500 3.993 −8.780 0.231
500 1.009 7.509 0.081
1000 14.342 −4.990 0.154
1000 6.648 −8.142 0.248
1000 3.994 −9.261 0.620
1000 1.009 6.961 0.175
Open in a new tab

‘True Ne' is the true Ne of the simulated population; ‘Time' is the time period (generations in the past) to which the estimate refers; ‘Percent Bias' is the difference between the estimated and true Ne, as a percentage of the true Ne; ‘CV' is the coefficient of variation of the estimate, calculated following Hill (1981).

Bias, as measured by the distance between the harmonic mean of Ne estimates across replicates and the true Ne, scaled by true Ne, was <10% in all cases; direction and magnitude of the bias was dependent upon both Ne and number of generations in the past to which an estimate applied. Bias for estimates from the most distant past (14.35 generations) was smallest and positive (upward bias) for Ne=100 (2.29%) and negative (downward bias) for larger Ne (−0.35%, −4.85% and −4.99% for Ne=250, 500 and 1000, respectively). Bias for estimates from the most recent past (1.01 generations) was positive (3.54, 3.15, 7.51 and 6.96% for Ne=100, 250, 500 and 1000, respectively), whereas bias for intermediate time points in the past (3.99 and 6.65 generations) ranged from −2.42% to −9.26%. In all but one case, confidence intervals for estimates of Ne encompassed the true Ne. Because of a slight upward bias and high precision, the estimate of Ne from the most recent past (1.01 generations) for the simulation where Ne=100 had a confidence interval of 100.6–107.5.

Precision was greatest for estimates from the more recent past (1.01 generations) and ranged from 0.017 (Ne of 100) to 0.081 (Ne of 1000). The next highest level of precision was obtained for estimates from the most distant past (14.35 generations) and ranged from 0.053 (Ne of 100) to 0.096 (Ne of 1000). Intermediate time points (3.99 and 6.65 generations) were the least precise, ranging from 0.054 (t=6.65 generations; Ne of 100) to 0.620 (t=3.99 generations; Ne of 1000).

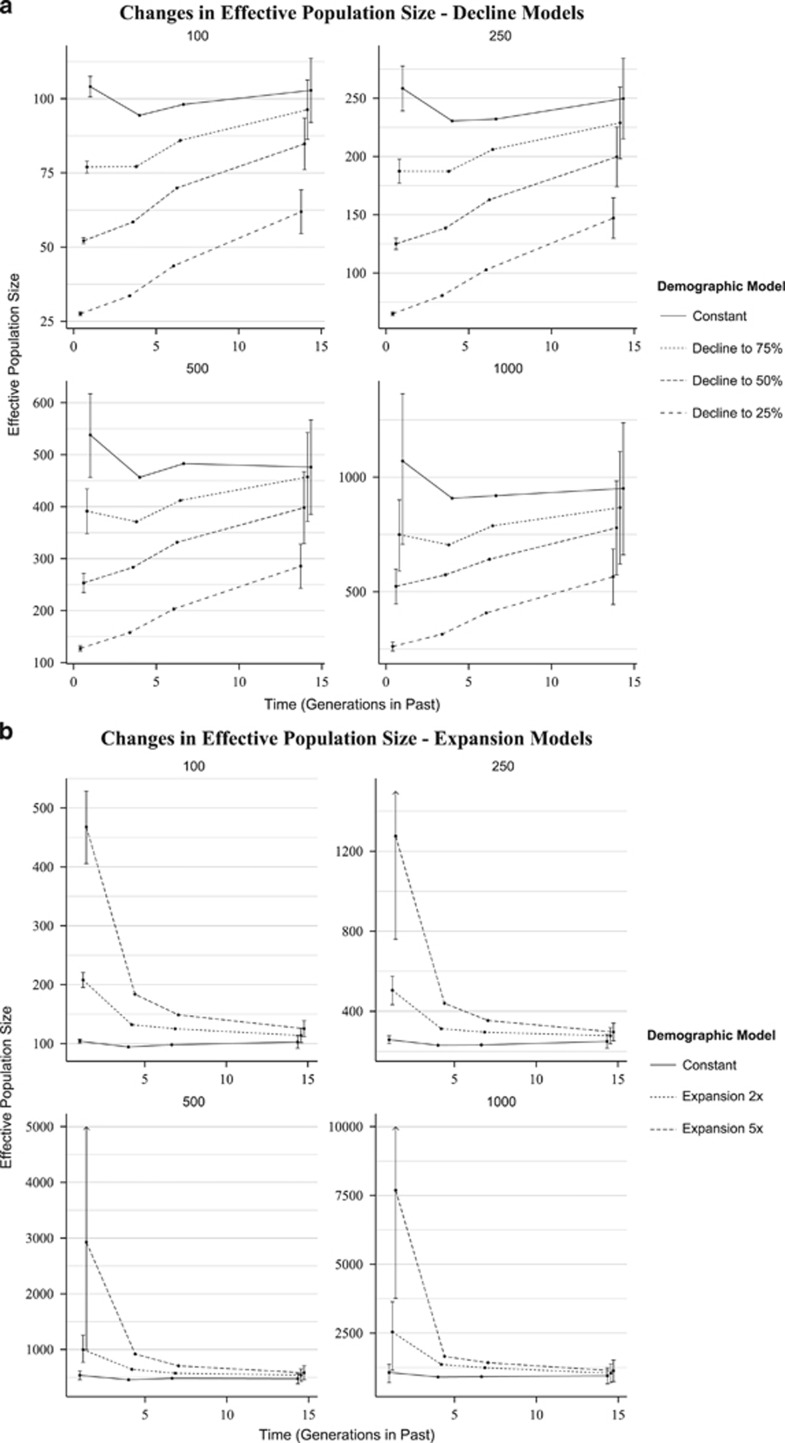
Results of simulations to investigate the ability of the linkage approach to detect declines and expansions in Ne are summarized in Figure 1. For the models where Ne remained constant, confidence intervals always overlapped; thus, a change in Ne was never falsely detected. A change in Ne was detected in 80% of all decline/expansion models where a change in Ne had occurred. Changes in Ne were detected more often when initial effective population size was small and/or when the magnitude of change was great. This was due in part to greater precision of estimates of Ne in smaller populations. A summary of demographic models and whether a change in Ne was detected in each model is presented in Table 3.

Figure 1.

Figure 1

Open in a new tab

Estimates of Ne over time in the past for various demographic models, produced with LinkNe. Each panel represents a different starting effective population size (Ne). Confidence intervals are shown only for estimates from the most recent and most distant past. Time points within a plot are adjusted horizontally so that confidence intervals could be distinguished. (a) Trend lines for constant and decline models. (b) Trend lines for constant and expansion models. Upper confidence limits for estimates of Ne for the expansion to 5 × model and for starting Ne of 250, 500 and 1000 were truncated for clarity and are marked with an arrow to indicate that the interval extends beyond the limits of the plot.

Table 3. Sensitivity of detection of changes in effective population size (Ne) for different demographic models.

Demographic model Initial Ne Change in Ne detected
Constant 100 No
  250 No
  500 No
  1000 No
Decline to 75% 100 Yes
  250 Yes
  500 No
  1000 No
Decline to 50% 100 Yes
  250 Yes
  500 Yes
  1000 No
Decline to 25% 100 Yes
  250 Yes
  500 Yes
  1000 Yes
Expansion to 2 × 100 Yes
  250 Yes
  500 Yes
  1000 No
Expansion to 5 × 100 Yes
  250 Yes
  500 Yes
  1000 Yes
Open in a new tab

Change in Ne was estimated using LinkNe for each model based on 1000 single-nucleotide polymorphism (SNP) loci and a sample size of 50 except where the change in Ne generated a population of <50 individuals (in which case all individuals were sampled). Change in Ne was detected when confidence intervals between estimates from the most distant past (14.3 generations) and those from the most recent past (1.01 generations) did not overlap.

Estimates of Ne over time for constant and decline models are shown in Figure 1a. The linkage approach was always able to detect declines to 25% of initial Ne. Declines to 50% were detected for initial Ne of 100, 250 and 500 but not 1000; declines to 75% were only detected for initial Ne of 100 and 250. Estimates of Ne at 1.01 generations in the past were fairly accurate as bias for models of decline to 25, 50 and 75% (averaged across simulations for all starting values of Ne) were 4.06%, 2.15% and 1.35%, respectively. Estimates of Ne for the most distant time in the past (14.3 generations) were downwardly biased for all decline models; bias for declines of initial Ne to 25, 50 and 75% were −41.5%, −19.6% and −8.71%, respectively.

Expansions in Ne (Figure 1b) were detected in all but one model (initial Ne of 1000 and a 2 × expansion); confidence intervals between the most recent (1.01 generations) and most distant (14.3 generations) times in the past overlapped slightly. Bias for estimates of Ne at 1.01 generations in the past, averaged across starting values of Ne, was positive and <10% for expansions of 2 × and 5 × (7.88% and 1.95%, respectively); bias varied considerably over each time period for different values of Ne (2 × : −0.23 to 27.08% 5 × : −41.5 to 53.77%). Estimates of Ne in the past were influenced less by expansions in population size than by declines.

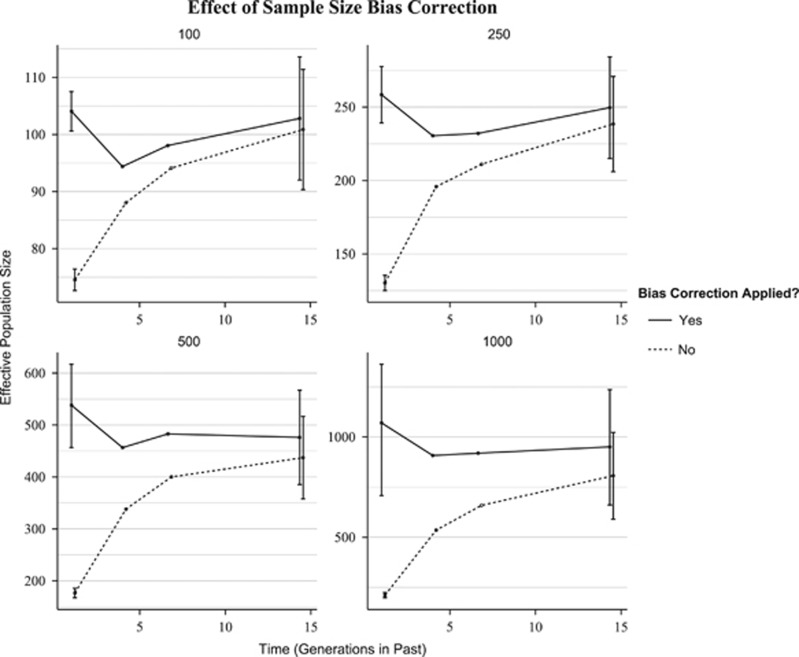
The sample size bias proposed by Waples (2006) influenced estimates of Ne in the recent past to a greater extent than estimates in the more distant past (Figure 2). When the bias correction was not applied, a downward bias was present for estimates at all points in time and was larger for more recent time periods, with an average bias of −7.93% (14.3 generations), −18.7% (6.65 generations), −26.9% (3.99 generations) and −50.9% (1.01 generations). There also was an effect of Ne on bias, as downward bias increased with increasing Ne. Overall, failure to apply the bias correction resulted in a significant downward trend, falsely indicating that the model of constant size had experienced a recent decline in Ne.

Figure 2.

Figure 2

Open in a new tab

Effect of sample-size (S) bias correction proposed by Waples (2006) on estimates of Ne over time. Estimates were produced with LinkNe. Solid lines represent estimates of Ne, with bias correction applied, for the constant population size model. Dashed lined represent estimates where r2sample was measured as 1/S.

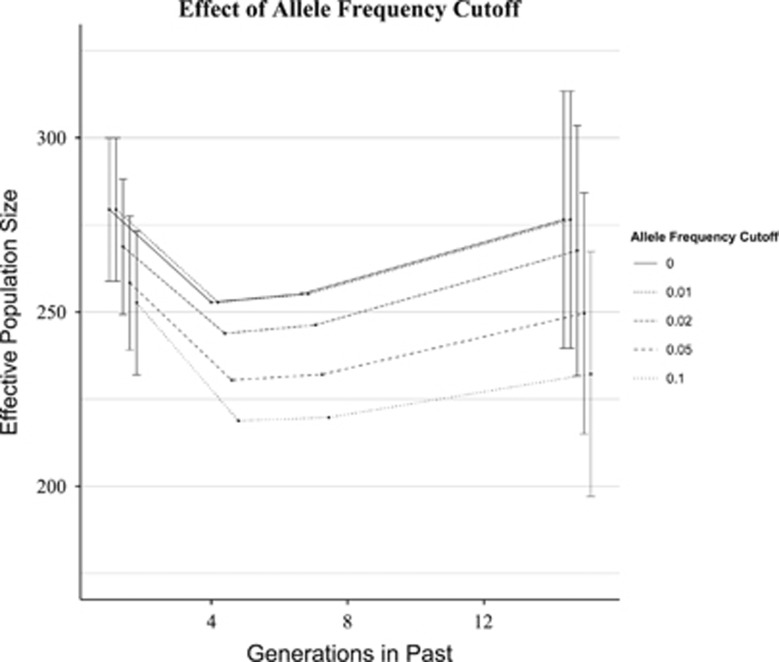
The cutoff value for excluding rare alleles had the most influence on estimates of Ne from the most distant past (Figure 3). For estimates of Ne in the recent past (1.01 generations), mean values of Ne ranged from 252.7 to 274.4 (range=26.74); for estimates of Ne in the most distant past (14.3 generations), values ranged from 232.2 to 276.5 (range=44.28). For all allele-frequency cutoff values evaluated, estimates of Ne in the recent past were upwardly biased, whereas the direction of bias for estimates in the more distant past depended on the level of cutoff chosen. No cutoff value was the least biased for all time points, although a cutoff value of 0.05 appeared to be the best compromise, as it resulted in the least bias, on average, across all time points (Figure 3).

Figure 3.

Figure 3

Open in a new tab

Effect of excluding rare alleles at various thresholds (0.10, 0.05, 0.02, 0.01 and 0), using the constant population model with N=250.

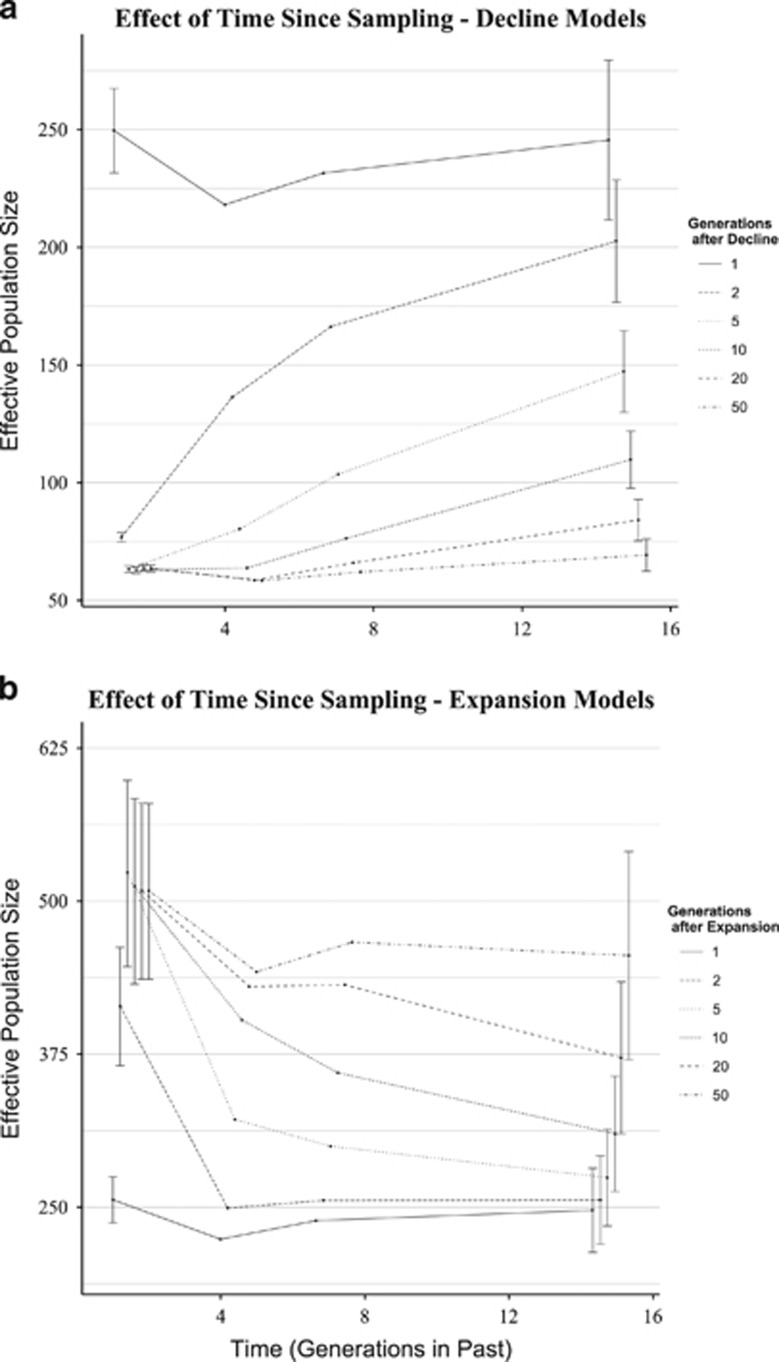
The number of generations between demographic change and sampling had a large effect on resulting estimates of Ne (Figure 4). For all demographic change models, estimates of Ne derived from unlinked and moderately linked loci (c>0.15 M) equilibrated to the correct Ne within five generations, whereas estimates from tightly linked loci (c⩽0.15 M) approached the new Ne more slowly. Both population expansions and declines could be detected up to 20 generations in the past. Estimates from the distant past (14.3 generations) tended to equilibrate more slowly for demographic expansions than for declines.

Figure 4.

Figure 4

Open in a new tab

Effect of length of time between demographic change and sampling. (a) Results for decline to 25% of initial Ne of 250 when sampling was conducted 1, 2, 5, 10, 20 and 50 generations after a decline. (b) Results for an expansion to 2 × of initial Ne of 250 when sampling was conducted 1, 2, 5, 10, 20 and 50 generations post expansion.

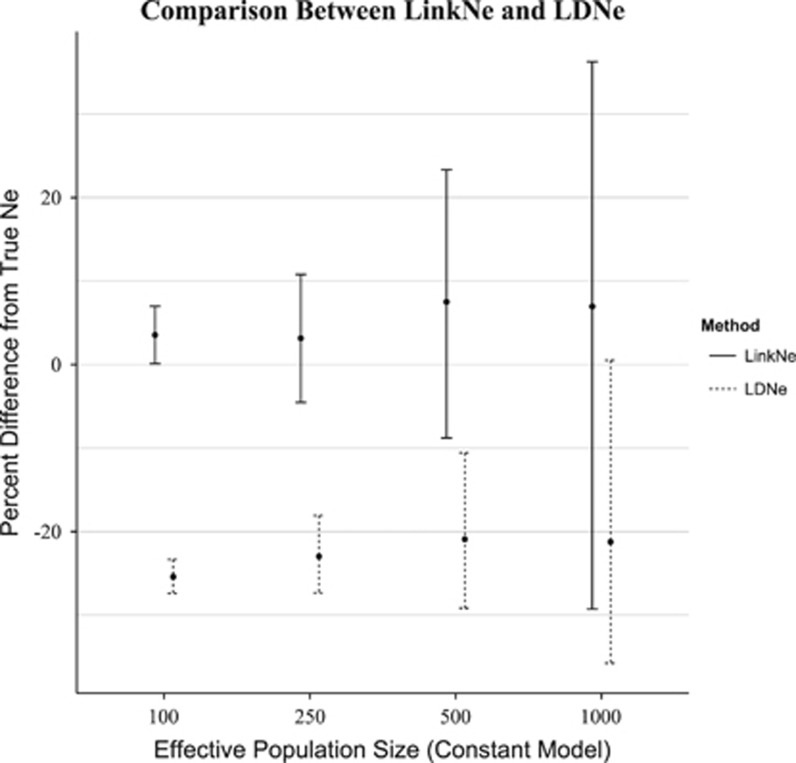
For all values of Ne under the constant model, estimates of current Ne based on NeEstimator2 were biased downward by >20% (Figure 5). Bias for initial Ne of 100, 250, 500 and 1000 was −25.4%, −23.0%, −20.9% and −21.2%, respectively. Estimates generated using LinkNe had a small upward bias of 3.54%, 3.15%, 7.51% and 6.96% for initial Ne of 100, 250, 500 and 1000, respectively.

Figure 5.

Figure 5

Open in a new tab

Comparison of bias in measures of Ne using LinkNe and the LDNe method (as implemented in NeEstimator2). Bias was measured as the difference between the estimated and true Ne and is expressed a percentage of the true Ne. Estimates of Ne based on linkage disequilibrium can be biased downward when linked loci are assumed to be unlinked.

Empirical data

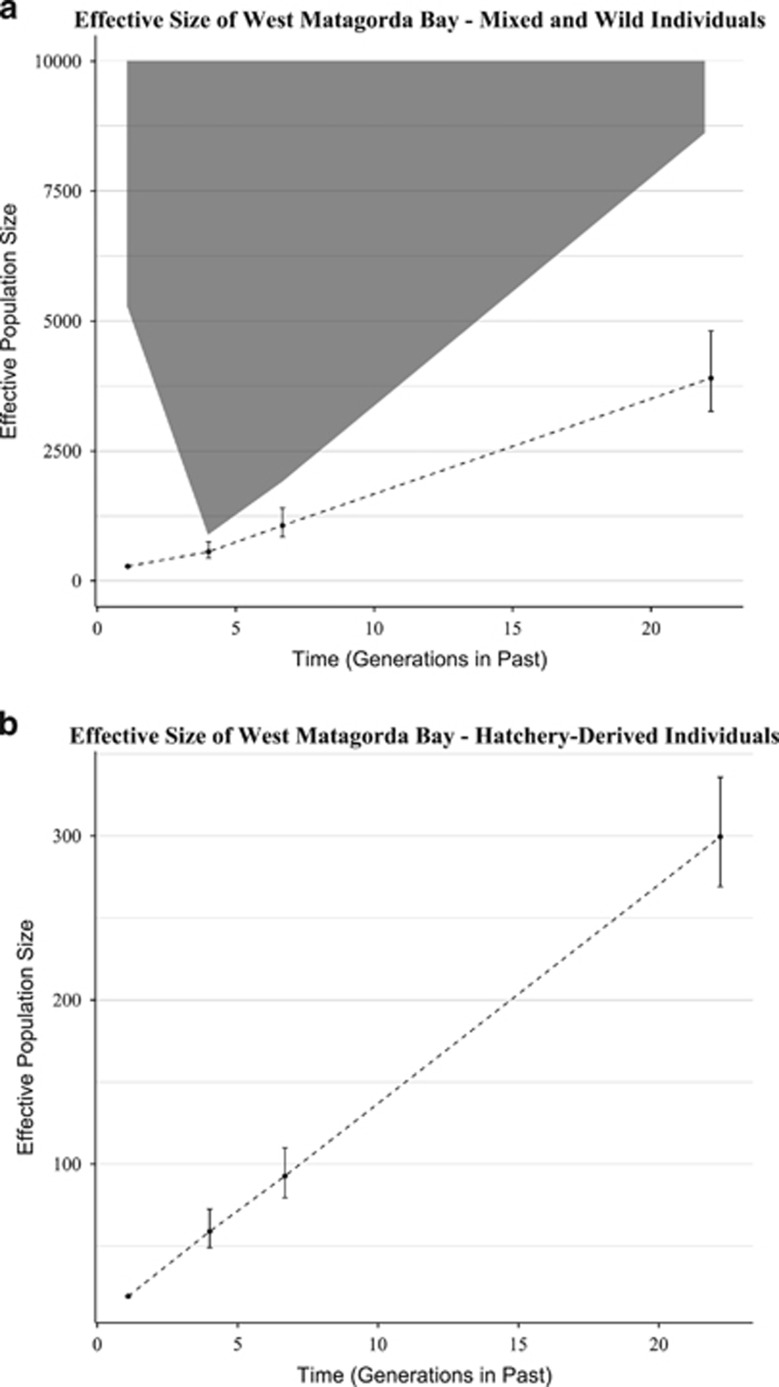
The trend line for the sample from West Matagorda Bay (Figure 6a, dashed line) was suggestive of a recent decrease in Ne, consistent with the presence of hatchery-raised individuals in the sample. Separating the sample into hatchery-raised and wild fish revealed that estimates of Ne over time for wild fish were large and featured no observable trend (Figure 6a, gray ribbon); estimates from hatchery-raised individuals alone (Figure 6b) were consistent with the expected bottleneck (based on Gold et al., 2008) of progeny from the parental brood stock. Trend lines for both the mixed sample and the hatchery-raised individuals were consistent with results of simulations (see Figure 1a, decline to 25%); estimates of Ne for the more distant past appeared lower than expected and the slope of the trend line less steep than expected, given that the decrease was known to have occurred in the previous generation.

Figure 6.

Figure 6

Open in a new tab

Results of analysis, using LinkNe, of a sample of red drum juveniles from Matagorda Bay, TX. (a) Trend line (dashed) for Ne produced using all sampled individuals and confidence interval (CI) of Ne when F1 hatchery individuals are removed (shaded area). Note that when ‘wild' individuals are assessed, only the lower bounds of the CI are estimable from the data; for clarity, the CI is truncated at 10 000. (b) Trend line for F1 hatchery-raised individuals, indicative of a large decline in Ne in the parental generation that consisted of hatchery brood stock.

Discussion

Simulations

The ability of this or any approach to identify changes in Ne over time is largely dependent on precision and potential bias. If estimates of Ne at different times in the past are systematically biased, inferences regarding demographic trends will be compromised. Results of simulations revealed <10% bias in estimates of Ne for populations of constant size over the time period (~1–15 generations in the past) assessed. However, the magnitude and direction of the bias depended on both the time to which an estimate referred and the true Ne. This suggests that although the precision provided by the number of simulated loci (1000) was such that confidence intervals for estimates of Ne across time tended to overlap for the constant population at all initial effective sizes, increasing the number of loci could produce estimates so precise that confidence intervals would not overlap, even for populations of constant size. However, because bias for all estimates was small (<10%), it would be unlikely that such a situation would be confused for a large change in Ne.

Further study is needed to evaluate the source of bias at different periods in time. For example, it is not clear why estimates from intermediate time points tend to be more biased and in a downward direction. It should be noted that in addition to the sample-size bias correction, a simulation-based bias correction for the drift component of r2 was proposed by Waples (2006) for unlinked loci. An applied correction for linked loci might eliminate some of the bias, but the correction factor would be challenging to implement because a correction factor would have to be calculated for all values of c across the spectrum of possible linkage values. Although Waples (2006) found little bias in Ne due to drift for unlinked loci when initial Ne was >100, the smallest initial Ne evaluated in our study, it is unclear whether this also is true for linked loci.

Our findings regarding precision of Ne estimates over time are in agreement with Hill (1981) who showed that the coefficient of variation of Ne decreases as the recombination rate decreases and the number of pairwise locus comparisons increases. This means, given an equal number of pairwise comparisons, estimates of Ne in the past should be more precise than recent estimates (Hill, 1981; Hayes et al., 2003). However, the vast majority of locus pairs in a genome are unlinked, and hence the large number of pairwise comparisons available should yield recent estimates with a high level of precision. Consistent with this, intermediate time periods (corresponding to intermediate values of c) had the lowest level of precision, most likely as a consequence of having the fewest number of pairwise comparisons.

Results of simulations demonstrated that for ideal populations, recent changes in Ne can be reliably detected by comparing estimates of Ne based on LD from pairs of linked and unlinked loci. In our simulations, trend lines for the constant population at all initial effective sizes never indicated a change in Ne, although trend lines for models with a change in Ne in some models indicated stability. This has important implications for interpretation of results when using the linkage approach as it indicates that although detected changes in Ne are robust, results indicating constant size need to be carefully scrutinized. Our simulations revealed that changes in Ne are more readily detected when Ne is small, largely because of increased precision of LD-based estimators at smaller Ne. In fact, even relatively small changes in Ne (declines to 75% of the original value) were detected provided that the initial Ne was 250 or less. The linkage approach was less effective in populations with larger initial Ne as only changes in Ne of relatively large magnitude could be detected. However, increasing the sample size, which was fixed at 50 individuals for all simulations, should improve resolution to detect changes for populations of larger initial Ne.

Estimates of Ne were fairly accurate for more recent time (t≈1 generation) in the past. This is because sampling was conducted five generations after the change occurred and unlinked (or moderately linked (c >0.15 M)) loci are expected to equilibrate to the new steady-state level of LD in three to four generations (Sved, 1971; Waples, 2006). Estimates from the more distant past (>3.33 generations) reflected Ne of the population before the change in Ne; however, these estimates tended to be influenced by more recent Ne. This effect was particularly pronounced for decline models, where estimates reflecting prior generations showed a considerable downward bias, causing trend lines to be less steep than expected. In addition, the bias was exaggerated for declines of large magnitude. Estimates of Ne in the past during expansion models were less influenced by more recent Ne, and it is likely that the different effects on estimates of Ne in the past observed in decline and expansion models relate to the relative contribution of drift and recombination to steady-state levels of LD. In the case of a decline, LD accumulates between loci at every linkage interval relatively quickly because of the increased importance of drift. Alternatively, in an expanding population drift becomes less important as time is required for recombination to dissolve LD between linked loci. In practice, this suggests that the true magnitude of a decline in Ne would be difficult to detect with certainty because past estimates would be influenced by effects of drift in more recent generations; estimates of past Ne following a population expansion, however, may provide a more reliable estimate of the magnitude of the change in Ne.

A critical component of the linkage approach is establishment of a relationship between recombination rate and time. Although an approximate relationship was suggested by Hayes et al. (2003), it was derived under the limiting assumptions that c is small and that Ne changes linearly with respect to time. Despite the fact that these assumptions are clearly violated, trend lines from our simulations agreed reasonably well with known timing of changes in Ne, particularly for expansion models. The results were less concordant for decline models, as trend lines suggested more gradual declines than expected. This is likely because of effects of increased genetic drift following a decline. Organizing locus pairs into bins and using a mean value for c, although necessary for achieving acceptable levels of precision, is one source of discordance between theoretical and observed results. Depending on the size of the bin and the degree of linkage, estimates of LD at locus pairs in genomic regions reflecting Ne across multiple generations are collapsed into a single estimate that may obscure fine-scale trends.

The simulations evaluated consisted of ideal populations with non-overlapping generations, even sex ratios, and binomially distributed reproductive success, such that N≈Ne. More rigorous investigation is necessary to evaluate effects on estimates made when these assumptions are violated. Effects of skewed sex ratio and increased variance in reproductive success on estimates of contemporary Ne generated with the LD method have been investigated to some extent by Waples (2006), with the conclusion that the assumptions are fairly robust to the influence of these effects, that is, an ideal population with a given Ne is a reasonable proxy for nonideal populations with the same Ne (Waples, 2006). However, the biological characteristics of the species tend to determine the Ne/N ratio (Portnoy et al., 2009), and it is likely that changes in census size (N) influence estimates of Ne differently. Therefore, although the linkage method can robustly detect changes in Ne, care must be taken when interpreting the results in terms of changes in census size. Additional study will be necessary to understand the influence of other factors that shape patterns of genome-wide LD in natural populations on estimates of past Ne; these factors include selection, migration, admixture and complicated demographic patterns.

Our simulations demonstrate the importance of sample-size (S) bias correction for accurately assessing changes in Ne. England et al. (2006) and Waples (2006) demonstrated that estimates of Ne can be downwardly biased when S is small relative to the true Ne and that this bias is more pronounced for estimates of Ne in the more recent past. When bias correction was not applied, the linkage method produced trend lines characteristic of a decline in Ne, even for the constant populations that had not experienced a decline. This is an important consideration, and little attention has been given to the effects of S on estimates of Ne in studies applying similar methods. Although the bias correction applied to the data was derived from simulations using only unlinked loci (Waples, 2006), the fact that the bias appears to be less important for linked loci suggests that the bias correction is appropriate for this analysis. It is important to note that the effect of S may be dependent on the way in which r2 is estimated, with estimators where marker phase is known requiring a smaller correction factor (Corbin et al., 2012).

The effect of modifying the cutoff value for excluding rare alleles varied depending on the time in the past to which estimates applied, and there was no single, optimal allele-frequency cutoff. In general, a cutoff at an allele frequency of 0.05 produced estimates of Ne across the range of time points that were closest to the true Ne. In addition, results for estimates based on unlinked loci were consistent with the findings of Waples and Do (2008) that indicated that larger cutoff values minimized upward bias caused by occurrence of rare alleles. Furthermore, our results paralleled that of a previous study (Corbin et al., 2012) where effects of modifying rare allele cutoffs for estimates of past Ne, using phase-known data, were explored. It was concluded from that study that a cutoff value between 0.05 and 0.1 produced the most accurate estimates. Applying a separate cutoff to locus pairs in different bins may produce more accurate estimates across all time points, if increased cutoff values were used for estimates further back in time.

Several insights were gained by modifying time of change in Ne relative to sampling. First, based on evaluating overlap of confidence intervals between past and present estimates, the linkage approach was able to detect both expansions and declines in Ne at least 20 generations in the past. In theory, it is possible to obtain estimates of Ne in the much more distant past (and to thus detect older demographic changes) if LD can be measured between very tightly linked loci (<0.01 M). However, simulations by Corbin et al. (2012) suggest that estimating long-term trends can be problematic, in part because the effect of mutation is important over long periods of time. Second, analysis of trend lines for decline and expansion models reinforced the idea that past estimates of Ne are influenced more by declines than expansion, as past estimates of Ne rapidly approach the new steady-state level of LD after a decline but approach the new level more slowly following an expansion. When the change in Ne occurred 50 generations in the past, neither declines nor expansions could be statistically differentiated from stasis. In the case of declines, the mean estimate of Ne was the same between the most recent generation and the generation furthest in the past. For expansions, the mean estimate of Ne was larger in the most recent generation than the generation furthest in the past; however, precision was limiting and confidence intervals overlapped. This further suggests that genomic patterns of LD indicating an expansion in Ne persist for longer, enabling expansions in the more distant past to be detected.

Results from simulations indicated that the assumption that all loci in a genome-wide data set are unlinked can downwardly bias estimates of contemporary Ne by as much as 25%. In the absence of marker linkage or genomic position data, it is unclear what should be the best strategy for avoiding this bias. One approach is to remove estimates from locus pairs with excessively high LD as they possibly are influenced by physical linkage (Gruenthal et al., 2014); in practice, however, the decision to remove such loci is fairly arbitrary. Regardless, in the absence of known linkage relationships, acknowledging that estimates of Ne from the LDNe method likely underestimate the true value is a conservative approach; the fact that the bias is downward is favorable from a biological risk assessment standpoint because overestimating Ne likely will have more dire consequences for imperiled species than underestimating Ne.

Empirical data

A decrease in Ne in the sample of juvenile red drum from Matagorda Bay in 2008 was detected using the linkage approach. Presumably the decline in Ne was because of the presence of an inordinately large proportion of hatchery-raised juveniles in the sample. The effect, as expected, was temporary as the current Ne of a second sample from the same locality, taken in 2015, was considerably larger than the estimate of current Ne in the wild fish in the 2008 sample (unpublished data). This highlights that interpretation of trends in Ne based on LD should be made with caution. If the trend line for the mixed sample had been generated with no knowledge about the constituents of the population, one might have hypothesized erroneously that the population of red drum in Matagorda Bay had experienced a recent, large decline in Ne possibly caused by a decline in census population size rather than an unequal contribution of progeny from a limited number of breeders in the parental generation. In addition, despite the rapidity of the decrease in Ne, the trend line indicated a more gradual decline that suggested that the decline occurred in the more distant past. This likely occurred for several reasons, including uncertainty in estimating recombination rates from the mapping cross and the necessity of binning loci over large genomic distances.

One consideration important to interpretation of these data is the effect of overlapping generations on estimates of Ne. It has been demonstrated that for samples taken from a single cohort or multiple consecutive cohorts, estimates of Ne based on LD are influenced by both the effective number of breeders (Nb) contributing to the sampled cohorts and Ne, with the amount of bias in the estimates being related to the ratio of Nb/Ne (Waples et al., 2014). Red drum has been estimated to have a ratio of Nb/Ne≈1.2 (Waples et al., 2013), and based on simulated estimates of bias for samples of two consecutive cohorts, the expected downward bias for estimates based on unlinked loci should be <30% (Waples et al., 2014). Interpretation of estimates based on linked markers relative to Nb and Ne is more difficult, but because past estimates are based on LD that has accumulated on generational time scales, they should represent the combined effects of all cohorts in an age-structured population, and should thus refer primarily to Ne. However, the effects of age-structure should be investigated more thoroughly in future research. Regardless of how estimates at various points in time are to be interpreted in terms of Nb and Ne, it should be stressed that although historical trends can be identified with some confidence, care should be taken when interpreting particular point estimates made with this method.

Another important consideration when evaluating potential changes in Ne using large, empirical data sets is that parametric confidence intervals (calculated based on the χ2 approximation; Hill, 1981) may be too narrow when many loci are utilized (see Waples et al., 2016). This is because, as the number of utilized loci increases, there are more correlations among r2 values for locus pairs that share common loci, and this increasingly violates the assumption of independence of comparisons implicit in the parametric model (Waples, 2006; Waples and Do, 2010). As a result, parametric confidence intervals do not adequately convey the uncertainty in r2, and the standard jackknife procedure for correcting confidence intervals (Waples and Do, 2008) will not alleviate the problem when a large number of loci are used (Do et al., 2014). Because the linkage method presented here tends to separate pairwise comparisons from the same locus into different bins, the effect is likely relatively less pronounced as compared with a single estimate of Ne using all loci when linkage data are unavailable. However, when comparing confidence intervals of Ne across different points in time it is important to consider the possibility of overly precise and inaccurate estimates. Further study will be needed to quantify the extent to which this problem affects genome-scale data sets. Regardless, considering that bias appears to be relatively low, overly tight confidence intervals are unlikely to result in false detection of large changes in Ne.

Conclusions

We have shown that when linkage or genomic position data are available, the LD approach of estimating Ne from unphased genetic markers (Waples, 2006; Waples and Do, 2008) can be extended to estimate Ne in the recent past and, importantly, to detect recent changes in effective population size (Ne). Results of simulations suggested that even with a moderate number of loci, relatively small changes in Ne (25%) could be detected provided that initial Ne was not large. Furthermore, we explored the effects that sample-size bias correction, rare allele cutoff and time since the change occurred have on estimates of Ne across points in time and quantified the bias in Ne associated with the assumption that all SNPs in a genome-wide data set are unlinked. Finally, we demonstrated the utility of the linkage method for detecting recent changes in Ne on an empirical data set. Overall, results of the analysis of both simulated and empirical data suggest that this approach will be useful for genetic monitoring, particularly when prior genetic samples are not available. This strategy should become increasingly available to species of conservation concern as genotyping-by-sequencing techniques are widely adopted and as genome sequences and linkage maps become more available.

Data archiving

Genepop files for empirical and simulated data can be found in the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.73s46. The LinkNe program can be accessed online at: https://github.com/chollenbeck/LinkNe.

Acknowledgments

We thank Robin Waples for helpful discussion and comments on a draft of the manuscript and Jonathan Puritz and Stuart Willis for helpful discussions regarding analytical methods. This work was supported in part by an Institutional Grant (NA10OAR4170099) to the Texas Sea Grant College Program from the National Sea Grant Office, National Oceanic and Atmospheric Administration, US Department of Commerce and by Grant 447715 from the Texas Parks and Wildlife Department. Additional funding for CMH was provided by the Harte Research Institute for Gulf of Mexico Studies and by a grant (NA14AR4170102) from Texas Sea Grant. This paper is number 105 in the series ‘Genetic Studies in Marine Fishes' and contribution number 11 of the Marine Genomics Laboratory.

The authors declare no conflict of interest.

Footnotes

Supplementary Information accompanies this paper on Heredity website (http://www.nature.com/hdy)

Supplementary Material

Supplementary Appendix 1
Click here for additional data file. (293.3KB, pdf)
Supplementary Appendix 2
Click here for additional data file. (84.2KB, pdf)

References

  1. Alam M, Han KI, Lee DH, Ha JH, Kim JJ. (2012). Estimation of effective population size in the Sapsaree: a Korean native dog (Canis familiaris. Asian-Australas J Anim Sci 25: 1063–1072. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Allendorf FW, Hohenlohe Pa, Luikart G. (2010). Genomics and the future of conservation genetics. Nat Rev Genet 11: 697–709. [DOI] [PubMed] [Google Scholar]
  3. Antao T, Perez-Figueroa A, Luikart G. (2011). Early detection of population declines: high power of genetic monitoring using effective population size estimators. Evol Appl 4: 144–154. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Balloux F. (2004). Heterozygote excess in small populations and the heterozygote-excess effective population size. Evolution 58: 1891–1900. [DOI] [PubMed] [Google Scholar]
  5. Carson EW, Bumguardner BW, Fisher M, Saillant E, Gold JR. (2014). Spatial and temporal variation in recovery of hatchery-released red drum (Sciaenops ocellatus in stock-enhancement of Texas bays and estuaries. Fish Res 151: 191–198. [Google Scholar]
  6. Corbin LJ, Blott SC, Swinburne JE, Vaudin M, Bishop SC, Woolliams JA. (2010). Linkage disequilibrium and historical effective population size in the Thoroughbred horse. Anim Genet 41 (Suppl 2): 8–15. [DOI] [PubMed] [Google Scholar]
  7. Corbin LJ, Liu AYH, Bishop SC, Woolliams JA. (2012). Estimation of historical effective population size using linkage disequilibria with marker data. J Anim Breed Genet 129: 257–270. [DOI] [PubMed] [Google Scholar]
  8. Do C, Waples RS, Peel D, Macbeth GM, Tillett BJ, Ovenden JR. (2014). NeEstimator v2: re-implementation of software for the estimation of contemporary effective population size (Ne from genetic data. Mol Ecol Resour 14: 209–214. [DOI] [PubMed] [Google Scholar]
  9. England PR, Cornuet J-M, Berthier P, Tallmon DA, Luikart G. (2006). Estimating effective population size from linkage disequilibrium: severe bias in small samples. Conserv Genet 7: 303–308. [Google Scholar]
  10. Flury C, Tapio M, Sonstegard T, Drögemüller C, Leeb T, Simianer H et al. (2010). Effective population size of an indigenous Swiss cattle breed estimated from linkage disequilibrium. J Anim Breed Genet 127: 339–347. [DOI] [PubMed] [Google Scholar]
  11. Gibbs RA, Belmont JW, Hardenbol P, Willis TD, Yu F, Yang H et al. (2003). The International HapMap Project. Nature 426: 789–796. [DOI] [PubMed] [Google Scholar]
  12. Gold JR, Ma L, Saillant E, Silva PS, Vega RR. (2008). Genetic effective size in populations of hatchery-raised red drum released for stock enhancement. Trans Am Fish Soc 137: 1327–1334. [Google Scholar]
  13. Gruenthal KM, Witting DA, Ford T, Neuman MJ, Williams JP, Pondella DJ et al. (2014). Development and application of genomic tools to the restoration of green abalone in southern California. Conserv Genet 15: 109–121. [Google Scholar]
  14. Hayes BJ, Visscher PM, Mcpartlan HC, Goddard ME. (2003). Novel multilocus measure of linkage disequilibrium to estimate past effective population size. Genome Res 13: 635–643. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Herrero-Medrano JM, Megens H-J, Groenen MAM, Ramis G, Bosse M, Pérez-Enciso M et al. (2013). Conservation genomic analysis of domestic and wild pig populations from the Iberian Peninsula. BMC Genet 14: 106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Hill WG. (1981). Estimation of effective population size from data on linkage disequilibrium. Genet Res 38: 209–216. [Google Scholar]
  17. Hollenbeck CM, Portnoy DS, Gold JR. (2015). A genetic linkage map of red drum (Sciaenops ocellatus and comparison of chromosomal syntenies with four other fish species. Aquaculture 435: 265–274. [Google Scholar]
  18. Karlsson S, Saillant E, Bumguardner BW, Vega RR, Gold JR. (2008). Genetic identification of hatchery-released red drum in Texas bays and estuaries. North Am J Fish Manag 28: 1294–1304. [Google Scholar]
  19. Larson WA, Seeb LW, Everett MV, Waples RK, Templin WD, Seeb JE. (2014). Genotyping by sequencing resolves shallow population structure to inform conservation of Chinook salmon (Oncorhynchus tshawytscha. Evol Appl 7: 355–369. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Luikart G, Ryman N, Tallmon Da, Schwartz MK, Allendorf FW. (2010). Estimation of census and effective population sizes: the increasing usefulness of DNA-based approaches. Conserv Genet 11: 355–373. [Google Scholar]
  21. Nei M, Tajima F. (1981). Genetic drift and estimation of effective population size. Genetics 98: 625–640. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Peng B, Kimmel M. (2005). simuPOP: a forward-time population genetics simulation environment. Bioinformatics 21: 3686–3687. [DOI] [PubMed] [Google Scholar]
  23. Peterson BK, Weber JN, Kay EH, Fisher HS, Hoekstra HE. (2012). Double digest RADseq: an inexpensive method for de novo SNP discovery and genotyping in model and non-model species. PLoS One 7: e37135. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Pollak E. (1983). A new method for estimating the effective population size from allele frequency changes. Genetics 104: 531–548. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Portnoy DS, McDowell JR, McCandless CT, Musick JA, Graves JE. (2009). Effective size closely approximates the census size in the heavily exploited western Atlantic population of the sandbar shark, Carcharhinus plumbeus. Conserv Genet 10: 1697–1705. [Google Scholar]
  26. Puritz JB, Hollenbeck CM, Gold JR. (2014). dDocent: a RADseq, variant-calling pipeline designed for population genomics of non-model organisms. PeerJ 2: e431. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Qanbari S, Hansen M, Weigend S, Preisinger R, Simianer H. (2010). Linkage disequilibrium reveals different demographic history in egg laying chickens. BMC Genet 11: 103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. R Core Team. (2015). R: a language and environment for statistical computing. R Found Stat Comput 1: 409. [Google Scholar]
  29. Sved JA. (1971). Linkage disequilibrium and homozygosity of chromosome segments in finite populations. Theor Popul Biol 2: 125–141. [DOI] [PubMed] [Google Scholar]
  30. Sved JA, Cameron EC, Gilchrist AS. (2013). Estimating effective population size from linkage disequilibrium between unlinked loci: theory and application to fruit fly outbreak populations. PLoS One 8: e69078. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Tenesa A, Navarro P, Hayes BJ, Duffy DL, Clarke GM, Goddard ME et al. (2007). Recent human effective population size estimated from linkage disequilibrium. Genome Res 17: 520–526. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Vega RR, Chavez C, Stolte CJ, Abrego D. (2003) Marine Fish Distribution Report, 1991–1999. Austin, TX.
  33. Waples RS. (2006). A bias correction for estimates of effective population size based on linkage disequilibrium at unlinked gene loci. Conserv Genet 7: 167–184. [Google Scholar]
  34. Waples RS, Do C. (2008). LDNE: a program for estimating effective population size from data on linkage disequilibrium. Mol Ecol Resour 8: 753–756. [DOI] [PubMed] [Google Scholar]
  35. Waples RS, Do C. (2010). Linkage disequilibrium estimates of contemporary Ne using highly variable genetic markers: a largely untapped resource for applied conservation and evolution. Evol Appl 3: 244–262. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Waples RS, Luikart G, Faulkner JR, Tallmon DA. (2013). Simple life-history traits explain key effective population size ratios across diverse taxa. Proc Biol Sci 280: 20131339. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Waples RS, Antao T, Luikart G. (2014). Effects of overlapping generations on linkage disequilibrium estimates of effective population size. Genetics 197: 769–780. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Waples RK, Larson WA, Waples RS. (2016). Estimating contemporary effective population size in non-model species using linkage disequilibrium across thousands of loci. Heredity (Edinb). (this volume). [DOI] [PMC free article] [PubMed]
  39. Wickham H. (2009) ggplot2: Elegant Graphics for Data Analysis. Springer: New York. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Appendix 1
Click here for additional data file. (293.3KB, pdf)
Supplementary Appendix 2
Click here for additional data file. (84.2KB, pdf)

Articles from Heredity are provided here courtesy of Nature Publishing Group

RESOURCES