Skip to main content
PMC home page
Heredity logoLink to Heredity
. 2016 Aug 24;117(4):233–240. doi: 10.1038/hdy.2016.60

Estimating contemporary effective population size in non-model species using linkage disequilibrium across thousands of loci

R K Waples 1,3,*, W A Larson 1,4, R S Waples 2
PMCID: PMC5026758  PMID: 27553452

Abstract

Contemporary effective population size (Ne) can be estimated using linkage disequilibrium (LD) observed across pairs of loci presumed to be selectively neutral and unlinked. This method has been commonly applied to data sets containing 10–100 loci to inform conservation and study population demography. Performance of these Ne estimates could be improved by incorporating data from thousands of loci. However, these thousands of loci exist on a limited number of chromosomes, ensuring that some fraction will be physically linked. Linked loci have elevated LD due to limited recombination, which if not accounted for can cause Ne estimates to be downwardly biased. Here, we present results from coalescent and forward simulations designed to evaluate the bias of LD-based Ne estimates (N̂e). Contrary to common perceptions, increasing the number of loci does not increase the magnitude of linkage. Although we show it is possible to identify some pairs of loci that produce unusually large r2 values, simply removing large r2 values is not a reliable way to eliminate bias. Fortunately, the magnitude of bias in N̂e is strongly and negatively correlated with the process of recombination, including the number of chromosomes and their length, and this relationship provides a general way to adjust for bias. Additionally, we show that with thousands of loci, precision of N̂e is much lower than expected based on the assumption that each pair of loci provides completely independent information.

Introduction

Effective population size (Ne) is a fundamental population genetics concept (Wright, 1931), which determines the rate of evolutionary change due to genetic drift and informs the equilibrium level of genetic variation and the effectiveness of selection. Ne is often much lower than census size (Frankham, 1995), demonstrating that simply counting individuals is insufficient to predict rates of evolutionary change. In addition to the number of mating individuals, Ne is affected by sex ratio, variation in reproductive success, age structure, migration and other demographic factors. It is an extremely relevant metric in conservation biology, with low Ne leading to inbreeding and reduced genetic diversity (Ellstrand and Elam, 1993). See Charlesworth (2009) for a primer on Ne, and Wang (2005) for a review of estimation methods.

Populations with smaller Ne undergo more genetic drift than larger populations. This genetic drift randomly generates associations between alleles at different loci, known as linkage (or gametic) disequilibrium (LD) at a rate inversely proportional to Ne. As a result, measures of LD between independently-segregating loci can be used to provide an estimate of Ne (Sved, 1971; Hill, 1981; Waples, 1991). Over the past decades, many studies have leveraged data sets consisting of a few dozen loci for genetic estimates of Ne (Luikart et al., 2010). While these studies continue to be useful, especially for long-running projects, biologists now have access to genomic methods that generate orders of magnitude more data. These technologies are growing quickly and have made it feasible to genotype many thousands of loci and improve inference of demographic parameters, provided that the scale and particularities of these new data sets are managed well. Here, we examine the benefits of applying the LD method to estimate contemporary Ne with high-throughput genomic data, and address implications for both bias and precision.

To estimate contemporary Ne with the LD method, it is necessary to measure LD between loci that are inherited independently (that is, recombination fraction (c) equal to 0.5). Estimates of past Ne are available by measuring LD between physically-linked loci with recombination fraction less than 0.5 (Hill, 1981); however, recombination fractions must be known with high precision to look more than a few generations in the past. Recombination fractions are rarely known for non-model species, so this effectively limits their application to model species (for example, Tenesa et al., 2007; Hollenbeck et al., 2016). For non-model species, a blanket assumption of no linkage among loci is often made. This assumption can be reasonable, as the chance that any two loci are physically linked is small, and many analyses are robust to a minor degree of ‘background' LD (for example, Falush et al., 2003). However, with data sets spanning thousands of loci, assuming a complete absence of physical linkage is no longer tenable for methods that are sensitive to linkage, such as estimating relatedness (Thompson, 2013) and Ne.

Here, we empirically examine the bias of Ne estimation due to physical linkage in a simulation study designed to evaluate the common situation where a researcher has genomics-scale data sets (for example, 1000s of loci) but limited other genomic resources. We explore factors underlying bias in terms of genetic architecture and relate this bias to the number and length of chromosomes. We focus on the simple case of a single sample taken from a single population. Simulated data are generated using a 'sideways' approach that combines both coalescent and forward simulations. Coalescent simulations ensure equilibrium and allow simple modeling of ascertainment, while forward simulations provide precise control over important parameters such as mating structure. This hybrid simulation procedure allows us to explore and quantify the effect of these aspects on bias in Ne estimates.

We show that the presence of physically-linked loci downwardly biases estimates of contemporary Ne based on the LD method, and that basic aspects of genomic architecture, such as the number of chromosomes and genome size, influence the amount of physical linkage. For example, bias created by physical linkage decreases as the number of chromosomes increases, as larger genomes house more independently assorting loci. Using these gross measures of genome architecture and our simulated data, we develop approximate bias corrections to account for the effects of linkage. We illustrate our results by calculating biased and putatively unbiased estimates of Ne from a published data set that includes 28 populations of Atlantic salmon (Salmo Salar) sampled across their range in Europe and North America (Bourret et al., 2013) and an Atlantic salmon linkage map. We also show that, although high-throughput sequencing techniques will increase precision of Ne estimates, the lack of independence of the vast numbers of pairwise comparisons means that precision in N̂e does not increase nearly as fast as naive expectation.

Materials and methods

Simulation procedure

Genetic data were generated in a two-step backward/forward procedure. First, a coalescent simulation program, SIMCOAL2 (Laval and Excoffier, 2004) was used to produce populations in approximate mutation-drift equilibrium. These populations were then used to initialize the forward-time simulation program SimuPop (Peng and Kimmel, 2005). In the forward simulation, populations were held to a 1:1 sex ratio with random mating. In this scenario, the expected Ne is equal to the census size (N), although the realized Ne varies each generation due to random fluctuation in family sizes (Waples and Faulkner, 2009).

The simulation procedure involved four nested steps, each replicated independently. (1) We created a genomic architecture, by randomly placing loci on chromosomes. (2) Informed by the genomic architecture, we used coalescent simulations to produce populations of constant size in mutation-drift-recombination equilibrium. (3) We initialized forward-time simulations with the coalescent results and progressed 10 generations forward in time, without mutation. (4) In the final generation, we selected a subsample of individuals for analysis. See Supplementary materials for detailed information on the simulation procedure.

We were interested in evaluating bias and precision of estimates of Ne. To investigate bias due to physical linkage, we created simulation scenarios that varied the population size (50, 200, 800), number of loci (1024, 4096), number of chromosomes (2–64) and sample sizes of individuals (50, 100), in a fully factorial design (Table 1); see Supplementary materials for results for smaller numbers of loci. Generally, two parents were randomly selected to produce each offspring and simulated chromosomes were 100 centimorgans (cM) long, except where noted below. To examine the effect of chromosomes length and recombination rate on the bias, we re-ran a subset of scenarios (number of chromosomes=4, 8) with both shortened (50 cM) and lengthened (200 cM) chromosomes. To examine precision of Ne estimates, we used a single parameter set with population size=200, 8 chromosomes, 4096 loci, sample size=100, and conducted 1000 forward simulations based on a single genomic architecture started from the same coalescent initialization and held the realized Ne constant each generation.

Table 1. Simulation parameters and replication, full factorial design, all possible combinations of parameters were simulated.

Simulation type Simulation parameters
 Replication
  # Loci # Chrs N Sample size Coalescent Forward Sampling Total replicates
Bias 1024, 4096 2, 4, 8, 16, 32, 64 50, 200, 800 50, 100a 2 10 4 80
Precision 16, 32, 64, 128, 256, 512, 1024, 2048, 4096 8 200 100 1 1000 1 1000
Open in a new tab
a

For a simulated population size of 50, no sample size of 100 is possible, and replication across sample sizes of 50 is not meaningful. N is the number of simulated individuals.

Notice that for a simulated population size of 50, no sample size of 100 is possible and that all samples of 50 individuals will be identical. For each genome created in step 1, steps 2, 3, and 4 were replicated 2, 10, and 4 times, respectively. This generally produced 80 replicates for each combination of parameters.

Estimation of Ne

Ne was estimated from the mean amount of LD present in the genome remaining after accounting for sampling-induced LD. We used PLINK ver. 1.07 (Purcell et al., 2007) to calculate Pearson's squared correlation coefficient (r2) of the genotype vectors for each pair of loci as a measure of LD. Genotypes were coded as the number of non-reference alleles, with possible values in [0, 1, 2]. With genotypes coded in this way, r2 is identical to Burrows' composite measure of linkage disequilibrium (rΔ) (Weir, 1996; Zaykin, 2004). To mirror the approach implemented in the software LDNe (Waples and Do, 2008), where a sample-size adjustment factor of [S/(S−1)]2 was used (Weir, 1979), we multiplied each r2 value by this term, subtracted the expected contribution from sampling error to obtain the adjusted r2', and then calculated N̂e as in Waples (2006).

For each simulation, mean r2 was calculated as the mean across all pairs of loci. Other methods have computed a weighted mean based on allele frequencies, number of alleles and/or missing data (for example, Peel et al., 2013; Sved et al., 2013), but here we simulate only bi-allelic loci without missing data and did not compute a weighted mean. Alleles observed in low numbers (⩽2) provide little information on LD and can upwardly bias estimates of r2 (Waples and Do, 2010), so we excluded loci with an observed minor allele frequency of <0.05 in each replicate. Using the LD method, after correcting for sampling-induced LD, it is possible to produce estimates of infinite Ne; to incorporate these values into summary statistics we replaced infinite estimates with 10 000.

For each pair of loci, an expected value for r2 (E(r2)) was calculated as a function of Ne and c, the recombination fraction of the two loci. We used a hybrid of two different formulas for E(r2): equation 2 in Weir and Hill (1980) and equation 3 in Sved and Feldman (1973). The Sved and Feldman formula is incorrect for unlinked loci (c=0.5) (Sved et al., 2013), while the Weir and Hill (1980) formula produces non-sensical values (E(r2)>1) for closely linked loci. Accordingly, we used the minimum E(r2) across the two equations. See supplementary Figure S1 for an illustration of the relationship between E(r2) and c for each equation.

For pairs of bi-allelic loci observed within a population, the statistic (r2/mean(r2)) follows a chi-squared distribution with one degree of freedom (Hill, 1981). To form the E(r2) distribution for pairs of loci with a known recombination fraction, we re-scaled the chi-squared distribution to have a mean equal to E(r2) and bounded it at 1.0. This allowed us to evaluate the extent to which the empirical distribution of r2 within our simulations departed from the expected values. To form a distribution of E(r2) for many pairs of loci with different values for c, we computed a weighted sum of their expected distributions. Using this approach, we were able to closely approximate the empirical distribution of pairwise r2 values, matching the E(r2) distribution for both unlinked loci and across the full range of simulated recombination fractions (Supplementary Figure S2).

Bias

LD between neutral and independently-segregating loci should provide a nearly unbiased estimate of Ne (Hill, 1981; Waples and Do, 2010). Bias in Ne estimates was assessed by comparing estimates with census sizes (N) of Wright–Fisher ideal populations. We evaluated this bias before and after excluding within-chromosome comparisons from LD measurements. This method leverages our complete knowledge of the genomic architecture in the simulated data, and allows an assessment of estimates of Ne based on r2 for all pairs of loci (biased by physical linkage) to estimates derived from the mean r2 for pairs of loci on different chromosomes (unbiased by physical linkage). Any increase in bias based on the within-chromosome LD measures can be attributed to physical linkage between loci.

In addition to characterizing the degree of bias, we evaluated two types of bias correction methods: (1) set a cutoff r2 value and exclude all pairwise r2 values above it from the calculation of mean r2 and (2) adjust estimates of Ne directly based on the number of chromosomes or their total genetic length in cM.

Empirical example

While simulations are ideal at replicating simple scenarios, real populations have many complexities not matched in simulated data. To investigate how the above methods can be applied to real populations, genetic data from 28 populations of Atlantic salmon (Bourret et al., 2013) were used to estimate Ne. From the published data set, we excluded populations with mean sample sizes <30 and samples that combined individuals from multiple years, as these issues can also bias estimates of Ne (Waples et al., 2014). We restricted our analysis to loci present on the linkage map of Lien et al. (2011) and the linkage groups of this map were treated as chromosomes. Any loci identified by Bourret et al. (2013) as putatively under selection, or with minor allele frequency <0.05, were excluded. We placed the r2 values for each pair of loci into sets of ‘unlinked' (loci on different chromosomes), and ‘linked' (loci co-located on a chromosome) following Larson et al. (2014). Mean r2 within the ‘unlinked' set provides an unbiased estimate of contemporary Ne, while the mean r2 across both sets represents a naive approach blind to the effects of the physical linkage. This naive approach mirrors the lack of genomic resources, such as a reference genome or linkage map, that is present in most non-model species and in nearly all species of conservation concern. Ne estimates were generated with a custom version of the LDNe program (Waples and Do, 2008) available from the authors upon request. This estimation procedure closely matches the calculations made in the analysis of the simulated data, except a weighted mean r2 was calculated based on the sample size of each locus due to some missing data.

Our simulations model simplified scenarios in which all chromosomes are the same length in cM and have the same number of ascertained loci. In real species, recombination (and thus chromosome length in cM) varies, thus we applied bias corrections for the Atlantic salmon data that incorporate both the size and number of linkage groups. These two bias corrections require different degrees of knowledge about genome structure and reflect the range of commonly-available information for non-model species.

Precision

Due to a limited number of recombination events each generation, loci do not segregate independently. This lack of independence between loci, coupled with the fact that each locus contributes to many pairwise r2 measurements, is not accounted for when generating standard confidence intervals (CIs) around the mean r2 or N̂e. To evaluate how much these effects reduce precision, we conducted a separate round of simulations and compared two measures of confidence: (1) nominal CIs around N̂e that assume all pairwise comparisons of loci are independent (Waples, 2006) and (2) empirical 95% intervals observed in the simulated data. Forward simulations of populations following a random Wright–Fisher mating model produce random variation in realized Ne as the variance in reproductive success varies each generation, even if census size stays constant. This inflates the variance of N̂e among replicate forward simulations (Waples and Faulkner, 2009). In most cases, this variation is confounded with other sampling processes, making it difficult to independently quantify them all. Therefore, for the simulations evaluating precision, we departed from a fully-random Wright–Fisher mating model and instead manually controlled mating to ensure that the realized variance in reproductive success was equal to the binomial variance, so that realized effective size was equal to the census size each generation. This excluded demographic fluctuations in realized Ne and allowed us to attribute all the variance of mean r2 values among replicates to the processes of sampling individuals and loci. These manually-controlled matings were specified by randomly permuting individuals across a pedigree known to produce the desired Ne.

Results

Bias

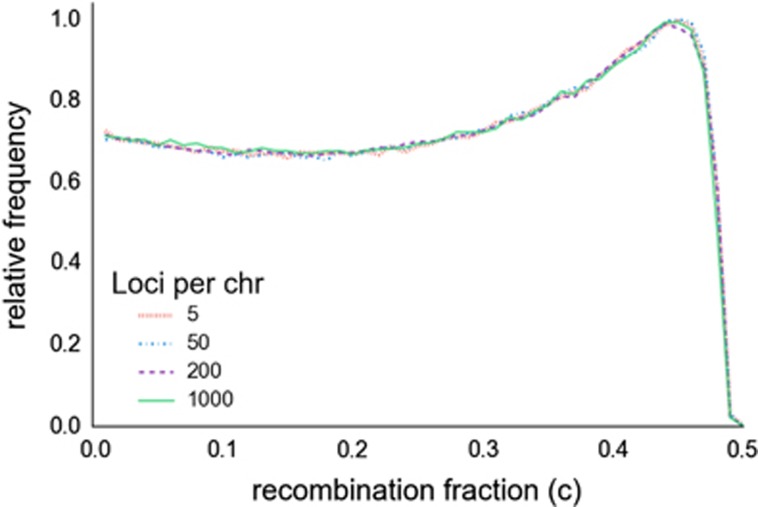
Within a chromosome, the distribution of locus pairs with a given recombination fraction is independent of the number of loci (Figure 1). Expected LD is a function of recombination fraction, so increasing the number of loci does not change the expected pattern or magnitude of LD. Because separate chromosomes segregate independently, increasing the number of loci does not increase the expected fraction of locus pairs that are physically linked. Although this result is not necessarily intuitive, it follows directly from the fact that the probability that any randomly-chosen pair of loci is linked is the same regardless how many other loci exist. Consistent with this expectation, the absolute number of loci measured was not found to have any systematic effect on estimates of mean r2 or on estimates of Ne (Supplementary Figure S3). See Supplementary Table S1 for a summary of each simulation.

Figure 1.

Figure 1

Open in a new tab

The distribution of recombination fractions among pairs of loci on a simulated chromosome. Simulated chromosomes are 100 cM in length; loci at opposite ends have c values near 0.5.

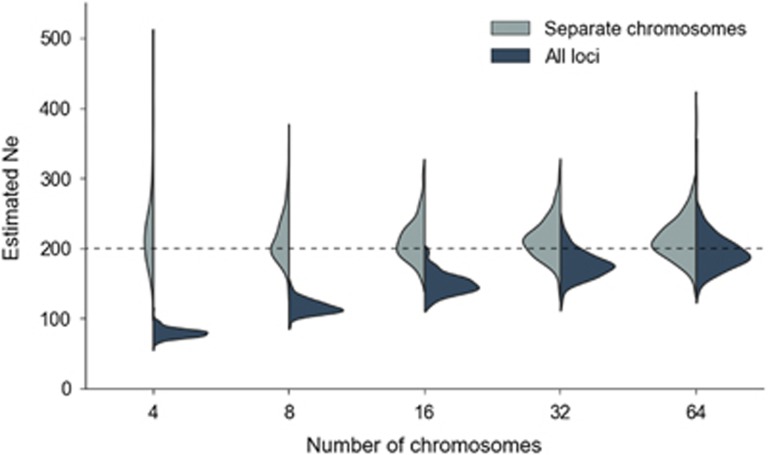
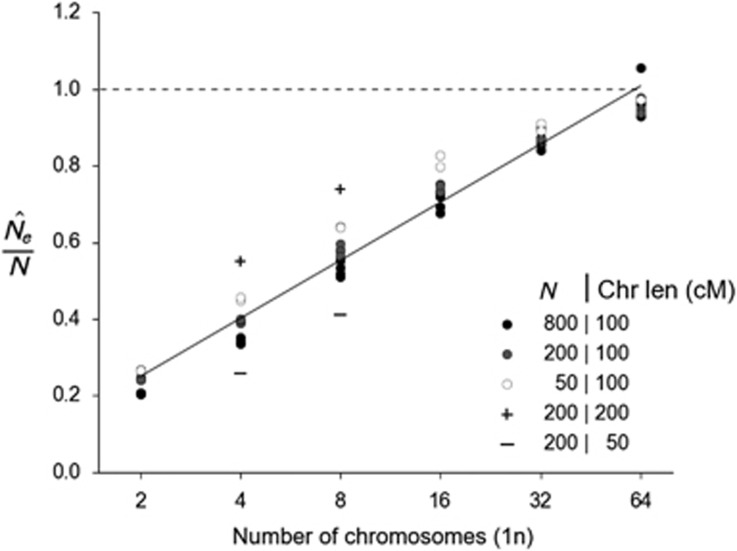
Although bias in N̂e depends to a limited extent on population size and sample size (see Supplementary Figure S4), by far the strongest indicator of the N̂e ratio is the number of chromosomes and their length in cM (Figures 2 and 3, Supplementary Table S2). This bias is caused by physically-linked loci and can be substantial. For example, with four chromosomes of 100 cM, the bias in and can be substantial. For example, with is about −60% of true Ne, with slightly less bias associated with small populations. With 32 chromosomes, however, the bias in N̂e is reduced to about −10–20%. We also see that the chromosome length in cM (proportional to the expected number of recombination events per generation) also has an effect, with eight 50 cM chromosomes generating a similar degree of bias to four 100 cM chromosomes (Figure 3). This suggests that the bias is a function of the total length of the genome in cM.

Figure 2.

Figure 2

Open in a new tab

Relationship between bias in N̂e and the number of haploid chromosomes. The distribution of N̂e from all loci is shown in dark shading; estimates using only unlinked loci are shown in light shading. The horizontal dashed line shows the simulated population size.

Figure 3.

Figure 3

Open in a new tab

Pattern of bias in N̂e for simulated data as a function of the number haploid chromosomes. Results are based on mean r2 values computed across all pairs of loci. Symbols are harmonic means of N̂e/Ne across all replicates for each parameter set. The solid line is a linear regression of N̂e/Ne on the natural log of the number of chromosomes (Chr): y=0.098+0.219 × ln(Chr). Plus symbols show results from simulations with N=200 with longer chromosomes (200 cM) for the 4 and 8 chromosome scenarios; minus symbols show the effects of shorter chromosomes (50 cM). Dashed line is the relationship between the harmonic mean of N̂e and N for an unbiased estimate.

We considered an initial approach to bias adjustment that is analogous to the identification of 'outlier' loci that show levels of genetic differentiation among populations that are not consistent with neutral genetic drift (Beaumont and Nichols, 1996). With limited information about genomic architecture, from the mean r2 across all pairs of loci one can compute the expected distribution of r2 values for individual pairs of loci, under the assumption that they all are unlinked (see Materials and methods). This expected distribution can be compared with the observed r2 values to identify r2 values unlikely to occur for unlinked loci. Figure 4 shows the distribution of r2 values for comparisons of 4096 loci on 4 chromosomes in a population of size N=200 and a sample size of 100 individuals. Figure 4a shows the raw data with the r2 measurements from linked and unlinked loci confounded, and the black dashed line shows the expected distribution of r2 values under the assumption that all locus pairs are unlinked and therefore come from a single distribution. Figure 4b breaks down the data from (Figure 4a) into within- and between-chromosome measurements. The distribution of r2 values for co-located loci is right-shifted compared with unlinked loci, but there is still significant overlap. The fit of the expected distribution to the unlinked loci (Figure 4b) is very good. In contrast, when all locus pairs are used (Figure 4a), there is an excess of large r2 values compared with the expectation.

Figure 4.

Figure 4

Open in a new tab

(a) is a histogram of r2 values across all loci. The 'expected' line is calculated from the overall mean r2. (b) is a stacked histogram and separates the same data into within-chromosome (dark) and between-chromosome (light) r2 measurements. The ‘expected' line is calculated from the mean r2 of all between-chromosome values. Data presented are from a simulation with population size=200, with 4096 loci on 8 chromosomes, and a sample size of 100. Note the log-scaled y-axis.

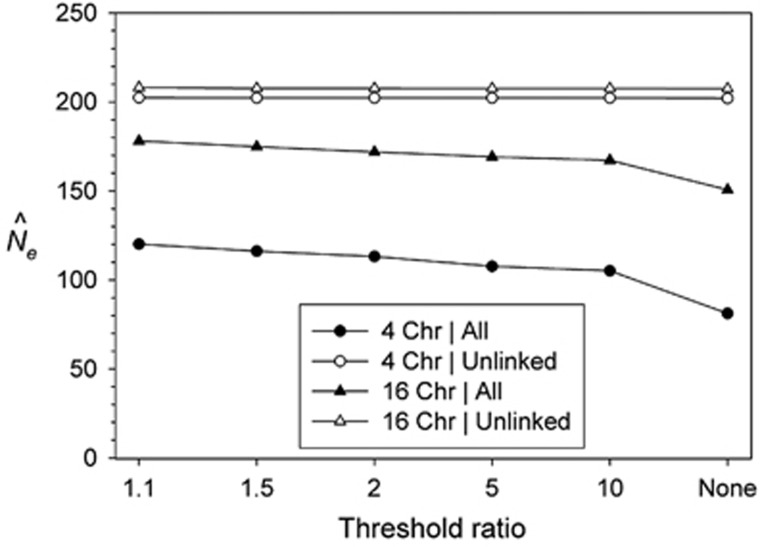
We explored various criteria for defining a threshold for truncating unusually large r2 values that presumably reflect linkage and hence will downwardly bias estimates of Ne. Figure 5 shows results of applying a threshold X to small bins of r2 values such that bins for which the ratio of the number of observed to expected r2 values was larger than X were removed. Using a more stringent threshold (X closer to 1) was more effective in reducing bias, but we found a strong asymptotic effect that limits effectiveness of the bias adjustment. Even using a stringent X=1.1 criterion, downward bias in N̂e/Ne was only reduced from −67% for no adjustment to −40% for simulations with 4 chromosomes, and from −25 to −11% for simulations with 16 chromosomes. This one-pass truncation method is safe, in the sense that it does not have an appreciable effect on data that have no linked loci, but it is also conservative in that it only removes part of the bias (Gruenthal et al., 2014; Candy et al., 2015; Stockwell et al., 2016). We also evaluated iterative truncation methods, whereby mean r2 is recalculated after removing the outlier pairs of loci and the new expected distribution is used to identify more outliers. However, this iterative approach is not conservative and is prone to overshooting the bias reduction and excluding many r2 values that legitimately arise from unlinked loci (data not shown).

Figure 5.

Figure 5

Open in a new tab

Effectiveness of removing outlier r2 values to reduce bias. Results are shown for simulations with 4 and 16 chromosomes and estimates based on all loci (biased downwards) or only pairs of loci on different chromosomes (‘unlinked' little or no bias with respect to true Ne=200). For each scenario, the expected distribution of pairwise r2 values was generated based on the overall mean r2. Values on the x axis are different ratios of observed/expected r2 values that were used to truncate the distribution, after which mean r2 and N̂e were recalculated.

Without information on the chromosome placement of loci, it is not possible to fully determine whether two loci are co-located based on LD. Figure 4 illustrates the impossibility of fully removing the bias in N̂e from any truncation method based on the overall mean r2. Ideally, we want to identify and exclude r2 values generated by linked loci. However, because of the large overlap in the distribution of r2 values for linked and unlinked comparisons, any fixed truncation threshold will either fail to remove many linked comparisons (many false negatives) or will remove many valid comparisons of loci on different chromosomes (many false positives).

A second, and more promising, approach is to take advantage of the strong correlation between the magnitude of bias in N̂e/Ne and the number of chromosomes and genome length in cM (Figures 2 and 3). The relationship shown in Figure 3 can be used to generate a rough estimate of the magnitude of downward bias in N̂e due to physical linkage. In this figure, the symbols represent harmonic means of N̂e/Ne across 80 replicate simulations for each parameter set, with N̂e calculated from mean r2 across all pairs of loci. The solid line is the least-squares regression of N̂e/Ne on the natural log of the number of chromosomes (Chr):

graphic file with name hdy201660e1.jpg

which explains 97% of the variance in these harmonic mean estimates. Accounting for sample size (S=50 or 100) did not significantly improve the fit. Adding a term for ln(Ne) led to a statistically significant improvement (P<0.01) that, however, led to only a negligible (<1%) increase in adjusted R2. This weak dependence of the bias on true Ne is convenient because Ne is the quantity we are trying to estimate. Thus, a simple, quantitative adjustment for bias in an estimate of Ne can be achieved by inserting the haploid chromosome number into Equation (1a) and (1b) and dividing the naive N̂e estimate by the regression result.

Alternatively, we can specify the total length of the genome in cM to predict the bias.

graphic file with name hdy201660e2.jpg

Equation (1b) differs from Equation (1a) only in the constant term. In our simulations, each chromosome was 100 cM in length, but real species will have chromosomes of variable length.

Empirical example

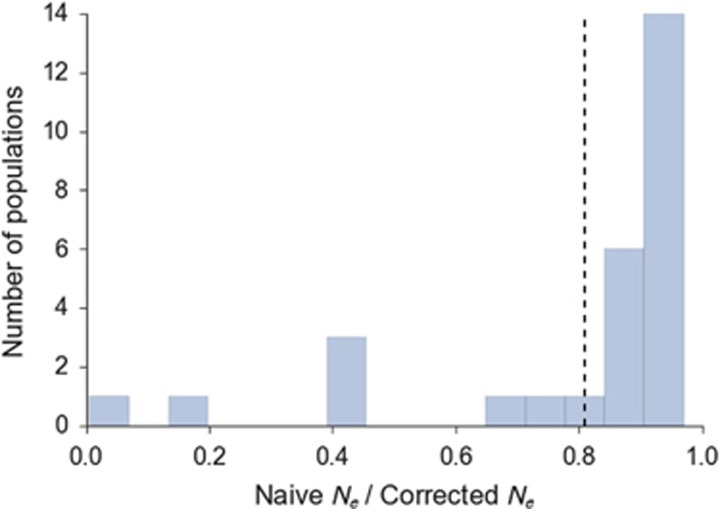
We examine how the bias correction procedure developed above can be applied to data from natural populations: 28 populations of Atlantic salmon from across their range. Importantly, a linkage map in Atlantic salmon (Lien et al., 2011) supplies chromosomal information for each locus. Across the populations investigated, mean naive N̂e was 255, range=15–1801, s.d.=406. Mean bias-corrected N̂e based on loci not co-located on chromosomes was 834, range=18–10 000, s.d.=2016. Figure 6 shows the effect of removing within-chromosome LD from Ne estimates. For all populations, mean r2 was lower and N̂e was larger after excluding co-located loci. The female linkage map has 29 (haploid) chromosomes and a total length of 2402 cM. Based on Equation (1a), we expect that Ne estimates for a species with 29 haploid chromosomes should be approximately the fraction −0.910+0.219 × ln(29)=0.83 of true Ne, indicating an expected downward bias of 17%. Alternatively, using the genome length in cM 2402, Equation (1b) predicts a bias of −0.910+0. 219 × ln(2402)=0.79 of true Ne, indicating an expected downward bias of 21%. Using the correction based on knowledge of genomic location of each locus, the geometric mean of the downward bias in the Atlantic salmon data is 34.5% and the median is 9.8%. Our estimates are between these two measures of the central tendency of the bias. Most of the populations fell in the range of 0–20% downward bias (0.8–1.0, Figure 6,Supplementary Table S3), consistent with a moderate amount of downward bias. The populations with larger naive estimates of Ne in general had larger corrections (Supplementary Figure S5), consistent with Figure 3.

Figure 6.

Figure 6

Open in a new tab

Effect of removing within-chromosome LD from Ne estimates in 28 Atlantic salmon populations. Values on x axis are the ratio of N̂e for naive (all locus comparisons) and corrected comparisons (only among loci on different chromosomes). Dashed line shows the predicted correction level based on 29 chromosomes.

Precision

The precision of estimates of Ne is grossly overestimated when large numbers of loci are observed (Figure 7). For example, with 4096 loci and true Ne=200, under the assumption that all comparisons are independent (that is, mean r2 is the result of 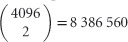Inline graphic independent measures), the parametric 95% CI on the point estimate of N̂e (202) is extremely small: (201–203, Supplementary Table S4). In contrast, we show that in simulations of 4096 loci on 8 chromosomes we achieve empirical 95% intervals for N̂e that are equivalent to those produced by only 160 fully independent loci (that is, Inline graphic independent measures). The empirical 95% interval is 20 times wider (168–242) than this naive assumption, indicating that the effective degrees of freedom associated with the point estimate are only a fraction of the nominal degrees of freedom. This overly optimistic precision implied by the naive CI is especially egregious as the parametric CI is so narrow that it does not even include the true population size of 200, even though the point estimate is off by only 1%.

Figure 7.

Figure 7

Open in a new tab

Relationship between theoretical and empirical (light) precision for estimates of Ne. Dark shaded area shows naive 95% CIs (which assume that all pairwise comparisons are independent), light shaded area shows empirical CIs from simulated data. True Ne was 200, sample size was 100 and number of chromosomes was 8. Notice both the x and y axes are log-scaled.

Discussion

Implications for genomic data sets

Observing more loci does not increase the probability that any randomly-chosen pair of loci will be linked, nor increase the fraction of loci that are physically linked. However, as the number of loci increases, the fraction of pairs that are linked will converge on the expected fraction, which means that results are easier to predict in a statistical sense.

We showed how to compare the observed distribution of r2 estimates for pairs of loci with the expected distribution under the assumption that all are neutral and unlinked. With this approach, it is easy to identify outlier pairs of loci with r2 values that are unlikely to be generated under the assumed model. We explored various criteria for one-pass truncation of the r2 values and showed that this approach can only be partially effective at reducing the downward bias in N̂e. The problem with this approach is that physical linkage encompasses the full range of recombination fractions from 0.5 to near zero. Only a relatively small number of strongly-linked loci produce outlier r2 values above any given threshold, while vastly more pairs of loosely linked loci create slightly elevated r2 values that cumulatively contribute to bias but cannot be easily distinguished from unlinked pairs that produce similar r2 values.

Here, we are cognizant of the benefits of simplicity and recognize the lack of genomic resources for many species. In the simulated data, the relationship between downward bias in N̂e and chromosome length/number is nearly log-linear (Figure 3). For example, eight 200 cM chromosomes results in less bias than eight 50 cM chromosomes, but a similar amount of bias to 16 100 cM chromosomes. The simplest adjustment based on the number of chromosomes (Equation 1a) assumes an average of 100 cM per chromosome. With more detailed information on recombination rates, it is possible to incorporate relative lengths of chromosomes into the bias correction as well (Equation 1b).

This method should improve estimates of downward bias in N̂e for species with limited genomic resources. Realistically, the pattern of bias in N̂e due to physical linkage is constrained to the range 0–1, so the relationship depicted in Figure 3 must be sigmoidal as the bias asymptotes near these boundaries. Therefore, we do not suggest using Equations (1a) and (1b) to correct for bias outside the range of the simulated data here, that is, 2–64 chromosomes, 200–6400 cM. Within that range, however, the pattern of bias is nearly log-linear and hence amenable to correction using this simple adjustment.

We see a very slight upward bias in N̂e when applying the LDNe estimation method to sets of loci on different chromosomes. This effect is larger with smaller sample sizes (S). This has been noted previously (for example, Waples and Do, 2010) and is likely due to a slight bias overcorrection in LDNe method relative to the original Hill method. Our results thus allow the user to simultaneously correct for bias due to linkage and the slight upward bias that occurs in LDNe. Besides drift and physical linkage, other factors affecting LD include selection, migration and admixture (Slatkin, 2008). The LD generated by these other evolutionary forces also has the potential to bias estimates of Ne (Waples and England, 2011; Gilbert and Whitlock, 2015). The simulations conducted here, while extensive, were limited in many respects and did not attempt to address these forces. Specifically, we simulated isolated populations of constant size. The simulated genome architecture was also greatly simplified; all chromosomes were the same size, measured in recombination units and loci were distributed randomly with respect to local recombination rate and were strictly neutral.

In this study, we simulated loci that are randomly placed on chromosomes. However, both biological and methodological factors may conspire to produce loci that are non-randomly distributed with respect to recombination. Many genotyping-by-sequencing methods, such as those based on restriction enzymes, are likely to produce loci that are closer together than random expectation. We note this may contribute to excess LD and further downward bias in Ne estimates, but we do not examine this further.

We evaluated our suggested approach with a published genetic data set of 28 populations of Atlantic salmon. Given 29 haploid chromosomes, our simulations predict there should be a downward bias in N̂e of about 17% (Figure 3). Alternatively, using the total length of the linkage map (2402 cM), our simulations predict a downward bias N̂e of about 21%. These corrections are conservative relative to the correction we observed by excluding loci co-located on chromosomes (geometric mean 34.5%). Although we do not know the true Ne of these populations and therefore cannot determine the true bias, we found that Ne always increased when comparisons of loci on the same chromosome were excluded, which clearly demonstrates the potential for bias. The populations with large corrections (>50%) were mostly for populations already estimated to be large, where precise estimation of Ne is known to be difficult; furthermore, some of the samples could be affected by admixture associated with artificial propagation or other anthropogenic factors not considered here.

The number of possible LD measurements increases with the square of the number of loci, so large genomics data sets vastly increase the number of pairwise r2 values that are available to estimate Ne. However, because these comparisons are not all independent, precision is greatly reduced from the theoretical value. Previously, this problem of assessing precision for the LD method has been pointed out and illustrated with small numbers of loci (Waples, 2006; Waples and Do, 2010). We show that the magnitude of this problem increases dramatically for genomics-scale data sets, to the extent that realized precision will be much less than predicted from standard models that assume complete independence among loci. This is an important topic that merits a more detailed treatment than we can provide here. In the meantime, users should be aware that precision is greatly overestimated for large numbers of loci if CIs are generated under the assumption that all pairwise comparisons are independent.

Related approaches

We found a consistent increase in N̂e when loci known to be physically linked are excluded, in both simulated and wild populations. In contrast, in the Queensland fruit fly (Bactrocera tryoni). Sved et al. (2013) did not find a consistent change in N̂e across a set of ~30 microsatellite loci when co-located loci were excluded. This difference may be due to increased number of loci in this study, and/or the simplified nature of simulated data, both of which can tend to reduce noise in estimates. Our results are consistent with those of Larson et al. (2014), who showed a significant increase in N̂e in multiple populations of Chinook salmon (Oncorhynchus tshawytscha) when co-located single-nucleotide polymorphism loci were removed from analyses, the expected pattern if N̂e was downwardly biased by linkage. Notably, in all three studies of wild populations (B. tryoni, and two salmonids), the degree of difference in unlinked vs all estimates was not consistent across populations, suggesting population-specific factors that affect within-chromosome LD, such as historic bottlenecks and recent metapopulation dynamics (Slatkin, 2008), could have important implications for estimating contemporary Ne.

There are other methods available to estimate recent effective population size from genetic data. However, most of these methods require data types not available in many species. When available, genetic samples spaced in time can powerfully inform estimates of genetic drift and thus Ne, for example, SPATPG (Gompert, 2016). With a detailed recombination map, equations relating the recombination fraction to expectations of LD can be used to estimate the recent history of Ne, for example, SNeP (Barbato et al., 2015) and Hollenbeck et al. (2016). Finally, with dense, phased genotype data, powerful new methods allow inference of complex demographic histories, including Ne, for example, the multiple sequentially markovian coalescent (Schiffels and Durbin, 2014) and diCal (Sheehan et al., 2013), but these data are not yet available for most species.

Practical applications

Ne estimates are useful in planning conservation actions and assessing genetic risk, and bias in Ne estimates can lead to inappropriate conservation decisions (Schwartz et al., 2007). For conservation applications, not correcting for the bias demonstrated here can be seen as conservative, as it will result in the prediction of smaller Ne, but it could lead to false alarms that waste scarce resources on populations that are not actually at high genetic risk.

For species without many genomic resources, the most reliable means of adjusting bias in N̂e related to linkage is to use a correction factor based on the number of chromosomes or their total length in cM. With knowledge of the chromosome location of each locus, either from a linkage map or reference genome, it is possible to correct for the downward bias in Ne estimates. Although reference genomes are not available for most non-model species, a researcher will often know the number of chromosomes. In cases where this chromosomal information is lacking, the relationship given in Equations (1a) and (1b) and shown in Figure 3 can be used to partially correct for this bias. In both cases, we suggest practitioners exclude any loci expected to be under selection from use as estimators of Ne. The results and conclusions presented are relevant for studies that leverage LD to estimate contemporary Ne with any number of loci.

Data accessibility

This study contains no new empirical data. The scripts used in the simulation analyses are available in Dryad (http://dx.doi.org/10.5061/dryad.1ms70). Atlantic salmon data were accessed from Dryad repository: doi:10.5061/dryad.gm367 (Bourret et al., 2012).

Acknowledgments

We would like to thank Chi Do for making available a beta version of LDNe that facilitated computation of mean r2 across loci on different chromosomes. RKW was supported by the Alaska Sustainable Salmon Fund under Projects 44714 and 44812 from the National Oceanic and Atmospheric Administration, US Department of Commerce, administered by the Alaska Department of Fish and Game. WAL was supported by the H Mason Keeler Endowment for Excellence and a US National Science Foundation Graduate Research Fellowship (grant # DGE-0718124).

Author contributions

RSW conceived the study, along with RKW and WAL. RKW conducted all simulations. RKW, WAL and RSW analyzed data; writing and editing the manuscript was conducted by RKW with help from WAL and RSW.

The authors declare no conflict of interest.

Footnotes

Supplementary Information accompanies this paper on Heredity website (http://www.nature.com/hdy)

Supplementary Material

Supplementary Material
Click here for additional data file. (1MB, pdf)
Supplementary Table S1
Click here for additional data file. (522.1KB, txt)
Supplementary Table S2
Click here for additional data file. (24.5KB, doc)
Supplementary Table S3
Click here for additional data file. (2.1KB, txt)
Supplementary Table S4
Click here for additional data file. (35KB, doc)

References

  1. Barbato M, Orozco-terWengel PA, Tapio M, Bruford MW. (2015). SNeP: a tool to estimate trends in recent effective population size trajectories using genome-wide SNP data. Front Genet 6: 109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Beaumont MA, Nichols RA. (1996). Evaluating loci for use in the genetic analysis of population structure. Proc R Soc B 263: 1619–1626. [Google Scholar]
  3. Bourret V, Kent MP, Primmer CR, Vasemägi A, Karlsson S, Hindar K et al. (2013). SNP-array reveals genome-wide patterns of geographical and potential adaptive divergence across the natural range of Atlantic salmon (Salmo salar). Mol Ecol 22: 532–551. [DOI] [PubMed] [Google Scholar]
  4. Bourret V, Kent MP, Primmer CR, Vasemägi A, Karlsson S, Hindar K et al. (2012). Data from: SNP-array reveals genome wide patterns of geographical and potential adaptive divergence across the natural range of Atlantic salmon (Salmo salar). Mol Ecol 22: 532–551. [DOI] [PubMed] [Google Scholar]
  5. Candy JR, Campbell NR, Grinnell MH, Beacham TD, Larson WA, Narum SR. (2015). Population differentiation determined from putative neutral and divergent adaptive genetic markers in Eulachon (Thaleichthys pacificus, Osmeridae), an anadromous Pacific smelt. Mol Ecol Resour 15: 1421–1434. [DOI] [PubMed] [Google Scholar]
  6. Charlesworth B. (2009). Fundamental concepts in genetics: effective population size and patterns of molecular evolution and variation. Nat Rev Genet 10: 195–205. [DOI] [PubMed] [Google Scholar]
  7. Ellstrand NC, Elam DR. (1993). Population genetic consequences of small population-size - implications for plant conservation. Annu Rev Ecol Syst 24: 217–242. [Google Scholar]
  8. Falush D, Stephens M, Pritchard JK. (2003). Inference of population structure using multilocus genotype data: linked loci and correlated allele frequencies. Genetics 164: 1567–1587. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Frankham R. (1995). Effective population-size adult-population size ratios in wildlife - a review. Genet Res 66: 95–107. [DOI] [PubMed] [Google Scholar]
  10. Gilbert KJ, Whitlock MC. (2015). Evaluating methods for estimating local effective population size with and without migration. Evolution 69: 2154–2166. [DOI] [PubMed] [Google Scholar]
  11. Gompert Z. (2016). Bayesian inference of selection in a heterogeneous environment from genetic time-series data. Mol Ecol 25: 121–134. [DOI] [PubMed] [Google Scholar]
  12. Gruenthal KM, Witting DA, Ford T, Neuman MJ, Williams JP, Pondella II DJ et al. (2014). Development and application of genomic tools to the restoration of green abalone in southern California. Conserv Genet 15: 109–121. [Google Scholar]
  13. Hill WG. (1981). Estimation of effective population-size from data on linkage disequilibrium. Genet Res 38: 209–216. [Google Scholar]
  14. Hollenbeck CM, Portnoy DS, Gold JR. (2016). A method for detecting recent changes in contemporary effective population size from linkage disequilibrium at linked and unlinked loci. Heredity e-pub ahead of print 11 May 2016 doi:10.1038/hdy.2016.30. [DOI] [PMC free article] [PubMed]
  15. Larson WA, Seeb LW, Everett MV, Waples RK, Templin WD, Seeb JE. (2014). Genotyping by sequencing resolves shallow population structure to inform conservation of Chinook salmon (Oncorhynchus tshawytscha. Evol Appl 7: 355–369. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Laval G, Excoffier L. (2004). SIMCOAL 2.0: a program to simulate genomic diversity over large recombining regions in a subdivided population with a complex history. Bioinformatics 20: 2485–2487. [DOI] [PubMed] [Google Scholar]
  17. Lien S, Gidskehaug L, Moen T, Hayes BJ, Berg PR, Davidson WS et al. (2011). A dense SNP-based linkage map for Atlantic salmon (Salmo salar reveals extended chromosome homeologies and striking differences in sex-specific recombination patterns. BMC Genomics 12: 615. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Luikart G, Ryman N, Tallmon DA, Schwartz MK, Allendorf FW. (2010). Estimation of census and effective population sizes: the increasing usefulness of DNA-based approaches. Conserv Genet 11: 355–373. [Google Scholar]
  19. Peel D, Waples RS, Macbeth GM, Do C, Ovenden JR. (2013). Accounting for missing data in the estimation of contemporary genetic effective population size (N(e)). Mol Ecol Resour 13: 243–253. [DOI] [PubMed] [Google Scholar]
  20. Peng B, Kimmel M. (2005). simuPOP: a forward-time population genetics simulation environment. Bioinformatics 21: 3686–3687. [DOI] [PubMed] [Google Scholar]
  21. Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MA, Bender D et al. (2007). PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet 81: 559–575. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Schiffels S, Durbin R. (2014). Inferring human population size and separation history from multiple genome sequences. Nat Genet 46: 919–925. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Schwartz MK, Luikart G, Waples RS. (2007). Genetic monitoring as a promising tool for conservation and management. Trends Ecol Evol 22: 25–33. [DOI] [PubMed] [Google Scholar]
  24. Sheehan S, Harris K, Song YS. (2013). Estimating variable effective population sizes from multiple genomes: a sequentially Markov conditional sampling distribution approach. Genetics 194: 647–662. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Slatkin M. (2008). Linkage disequilibrium—understanding the evolutionary past and mapping the medical future. Nat Rev Genet 9: 477–485. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Stockwell BL, Larson WA, Waples RK, Abesamis RA, Seeb LW, Carpenter KE. (2016). The application of genomics to inform conservation of a functionally important reef fish (Scarus niger) in the Philippines. Conserv Genet 1–11.
  27. Sved JA. (1971). Linkage disequilibrium and homozygosity of chromosome segments in finite populations. Theor Popul Biol 2: 125–141. [DOI] [PubMed] [Google Scholar]
  28. Sved JA, Cameron EC, Gilchrist AS. (2013). Estimating effective population size from linkage disequilibrium between unlinked loci: theory and application to fruit fly outbreak populations. PLoS One 8: e69078. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Sved JA, Feldman MW. (1973). Correlation and probability methods for one and two loci. Theor Popul Biol 4: 129–132. [DOI] [PubMed] [Google Scholar]
  30. Tenesa A, Navarro P, Hayes BJ, Duffy DL, Clarke GM, Goddard ME et al. (2007). Recent human effective population size estimated from linkage disequilibrium. Genome Res 17: 520–526. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Thompson EA. (2013). Identity by descent: variation in meiosis, across genomes, and in populations. Genetics 194: 301–326. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Wang J. (2005). Estimation of effective population sizes from data on genetic markers. Philos Trans R Soc Lond B Biol Sci 360: 1395–1409. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Waples RS. (1991). Genetic methods for estimating the effective size of cetacean populations. Report - International Whaling Commission, Special Issue 13: 279–300. [Google Scholar]
  34. Waples RS. (2006). A bias correction for estimates of effective population size based on linkage disequilibrium at unlinked gene loci. Conserv Genet 7: 167–184. [Google Scholar]
  35. Waples RS, Antao T, Luikart G. (2014). Effects of overlapping generations on linkage disequilibrium estimates of effective population size. Genetics 197: 769–780. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Waples RS, Do C. (2008). ldne: a program for estimating effective population size from data on linkage disequilibrium. Mol Ecol Resour 8: 753–756. [DOI] [PubMed] [Google Scholar]
  37. Waples RS, Do C. (2010). Linkage disequilibrium estimates of contemporary Ne using highly variable genetic markers: a largely untapped resource for applied conservation and evolution. Evol Appl 3: 244–262. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Waples RS, England PR. (2011). Estimating contemporary effective population size on the basis of linkage disequilibrium in the face of migration. Genetics 189: 633–644. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Waples RS, Faulkner JR. (2009). Modelling evolutionary processes in small populations: not as ideal as you think. Mol Ecol 18: 1834–1847. [DOI] [PubMed] [Google Scholar]
  40. Weir BS. (1979). Inferences about linkage disequilibrium. Biometrics 35: 235–254. [PubMed] [Google Scholar]
  41. Weir BS. (1996) Genetic Data Analysis II: Methods for Discrete Population Genetic Data. Sinauer Associates: Sunderland, MA, USA. [Google Scholar]
  42. Weir BS, Hill WG. (1980). Effect of mating structure on variation in linkage disequilibrium. Genetics 95: 477–488. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Wright S. (1931). Evolution in Mendelian populations. Genetics 16: 97. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Zaykin DV. (2004). Bounds and normalization of the composite linkage disequilibrium coefficient. Genet Epidemiol 27: 252–257. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Material
Click here for additional data file. (1MB, pdf)
Supplementary Table S1
Click here for additional data file. (522.1KB, txt)
Supplementary Table S2
Click here for additional data file. (24.5KB, doc)
Supplementary Table S3
Click here for additional data file. (2.1KB, txt)
Supplementary Table S4
Click here for additional data file. (35KB, doc)

Data Availability Statement

This study contains no new empirical data. The scripts used in the simulation analyses are available in Dryad (http://dx.doi.org/10.5061/dryad.1ms70). Atlantic salmon data were accessed from Dryad repository: doi:10.5061/dryad.gm367 (Bourret et al., 2012).

Articles from Heredity are provided here courtesy of Nature Publishing Group

RESOURCES