Skip to main content
PMC home page
Heredity logoLink to Heredity
. 2016 Aug 17;117(4):268–278. doi: 10.1038/hdy.2016.62

Making sense of the relationships between Ne, Nb and Nc towards defining conservation thresholds in Atlantic salmon (Salmo salar)

A-L Ferchaud 1,*, C Perrier 1,2, J April 3, C Hernandez 1, M Dionne 3, L Bernatchez 1
PMCID: PMC5026759  PMID: 27530910

Abstract

Effective population size over a generation (Ne) or over a reproductive cycle (Nb) and the adult census size (Nc) are important parameters in both conservation and evolutionary biology. Ne provides information regarding the rate of loss of genetic diversity and can be tracked back in time to infer demographic history of populations, whereas Nb may often be more easily quantified than Nc for short-term abundance monitoring. In this study, we propose (1) an empirical context to Waples et al. (2014) who introduced a correction to bias due to overlapping generations, and (2) a mathematical relationship between Ne and Nb for direct application in Atlantic salmon populations in Québec, Canada. To achieve this, we investigate the relationships between Ne, Nb and Nc in 10 Atlantic salmon populations, Canada, for which we genotyped 100 randomly sampled young-of-the year individuals for 5 consecutive years. The results show a positive correlation between Ne, Nb and Nc, suggesting that Nb is an indicative parameter for tracking effective population size and abundance of Atlantic salmon. However, our model allows predicting Nc from Nb values at 27% that can be partly explained by high variance in Nb/Nc both among populations (37%) and among years (19%). This result illustrates the need for thorough calibration of Nb/Nc before using Nb in monitoring programs, as well as a full understanding of the limits of such an approach. Finally, we discuss the importance of these results for the management of wild populations.

Introduction

In many ecological and evolutionary research contexts, two important variables to be estimated in natural populations are the effective population size (over a generation (Ne) or over a reproductive cycle (Nb or effective number of breeders)) and the adult census size (Nc) (Frankham, 1995; Waples, 2005; Waples et al., 2014). In conservation biology, Ne is important chiefly because it determines the rate of loss of genetic variability and the rate of increase in inbreeding in a population. Ne is defined as the size of an ideal Wright–Fisher population exhibiting the same amount of genetic drift and inbreeding as the population under consideration (Wright, 1931). Ne may be complicated to estimate in most populations because of age structure, generation overlap and iteroparity (Waples et al., 2014). Nb is a concept derived from Ne that refers to the effective number of breeders during a single breeding event (Waples, 1989). The two measures are directly connected because Nb times the generation time approximates Ne (Waples, 1989). For Nb, only one season of data collection is needed. This parameter is thus generally more easily quantifiable than Ne as it can be inferred from a single cohort (for taxa with easy distinguishable cohorts), and might be a more accessible parameter for managers dealing with yearly conservation decisions (Waples, 2005; Luikart et al., 2010; Tallmon et al., 2010). Nc, the adult census population size, is generally defined as the total number of potential (sexually mature) breeders that can sometimes be assessed by directly counting individuals. However, this task is often problematic when Nc is large or because detecting all individuals is difficult and we thus often must estimate Nc. Therefore, estimates of Nb from genetic methods would be useful for tracking population trends if Nb reflects the number of adults in a population (that is, if a positive correlation is observed between Nc and Nb). In this case, Nb estimates would provide a complementary metric or could potentially be used in the place of abundance monitoring (Tallmon et al., 2010).

Knowledge of the relative magnitudes of these three parameters (Ne, Nb and Nc), as expressed by the ratios Ne/Nc and Nb/Nc, is important for disentangling the relative risks that demographic, environmental and genetic factors might pose for population persistence in the short term (Frankham, 1995; Palstra and Ruzzante, 2008). Expressed simply, for a given Ne, a population with a small Ne relative to Nc (that is, small Ne/Nc ratio) will lose gene diversity more quickly than an equal-sized population with a greater Ne/Nc ratio. Factors that can maximize this ratio are (1) a maximum number of breeders in each subsequent generation (or year), (2) more equal family sizes, (3) more equal sex ratios of breeders and (4) a reduced fluctuation in population size. Temporal fluctuations in effective size and the Ne/Nc ratio are not uncommon in natural populations and can be larger than differences between populations (see, for example, Miller and Kapuscinski, 1997; Heath et al., 2002, Waples, 2002, Shrimpton and Heath, 2003; Fraser et al., 2007). Several studies have suggested that no simple relationship between Ne and Nc may exist, either because of habitat factors or because of population expansion and contraction (Ardren and Kapuscinski, 2003; Watts et al., 2007; Fraser et al., 2007; Belmar-Lucero et al., 2012, and see review in Palstra and Fraser, 2012). Although these authors argued that more empirical studies are needed, they gave recommendations to accurately approximate such a relationship with a particular emphasis to better report the uncertainties in variables (Palstra and Fraser, 2012).

Genetic methods often represent the only feasible way to estimate effective sizes (Nb and Ne). The so-called temporal methods—which use genetic data in two or more temporally spaced samples taken from the same population (Waples, 1989) —exploit the temporal changes in allele frequencies and are in general more accurate and robust than other genetic methods. However, collecting temporal data separated by at least one generation could be expensive, especially for long-lived species that have large generation intervals and are usually more of conservation concern. Furthermore, such species usually have overlapping generations and a sampling interval much larger than a generation is necessary to yield accurate Ne estimates. The most widely used single-sample method calculates Ne from linkage disequilibrium (LD) among loci that are unliked (Waples and Do, 2008). The method relies on the fact that in a system where gametes are distributed at random among a small number of zygotes, there will be departures from expected genotype and gametic frequencies, both of which can be used to estimate Ne. In the case of age-structured populations, genetic estimates using the LD methods are strongly affected by both Ne per generation and Nb per breeding season. Samples from single cohort are the most amenable to quantitative bias adjustments resulting from overlapping generations. In this way, Waples et al. (2014) showed that single-cohort samples can be used to estimate Ne with little bias. They proposed formulas to adjust genetic estimates of effective size (Nb and Ne) to correct bias because of age structure using two or three simple life-history traits.

The Atlantic salmon (Salmo salar, L.) is a well-known iteroparous species with overlapping generations and has a complex life history that includes spawning, juvenile rearing in rivers and extensive feeding migrations on the high seas. As a result, Atlantic salmon goes through several distinct phases that can be identified by specific changes in behavior, physiology and habitat requirements. It is an anadromous fish, typically spending 2–3 years in fresh water, migrating to the ocean where it also spends 2–3 years and then returning to its natal river to spawn. The abundance (Nc) of Atlantic salmon has been declining worldwide over the past decades (Friedland et al., 2003; Chaput, 2012; Dionne and Cauchon, 2014). This decline has been attributed to several causes including most ocean productivity decrease because of climate change (Mills, 2013), commercial fisheries (Friedland et al., 2003) as well as habitat disconnection and deterioration (Hall et al., 2012; Nieland et al., 2015). As an indirect consequence of the drop of Nc, Nb and Ne may also decrease, potentially resulting in increased inbreeding depression, loss of local diversity and of evolutionary potential in small populations. Although international management plans have been deployed to mitigate this worldwide decline (that is, cessation of commercial fishing, although with few exceptions), populations trends are mostly not reversing (Hermansen et al., 2015). Meanwhile, based on descriptors of population health, fine-tuned management and conservation actions have been undertaken at the population level (Parrish et al., 1998; Limburg and Waldman, 2009). In this context, monitoring trends in Ne, Nb and Nc and understanding the links among these parameters may help to refine Atlantic salmon population health indices and ultimately conserve more adequately the genetic integrity of threatened populations. Monitoring these parameters and especially extrapolating a Nc value from a Nb or Ne estimate could also possibly replace direct abundance monitoring in rivers where such classic operation can be logistically challenging.

The main goal of this study is to empirically explore the relationship between the three estimates, Nc, Nb and Ne, taking into consideration different demographic factors and temporal fluctuations (sampling over a generation time) in 10 populations of Atlantic salmon. We took advantage of a large data set partly published in Perrier et al. (2016). To the data set of Perriers et al. (2016), we added one population and two additional years on all populations, thus comprising an entire generation time (that is, 5 years; Dionne and Cauchon, 2014). We genotyped ∼5000 1-year-old Atlantic salmon at 15 highly variable microsatellite markers in 10 different populations for 5 consecutive years (∼100 individuals per river and per year). Being an iteroparous and anadromous species, the Atlantic salmon appears a suitable species to propose an empirical context to Waples et al. (2014), who introduced a correction to bias because of overlapping generations on simulated data. Although fastidious, counts of spawn adult breeders returning to their natal river can be done to get an estimate of Nc. Atlantic salmon has also been well studied and described in terms of variation among rivers and several key life-history traits. In this context, the large data set used in this study offers the opportunity to propose an empirical relationship between Ne and Nb for direct application in Atlantic salmon populations in Québec, Canada. Finally, we also aim to test how much Nb reflects an Nc estimate by examining the correlation between these two measures.

Materials and methods

Study sites, sampling and estimates of census size (Nc)

A total of 4730 1-year-old parr (juveniles) were sampled using electrofishing in 10 rivers during summer in 2010, 2011, 2012, 2013 and 2014 corresponding to the breeding years 2008, 2009, 2010, 2011 and 2012 (Table 1 and Figure 1; Perrier et al., 2016). These rivers were chosen according to the (1) representation of the different regional genetic groups identified in the studied area (Dionne et al., 2008; Moore et al., 2014), (2) variation in census size estimates, (3) levels of stocking and (4) logistical feasibility of sampling. Individuals were sampled with respect to the guidelines of the Canadian Council on animal care and details for the sampling within river are provided in Perrier et al. (2016). Whole fish were stored immediately in 50 ml tubes with 95% ethanol. The median number of juveniles effectively genotyped per river and per year was 98 individuals (Table 1).

Table 1. River name, sample abbreviation, breeding year, sample size and counted number of anadromous breeders (Nc) for Atlantic salmon populations from Québec.

River Sample abbreviation Breeding year Sample size Nc
Laval LAV08 2008 60 103
  LAV09 2009 95 131
  LAV10 2010 95 55
  LAV11 2011 91 34
  LAV12 2012 94 35
Grand-Pabos GPA08 2008 64 150
  GPA09 2009 100 103
  GPA10 2010 97 284
  GPA11 2011 100 289
  GPA12 2012 98 137
Petite-Cascapedia PCA08 2008 98 285
  PCA09 2009 94 245
  PCA10 2010 100 338
  PCA11 2011 100 384
  PCA12 2012 94 130
Trinite TRI08 2008 98 838
  TRI09 2009 100 420
  TRI10 2010 100 763
  TRI11 2011 100 1060
  TRI12 2012 94 484
Sainte-Marguerite SMA08 2008 96 743
  SMA09 2009 100 618
  SMA10 2010 99 744
  SMA11 2011 100 1400
  SMA12 2012 95 287
Malbaie MAL08 2008 43 931
  MAL09 2009 99 625
  MAL10 2010 100 590
  MAL11 2011 100 687
  MAL12 2012 99 349
Godbout GOD08 2008 99 615
  GOD09 2009 100 767
  GOD10 2010 97 842
  GOD11 2011 100 1160
  GOD12 2012 98 821
Aux-Rochers ROC08 2008 54 615
  ROC09 2009 99 615
  ROC10 2010 97 1069
  ROC11 2011 100 1381
  ROC12 2012 97 850
Saint-Jean SJE08 2008 87 947
  SJE09 2009 100 796
  SJE10 2010 94 917
  SJE11 2011 100 779
  SJE12 2012 96 617
Matane MAT08 2008 92 1977
  MAT09 2009 99 1555
  MAT10 2010 100 1498
  MAT11 2011 100 2103
  MAT12 2012 97 1362
Average     98 622
Minimum     43 34
Maximum     100 2103
Open in a new tab

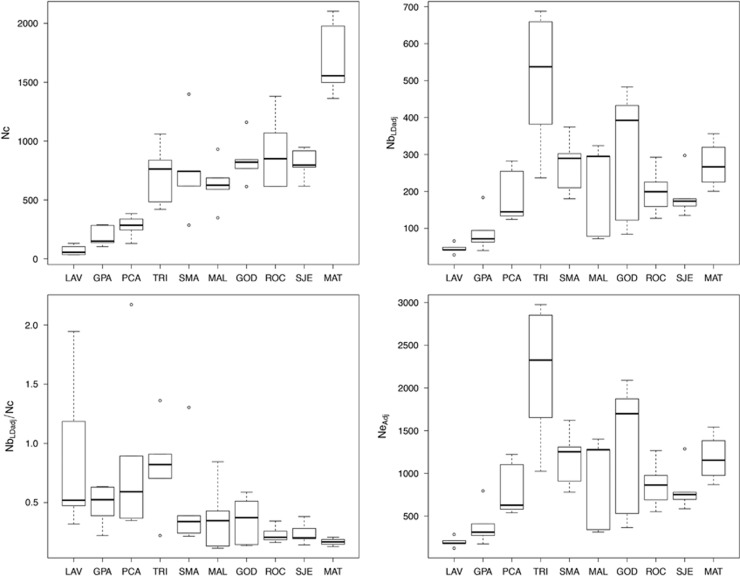
Figure 1.

Figure 1

Open in a new tab

Boxplots displaying the variation in census size (Nc), adjusted effective number of breeders (NbLDadj) and the ratio of the adjusted effective number of breeders over census size (NbLDadj/Nc) across 5 years within each river. Rivers are ordered according to their census size.

The number of anadromous adults returning to a river for a given year has been assessed for each river allowing an estimate of Nc for each sample. Basically, the number of spawners for each river is estimated using migratory pass, count barriers or snorkeling methods that are considered to provide the most reliable evaluation for a given river (Fontaine and Caron, 1999; see Perrier et al., 2016 for details). Such estimates for the Laval River were not available for the corresponding 5 years. Instead, according to the standard protocol of the Ministère des Forêts, de la Faune et des Parcs du Québec (Fontaine and Caron, 1999), data for the Laval River were estimated assuming that interannual variations are approximately the same as those observed in the other rivers of the region. The census size within a river across a generation (hereafter named Ncpool) was obtained by summing Nc over years × (α/number of sampled years), with α=age at maturity (=3.4 years).

Genotyping, genetic diversity and differentiation

All methodological steps from DNA extraction to genotyping through amplifications at 15 microsatellites are detailed in Perrier et al. (2016). Potential presence of null alleles and large allelic dropout were tested using the software MICROCHECKER (Van Oosterhout et al., 2004). Fis, Ho and He for each marker and river were estimated using FSTAT 2.9.3 (Goudet, 1995) and were mainly used to ensure the absence of technical problems that may have led to abnormal heterozygotes excess or deficit. Using Genepop v 4.2.2 (Rousset, 2008), we estimated Fst between rivers to assess the potential structure among rivers and Fis for each river. The stability across years of the genetic structure between rivers was tested computing Pearson's correlation coefficient between Fst estimates for each pairwise comparison year. Moreover, an analysis of molecular variance conducted with rivers nested within year was also performed with Arlequin version 3.5.1.2 (Excoffier and Lischer, 2010). The relationship between Fis values and NbLDadj/Nc ratio was subsequently tested by a linear regression model in order to test for a putative within-river Wahlund or Allendorf–Phelps effects (Allendorf and Phelps, 1981; Waples, 1998; Castric et al., 2002). Migrants across populations were identified using Geneclass2 (Piry et al., 2004) and then removed for subsequent analyses.

Estimates of effective number of breeders (Nb), effective population size (Ne) and their ratio to census size (Nc)

Our sampling design allowed assessing (1) Nb estimates from each consecutive cohort (from 2008 to 2012) of the 10 rivers and (2) Ne estimates over a generation by analyzing consecutive cohorts from a same river jointly. We estimated Nb for each of the 50 samples using two different single-sample estimator methods. The first was the Sibship assignment method (Wang, 2009) that uses sibship frequencies estimated from randomly sampled pairs of individuals as being sibs sharing one or two parents. The program Colony2 (Wang, 2009) was run under the full likelihood model to estimate Nbsib by considering polygamous breeding systems for both sexes (Garant et al., 2001; Richard et al., 2013), and no prior information on candidate parents or sibship sizes. Second, we estimated NbLD by applying the LD (Waples and Do, 2008) method that uses the unbiased estimators of Burrow's Δ (Weir, 1979) to test for nonrandom associations between unlinked loci. For this, we used the program NeEstimator 2 (Do et al., 2014) that implements an improved version of the LDNe algorithm (Waples and Do, 2008) to better deal with missing data (Peel et al., 2013). We used a threshold of 0.05 as the lowest allele frequency that gives the least biased results according to Waples and Do (2010). We then used the method developed by Waples et al. (2014) that corrects bias due to overlapping generations using three simple life-history traits, and the following equation:

graphic file with name hdy201662e1.jpg

Where Al, α and CVf correspond to adult life span, age at maturity and variation in age-specific fecundity, respectively. We used Al=2, α=3.4 and CVf=0.88 (these parameters were computed using the data published in Perrier et al., 2014 and according to Dionne and Cauchon, 2014). Then, in order to obtain a Ne estimate for each river, we used the following equation from Waples et al. (2014) Table 3:

Table 3. Linear mixed effects models accounting for the effects of the river and of the year on NbAdj/N C.

Explained variable Models Log likelihood The χ2 test P-value Variance explained by the river Variance explained by the year
NbAdj/NC lmer (log(NbAdj/NC)~1+(1 | river)+(1 | breeding year)) −48.78   0.37 0.19
  lmer (log(NbAdj/NC)~1+(1 | river)) −52.52 0.006    
  lmer (log(NbAdj/NC)~1+(1 | breeding year)) −54.55 0.000    
Open in a new tab

The χ2 tests were used to compare the models including only the river or the breeding year to the model including both terms.

graphic file with name hdy201662e2.jpg

As these estimates (from each year and river) reflect temporal (across years) and demographic (across rivers) variation, they were subsequently used for modeling the prediction of Ne estimate from Nb estimate (see below). For each river, the ratio of number of breeders to census size was assessed dividing NeLDadj by the Nc values within each river (Waples, 2005).

Ne for each river was also estimated pooling all consecutive cohorts into a single analysis by river using the two methods previously employed. First, the program Colony2 (Wang, 2009) was run with the same setting used for Nbsib estimates to get Ne estimates from pooled temporal samples (hereafter named NepoolSib). Second, the LDNe approach was performed to estimate the Nepool. Pearson's correlation was computed to test the congruence between NbLDadj and Nbsib estimates and between Nepool and NepoolSib estimates, as well as between the mean of NeAdj within a river and the corresponding Nepool. For each river, the ratio of effective size to census size was assessed dividing Nepool by the Ncpool values (Waples, 2005). As the ratios Nb/Nc and Ne/Nc could differ among populations and hence reflect differences in sex ratios, nonrandom mating, variance in individual reproductive success and family size and fluctuating Nc over generations, we tested whether NbLDadj/Nc varied among rivers and among years. The results of this analysis directly reflect the variation of NeAdj/Nc as NeAdj was directly estimated from NbLDadj. We used the function LMER from the R package LME4 to fit linear mixed effects models accounting for the effects of river and breeding year on NbLDadj/Nc, considered as random variables. The function BOXCOC from the library MASS in R (Venables and Ripley, 2002) was used to determine the best normalization transformation to apply to NbLDadj/Nc. NbLDadj/Nc values were thereafter log transformed. The χ2 tests were used to compare the log likelihood of the models built using only one variable with models including two variables. From the best models, we inferred the variance of log (NbLDadj/Nc) attributable to the river and to the year. Finally, the relationship between log(NeAdj/Nc) and Nc on one hand and between log(NbLDadj) and Nc on the other hand were explored using Pearson's correlation test.

Predicting Ne and Nc from Nb

Taking into account the variability across rivers and years, we used a hierarchical linear mixed effects model to predict (1) NeAdj from NbLDadj and (2) Nc from NbLDadj. This model includes the NbAdj and NeAdj variability (95% confidence interval) within each river by an extension of bootstrapped type II regression model with random effect of 1000 iterations (Sokal and Rohlf, 1995; Legendre and Legendre, 1998) using a custom R-script. Linear model were run using the function lme() of the NLME R-cran package (Pinheiro et al., 2015). The function BOXCOC from the library MASS in R (Venables and Ripley, 2002) was used to determine the best normalization transformation to apply to NeAdj, NbLDadj and Nc. NeAdj, NbLDadj and Nc values were thereafter log transformed.

Results

Genetic diversity within and among rivers

A total of 4730 juveniles were genotyped for the 15 microsatellites with an average of 3.03% of missing genotypes. The median number of juveniles genotyped per river and per year was 98 and ranged from 43 to 100 (Table 1). The mean number of alleles per locus was 27 and ranged from 10 to 47, whereas the number of alleles per locus per population varied from 4 to 31 with an average of 15. MICROCHECKER analysis was performed that confirmed the absence of null alleles and allele dropout. He estimates per population per year varied from 0.79 to 0.86 with an average of 0.81 (Supplementary Material 1). Average Fis per population per year ranged from −0.02 to 0.04 with an average of 0.01 (Supplementary Material 1), and no significant relationship was found between Fis and NbAdj/Nc (r2Adj=0.016, P=0.19, F=1.854), confirming the absence of significant within-river Wahlund or Allendorf–Phelps effects. Fst among rivers within a given year were significant (P<0.001) and ranged from 0.005 (PCA10-MAT10) to 0.063 (LAV12-GOD12) with an average of 0.0288 (Supplementary Material 2). The genetic structure between rivers was stable across years as t Pearson's correlation coefficient between Fst estimates between years was highly significant (P<2.2e−16) for all comparisons and ranged between 0.83 (2008–2012) and 0.96 (2009–2010) (Supplementary Material 2). The hierarchical analysis of molecular variance conducted with rivers nested within year revealed that the genetic variation is 2.75 times as important among rivers within a year as among years.

Estimates of census size (Nc), effective number of breeders (Nb), effective population size (Ne) and their ratio to census size

Census size varied from 34 (LAV11) to 2103 (MAT11), with an average of 691 and a median value of 622 (Table 1 and Figure 1). Average Nc values per river across the 5 years ranged from 72 (LAV) to 1699 (MAT), with an average of 691 and a median of 736.

Nbsib estimates varied from 46 (LAV10) to 186 (SMA12), with an average of 127 and a median of 139 (Table 2). NbLD estimates varied from 34 (LAV10) to 815 (TRI08) with an average of 269, and NbLDadj estimates varied from 29 (LAV10) to 688 (TRI08), with an average of 227 and a median of 199. The 95% confidence intervals ranged from ±25 (LAV10) to infinite (MAT08, TRI08 and TRI12). Over the 50 samples, we obtained a single ‘infinite' value, for MAT08, for which the lower limit of the confidence interval was 521 (Table 2). Overall, the mean coefficient of variation across rivers was 0.41 and varied from 0.24 (MAT) to 0.61 (GOD). Overall, NbLDadj and Nbsib were positively correlated (r2=0.70, P-value=2.33e−08). NbLDadj/Nc varied from 0.12 (MAL09) to 2.17 (PCA12). Average NbLDadj/Nc values per river over 5 years ranged from 0.17 (MAT) to 0.89 (LAV), with an average value of 0.50 and a median value of 0.35. The estimations of effective sizes across a generation (Ne) were first assessed from single-cohort samples estimates using the equation of Waples et al. (2014). NeAdj values estimated from NbLDadj varied from 124 (LAV10) to 2976 (TRI08), with an average of 980 and a median value of 863. NeAdj estimates averaged per river varied from 196 (LAV) to 2167 (TRI), with a mean of 984 and a median value of 895. The mean coefficient of variation across rivers for NeAdj was 0.41 and varied from 0.24 (MAT) to 0.61 (GOD). Ne estimates were also obtained by pooling all consecutive cohorts into a single analysis by river. Nepool estimated per river ranged from 132 (LAV) to 643 (MAT), with a mean of 352 and a median value of 375. A significant positive correlation was found between the mean of NeAdj within a river and the corresponding Nepool (r2=0.63, P-value=0.04). NepoolSib estimates per river ranged from 246 (LAV) to 646 (MAT), with an average of 496 and a median value of 542. Nepool and NepoolSib were also significantly and positively correlated (r2=0.89, P-value=0.0006013, Supplementary Material 3). The mean ratio Nepool/ Ncpool was 0.22 and ranged from 0.11 (MAT, GOD and MAL) to 0.54 (LAV) (Table 2).

Table 2. Sample abbreviation, Nbsib, NbLD, NbLDadj, NbLDadj/Nc, NeAdj, NepoolAdj and NepoolAdj/Ncpool estimated using the LDNe method (Waples and Do, 2008) and NepoolSib estimated using the Sibship method (Wang, 2009).

Sampling abbreviation Nbsib NbLD NbLDadj NbLDadj/Nc NeAdj Nesib Nepool Nepool/Ncpool
LAV08 51 (34–78) 58 (47–73) 49 (40–62) 0.47 211 (172–268) 246 (205 –299) 132 (121–145) 0.54
LAV09 81 (59–114) 50 (43–57) 42 (36–48) 0.32 181 (158–210)      
LAV10 47 (32–72) 34 (30–38) 29 (25–32) 0.52 124 (110–139)      
LAV11 72 (50–104) 78 (66–96) 66 (55–81) 1.94 286 (239–349)      
LAV12 69 (26–62) 49 (43–57) 41 (36–48) 1.19 180 (157–208)      
GPA08 77 (54–110) 112 (82–169) 95 (69–142) 0.63 409 (299–617) 304 (258 –360) 167 (152–184) 0.26
GPA09 66 (47–95) 48 (42–55) 40 (35–46) 0.39 173 (152–199)      
GPA10 90 (66–124) 75 (64–89) 63 (54–75) 0.22 272 (232–324)      
GPA11 128 (95–174) 218 (158–333) 184 (134–281) 0.64 794 (578–1217)      
GPA12 81 (67–105) 85 (72–102) 72 (61–86) 0.52 311 (264–373)      
PCA08 155 (116–206) 302 (201–565) 255 (170–477) 0.89 1102 (734–2063) 522 (453–599) 391 (339–457) 0.42
PCA09 107(80–142) 172 (130–246) 145 (109–207) 0.59 627 (474–897)      
PCA10 99 (73–135) 148 (116–199) 124 (97–168) 0.37 539 (422–726)      
PCA11 104 (76–141) 159 (124–216) 134 (104–182) 0.35 580 (451–788)      
PCA12 177 (154–208) 335 (213–715) 282 (180–603) 2.17 1222 (777–2608)      
TRI08 146 (111–194) 815 (344-Inf) 688 (290-Inf) 0.82 2976 (1256–10 951) 602 (526–683) 469 (395–568) 0.19
TRI09 147 (113–191) 453 (266–1312) 382 (224–1107) 0.91 1654 (971–4791)      
TRI10 158 (118–215) 637 (317–10 641) 537 (267–8975) 0.7 2326 (1156–38 844)      
TRI11 155 (114–207) 281 (186–527) 237 (157–444) 0.22 1024 (680–1922)      
TRI12 184 (165–214) 782 (346-Inf) 659 (292-Inf) 1.36 2853 (1262–10 951)      
SMA08 143 (109–192) 214 (153–339) 180 (129–286) 0.24 780 (557–1237) 643 (562 –738) 412 (356–483) 0.16
SMA09 154 (116–206) 249 (176–408) 210 (148–344) 0.34 909 (641–1488)      
SMA10 158 (121–208) 343 (219–721) 290 (185–608) 0.39 1253 (801–2632)      
SMA11 151 (116–201) 359 (235–708) 302 (198–598) 0.22 1309 (856–2586)      
SMA12 186 (168–215) 444 (259–1322) 374 (219–1115) 1.3 1621 (946–4826)      
MAL08 84 (55–135) 384 (155–3000) 324 (130–2530) 0.35 1401 (564–10 951) 401 (340–470) 234 (210–262) 0.11
MAL09 95 (69–129) 86 (73–102) 72 (61–86) 0.12 312 (265–373)      
MAL10 107 (80–145) 93 (79–112) 79 (67–94) 0.13 340 (289–407)      
MAL11 145 (109–193) 350 (231–675) 295 (195–570) 0.43 1277 (842–2466)      
MAL12 102 (86–126) 350 (112–180) 295 (94–152) 0.85 1277 (409–658)      
GOD08 96 (72–130) 100 (82–125) 84 (69–106) 0.14 365 (299–457) 562 (493–647) 303 (266–347) 0.11
GOD09 148 (113–197) 465 (260–1727) 392 (219–1457) 0.51 1699 (949–6305)      
GOD10 149 (115–178) 145 (114–195) 123 (96–165) 0.15 530 (416–713)      
GOD11 151 (117–203) 513 (287–1936) 433 (242–1633) 0.37 1872 (1047–7067)      
GOD12 165 (41–88) 573 (275–114 861) 483 (232–96 880) 0.59 2090 (1005–419 296)      
ROC08 88 (61–131) 151 (101–279) 127 (85–235) 0.21 551 (368–1018) 493 (428–569) 359 (310–421) 0.12
ROC09 128 (96–172) 189 (145–265) 159 (122–223) 0.26 689 (527–966)      
ROC10 136 (102–182) 236 (167–384) 199 (141–324) 0.19 863 (611–1401)      
ROC11 132 (97–178) 267 (189–438) 225 (159–369) 0.16 976 (688–1599)      
ROC12 183 (162–218) 347 (222–729) 293 (187–615) 0.34 1267 (811–2660)      
SJE08 123 (90–168) 160 (120–234) 135 (101–197) 0.14 585 (436–854) 543 (476–620) 416 (354–497) 0.15
SJE09 131 (98–176) 190 (140–285) 161 (118–240) 0.2 695 (512–1040)      
SJE10 116 (87–156) 213 (153–336) 180 (129–284) 0.2 779 (559–1227)      
SJE11 141 (107–187) 353 (223–767) 298 (188–647) 0.38 1289 (814–2799)      
SJE12 160 (141–189) 206 (152–307) 174 (128–259) 0.28 752 (556–1119)      
MAT08 146 (112–196) Inf (618–Inf) Inf (521–Inf) Inf Inf (2256–10 951) 646 (571–734) 643 (524–815) 0.11
MAT09 157 (118–208) 238 (170–377) 201 (144–318) 0.13 868 (622–1377)      
MAT10 159 (121–212) 297 (200–539) 250 (169–454) 0.17 1084 (731–1967)      
MAT11 157 (120–213) 422 (251–1154) 356 (212–974) 0.17 1542 (916–4214)      
MAT12 179 (152–198) 335 (220–654) 283 (186–552) 0.21 1224 (804–2387)      
Average 127 (96–164) 269 (173–3153) 227 (146–2659) 0.5 980 (633–11 510) 496 (431–572) 352 (303–418) 0.22
Minimum 47 (26–62) 34 (30–38) 29 (25–32) 0.12 124 (110–139) 246 (205–299) 132 (121–145) 0.11
Maximum 186 (168–218) 815 (618–114 861) 688 (521–96 880) 2.17 2976 (2256–419 296) 646 (571–738) 643 (524–815) 0.54
Open in a new tab

Values in brackets represent the 95% confidence interval.

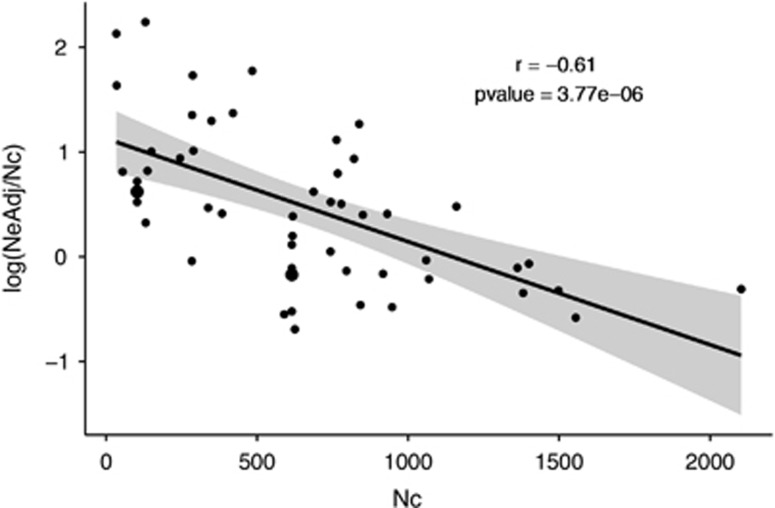
The LMER model that best predicted log (NbLDadj/Nc) variation integrated both the effects of the river and that of year (log likelihood=−48.78). Overall, 37% of the variance in log (NbLDadjj/Nc) was explained by the river and 19% was explained by the year, leaving 44% of the variance unexplained (Table 3). A significant negative correlation was also found between log(NbLDadj/Nc) and Nc (r2=−0.62, P-value=1.58e−06), as well as between log(NeAdj/Nc) and Nc (r2=−0.61, P-value=3.77e−06; Figure 2).

Figure 2.

Figure 2

Open in a new tab

Relationship between log(NeAdj/Nc) and Nc. Each dot represents a single sample (one population for a specific year) and the line was fitted with a linear regression including the 95% confidence interval (display in gray area Pearson's correlation coefficient and the associated P-value are also reported.

Predictions of Ne and Nc from Nb

Because we applied a log transformation on Nc, NbAdj and NeAdj variables, the linear model that actually describe our data is:

graphic file with name hdy201662e3.jpg

where b0 is the intercept, b1 corresponds to the slope and e is the error term.

We convert to raw data by taking the exponential of independent and dependent variables of this model, and thus we get:

graphic file with name hdy201662e4.jpg

Similarly, the equation obtained for the relationship between NeAdj and NbLDadj is

graphic file with name hdy201662e5.jpg

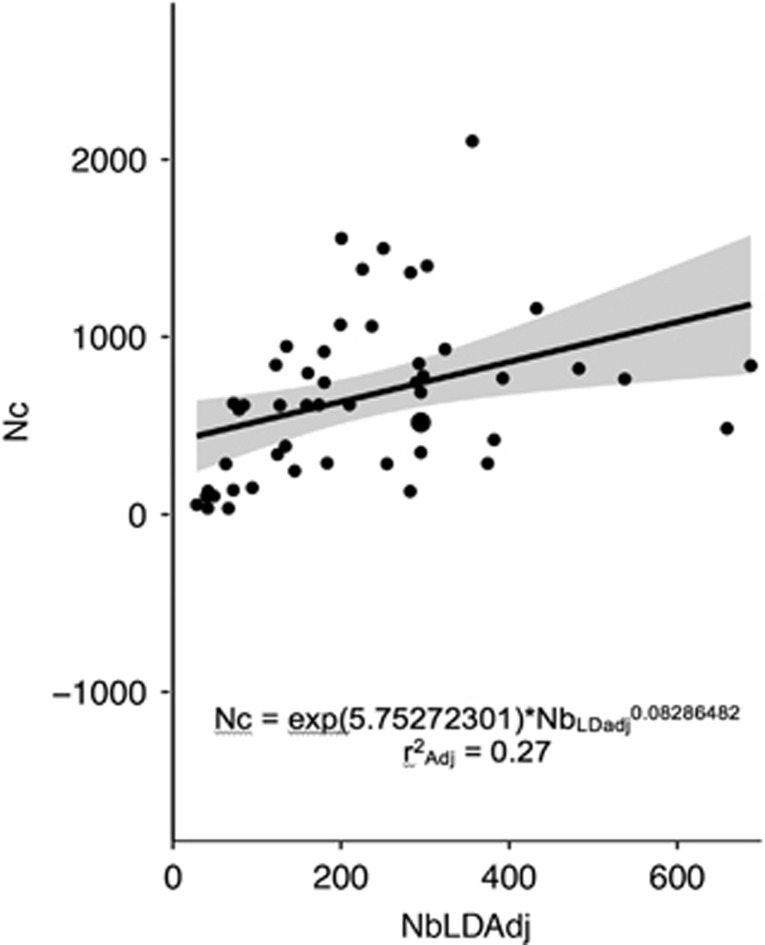
Here, a quasi-perfect correlation is obviously expected as Ne was directly estimated from Nb estimates. However, the main point here was to use our empirical data set to propose an empirical equation directly applicable in our system. Figure 3 shows the fit between the observed data and the hierarchical linear model for the relation between NbAdj and Nc. The mean correlation between NbLDadj and Nc among years within a river is 0.68. For the relationship between NbLDadj and Ne the mean correlation between NbLDadj and Nc among years within river is 0.15.

Figure 3.

Figure 3

Open in a new tab

Relationship between NbLDadj and Nc variables including the 95% confidence interval (in gray area). Each dot represents a single sample (one population for a specific year) and curves were fitted based on the coefficients of the hierarchical linear mixed model.

Discussion

The goal of this study was to empirically explore the relationship between the three parameters, Nc, Nb and Ne, taking into consideration different demography factors (including genetically distinct populations) and temporal fluctuations (sampling 5 consecutive years) in 10 populations of Atlantic salmon. To achieve this, we generated one of the most comprehensive microsatellite data sets generated to date in Atlantic salmon. Our results allow performing a detailed empirical assessment of the mathematical relationship between Ne and Nb developed by Waples et al. (2014). Precise estimates of cohort-specific Nb were quantified across a wide range of population sizes that allowed drawing the relationship with census size (Nc). In the following sections, we first discuss about factors potentially affecting Nb, Ne and their ratio to Nc in comparison with other studies conducted on the same species as well as on other taxa. Then, we consider the reliability of these relationships for wild populations and specifically for Atlantic salmon conservation.

Factors potentially affecting Nb, Ne and their ratios to Nc

In our study, NbLDadj (from 29 to 696), NeAdj (from 106 to 2538) and Nc (from 34 to 2103) estimates generally fall within the range of values reported in other northeast Atlantic salmon populations. Nb was estimated at 198 in the Escoumins River (Québec, Canada, Perrier et al., 2014), ranged from 70 to 352 over a 30-year study in the Northeast Brook (Newfounland, Johnstone et al., 2013) and ranged from 42 to 3784 with an average of 1016 among 9 rivers in Newfounland (Palstra et al., 2009). Moreover, when estimating Ne from pooled years, NepoolSib estimates were downwardly biased for large populations in comparison with estimates from the LDNE approach (NepoolAdj). Comparison between NbLD, NbLDadj and Nbsib estimates in our study also strengthens the point that Nbsib is likely downwardly biased because of overlapping generations. A putative explanation that has already been inferred either in Atlantic salmon (Johnstone et al., 2013) or in the threespine stickleback (DeFaveri and Merilä, 2015) is that in large populations, the Sibship method as implemented in Colony2 (Jones and Wang, 2010) would be more sensitive to sample size (that is, a bigger sample size would better reflect the entire Sibship network (Carrea, 2011, but see Wang, 2016). In contrast, NeAdj inferred from each year seems to better reflect the extent of LD within the cohort. Moreover, to overcome the bias due to overlapping generations using the LDNe method (which assumes discrete generations), we corrected Nb and Ne estimates according to Waples et al. (2014) using three life-history traits that were identically set for the 10 rivers because river-specific data were not available. These NbLDadj and NeAdj estimates could therefore be refined for each river in the future given that adult life span, age at maturity and age-specific fecundity probably differ among rivers. The age at maturity is probably the parameter that varies the most among Atlantic salmon populations and consequently could have the most considerable effect on effective size estimates. However, it is difficult to obtain a good estimate for such a parameter. In particular, this would require knowing the exact proportion of mature male parr (which are early sexually maturing male salmon that are not counted in Nc estimates) in a population that could also vary among years.

With a mean Nepool/Ncpool ratio of 0.22 across sampled rivers, our results are in agreement with the review of Palstra and Ruzzante (2008) reporting a low median ratio (=0.14) across studies. However, we observed a pronounced variability for Nepool/Ncpool estimates across populations (from 0.11 for the largest population MAT to 0.54 for the smallest population LAV). Consistently, the median Nepool/Ncpool ratio has previously been shown to be highly variable within species (Shrimpton and Heath, 2003; Palstra and Fraser, 2012) and generally larger in small than in large populations, suggesting changes in biological interactions with populations abundance (Frankham, 1995; Palstra and Fraser, 2012). Values of <1 in our populations could probably be attributed to common factors found in the wild and already reported in several studies, such as skewed sex ratios, high variance in reproductive success and fluctuations in population size through time (Nunney, 1993; Vucetich et al., 1997; Hedrick, 2005). The inverse relationship between NeAdj/Nc and Nc found in this study and other previous studies (Pray et al., 1996; Ardren and Kapuscinski, 2003; Araki et al., 2007; Fraser et al., 2007; Watts et al., 2007) could potentially be explained by an increase of the standardized variance in family size as Nc increases, and conversely, that this variance decreases as Nc decreases (Hedrick, 2005). At low abundance, lower variance in reproductive success leads to relatively higher effective size, either per generation (Ne) or per cohort (Nb) (Ardren and Kapuscinski, 2003). Indeed, Palstra and Ruzzante (2008) argue that mechanisms of genetic compensation may counteract reductions of Ne (and hence increase Ne/Nc). Such genetic compensation can be viewed as resulting in a buffering effect against loss of genetic diversity at low Nc. For salmonid fishes, genetic compensation can be reconciled with aspects of their breeding ecology (Fleming, 1996, 1998). Specifically, it is hypothesized to be due to density dependence in competition for spawning territories, competition for mates, redd superimposition or embryo mortality caused by delayed spawning (Ardren and Kapuscinski, 2003). Contrarily, Ne/Nc ratios in large populations are generally lower because there is higher variance in breeding success.

Making sense of the relationships between Nb, Ne and Nc in the context of salmon conservation

Estimating Ne over an entire generation can be challenging, whereas Nb can more easily be quantified from a single-cohort sample (Waples, 2005) and be a more practical parameter for managers. Here, we presented the first empirical application to the correction for overlapping generations estimating NbLDadj and NeAdj (Waples et al., 2014). Our sampling design incorporated the temporal, environmental and demographic variability and thus allows proposing an accurate prediction for this model. Therefore, for future management of Québec Atlantic salmon populations (or elsewhere in the species range), our results suggest that a single-cohort sample would be enough to get an estimate of Nb and then an extrapolated estimate of Ne.

In the present study, Nb/Nc fluctuated temporally; this also corroborates previous studies in Atlantic salmon (see, for example, Palstra et al., 2009; Johnstone et al., 2013; Perrier et al., 2013, 2016). Nb/Nc temporal variation has also been reported in other salmonid species (Heath et al., 2002; Palm et al., 2003). Frankham (1995) and Vucetich et al. (1997) suggested that fluctuation in census size was the largest contributor to the reduction of effective to census size ratios on both theoretical and empirical grounds, whereas Storz et al. (2001) suggested that variance in reproductive success has a pivotal role based on results of paternity analysis. If the former is correct, then genetic monitoring may be an efficient and independent means of estimating abundance of exploited populations of conservation and/or commercial interest (Ovenden et al., 2007; Waples et al., 2008). A significant positive correlation between Nb and Nc has also been reported in several long-term studies (Osborne et al., 2010; Charlier et al., 2012) but not in others (Ardren and Kapuscinski, 2003; Palstra et al., 2009; Berry and Kirkwood, 2010; Serbezov et al., 2012; Duong et al., 2013; Johnstone et al., 2013; Dowling et al., 2014; Whiteley et al., 2015). The positive correlation between Nb and Nc suggests that in the case of Québec Atlantic salmon populations, NbAdj is an indicative parameter for tracking temporal trends within populations and that genetic monitoring can be used for detecting fluctuations in abundance. However, it is noteworthy that our model allows explaining only 27% of the variance in Nc value from NbAdj estimates, and that 73% of the remaining variation could be explained by other factors. As reported in Perrier et al. (2016), most of the variance in NbAdj/Nc was explained by the river rather than year, suggesting that NbAdj/Nc differ among rivers according to their biological characteristics. Such variability in NbAdj/Nc could be attributed to various biological processes including differences in variance of individual reproductive success and in sex ratio (Crow and Kimura, 1970; Nunney, 1993; Frankham, 1995; Kalinowski and Waples, 2002; Hedrick, 2005). Moreover, estimates of Nc employed in this study correspond to adult run size, ignoring the reproductive potential of individuals that mature without going to the sea. In Atlantic salmon such individuals are primarily males (Klemetsen et al., 2003) and known as mature male parr (Verspoor et al., 2007). It has been recently shown that these mature male parr can contribute importantly to the effective population size via both their reproductive effort and the fact that they are generally maturing asynchronously from females they mate with. Thus, several studies have shown that mature male parr may fertilize relatively large proportions of eggs in the wild, ranging typically from 30 to 60% (Martinez et al., 2000; Saura et al., 2008; Grimardias et al., 2010; Richard et al., 2013). Thus, NeAdj/Nc and NbAdj /Nc reports using Nc inferred from anadromous run are expected to be upwardly biased as Nc does not include mature male parr (Perrier et al., 2014). This bias could be especially problematic because anadromous adults often contain fewer males than females (Dalley et al., 1983; Myers and Hutchings, 1987), potentially resulting in a high degree of polygamy that may cause more pronounced reductions in NeAdj/Nc ratios. Hence, the efficacy of Ne as a predictor of abundance may depend on intrinsic population characteristics of the species, and in particular the proportion of mature male parr and skewed sex ratio.

Conclusion

Here, we showed the utility of using a comprehensive empirical data set to obtain robust census and effective population or breeder sizes and depict demographic and temporal fluctuations. Nb and Ne estimates from the LDNe method and the Sibship method were congruent overall. The results show a significant correlation between Nb and Nc and between Nb and Ne, suggesting that in the case of Atlantic salmon populations, Nb offers potential to be used for tracking population abundance and effective population size. Moreover, based on Waples et al. (2014) we proposed an empirical relationship between Ne and Nb for a direct application in the conservation of the Atlantic salmon. However, our model allows explaining only 27% of the variation in Nc from Nb estimates, indicating that a large proportion of the variance in Nb/Nc exists both among populations (37%) and among years for the same population (19%). This result illustrates the need for a thorough calibration of Nb/Nc before using Nb in monitoring programs, as well as a full awareness of the limits of such approach.

Data accessibility

Empirical data (genepop file) available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.jh146.

Acknowledgments

We thank all biologists and technicians of the Ministère des Forêts, de la Faune et des Parcs du Québec (MFFP) for their implication in the project and their field assistance. We are grateful to E Normandeau for his help while analyzing the data. We are also grateful to the associated editor and three anonymous reviewers for their constructive comments on a previous version of this manuscript. This research was funded by the MFFP and the Canadian Research Chair in Genomics and Conservation of Aquatic Resources.

Author contributions

LB and MD conceived the study. MD supervised the sampling. CH performed lab analysis for the two last years. A-LF conducted analysis and writing and editing the manuscript with help from JA, CP, MD and LB.

The authors declare no conflict of interest.

Footnotes

Supplementary Information accompanies this paper on Heredity website (http://www.nature.com/hdy)

Supplementary Material

Supplementary Table 1
Click here for additional data file. (54.2KB, xlsx)
Supplementary Information
Click here for additional data file. (318KB, pdf)

References

  1. Allendorf FW, Phelps SR. (1981). Use of allelic frequencies to describe population structure. Can J Fish Aquat Sci 38: 1507–1514. [Google Scholar]
  2. Araki H, Waples R, Ardren W, Cooper B, Blouin M. (2007). Effective population size of steelhead trout: influence of variance in reproductive success, hatchery programs, and genetic compensation between life-history forms. Mol Ecol 16: 953–966. [DOI] [PubMed] [Google Scholar]
  3. Ardren W, Kapuscinski A. (2003). Demographic and genetic estimates of effective population size (Ne) reveals genetic compensation in steelhead trout. Mol Ecol 12: 35–49. [DOI] [PubMed] [Google Scholar]
  4. Belmar-Lucero S, Wood J, Scott S, Harbicht A, Hutchings J, Fraser D. (2012). Concurrent habitat and life history influences on effective/census population size ratios in stream-dwelling trout. Ecol Evol 2: 562–573. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Berry O, Kirkwood R. (2010). Measuring recruitment in an invasive species to determine eradication potential. J Wildl Management 74: 1661–1670. [Google Scholar]
  6. Carrea C. (2011). Ecologia, genetica e historia de vida de Galaxias maculatus en dos grandes cuencas de Patagonia. PhD dissertation, Universidad Nacional del Comahue, Argentina.
  7. Castric V, Bernatchez L, Belkhir K, Bonhomme F. (2002). Heterozygote deficiencies in small lacustrine populations of brook charr Salvelinus Fontinalis Mitchill (Pisces, Salmonidae): a test of alternative hypotheses. Heredity 89: 27–35. [DOI] [PubMed] [Google Scholar]
  8. Charlier J, Laikre L, Ryman N. (2012). Genetic monitoring reveals temporal stability over 30 years in a small, lake-resident brown trout population. Heredity 109: 246–253. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Chaput G. (2012). Overview of the status of Atlantic salmon (Salmo salar) in the North Atlantic and trends in marine mortality. ICES J Mar Sci 69 (9): 1538–1548. [Google Scholar]
  10. Crow JF, Kimura M. (1970) An Introduction to Population Genetics Theory. Harper and Row: New-York. [Google Scholar]
  11. Dalley EL, Andrews CW, Green JM. (1983). Precocious male Atlantic salmon parr (Salmo salar) in insular Newfoundland. Can J Fish Aquat Sci 40: 647–652. [Google Scholar]
  12. DeFaveri J, Merilä J. (2015). Temporal stability of genetic variability and differentiation in the three-spined stickleback (Gasterosteus aculeatus. PLoS One 10: e0123891. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Dionne M, Caron F, Dodson J, Bernatchez L. (2008). Landscape genetics and hierarchical genetic structure in Atlantic salmon: the interaction of gene flow and local adaptation. Mol Ecol 17: 2382–2396. [DOI] [PubMed] [Google Scholar]
  14. Dionne M, Cauchon V. (2014). Écologie et évolution des populations témoins de saumon atlantique au Québec: rapport de recherche 2014. Ministère des Forêts, de la Faune et des Parcs, Direction générale de l'expertise sur la faune et ses habitats, Direction de la faune aquatique, Québec, 86p.
  15. Do C, Waples RS, Peel D, Macbeth GM, Tillett BJ, Ovenden JR. (2014). NeEstimator v2: re-implementation of software for the estimation of contemporary effective population size (Ne) from genetic data. Mol Ecol Resour 14: 209–214. [DOI] [PubMed] [Google Scholar]
  16. Dowling T, Turner T, Carson E, Saltzgiver M, Adams D, Kesner B et al. (2014). Time-series analysis reveals genetic responses to intensive management of razorback sucker (Xyrauchen texanus. Evol Appl 7: 339–354. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Duong TY, Scribner KT, Forsythe PS. (2013). Interannual variation in effective number of breeders and estimation of effective population size in long-lived iteroparous lake sturgeon (Acipenser fulvescens. Mol Ecol 22: 1282–1294. [DOI] [PubMed] [Google Scholar]
  18. Excoffier L, Lischer HE. (2010). Arlequin suite ver 3.5: a new series of programs to perform population genetics analyses under Linux and Windows. Mol Ecol Resour 10: 564–567. [DOI] [PubMed] [Google Scholar]
  19. Fleming I. (1996). Reproductive strategies of Atlantic salmon: ecology and evolution. Fish Biol Fish 6: 379–416. [Google Scholar]
  20. Fleming IA. (1998). Pattern and variability in the breeding system of Atlantic salmon (Salmo salar, with comparisons to other salmonids. Can J Fish Aquat Sci 55: 59–76. [Google Scholar]
  21. Fontaine P-M, Caron F. (1999). Re-evaluation of spawner and return salmon numbers in Québec, 1967–1998. Report to the Working Group on North Atlantic Salmon of the International Council for the Exploration of the Sea (ICES). Service de la faune aquatique. Direction générale du patrimoine faunique et naturel. Gouvernement du Québec. Québec, Canada. 14p.
  22. Frankham R. (1995). Effective population size - adult size ratios in wildlife - a review. Genetical research 66: 95–107. [DOI] [PubMed] [Google Scholar]
  23. Fraser D, Jones M, McParland T, Hutchings J. (2007). Loss of historical immigration and the unsuccessful rehabilitation of extirpated salmon populations. Conserv Genet 8: 527–546. [Google Scholar]
  24. Friedland KD, Reddin DG, McMenemy JR, Drinkwater KF. (2003). Multidecadal trends in North American Atlantic salmon (Salmo salar stocks and climate trends relevant to juvenile survival. Can J Fish Aquat Sci 60: 563–583. [Google Scholar]
  25. Garant D, Dodson J, Bernatchez L. (2001). A genetic evaluation of mating system and determinants of individual reproductive success in Atlantic salmon (Salmo salar L.). J Hered 92: 137–145. [DOI] [PubMed] [Google Scholar]
  26. Goudet J. (1995). FSTAT (version 1.2): a computer program to calculate F-statistics. J Hered 86: 485–486. [Google Scholar]
  27. Grimardias D, Merchermek N, Manicki A, Garnier J, Gaudin P, Jarry M et al. (2010). Reproductive success of Atlantic salmon (Salmo salar mature male parr in a small river, the Nivelle: influence of shelters. Ecol Freshw Fish 19: 510–519. [Google Scholar]
  28. Hall C, Jordaan A, Frisk M. (2012). Centuries of anadromous forage fish loss: consequences for ecosystem connectivity and productivity. Bioscience 62: 723–731. [Google Scholar]
  29. Heath D, Busch C, Kelly J, Atagi D. (2002). Temporal change in genetic structure and effective population size in steelhead trout (Oncorhynchus mykiss. Mol Ecol 11: 197–214. [DOI] [PubMed] [Google Scholar]
  30. Hedrick P. (2005). A standardized genetic differentiation measure. Evolution 59: 1633–1638. [PubMed] [Google Scholar]
  31. Hermansen S, Hansen J, Hutchinson P. (2015) Report of the Thirty-Second Annual Meeting of the Council of the North Atlantic Salmon Conservation Organization Hotel North 2, Happy Valley-Goose Bay, Canada.
  32. Johnstone D, O'Connell M, Palstra F, Ruzzante D. (2013). Mature male parr contribution to the effective size of an anadromous Atlantic salmon (Salmo salar population over 30 years. Mol Ecol 22: 2394–2407. [DOI] [PubMed] [Google Scholar]
  33. Jones O, Wang J. (2010). COLONY: a program for parentage and sibship inference from multilocus genotype data. Mol Ecol Resour 10: 551–555. [DOI] [PubMed] [Google Scholar]
  34. Kalinowski ST, Waples RS. (2002). Relationship of effective to census size in fluctuating populations. Conserv Biol 16: 129–136. [DOI] [PubMed] [Google Scholar]
  35. Klemetsen A, Amundsen P-A, Dempson JB, Jonsson B, Jonsson N, O'Connel MF et al. (2003). Atlantic salmon Salmo salar L., brown trout Salmo trutta L. and Arctic charr Salvelinus alpinus (L.): a review of aspects of their life histories. Ecol Freshw Fish 12: 1–59. [Google Scholar]
  36. Legendre P, Legendre L. (1998) Numerical Ecology, 2nd English edition. Elsevier Science BV: Amsterdam. 853p. [Google Scholar]
  37. Limburg K, Waldman J. (2009). Dramatic declines in North Atlantic diadromous fishes. Bioscience 63. [Google Scholar]
  38. Luikart G, Ryman N, Tallmon DA, Schwartz MK. (2010). Estimation of census and effective population sizes: the increasing usefulness of DNA-based approaches. Conserv Genet 11: 355–373. [Google Scholar]
  39. Martinez JL, Moran P, Perez J, De Gaudemar B, Beall E, Garcia-Vazquez E. (2000). Multiple paternity increases effective size of southern Atlantic salmon populations. Mol Ecol 9: 293–298. [DOI] [PubMed] [Google Scholar]
  40. Miller L, Kapuscinski A. (1997). Historical analysis of genetic variation reveals low effective population size in a northern pike (Esox lucius population. Genetics 147: 1249–1258. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Mills K. (2013). Climate and ecosystem linkages explain widespread declines in North American Atlantic salmon populations. Glob Change Biol 19: 3046–3061. [DOI] [PubMed] [Google Scholar]
  42. Moore J, Bourret V, Dionne M, Bradbury I, O'Reilly P, Kent M et al. (2014). Conservation genomics of anadromous Atlantic salmon across its North American range: outlier loci identify the same patterns of population structure as neutral loci. Mol Ecol 23: 5680–5697. [DOI] [PubMed] [Google Scholar]
  43. Myers RA, Hutchings JA. (1987). Mating of anadromous Atlantic salmon, Salmo salar L., with mature male parr. J Fish Biol 31: 143–146. [Google Scholar]
  44. Nieland JL, Sheehan TF, Saunders R. (2015). Assessing demographic effects of dams on diadromous fish: a case study for Atlantic salmon in the Penobscot River, Maine. ICES J Mar Sci 72: 2423–2437. [Google Scholar]
  45. Nunney L. (1993). The influence of mating system and overlapping generations on effective population size. Evolution 47: 1329–1341. [DOI] [PubMed] [Google Scholar]
  46. Osborne M, Davenport S, Hoagstrom C, Turner T. (2010). Genetic effective size, Ne, tracks density in a small freshwater cyprinid, Pecos bluntnose shiner (Notropis simus pecosensis. Mol Ecol 19: 2832–2844. [DOI] [PubMed] [Google Scholar]
  47. Ovenden JR, Peel D, Street R, Courtney AJ, Hoyle SD, Peel SL et al. (2007). The genetic effective and adult census size of an Australian population of tiger prawns (Penaeus esculentus. Mol Ecol 16: 127–138. [DOI] [PubMed] [Google Scholar]
  48. Palm S, Laikre L, Jorde P, Ryman N. (2003). Effective population size and temporal genetic change in stream resident brown trout (Salmo trutta, L.). Conserv Genet 4: 249–264. [Google Scholar]
  49. Palstra F, Ruzzante D. (2008). Genetic estimates of contemporary effective population size: what can they tell us about the importance of genetic stochasticity for wild population persistence? Mol Ecol 17: 3428–3447. [DOI] [PubMed] [Google Scholar]
  50. Palstra F, O'Connell M, Ruzzante D. (2009). Age structure, changing demography and effective population size in Atlantic Salmon (Salmo salar. Genetics 182: 1233–1249. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Palstra F, Fraser D. (2012). Effective/census population size ratio estimation: a compendium and appraisal. Ecol Evol 2: 2357–2365. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Parrish DL, Behnke RJ, Gephard SR, McCormick SD, Reeves GH. (1998). Why aren't there more Atlantic salmon (Salmo salar? Can J Fish Aquat Sci 55: 281–287. [Google Scholar]
  53. Peel D, Waples RS, Macbeth GM, Do C, Ovenden JR. (2013). Accounting for missing data in the estimation of contemporary genetic effective population size (N(e)). Mol Ecol Resour 13: 243–253. [DOI] [PubMed] [Google Scholar]
  54. Perrier C, Guyomard R, Bagliniere J, Nikolic N, Evanno G. (2013). Changes in the genetic structure of Atlantic salmon populations over four decades reveal substantial impacts of stocking and potential resiliency. Ecol Evol 3: 2334–2349. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Perrier C, Normandeau É, Dionne M, Richard A, Bernatchez L. (2014). Alternative reproductive tactics increase effective population size and decrease inbreeding in wild Atlantic salmon. Evol Appl 7: 1094–1106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Perrier C, April J, Cote G, Bernatchez L, Dionne M. (2016). Effective number of breeders in relation to census size as management tools for Atlantic salmon conservation in a context of stocked populations. Cons Genet 17: 31–44. [Google Scholar]
  57. Pinheiro J, Bates D, DebRoy S, Sarkar D, R Core Team. (2015) nlme: Linear and Nonlinear Mixed Effects Models. R package version 3.1-122. Available at: http://CRAN.R-project.org/package=nlme.
  58. Piry S, Alapetite A, Cornuet J, Paetkau D, Baudouin L, Estoup A. (2004). GENECLASS2: a software for genetic assignment and first-generation migrant detection. J Hered 95: 536–539. [DOI] [PubMed] [Google Scholar]
  59. Pray LA, Goodnight CJ, Stevens L, Schwartz JM, Yan G. (1996). The effect of population size on effective population size: an empirical study in the red flour beetle Tribolium castaneum. Genet Res 68: 151–155. [Google Scholar]
  60. Richard A, Dionne M, Wang J, Bernatchez L. (2013). Does catch and release affect the mating system and individual reproductive success of wild Atlantic salmon (Salmo salar L.)? Mol Ecol 22: 187–200. [DOI] [PubMed] [Google Scholar]
  61. Rousset F. (2008). Genepop'007: a complete reimplementation of the Genepop software for Windows and Linux. Mol Ecol Resour 8: 103–106. [DOI] [PubMed] [Google Scholar]
  62. Tallmon D, Gregovich D, Waples R, Baker C, Jackson J, Taylor B et al. (2010). When are genetic methods useful for estimating contemporary abundance and detecting population trends? Mol Ecol Resour 10: 684–692. [DOI] [PubMed] [Google Scholar]
  63. Saura M, Caballero A, Moran P. (2008). Impact of precocious male parr on the effective size of a wild population of Atlantic salmon. Freshw Biol 53: 2375–2384. [Google Scholar]
  64. Serbezov D, Jorde P, Bernatchez L, Olsen E, Vøllestad L. (2012). Life history and demographic determinants of effective/census size ratios as exemplified by brown trout (Salmo trutta. Evol Appl 5: 607–618. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Shrimpton JM, Heath DD. (2003). Census vs. effective population size in chinook salmon: large- and small-scale environmental perturbation effects. Mol Ecol 12: 2571–2583. [DOI] [PubMed] [Google Scholar]
  66. Sokal RR, Rohlf FJ. (1995) Biometry: The Principles and Practice of Statistics in Biological Research, 4th edn. Freeman & Co: New York. p 887. [Google Scholar]
  67. Storz J, Bhat H, Kunz T. (2001). Genetic consequences of polygyny and social structure in an Indian fruit bat, Cynopterus sphinx. II. Variance in male mating success and effective population size. Evolution 55: 1224–1232. [DOI] [PubMed] [Google Scholar]
  68. Van Oosterhout C, Hutchinson WF, Wills DP, Shipley P. (2004). MICRO CHECKER: software for identifying and correcting genotyping errors in microsatellite data. Mol Ecol Notes 4: 535–538. [Google Scholar]
  69. Venables WN, Ripley BD. (2002) Modern Applied Statistics with S, 4th edn. Springer: New York. [Google Scholar]
  70. Verspoor E, Stradmeyer L, Nielsen J. (2007) The Atlantic salmon: Genetics, Conservation and Management. Blackwell: Oxford, UK. pp 500. [Google Scholar]
  71. Vucetich JA, Waite TA, Nunney L. (1997). Fluctuating population size and the ratio of effective to census population size. Evolution 51: 2017–2021. [DOI] [PubMed] [Google Scholar]
  72. Wang J. (2009). A new method for estimating effective population sizes from a single sample of multilocus genotypes. Mol Ecol 18: 2148–2164. [DOI] [PubMed] [Google Scholar]
  73. Wang J. (2016). A comparison of single-sample estimators of effective population sizes from genetic marker data. Mol Ecol e-pub ahead of print 9 July 2016 doi:10.1111/mec.13725. [DOI] [PubMed]
  74. Waples R. (1989). A generalized approach for estimating effective population size from temporal changes in allele frequency. Genetics 121: 379–391. [DOI] [PMC free article] [PubMed] [Google Scholar]
  75. Waples RS. (1998). Separating the wheat from the chaff: patterns of genetic differentiation in high gene flow species. J Hered 89: 438–450. [Google Scholar]
  76. Waples R. (2002). Effective size of fluctuating salmon populations. Genetics 161: 783–791. [DOI] [PMC free article] [PubMed] [Google Scholar]
  77. Waples R. (2005). Genetic estimates of contemporary effective population size: to what time periods do the estimates apply? Mol Ecol 14: 3335–3352. [DOI] [PubMed] [Google Scholar]
  78. Waples RS, Do C. (2008). LDNE: a program for estimating effective population size from data on linkage disequilibrium. Mol Ecol Resour 8: 753–756. [DOI] [PubMed] [Google Scholar]
  79. Waples RS, Punt AE, Cope JM. (2008). Integrating genetic data into management of marine resources: how can we do it better? Fish and Fisheries 9: 423–449. [Google Scholar]
  80. Waples R, Do C. (2010). Linkage disequilibrium estimates of contemporary Ne using highly variable genetic markers: a largely untapped resource for applied conservation and evolution. Evol Appl 3: 244–262. [DOI] [PMC free article] [PubMed] [Google Scholar]
  81. Waples RS, Antao T, Luikart G. (2014). Effects of overlapping generations on linkage disequilibrium estimates of effective population size. Genetics 197: 769–780. [DOI] [PMC free article] [PubMed] [Google Scholar]
  82. Watts IC, Saccheri IJ, Kemp SJ, Thompson DJ. (2007). Effective population sizes and migration rates in fragmented populations of an endangered insect (Coenagrion mercuriale: Odonata). J Anim Ecol 76: 790–800. [DOI] [PubMed] [Google Scholar]
  83. Weir BS. (1979). Inferences about linkage disequilibrium. Biometrics 35: 235–254. [PubMed] [Google Scholar]
  84. Whiteley A, Coombs J, Cembrola M, O'Donnell M, Hudy M, Nislow K et al. (2015). Effective number of breeders provides a link between interannual variation in stream flow and individual reproductive contribution in a stream salmonid. Mol Ecol 24: 3585–3602. [DOI] [PubMed] [Google Scholar]
  85. Wright S. (1931). Evolution in Mendelian populations. Genetics 16: 97–159. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Table 1
Click here for additional data file. (54.2KB, xlsx)
Supplementary Information
Click here for additional data file. (318KB, pdf)

Data Availability Statement

Empirical data (genepop file) available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.jh146.

Articles from Heredity are provided here courtesy of Nature Publishing Group

RESOURCES