Bayesian longitudinal segmentation of hippocampal substructures in brain MRI using subject-specific atlases

Abstract

The hippocampal formation is a complex, heterogeneous structure that consists of a number of distinct, interacting subregions. Atrophy of these subregions is implied in a variety of neurodegenerative diseases, most prominently in Alzheimer’s disease (AD). Thanks to the increasing resolution of MR images and computational atlases, automatic segmentation of hippocampal subregions is becoming feasible in MRI scans. Here we introduce a generative model for dedicated longitudinal segmentation that relies on subject-specific atlases. The segmentations of the scans at the different time points are jointly computed using Bayesian inference. All time points are treated the same to avoid processing bias. We evaluate this approach using over 4,700 scans from two publicly available datasets (ADNI and MIRIAD). In test-retest reliability experiments, the proposed method yielded significantly lower volume differences and significantly higher Dice overlaps than the cross-sectional approach for nearly every subregion (average across subregions: 4.5% vs. 6.5%, Dice overlap: 81.8% vs. 75.4%). The longitudinal algorithm also demonstrated increased sensitivity to group differences: in MIRIAD (69 subjects: 46 with AD and 23 controls), it found differences in atrophy rates between AD and controls that the cross sectional method could not detect in a number of subregions: right parasubiculum, left and right presubiculum, right subiculum, left dentate gyrus, left CA4, left HATA and right tail. In ADNI (836 subjects: 369 with AD, 215 with early cognitive impairment – eMCI – and 252 controls), all methods found significant differences between AD and controls, but the proposed longitudinal algorithm detected differences between controls and eMCI and differences between eMCI and AD that the cross sectional method could not find: left presubiculum, right subiculum, left and right parasubiculum, left and right HATA. Moreover, many of the differences that the cross-sectional method already found were detected with higher significance. The presented algorithm will be made available as part of the open-source neuroimaging package FreeSurfer.

1. Introduction

1.1. Background

The study of the human hippocampus has traditionally attracted considerable attention from the neuroscience and neuroimaging communities due to its connection with memory [1, 2] and an array or neurological disorders, especially Alzheimer’s disease (AD) [3, 4, 5]. Limits in MR acquisition have for many years forced in vivo studies to treat the hippocampus as a single structure. However, the hippocampus consists of a number of subregions that have been shown to have different memory functions using animal models [6, 7]. In humans, there is increasing evidence that hippocampal subregions play different roles in memory [8, 9, 6, 10], and that they are differently affected by AD [11, 12]. Therefore, in vivo analysis of hippocampal subregions holds great promise to improve our understanding of normal aging and AD, as well as to deliver more sensitive biomarkers of AD and other neurological disorders.

Recent advances in MRI acquisition have made it possible to study the hippocampal subregions in vivo. Earlier studies had to rely on manual segmentations [13, 14], typically performed on T2 scans acquired coronally with high in-plane resolution and relatively thick slices. Automated methods have since been proposed to bypass the manual segmentation procedure, which requires extensive expertise, is extremely time consuming, and cannot be reproduced easily. Yushkevich et al. [15, 16] proposed a multi-atlas segmentation algorithm using a library of manually labeled T1 and T2 scans, whose output was refined by a machine learning bias correction strategy. Wang et al. [17, 18] employed a surface-based atlas approach. Our group, in previous work, used a probabilistic atlas to produce segmentations with a Bayesian inference algorithm within a generative framework. In a first version [19], the atlas was constructed using high-resolution in vivo MRI scans (coronal slices with .38 mm in-plane resolution, .8 mm slice separation). More recently, we acquired ultrahigh resolution ex vivo MRI, which enabled us to produce very detailed manual segmentations and, in turn, a much more accurate atlas [20]. It is the use of generative techniques that enables the application of ex vivo atlases to the segmentation of in vivo scans, since they do not require the intensity characteristics of the training and test datasets to match – in contrast with registration-based algorithms such as Yushkevich’s and Wang’s.

Many large scale studies, including the Alzheimer’s Disease Neuroimaging Initiative (ADNI), are now collecting longitudinal MRI data. Since they remove the confounding inter-subject variability, longitudinal studies enable us to accurately quantify within-subject neuroanatomical changes, and provide higher sensitivity than their cross-sectional counterparts [21]. However, until now, no dedicated method exists (to the best of our knowledge) for the longitudinal segmentation of hippocampal subregions.

In this paper, we introduce a novel Bayesian approach for the joint segmentation of hippocampal subregions across multiple time points. The method is based on a generative model of longitudinal MRI scans, extending our cross-sectional approach [20] to longitudinal datasets. Rather than by a population-wide atlas, the scans at the different time points are assumed to have been generated by a subject-specific atlas, which introduces a statistical dependence between the time points and ensures that the different images and corresponding segmentations are similar to each other. This subject-specific atlas is simply a deformed version of the population-wide atlas. Within this framework, the segmentations of all time points are computed simultaneously with a Bayesian inference algorithm; the subject-specific atlas is obtained as a by-product. Due to its generative nature and unsupervised intensity model, the algorithm is robust against changes in MRI contrast.

1.2. Further related work on longitudinal segmentation

Longitudinal segmentation algorithms exploit the prior knowledge that a set of images belongs to the same subject, in order to produce more accurate and consistent segmentations than when the images are processed independently. A crucial aspect of longitudinal methods is the need to keep them unbiased: algorithms that do not treat all time points the same way introduce processing bias due to the additional processing steps applied to selected images [22].

Many longitudinal segmentation approaches rely on a non-linear, group-wise registration that brings the images from the different time points into a common coordinate space. The registration should be computed in an intermediate space [23], in order to avoid biases due to image resampling in the space to a selected scan – typically the baseline [24, 25]. In some methods, the group-wise alignment is precomputed with a registration algorithm. For example, Gao et al. [26] used pre-aligned scans to optimize a cost function that included an intensity correction term matching the intensity profiles across time points. Other approaches integrate the registration into the segmentation framework. For instance, Shi et al. [27] used a multichannel (T1/T2) segmentation algorithm guided by prior tissue probability maps; the spatial mapping of the tissue maps across time points was estimated simultaneously with the segmentation using an expectation maximization algorithm. Xue et al. [28, 29] proposed a similar approach, which iteratively used the estimate of the segmentations to update the registrations and vice versa.

Some approaches do not require non-linear registration to produce the segmentations – though rigid registrations are still used to bring the images into rough alignment. In the context of whole hippocampus segmentation, Wolz et al. [30] built a 4D graph in which a voxel had 6 spatial neighbors and 2 temporal neighbors (from the preceding and following time points). In their model, unary terms included intensity and anatomical priors, whereas pairwise terms were engineered to enforce spatial and temporal smoothness in the segmentation. The segmentation of all time points was then computed simultaneously with graph cuts. In a similar framework, Bauer et al. [31] used a random forest classifier in the unary term. Other papers have exploited expert knowledge to drive the segmentation. For example, Wang et al. [32] constrained the distance across the serial images to remain within a biologically plausible range, and used a similar strategy in a more recent paper [33] to segment the brain cortex (keeping the thickness within a reasonable range).

Finally, some longitudinal segmentation approaches have used a subject-specific atlas to produce consistent segmentations. In the context of neonate brain segmentation, Shi et al. [34] registered a population-wide atlas to the latest time point, which is normally the most reliable one in infants (least motion, and most contrast between gray and white matter), in order to produce subject-specific tissue probability maps. Rather than using a single time point as the target of the registration, Aubert-Broche et al. [35] built a subject-specific atlas by non-linearly coregistering the time points; then, they registered a population-wide atlas to the output to obtain subject-specific probability maps.

1.3. Contribution: an unbiased, longitudinal segmentation method for hippocampal subregions based on a subject-specific atlas

The contribution of this article is twofold. In first place, it presents the first available automated algorithm for longitudinal segmentation of the hippocampal subregions; prior works have only addressed the longitudinal segmentation of the hippocampus as a whole [30]. Additionally, it presents a novel generative model for longitudinal segmentation based on subject-specific atlases, which is unbiased and adaptive to changes in MRI contrast. The models assumes that the images are generated by a hidden subject-specific atlas, which is in turn generated by a population-wide atlas. Even though the idea of using subject-specific atlases is not original, our model is novel: as opposed to works like Aubert-Broche et al. [35], we estimate the subject-specific atlas along with the registrations and segmentations in a probabilistic framework, rather than precomputing it based solely on image intensities. This has the advantage that the segmentation and registration can iteratively improve each other.

The rest of this paper is organized as follows. Section 2 describes the generative framework that our method is based on, as well as the Bayesian inference algorithm that we used to obtain the segmentations. In Section 3, we describe a set of experiments that evaluated the test-retest reliability and sensitivity to group differences; since the hippocampal subregions cede to neurodegenerative pathology that worsens over time, we tested our approach on two public MRI datasets of AD patients (ADNI and MIRIAD). The experiments compared our algorithm with two competing methods; the results are discussed in Section 4, while Section 5 concludes the article.

2. Methods

Our segmentation framework is based on a generative model of longitudinal MRI data. In this section, we first describe the forward generative model, in which longitudinal MRI scans are assumed to have been generated by a probabilistic atlas of anatomy. Then, we present an inference algorithm that “inverts” the model with Bayes rule in order to estimate longitudinal segmentations from MRI data.

2.1. Forward generative model of longitudinal MRI scans

Let {y₁, …, y_T} be the image intensities of a set of T longitudinal MRI scans from the same subject. Each scan is represented by a vector of intensities corresponding to J voxels, i.e., y_t = [y_t1, …, y_tJ]. Here we follow the literature of probabilistic atlases with unsupervised intensity models [36, 37, 38, 39], but modify the framework in order to adapt it to the longitudinal nature of the data. The image intensities are assumed to have been generated by the following process (the graphical model is displayed in Figure 1, and further illustrated in Figure 2):

Figure 1.

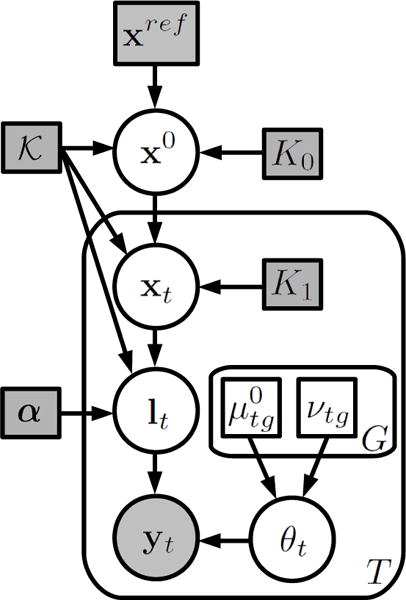
Generative model for longitudinal MRI data. Random variables are in circles, parameters in squares. Shaded variables are observed. Plates indicate replication.

Figure 2.

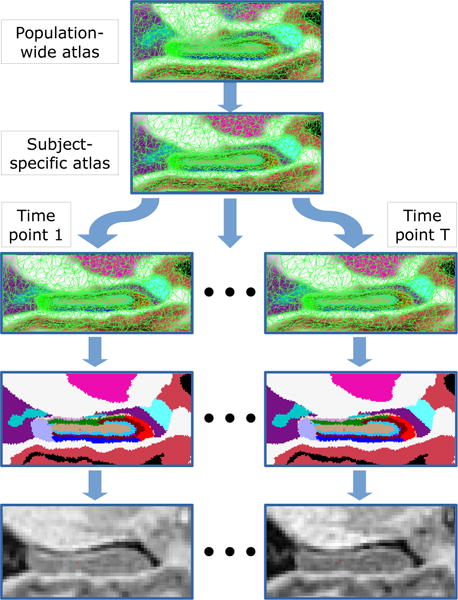
Illustration of the generative process through which the longitudinal MRI data are assumed to be generated: the population-wide atlas is first deformed into a subject-specific atlas, which is subsequently deformed T times – once per time point. Segmentations are sampled from these deformed atlases, and image intensities are generated from the segmentations through a Gaussian mixture model.

1. We are given a probabilistic, population-wide atlas of anatomy, which is encoded as a tetrahedral mesh [39] that covers the region of interest (in our case, a cuboid containing the hippocampus). The mesh is defined by its position x_ref (a vector with the coordinates of its N nodes) and its connectivity. Each node n has a corresponding vector of label probabilities [α_n = [α_n1, …, α_nL], where α_nl is the frequency with which label l is expected at node n, and L is the number of neuroanatomical labels modeled by the atlas.

2. The mesh is deformed from its reference position x_ref to a new position x₀, which is specific to the subject at hand, and yields the corresponding subject-specific atlas. The deformation is governed by a prior probability distribution that penalizes deformations and explicitly forbids collapsing tetrahedra, thereby preserving the topology of the mesh [40]:

   $$p({\mathit{x}}_0)\propto \text{exp}\left[-K_0{\displaystyle \sum _d{U}_d^{\mathcal{K}}({\mathit{x}}_0,{\mathit{x}}_{\mathit{\text{ref}}})}\right],$$ (1)

   where d loops over the tetrahedra in the mesh, K₀ is the stiffness parameter, and $U_d^{\mathcal{K}}({\mathit{x}}_0,{\mathit{x}}_{\mathit{\text{ref}}})$ is the cost of deforming the d^th tetrahedron (see further details in [40]).
3. The mesh in position x₀ (i.e., the subject-specific atlas) is further deformed T times to positions {x₁, …, x_T} (corresponding to the T time points) – but this time using x₀ as reference position:

   $$p({\mathit{x}}_t|{\mathit{x}}_0)\propto \text{exp}\left[-K_1{\displaystyle \sum _d{U}_d^{\mathcal{K}}({\mathit{x}}_t,{\mathit{x}}_0)}\right],$$ (2)

   for t = 1, …, T. Note that the deformed mesh positions {x_t} are conditionally independent given the subject-specific atlas x₀, which is the variable that creates the statistical dependence between the time points. A consequence of this conditional independence is that no particular temporal trajectory (e.g., atrophy) is assumed. This choice increases the flexibility of the method, by enabling it to model trajectories that involve changes in trend over time (e.g., crossover studies, cyclic patterns).
4. Using the deformed mesh positions, label probabilities at each time point and voxel are computed by interpolating the values at the vertices of the tetrahedron enclosing the voxel. Let r_j be the 3D coordinates of voxel j, and let ${\varphi }_{tn}^{\mathcal{K}}$ be a deformed interpolation basis function linked to node n at time point t. The interpolated label probabilities at voxel j of time point t are then given by²:

   $$p_j(l|{\mathit{x}}_t)={\displaystyle \sum _{n=1}^N{\alpha }_{nl}{\varphi }_{tn}^{\mathcal{K}}({\mathit{r}}_j;{\mathit{x}}_t)}.$$

   Segmentation images {l₁, …, l_T} are then created by independently sampling these categorical distributions at each voxel:

   $$p({\mathit{l}}_t|{\mathit{x}}_t)={\displaystyle \prod _{j=1}^J{p}_j(l_{tj}|{\mathit{x}}_t)}$$

   where l_tj is the label of voxel j in time point t.
5. The intensities of the voxels are generated following three assumptions. First, that they are conditionally independent, given the segmentations. Second, that they follow a Gaussian distribution for each label and time point. And third, that labels describing structures of the same tissue type share their Gaussian parameters (means and variances) through G global classes. For example, gray matter structures such as the amygdala, the cerebral cortex, and many of the hippocampal subregions will belong to the same global class (see details in Section 2.2.5). Under these assumptions, the probability of observing the image at time point t is:

   $$\begin{array}{l}p({\mathit{y}}_t|{\mathit{l}}_t,{\mathit{\theta }}_t)={\displaystyle \prod _{j=1}^{J}p(y_{tj}|l_{tj}|{\mathit{\theta }}_t)}\\ ={\displaystyle \prod _{j=1}^J\mathcal{N}\left(y_{tj};{\mu }_{t\mathcal{G}(l_{ti})},{\sigma }_{t\mathcal{G}(l_{ti})}^2\right)},\end{array}$$

   where $\mathcal{N}$ is the Gaussian distribution, $\mathcal{G}(l)\in \{1,\dots ,G\}$ is the global class corresponding to label l, $({\mu }_{tg},{\sigma }_{tg}^2)$ are the Gaussian parameters for time point t and global class g, and ${\mathit{\theta }}_t=\left\{\right\{{\mu }_{tg}\},\{{\sigma }_{tg}^2\left\}\right\}$ represents all Gaussian parameters for time point t. Note that we allow the Gaussian parameters to be different for each time point, which removes the need to standardize the intensities across time points, and also models possible changes in contrast induced by disease. The parameters of each Gaussian $({\mu }_{tg},{\sigma }_{tg}^2)$ are assumed to be independent samples of normal-inverse gamma (NIG) distributions, which is the conjugate prior for a Gaussian distribution with unknown mean and variance:

   $$\begin{array}{l}p({\mathit{\theta }}_t)={\displaystyle \prod _{g=1}^{G}p({\mu }_{tg},{\sigma }_{tg}^2)}\\ p({\mu }_{tg},{\sigma }_{tg}^2)=\mathit{\text{NIG}}({\mu }_{tg}^0,{\nu }_{tg},0,0)\\ =\mathcal{N}({\mu }_{tg};{\mu }_{tg}^0,{\sigma }_{tg}^2/{\nu }_{tg}),\end{array}$$

   where we have assumed that the variance-related parameters of the NIG are equal to zero (i.e., the prior on the variance is a uniform distribution), and the remaining hyperparameters ${\mu }_{tg}^0$ and ν_tg encode any prior knowledge that we might have on the image intensities of each time point: ${\mu }_{tg}^0$ represents the expected mean of class g at time point t, which is assumed to have been obtained as the sample mean of ν_tg prior observations. Details on how these hyperparameters are computed are given in Section 2.2.5 and Table 1.

Table 1.

Global tissue classes grouping structures with similar image intensity properties. GC-DG stands for granule cell layer of the dentate gyrus, and HATA for hippocampus-amygdala transition area.

Global class	Structures
Gray matter	Cerebral cortex, amygdala, parasubiculum, presubiculum, subiculum, CA1, CA2/3, CA4, GC-DG, HATA
White matter	Cerebral white matter, fimbria
Cerebrospinal fluid	Ventricle, hippocampal fissure
Dicencephalon	Diencephalon
Thalamus	Thalamus
Pallidum	Pallidum
Putamen	Putamen
Choroid plexus	Choroid plexus

2.2. Segmentation as Bayesian inference

Given the model described above, segmentation can be cast as a Bayesian inference problem:

$$\{{\widehat{\mathit{l}}}_t\}=\underset{\{{\mathit{l}}_t\}}{\text{argmax}}p(\{{\mathit{l}}_t\}|\{{\mathit{y}}_t\}).$$

Solving this problem exactly leads to an intractable integral over the model parameters, so we make the standard approximation that the posterior distribution of the parameters is heavily peaked. If we group all Gaussian parameters in θ = {θ₁, …, θ_T}, and all deformations (subject-specific atlas and time points) in x = {x₀, x₁, …, x_T}, we have:

$$\begin{array}{l}\{{\widehat{\mathit{l}}}_t\}=\underset{\{{\mathit{l}}_t\}}{\text{argmax}}{\displaystyle {\int }_{\mathit{x}}{\displaystyle {\int }_{\mathit{\theta }}p(\{{\mathit{l}}_t\}|\mathit{x},\mathit{\theta },\{{\mathit{y}}_t\})p(\mathit{x},\mathit{\theta }|\{{\mathit{y}}_t\})d\mathit{x}d\mathit{\theta }}}\\ \approx \underset{\{{\mathit{l}}_t\}}{\text{argmax}}p(\{{\mathit{l}}_t\}|\widehat{\mathit{x}},\widehat{\mathit{\theta }},\{{\mathit{y}}_t\}),\end{array}$$

where the point estimates of the model parameters are given by:

$$\{\widehat{\mathit{x}},\widehat{\mathit{\theta }}\}=\underset{\mathit{x},\mathit{\theta }}{\text{argmax}}p(\mathit{x},\mathit{\theta }|\{{\mathit{y}}_t\}).$$

Using Bayes’ rule, we can rewrite this problem as:

$$\begin{array}{l}\{\widehat{\mathit{x}},\widehat{\mathit{\theta }}\}=\underset{\mathit{x},\mathit{\theta }}{\text{argmax}}p(\{{\mathit{y}}_t\}|\mathit{x},\mathit{\theta })p(\mathit{x})p(\mathit{\theta })\\ =\underset{\mathit{x},\mathit{\theta }}{\text{argmax}}p({\mathit{x}}_0){\displaystyle \prod _{t=1}^{T}p({\mathit{y}}_t|{\mathit{x}}_t,{\mathit{\theta }}_t)p({\mathit{x}}_t|{\mathit{x}}_0)p({\mathit{\theta }}_t)}.\end{array}$$

Finally, taking the logarithm of this expression, and expanding:

$$\begin{array}{l}p({\mathit{y}}_t|{\mathit{x}}_t,{\mathit{\theta }}_t)={\displaystyle \sum _{{\mathit{l}}_t}p({\mathit{y}}_t|{\mathit{l}}_t,{\mathit{\theta }}_t)p({\mathit{l}}_t|{\mathit{x}}_t)}\\ ={\displaystyle \sum _{{\mathit{l}}_t}{\displaystyle \prod _{j=1}^{J}p(y_{tj}|l_{tj},{\mathit{\theta }}_t)}}{\displaystyle \prod _{j=1}^J{p}_j(l_{tj}|{\mathit{x}}_t)}\\ ={\displaystyle \prod _{j=1}^J{\displaystyle \sum _{l=1}^{L}p(y_{tj}|l,{\mathit{\theta }}_t)p_j(l|{\mathit{x}}_t)}},\end{array}$$

we obtain the following objective function of the variables x₀, {x_t}, and {θ_t}:

$$\begin{array}{c}\text{log}p({\mathit{x}}_0)+{\displaystyle \sum _{t=1}^T\text{log}p({\mathit{x}}_t|{\mathit{x}}_0)+}{\displaystyle \sum _{t=1}^T\text{log}p({\mathit{\theta }}_t)}\\ +{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{j=1}^J\text{log}}\left[{\displaystyle \sum _{l=1}^{L}p(y_{tj}|l,{\mathit{\theta }}_t)p_j(l|{\mathit{x}}_t)}\right].\end{array}$$ (3)

The optimization of this objective function solves a joint registration, segmentation and subject-specific atlas estimation problem. We use a coordinate ascent scheme, in which one variable is updated at a time in an iterative fashion. In the rest of this section, we first describe the optimization procedure for each of the variables; then, we describe how the final segmentation is obtained once the point estimates have been computed; next, we provide details on our implementation; and finally, we close the section with a description of our strategy to avoid biases in the longitudinal analysis.

2.2.1. Optimization of x_t, t > 0

The deformations of the individual time points can be updated independently of each other. Dropping any terms that are independent of x_t in Eq. (3), the problem reduces to:

$$\underset{{\mathit{x}}_t}{\text{argmax}}\text{log}p({\mathit{x}}_t|{\mathit{x}}_0)+{\displaystyle \sum _{j=1}^J\text{log}\left[{\displaystyle \sum _{l=1}^{L}p(y_{tj}|l,{\mathit{\theta }}_t)p_j(l|{\mathit{x}}_t)}\right]}.$$ (4)

This is a registration problem, which includes a regularization term (the first) and a data term (the second). As in [20], we solve this problem directly with a conjugate gradient optimizer. The problem is actually identical to that of [20], with the only difference that the node positions of the population-wide atlas x_ref are replaced by those of the subject-specific atlas x₀.

2.2.2. Optimization of θ_t

As with x_t, the Gaussian parameters can be updated one time point at a time. The problem of Eq. (3) becomes:

$$\underset{{\mathit{\theta }}_t}{\text{argmax}}\text{log}p({\mathit{\theta }}_t)+{\displaystyle \sum _{j=1}^J\text{log}\left[{\displaystyle \sum _{l=1}^{L}p(y_{tj}|l,{\mathit{\theta }}_t)p_j(l|{\mathit{x}}_t)}\right]},$$ (5)

which can be solved with an Expectation-Maximization (EM) algorithm [43]. The method iterates between an expectation (E) and a maximization (M) step until convergence. In the E step, a lower bound of the objective function in Eq. (5) that touches it at the current estimate of θ_t is built, which involves computing a soft classification of each voxel in the image corresponding to the time point t:

$$W_{\mathit{\text{tjl}}}=\frac{p(y_{tj}|l,{\mathit{\theta }}_t)p_j(l|{\mathit{x}}_t)}{{\displaystyle {\sum }_{l\prime =1}^{L}p(y_{tj}|l\prime ,{\mathit{\theta }}_t)p_j(l\prime |{\mathit{x}}_t)}}.$$ (6)

In the subsequent M step, this bound is optimized with respect to θ_t, thereby guaranteeing to improve the original objective function of Eq. (5) compared to the previous iteration [43]. Taking derivatives and setting them to zero, we obtain the following update equations:

$${\mu }_{tg}\leftarrow \frac{{\nu }_{tg}{\mu }_{tg}^0+{\displaystyle {\sum }_{j=1}^J{\mathrm{\Omega }}_{\mathit{\text{tjg}}}{y}_{tj}}}{{\nu }_{tg}+{\displaystyle {\sum }_{j=1}^J{\mathrm{\Omega }}_{\mathit{\text{tjg}}}}},$$ (7)

$${\sigma }_{tg}^2\leftarrow \frac{{\nu }_{tg}{\left({\mu }_{tg}-{\mu }_{tg}^0\right)}^2+{\displaystyle {\sum }_{j=1}^J{\mathrm{\Omega }}_{\mathit{\text{tjg}}}{\left(y_{tj}-{\mu }_{tg}\right)}^2}}{{\displaystyle {\sum }_{j=1}^J{\mathrm{\Omega }}_{\mathit{\text{tjg}}}}},$$ (8)

where we have defined ${\mathrm{\Omega }}_{\mathit{\text{tjg}}}={\displaystyle {\sum }_{\mathcal{G}(l)=g}{W}_{\mathit{\text{tjl}}}}$.

2.2.3. Optimization of x₀

Considering only terms depending on x₀, Eq. (3) becomes:

$$\underset{{\mathit{x}}_0}{\text{argmax}}\left[\text{log}p({\mathit{x}}_0)+{\displaystyle \sum _{t=1}^T\text{log}p({\mathit{x}}_t|{\mathit{x}}_0)}\right],$$

which is independent of the image intensities. Since the function $U_d^{\mathcal{K}}({\mathit{x}}_a,{\mathit{x}}_b)$ in Eqs. (1) and (2) is symmetric [40], we can rewrite:

$$\underset{{\mathit{x}}_0}{\text{argmin}}{\displaystyle \sum _d\left[K_0{U}_d^{\mathcal{K}}({\mathit{x}}_0,{\mathit{x}}_{\mathit{\text{ref}}})+K_1{\displaystyle \sum _{t=1}^T{U}_d^{\mathcal{K}}({\mathit{x}}_0,{\mathit{x}}_t)}\right]}.$$ (9)

Eq. (9) can be seen as a weighted “average” of the mesh positions of the time points and that of the population-wide atlas x_ref. The atlas essentially plays the role of an additional time point, though with a different weight (K₀, rather than K₁). We solve this problem numerically with a conjugate gradient algorithm.

2.2.4. Computation of final segmentation

Once the point estimates of the model parameters have been computed, the conditional posterior label probabilities for each voxel are given by the soft classifications provided by the E step of the EM algorithm used to update the Gaussian parameters (Eq. (6)):

$$\begin{array}{l}p(\{{\mathit{l}}_t\}|\widehat{\mathit{x}},\widehat{\mathit{\theta }},\{{\mathit{y}}_t\})={\displaystyle \prod _{t=1}^{T}p({\mathit{l}}_t|{\widehat{\mathit{x}}}_t,{\widehat{\mathit{\theta }}}_t,{\mathit{y}}_t)}\\ ={\displaystyle \prod _{t=1}^T{\displaystyle \prod _{j=1}^J{W}_{tj{l}_{tj}}}}.\end{array}$$ (10)

If we desire to compute discrete segmentations, the MAP (maximum-a-posteriori) estimate can be computed voxel by voxel as:

$${\widehat{l}}_{tj}=\underset{l}{\text{argmax}}{W}_{\mathit{\text{tjl}}},$$

whereas if we are interested in the volumes of the structures, their expected value can be shown to be equal to:

$$V_{tl}={\displaystyle \sum _{j=1}^J{W}_{\mathit{\text{tjl}}}},$$

where V_tl is the volume of the structure with label l in the image acquired at time point t.

2.2.5. Implementation details

Given a set of longitudinal scans, we first preprocess the data using the FreeSurfer [44, 45, 46, 47] longitudinal stream [48, 22]. The longitudinal stream creates an unbiased within-subject template space and image (“base”) [48] using an inverse consistent registration method [49]. This template is a robust representation of the average subject anatomy and is processed with a modified FreeSurfer pipeline. The original time point images are conformed and resampled to the template space via a single cubic b-spline interpolation step. Several processing steps of the FreeSurfer pipeline are then initialized for each time point with common information from the subject template to increase reliability and thus statistical power. The normalized, bias-field corrected, skull-stripped images (“norm.mgz”) corresponding to the different time points are then used as input for the proposed longitudinal segmentation algorithm (i.e., {y_t}).

To initialize the mesh positions, we first use an affine registration procedure to align the modeled image region with the cuboid in which the population-wide atlas is defined. As reference image, the registration uses a binary hippocampal mask extracted from the automated segmentation (FreeSurfer’s “aseg.mgz”) of the subject template. As moving image, the registration uses a soft segmentation of the hippocampus estimated from x_ref. After the affine registration, we further deform the mesh (non-linearly, using Eq. 1) to the same automated segmentation of the subject template. This mesh deformation is used to initialize the node positions of subject-specific atlas x₀, as well as the deformations of the time points x₁, …, x_T.

The hyperparameters of the different time points and global tissue classes are computed from the corresponding norm and aseg images as follows: for each global class g, we extract the intensities of the voxels of norm labeled as any of the compatible labels by aseg (i.e., l, s.t. $\mathcal{G}(l)=g$). We set ${\mu }_{tg}^0$ to the median value of such intensities, and ν_tg to a conservative value equal to one half of the number of such voxels. The complete mapping of labels to global tissue classes is detailed in Table 1. Note that voxels from outside the hippocampus to estimate the intensity properties of the hippocampal subregions, which makes the algorithm more robust. For example: since they both consist of white matter, the intensity distribution of the fimbria can be more easily estimated from the cerebral white matter, which is much bigger and easier to segment.

We set the stiffness parameters to K₀ = K₁ = 0.05, which is the default value for the cross-sectional method currently implemented in FreeSurfer [20]. We rasterize (i.e., interpolate) the mesh at 0.333 mm isotropic resolution, which is also the default value in the current Free-Surfer implementation. This resolution represents the voxel size at which the final segmentations are obtained.

Algorithm 1.

Longitudinal segmentation

Compute ${\mu }_{tg}^0$, νtg, x0 with norm.mgz, aseg.mgz

${\mu }_{tg}\Leftarrow {\mu }_{tg}^0$, ∀t, g; ${\sigma }_{tg}^2\Leftarrow 100$, ∀t, g; xt ⇐ x0 ∀t > 0

for its = 1 to 10 do

for t = 1 to T do

LogPprev ⇐ −∞; LogPcurr ⇐ 0

while LogPcurr – LogPprev > 10−5 do

LogPprev ⇐ LogPcurr

LogPcurr ⇐ Eq. 5

Wtjl ⇐ Eq. 6; μtg ⇐ Eq. 7; ${\sigma }_{tg}^2$ ⇐ Eq. 8

end while

if its < 10 then

itDef ⇐ 0; maxDef ⇐ ∞

while itDef < 20 and maxDef > 10−5 do

itDef ⇐ itDef + 1

(xt, maxDef) ⇐ conjugate gradient on Eq. 4

end while

end if

end for

if its < 10 then

itDef ⇐ 0; maxDef ⇐ ∞

while itDef < 20 and maxDef > 10−5 do

itDef ⇐ itDef + 1

(x0, maxDef) ⇐ conjugate gradient on Eq. 9

end while

end if

end for

${\widehat{l}}_{tj}\Leftarrow {\text{argmax}}_l{W}_{\mathit{\text{tjl}}}$, ∀t, j

$V_{tl}\Leftarrow {\displaystyle {\sum }_{j=1}^J{W}_{\mathit{\text{tjl}}}}$, ∀t, l

For the optimization, we use the following scheme: we first alternately update {θ_t} and {x_t} 10 times. Each up-date of θ_t iterates between the E and M steps until the change in the objective function is less than 10⁻⁵, whereas each update of x_t takes at most 20 iterations of the conjugate gradient method (it stops early if the maximum shift across mesh nodes is less than 10⁻⁵). Next, x₀ is updated with the conjugate gradient algorithm (maximum 100 steps; the early termination criterion is the same as for x_t). The optimization then returns to the update of {θ_t}, starting a new external iteration. We set the maximum number of external iterations to 10. The complete segmentation algorithm is summarized in Algorithm 1.

2.2.6. Avoiding biases

As mentioned in the introduction, processing bias can be introduced if all the time points are not treated in exactly the same way. In our algorithm, the initialization is computed with the output from the FreeSurfer longitudinal pipeline, which is designed to avoid processing bias [49, 48]. The segmentation algorithm is also unbiased, since all images are treated identically. Moreover, subjects with a single time point are treated as if they were longitudinal, which makes the measures derived from them comparable with those obtained from subjects with multiple time points. More specifically, the FreeSurfer longitudinal pipeline includes a pose normalization step that introduces resampling artifacts and a subject template, and the hippocampal segmentation estimates the mesh position for a subject-specific atlas (rather than using the population-wide atlas directly). This procedure makes it possible to include all subjects in analyses that support single time point data, such as linear mixed effects models [50].

3. Experiments and Results

3.1. MRI data

We used two publicly available datasets in the experiments in this study: MIRIAD and ADNI. The MIRIAD dataset consists of T1-weighted brain MRI scans of AD patients (n = 46) and cognitively normal (CN) controls (n = 23) acquired at intervals from two weeks to two years. All 69 subjects were scanned at 0, 2, 6, 14, 26, 38 and 52 weeks from baseline; 39 subjects were also scanned at 18 months; 22 of these 39 were further scanned at 24 months. At 0, 6 and 38 weeks, two back-to-back scans were conducted without removing the subject from the scanner in between. The mean age at baseline of the subjects was 69.6±6.9 years. All the scans were acquired on the same 1.5 T scanner (GE Signa) with an IR-FSPGR sequence (coronal slices with 0.9375×0.9375 mm resolution, 1.5 mm slice thickness, TR=15ms, TE=5.4ms, TI=650ms, flip angle 15°). Further information can be found at https://www.ucl.ac.uk/drc/research/miriad-scan-database.

The ADNI dataset consists of longitudinal T1-weighted scans from 836 subjects of the ADNI dataset. The subjects are divided into four classes: elderly controls (n = 252), early mild cognitive impairment (eMCI, n =215), late MCI (lMCI, n = 176), and AD (n = 193). The subjects were scanned on average 4.8 times (minimum: a single time; maximum: 11 times; 4013 scans in total), with a mean interval between scans equal to 286 days (minimum: 23 days, maximum: 1567 days). The mean age at baseline of the subjects was 75.1±6.6 years. Since the ADNI project spans multiple sites, different scanners were used to acquire the images; further details on the acquisition can be found at http://www.adni-info.org.

The ADNI was launched in 2003 by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, the Food and Drug Administration, private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year public-private partnership. The main goal of ADNI is to test whether MRI, positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to analyze the progression of MCI and early AD. Markers of early AD progression can aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as decrease the time and cost of clinical trials. The Principal Investigator of this initiative is Michael W. Weiner, MD, VA Medical Center and University of California - San Francisco. ADNI is a joint effort by co-investigators from industry and academia. Subjects have been recruited from over 50 sites across the U.S. and Canada. The initial goal of ADNI was to recruit 800 subjects but ADNI has been followed by ADNI-GO and ADNI-2. These three protocols have recruited over 1,500 adults (ages 55–90) to participate in the study, consisting of cognitively normal older individuals, people with early or late MCI, and people with early AD. The follow up duration of each group is specified in the corresponding protocols for ADNI-1, ADNI-2 and ADNI-GO. Subjects originally recruited for ADNI-1 and ADNI-GO had the option to be followed in ADNI-2.

3.2. Experimental setup

3.2.1. Competing methods

We compared the performance of our algorithm with that of two other approaches. The competing methods were:

1. Cross-sectional segmentation (henceforth “C-S”): the algorithm described in [20] was used to segment each time point independently of the others in a cross-sectional fashion (i.e., as if they were different subjects).

2. Cross-sectional segmentation with longitudinal initialization (henceforth “L-INIT”): same as C-S, but initializing the algorithm with the automated segmentation (aseg) from the longitudinal FreeSurfer stream (rather than the cross-sectional aseg).

3. Longitudinal segmentation (henceforth “LONG”): the algorithm described in this paper was used to segment all the time points corresponding to each subject simultaneously.

The motivation for testing L-INIT is twofold. First, it is currently the recommended setup for longitudinal hippocampal subfield segmentation in FreeSurfer. And second, it enables us to isolate the contribution of our proposed generative model to the results of LONG, separating it from the contribution of the longitudinal initialization.

In order to assess the segmentation accuracy of the methods, we would ideally use ground truth labels obtained from manual delineations of the hippocampal substructures made on the in vivo MRI scans. However, such manual annotations would have to be made with the protocol that we used to build the ultra-high resolution ex vivo, which is not possible. Instead, we validated the method indirectly through two sets of experiments: test-retest reliability, and group differentiation with linear mixed effect (LME) modeling.

3.2.2. Experiment 1: test-retest reliability

In order to evaluate the test-retest reliability of the methods, we used them to segment the scan-rescan data of the MIRIAD dataset. For each subject, we took the scan-rescan session corresponding to the first time point (therefore including both AD subjects and controls). After segmenting each of the n = 69 pairs of scans with the three competing algorithms, we compared their performance with two different metrics. First, we measured the absolute difference in volume estimates for each of the segmented hippocampal subregions. The smaller this difference, the larger the agreement across the two scans. Second, we computed the Dice overlap between the MAP segmentations of each subregion in the two scans. The Dice coefficient between two binary masks X and Y is defined as:

$$\mathit{\text{Dice}}(X,Y)=2\frac{|X\cap Y|}{|X|+|Y|},$$

and is bounded by 0 (no overlap) and 1 (perfect overlap). When the C-S method is used, computing the Dice overlap requires a rigid registration between the two scans, which was computed with the robust registration tool in FreeSurfer [49]. In order to mitigate the effect of image resampling on the Dice overlaps in this scenario, we used linear resampling to warp the scans to the intermediate space (the base) and replaced the Dice coefficient by a soft counterpart:

$${\mathit{\text{Dice}}}_s(X_s,Y_s)=2\frac{{\sum }_{\mathit{r}}{X}_s(\mathit{r})Y_s(\mathit{r})}{{\sum }_{\mathit{r}}{X}_s(\mathit{r})+{\sum }_{\mathit{r}}{Y}_s(\mathit{r})},$$

where r represents spatial locations, and X_s(r), Y_s(r) are resampled masks defined between zero and one³.

3.2.3. Experiment 2: group analysis with LME

The test-retest experiment described above only evaluated one aspect of the longitudinal algorithms: their ability to produce consistent segmentations. Additionally, it is necessary to test the performance when capturing the temporal evolution of the segmented structures. For example, an algorithm that always produces the same output yields perfect test-retest reliability, but also fails to capture any anatomical changes over time or differentiate groups based on such changes.

We carried out two experiments using group analyses: one with MIRIAD, and one with ADNI. The setup was identical in both cases, with the only difference that the datasets have different numbers of classes. For each hippocampal subregion, we built an LME model for the estimated volume in which subject intercept and slope were random effects, intracranial volume (ICV) and age at baseline were fixed effects, and each group had its own (fixed) bias and slope. The model fit and and computation of p values for F tests comparing the fixed slopes of the different groups was done with the LME toolbox in Free-Surfer [50]. We then took the ability of the measurements to separate the (fixed) slopes of the groups as a measure of the sensitivity of the longitudinal segmentation to detect anatomical change associated with disease.

For the ADNI dataset, we chose to merge the late MCI and AD classes into a single class (“lMCI/AD”). This choice was motivated by the fact that a pilot LME analysis using whole hippocampal volumes from FreeSurfer’s longitudinal stream did not reveal any differences in atrophy rates between the two classes. This is consistent with the results of other studies based on manual [51, 52] and automated segmentations [53]. This lack of differences between the late MCI and AD groups may be explained by the continuous nature of pathology; current in vivo imaging technology cannot identify the subtle differences in atrophy rates between the two groups. It is necessary to examine the patient serially to be sure of the clinical findings, and 10–20% of patients with MCI will worsen and convert to AD (in fact, many lMCI subjects are diagnosed as AD at other time points in ADNI). In addition, the presence of co-morbidities and other dementia etiologies (e.g., vascular dementia or dementia of the Lewy body disease [54]) makes it difficult to decipher the stage of the pathology at this point with in vivo imaging.

3.3. Results

3.3.1. Test-retest

Figure 3 displays the absolute differences (in %) between the volumes of the hippocampal subregions estimated from the scan-rescan data of the MIRIAD dataset. The average differences across structures are: 6.5% for C-S, 5.9% for L-INIT, and 4.5% for LONG. L-INIT provides a slight improvement over the purely cross-sectional (C-S) method, thanks to the implicit regularization introduced by the use of the FreeSurfer longitudinal stream in the initialization. Despite being quite consistent across subregions, this improvement is only significant (as measured with a two-tailed paired t-test) for one of them: the left granule cell layer of the dentate gyrus (DG). The proposed longitudinal method (LONG), which explicitly regularizes the segmentations, produces the lowest difference for all structures except for the right fimbria. The improvements over the C-S method are statistically significant for all structures except for the presubiculum and fimbria (both sides); left molecular layer; and left whole hippocampus. In absolute terms, the errors are below 5% for all structures except for the parasubiculum, hippocampus-amygdala transition area (HATA) and fimbria. These three subregions suffer from the highest variability in volume estimates: the parasubiculum because it represents the transition of the hippocampus with the entorhinal cortex, and its boundaries are not well defined; the HATA because it is a transitional region with the head of the hippocampus (dorsal subiculum) and amygdala; and the fimbria due to its occasional low contrast.

Figure 3.

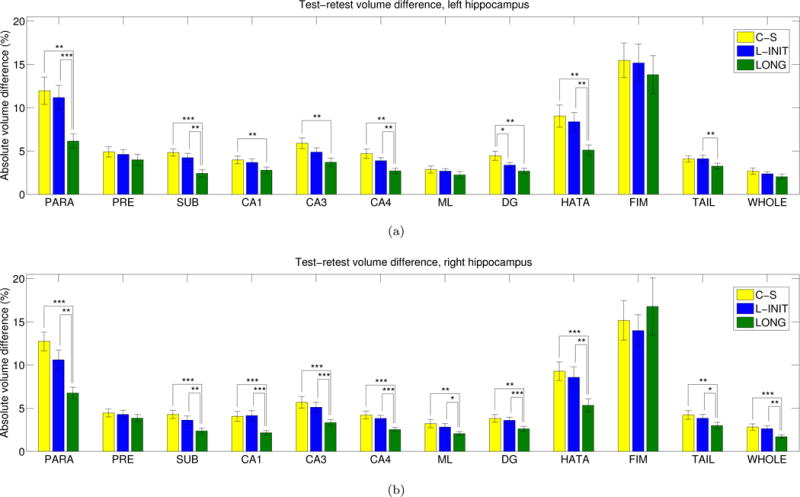
Absolute volumes differences (in % of total volume) for the hippocampal subregions in the back-to-back scans of the MIRIAD dataset: (a) left hippocampus, (b) right hippocampus. The bars represent the mean, and the error bars, one standard deviation. A two-tailed paired t-test was used to assess whether there were significant differences between the methods: one asterisk represents p < 0.05, two asterisks represent p < 0.01, and three asterisks represent p < 0.001. The abbreviations of the hippocampal subregions are: SUB = subiculum, PRE = presubiculum, PARA = parasubiculum, ML = molecular layer, DG = granule cell layer of the dentate gyrus, CA3 = CA2+CA3, FIM = fimbria, HATA = hippocampus-amygdala transition area, WHOLE = whole hippocampus. For anatomical and morphological definitions of these subregions, see [20].

Figure 4 displays the Dice coefficient for the different hippocampal subregions and competing methods. The averages across subregions are: 0.754 for C-S, 0.775 for L-INIT, and 0.818 for LONG. L-INIT outperforms C-S for nearly all structures, in a statistically significant manner in most cases (once more, significance was assessed with a two-tailed paired t-test). LONG provides the highest Dice for all subregions except for the left tail, right tail and right fimbria. Moreover, it yields a statistically significant increase with respect to the other two methods in all hippocampal subregions except for the tail and fimbria. It is worth noting that the Dice scores for C-S are negatively affected (to a very small extent) by the resampling that is required to compute them.

Figure 4.

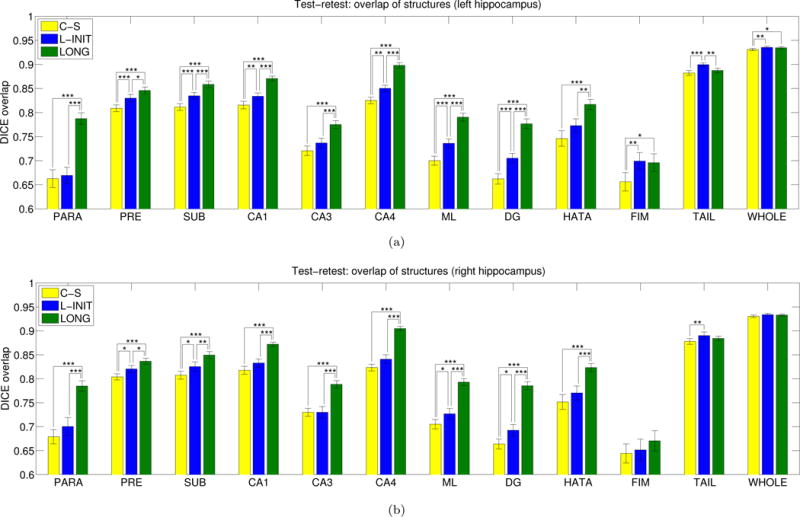
Dice overlaps for the different subregions in the back-to-back scans of the MIRIAD dataset: (a) left hippocampus, (b) right hippocampus. Please see the caption of Figure 3 for the abbreviations of the hippocampal subregions and the convention for representation of statistical significance.

Figure 5 shows a coronal slice of a test-retest scan illustrating the differences between the algorithms. In this sample subject, C-S undersegments the superior region of the hippocampus (pointed red arrow) only in the first scan, creating a large difference with the second scan. While this issue is fixed by L-INIT, some undersegmentation still occurs in the subicular region of the first scan (blue arrow), and some inconsistencies are observed in the presubiculum and molecular layer (green arrow). The proposed longitudinal framework (LONG), on the other hand, produces segmentations that are more consistent with each other.

Figure 5.

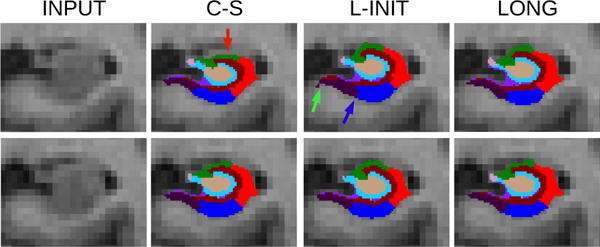
Registered coronal slices of back-to-back scans of a sample subject of the MIRIAD dataset. From left to right: input, cross-sectional segmentation, segmentation with FreeSurfer longitudinal initialization, and proposed longitudinal method. The top row corresponds to the first scan, and the bottom row to the second scan.

3.3.2. Group analysis

Figures 6 and 7 show the atrophy rates for the MIRIAD dataset (computed for each group as the fixed slope divided by the fixed intercept) as estimated by the three competing methods. The cross sectional method (C-S) can detect the differences in some of the subregions and in the whole hippocampal volume, particularly in the right hemisphere (which is known to atrophy at a faster rate [55]). When L-INIT is used, effects that the C-S method could not detect are now found: moderate effects on the right tail and subiculum, and mild effects on the left dentate gyrus and CA4, though a strong effect is lost for the left subiculum. Our new algorithm (LONG) improves group differentiation even further: in addition to all the effects that the other two approaches could detect combined, it also finds a strong effect on the left presubiculum, a moderate effect on the right presubiculum, and mild effects on the left HATA and right parasubiculum.

Figure 6.

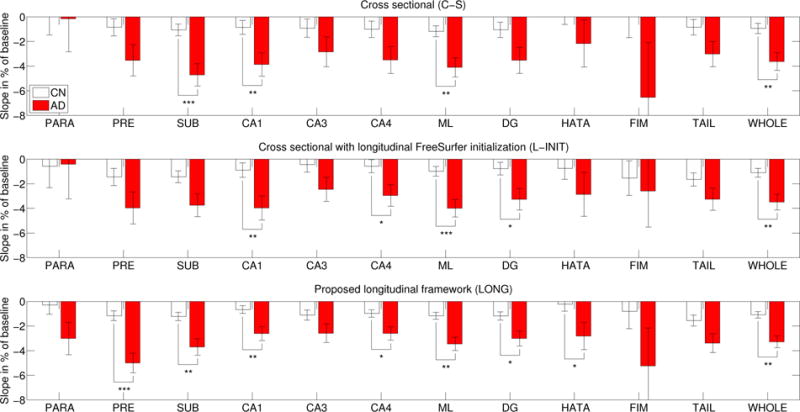
MIRIAD dataset: atrophy rates (percentage of baseline, per year) for the hippocampal subregions of the left hemisphere as estimated by the three competing methods. The abbreviations for the subregions and the conventions for statistical significance can be found in Figure 3.

Figure 7.

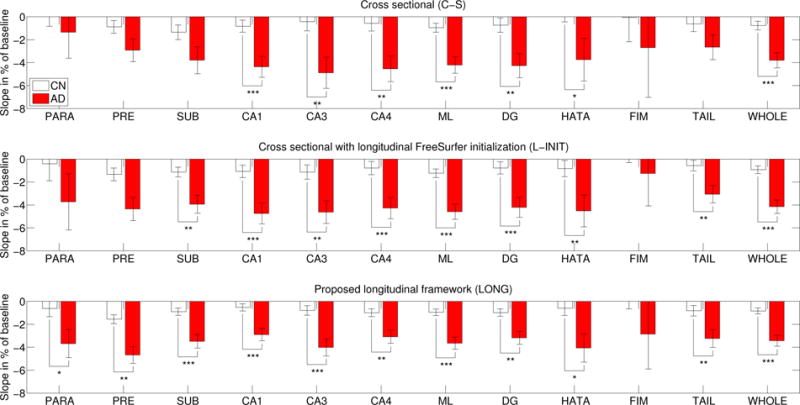
MIRIAD dataset: atrophy rates for the hippocampal subregions of the right hemisphere. The abbreviations for the subregions and the conventions for statistical significance can be found in Figure 3.

Figures 8 and 9 show the atrophy rates for the ADNI dataset. When comparing the controls with the lMCI/AD group, strong effects are found by all three methods for almost every hippocampal subregion (except for the highly variable fimbria). However, when comparing controls with eMCI and lMCI/AD with eMCI, the longitudinal methods reveal differences that the cross-sectional version could not find. Initializing with the longitudinal FreeSurfer segmentation (L-INIT) yields stronger signal for a number of subregions, such as the left CA3, left HATA, and right subiculum. The proposed longitudinal model (LONG) detects even more effects, such as slight differences in the left subiculum and presubiculum, and the right parasubiculum. LONG also detects stronger effects for many other subregions, such as the left DG, left CA4, or right CA1.

Figure 8.

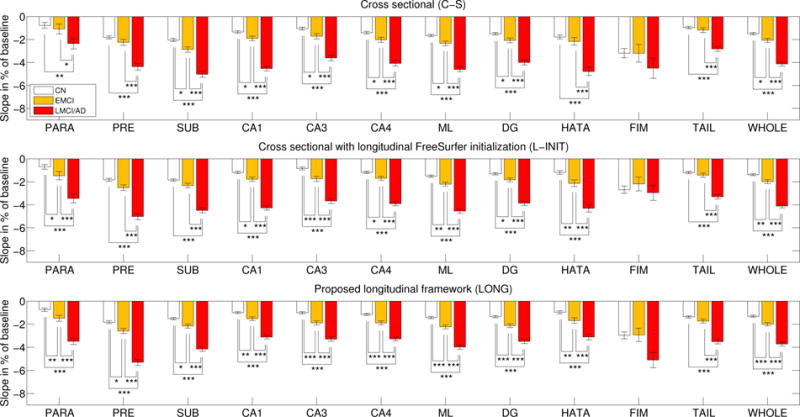
ADNI dataset: atrophy rates (percentage of baseline, per year) for the hippocampal subregions of the left hemisphere as estimated by the three competing methods. The abbreviations for the subregions and the conventions for statistical significance can be found in Figure 3.

Figure 9.

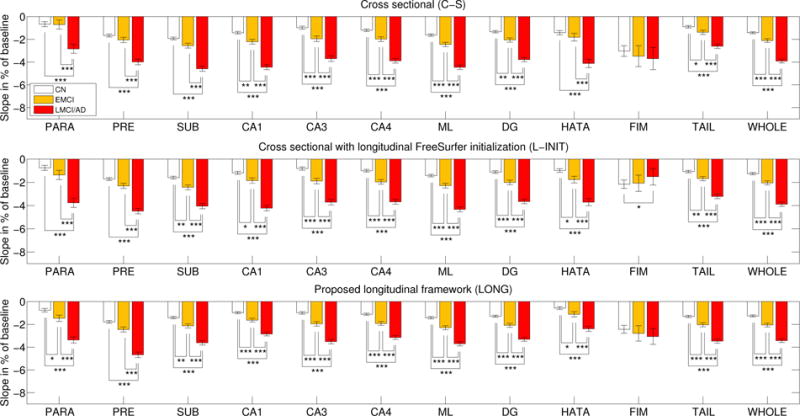
ADNI dataset: atrophy rates (percentage of baseline, per year) for the hippocampal subregions of the right hemisphere. See caption of Figure 8 for an explanation of this figure.

4. Discussion

The model we propose in this paper assumes that longitudinal scans of a certain individual have been generated by a hidden subject-specific atlas. This spatio-temporal approach allows a completely symmetric setup (all time points are treated identically), thus avoiding potential processing bias. The subject-specific atlas explicitly regularizes the segmentation across scans from different time points, which consistently increases the test-retest reliability while improving sensitivity. Perfect reliability can, of course, be enforced by reporting the same result across time independent of the image (over-constraining the method). However, this will prevent the detection of longitudinal changes and group differences. The presented approach aims at optimizing the trade-off between noise reduction and over-regularization by keeping the model flexible enough to follow temporal morphometric changes.

The proposed longitudinal segmentation method was evaluated against a purely cross-sectional implementation (C-S) and a variant of it (L-INIT) that uses the FreeSurfer longitudinal stream in the initialization. The test-retest experiments revealed that taking advantage of the longitudinal stream already enabled L-INIT to consistently outperform C-S in terms of volume error and Dice coefficient. The generative model takes the performance one step further, and enables our proposed method (LONG) to outperform L-INIT for both metrics and nearly every hippocampal subregion. It is worth noting that the Dice coefficients computed for C-S are negatively affected by the registration it requires. However, given that all other metrics (including the sensitivity to differences in atrophy rates) support the superiority of L-INIT and LONG, and given that we used a soft version of the Dice coefficient to reduce the impact of resampling, there is no reason to believe that the observed differences can be attributed exclusively to interpolation artifacts.

When comparing atrophy rates across disease groups, we observed a similar trend as in the test-retest experiments. L-INIT revealed effects that C-S could not detect, and we also demonstrated that the regularization scheme in LONG increases the ability to separate various groups in the two datasets (MIRIAD and ADNI) even further. This is essential as significance in group comparisons is affected both by the measurement noise and the effect size.

In absolute terms, the three competing methods yielded approximately the same annual rates of atrophy for the whole hippocampus in controls: 1% in MIRIAD, and 1.5% in ADNI. For early MCI (in ADNI), they all produced similar estimates as well (2%). In the AD group, however, the rates dropped from 3.75% to 3.35% in MIRIAD and from 4% to 3.6% in ADNI for the proposed method. This could indicate that the regularization scheme used by our method (i.e., the subject-specific atlas) might slightly over-smooth trajectories corresponding to larger atrophy rates (i.e., those corresponding to AD patients).

We also need to emphasize that higher atrophy rates do not necessarily correspond to more accurate segmentations. Ideally, one would evaluate such accuracy directly with the help of manual delineations, but this was not possible in this study because the 1 mm in vivo images cannot be manually annotated with our ex vivo delineation protocol. Nevertheless, the atrophy rates estimated by our method agree well with previously published data. In MIRIAD, our estimates are very similar to those reported by Cash et al. [56], who surveyed the output from 13 automated methods, and reported 0.7% for controls and 3.8% for AD. In ADNI, our estimates for late MCI/AD are also very close to those reported by [51] (3.5%) and [52](3.3%-3.6%) using manual segmentations, even though higher values have also been reported by other studies (e.g., Henneman et al. [57] reported 4.0%). A more thorough analysis of hippocampal atrophy rates estimated with neuroimaging can be found in [58].

5. Conclusion

In this article, we have proposed a novel Bayesian longitudinal segmentation algorithm for hippocampal subregions based on a hidden subject-specific atlas. The method is general and could in principle be applied to other brain regions, though such a setup would require further evaluation in future work. Also, the method does not make any assumptions on the shape or temporal smoothness of the trajectories, i.e., it treats all time points the same way. This design increases the flexibility of the proposed segmentation method. Further information on ordering and time spacing, as well as further assumptions on the shape of the trajectories (e.g., linear) can be exploited byy the statistical tools that are used to analyze the output of the segmentation. For example, in this study, we used a linear mixed effect model that accounted for the time spacing a correlations between repeated measures, while assuming linear trajectories (which approximately holds in atrophy studies).

Our approach builds on the literature of Bayesian segmentation with unsupervised intensity models, and inherits the robustness of such methods against changes in MRI contrast – which stems from the fact that intensity properties are inferred directly from the images to be segmented. This is actually a requirement if the atlas is constructed using ex vivo data (which enables ultra-high-resolution), since fixation and death radically change MRI contrast. Therefore, the algorithm does not require and intensity standardization across time points, and can handle changes in contrast induced by disease. That said, if the image intensities at all time points are know to be normalized and not affected by pathology, the robustness of the algorithm could be enhanced by forcing the Gaussian parameters to be equal across time points, i.e., ${\mathit{\theta }}_t=\overline{\mathit{\theta }}$, ∀t. However, the potential gain would be minimal because there are sufficient voxels in each time point to estimate θ_t with high certainty [59].

Another advantage of Bayesian segmentation with probabilistic atlases that our algorithm also inherits is its computational efficiency. Our implementation runs in approximately 15T − 20T minutes on a modern desktop, where T is the number of time points⁴. The implementation will be publicly shared as part of the popular neuroimaging package FreeSurfer, and will be (to the best of our knowledge) the first available method to longitudinally segment the hippocampal subregions.

As in the original cross-sectional method [20], the volumetric results from individual subfields need to be interpreted with caution when segmenting 1 mm images; at that resolution, the molecular layer is not visible, and the fitting of the internal boundaries of the hippocampal atlas relies mostly on the prior. In that sense, the statistical dependence introduced by the subject-specific atlas helps increase the stability of the segmentation of such internal boundaries across time points. Nevertheless, we would only recommend complex analyses (e.g., shape analysis) of the segmentations if the proposed method is applied to longitudinal data acquired at a higher resolution (e.g., 0.4 × 0.4 × 2.0 mm scans as in [20].)

As a growing number of studies are beginning to collect longitudinal MRI data, the development of dedicated algorithms that exploit the relationship between scans of the same subject is paramount. Longitudinal methods that provide higher sensitivity than their cross-sectional counterparts permit reduction of sample sizes in neuroimaging studies and the detection of much smaller effects. Moreover, longitudinal segmentation algorithms for the hippocampal subregions hold great promise to increase our understanding of AD progression and disease etiology; to provide powerful biomarkers for computer-aided diagnosis at presymptomatic stages; and to allow a highly accurate and localized quantification of treatment response in AD and other neurological disorders.

Highlights.

• -A segmentation method for the hippocampal substructures in longitudinal MRI scans
• -Increased test-retest reliability compared with cross-sectional analyisis
• -Increased power to detect group differences in atrophy rates in LME framework
• -Algorithm will be made publicly available as part of FreeSurfer