Communication shapes sensory response in multicellular networks

Significance

Cells routinely sense and respond to their environment, and they also communicate with each other. Exactly how communication impacts sensing remains poorly understood. We study a population of fibroblast cells that responds to a chemical stimulus (ATP) and communicates by molecule exchange. Combining experiments and mathematical modeling, we find that cells exhibit calcium oscillations in response to not only the ATP stimulus but also, increased cell–cell communication. Our results show that, when cells are together, their sensory responses reflect not just the stimulus level but also, the degree of communication within the population.

Abstract

Collective sensing by interacting cells is observed in a variety of biological systems, and yet, a quantitative understanding of how sensory information is collectively encoded is lacking. Here, we investigate the ATP-induced calcium dynamics of monolayers of fibroblast cells that communicate via gap junctions. Combining experiments and stochastic modeling, we find that increasing the ATP stimulus increases the propensity for calcium oscillations, despite large cell-to-cell variability. The model further predicts that the oscillation propensity increases with not only the stimulus, but also the cell density due to increased communication. Experiments confirm this prediction, showing that cell density modulates the collective sensory response. We further implicate cell–cell communication by coculturing the fibroblasts with cancer cells, which we show act as “defects” in the communication network, thereby reducing the oscillation propensity. These results suggest that multicellular networks sit at a point in parameter space where cell–cell communication has a significant effect on the sensory response, allowing cells to simultaneously respond to a sensory input and the presence of neighbors.

Decoding the cellular response to environmental perturbations, such as chemosensing, photosensing, and mechanosensing, has been of central importance in our understanding of living systems. To date, most studies of cellular sensation and response have focused on single isolated cells or population averages. An emerging picture from these studies is the set of design principles governing cellular signaling pathways: these pathways are organized into an intertwined, often redundant network with architecture that is closely related to the robustness of cellular information processing (1, 2). However, many examples suggest that collective sensing by many interacting cells may provide another dimension for the cells to process environmental cues (3). Examples, such as quorum sensing in bacterial colonies (4), olfaction in insects (5) and mammals (6), glucose response in the pancreatic islet (7), and the visual processing of retinal ganglion cells (8), suggest a fundamental need to revisit cellular information processing in the context of multicellular sensation and response, because even weak cell-to-cell interaction may have strong impact on the states of multicellular network dynamics (9). In particular, we seek to examine how the sensory response of cells in a population differs from that of isolated cells and whether we can tune between these two extremes by controlling the degree of cell–cell communication.

Previously, we described the spatial–temporal dynamics of collective chemosensing of a mammalian cell model system (10, 11). In this system, high-density mouse fibroblast cells (NIH 3T3) form a monolayer that allows nearest neighbor communications through gap junctions (12). When extracellular ATP is delivered to the monolayer, store-operated calcium dynamics is mediated by second messenger inositol 1,4,5-trisphosphate (IP3) (13). The dynamics is complicated by nonlinear feedback between Ca²⁺ and the ion channel opening probability, which leads to rich behaviors, such as cytosolic calcium oscillations (14). In the situation of collective ATP sensing, we have found that gap junction communications dominate intercellular interactions (10). Furthermore, these short-range interactions propagate and turn the cell monolayer into a percolating network (11). These characteristics make the system ideal for studying how sensory response is modulated by communication in multicellular networks.

Here, we use this model system to examine how cell–cell communication affects collective chemosensing. Combining experiments with stochastic modeling, we find that cells robustly encode the ATP stimulus strength in terms of their propensity for calcium oscillations, despite significant cell-to-cell variability. The model further predicts that the oscillation propensity depends on not only the stimulus but also the density of cells, and that denser monolayers have narrower distributions of oscillation frequencies. We confirm both predictions experimentally. To verify that the mechanism behind the density dependence is the modulation of cell–cell communication, we introduce cancer cells (MDA-MB-231) into the fibroblast cell monolayer. As we show, MDA-MB-231 cells act as “defects” in the multicellular network, because they have distinct calcium dynamics compared with the fibroblasts caused by reduced gap junction communication (15–17). We find that the oscillation propensity of the fibroblasts decreases as the fraction of cancer cells increases, confirming that the sensory response is directly affected by the cell–cell communication.

Results

To study the sensory responses of a multicellular network, we use single-channel microfluidic devices and deliver ATP solutions to monolayers of fibroblast (NIH 3T3) cells. The ATP concentrations vary from 0 to 200 μM, and the calcium dynamics of individual cells is obtained with fluorescent calcium indicator at 4 frames per second (more details are in SI Appendix, section 1).

We modulate the degree of communication in two ways. First, we vary the cell density. Smaller cell densities correspond to larger cell-to-cell distances, which we expect to reduce the probability of forming gap junctions. Second, we coculture the fibroblasts with breast cancer (MDA-MB-231) cells in the flow channel (SI Appendix, section 1). As we later show, MDA-MB-231 cells have reduced communication properties and therefore, act as defects in the multicellular network. To distinguish the two cell types, MDA-MB-231 cells are prelabeled with red fluorescent dye (Cell Tracker Red CMTPX; Life Technologies). Varying cell density and the fraction of cancer cells allow us to control the architecture of the multicellular network over a wide range.

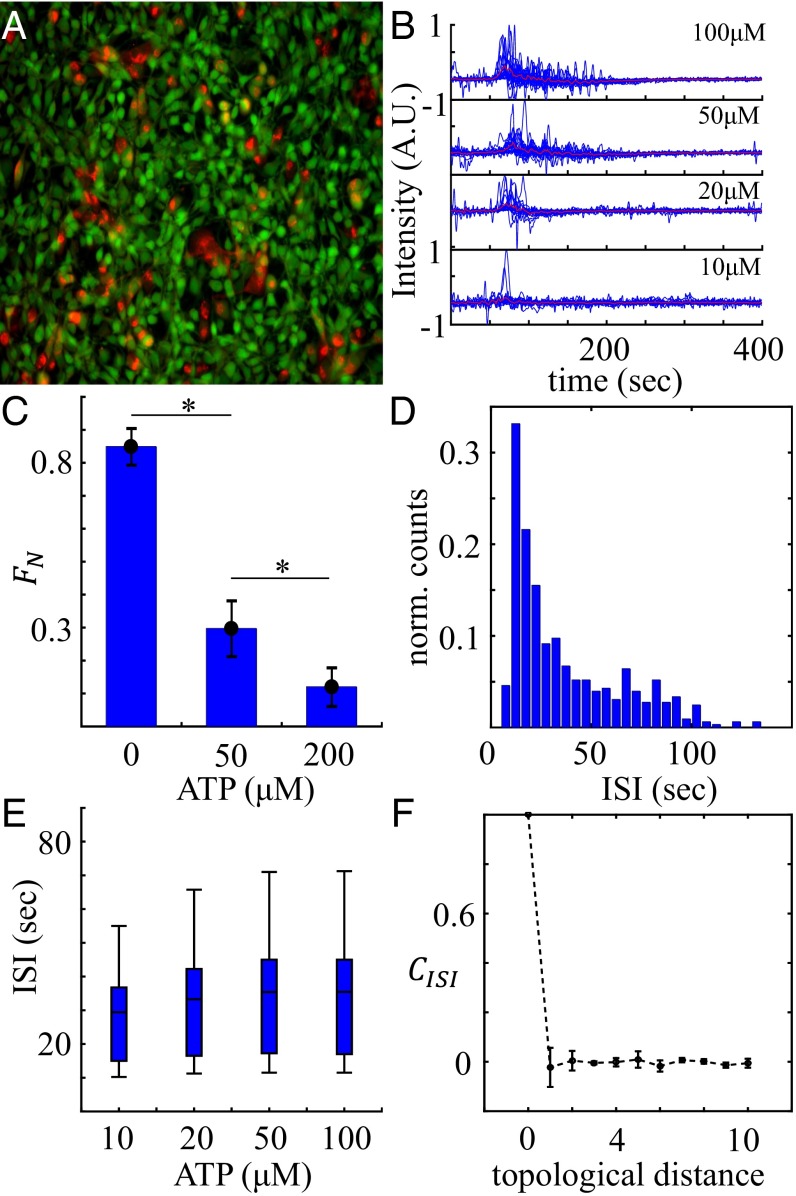
Fig. 1A shows the composite image of a high-density cell monolayer with cocultured fibroblast and cancer cells. In this example, MDA-MB-231 cells make up a fraction $F_C=$ 15% of the total population, which has a total cell density of ${\text{ρ}}_T=$ 2,500 cells per 1 mm². At this density, each cell has an average of six nearest neighbors, from which extensive gap junction communication is expected. After identifying cell centers from the composite image (SI Appendix, section 1), we compute the time-dependent average fluorescent intensity near the center of each cell, which represents the instantaneous intracellular calcium concentration at the single-cell level.

Fig. 1.

Calcium dynamics of cell monolayer in response to extracellular ATP. (A) Composite image showing the multicellular network of cocultured fibroblast (NIH 3T3) and breast cancer cells (MDA-MB-231). Green, fluorescent calcium signal for both cell types; red, MDA-MB-231. (B) Normalized fluorescence intensity profiles of one typical experiment for each ATP concentration tested. Blue, randomly selected single-cell calcium responses; red, average intensity profiles of all cells in each experiment. All time series begin ∼50 s before arrival of ATP stimuli. Intensity profiles of individual cells have been rescaled to $\left[-1,1\right]$. (C) Fraction of nonoscillating cells $F_N$ as a function of ATP concentration at fixed cell density. Error bars: SEMs for $n\ge 4$. *P < 0.05. (D) ISI event counts normalized by number of cells for only NIH 3T3 cells. (E) Average experimentally measured ISI values of NIH 3T3 cells at varying ATP concentrations at fixed cell density. In B, C, and E, cell density ${\text{ρ}}_T=\mathrm{1,200}\pm 200$ cells per 1 mm², and cancer cell fraction $F_C=15\pm 6\%$. (F) ISI cross-correlation as a function of topological distance. Data from experiments with 50 μM ATP at fixed cell density (${\text{ρ}}_T=\mathrm{1,400}\pm 400$ cells per 1 mm²) and cancer fraction ($F_C=20\pm 5\%$). Error bars show SDs from five experiments.

Collective Response to ATP Stimuli.

Typical responses of cells to excitation by ATP are shown in Fig. 1B. We see that, on average, higher concentrations of ATP trigger larger increases in calcium levels. Cell-to-cell variations are significant; for example, response times as well as subsequent calcium dynamics of individual cells vary dramatically. In many cells, the initial calcium increase is followed by transient calcium oscillations. We quantify the oscillation propensity by computing the fraction of nonoscillating cells $F_N$ using a peak-finding algorithm (SI Appendix, section 2). We see in Fig. 1C that higher concentrations of ATP cause a larger percentage of cells to oscillate and thus, a smaller $F_N$.

The period of the oscillation is characterized by the interspike interval (ISI), which has been proposed to dynamically encode information about the stimuli (18, 19). To investigate the characteristics of ISI in the context of collective chemosensing, we study the statistics of the ISI from 30,000 cells. Fig. 1D shows the histogram (event counts) of ISI values normalized by the number of cells of a typical experiment where the ATP concentration is 50 μM. We see that the distribution is broad, which underscores the high degree of cell-to-cell variability in the responses. Fig. 1E summarizes the distribution at each ATP concentration using a box and whisker plot. We see that there is no significant dependence of the ISI on the ATP concentration. This observation is at odds with a familiar property of calcium oscillations, termed frequency encoding, in which the oscillation frequency (or ISI) depends on the strength of the stimulus (14, 18, 20, 21). However, we will see in the next section that the lack of a dependence here is likely caused by the high degree of cell-to-cell variability.

Finally, we characterize the spatial correlations of the ISI within the monolayer by computing the cross-correlation function $C_{ISI}$ as a function of topological distance d between cells [defined by Delaudry triangulation (10)]. For each experiment, we compute the average ISI $T_i$ for each oscillatory cell i. We then define $\text{δ}{T}_i=T_i-\langle T_i\rangle$ and $C_{ISI}\left(d\right)={\langle \text{δ}{T}_i\text{δ}{T}_j\rangle }_{D_{ij}=d}/\langle \text{δ}{T}_i^2\rangle$, where $D_{ij}$ is the topological distance between cells i and j. Fig. 1F shows that $C_{ISI}$ falls off immediately for $d>0$. This observation is surprising, because one might hypothesize that communication between cells would result in ISI values for nearby cells being correlated. However, as described next, evidence from mathematical modeling suggests that this correlation is removed by the cell-to-cell variability.

Stochastic Modeling of the Collective Response.

To obtain a mechanistic understanding of the experimental observations, we turn to mathematical modeling. We develop a stochastic model of collective calcium signaling based on the works of Tang and Othmer (18, 22). Their model captures the ATP-induced release of IP3, the IP3-triggered opening of calcium channels, and the nonlinear dependence of the opening probability on the calcium concentration as illustrated in Fig. 2A. The model neglects more complex features of calcium signaling observed in some cell types, such as upstream IP3 oscillations (23, 24) and spatial correlations among channels (25, 26). The model predicts that, at a critical ATP concentration, the calcium dynamics transitions from nonoscillating to oscillating. However, it was previously only analyzed deterministically for a single cell (18, 22). Therefore, we extend it to include both intrinsic noise and cell–cell communication via calcium exchange (SI Appendix, section 3). We also explicitly include the dynamics of IP3, which has a constant degradation rate and a production rate α that we take as proportional to the ATP concentration. We simulate the dynamics using the Gillespie algorithm (27), and we vary the density ${\text{ρ}}_T$ of cells on a square grid, which modulates the degree of communication.

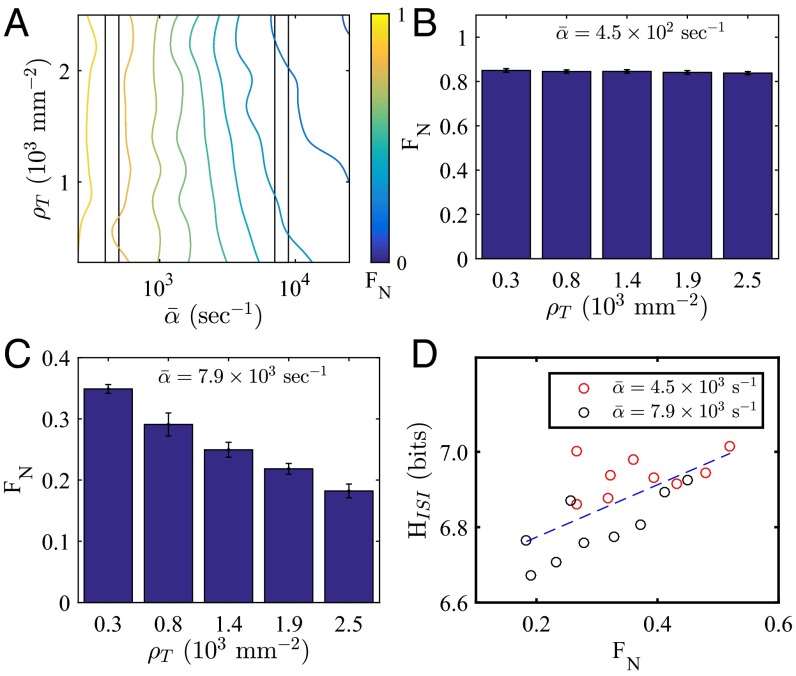
Fig. 2.

Model development and validation. (A) Schematic of the model. ATP stimulates IP3 release at rate α, and IP3 acts jointly with Ca²⁺ to open the endoplasmic reticulum (ER) calcium channels (positive feedback), whereas additional Ca²⁺ binding closes channels (negative feedback). Communication is modeled via diffusion of Ca²⁺ between adjacent cells. (B) Fraction of nonoscillating cells $F_N$ as a function of ATP-induced IP3 production rate α. (C) ISI decreases with $\overline{\text{α}}$ (green). The decrease is severely weakened by cell-to-cell variability (blue). (D) ISI cross-correlation as a function of topological distance d (green). Cell-to-cell variability removes correlations for $d>0$ (blue). (E) Distribution of ISI values (green). Cell-to-cell variability significantly broadens distribution (blue). (F) $F_N$ vs. $\overline{\text{α}}$ with cell-to-cell variability. Cells are simulated on a (B, C, E, and F) $3\times 3$ or (D) $7\times 7$ grid with density (B, D, and F) ${\text{ρ}}_T=2.5\times {10}^3$ or (C and E) $1.4\times {10}^3$ mm⁻². In B and F, error bars are SEMs for $n=5$ subsamples.

Fig. 2B shows the dependence of $F_N$ on α, the model analog of the ATP concentration. Consistent with the experimental findings in Fig. 1C, we see that $F_N$ decreases with α. In the model, the decrease is caused by the fact that intrinsic noise broadens the transition from the nonoscillating to the oscillating regime. Thus, instead of a sharp transition from $F_N=1$ to $F_N=0$ as predicted deterministically, the transition occurs gradually over the range of α shown in Fig. 2B. Fig. 2C shows the dependence of the ISI on α in the model (Fig. 2C, green box plots). We see that the ISI decreases with α, which is expected, because frequency encoding is a component of the Tang–Othmer model (18, 22). However, this property is not consistent with the experimental observation in Fig. 1E, where the ISI shows no clear dependence on ATP concentration. Furthermore, Fig. 2D shows the dependence of the correlation function $C_{ISI}$ on the topological distance d in the model (green dashed curve in Fig. 2D). We see that $C_{ISI}$ decreases gradually with d, indicating nonzero spatial correlations in the ISI, again inconsistent with the experimental findings (Fig. 1F).

Motivated by the high level of cell-to-cell variability evident in Fig. 1 B and D, we hypothesize that cell-to-cell variability is responsible for these discrepancies between the model and the experiments. Indeed, inspecting the ISI histogram from the model reveals a very narrow distribution of ISI values, as seen in Fig. 2E, green bars, which is in contrast to the broad distribution observed experimentally in Fig. 1D. To incorporate cell-to-cell variability, we allow the model parameters to vary from cell to cell. Lacking information about the susceptibility of particular parameters to variation, we allow all model parameters to vary by the same maximum fold change F. F is found by equating the variance of the resulting ISI distribution with that from the experiments, which yields $F=2$ (SI Appendix, section 3). As seen in Fig. 2E, blue bars, the resulting ISI distribution is consistent with that observed in Fig. 1D in both width and shape.

We see in Fig. 2C, blue box plots, that including cell-to-cell variability in the model severely weakens the decrease of the ISI with $\overline{\text{α}}$, therefore agreeing with the experimental results shown in Fig. 1E (with variability, $\overline{\text{α}}$ is defined as the mean of the α values sampled for each cell). We also see in Fig. 2D, blue curve, that variability removes the correlation $C_{ISI}$ for $d>0$, which is consistent with the immediate fall off observed experimentally in Fig. 1F. Importantly, even with variability, the decrease of $F_N$ with α seen in Fig. 2B persists, as shown in Fig. 2F. This decrease remains consistent with the experimental observation in Fig. 1C. Indeed, variability significantly broadens the range of $\overline{\text{α}}$ values over which the transition occurs, as expected (compare Fig. 2 B and F), which is consistent with the broad range over which the transition occurs experimentally (Fig. 1C).

Effects of Communication on the Sensory Response.

Having validated the model, we now use it to make predictions about the effect of cell–cell communication on collective calcium dynamics. Communication in the model is controlled by cell density, with higher density leading to more cell-to-cell contacts and thus, a higher degree of communication. Therefore, we first investigate the dependence of the oscillation propensity on the cell density. Fig. 3A shows $F_N$ as a function of both cell density ${\text{ρ}}_T$ and the ATP-induced IP3 production rate $\overline{\text{α}}$. We see that the fraction of nonoscillating cells transitions from $F_N=1$ to $F_N=0$ as a function of $\overline{\text{α}}$ and that there is also a dependence of $F_N$ on ${\text{ρ}}_T$. At low $\overline{\text{α}}$, $F_N$ is everywhere large and independent of ${\text{ρ}}_T$ (Fig. 3 A, Left and B). However, at intermediate $\overline{\text{α}}$, $F_N$ is a decreasing function of ${\text{ρ}}_T$ (Fig. 3 A, Right and C). In this regime, increasing the cell density causes more cells to exhibit oscillatory calcium dynamics (thus decreasing $F_N$), even with a fixed sensory stimulus $\overline{\text{α}}$. At large $\overline{\text{α}}$ (beyond the range shown in Fig. 3A), we have checked that the nonoscillating fraction is driven to low values as expected, and the density dependence of $F_N$ is weakened (SI Appendix, section 3).

Fig. 3.

Model predictions. (A) Fraction of nonoscillating cells $F_N$ as a function of cell density ${\text{ρ}}_T$ and ATP-induced IP3 production rate $\overline{\text{α}}$. Left and right boxes correspond to B and C, respectively. (B) At small $\overline{\text{α}}$, $F_N$ is large and density-independent. (C) At intermediate $\overline{\text{α}}$, $F_N$ decreases with density. In B and C, error bars are SEMs for $n=5$ subsamples. (D) Entropy of ISI distribution $H_{ISI}$ increases with $F_N$. SI Appendix, section 2 has details of calculating the differential entropy.

The prediction in Fig. 3C is striking, because it implies that cell–cell communication causes more cells to oscillate, even while cell-to-cell variability causes their ISI values to be spatially uncorrelated (Fig. 2D). Therefore, we wondered whether communication would have an effect on the width of the ISI distribution in this regime. The width or more generally, the amount of uncertainty in the ISI distribution is characterized by the entropy. For a continuous variable x, the entropy becomes the differential entropy defined as $H_{ISI}=-{\displaystyle \int \text{ρ}\left(x\right)\log \text{ρ}\left(x\right)dx}$, where $\text{ρ}\left(x\right)$ is the probability density. As seen in Fig. 3D, the entropy of the ISI distribution increases with $F_N$. This result indicates that, as communication decreases $F_N$, it also narrows the distribution of ISI values.

We now test these predictions in our experimental system. To test our predictions about how the nonoscillating fraction of cells should depend on cell density, we measure $F_N$ as a function of ${\text{ρ}}_T$ for various ATP concentrations. We see in Fig. 4A that, with no ATP, $F_N$ is large at both low and high densities, and there is no statistically significant correlation between $F_N$ and ${\text{ρ}}_T$. Then, we see in Fig. 4B that, at intermediate ATP concentrations (10–100 μM), $F_N$ significantly decreases with ${\text{ρ}}_T$. Finally, we see in Fig. 4C that, at large ATP concentration (200 μM), $F_N$ is small at both low and high densities, and again, there is no statistically significant correlation between $F_N$ and ${\text{ρ}}_T$. These results confirm the predictions in Fig. 3.

Fig. 4.

Experimental tests of model predictions. (A) Fraction of nonoscillating NIH 3T3 cells $F_N$ as a function of cell density ${\text{ρ}}_T$ when stimulated by 0 μM ATP. Error bars: SEMs for $n>4$. (B) As in A but with intermediate concentrations 10–100 μM ATP. *P < 0.05. (C) As in A but with 200 μM ATP. In A–C, the cancer cell fraction is fixed at $F_C=15\pm 6\%$. (D) $F_N$ is positively correlated with the differential entropy of ISIs $H_{ISI}$ (${\text{ρ}}_T$ between 600 and 2,500 cells per 1 mm²; $F_C$ between 5% and 80%). Error bars represent SDs of 1,000 bootstrap resampled results (more details are in SI Appendix, section 2). ns, not significant.

To test the prediction that the entropy of the ISI distribution increases with the nonoscillating fraction of cells, we measure $H_{ISI}$ as function of $F_N$. As seen in Fig. 4D, $H_{ISI}$ increases with $F_N$, consistent with the prediction in Fig. 3D. This result implies that increasing the degree of communication narrows the distribution of ISI, making the ISI values less variable across the population. We have also checked that the entropy of the distribution of cross-correlation values for nearest neighbors’ entire calcium trajectories $C_{NN}$ (10, 11) decreases as a function of cell density (SI Appendix, section 4). Together, these results imply that cell–cell communication has a significant effect on the collective sensory response. This finding is especially striking given the strong effects of cell-to-cell variability (Fig. 1 E and F). We conclude that the effects of communication observed here persist, despite extensive variability.

Effect of Cancer Cell Defects.

We have seen that increasing cell density increases the propensity of cells to oscillate in response to an ATP stimulus. This behavior is consistent with our model, which predicts that the mechanism is through increased cell–cell communication. However, it could be in the experiments that increasing the cell density introduces other effects beyond increased gap junction communication, such as mechanical coupling between cells or coupling to the substrate (28). To modulate the communication directly, we vary the fraction $F_C$ of cancer cells with which the fibroblasts are cocultured, while keeping the density of all cells fixed. Because cancer cells are known to have reduced gap junction communication (15–17), we expect the fraction of nonoscillating cells $F_N$ to have the opposite dependence on $F_C$ that it does on cell density (Fig. 4B).

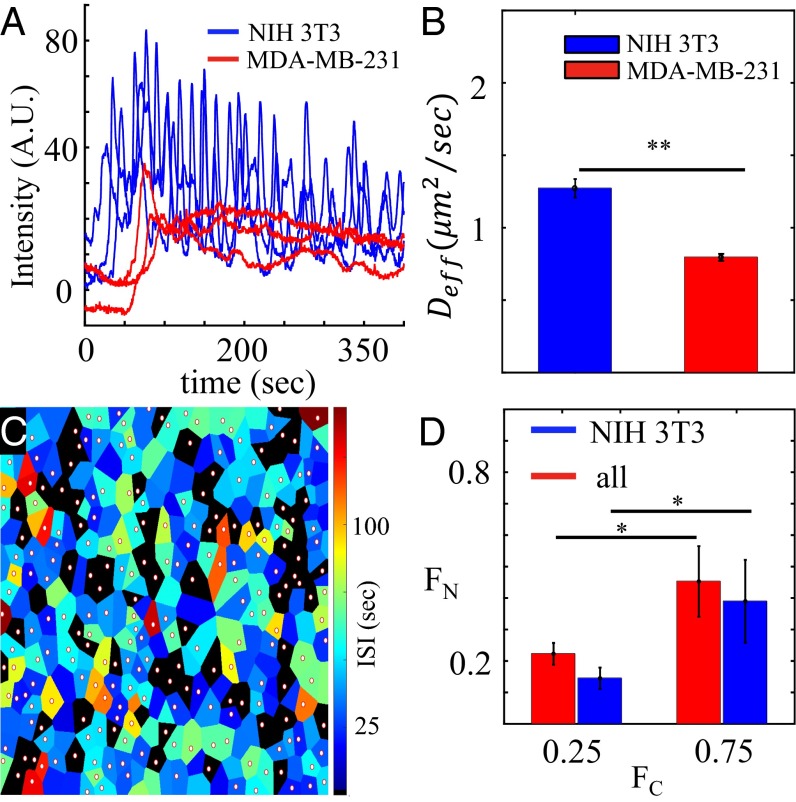
We first investigate whether MDA-MB-231 cells indeed have reduced communication in our system. Fig. 5A shows several examples of single-cell calcium dynamics for NIH 3T3 and MDA-MB-231 cells in a typical experiment. We see that both cell types exhibit immediate increases in cytosolic calcium levels at the arrival of ATP, but cancer cells typically show long relaxation times, whereas fibroblast cells tend to more often exhibit oscillations after stimulation. These qualitative features are maintained across all ATP concentrations. Fig. 5B shows a comparison of the intercellular diffusion coefficients in the two cell types obtained from a fluorescence recovery after photobleaching analysis (29) (SI Appendix, section 1). We see in Fig. 5B that gap junction-mediated diffusion between MDA-MB-231 cells is significantly weaker than that between NIH 3T3 cells, consistent with previous reports (15–17). Therefore, it is evident that MDA-MB-231 cells can be treated as communication defects in the cocultured multicellular network. Indeed, Fig. 5C shows the spatial distribution of these defects in the monolayer. In Fig. 5C, the mean ISI for each cell is shown in color, with nonoscillating cells in black. We see that cancer cells, labeled by white circles, are more likely to be nonoscillating, which is consistent with the qualitative characteristics shown in Fig. 5A. We have further quantified the distinction between the two cells types in SI Appendix, section 2, where we show using the distributions of ISI values that oscillatory events are at least five times less likely to occur for the MDA-MB-231 cells.

Fig. 5.

Effects of cancer cell defects on collective response. (A) Typical fluorescence intensity profiles showing the calcium dynamics on the single-cell level, where basal-level intensity has been subtracted. For each cell, basal-level intensity is estimated by averaging 100 s of its fluorescent intensity before ATP arrival (ATP concentration = 50 μM; ${\text{ρ}}_T$ = 2,400 cells per 1 mm²; $F_C$ = 12%). (B) Fluorescence recovery after photobleaching experiments confirm that MDA-MB-231 cells have weaker gap junction communication compared with NIH 3T3 cells (error bars: SEMs for $n>100$). **P < 0.01. More details are in SI Appendix, section 1. (C) Spatial map of average ISI of each individual cell. ATP concentration is 50 μM. Black, nonoscillating cell; circle, MDA-MB-231 cell. (D) When stimulated by an intermediate range of ATP concentrations (10–100 μM), the fraction of nonoscillating cells $F_N$ increases with increased cancer fraction $F_C$ at fixed total cell density (${\text{ρ}}_T=\mathrm{1,200}\pm 200$ cells per 1 mm²). *P < 0.05. Blue, fraction of nonoscillating NIH 3T3 cells; red, fraction of nonoscillating cells including both cell types.

Having established that the presence of cancer cells reduces the degree of cell–cell communication in the monolayer, we now vary the fraction of cancer cells and measure the oscillation propensity of the remaining fibroblasts. Fig. 5D shows the nonoscillating fraction of fibroblasts $F_N$ (blue bars) as a function of the cancer cell fraction $F_C$ for a typical experiment at fixed cell density (${\text{ρ}}_T=\mathrm{1,200}\pm 200$ cells per 1 mm²). We see that $F_N$ significantly increases with $F_C$. We also see that $F_N$ for all cells (both fibroblasts and cancer cells) (red bars in Fig. 5D) significantly increases with $F_C$ and that, as expected, $F_N$ is larger for all cells than for just fibroblasts. These findings imply that reduced cell–cell communication decreases the propensity for calcium oscillations, which is consistent with the effects of varying cell density (Fig. 4B). Finally, we also investigate the effect of cancer cells on the entropy of the ISI distribution. As shown in SI Appendix, section 2, $H_{ISI}$ is higher for cells that are surrounded by a large number of cancer cells and lower for cells with pure fibroblast neighbors. In the latter case, $H_{ISI}$ also increases as the number of nearest neighbors decreases. These findings imply that reduced cell–cell communication increases the entropy of the ISI values, even at the local level of a cell’s microenvironment, which is consistent with the effects seen in Fig. 4D. Taken together, we conclude that the calcium dynamics of individual cells is strongly regulated by the degree of gap junction communication inside the cell monolayer.

Discussion

We have characterized the collective calcium dynamics of multicellular networks with varying degrees of cell–cell communication when they respond to extracellular ATP. We have found that increasing the ATP stimulus increases the propensity for cells to exhibit calcium oscillations, which is expected at the single-cell level. However, we have also found that increasing the cell density alone, while keeping the stimulus fixed, has a similar effect, revealing a purely collective component to the sensory response. Modeling suggests that this effect is caused by an increased degree of molecular communication between cells. In line with this prediction, we have found that increasing the fraction of cancer cells in the monolayer reduces the oscillation propensity, because cancer cells act as defects in the communication network. Based on these results, we conclude that the collective sensory response, in which nonlinear signaling dynamics is coupled with strong intrinsic and extrinsic noise, encodes both stimulus strength and degree of communication.

Our results suggest that the calcium response to extracellular ATP encodes multiplexed information under physiological conditions. Typical plasma and pericellular concentrations of ATP in animals and human have been reported to range from submicromolar to tens of micromolar (30–32), whereas hundreds of micromolar have been associated with tumor because of the hypoxia microenvironment (33). The concentration range of ATP in Fig. 4B is associated with several physiological phenomena, including immunomodulation (34, 35), traumatic shock (36), and platelet activation (37). Within this range, our results show that calcium dynamics encodes both stimuli strength in the magnitude of intracellular calcium concentration (Fig. 1B) and cell density in the propensity of calcium oscillation (Fig. 4B). Such multiplexing has been shown to be possible with simple biochemical networks (38), and it is thought to underlie the ability of single networks to respond with specificity to multiple inputs, such as neuronal growth factor and EGF in the rat PC-12 system (39). A possible reason for multiplexing is that it is beneficial for the responses to each input to be dependent on each other (40), which in our case, suggests a benefit for a collective component to the ATP sensory response. The ways in which dynamic information is stored in and extracted from cellular signals are a topic of ongoing research (41, 42).

Recent experiments have put our results in the context of a unique paradigm of cell signaling: cells may decode information from the dynamics and not just the magnitude of signaling molecules (43). For instance, UV and γ-radiation differentially trigger nonoscillatory and oscillatory p53 dynamics (44). Similarly, when endothelial cells are stimulated by VEGF, nonoscillatory and oscillatory calcium dynamics leads to migration and proliferation, respectively (45). In light of these developments, our results suggest that cell density, via gap junctional communication and nonlinear signaling dynamics, can impact cellular function, similar to so-called dynamical quorum sensing (46–48).

Our results suggest that the dependence of the calcium response on both sensory and collective parameters persists, despite significant cell-to-cell variability. Certain measures are robust to variability, such as the oscillation propensity and the entropy of the ISI distribution, whereas others are not, such as spatial correlations in the ISI and its dependence on the ATP input (frequency encoding). This result implies that our main finding of communication-dependent sensing is generic, because it persists despite large variability, but that traditional measures of information processing, such as frequency encoding, may have to be rethought in contexts where cell-to-cell variability is pronounced. It is becoming increasingly understood that variability is common in cell populations, and recent examples suggest that it may even be beneficial. For example, recent studies in a related system (NF-κB oscillations in fibroblast populations) also found a large degree of cell-to-cell variability (49) and showed that this variability allows entrainment of the population to a wider range of inputs (50).

In our model, the transition from the nonoscillatory to the oscillatory regime occurs because of a saddle-node bifurcation, a critical point in parameter space where the number of dynamical fixed points changes (SI Appendix, section 3). This transition is broadened by intrinsic noise and cell-to-cell variability into a critical “region,” and cell–cell communication causes the oscillation propensity to depend on cell density within this region (Fig. 3A). Our finding that this region is broad and our suggestion that it may be of some functional use for the system resonate with recent studies that have argued that biological systems are poised near critical points in their parameter space (51–53). The connection between dynamical criticality, as in our model, and criticality in many-body statistical systems remains to be fully explored.

Gap junctional communications exist among many types of cells. Therefore, our results may have far-reaching implications for other biological model systems, such as neuronal networks or cardiovascular systems. Because gap junctions mediate fast, nearest neighbor communication, we expect our conclusions to also hold for 3D cell aggregates, such as tissue organoids. It will be interesting to explore whether distinctions in the calcium dynamics in these systems originate from differences in their degrees of cell–cell communication.

Materials and Methods

SI Appendix, section 1 has details of sample preparation and data collection, and SI Appendix, section 3 has details of stochastic modeling.