Wettability control on multiphase flow in patterned microfluidics

Significance

The simultaneous flow of multiple fluid phases through a porous solid occurs in many natural and industrial processes—for example, rainwater infiltrates into soil by displacing air, and carbon dioxide is stored in deep saline aquifers by displacing brine. It has been known for decades that wetting—the affinity of the solid to one of the fluids—can have a strong impact on the flow, but the microscale physics and macroscopic consequences remain poorly understood. Here, we study this in detail by systematically varying the wetting properties of a microfluidic porous medium. Our high-resolution images reveal the fundamental control of wetting on multiphase flow, elucidate the inherently 3D pore-scale mechanisms, and help explain the striking macroscopic displacement patterns that emerge.

Abstract

Multiphase flow in porous media is important in many natural and industrial processes, including geologic CO₂ sequestration, enhanced oil recovery, and water infiltration into soil. Although it is well known that the wetting properties of porous media can vary drastically depending on the type of media and pore fluids, the effect of wettability on multiphase flow continues to challenge our microscopic and macroscopic descriptions. Here, we study the impact of wettability on viscously unfavorable fluid–fluid displacement in disordered media by means of high-resolution imaging in microfluidic flow cells patterned with vertical posts. By systematically varying the wettability of the flow cell over a wide range of contact angles, we find that increasing the substrate’s affinity to the invading fluid results in more efficient displacement of the defending fluid up to a critical wetting transition, beyond which the trend is reversed. We identify the pore-scale mechanisms—cooperative pore filling (increasing displacement efficiency) and corner flow (decreasing displacement efficiency)—responsible for this macroscale behavior, and show that they rely on the inherent 3D nature of interfacial flows, even in quasi-2D media. Our results demonstrate the powerful control of wettability on multiphase flow in porous media, and show that the markedly different invasion protocols that emerge—from pore filling to postbridging—are determined by physical mechanisms that are missing from current pore-scale and continuum-scale descriptions.

Multiphase flow in porous media is important in many natural and industrial processes, including geologic CO₂ sequestration (1), enhanced oil recovery (2), water infiltration into soil (3), and transport in polymer electrolyte fuel cells (4). Much of the research on multiphase flow in porous media has focused on the effect of fluid properties and flow conditions. Much less emphasis has been given to the fluids’ affinity to the porous media (i.e., wettability), even though wettability has a profound influence on fluid–fluid interactions in the presence of a solid surface (5–7). Despite recent advances in our ability to accurately measure wettability under reservoir conditions (8, 9), and to engineer wettability in the subsurface (10–13), the complex physics of wetting continues to challenge our microscopic and macroscopic descriptions (14).

Fluid–fluid displacement in the presence of a solid surface can be characterized as either drainage or imbibition, depending on the system’s wettability. Drainage refers to the regime where the invading fluid is less wetting to the solid surface than the defending fluid. Imbibition refers to the opposite case, where the invading fluid is more wetting to the solid surface than the defending fluid. Drainage in porous media has been studied extensively through laboratory experiments and computer simulations (15–18), and we now have a fairly good understanding of the different displacement patterns, which include compact displacement, capillary fingering, and viscous fingering. The key dimensionless parameters that control these displacement patterns are the viscosity ratio $\mathrm{ℳ}$ (the ratio of the viscosity of the defending fluid to that of the invading fluid) and the capillary number $\text{Ca}$ (a measure of the strength of viscous forces relative to capillary forces).

In contrast with the wealth of observations in the drainage regime, imbibition (especially for viscously unstable displacement) remains relatively unexplored, even though early experiments have shown significant differences between drainage and imbibition (19). Specifically, the morphology of the displacement pattern broadens as the invading fluid becomes more wetting to the medium. This observation was confirmed by recent experiments (20) and pore-scale simulations (21), which found that increasing the medium’s affinity to the invading fluid makes the invasion pattern more compact at all Ca. However, the complete range of wetting conditions in imbibition is yet to be fully explored, especially in the regime where the invading fluid is strongly wetting to the porous medium.

Here, we use patterned microfluidic flow cells to study viscously unfavorable fluid–fluid displacement (i.e., $\mathrm{ℳ}>1$) in porous media under an unprecedentedly wide range of wettability conditions. We image the system at high resolution, providing simultaneous visualization of both the physics of wetting at the pore scale and the impact of wetting on the macroscopic displacement pattern. We find that wettability has a nonmonotonic effect on two-phase flow in porous media: Increasing the medium’s affinity to the invading fluid results in more efficient displacement of the defending fluid until a critical wetting transition, after which the displacement becomes significantly less efficient. We show that this dramatic transition is caused by corner flow, which allows the invading fluid to propagate without filling the pore bodies. We further show that the pore-scale displacement becomes incomplete at large $\text{Ca}$ due to the formation of wetting films on the solid surfaces, which can be either the viscous defending fluid or the less viscous invading fluid depending on the wettability condition. Our results demonstrate the complex nature of wettability control on multiphase flow in porous media, which involves key physical mechanisms that are likely to play an important role in natural porous media such as rocks and soils.

Experiments in Patterned Microfluidics

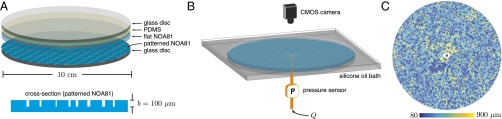
We conduct fluid–fluid displacement experiments in quasi-2D microfluidic flow cells patterned with vertical posts (Fig. 1). This system allows for clear visualization of flow in a porous medium with a known and controllable microstructure, eliminating the uncertainty of natural media and enabling reproducibility (22–24). We fabricate the flow cells with a photocurable polymer (NOA81, Norland Optical Adhesives) via soft imprint lithography. To make the NOA81 surface more hydrophilic, we expose it to high-energy UV radiation—it becomes increasingly hydrophilic with longer exposure time (25, 26). To make the NOA81 surface more hydrophobic, we apply chemical vapor deposition (CVD) of trimethoxysilane in an enclosed chamber (20) (SI Appendix, Fig. S3). These techniques allow us to access a wide range of wettability conditions, which we characterize using the static advancing contact angle of water immersed in silicone oil. Specifically, we achieve stable contact angles of $\theta =150°$ (strong drainage), $\theta =120°$ (weak drainage), $\theta =90°$ (neutral), $\theta =60°$ (weak imbibition), and $\theta =7°$ (strong imbibition); SI Appendix, Fig. S3. We fabricate a new flow cell for each experiment to ensure precise control over its wettability.

Fig. 1.

We conduct radial fluid–fluid displacement experiments by injecting water into viscous silicone oil in quasi-2D microfluidic flow cells patterned with vertical posts. (A) The core of the flow cell is made of a photocurable polymer (NOA81) patterned with circular posts of height $b=$ 100 μm. The flow cell has porosity $\varphi =0.45$, pore volume $V=0.38$ mL, and intrinsic permeability $k\approx 2.4\times {10}^{-10}$ m². (B) The flow cell is initially saturated with a viscous silicone oil (${\eta }_{\text{oil}}=340$ mPa $\cdot$ s) and placed in a bath of the same fluid to avoid capillary edge effects. We inject water into the center of the flow cell at a constant rate Q. A pressure sensor records the injection pressure throughout the experiment. We image the experiment from above with a CMOS camera, measuring the gap-averaged water saturation at high spatial and temporal resolution from calibrated light intensity. (C) We design the pattern of posts to introduce disorder, but such that it is macroscopically homogeneous at the scale of the flow cell. Here, we show the spatial distribution of pore-throat sizes, which range from 80 to 900 μm (SI Appendix, Fig. S1).

To perform an experiment, we first fully saturate the flow cell with silicone oil (${\eta }_{\text{oil}}=340$ mPa $\cdot$ s). We then inject deionized water (${\eta }_{\text{water}}=0.99$ mPa $\cdot$ s) into the center of the flow cell at a constant rate Q, forcing radially outward displacement of the defending silicone oil. This is a viscously unfavorable displacement, with viscosity ratio $\mathrm{ℳ}={\eta }_{\text{oil}}/{\eta }_{\text{water}}\approx 340$. We characterize the importance of viscous forces relative to capillary forces using the classical macroscopic capillary number $\text{Ca}={\eta }_{\text{oil}}{\text{v}}_{\text{inj}}/\gamma$ (18), where $\gamma =13\pm 2$ mN/m is the interfacial tension between the fluids and ${\text{v}}_{\text{inj}}=Q/\left(bd\right)$ is the characteristic injection velocity for a gap thickness b and a median pore-throat size d. By varying the injection rate ($Q=0.002$, 0.02, and 0.2 mL/min), we conduct experiments at three capillary numbers spanning 2 orders of magnitude ($\text{Ca}=2.9\times {10}^{-3}$, $2.9\times {10}^{-2}$, and $2.9\times {10}^{-1}$, respectively) for each of the 5 wettability conditions described above.

Results and Discussion

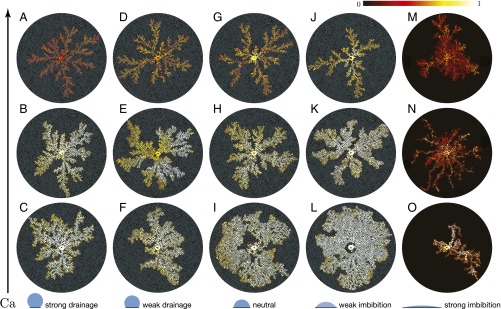
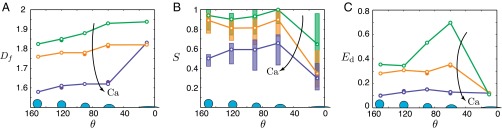
Our main result is an experimental phase diagram of the displacement patterns obtained under a wide range of wettability conditions and capillary numbers (Fig. 2 and Movies S1–S3). The phase diagram is a striking qualitative demonstration of the remarkable control wettability exerts on multiphase flow in porous media. To provide quantitative insight into these patterns, we calculate three metrics for each experiment: (i) We quantify the patterns in 2D by calculating their fractal dimension $D_f$ via the box-counting method (Fig. 3A); this is a classical measure of the degree to which a pattern fills space in 2D. (ii) We quantify the displacement in 3D using the gap-averaged water saturation S measured via light-intensity calibration (Fig. 3B and SI Appendix, Fig. S4). (iii) We also introduce an additional 3D metric, the displacement efficiency $E_d$, which is the fraction of the defending fluid that has been displaced from the flow cell at the end of the experiment (Fig. 3C).

Fig. 2.

Displacement patterns for different wettability conditions (left to right: $\theta =150°,120°,90°,60°,7°$) and capillary numbers (bottom to top: $\text{Ca}=2.9\times {10}^{-3}$, $2.9\times {10}^{-2}$, $2.9\times {10}^{-1}$). These patterns correspond to the end of the experiment, which is when the invading fluid reaches the perimeter of the flow cell. The colormap shows the gap-averaged saturation of the invading water. The pattern of circular posts is overlaid on the experimental images and all images are oriented in the same way to aid visual comparison. Generally, the displacement becomes more efficient as the flow cell becomes more hydrophilic (i.e., decreasing θ), or as Ca decreases. These trends do not hold for strong imbibition (M–O), which has a very low displacement efficiency for all Ca.

Fig. 3.

(A) Fractal dimension $D_f$ of the 2D invasion pattern as a function of the static contact angle θ, computed using the box-counting method. The open circles correspond to the snapshots presented in the phase diagram (Fig. 2) and the filled circles represent additional experiments conducted at the same conditions (SI Appendix, Fig. S6). (B) Box plots of the gap-averaged water saturation S of the invaded regions as a function of θ. The open circles correspond to the median S, and the lower and upper edges of each box represent the first and third quartiles of S, respectively. (C) Displacement efficiency $E_{\text{d}}$ as a function of θ, where $E_{\text{d}}$ is defined as the fraction of the defending fluid that has been displaced from the flow cell at the end of the experiment.

Certain regions of the phase diagram correspond to flow regimes that have been well studied. In strong drainage, for example, we see the classical transition from capillary fingering ($D_f\approx 1.82$) to viscous fingering ($D_f\approx 1.62$) as Ca increases (Figs. 2 C–A and 3A) (15–18).

Although the 2D morphology of these classical patterns is well known, our results provide insight into the displacement in 3D. We uncover and analyze a wide range of other behaviors for conditions that were previously unexplored.

Incomplete Pore-Scale Displacement.

The saturation profile of the experimental phase diagram clearly reveals incomplete pore-scale displacement for all wettability conditions as $\text{Ca}$ increases (Fig. 2). That is, the saturation of the invading fluid decreases as an increasing fraction of the defending fluid is left behind (Fig. 3B).

Incomplete displacement and rate dependence in fluid–fluid displacement was first studied in the context of drainage in capillary tubes (27, 28). In the classical experiments of Taylor (27), air is injected into a cylindrical tube that is initially filled with a wetting, viscous fluid. At small $\text{Ca}$, the air advances via contact-line motion and the displacement is complete. At large $\text{Ca}$, however, viscous forces dominate capillarity and the invading air forms a single finger that advances along the center of the tube, leaving a macroscopic trailing film of the defending fluid on the tube walls. We observe similar behavior in our experiments for all wettability conditions except strong imbibition: The invading water fully saturates the cell gap at small $\text{Ca}$ ($S\approx 1$), but a trailing film of defending oil is left on the walls at large $\text{Ca}$ ($S\approx 0.6$).

In strong imbibition, the water saturation at large $\text{Ca}$ ($S\approx 0.3$) is significantly lower than the saturations measured at other wettability conditions at the same $\text{Ca}$ (Fig. 3B). In addition, the interface between the invading water and the defending oil becomes diffuse rather than sharp (Fig. 2M). These observations are consistent with the formation of thin leading films of water, as recently observed in forced imbibition experiments in Hele–Shaw cells (26). Mechanistically, the dynamic contact angle of the meniscus between a low-viscosity wetting fluid displacing a viscous nonwetting fluid decreases with increasing $\text{Ca}$, approaching zero at a critical capillary number ${\text{Ca}}^{*}$. For $\text{Ca}>{\text{Ca}}^{*}$, this then enables displacement via thin leading films of wetting fluid that propagate along the solid surfaces, leaving residual nonwetting defending fluid in the pore bodies. In our experiments, this condition occurs in the transition between $\text{Ca}=2.9\times {10}^{-2}$ and $\text{Ca}=2.9\times {10}^{-1}$.

Compact Displacement via Cooperative Pore Filling.

Increasing the medium’s affinity to the invading fluid (i.e., decreasing θ; left to right in Fig. 2) leads to an increasingly compact displacement pattern in the transition from strong drainage to weak imbibition. Quantitatively, $D_f$ and $E_d$ increase with decreasing θ in the transition from strong drainage to weak imbibition for all Ca. This effect is most striking in weak imbibition at low Ca (Fig. 2L), where the invading water sweeps the medium uniformly and forms a remarkably compact displacement pattern ($D_f=1.92$; $E_d=0.68$).

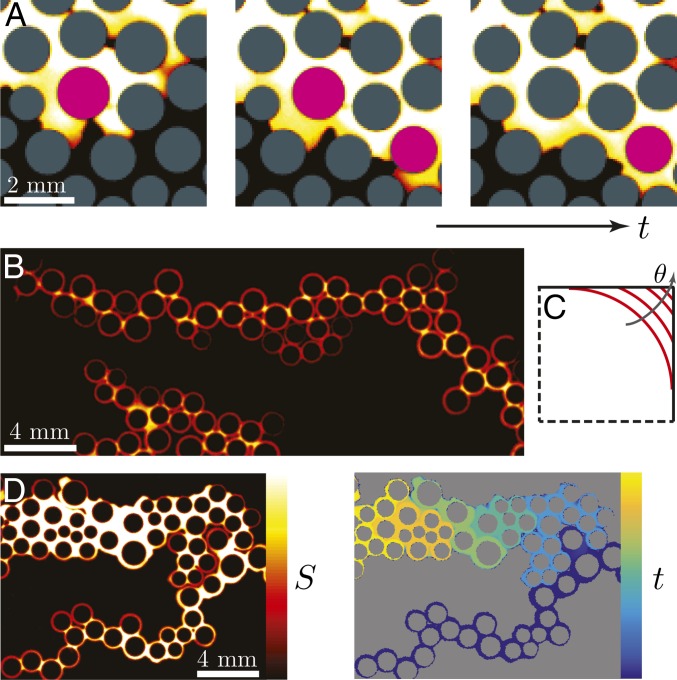
The mechanistic origin of why wettability can lead to more compact displacement patterns was first studied using quasi-static, pore-scale simulations (29–31). The simulation results suggested that this is due to cooperative pore filling, in which two or more neighboring menisci overlap and merge into a new, stable meniscus (29–31). Here, we provide direct experimental observations of these events (Fig. 4A).

Fig. 4.

(A) Sequence of snapshots from weak imbibition at $\text{Ca}=2.9\times {10}^{-3}$ (Fig. 2L). Here, the invading water displaces the defending silicone oil in a cooperative manner: neighboring menisci overlap and form a new, stable meniscus. The posts where this occurs are highlighted in pink. This pore-scale mechanism is directly responsible for the increasing compactness of the macroscopic displacement pattern as θ decreases. (B) Snapshot from strong imbibition at $\text{Ca}=2.9\times {10}^{-2}$ (Fig. 2N) illustrating invasion by corner flow: the invading fluid advances by coating the perimeters of the posts rather than by filling the pore bodies. Pendular rings link the coated posts, forming chains. (C) For a given interfacial curvature, the interface is forced farther into the corner as θ increases, thereby reducing the cross-sectional area available for corner flow. The critical contact angle for corner flow in this geometry is ${\theta }_{\mathrm{⌞}}=45°$. (D, Left) A snapshot from strong imbibition at $\text{Ca}=2.9\times {10}^{-3}$ (Fig. 2O) shows that the corner films coating the posts swell and expand over time. (Right) The same snapshot color coded by invasion time illustrates that strong imbibition at low Ca occurs in a burst-like manner, where groups of closely spaced posts are coated in rapid succession, followed by periods of inactivity.

Cooperative pore filling is thought to become important below a critical contact angle ${\theta }_c$ (29, 30). Above ${\theta }_c$, the invading fluid advances pore-by-pore and the macroscopic displacement pattern is nearly θ-independent. Below ${\theta }_c$, the displacement becomes increasingly compact due to cooperative pore filling as θ decreases. Cieplak and Robbins (29, 30) found that ${\theta }_c$ itself decreases with porosity, and that cooperative pore filling is promoted by narrower pore throats. In our experiments, ${\theta }_c$ lies in the transition between strong drainage and weak drainage ($120°<{\theta }_c<150°$).

Wetting Transition and Corner Flow in Strong Imbibition.

Intuitively, one would expect the invasion front to become increasingly compact with decreasing θ, and a stable flood as the invading fluid becomes perfectly wetting to the medium. Surprisingly, this is not what we see in strong imbibition—instead, we observe a dramatic change in both pore-scale displacement mechanisms and macroscopic displacement patterns (Fig. 2 M–O). Specifically, the invading fluid advances preferentially along the solid surfaces at all Ca (Fig. 4B).

For high $\text{Ca}$, the invading fluid advances in leading films along the solid surfaces. For low $\text{Ca}$, the invading fluid instead advances by sequentially coating the perimeters of neighboring posts. The invading fluid bypasses the pore bodies as a result of capillary suction in the corners where the posts meet the top and bottom surfaces of the flow cell. This phenomenon is known as corner flow, and has been studied extensively in the context of spontaneous imbibition into angular capillaries (32–37). For the wetting fluid to invade the corners, the contact angle must satisfy the geometric relation $\theta <\left(\pi -\alpha \right)/2$, where α is the corner angle (32). For the right-angled corners present in our flow cell, the critical contact angle for corner flow is then ${\theta }_{\mathrm{⌞}}=45°$, which is between weak imbibition ($\theta =60°$) and strong imbibition ($\theta =7°$).

The macroscopic manifestation of corner flow in strong imbibition is the formation of “chains” of coated posts, where neighboring posts are linked by pendular rings of water (Fig. 4B and Movie S4). The propagation of these post chains has certain features in common with strong drainage; for example, the chains propagate outward in a radially symmetric fashion at high Ca (compare: viscous fingering, Fig. 2N), but become asymmetric at small Ca (compare: capillary fingering, Fig. 2O).

The pore-scale invasion speed in strong imbibition can be characterized by the coating speed of corner flow, ${\mathrm{v}}_{\mathrm{⌞}}$. We find ${\mathrm{v}}_{\mathrm{⌞}}\approx 2$ mm/s in our experiments over more than an order of magnitude change in the injection rate (SI Appendix, Fig. S5). When the characteristic injection velocity ${\text{v}}_{\text{inj}}=Q/\left(bd\right)$ far exceeds the coating speed, as in our experiments at high Ca, corner flow is overwhelmed by the formation of leading films. When the injection velocity is comparable to the coating speed, as in our experiment at intermediate Ca, we see a continuous coating process (Movie S4). For even lower injection velocities, as in our experiment at low Ca, we instead see a burst-like invasion process in which clusters of closely spaced posts are rapidly coated, followed by quiescent periods during which the corner films gradually swell (Fig. 4D and Movie S4). This burst-like invasion is analogous to the well-studied phenomenon of “Haines jumps” in slow drainage, in which clusters of pores are rapidly invaded, followed by quiescent periods during which the nonwetting fluid slowly swells into the pore throats (38–41).

The curvature of the interface in corner flow is set by the pressure balance between the capillary pressure in the corner and the pressure difference between the two fluids, as described by the Young–Laplace equation: $\gamma /R=P_{\text{oil}}-P_{\text{water}}$. This suggests that the radius of curvature R will decrease as Ca increases because higher flow rates increase the absolute pressure difference between the two fluids (i.e., both fluid pressures increase proportional to their own viscosities). We therefore expect corner flow to become less favorable as Ca increases.

For a given interfacial curvature, larger θ ($\theta <{\theta }_{\mathrm{⌞}}$) forces the interface farther into the corner, making corner flow less favorable (Fig. 4C) (33, 34). We have validated this prediction with an additional experiment in intermediate imbibition ($\theta =28°$), which exhibits the coexistence of pore-body displacement and corner flow, as well as thinner corner films (SI Appendix, Fig. S7).

We expect corner flow to play an important role in strong imbibition in natural porous media like rocks and soils. Natural media typically have angular and irregular grains, which promote corner flow (42). These grains are also rough, and surface roughness is known to act as an amplifier for wettability: Molecularly hydrophobic and hydrophilic surfaces become macroscopically more hydrophobic and more hydrophilic, respectively, after being roughened (43). In addition, the greater connectivity between grains in a truly 3D porous medium should further facilitate corner flow.

Evolution of Injection Pressure.

To develop further insight into the macroscopic impact of wettability on fluid–fluid displacement, we measure the evolution of the injection pressure (Fig. 5). Pressure information in fluid–fluid displacement is of great practical interest in many subsurface technologies, including wastewater disposal (44), geologic sequestration of carbon dioxide (1), and hydraulic fracturing (45), because perturbations in the pore pressure are intimately linked with mechanical deformation of the medium (46).

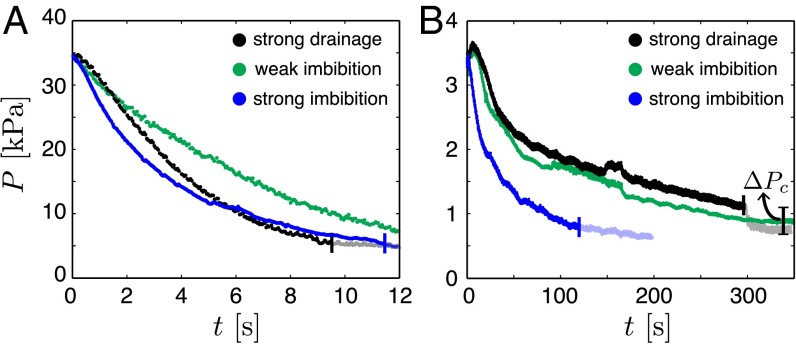
Fig. 5.

Evolution of the injection pressure during strong drainage, weak imbibition, and strong imbibition at (A) $\text{Ca}=2.9\times {10}^{-1}$ and (B) $\text{Ca}=2.9\times {10}^{-2}$. The pressure measurements are shifted in time so that $t=0$ $\text{s}$ is the time when the invading water first enters the flow cell. The end of each experiment (i.e., the time when the water first reaches the perimeter of the flow cell) is marked with a vertical line and subsequent measurements are translucent. (B) The sudden drop in injection pressure as the water exits the flow cell in strong drainage corresponds to the capillary pressure $\mathrm{\Delta }{P}_c$ across the oil–water interface.

We place the flow cell in a silicone oil bath to enforce a uniform and constant pressure along the perimeter, and to remove capillary edge effects (Fig. 1B). The measured pressure is the sum of the capillary pressure across the oil–water interface $\mathrm{\Delta }{P}_c$ and the combined viscous pressure loss in the water and oil phases. The viscous pressure loss decreases as the silicone oil is displaced by the much less viscous water. The characteristic capillary pressure in strong drainage is $\mathrm{\Delta }{P}_c\approx 2\gamma \left(1/b+1/d\right)\approx 0.3$ kPa, where b is the gap thickness of the flow cell and d is the median pore-throat size (22). This is consistent with the observed $\mathrm{\Delta }{P}_c$ in strong drainage (Fig. 5B).

One might expect wettability to have a weak impact on injection pressure at moderate to high Ca, where the capillary pressure itself becomes small relative to the viscous pressure loss. Instead, we find that wettability exerts a powerful control over the evolution of the injection pressure at all Ca, and the injection pressures for different wettability conditions differ by much more than the capillary pressure itself (Fig. 5). The injection pressure also decreases much more sharply in strong imbibition than in strong drainage or weak imbibition, reflecting the unique displacement mechanisms in strong imbibition: The invading fluid advances along the corners, bypassing the pore bodies, and this rapidly reduces the viscous pressure loss.

Conclusions

We have systematically investigated the impact of wettability on multiphase flow in porous media via fluid–fluid displacement experiments in patterned microfluidic flow cells with controlled wetting properties.

We have shown that fluid–fluid displacement at high Ca is dominated by the formation of wetting films on the solid surfaces for all wettability conditions, which leads to incomplete displacement at the pore scale. In drainage, these are trailing films of the more viscous defending fluid; in imbibition, they are leading films of the less viscous invading fluid. We have further shown that the displacement pattern becomes more compact as the invading fluid becomes more wetting to the medium (i.e., decreasing θ; Fig. 2), which leads to more efficient displacement of the defending fluid (Fig. 3). Through visualization of fluid flow at the pore scale, we have provided direct experimental evidence that the more compact invasion front stems from cooperative pore filling (Fig. 4A). Our experiments have revealed that the trend of increasingly compact displacement with decreasing θ is unexpectedly reversed as the system exhibits a wetting transition between weak imbibition ($\theta =60°$) and strong imbibition ($\theta =7°$). We have shown that this dramatic change is caused by corner flow, which allows the invading fluid to propagate without filling the pore bodies. We have observed marked differences in the evolution of the injection pressure between experiments under different wettability conditions, even at large capillary numbers where viscous pressure dominates over capillary pressure. This finding underscores the significant control wettability exerts on the efficiency of the displacement, which is strongly connected to the viscous pressure drop across the flow cell.

Our results highlight the inherently 3D nature of multiphase flow in porous media, which manifests itself through physical mechanisms such as film formation and corner flow. These wettability-controlled mechanisms have a fundamental impact on multiphase flow, making them challenging but essential ingredients in pore-scale and continuum-scale descriptions. Our microfluidics study of the fundamental mechanisms paves the way for the interpretation and further investigation of wettability control on multiphase flow in natural porous media, which often exhibit spatial heterogeneity in wettability (47, 48), surface roughness (43, 49), and preexisting wetting layers (50).

Materials and Methods

Post Pattern Design.

To create the post pattern, we first generate an irregular triangular mesh inside a circle using the pdemesh tool in MATLAB. We use the nodes of the triangular mesh as the centers of the posts. We then assign the radius of each post to be 45% of the distance to its nearest neighbor, which provides a random distribution of nonoverlapping posts. Detailed statistics of the post size and the pore-throat size distributions are provided in SI Appendix, Fig. S1.

Microfluidic Flow Cell Fabrication.

We fabricate the flow cells via soft imprint lithography following the procedures detailed in Bartolo et al. (51). We first generate a silicon master of the post pattern via conventional photolithography techniques. We use the silicon master to create a polydimethylsiloxane (PDMS; Sylgard 184, Dow Corning) cast of the post pattern. The PDMS cast forms a negative complement of the silicon master, consisting of wells rather than posts. The core of the flow cell is made of a photocurable polymer (NOA81, Norland Optics) and consists of a flat top half and a bottom half that contains the post structures (Fig. 1). To make the bottom half, we first deposit a puddle of NOA81 onto a 4-in. glass disk. We allow the NOA81 to spread across the disk before covering it with the PDMS cast. Upon contact, the NOA81 spontaneously imbibes into the wells in the PDMS cast. After removing excess NOA81 with a metal roller, we cure it with a collimated 365-nm UV light source (MA4-1, Karl Suss) for 15 s at 25 mW/cm². We peel off the PDMS cast after curing. The bottom half of the flow cell is now ready for wettability alteration (see the next section). To make the top half of the flow cell, we sandwich a puddle of NOA81 between two flat PDMS discs (4” diameter) separated by 100-μm-thick precision metal shims. After the NOA81 fills the gap between the PDMS discs, we cure it with the MA4-1 for 60 s at 25 mW/cm². We then peel off one of the PDMS discs. The top half of the flow cell is now ready for wettability alteration (see the next section). The entire fabrication workflow is illustrated in SI Appendix, Fig. S2.

Wettability Alteration.

We characterize the wettability of our system by placing a small drop of deionized (DI) water on a treated NOA81 surface submerged in a silicone oil-filled reservoir. We image the water drop with a contact angle goniometer (model 250, ramé-hart), which measures the water/silicone oil contact angle via its DROPimage software. The images obtained from the contact angle measurements are provided in SI Appendix, Fig. S3. The contact angle of water on an untreated NOA81 surface immersed in silicone oil is $\theta =120°\pm 3°$. NOA81 is a thiolene-based polymer that gains surface energy through deep UV radiation, due to the formation of peroxide groups (25). We make the NOA81 surface more hydrophilic by exposing it to high-energy UV light in a UV-ozone cleaner (UV-1, Samco, Japan). By varying the duration of UV exposure ($t_{\text{UV}}$), we achieve $\theta =90°\pm 7°$ ($t_{\text{UV}}=85$ s), $\theta =60°\pm 5°$ ($t_{\text{UV}}=210$ s), and $\theta =7°\pm 3°$ ($t_{\text{UV}}=\mathrm{1,800}$ s). To make the NOA81 surface more hydrophobic, we apply CVD of trimethoxysilane in a desiccator for 30 min, which yields $\theta =150°\pm 5°$.

Experimental Setup.

To perform an experiment, we first inject silicone oil (350 cSt, Sigma-Aldrich) into the flow cell, which sits in an empty reservoir. After the flow cell is fully saturated, we pour silicone oil into the reservoir until the gap is fully submerged. We then inject DI water at a prescribed volume flow rate using a syringe pump (PHD 2000, Harvard Apparatus). We image the displacement via a scientific camera (Orca Flash 4.0, Hamamatsu) mounted directly above the center of the flow cell. The scientific camera has a complementary metal–oxide–semiconductor (CMOS) sensor with 2,048 $\times$ 2,048 pixels, which yields a spatial resolution of $a=52$ μm per pixel.

Water Saturation Quantification.

We seed the injected water with a light-absorbing dye (Brilliant Blue G, Alfa Aesar) at 800 mg/L concentration. We experimentally generate a calibration curve that relates the transmitted-light intensity to the dye concentration in the water solution, which is well-described by the Beer–Lambert law. We further find an one-to-one relationship in the transmittance of water films of different dye concentrations at a fixed thickness, and water films of different thicknesses at a fixed concentration. This allows us to convert the measured transmitted-light intensity to the gap-averaged water saturation. The calibration curve is presented in SI Appendix, Fig. S4. We test the accuracy of the quantified water saturation by calculating the total injected volume as $V={\displaystyle \sum abS}$, which corresponds well to the actual injected volume (SI Appendix, Fig. S4).

Pressure Measurements.

We connect a pressure transducer (uPS0250-T116-10, Labsmith) to a stiff injection tube (TUBE116-030P, Labsmith) via a T-connector 3 cm below the flow cell. The transducer operates within a pressure range of 0–250 kPa and at a sampling frequency of 50 Hz, with a resolution of 1 Pa.