Comprehensive structural and dynamical view of an unfolded protein from the combination of single-molecule FRET, NMR, and SAXS

Significance

Proteins are the most versatile components of the molecular machinery of life. Synthesized as linear polymers of amino acids, proteins start out in their unfolded state and perform their function either in well-defined folded conformations or as intrinsically disordered proteins (IDPs) lacking tertiary structure. Both for the folding process and the properties of IDPs, a quantitative understanding of the conformational distributions and dynamics of unfolded proteins is thus essential. However, reaching this goal has been challenging owing to the large conformational heterogeneity and rapid dynamics of these systems. Here we combine three of the most powerful biophysical methods available to obtain a comprehensive view of an unfolded protein that would not be available from any of the individual methods.

Abstract

The properties of unfolded proteins are essential both for the mechanisms of protein folding and for the function of the large group of intrinsically disordered proteins. However, the detailed structural and dynamical characterization of these highly dynamic and conformationally heterogeneous ensembles has remained challenging. Here we combine and compare three of the leading techniques for the investigation of unfolded proteins, NMR spectroscopy (NMR), small-angle X-ray scattering (SAXS), and single-molecule Förster resonance energy transfer (FRET), with the goal of quantitatively testing their consistency and complementarity and for obtaining a comprehensive view of the unfolded-state ensemble. Using unfolded ubiquitin as a test case, we find that its average dimensions derived from FRET and from structural ensembles calculated using the program X-PLOR-NIH based on NMR and SAXS restraints agree remarkably well; even the shapes of the underlying intramolecular distance distributions are in good agreement, attesting to the reliability of the approaches. The NMR-based results provide a highly sensitive way of quantifying residual structure in the unfolded state. FRET-based nanosecond fluorescence correlation spectroscopy allows long-range distances and chain dynamics to be probed in a time range inaccessible by NMR. The combined techniques thus provide a way of optimally using the complementarity of the available methods for a quantitative structural and dynamical description of unfolded proteins both at the global and the local level.

Proteins exist as ensembles of interconverting conformations. Obviously, unfolded polypeptide chains, such as chemically or physically denatured proteins and intrinsically disordered proteins (IDPs), can access extremely large numbers of conformations (1). A comprehensive description of their structural and dynamical behavior is a prerequisite for understanding protein folding (2–4) and the function of IDPs in health and disease (5, 6). Due to the very large number of conformational degrees of freedom of the unfolded polypeptide ensemble, it is of utmost importance to obtain as many independent experimental parameters as possible for a quantitative description of its behavior. Three experimental methods have been particularly informative in this respect: NMR spectroscopy (2, 5, 7–9), small angle X-ray scattering (SAXS) (10, 11), and single-molecule Förster resonance energy transfer spectroscopy (single-molecule FRET) (12, 13).

NMR in solution provides very rich local structural and dynamical information at virtually any atom site with the exception of oxygen. Distance and angular information can be obtained from nuclear Overhauser enhancements (14), three-bond scalar couplings (15), paramagnetic relaxation enhancements (PREs) (16), pseudo contact shifts (17), residual dipolar couplings (RDCs) (8, 18), chemical shifts (19), and hydrogen bond scalar couplings (20). Thus, on the order of 10 geometric parameters per amino acid can be obtained with relative ease on unfolded polypeptides (21). Information on dynamics is also available from solution NMR but is restricted to three timescales: the pico- to low nanosecond range of the Larmor frequencies, the micro- to low millisecond range of the chemical shift (19), and the larger-than-seconds range of real-time NMR (22). The large number of experimental data from NMR on the geometry of unfolded polypeptide ensembles together with the knowledge on the covalent structure of the polypeptide chain provide powerful input for computer models of representative ensembles of the unfolded state. Typically, ensembles containing tens of thousands of conformers are simulated in an unrestrained manner and reduced by various methods (23–26) to smaller-size ensembles that satisfy the measured parameters. As an alternative, we have recently used restrained ensemble structure calculations (27) to create minimal-size ensembles of urea-denatured ubiquitin (76 aa) that satisfy a very high number of 419 RDC and 253 PRE restraints obtained by NMR (21). The analysis of the ensemble revealed significant (10–20%) populations of a native-like first β-hairpin and α-helix and nonnative α-helical conformations in the C-terminal half. Thus, the urea-denatured state has similarities to ubiquitin’s methanol/acid-denatured A-state (28).

Information from SAXS comes at lower resolution but provides important information on the overall shape of a biomolecule in solution (10, 11), which ideally complements the predominantly local information from NMR. The SAXS scattering profiles yield the solution-averaged autocorrelation of the molecular electron density, often reported in simplified form as a radius of gyration, R_g.

Single-molecule FRET has recently emerged as an additional method to study unfolded proteins (12, 13). Single-molecule FRET provides intramolecular distance information in the range of tens of angstroms by measuring the Förster transfer between fluorescence donor and acceptor dyes attached to the polypeptide. Because the signal is recorded on single molecules, structural and dynamic heterogeneity can be resolved that is often impossible to detect by ensemble-averaged methods. An example is the investigation of the properties of the unfolded state of a protein in the presence of a folded subpopulation, as it is commonly the case under near-physiological conditions or for IDPs in the presence of ligands (29, 30). The resulting subpopulation-specific transfer efficiencies and fluorescence lifetime distributions can be analyzed in terms of intramolecular distance distributions based on models from polymer physics (3, 31) or combined with molecular simulations (32–34) to quantify global parameters such as mean-squared distances, radius of gyration, or persistence length. In addition to this information relating to equilibrium distances, distance dynamics can be determined on a broad range of timescales with methods such as fluorescence correlation spectroscopy (FCS, ∼10⁻⁸ to 10⁻³ s), transfer efficiency histogram analysis (∼10⁻⁴ to 10⁻¹ s), microfluidic mixing (∼10⁻³ to 10² s) and measurements on immobilized molecules (∼10⁻⁵ to 10³ s) (4). Typical reconfiguration times of unfolded proteins as measured by nanosecond-FCS (nsFCS) (30, 35) range between ∼20 ns and ∼200 ns, a time window that is not accessible by NMR in solution. Thus, the precise long-range and the dynamical information on the >10-ns timescale makes single-molecule FRET highly complementary to both NMR and SAXS.

Despite their obvious complementarity, SAXS, NMR, and single-molecule FRET data on unfolded proteins or IDPs have only rarely been directly combined or compared, and concerns have been raised about the validity of the individual methods for correctly quantifying unfolded-state properties (36, 37). Here we present a direct comparison of the properties of urea-denatured ubiquitin as quantified from all three methods and enhance the description of the ensemble by the FRET-specific single-molecule, time-dependent, and long-range distance information. Compared with previous structural ensembles calculated only from NMR restraints (21), the addition of SAXS restraints (38) did not change significantly either the overall dimensions of the ensemble or its 10–20% secondary structure content similar to ubiquitin’s A-state. To obtain a detailed description of the denatured ensemble by single-molecule FRET, seven double-cysteine variants of ubiquitin were created, labeled for FRET, and analyzed. The resulting FRET distance distributions were then compared with the structural ensembles based on NMR and SAXS restraints. The results show good agreement of not only the FRET- and NMR/SAXS ensemble-derived average distances, but also of their distributions. Furthermore, the single-molecule FRET data reveal the reconfiguration times of the unfolded chain in the range of 50–100 ns. Thus, the combined data from all methods provide a detailed and consistent description of the conformational ensemble of urea-denatured ubiquitin at unprecedented spatial and temporal detail.

Results

Structural Ensembles of Urea-Denatured Ubiquitin Calculated from NMR and SAXS Restraints.

We had previously calculated structural ensembles of ubiquitin denatured in 8 M urea at pH 2.5 based on experimental NMR observations comprising 419 RDC (20, 39) and 253 PRE restraints determined on eight S-(1-oxyl-2,2,5,5-tetramethyl-2,5-dihydro-1H-pyrrol-3-yl)methyl methanesulfonothioate (MTSL)-labeled cysteine variants (21). Ensemble sizes of at least 10 conformers had been sufficient to obtain average back-calculated NMR parameters and radii of gyration that matched the experimental data within the expected error. Here we have extended these calculations by including restraints from the SAXS intensity profile (38) and 71 backbone ³J_HNHα-couplings (40) of urea-denatured ubiquitin as well as increasing the ensemble size to 20. The newly generated ensembles are very similar to the previous ones (21), as can be appreciated from the C^α–C^α contact map of 400 such ensembles (Fig. 1) that shows highly similar intramolecular interactions corresponding to both native and nonnative structure elements. It is noted that whereas each individual ensemble of 20 conformers matches all experimental data within the error, the different ensembles contain very different structures, because their degrees of freedom largely exceed the number of structural restraints. We have shown previously (21) that the probability for observing individual C^α–C^α contacts within the total of all structures follows a binomial distribution and that observations of contacts in the low percent range are highly significant for a total of several thousand structures.

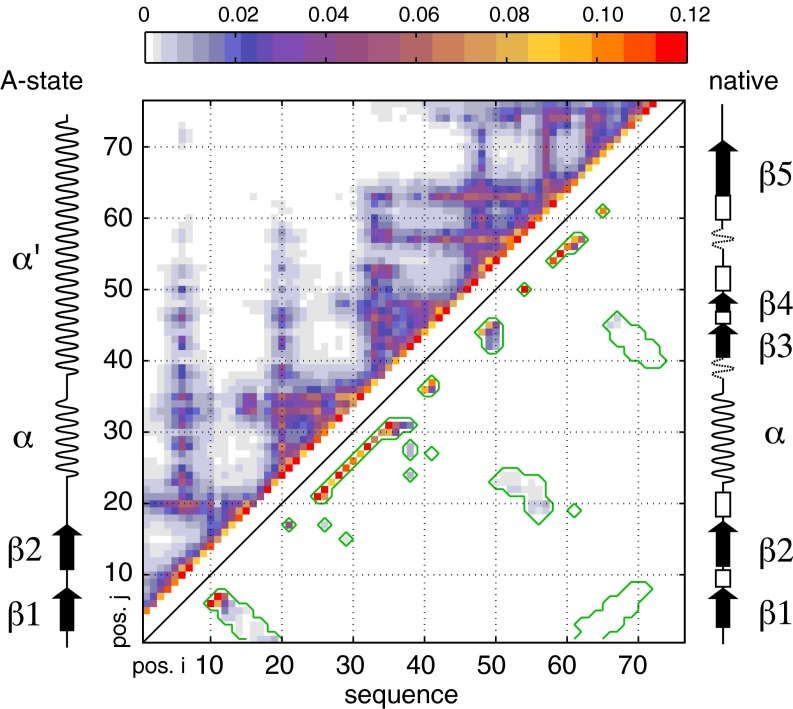
Fig. 1.

C^α–C^α contact map of urea-denatured ubiquitin. Four hundred low-energy structural ensembles of 20 conformers each were generated as described in Methods using X-PLOR simulations with restraints derived from RDC, PRE, J-coupling, and SAXS data. Contact probabilities p(i,j) between residue i and residue j were determined as the total number of contacts observed in all conformers with C^α–C^α distances smaller than 8 Å divided by the total number of conformers (i.e., 8,000). The contact probabilities p(i,j) are color-coded as indicated by the color bar at the top and plotted versus sequence positions i and j. The upper left part of the contact map represents all observed contacts; the lower right part shows only contacts also present in the native state of ubiquitin (delimited by green contour lines). Merely for comparison, the secondary structures of native state and A-state ubiquitin are shown schematically at the right and left sides, respectively.

In particular, and similar to previous findings, significant contact populations on the order of 10% are observed between residues 6 and 10 as well as 7 and 11 at the location of the native β-turn (Fig. 1). In addition, strong α-helical i to i+4 contacts exist along the entire peptide sequence, covering both the native helix of residues 22–35 and the nonhelical C-terminal part of the native protein. Thus, the structural ensemble has similarities to ubiquitin’s methanol/acid-denatured A-state, in which the first β-hairpin, the α-helix, and a long C-terminal α-helix are formed but move on the nanosecond timescale as independent elements connected by flexible linkers (28). Many further, weaker, native and nonnative long-range contacts are also observed, among them a patch comprising the native contacts between amino acid stretches 18–24 and 50–57. The presence of such long-range contacts on the order of 1% in the calculated ensemble seems to indicate that the protein samples tertiary interactions of the fully folded native form even in 8 M urea to a detectable extent.

Distance Distributions in the Unfolded Ensemble from Single-Molecule FRET.

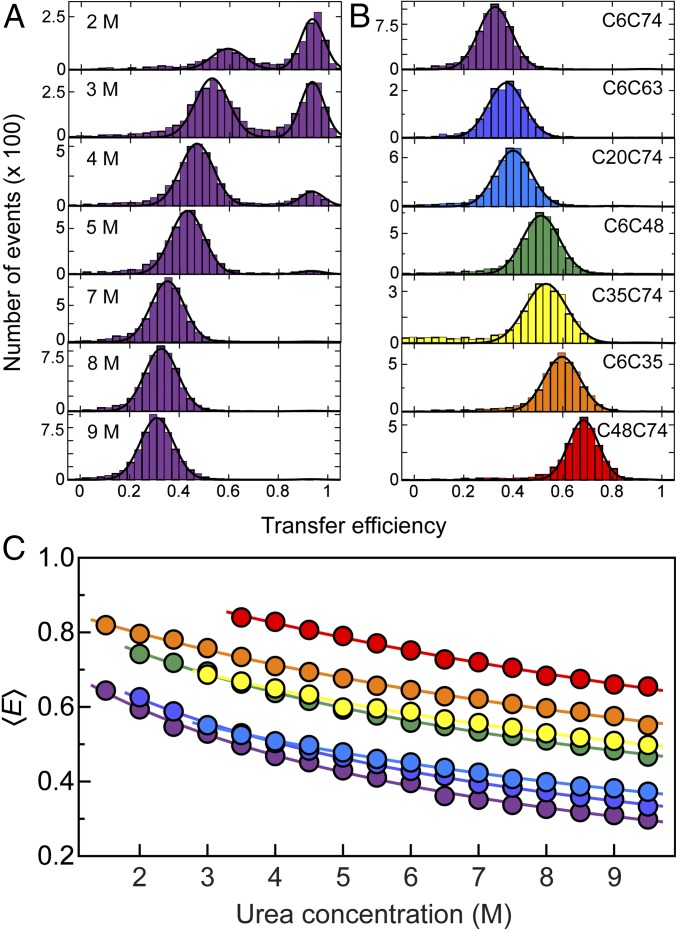
To probe the distances between different segments of the polypeptide chain in single-molecule FRET experiments and to compare them to the NMR/SAXS ensemble, we created seven double-cysteine variants of ubiquitin with cysteine residues bracketing between 26 and 68 peptide segments. The variants were labeled with Alexa Fluor 488 and Alexa Fluor 594 as FRET donor and acceptor, respectively. We then used confocal single-molecule fluorescence spectroscopy of freely diffusing molecules to obtain transfer efficiency histograms of ubiquitin at different urea concentrations (Fig. 2A). The peak at high transfer efficiency corresponds to folded ubiquitin molecules, and the peak at lower transfer efficiencies to unfolded ubiquitin. With increasing concentration of urea, we observe a gradual change in the relative populations of folded and unfolded states and a disappearance of the folded peak at urea concentrations above ∼5.5 M, as expected for urea-induced unfolding of ubiquitin. However, whereas the position of the folded state is unaffected by the addition of urea to within experimental uncertainty in this high transfer efficiency range, the unfolded peak shifts to lower transfer efficiencies, indicating a continuous expansion of the chain with increasing concentration of urea, as previously observed for many unfolded proteins (3, 31, 41–46).

Fig. 2.

(A) Single-molecule FRET efficiency (E) histograms of the C6C74 variant of ubiquitin at different concentrations of urea, pH 2.5, illustrating the unfolding transition and the unfolded-state expansion. The peak at E ≈ 0.9 corresponds to folded and the peak at lower E to unfolded molecules. To determine mean transfer efficiencies, 〈E〉, peaks were fitted with Gaussian peak functions (black lines). (B) Histograms at 8 M urea, pH 2.5 for all ubiquitin variants investigated, with the positions of labeled Cys residues indicated for each panel. The color code is the same as in Table 1. (C) Dependencies of mean transfer efficiencies of the unfolded subpopulation on the urea concentration for all variants (color code as in B). The solid lines are fits with a weak binding model (43, 74) of the form E(c_D) = E₀ + ΔE Kc_D/(1 + Kc_D) for interpolation, where c_D is the denaturant concentration, and K, ΔE, and E₀ are fit parameters.

As expected for a disordered chain (30, 43), we also observe a decrease in transfer efficiency for the unfolded state with increasing sequence separation between the two fluorophores at a given urea concentration, as shown in Fig. 2B for 8 M urea. For all seven variants of ubiquitin we detect a similar trend for the expansion of the unfolded chain with increasing concentration of urea, but offset corresponding to the length of the segments probed (Fig. 2C). To quantify the dimensions of unfolded ubiquitin from the single-molecule FRET data, we converted the mean transfer efficiencies into root-mean-squared distances (RMSDs) using the intrachain distance distributions for a Gaussian chain, previously shown to be a useful approximation for unfolded proteins (32, 41–43, 47). To complement our information on the distances within the unfolded chain of ubiquitin, we additionally performed an analysis of fluorescence intensity decays, which occur on much shorter timescales than unfolded chain reconfiguration (35) and thus provide more direct and robust information about the shape of the underlying distance distribution function (43, 48, 49). For that purpose, we extracted from our single-molecule measurements subpopulation-specific time-correlated single-photon counting histograms of both donor and sensitized acceptor emission for the different variants of ubiquitin at 8 M urea, an example of which is shown in Fig. 3. We then fitted the donor and acceptor signal globally, assuming distributions of transfer rates corresponding to the distribution of donor–acceptor distances for a Gaussian chain (43) and obtained the RMSD values for all variants (see Methods for details). The good agreement between the values of RMSD obtained from the mean transfer efficiencies and the fluorescence intensity decays supports the robustness of the analysis (Fig. 3D).

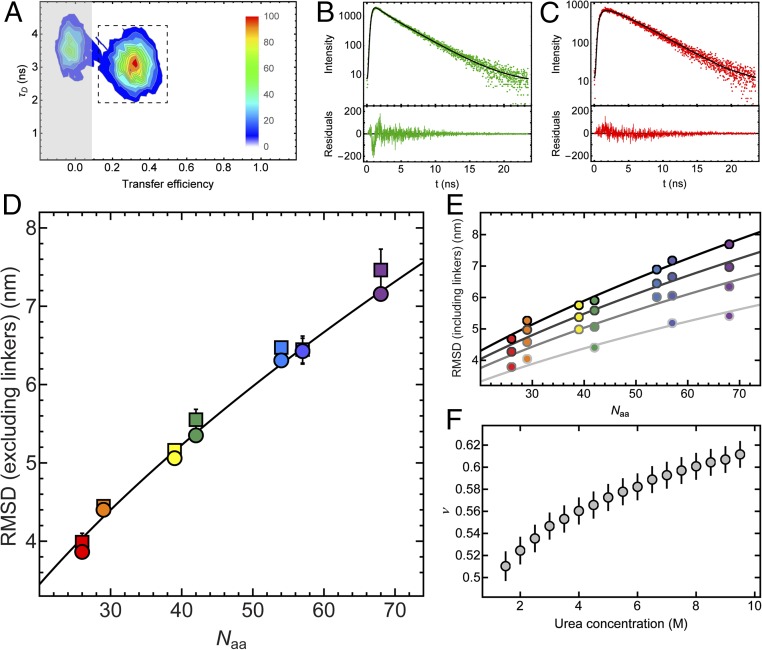
Fig. 3.

(A) Contour plot of donor fluorescence lifetime, τ_D, versus transfer efficiency for the C6C74 variant in 8 M urea, pH 2.5. Relative amplitudes are indicated as a color scale. For the subpopulation-specific fluorescence lifetime analysis, only the photons from fluorescence bursts in the region indicated by the dashed box were used to exclude the influence of the population containing no active acceptor dye (“donor-only,” shaded region). [Note that at lower denaturant concentrations, a population corresponding to folded molecules appears (Fig. 2), whose influence on the lifetime analysis can also be excluded in this way.] (B and C) The resulting time-correlated single-photon counting histograms of donor (B) and acceptor (C) emission with residuals below each panel. The donor and acceptor decays were fitted globally based on the distribution of transfer rates resulting from the distance distribution of a Gaussian chain (black lines), with the RMSD as the only free fit parameter apart from the two overall amplitudes for donor and acceptor decays (see Methods for details). (D) The values of the intrachain RMSDs excluding the dye linkers obtained from the mean transfer efficiencies, either from the numbers of donor and acceptor photons, i.e., the transfer efficiency histograms (Fig. 2), (circles) or from the fluorescence lifetime analysis (squares) for all variants of ubiquitin at 8 M urea are plotted as a function of sequence separation between the labeling sites, N_aa. The line corresponds to the equation ${\langle r^2\rangle }^{1/2}=\sqrt{2l_p\hspace{0.17em}b}\hspace{0.17em}{N}_{aa}^{\nu }$, where b = 0.38 nm is the distance between two C^α atoms, and l_p = 0.43 nm and ν = 0.60 are the parameters obtained from the global fit (E). The colors correspond to the different variants of ubiquitin, with the same color code as in Table 1 and Fig. 2. (E) Representative examples of RMSD values from transfer efficiency histograms (including the dye linkers) as a function of N_aa for all ubiquitin variants at 2, 4, 6, and 8 M urea [from light gray to black; note that all urea concentrations from 1.5 to 9.5 M (Fig. 2C) were used for the analysis] with a global fit to ${\langle r^2\rangle }^{1/2}=\sqrt{2l_p\hspace{0.17em}b}\hspace{0.17em}{N}_{aa}^{\nu }$, where l_p was a shared fit parameter for all datasets and ν was allowed to vary with urea concentration. (F) The resulting values of ν as a function of urea concentration. Error bars represent standard errors of the fit.

Finally, because the single-molecule experiments enable us to quantify unfolded-state expansion over a broad range of denaturant concentrations owing to the separation of folded and unfolded subpopulations in transfer efficiency histograms (Fig. 2), we can use the results to quantify the dependence of unfolded-state dimensions on urea concentration. Concentrated solutions of denaturants such as urea and guanidinium chloride are good solvents for unfolded proteins (50, 51); correspondingly, an increase in the denaturant concentration usually leads to an expansion of the unfolded state (3, 4, 41), as we observe here for ubiquitin (Figs. 2 and 3). This expansion can be expressed in terms of a change in the scaling coefficient, ν, that quantifies the dependence of the RMSD, ${\langle r^2\rangle }^{1/2}$, on chain length, N_aa, in scaling laws of the form ${\langle r^2\rangle }^{1/2}=r_0{N}_{aa}^{\nu }$. In bad solvent, ν is expected to be 1/3, in good solvent ∼3/5, and under Θ conditions ∼1/2 (52). Taking advantage of the observation that the prefactor, r₀, for proteins only varies within a narrow range (53) (see Methods for details), we estimated the scaling exponent as a function of urea concentration (Fig. 3). Interestingly, we find a continuous increase of ν from ∼0.5 to ∼0.6 between 1.5 M and 9.5 M urea (Fig. 3), indicating that the expansion of unfolded ubiquitin resembles a transition from Θ conditions to the good solvent regime.

Comparison of Distances Derived from Single-Molecule FRET and Computed Ensembles.

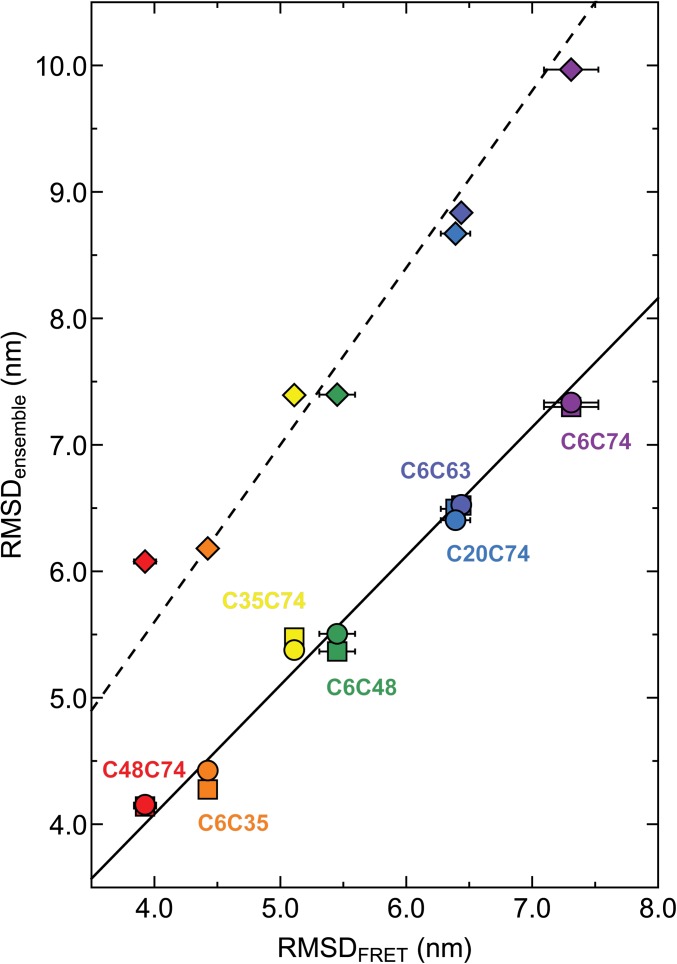
The average distances between amino acids determined by the single-molecule FRET experiments at 8 M urea can be compared directly to distances in the structural ensembles calculated using X-PLOR-NMR. Fig. 4 shows a comparison of the RMSDs between these amino acids in the ensembles versus the respective RMSDs from the single-molecule FRET measurements. For ensembles generated without any experimental restraints, the RMSDs are systematically larger than those from FRET (RMSD_ensemble ≈ 1.40·RMSD_FRET), but still show a correlation coefficient of r = 0.996 with the FRET results. The respective average radius of gyration R_g of the ensemble is 39.3 Å and thus considerably larger than the R_g value from SAXS experiments [28.0 ± 3.5 Å (38)]. Including SAXS or NMR+SAXS restraints reduces R_g to values close to the experiment (SAXS: 28.9 Å; NMR+SAXS: 29.3 Å) and gives excellent agreement with the FRET-derived distances (SAXS: RMSD_ensemble ≈ 1.02·RMSD_FRET, r = 0.988; NMR+SAXS: RMSD_ensemble ≈ 1.02·RMSD_FRET, r = 0.996). The rms deviation between average distances derived from the NMR+SAXS_ensemble and the FRET data is only 1.39 Å. The overall good agreement of distances from the NMR+SAXS-based ensemble and the single-molecule FRET experiments also leads to a good match of the length scaling exponents, ν (NMR+SAXS: 0.61 ± 0.03, FRET: 0.60 ± 0.03; see Methods for details). This indicates that the X-PLOR calculations under experimental restraints reproduce the long-range behavior of a random chain, even in the presence of the local, partially ordered structure evident from the C^α–C^α contact map in Fig. 1.

Fig. 4.

RMSDs obtained from ensemble calculations versus RMSDs obtained from single-molecule FRET measurements (the average values of RMSDs calculated from mean transfer efficiencies and fluorescence lifetime distribution analysis are corrected for dye linker lengths). Ensemble calculations were carried out with NMR and SAXS restraints (circles), only SAXS restraints (squares), or without any experimental restraints (diamonds), respectively. Color-coding corresponds to respective ubiquitin mutants in Table 1 and Fig. 2. The lines represent least-squares fits to the data of the form RMSD_ensemble = m·RMSD_FRET, with m = 1.02 (NMR+SAXS, solid line), 1.02 (SAXS, solid line), 1.40 (no restraints, dashed line).

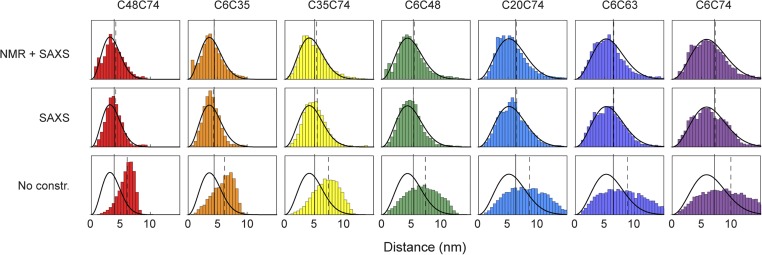
However, not only the average distances in the ensembles calculated under NMR/SAXS or SAXS restraints closely match the FRET-derived distances, but even the distance distributions within the ensembles are remarkably similar to the distance distributions of a Gaussian chain used for the interpretation of the FRET data (Fig. 5). For the NMR/SAXS-restrained ensemble, the distributions agree almost quantitatively. Any remaining small differences may have several causes: (i) genuine specific conformations and local structure induced by the NMR and SAXS data, which are not captured by the simple polymer model used to interpret the FRET observables, (ii) incomplete sampling of conformational space in the calculated ensembles, and (iii) unknown details of the alignment mechanism for RDCs and the incomplete knowledge of dynamics for PREs, which lead to inaccuracies when incorporating them as quantitative restraints (21). Corresponding to their larger average distances (Fig. 4), the distributions obtained from unrestrained ensemble calculations are much more expanded than those from the restrained ensembles or the FRET-based data (Fig. 5). This behavior is expected for unrestrained X-PLOR calculations, because the remaining nonbonded energy terms contain only repulsive van der Waals terms and a database potential for torsion angles (54) without any further attractive interactions.

Fig. 5.

Comparison of C^α–C^α distance distributions derived from restrained ensemble calculations and single-molecule FRET. Bars show C^α–C^α distance distributions from the molecular ensembles calculated under different types of experimental restraints: NMR+SAXS, SAXS, and without experimental constraints (No constr.) (color-coded as in Table 1). Solid black lines depict the distance distributions as obtained from single-molecule FRET measurements for each ubiquitin variant. The vertical black solid and dashed lines indicate the values of RMSDs from FRET measurements and ensemble calculations, respectively.

Reconfiguration Times of the Unfolded-State Ensemble.

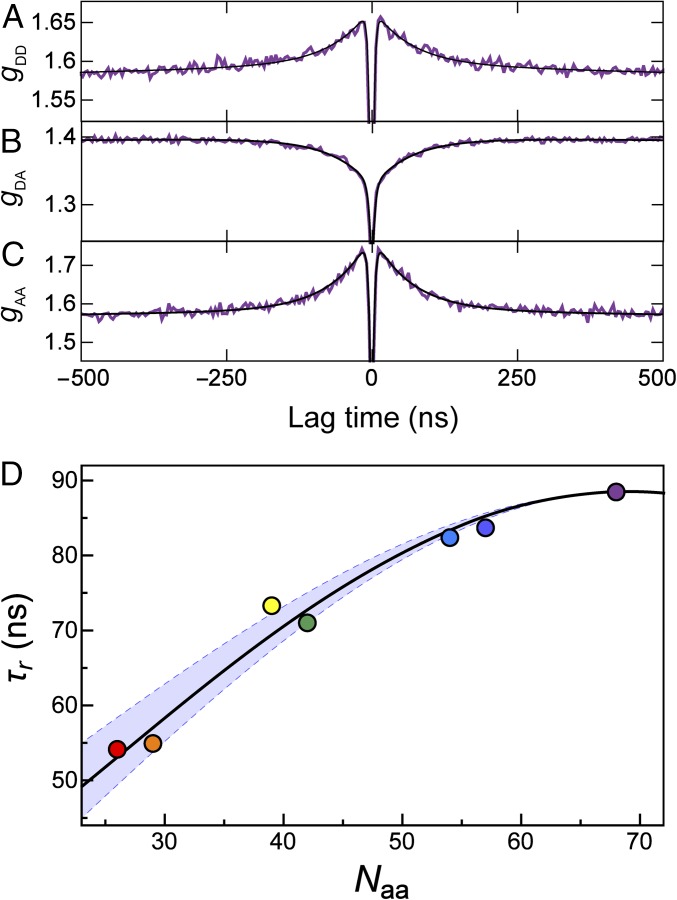
Single-molecule fluorescence spectroscopy additionally allows us to obtain information about the reconfiguration dynamics of unfolded ubiquitin, which is difficult to access with other methods. For this purpose we used nsFCS to determine the distance dynamics between the donor and acceptor fluorophores attached to the protein (30, 35, 55). Because distance fluctuations in the chain are directly connected to intensity fluctuations of the dyes, the decay of the fluorescence intensity correlation function can be related quantitatively to the relaxation of the distance correlation function (i.e., the reconfiguration time of the polypeptide chain) (35, 56, 57). Examples of fluorescence intensity correlation functions for the C6C74 variant of ubiquitin at 8 M urea are shown in Fig. 6 A–C, with the characteristic correlated component in the autocorrelation functions and the anticorrelated component in the donor–acceptor cross-correlation in the submicrosecond range (30). The reconfiguration times, τ_r, for all variants of ubiquitin are found to be in the range of 50 ns to 90 ns (Fig. 6D), similar to the times observed for other denaturant-unfolded proteins or IDPs (30, 31, 35, 58). We also observe a pronounced dependence of τ_r on the sequence separation of the dyes in the different variants of ubiquitin. We compare our results with the prediction from the Rouse model with internal friction (RIF) (30, 59, 60) (black line in the Fig. 6D) and find good agreement between our experimental data and the RIF model with a value for the internal friction time in the range of 10–40 ns. This result indicates a significant contribution of internal friction, slowing down the reconfiguration dynamics of the chain beyond what is expected from solvent friction alone. The value of the internal friction time we observe for ubiquitin in 8 M urea at pH 2.5 is similar in magnitude to that of cold shock protein at ∼4 M GdmCl, pH 7 (30) or spectrin domains between 4 and 8 M GdmCl, pH 7 (58). The molecular origin of internal friction in unfolded proteins is currently unclear; simulations have indicated an important role of dihedral angle rotation (61, 62), but because internal friction is absent in some proteins at very high denaturant concentrations (30, 35), the influence of attractive intrachain interactions (63) and residual structure formation as detected here (Fig. 1) is likely to also contribute.

Fig. 6.

(A–C) nsFCS measurements of the donor–acceptor distance dynamics for the C6C74 ubiquitin variant at 8 M urea. The global fit of donor–donor (A), donor–acceptor (B), and acceptor–acceptor (C) correlations is used to determine the reconfiguration time, τ_r, of the unfolded chain. (D) The resulting reconfiguration times for all variants as a function of sequence separation show distance dynamics of the unfolded chain in the range of 50–90 ns. The black line represents the fit with a modified RIF model, resulting in an internal friction time of τ_i = 25 ns (see Methods for details). The lower and upper bounds of the light blue band are determined by the same fit with internal friction times τ_i = 10 ns and τ_i = 40 ns, respectively. The color code for the variants is the same as in Table 1. Note that the rapid drop in the correlation functions in the low nanosecond range is caused by photon antibunching on the timescale of the excited state lifetime (93) and not related to chain dynamics.

Discussion

We present here a comparative analysis using single-molecule FRET, NMR, and SAXS to characterize the urea-denatured state of ubiquitin at pH 2.5. Using a previously described approach (21), we generated large sets of ensembles, each containing 20 structures restrained by NMR and SAXS data, and compared them to distance information from single-molecule FRET measurements. Chain dimensions were derived from the single-molecule FRET data on seven donor/acceptor pairs in terms of RMSD, ${\langle r^2\rangle }^{1/2}$, using the distance distribution of a simple polymer model as an approximation (32, 41–43, 47). The seven RMSD values show excellent agreement with RMSD values calculated from the atomistic model ensembles that were restrained by NMR and SAXS or SAXS-only data (Fig. 4). Even the distance distributions in the ensembles calculated based on NMR and SAXS restraints agree surprisingly well with the Gaussian chain distance distributions assumed for the interpretation of the FRET data (Fig. 5). Only minor differences exist between the long-range distance distributions of ensembles calculated under NMR+SAXS or SAXS-only constraints, respectively. This observation indicates that the 743 predominantly local NMR restraints can be incorporated into the ensemble structures without disturbing the overall dimensions of the chain. Calculations carried out without experimental restraints show considerably larger average distances and much stronger deviations from the single-molecule FRET data. Thus, the intrinsic X-PLOR force field for the protein bonded and nonbonded interactions (21, 64) does not lead to agreement between the simulated ensembles and the FRET measurements; rather, this agreement has to be enforced by the experimental restraints (Figs. 4 and 5). This is not surprising because the intrinsic X-PLOR force field used contains (besides standard terms for covalent geometry and a conformational database potential for torsion angles) only repulsive van der Waals terms (54), but no attractive interactions such as hydrogen bonding, electrostatics, or hydrophobic effects (65).

The C^α–C^α contacts of the NMR/SAXS-restrained ensembles are very similar to those of previous ensembles restrained only by NMR RDC and PRE data (21). In particular, we observe prominent contacts of about 15% population between T7 and G10 and between L8 and K11, which indicate the respective population of a β-turn at the location of ubiquitin’s native first β-hairpin. This is consistent with earlier findings from ¹⁵N and ¹³C secondary chemical shifts and hydrogen bond scalar couplings of a ∼10–20% population of this β-hairpin even in 8 M urea at pH 2.5 (20). In addition, many further medium to strong (∼5–10%) i to i+4 C^α–C^α contacts are observed throughout the entire protein sequence (Fig. 1), comprising the native helix in the region of residues 21–31 as well as in the C-terminal half. The location of both the β-hairpin and helical propensities are reminiscent of ubiquitin’s A-state induced at low pH and ∼60% methanol (28, 66, 67). However, in the A-state, these secondary structure elements have significantly higher average populations (67). Fig. 1 also shows the presence of residual long-range, native-like contacts in the urea-denatured state at the level of about 1%, which is consistent with a bias required for directing the folding process to the native state (1). The good agreement of the single-molecule FRET-based distance distributions with the NMR/SAXS-restrained ensembles illustrates that such local and residual long-range structure is not inconsistent with the global properties based on simple polymer models (65, 68). We also note that the range of segment lengths accessible to PRE and FRET experiments is complementary. Whereas quantifiable PRE effects for highly unfolded ubiquitin are limited to segments of up to ∼20 residues (21) [corresponding to an average distance of 3.5 nm (Fig. 3D)], single-molecule FRET can only probe segments above this length quantitatively given the typical Förster radii of ∼5–6 nm.

Solution NMR provides only limited information on the long-range reconfiguration dynamics of the unfolded protein ensemble. Rotational diffusion of the polypeptide chain makes dynamics unobservable via dipolar, chemical shift anisotropy, or quadrupolar relaxation on timescales longer than the rotational time (69). Recently, Parigi et al. (70) have shown by ¹H T₁ relaxation dispersion that a number of IDPs exhibit long-range rotational correlation times in the one-digit nanosecond range, which are comparable to folded proteins of similar size. For urea-denatured ubiquitin, ¹⁵N relaxation data (71) indicate an isotropic reorientation of the N-H vectors, which is considerably faster than the rotational correlation time of 4 ns for folded ubiquitin (72). However, slower microsecond motions are evident from chemical exchange line broadening effects for residue T9 in the first β-turn, presumably corresponding to the transient formation of local secondary structure.

Information on long-range dynamics of unfolded proteins from NMR on the timescale of tens of nanoseconds to microseconds has thus been missing for denatured proteins. Here we fill this gap with nsFCS (30, 35), which determines the dynamics of long-range distance fluctuations between the fluorophores attached to the protein. In contrast to NMR relaxation, the FRET-based distance fluctuations observed by nsFCS are not affected by rotational diffusion of the chain if the relative rotational decorrelation of donor and acceptor is faster than the fluorescence lifetime (31, 35). Chain reconfiguration for the polypeptide segments of ∼30 and 70 residues of unfolded ubiquitin occurs on a timescale of 50–90 ns (Fig. 6), despite the residual structure evidenced by NMR. This residual structure may make an important contribution to the internal friction we quantified by analyzing the segment-dependent dynamics with the RIF model (30, 59) (Fig. 6D). The timescales derived from correlation spectroscopy agree with the observation that (with the exception of the first β-hairpin) the NMR spectra of unfolded ubiquitin are mostly in fast chemical exchange (39, 71), that is, the interconversion between all conformations is considerably faster than the microsecond timescale of chemical shifts. The NMR observables (i.e., chemical shifts, scalar couplings, RDCs, PREs, and other relaxation rates) are thus averages over all conformations (8).

Owing to these fast global reconfiguration dynamics, the expansion of the unfolded state with increasing concentration of urea is observed to be continuous, as reflected by a gradual shift in transfer efficiency (Fig. 2). This finding is in agreement with previous NMR results (73) showing that most resonances of the unfolded ubiquitin population shift continuously between 8 M and 2 M urea concentration and thus are in fast exchange over the entire urea concentration range. However, below about 3 M urea, a second set of NMR resonances becomes detectable that corresponds to native ubiquitin (73), in accord with the second population detected in the single-molecule FRET efficiency histograms (Fig. 2A). Both the NMR data and the single-molecule FRET efficiency histograms show that this folded state is in slow exchange with the unfolded state on a timescale larger than milliseconds. The previous NMR and SAXS data could be described well by a model in which about 30 urea molecules interact as H-bond acceptors with the ubiquitin backbone at 8 M urea, thereby expanding the chain (73). In particular, the continuous chemical shift changes for unfolded ubiquitin in the range of 2 M to 8 M point to a continuous increase in urea binding and chain expansion. This agrees well with the chain expansion observed by the FRET data for increasing amounts of urea, which can be described in terms of an effective weak binding model (74) (Fig. 2C). Although direct H-bond interactions with the backbone explain the data well, the exact mechanism of urea-induced denaturation is still under debate (75–78). We note that, based on time-resolved SAXS experiments, unfolded-state collapse of ubiquitin upon jumping from high to low denaturant concentration has been controversial [as for other proteins (36)], with some reports supporting (79, 80) and others contradicting collapse (81). Our results favor the former, but the extent of collapse can of course depend on the solution conditions and the net charge of the chain (53, 82). Resolving this controversy will require further concerted efforts involving a direct comparison of the different methods, either using time-resolved ensemble methods or proteins that remain unfolded even at low denaturant concentrations (83, 84).

In summary, we observe good agreement between distance distributions for unfolded ubiquitin derived from single-molecule FRET and NMR/SAXS-restrained ensembles. The consistency between these orthogonal approaches strongly validates these distance parameters and the underlying computed ensembles. NMR, SAXS and single-molecule FRET data are highly complementary. NMR yields exquisite details on mostly local structural propensities and dynamics, and even residual short- and long-range interactions that are only populated in the low percent range within unfolded protein states are detectable. However, the overall dimensions of the unfolded-state ensemble are difficult to define by NMR restraints alone. SAXS data can fill this gap and help to constrain the overall shape of the unfolded-state molecular ensemble. As in the case of most ensemble methods, however, a quantitative analysis is usually limited to conditions where the protein is fully unfolded, because the combined contributions of changes in unfolded-state dimensions and relative populations of folded and unfolded states to the scattering signal is difficult to disentangle. Single-molecule FRET, finally, provides relatively coarse-grained information in the form of average intramolecular distances and distance distributions that are often suitably captured by polymer-physics-based models (31) but cannot resolve the presence of local or transiently formed secondary structure. However, because it is a single-molecule method, conformational heterogeneity can often be resolved, enabling subpopulation-specific analysis; in the case of unfolded proteins, for example, the properties of the unfolded state can be determined even in the presence of folded molecules, and the range of accessible denaturant concentrations can thus be extended compared with ensemble methods. Additionally, segment-specific intramolecular distance information and chain reconfiguration times in the submicrosecond range are accessible, which cannot be obtained by either NMR or small angle scattering methods. Combining this information thus enables us to arrive at the currently most comprehensive description of the structural and dynamic properties of an unfolded protein. Our work thus paves the way for using restraints from all three methods for modeling unfolded states. We expect this type of integrated approach to be ideally suited both for reaching a deeper understanding of the role of unfolded state structure and dynamics in protein folding and for linking the conformational and dynamic properties of IDPs to their cellular functions (61, 62, 85, 86).

Methods

Protein Expression, Purification, and Labeling.

Seven double-cysteine variants (K6C-R74C, K6C-K63C, S20C-R74C, K6C-K48C, G35C-R74C, K6C-G35C, and K48C-R74C) of ubiquitin (Table 1) were generated by site-directed mutagenesis from single-cysteine mutants produced previously for MTSL labeling and subsequent PRE measurements (21). The variants were expressed and purified in ¹⁵N-labeled form as described before (21) and prepared as stock solutions of 400 μM protein, 50 mM sodium acetate, and 10 mM tris(2-carboxyethyl)phosphine, pH 4.6. The structural integrity of the mutants under these native-state conditions was verified by comparison of their ¹H-¹⁵N heteronuclear single-quantum correlation NMR spectra to wild-type ubiquitin. Stock solutions were then aliquoted and frozen for later use.

Table 1.

Sequences of the seven ubiquitin variants used in this work

The variant names are colored according to the color code used for the corresponding data throughout the paper. The cysteine residues used for FRET labeling are highlighted in red.

Ubiquitin variants C20C74 and C35C74 were labeled with Alexa Fluor 488 maleimide (Invitrogen) at a dye:protein molar ratio of 0.7:1 for 2 h at room temperature (using ∼200 μL of 0.5 mM protein solutions), and subsequently with Alexa Fluor 594 maleimide (Invitrogen) at a dye:protein molar ratio of 2:1 for 16 h at 4 °C. Unreacted dye was removed by gel filtration with a Superdex Peptide 10/300 GL column (GE Healthcare) in 100 mM sodium phosphate buffer, pH 7.1, and 6 M guanidinium chloride. The resulting sample contained ubiquitin labeled with Alexa Fluor 488 and 594, and ubiquitin doubly labeled with either Alexa Fluor 488 or Alexa Fluor 594, as shown by mass spectrometry. To increase the fraction of FRET-labeled protein for the other variants, purified ubiquitin was first labeled with Alexa Fluor 594 maleimide in 100 mM sodium phosphate buffer, pH 7.1, and 6 M guanidinium chloride, at a dye:protein molar ratio of 0.7:1 for 2 h at room temperature. Unreacted dye was removed by gel filtration using a Superdex Peptide 10/300 GL column (GE Healthcare) in 20 mM Tris⋅HCl and 4 mM DTT, pH 8.0. Singly labeled ubiquitin was separated from unlabeled and doubly labeled protein with ion exchange chromatography using a Mono Q 5/50 GL column (GE Healthcare). Labeled protein was eluted with a linear gradient of 0–1 M NaCl in 20 mM Tris⋅HCl and 4 mM DTT, pH 8.0. The fractions containing singly labeled ubiquitin were further labeled with Alexa Fluor 488 after concentration by ultrafiltration (Amicon Ultra, molecular-weight cutoff 3 kDa; Merck Millipore). Twofold excess of Alexa Fluor 488 was reacted with protein singly labeled with Alexa Fluor 594 in 100 mM sodium phosphate buffer, pH 7.1, and 6 M guanidinium chloride for 2 h at room temperature or overnight at 4 °C. After removal of the free unreacted dye, doubly labeled ubiquitin was separated by ion-exchange chromatography, as described above. The resulting sample mainly contained ubiquitin labeled with Alexa Fluor 488 and 594, as confirmed by mass spectrometry. Approximately 100 nmol of unlabeled protein were subjected to the labeling reaction per variant, and ∼10 nmol of pure doubly labeled protein were obtained.

Single-Molecule Fluorescence Spectroscopy.

Observations of single-molecule fluorescence were made using a MicroTime 200 confocal microscope equipped with a HydraHarp 400 counting module (PicoQuant) and an Olympus UplanApo 60×/1.20W objective. Alternating excitation of the dyes was achieved using pulsed interleaved excitation (87). The wavelength range used for acceptor excitation was selected with a z582/15 band-pass filter (Chroma) from the emission of a SC-450-4 supercontinuum fiber laser (Fianium) driven at 20 MHz, which triggers the 485-nm pulsed diode laser (LDH-D-C-485; PicoQuant) used for donor excitation. Emitted photons were collected through the microscope objective, focused onto a 100-μm pinhole, and then separated into four channels with a polarizing beam splitter and two dichroic mirrors (585DCXR; Chroma). Photons were additionally filtered by band-pass filters (ET525/50M and HQ650/100; Chroma) before being focused onto one of four single-photon avalanche detectors (SPADs) (Optoelectronics SPCM AQR-15; PerkinElmer or τ-SPADs; PicoQuant).

Samples of labeled protein were diluted from concentrations of ∼2–5 μM (in 6 M GdmCl and 100 mM sodium phosphate, pH 7.1) to a concentration of ∼25–50 pM in measurement buffer (10 mM glycine-HCl, pH 2.5, with concentrations of urea as indicated). Note that despite the low pH, the fluorescence quantum yields of the dyes are essentially unchanged compared with neutral pH (82). We used doubly recrystallized urea for the preparation of single-molecule buffers to minimize fluorescence background often present in commercially available urea. To reduce photobleaching of the chromophores and increase the brightness of the dyes, the photoprotective additive β-mercaptoethanol (143 mM) was added; 0.001% Tween 20 (Pierce) was included to prevent surface adhesion of the protein. All measurements were performed by exciting the donor dye with a laser power of 100 μW (measured at the back aperture of the objective). The power used for directly exciting the acceptor dye was adjusted to match the intensity of donor emission (50–70 μW). Measurements were performed by placing the confocal volume at an axial position 50 μm into the solution relative to the cover slide surface, with an acquisition time of 30 min each.

For the identification of fluorescence bursts caused by proteins diffusing through the confocal volume, we used only the photons detected after donor excitation (i.e., detected in time intervals of ∼25 ns following pulses from the 485-nm diode laser). Successive photons separated by interphoton times <100 μs were combined into one fluorescence burst. Only the bursts with a total number of photons >80, detected after donor excitation, were used for further analysis. Transfer efficiencies for each burst were calculated according to $E=n_A/(n_A+n_D)$, where $n_D$ and $n_A$ are the number of photons detected in the donor and acceptor detection channels, respectively, corrected for background, acceptor direct excitation, channel cross-talk, differences in detector efficiencies, and quantum yields of the dyes (88). The changes in refractive index caused by increasing concentrations of urea were measured with a digital Abbe refractometer (Krüss) and were used to recalculate the Förster radius (R₀) for every set of solution conditions. A value of R₀ in the absence of urea of 5.4 nm was used (41). Fluorescence anisotropies (determined for all urea concentrations based on the polarization-sensitive detection in the single-molecule instrument) were between 0.06 and 0.16 for the donor and between 0.04 and 0.13 for the acceptor, indicating rapid orientational averaging of the fluorophores (i.e., κ² ≈ 2/3), as usually observed for unfolded proteins (13, 55).

Determining RMSDs from Mean Transfer Efficiencies.

The calculation of the root-mean-squared distances of unfolded protein chains from the measured mean transfer efficiencies was performed assuming an interdye distance distribution of a Gaussian chain (32, 43, 47). Experimentally determined mean transfer efficiencies of the unfolded state can be calculated from a dye-to-dye distance distribution, P(r), according to

$$\langle E\rangle ={\displaystyle {\int }_0^{l}E\left(r\right)P\left(r\right)dr}/{\displaystyle {\int }_0^{l}P\left(r\right)dr},$$ [1]

with $E\left(r\right)=1/\left(1+{(r/R_0)}^6\right)$, where l is the contour length of the chain. The probability density function for the end-to-end distance of a Gaussian chain is

$$P\left(r\right)=4\pi r^2{\left(\frac{3}{2\pi \langle r^2\rangle }\right)}^{3/2}exp\left(-\frac{3r^2}{2\langle r^2\rangle }\right).$$ [2]

Given a measured value of $\langle E\rangle$, the RMSD, ${\langle r^2\rangle }^{1/2}$, can be calculated numerically. Note that an alternative analysis using Sanchez theory based on a reweighted Flory–Fisk distribution (42, 53, 89) instead of a Gaussian chain distribution resulted in very similar results (ΔRMSD ≤ 0.1 nm), supporting the robustness of our results with respect to the distance distribution used, as previously shown for other unfolded proteins and IDPs (46, 47).

The scaling of the RMSD with chain length was analyzed based on the equation ${\langle r^2\rangle }^{1/2}=r_0{N}_{aa}^v$ (52), where in the prefactor, $r_0=\sqrt{2l_{p}b}$, l_p is the persistence length, b is the peptide segment length of 0.38 nm, and ν is the length scaling exponent. For the analysis of the RMSD values as a function of the number of peptide segments, N_aa, and urea concentration based on the single-molecule FRET data (Fig. 3), l_p was used as a global fit parameter, resulting in l_p = (0.43 ± 0.04) nm. The values of ν given for the FRET-based and the constrained-ensemble-based data at 8 M urea were obtained using this value of l_p; the corresponding uncertainties given for ν reflect the change in ν resulting from the fit when l_p is varied in a range from the lower bound of l_p observed experimentally for proteins in high concentrations of denaturant (90) (l_p = 0.33 nm) to the average value for folded proteins (91) (l_p = 0.53 nm) (53). The RMSDs determined from the analysis of the FRET data include the length contribution from the dye linkers. For comparing the RMSDs of the chain segment probed between FRET and ensemble calculations at 8 M urea (Figs. 4 and 5), the ${\langle r^2\rangle }^{1/2}$ values from FRET were corrected for the linker length using ${\langle r^2\rangle }^{1/2}=\sqrt{2l_p\hspace{0.17em}b}\hspace{0.17em}\mathrm{\cdot }{N}^{0.6},$ where N = N_aa+L is the sequence length of the interdye segment, comprising both the number of peptide bonds, N_aa, and the contribution from both dye linkers, L. L was previously estimated to be equivalent to an additional nine amino acids (43, 53). A global analysis of the transfer efficiencies for all ubiquitin variants at all urea concentrations investigated (Figs. 2 and 3), with L as a free fit parameter, resulted in L = 9 ± 2 (uncertainty from varying l_p between 0.33 and 0.53 nm), supporting this estimate.

Subpopulation-Selective Fluorescence Lifetime Distribution Analysis.

Fluorescence lifetime analysis provides a way of quantifying distance distributions in unfolded proteins orthogonal to the analysis of burst-averaged ratiometric transfer efficiencies (43, 49). For a subpopulation-selective analysis, we use the following procedure. In a first step, for every fluorescence burst, the mean donor fluorescence lifetime was estimated from the average arrival time of the photons in each burst relative to the exciting laser pulse (92). From the resulting 2D histograms of estimated fluorescence lifetime versus ratiometrically determined transfer efficiency (43, 49), we selected the bursts corresponding to the unfolded state and, by using the combined photon counts from all unfolded molecules, obtained subpopulation-specific fluorescence intensity decays (Fig. 3 A–C). To avoid the common problem of overparameterization and numerical instability in this type of analysis, distance distributions, P(r), of polymer physics-based models can be used, as described previously (43). Here, we used the P(r) of a Gaussian chain (Eq. 3), which is uniquely defined by ${\langle r^2\rangle }^{1/2}$ as the only free parameter (43). The applicability of the Gaussian chain approximation is further supported by the agreement of the corresponding shapes with the distance distributions from the X-PLOR-NIH–derived ensembles (Fig. 5). Additional stability of the fit is achieved by analyzing donor and acceptor decays in a global fit based on the distribution of transfer rates resulting from the distribution of donor–acceptor distances (43, 49). Especially the rise in the acceptor intensity at early times provides a stringent additional constraint. Apart from ${\langle r^2\rangle }^{1/2},$ the only other fit parameters were the two overall amplitudes of the donor and acceptor decays. Acceptor direct excitation and cross-talk of donor emission into the acceptor detection channel were taken into account as previously described (43). Intrinsic donor and acceptor fluorescence intensity decay rates were determined independently and constrained in the fits (k_D = 0.275 ± 0.005 ns⁻¹ and k_A = 0.250 ± 0.005 ns⁻¹ at 8 M urea). Uncertainties in the RMSD values determined by this method (Fig. 3D) were obtained by taking into account the uncertainty of the donor fluorescence intensity decay rate in the absence of the acceptor.

nsFCS Measurements.

nsFCS measurements were performed in samples with a protein concentration of ∼2 nM, with the 485-nm diode laser operating in continuous-wave mode (100 μW) and with typical data acquisition times of 12–16 h to achieve sufficient statistics for interphoton times in the submicrosecond range (35, 55). All measurements were performed in 10 mM glycine-HCl, 8 M urea, pH 2.5, 143 mM β-mercaptoethanol, and 0.001% Tween 20. Autocorrelation curves of acceptor and donor channels and cross-correlation curves between acceptor and donor channels were calculated from the measurements as described previously (35, 55). The data for delay times up to 4 μs were fit with

$$g_{ij}\left(\tau \right)=1+\frac{1}{\langle N\rangle }\left(1-c_{AB}{e}^{-\frac{\tau -t_0}{{\tau }_{AB}}}\right)\left(1+c_{CD}{e}^{-\frac{\tau -t_0}{{\tau }_{CD}}}\right)\left(1+c_T{e}^{-\frac{\tau -t_0}{{\tau }_T}}\right),$$ [3]

where $i,\hspace{0.17em}j=A,\hspace{0.17em}D$ and 〈N〉 is the mean number of molecules in the confocal volume. The three multiplicative terms describe the contributions of photon antibunching (93) (AB), chain dynamics (CD), and triplet blinking of the dyes (T) with amplitudes c_AB, c_CD, and c_T and relaxation times τ_AB, τ_CD, τ_T, respectively. The three correlation curves from each measurement were fit globally with τ_CD and the time origin, t₀, as shared fit parameters. The amplitudes and the relaxation times of the antibunching and triplet components were fit with a free independent decay component for each correlation curve as described previously (30).

The analysis of our experimental data with the RIF model (30, 59, 60) was performed as described previously (30). Briefly, the effect of internal friction on the reconfiguration time of the chain, τ_r, is included in the model as an additional timescale, τ_i, as τ_r = τ_s + τ_i, where τ_s is the reconfiguration time of the ideal chain without internal friction. According to the RIF model, τ_s depends on the length of the segment probed owing to the length-dependent relaxation modes in polymer reconfiguration dynamics (30, 59, 94), but τ_i is independent of segment length. Fluorophores and linkers were taken into account explicitly and modeled as additional beads connected to the polymer chain via harmonic springs. We then calculated the reconfiguration times of the unfolded ubiquitin chain as a function of the segment length probed and adjusted the internal friction time, τ_i, to optimize the fit of the model to the experimental data (30). We note that based on this analysis the timescale of the dynamics within the linker segment of the dyes is approximately two orders of magnitude faster than the end-to-end dynamics of the polypeptide chain (30), implying a minor effect on the observed chain dynamics.

Ensemble Calculations.

Structural ensembles of urea-denatured ubiquitin were calculated by the program X-PLOR-NIH, version 2.39 (64), using protocols described previously (21) with standard X-PLOR force fields including a conformational database potential for torsion angles and repulsive-only van der Waals terms (54). The ensemble calculations used experimental restraints in different combinations derived from 419 RDCs (nine different types) and 256 PREs published previously (20, 21) that were supplemented by 71 backbone ³J_HNHα-couplings (40) and SAXS data (38). To speed up the calculation, the SAXS scattering curves were approximated by a 25-point spline fit. Unlike in the earlier work (21), where PRE restraints were introduced in a hypothetical mutant of ubiquitin containing all eight MTSL-labeled cysteines in a single molecule, the PRE restraints were introduced as originating from the C^β atoms or, in the case of glycine, from the C^α atom, of the respective native amino acids in native ubiquitin. Annealing results were independent of initial conformations (extended, folded, or random). Ensemble calculations were carried out using different combinations of restraints: (i) NMR and SAXS, (ii) SAXS only, and (iii) no experimental restraints, which served as a control. Even though an ensemble size of 10 conformers (21) was sufficient to match all experimental NMR and SAXS data within the expected error, larger ensembles led to increased convergence of the intrachain distance distributions, presumably because larger ensembles result in reduced correlations between multiple restraints that need to be matched by an individual conformer. Hence, all calculations were carried out using ensemble sizes of 20 as a compromise between accuracy and computational cost. A total of 800 ensembles with 20 conformers were calculated for each of the restraint sets, out of which the 50% lowest energy ensembles (8,000 total structures) were selected for further statistical analysis.