Origin of embrittlement in metallic glasses

Significance

Annealing embrittlement of metallic glasses is widely recognized as detrimental to their technological advancement, yet lacks fundamental understanding. Here, we identify a one-to-one correspondence between fracture toughness and shear modulus, which points to a correlation between liquid fragility and annealing embrittlement sensitivity. From a scientific perspective, this finding provides a thermodynamic and structural origin of annealing embrittlement, revealing that lower potential energy glass states having higher flow barriers and atomic structures with higher degree of order will demonstrate a lower fracture toughness. From a technological perspective, this result suggests that fragile glass formers would be more prone to annealing embrittlement compared with stronger glass formers, and as such, their fracture toughness would be more sensitive to their processing history.

Abstract

Owing to their glassy nature, metallic glasses demonstrate a toughness that is extremely sensitive to the frozen-in configurational state. This sensitivity gives rise to “annealing embrittlement,” which is often severe and in many respects limits the technological advancement of these materials. Here, equilibrium configurations (i.e., “inherent states”) of a metallic glass are established around the glass transition, and the configurational properties along with the plane-strain fracture toughness are evaluated to associate the intrinsic glass toughness with the inherent state properties and identify the fundamental origin of embrittlement. The established correlations reveal a one-to-one correspondence between toughness and shear modulus continuous over a broad range of inherent states, suggesting that annealing embrittlement is controlled almost solely by an increasing resistance to shear flow. This annealing embrittlement sensitivity is shown to vary substantially between metallic glass compositions, and appears to correlate well with the fragility of the metallic glass.

Unlike conventional oxide glasses, metallic glasses can be considerably tougher, often approaching values typical of engineering metals. Specifically, the toughness of metallic glasses can vary from values as high as 150–200 MPa·m^1/2 (1, 2), comparable to low-carbon steels, to as low as 2–3 MPa·m^1/2 (3, 4), which is more typical of oxide glasses. But, like any glass, metallic glasses tend to embrittle when annealed around the glass transition, as evidenced by a measurable drop in their toughness and their capacity to deform plastically. This phenomenon, typically referred to as annealing embrittlement, has broad scientific and technological ramifications. From a technological perspective, annealing embrittlement is at least partly responsible for the large variability in toughness observed when the glass is quenched at different cooling rates (5–7), thereby limiting their mechanical performance and engineering reliability. From a physics perspective, the physical origin of annealing embrittlement is still a topic of debate and controversy that is far from being settled, as varying and contradictory theories have been proposed by various groups over the years.

Wu and Spaepen (8) made the first attempt to relate the toughness of the metallic glass to its structure. They postulated that annealing embrittlement is associated with a reduction in “free volume” in the glass atomic structure as it is relaxed at incrementally lower temperatures, degrading its capacity for plastic rearrangement and flow. Their concept has been adopted by several other groups (9–11). In recent years, an alternative concept has emerged linking the toughness of the metallic glass to its elastic constants, particularly to the ratio of the bulk to shear modulus (or equivalently to Poisson’s ratio). This ratio is used to relate the resistances to cavitation and shear flow, respectively (12). Unlike free volume, the elastic constants of the glass are experimentally accessible so that this newer concept may be experimentally corroborated. Following this approach, one would expect annealing embrittlement to be associated with an increasing shear modulus, a decreasing bulk modulus, or a decreasing Poisson’s ratio. It was indeed found that as the glass relaxes at temperatures around the glass transition, the drop in toughness is associated with changes in the elastic constants, and particularly the shear modulus (13, 14). More recently Kumar et al. (15) proposed yet one more theory, pointing to a sharp drop in bending ductility at a well-defined annealing temperature as evidence of a thermodynamic transition controlling annealing embrittlement. Lastly, the modeling work of Rycroft and Bouchbinder (16) is notable, where a shear transformation model of amorphous plasticity is coupled with a condition for cavitation to effectively simulate annealing embrittlement.

When a glass is relaxed near the glass transition for sufficiently long time, an equilibrium liquid configuration is attained, often referred to as an “inherent state.” Quenching the equilibrium liquid freezes in such equilibrium configurations in the glass, where they give rise to properties (e.g., moduli, specific volume, etc.) that are unique and reversible. Thus, each of these properties is consistent with the definition of a state variable for thermodynamic equilibrium (17, 18). The fracture toughness of any material at the limit where it becomes size-independent (at the limit where the crack propagates in plane strain) is thought to be an intrinsic material property. It was recently shown that when the size requirements for plane-strain conditions and fracture toughness validity (according to ASTM standard E399) are met for a metallic glass, its fracture toughness value approaches a well-defined constant value (19). For an equilibrium glass configuration, one expects the “intrinsic” size-independent fracture toughness of a metallic glass to be consistent with the definition of an “inherent-state” property. As such, the intrinsic fracture toughness is expected to be uniquely associated with a specific equilibrium configuration, and to scale with other inherent state properties of that configuration (e.g., shear modulus, density, viscosity, etc.). A few studies have attempted to explore such fundamental relationships by correlating parameters that relate to fracture toughness (e.g., impact toughness or bending ductility) to inherent-state variables (e.g., configurational enthalpy or Poisson’s ratio) (10, 15). However, samples in those studies were either insufficiently relaxed to have attained thermodynamic equilibrium (10) or not sufficiently large to alleviate size effects on toughness (15). Thus, such fundamental relations may have been missed or obscured. Here, we seek to establish a fundamental correspondence between fracture toughness and inherent state that could reveal the underlying origin of embrittlement in metallic glasses. To ensure states of near-thermodynamic equilibrium, high-purity fully amorphous samples with size and geometry consistent with the E399 ASTM standard were produced and fully relaxed at well-defined temperatures in the equilibrium supercooled liquid regime.

Equilibrium configurational states of Zr₃₅Ti₃₀Cu_8.25Be_26.75 glass are carefully characterized at annealing temperatures near the glass transition for inherent-state properties and plane-strain fracture toughness. Fatigue-precracked rectangular beam samples were used to accurately evaluate the intrinsic fracture toughness. To establish near-thermodynamic equilibrium at a given temperature, each sample was annealed incrementally over multiple time steps followed by rapid quenching to room temperature. At each time step, the sound velocities and density ρ were measured and the shear modulus G, bulk modulus B, and Poisson’s ratio ν were calculated. An equilibrium state is assumed to be established when the modulus change with further annealing at constant time intervals is within the measurement error. Annealing temperatures from 40 degrees above/below the glass transition temperature of ∼573 K were considered to explore a sufficiently broad range of inherent states. Details on the measurements of the elastic constants and density are presented in Materials and Methods.

Fracture toughness tests were conducted in a three-point bending configuration using single-edge notched (precracked) beams in accordance with ASTM E399. Size requirements for both K-validity and plane-strain conditions were largely satisfied to rule out any effects of size and geometry on the intrinsic fracture toughness. For a linear-elastic K_IC measurement, the crack-tip plastic-zone size must be typically an order of magnitude smaller than (i) the in-plane dimensions of the crack length a and the remaining uncracked ligament b (a condition of small-scale yielding), and (ii) the out-of-plane specimen thickness dimension B (a condition of plane strain); this is generally written as a, b, B> 2.5 (K_IC/σ_y)², where σ_y is the yield strength. Using the average measured σ_y of 1,700 MPa (which was found not to vary appreciably between equilibrium states), the sample size (a, b, B ≈ 3.5 mm) is sufficient to meet fracture-mechanics requirements for a valid K_IC measurement (i.e., for valid stress intensity K-dominated crack-tip fields and/or for plane-strain constraint) if the measured toughness K_Q does not exceed ∼64 MPa·m^1/2. More details on the fracture toughness measurements can be found in Materials and Methods.

Processing and preparation of the samples was performed in a controlled manner to rule out any influence of extrinsic parameters such as crystallinity, oxygen, impurities, inclusions, or residual stresses on toughness. Specifically, to circumvent the adverse effects on toughness of either inclusions or crystallinity, the alloy ingots were prepared using high-purity elements with low oxygen content, alloyed under an ultrapure Ti-gettered inert atmosphere. The test samples were carefully inspected by X-ray diffraction (XRD) and differential scanning calorimetry to ensure the absence of detectable crystallinity. Long-range residual stresses arising in as-quenched samples, which may substantially influence toughness, were effectively eliminated by extensively grinding down cylindrical rods to obtain rectangular beams. The precracks were generated near the centerline of the original rods where residual stresses are expected to be near zero. Lastly, to obtain an accurate representation of the average configurational properties ahead of and in the plane of the crack tip, the ultrasound measurements were taken in the region just ahead of the crack tip and through the sample thickness. More details on the processing and preparation of samples can be found in Materials and Methods.

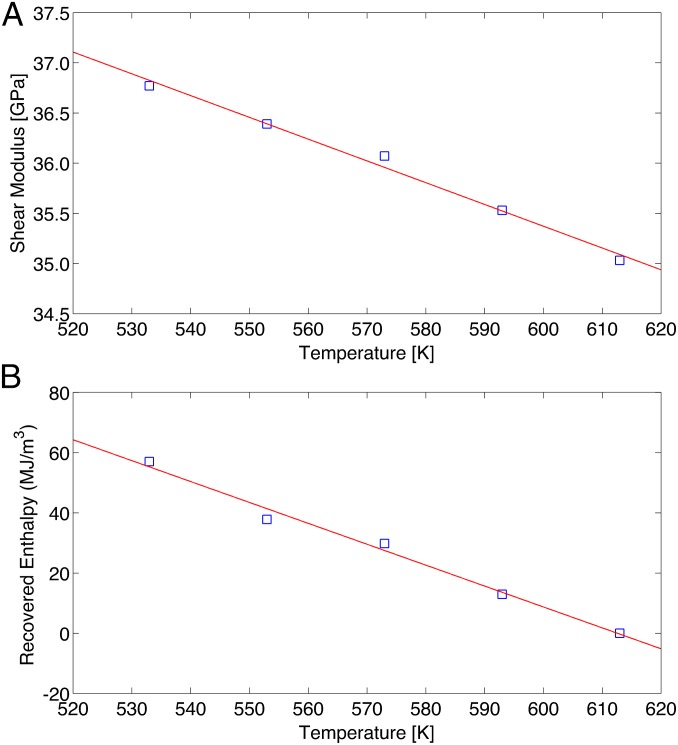
The measured ρ, G, B, and ν values associated with the relaxed states at temperatures T_R of 533, 553, 573, 593, and 613 K are listed in Table 1. G is shown to decrease systematically with annealing temperature, as expected (20–22). The decrease in G of ∼5% is considerably outside the measurement error. On the other hand, B changes by just ∼0.3%, roughly within the measurement error. Therefore, G more closely tracks the transitions between inherent states compared with B, and is regarded here as the state variable that best characterizes the inherent state for each equilibrium configuration. This has also been verified by simulations, where it was determined that local atomic order in the glass structure strongly influences the transverse correlations of shear forces, which determine G, but does not significantly affect the atomic pressure correlations which determine B (23). By plotting G vs. T_R in Fig. 1A, an expected near-linear trend emerges (17, 21) with a slope of –21.7 MPa/K. Data for the recovered enthalpy ∆H associated with each relaxed state are listed in Table 1. ∆H is directly related to the configurational energy of the glass; the larger the ∆H value, the lower the configurational energy of the glass (21). In Fig. 1B ∆H is plotted against T_R. Like G, ∆H decreases very systematically and consistently with T_R over a broad range. Fig. 1 A and B points to a one-to-one correspondence between G and ∆H (20), arising as G and ∆H decrease correspondingly by relaxing to increasingly higher and shallower potential energy basins in the potential energy landscape.

Table 1.

Data for the density ρ, shear modulus G, bulk modulus B, Poisson’s ratio ν, recovered enthalpy ΔH, fracture toughness K_IC, and rough zone width L_rough for amorphous Zr₃₅Ti₃₀Cu_8.25Be_26.75 in various relaxed states at temperatures T_R

TR, K	ρ, kg/m3	G, GPa	B, GPa	ν, —	∆H, MJ/m3	KIC, MPa·m1/2	Lrough, mm
533	5,372	36.77 ± 0.04	105.0 ± 0.33	0.3433	57.0	24.7	0.266
553	5,378	36.39 ± 0.03	105.8 ± 0.18	0.3457	37.8	25.8	0.315
573	5,376	36.07 ± 0.04	105.8 ± 0.27	0.3469	29.8	35.9	0.566
593	5,373	35.53 ± 0.07	105.6 ± 0.17	0.3488	12.9	60.9	0.899
613	5,367	35.03 ± 0.15	105.4 ± 0.30	0.3505	0	74.4	1.28

Fig. 1.

(A) Shear modulus G vs. relaxation temperature T_R, (B) recovered enthalpy ΔH vs. relaxation temperature T_R, for equilibrium configurational states of Zr₃₅Ti₃₀Cu_8.25Be_26.75 glass. Solid lines are linear fits through the data.

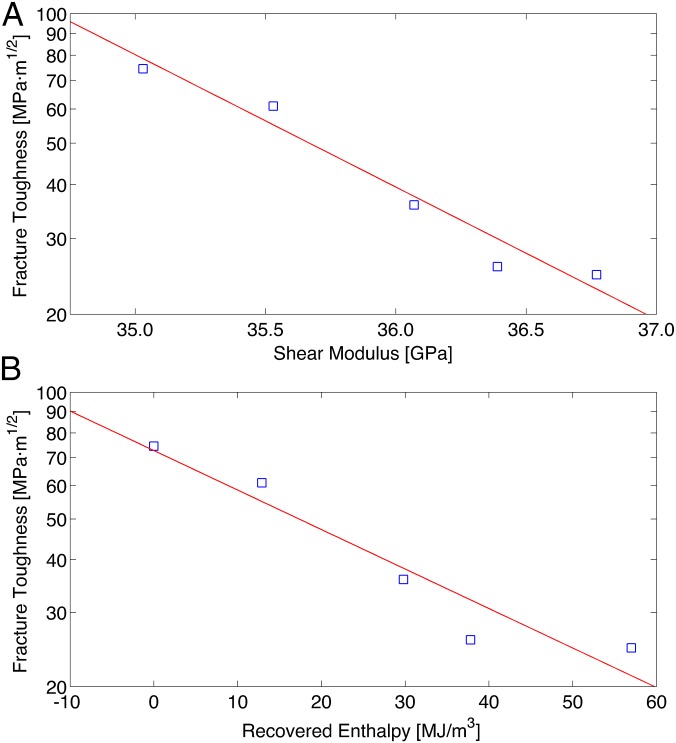
The critical stress intensity K_Q obtained at each relaxed state is listed in Table 1. K_Q varies broadly from about 25 MPa·m^1/2 to about 75 MPa·m^1/2 over the T_R range considered. The K_Q values corresponding to annealing temperatures from 533 to 573 K are valid K_IC measurements. Whereas the 75-MPa·m^1/2 value does not strictly meet the sample size requirements for K_IC validity, the sample thickness and uncracked ligament are more than 5 times larger than the plastic zone size, and as such, any plane-stress and small-scale-yielding effects are expected to be too small to undermine the trends described below in any substantial way. When the K_IC values are compared with the moduli, a correlation between K_IC and G is observed, but no clear correlation between K_IC and B (outside the margin of measurement error) is apparent. A correlation between K_IC and ν is also evident, as suggested previously (9), but this correlation arises almost entirely from the K_IC vs. G correlation. Not surprisingly, a correlation between K_IC and ∆H is as robust as the K_IC vs. G correlation. The strong K_IC vs. G and K_IC vs. ∆H correlations reveal a sharply decreasing toughness as the glass is relaxed to increasingly lower and deeper potential energy basins.

To clarify this trend, the logarithm of K_IC is plotted against G and ∆H in Fig. 2 A and B, respectively. A robust exponential relationship is established between K_IC and G as

$$\text{ln}\left(\frac{K_{\text{IC}}}{K_{\text{IC},\text{o}}}\right)=-CG,$$ [1]

where K_IC,o = 4.7 × 10¹² MPa·m^1/2 is a characteristic fracture toughness scale corresponding to a hypothetical toughness of a zero shear modulus state (i.e., the limit of an ideal “incompressible” liquid), and $C=d\text{ln}\left(K_{\text{IC}}/K_{\text{o}}\right)/dG$ = 7.1 × 10⁻¹⁰⋅Pa⁻¹ is the coefficient of the K_IC vs. G exponential dependence. A similar exponential relation between K_IC and ∆H can likewise be obtained, but such relation is less meaningful as ∆H is a relative property with an arbitrary reference. Fig. 2 A and B suggests that the “intrinsic” plane-strain fracture toughness K_IC follows exponentially decaying functions of G and ∆H. These relations appear to be continuous over a broad range of equilibrium configurational states of the glass, and no sharp drop in toughness at some “critical” annealing temperature of the type suggested by Kumar et al. (15) is evident.

Fig. 2.

(A) Logarithm of fracture toughness K_IC vs. shear modulus G, (B) logarithm of fracture toughness K_IC vs. recovered enthalpy ΔH, for equilibrium configurational states of Zr₃₅Ti₃₀Cu_8.25Be_26.75 glass. Solid lines are linear fits through the data.

To further investigate this apparent dependence of fracture toughness on the resistance to shear flow, we examined the fracture surface morphology. Scanning electron microscopy images of the fracture surfaces corresponding to the five relaxed states are shown in Fig. 3 A–E. The fractographs are presented with the precrack surfaces aligned, to exemplify the extent of shear sliding activity ahead of the precrack. Sliding along shear bands ahead of the crack tip is the key mechanism of crack blunting and potential crack arrest in metallic glasses, and is understood to be the mechanistic origin of fracture toughness in these materials (1). Here, the extent of the shear sliding region ahead of the precrack, which forms the “plastic zone,” is termed “rough zone width” and is designated by L_rough. The L_rough value in each fractograph is approximated graphically by determining the level where steep ridges and deep valleys roughly merge. The L_rough values are indicated in the fractographs of Fig. 3 and listed in Table 1. As seen, L_rough increases with increasing T_R. A one-to-one correspondence between K_IC vs. L_rough is evident from the data in Table 1, as first reported by Suh et al. (25). Such correspondence is shown graphically in Fig. 3F. Another characteristic fracture toughness scale arises from the K_IC vs. L_rough dependence by extrapolation to L_rough = 0, where K_IC∼10 MPa·m^1/2. This scale represents the opposite limit of K_IC,o, characterizing the limit of fracture toughness where G becomes large.

Fig. 3.

Scanning electron micrographs of the fracture surfaces from fractured specimens associated with equilibrium states of Zr₃₅Ti₃₀Cu_8.25Be_26.75 metallic glass at various relaxation temperatures T_R: (A) 533, (B) 553, (C) 573, (D) 593, and (E) 613 K. The precrack surfaces in the fractographs are aligned and designated by dotted lines. The extent of the rough zone width L_rough in each fractograph is also designated by a dotted line. (F) Fracture toughness K_IC vs. rough zone width L_rough for the conditions in A–E. The solid line is a linear fit through the data.

The correlations established here reveal that the plane-strain fracture toughness of samples equilibrated at different T_R is linked uniquely to properties characterizing the inherent state of the glass (e.g., G and ∆H). Analysis of the inherent states of a relaxed metallic glass (i.e., supercooled liquid states) based on potential energy landscape theory reveals that the isoconfigurational shear modulus G is proportional to the activation barrier for plastic shear flow (i.e., configurational hopping between inherent-state basins), which scales directly with ∆H (17). As such, the exponential relation between K_IC and G (and between K_IC and ∆H) suggests that the process of crack blunting by shear banding ahead of the crack tip is consistent with hopping across activation flow barriers separating potential energy wells that define inherent states of the glass.

It is interesting to examine how this sensitivity to annealing embrittlement varies among various metallic glasses. One may quantify the annealing embrittlement sensitivity by a parameter F defined as the relative drop in fracture toughness K_IC with respect to a relative drop in relaxation temperature T_R:

$$F=\frac{d\text{ln}\left(K_{\text{IC}}/K_{\text{IC},\text{g}}\right)}{d\left(T_{\text{R}}/T_{\text{g}}\right)},$$ [2]

where K_IC,g is the fracture toughness of a glass relaxed at its glass transition temperature (i.e., at T_R = T_g). With this definition, the larger the value of F, the greater the sensitivity to annealing embrittlement. Data for K_IC at varying T_R are readily available in the present work for the Zr₃₅Ti₃₀Cu_8.25Be_26.75 glass; however, finding reliable data for other glasses in the literature is challenging. This is because most studies on fracture in the literature involve tests on metallic glasses that were either as-quenched or not sufficiently relaxed. In the study of Kumar et al. (15), tests were performed on different metallic glass alloys that were sufficiently relaxed over a broad T_R range. Those tests were not actual fracture toughness tests but rather bending tests to failure. Nonetheless, one can estimate a critical Mode I stress intensity factor from the reported plastic strain to failure using the analytical expression of Conner et al. (26) (Supporting Information). Although a K_IC value estimated from such analysis is not strictly a plane-strain fracture toughness value, the drop of K_IC with decreasing T_R evaluated from such analysis is expected to be representative of the material’s tendency to anneal embrittle.

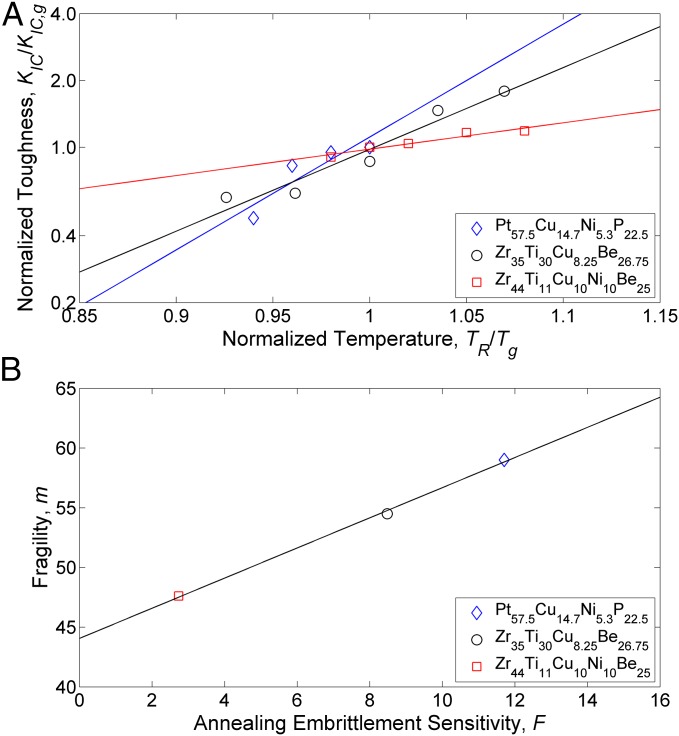
In Fig. 4A, we plot $\text{ln}\left(K_{\text{IC}}/K_{\text{IC},\text{g}}\right)$ vs. $T_{\text{R}}/T_{\text{g}}$ data for the Zr₃₅Ti₃₀Cu_8.25Be_26.75 glass gathered in the present work (T_g = 573 K; K_IC,g = 41.5 MPa·m^1/2), along with data for Pt_57.5Ni_5.3Cu_14.7P_22.5 and Zr₄₄Ti₁₁Cu₁₀Ni₁₀Be₂₅ reported by Kumar et al. (15) (Supporting Information, Figs. S1 and S2 and Table S1.). The plot reveals that the three metallic glasses exhibit very different propensities for annealing embrittlement, with Pt_57.5Ni_5.3Cu_14.7P_22.5 and Zr₄₄Ti₁₁Cu₁₀Ni₁₀Be₂₅ demonstrating the highest and lowest annealing embrittlement sensitivity, respectively, and Zr₃₅Ti₃₀Cu_8.25Be_26.75 falling in between. One may notice that the order of annealing embrittlement sensitivity actually follows the order of the fragility of the three glasses. The fragility m, defined by Angell as the steepness of the viscosity temperature dependence at T_g (27), is often used as a parameter characterizing the potential energy landscape morphology of a glass/liquid. The value of the parameter F evaluated as the fitting slope of the data in Fig. 4A according to Eq. 2 is 11.7 for Pt_57.5Ni_5.3Cu_14.7P_22.5, 8.5 for Zr₃₅Ti₃₀Cu_8.25Be_26.75, and 2.7 for Zr₄₄Ti₁₁Cu₁₀Ni₁₀Be₂₅. The reported fragility m is 59 for Pt_57.5Ni_5.3Cu_14.7P_22.5, 54.5 for Zr₃₅Ti₃₀Cu_8.25Be_26.75, and 47.6 for Zr₄₄Ti₁₁Cu₁₀Ni₁₀Be₂₅ (28–30) (Materials and Methods). By plotting F vs. m, as presented in Fig. 4B, a one-to-one correspondence between the annealing embrittlement sensitivity F and fragility m is suggested. With just three data points it may be premature to conclude that a “correlation” between F and m has been established, although from a thermodynamic perspective, such correlation is plausible. Fragility is understood to be controlled by the decrease of the isoconfigurational shear modulus G with increasing potential energy (or temperature) (18, 20, 21). Because a one-to-one correspondence between K_IC and G is demonstrated here (Fig. 2 and Eq. 1), it is conceivable that fragility can be associated with the steepness of the K_IC drop with temperature, or equivalently with the annealing embrittlement sensitivity F. This outcome would have significant scientific and technological implications. From a scientific perspective, this result suggests a thermodynamic origin of annealing embrittlement, but also a structural one. In Angell’s original conception, fragility quantifies how rapidly the “structure” (i.e., the local order) of an equilibrium liquid develops as the liquid cools toward T_g (27). Simulations verify that fragile glass formers indeed show a much more rapid rise of local order as the temperature decreases toward T_g (31). As such, the present result suggests that annealing embrittlement should be associated with the degree of order established in each equilibrium state at which the atomic structure of the glass is relaxed to. Considering the description recently proposed by Ma (32), one can relate annealing embrittlement to the distribution of inhomogeneous local structures (i.e., local motifs ordered to various degrees) established at each relaxed state, which varies from one equilibrium state to another. From a technological perspective, the present result suggests that more fragile glasses are more prone to embrittlement than stronger glasses. Specifically, it suggests that fragile glasses would tend to embrittle at low fictive temperatures and toughen at high fictive temperatures, whereas stronger glasses would have a more constant toughness with varying fictive temperature.

Fig. 4.

(A) Logarithm of normalized toughness $K_{\text{IC}}/K_{\text{IC},\text{g}}$ vs. normalized temperature $T_{\text{R}}/T_{\text{g}}$ for Zr₃₅Ti₃₀Cu_8.25Be_26.75, Pt_57.5Ni_5.3Cu_14.7P_22.5, and Zr₄₄Ti₁₁Cu₁₀Ni₁₀Be₂₅. Solid lines are regressions through the data. (B) Fragility m vs. tendency for annealing embrittlement F for Zr₃₅Ti₃₀Cu_8.25Be_26.75, Pt_57.5Ni_5.3Cu_14.7P_22.5, and Zr₄₄Ti₁₁Cu₁₀Ni₁₀Be₂₅. The line is a linear fit through the data.

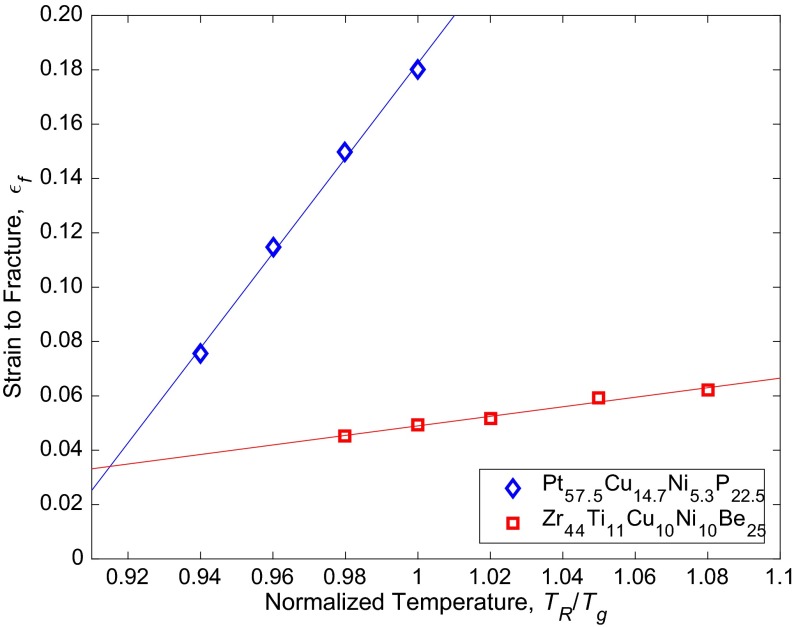
Fig. S1.

Strain to fracture ε_f vs. normalized temperature T_R/T_g as reported in ref. 15 for Pt_57.5Ni_5.3Cu_14.7P_22.5 and Zr₄₄Ti₁₁Cu₁₀Ni₁₀Be₂₅. Solid lines are linear fits to the data.

Fig. S2.

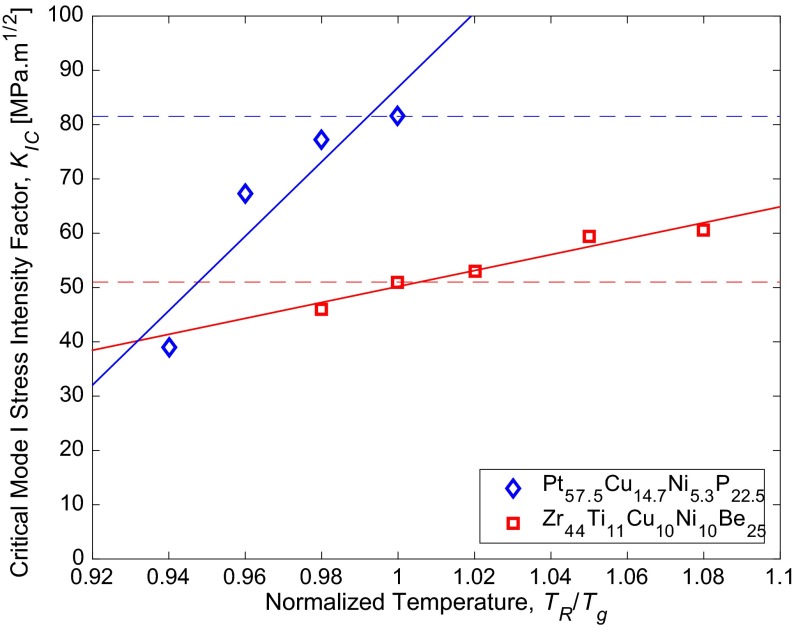
Evaluated K_IC data for Pt_57.5Ni_5.3Cu_14.7P_22.5 and Zr₄₄Ti₁₁Cu₁₀Ni₁₀Be₂₅ using Eq. S1 plotted against normalized temperature T_R/T_g. Solid lines are linear fits to the data. The upper dotted line designates the K_IC,g value of 81.5 MPa⋅m^1/2 for Pt_57.5Ni_5.3Cu_14.7P_22.5 (33), whereas the lower dotted line designates the K_IC,g value of 51 MPa⋅m^1/2 for Zr₄₄Ti₁₁Cu₁₀Ni₁₀Be₂₅ (11).

Table S1.

Model parameters used in the present analysis to evaluate K_IC from the reported ε_f data using Eq. S1

Model parameters	Pt57.5Ni5.3Cu14.7P22.5	Zr44Ti11Cu10Ni10Be25	Refs.
h, mm	0.3	0.3	(15)
εy	0.0153	0.020	(33, 34)
Gg, GPa	30.5	33.2	(21)
n	1.29	0.93	(21)
B, GPa	198.7	108.2	(33, 35)
KIC,g, MPa⋅m1/2	81.5	51	(33, 11)
Δu*, μm	4.4	1.3

In conclusion, we demonstrate here that in the fully relaxed state of the metallic glass, the fracture resistance and shear flow resistance exhibit a one-to-one correspondence. Specifically, the present experiments reveal that the intrinsic toughness (i.e., the plane-strain fracture toughness) decays exponentially with the shear modulus and stored configurational enthalpy, and the decay functions are continuous over a broad range of equilibrium configurational states of the glass. A comparison of data for toughness vs. relaxation temperature among three metallic glass alloys reveals very different tendencies for annealing embrittlement. The data further suggest a potential correlation between annealing embrittlement sensitivity and the fragility of the equilibrium glass-forming liquid. Such a correlation can be rationalized by considering the temperature dependence of the barrier for shear flow. In summary, annealing embrittlement sensitivity, liquid fragility, and the temperature dependence of shear elasticity appear to have a common underlying origin.

Materials and Methods

Sample Preparation.

Ingots of Zr₃₅Ti₃₀Cu_8.25Be_26.75 were prepared by weighing appropriate amounts of Zr (single crystal, 99.92% purity), Ti (single crystal, 99.99% purity), Cu (99.999% purity), and Be (99.9% purity). The ingots were alloyed by arc melting in a Ti-gettered argon atmosphere on a water-cooled copper hearth, and flipped at least four times to ensure chemical homogeneity. Rods 8 mm in diameter with lengths varying between 5 and 13 cm were produced by injection casting in a copper mold from the molten liquid state at 1,100 °C. Controlled melt heating was performed with rf induction power under argon atmosphere, and with the melt temperature being monitored by an infrared pyrometer. The amorphous nature of all specimens was verified by XRD with Cu Kα radiation.

Mechanical Testing.

Five single edge-notched bend SE(B) specimens were machined out of cylindrical rods with thicknesses B of 3.5 mm and widths W of 7 mm. The length L of the specimens was slightly longer than the testing span length S of 28 mm. The specimen faces perpendicular to the crack were mirror polished with 0.02-µm colloidal silica. All SE(B) specimens were fatigue precracked using a servo-hydraulic Materials Testing System in ambient air. Before fatigue precracking, notches having a length of ∼2 mm and a root radius of 125 µm were created using a wire saw with 1-µm diamond slurry. Fatigue precracks were created under load control using initial stress intensity ranges of ΔK = K_max − K_minof ∼11 MPa m^1/2 at a constant frequency of 10 Hz (sine wave) with a load ratio R = 0.1, where R is the ratio of minimum to maximum applied load, P_min/P_max. The samples were fatigue precracked in multiple increments and the precrack length between increments was checked on both sides of the sample to ensure one straight precrack grew from the notch until the total crack length (including the notch length)-to-width ratio, a/W, was 0.5. The lengths of the precracks were ∼1.5 mm, well above the ASTM E399 standard requirements. Final values of ΔK during fatigue precracking never exceeded 60% of even the most brittle K_Q result. Fracture toughness tests were performed in accordance with ASTM E399 under displacement control at a constant displacement rate of 0.3 mm/min. Load-displacement data were found to be linear to failure such that the value of K_Q was calculated from the peak load at fracture. Compression testing was also performed using plane-parallel square beams with a side length of ∼3.5 mm and an aspect ratio of ∼2 sectioned from each specimen postannealing. The stress–strain response was measured at a strain rate of 10⁻³⋅s⁻¹ in an Instron load frame, and the yield strength σ_y was assessed. A yield strength of 1,700 ± 20 MPa was determined, which appears to be nearly independent of the relaxed state.

Annealing Experiments and Acoustic Measurements.

Annealing of the precracked specimens was performed by sealing the specimen inside a quartz tube under an argon atmosphere, and annealing it in a furnace for sufficient time to relax the glass to a well-defined equilibrium liquid state. Subsequently, the specimens were directly quenched in room-temperature water by breaking the quartz tube immediately after immersing in water, to effectively retain the relaxed state established at the annealing temperature. The five specimens were annealed at the relaxation temperatures T_R of 533, 553, 573, 593, and 613 K. Multiple annealing steps were performed at each temperature and the shear and longitudinal wave speeds along with the density were measured after each annealing step. XRD was also performed after each annealing step to verify that the specimens remained amorphous. Equilibration was assessed by monitoring the relaxation of the shear and longitudinal wave speeds. Equilibrium is assumed to be established when the wave speeds change by less than 0.2%. The total annealing times at 533, 553, 573, 593, and 613 K were 15,000, 520, 170, 41, and 15 min, respectively. Measurements for the density and elastic constants were performed on the precracked specimens before the fracture tests. The density was measured using the entire specimen by the Archimedes method, according to the ASTM standard C693-93. The room-temperature shear and longitudinal wave speeds were measured in a zone immediately ahead of the precrack using the pulse–echo overlap technique with 25-MHz ultrasound transducers. Using the data for the elastic wave speeds and density ρ, the shear modulus G, bulk modulus B, and Poisson’s ratio ν of the samples were calculated. Following annealing, the recovered enthalpy ∆H at T_g was assessed by differential scanning calorimetry by scanning a small segment from each annealed specimen using a Netzsch 404C calorimeter at a rate of 10 K/min. The recovered enthalpy of each specimen was calibrated in reference to the specimen that displayed the lowest value of ∆H.

Fragility Evaluation.

The viscosity of Pt_57.5Ni_5.3Cu_14.7P_22.5 was studied by Harmon et al. (28), who directly evaluated a fragility of m = 59 by fitting the temperature-dependent viscosity using the cooperative shear model. The viscosity of Zr₃₅Ti₃₀Cu_8.25Be_26.75 was studied by Duan et al. (29) and that of Zr₄₄Ti₁₁Cu₁₀Ni₁₀Be₂₅ by Waniuk et al. (30), and in both studies the Vogel–Fulcher–Tamman (VFT) relation was used to fit the temperature-dependent viscosity. The VFT parameters and glass transition temperatures were reported to be D = 12.4, T_o = 422.6 K, and T_g = 578 K for Zr₃₅Ti₃₀Cu_8.25Be_26.75 (29) and D = 18.9, T_o = 412.5 K, and T_g = 623 K for Zr₄₄Ti₁₁Cu₁₀Ni₁₀Be₂₅ (30). The fragility can be related to D, T_o, and T_g as $m=D{T}_o{T}_g/\left[\text{ln}\left(10\right){\left(T_g-T_o\right)}^2\right]$, and can be calculated to be 54.5 for Zr₃₅Ti₃₀Cu_8.25Be_26.75 and 47.6 for Zr₄₄Ti₁₁Cu₁₀Ni₁₀Be₂₅.

Analysis of Shear Band Plasticity and Evaluation of Stress Intensity Factors

Using an analysis of shear band plasticity based on a model of an elastic-perfectly plastic solid, Conner et al. (26) derived an analytical expression to evaluate the stress intensity factor in bending of an unnotched metallic glass plate. In their analysis for symmetric bending of a plate having half-thickness h, the critical Mode I stress intensity factor K_IC is related to the bending strain at fracture ε_f according to

$$K_{IC}=\left\{\frac{2G}{\left(1-\nu \right)}{\epsilon }_y{\left[\frac{3}{2}-\frac{1}{2}\left(\frac{{\epsilon }_y}{{\epsilon }_f}\right)\right]}^2\right\}\sqrt{\pi c}\left[1.12-\frac{1.39}{2}\left(\frac{c}{h}\right)+\frac{7.3}{4}{\left(\frac{c}{h}\right)}^2-\frac{13}{8}{\left(\frac{c}{h}\right)}^3+\frac{14}{16}{\left(\frac{c}{h}\right)}^4\right]\hspace{0.17em},$$ [S1]

where G is shear modulus, ν the Poisson’s ratio, ε_y the elastic strain at yielding, and c is the length of the stable crack formed in the shear band before unstable fracture, and can be related to ε_f according to

$$c=h\sqrt{{\left[1-\left(\frac{{\epsilon }_y}{{\epsilon }_f}\right)\right]}^2-{\left(\frac{h\alpha }{{\epsilon }_f-{\epsilon }_y}\right)}^2}\hspace{0.17em},$$ [S2]

where α is a curvature parameter given by

$$\alpha =\frac{\left(1-\nu \right)}{\left(1-2\nu \right)}\frac{\mathrm{\Delta }{u}^{\ast }}{\sqrt{2}{h}^2},$$ [S3]

where Δu* is the critical shear offset attained in the shear band before transitioning into an unstable crack (i.e., before fast fracture). Δu* is considered a material constant, and for typical metallic glasses is on the order of a few micrometers. In principle, Δu* is an accessible length scale that may be measureable by microscopy. But, for the purpose of this model, Δu* can be regarded as a model parameter that can be adjusted such that the K_IC evaluated by Eq. S1 matches the measured K_IC.

Kumar et al. (15) tested 0.6-mm-thick metallic glass plates of Pt_57.5Ni_5.3Cu_14.7P_22.5, Pd₄₃Ni₁₀Cu₂₇P₂₀, and Zr₄₄Ti₁₁Cu₁₀Ni₁₀Be₂₅ in bending after annealing the plates at various relaxation temperatures T_R around the glass transition temperature T_g, and reported the strain to fracture as a function of relative temperature T_R/T_g.

The shear modulus G and Poisson’s ratio ν are known to vary strongly when the glass is relaxed at different relative temperatures T_R around T_g. The temperature dependence of the shear modulus G(T_R) is given by (21)

$$G\left(T_R\right)=G_g\text{exp}\left[n\left(1-T_R/T_g\right)\right],$$ [S4]

where G_g is the measured value of the shear modulus for a glass relaxed at T_g [i.e., G_g = G(T_g)] and n is a material constant related to the fragility of the glass. The bulk modulus B on the other hand is known to vary only slightly with varying T_R, an effect also corroborated in the present work (see Table 1 in the main text), and is hence considered to be a constant having the value measured in the as-cast glass state. The temperature dependence of the Poisson’s ratio under this assumption is solely due to G(T_R), and is given by

$$\nu \left(T_R\right)=\frac{3B-2G\left(T_R\right)}{2\left(3B+G\left(T_R\right)\right)}.$$ [S5]

For the purpose of this analysis, the critical shear offset Δu* is a model parameter determined by requiring Eq. S1 to produce a K_IC value at T_g [i.e., K_IC,g = K_IC(T_g)] equal to the measured value in the as-quenched glass state of each composition. In this manner, the K_IC values estimated from the model at various T_R are calibrated to the reported measured K_IC value for each composition. The critical Mode I stress intensity factor K_IC has been evaluated for Pt_57.5Ni_5.3Cu_14.7P_22.5 (33) and Zr₄₄Ti₁₁Cu₁₀Ni₁₀Be₂₅ (11), but no value has been reported for Pd₄₃Ni₁₀Cu₂₇P₂₀. Therefore, the present analysis is implemented to evaluate K_IC from ε_f data only in the Pt_57.5Ni_5.3Cu_14.7P_22.5 and Zr₄₄Ti₁₁Cu₁₀Ni₁₀Be₂₅ systems. Lastly, it should be noted that the K_IC values estimated from the model at various T_R are not necessarily “plane-strain fracture toughness” values, as the samples used in ref. 15 likely were not thick enough to ensure crack propagation in plane strain.

In the context of this analysis, only data for strain to fracture ε_f from ref. 15 that substantially exceed the material elastic yield strain ε_y are used in Eqs. S1 and S2, whereas data where ε_f is close to or equal to ε_y are neglected. This is because, as noted by Conner et al. (26), Eqs. S1 and S2 are valid only when the strain at the plate surface is substantially high to initiate a crack at the surface.

A plot of the strain to fracture ε_f vs. T_R/T_g reported in ref. 15 for Pt_57.5Ni_5.3Cu_14.7P_22.5 and Zr₄₄Ti₁₁Cu₁₀Ni₁₀Be₂₅ is presented in Fig. S1. All model parameters used in the present analysis to evaluate K_IC from the reported ε_f data using Eq. S1 for Pt_57.5Ni_5.3Cu_14.7P_22.5 and Zr₄₄Ti₁₁Cu₁₀Ni₁₀Be₂₅ are presented in Table S1. The evaluated K_IC data for Pt_57.5Ni_5.3Cu_14.7P_22.5 and Zr₄₄Ti₁₁Cu₁₀Ni₁₀Be₂₅ are plotted in Fig. S2 against T_R/T_g.