Interplay between hydrophobicity and the positive-inside rule in determining membrane-protein topology

Significance

Topology prediction is crucial for structure prediction, design, and analysis of membrane proteins. We describe a graphical algorithm, called TopGraph, which is based on a sequence search for minimum energy of insertion using the dsTβL experimental insertion scale rather than statistics derived from known structures. Unlike many existing predictors, TopGraph exhibits high accuracy even on large transporters with no structural homologues. Furthermore, results suggest that the positive-inside rule, which is known to orient segments with respect to the membrane, can also drive insertion of marginally hydrophobic segments in large membrane domains.

Abstract

The energetics of membrane-protein interactions determine protein topology and structure: hydrophobicity drives the insertion of helical segments into the membrane, and positive charges orient the protein with respect to the membrane plane according to the positive-inside rule. Until recently, however, quantifying these contributions met with difficulty, precluding systematic analysis of the energetic basis for membrane-protein topology. We recently developed the dsTβL method, which uses deep sequencing and in vitro selection of segments inserted into the bacterial plasma membrane to infer insertion-energy profiles for each amino acid residue across the membrane, and quantified the insertion contribution from hydrophobicity and the positive-inside rule. Here, we present a topology-prediction algorithm called TopGraph, which is based on a sequence search for minimum dsTβL insertion energy. Whereas the average insertion energy assigned by previous experimental scales was positive (unfavorable), the average assigned by TopGraph in a nonredundant set is −6.9 kcal/mol. By quantifying contributions from both hydrophobicity and the positive-inside rule we further find that in about half of large membrane proteins polar segments are inserted into the membrane to position more positive charges in the cytoplasm, suggesting an interplay between these two energy contributions. Because membrane-embedded polar residues are crucial for substrate binding and conformational change, the results implicate the positive-inside rule in determining the architectures of membrane-protein functional sites. This insight may aid structure prediction, engineering, and design of membrane proteins. TopGraph is available online (topgraph.weizmann.ac.il).

The plasma membrane is a complex physical environment comprising a hydrophobic core and a polar exterior, which is more negatively charged on its cytoplasmic side (1). Two hallmarks of membrane proteins are hydrophobic segments that span the membrane core, and positive charges at the membrane–cytoplasm interface (the positive-inside rule; ref. 2); these features drive insertion and orient segments relative to the membrane plane, respectively. Furthermore, recent work has shown that positive charges placed close to engineered segments can drive membrane insertion even of marginally polar segments (3, 4), suggesting a role for the positive-inside rule in insertion, and emphasizing the importance of accurate models of membrane-protein energetics for protein engineering and for understanding the physical basis of membrane-protein topology.

Topology prediction is a stringent test of our models of membrane-protein energetics. The most parsimonious membrane-topology predictor would locate the membrane-spanning segments and determine their orientations by a sequence search for minimum insertion energy. To achieve that, however, the insertion energy scale must at a minimum exhibit two properties: (i) to drive membrane insertion, the hydrophobic amino acids must make large contributions to insertion; and (ii) to orient the protein with respect to the membrane plane, positively charged residues must be strongly favored in the cytoplasm over the extracellular space. These properties, however, were not observed in previous insertion scales (5–9); instead, topology predictors have relied on machine learning, and used experimentally determined membrane-protein structures to train predictors with hundreds of fitting parameters (10–15). Although the accuracy of these predictors is high (80–90%; refs. 10–16), statistics-based predictors cannot be used to systematically investigate the interplay between different energy contributions to topology. Moreover, such methods are less useful than energy-based methods in predicting topology in targets that lack homology to previously characterized proteins (16), and cannot be used to design new proteins.

In a landmark study, von Heijne and coworkers measured translocon-mediated apparent membrane-insertion energetics of hydrophobic segments engineered into the leader peptidase (Lep) protein, and derived an insertion scale for every amino acid across the membrane (9, 17). Elofsson and coworkers subsequently incorporated this scale into a hidden Markov model-based topology predictor (10, 18). Although this predictor is a substantial improvement over the statistics-based methods in reducing the number of fitted parameters, the authors noted significant uncertainties; for instance, the Lep scale reported only a small driving force of 0.5 kcal/mol for membrane insertion of the most hydrophobic residues, Leu and Phe, compared with at least 2 kcal/mol in other scales (7, 19), leading Elofsson and coworkers to observe that the Lep scale assigns positive (unfavorable) insertion energies to a large fraction of membrane-spanning segments (10). Furthermore, although it is established that protein orientation with respect to the membrane plane is determined by the positive-inside rule, the Lep measurements reported only a small bias of around 0.5 kcal/mol in favor of Arg and Lys in the cytoplasm compared with the extracellular domain (20), and thereby could not be used to predict orientation. To overcome these problems, the predictor relied on corrections, parameter fitting, and empirical rules in addition to the Lep energetics.

To derive higher-confidence insertion energetics we recently developed an experimental method, called deep sequencing TOXCAT-β-lactamase (dsTβL), and measured apparent insertion free energies ($\mathrm{\Delta }{G}_{insertion}^{app}$) into the bacterial plasma membrane for each of the 20 amino acids at 27 positions across the membrane (21). The dsTβL scale was in good agreement with what theory and previous experiments suggested; for instance, the hydrophobicity at the membrane core was in line with biophysical measurements (22) and 3–4 times larger than measured with Lep (23). Furthermore, dsTβL reported large asymmetries (∼2 kcal/mol) for the localization of the positively charged residues Arg and Lys in the cytoplasmic side relative to the extracellular side of the membrane. Here, we develop a topology predictor, called TopGraph, which uses dsTβL to assign insertion energies to segments of a query protein and search for the topology of minimum insertion energy. We test TopGraph on experimentally determined topology databases. We further analyze large membrane domains of transporters, which have been challenging for statistics-based predictors, and describe cases where the positive-inside rule apparently drives the insertion of polar segments into the membrane.

Results

Assessing Topology-Prediction Accuracy.

We used three published datasets to test topology-prediction accuracy. First, prediction accuracy of membrane-span locations was assessed using the Reeb dataset, which is based on a nonredundant set of 188 high-resolution structures (with a pairwise sequence-identity cutoff of 20%; ref. 16). For each of the query sequences in the Reeb dataset we defined “overlap10” to represent whether the correct number of membrane-spanning segments was predicted, and whether at least 10 residues of each predicted segment overlapped with an inserted segment in the experimentally determined structure. Second, to assess orientation-prediction accuracy we used a set of 609 Escherichia coli inner membrane proteins, for which the location of the C terminus (cytoplasmic or periplasmic) was experimentally determined (24). Third, we assessed discrimination of soluble and membrane-spanning proteins using an annotated nonredundant set (<30% pairwise sequence identity) of 3,400 soluble proteins and 311 membrane proteins of known structure (13, 25). We compared the performance of TopGraph and TOPCONS, a topology predictor that uses the consensus of five statistical predictors (13, 26), in these three tests, and additionally analyzed the overlap10 performance of the Lep scale on the Reeb dataset.

A Graphical Algorithm for Membrane-Topology Prediction.

We set ourselves the goal of predicting membrane-protein topology based on insertion energies and without invoking statistical inference to predict insertion propensities. Given a query sequence we start by using a sliding window to extract all subsequences of lengths 21–30 amino acid residues. The dsTβL scales (21) do not report on secondary-structure propensity nor on the existence of signal peptides, which are often cleaved post translationally. We therefore eliminate all signal peptides predicted by TOPCONS (13) and any subsequence that is predicted to be nonhelical (27), as well as subsequences that contain several charged or polar residues (SI Methods). To the remaining segments we assign apparent insertion free energies according to the dsTβL scale (21) in each of the two orientations relative to the membrane (locating the C-terminus either in the cytoplasm or outside). Because segments vary in length, we estimate the location z of every amino acid position i in the segment relative to the membrane midplane:

$$z\left(i\right)=\frac{30}{n}i-15,$$ [1]

where n is the total number of residues in the segment and i is the amino acid position relative to the segment’s start; z(i) ranges from −15 to +15 Å, for cytoplasmic and extracellular locations, respectively. The segment’s apparent insertion free energy is then given by:

$$\mathrm{\Delta }{G}_{\mathit{insertion}}^{\mathit{app}}={\displaystyle {\sum }_{i=1}^n\mathrm{\Delta }{G}_{\mathit{AA}}^{\mathit{z}\left(\mathit{i}\right)},}$$ [2]

where $\mathrm{\Delta }{G}_{AA}^{z\left(i\right)}$ is the apparent insertion free energy for amino acid type AA at location z(i) according to dsTβL.

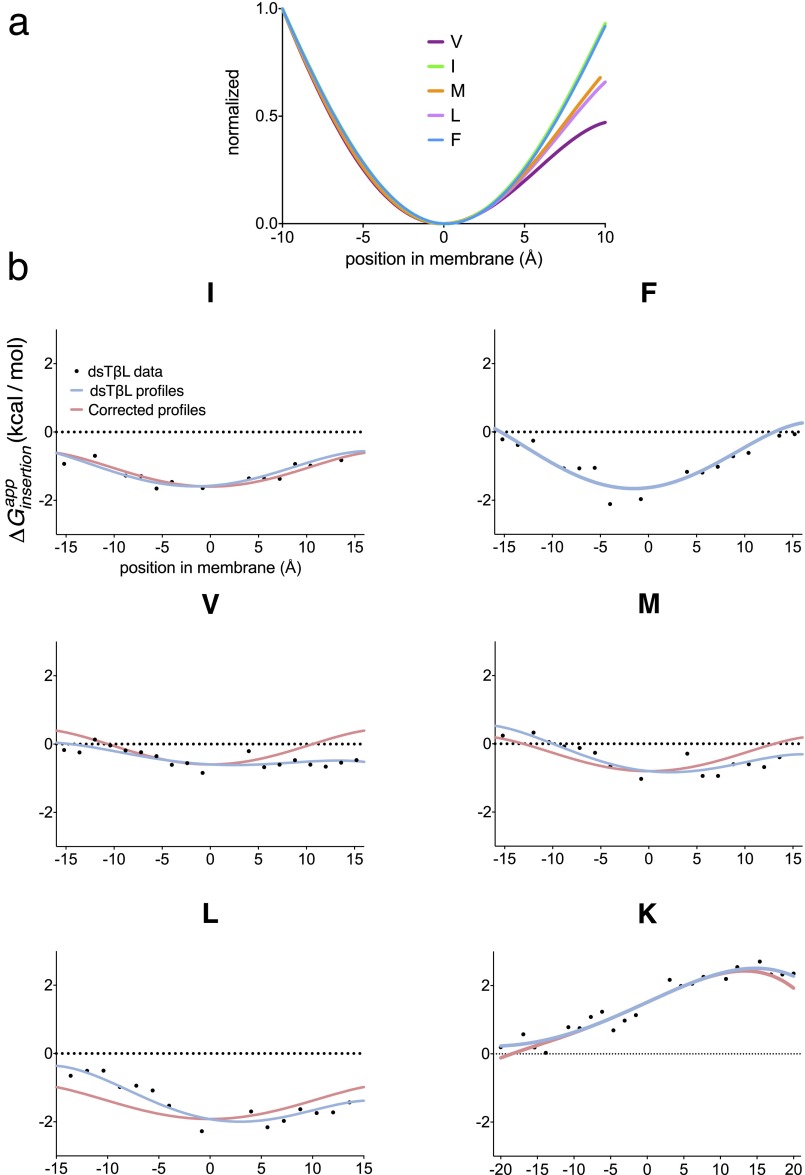
Before running predictions, we modified the dsTβL profiles for the positively charged residue Lys and for the hydrophobic residues Val, Leu, Ile, and Met (Fig. S1 and Table S1). Specifically, in the original dsTβL report (21), Val, Leu, and Met showed slightly nonsymmetric profiles, whereas the other hydrophobics, Ile and Phe, were close to symmetric, as expected. We therefore changed the hydrophobic residues’ profiles so that all were symmetric, and maintained the insertion energy at the membrane midplane as in the original dsTβL scales. Furthermore, the energy contribution of Lys at the cytoplasmic side of the membrane in the original dsTβL scale was slightly positive (+0.2 kcal/mol), thereby penalizing lysine-containing membrane-spanning segments. We therefore modified the Lys profile to be slightly negative (−0.1 kcal/mol) at the cytoplasm interface. These corrections increase the deviation between the polynomial functions used to fit the dsTβL data, but the most extreme deviation is only 0.84 kcal/mol (Leu at the membrane–cytoplasm interface; Fig. S1 and Table S1). In preliminary prediction runs we noticed that these changes do not affect prediction accuracy significantly.

Fig. S1.

Corrections to the dsTβL insertion energies. (A) The dsTβL insertion profiles for hydrophobic residues normalized to the interval 0 (most hydrophobic) to 1 (least hydrophobic). Whereas the Ile and Phe profiles are nearly symmetric, as expected, the other profiles are not. (B) The insertion profiles of Ile, Leu, Val, and Met were corrected to be symmetric, and maintain the same insertion energy at the membrane midplane as measured in the original dsTβL experiment. The profile for Lys was modified to be slightly negative at the cytoplasmic side (−15 Å); this change favors the extension of hydrophobic segment to include cytoplasmic Lys residues. Equations for the modified profiles are provided in Table S1. The corrected profiles (red) are different from the original profiles (blue) by at most 0.84 kcal/mol (Leu at the cytoplasm–membrane interface; Table S1).

Table S1.

Polynomial fit for the insertion profiles of amino acids that were modified relative to the dsTβL measurements (21)

Amino acid	${\text{a}}_0\mathrm{\cdot }\left({10}^{-5}\right)$	${\text{a}}_1\mathrm{\cdot }\left({10}^{-11}\right)$	${\text{a}}_2\mathrm{\cdot }\left({10}^{-3}\right)$	${\text{a}}_3\mathrm{\cdot }\left({10}^{-9}\right)$	$\text{c}$	Max diff* (kcal/mol)
K†	−0.4	$-1.0\ast {10}^{-7}$	$-8.0\ast {10}^{-2}$	$1.0\ast {10}^8$	1.51	0.45
I†	−1.0	−4.0	6.0	7.0	−1.60	0.24
V‡	−1.0	−4.0	6.0	7.0	−0.60	0.82
L‡	−1.0	−4.0	6.0	7.0	1.92	0.84
M‡	−1.0	−4.0	6.0	7.0	−0.80	0.59

The insertion data were fitted to the following fourth-order polynomial, where Z is given in angstroms (Z = 0 at the membrane midplane) and $\mathrm{\Delta }{G}_{insertion}^{app}$ is in kilocalories per mole:$\mathrm{\Delta }{G}_{insertion}^{app}={\mathrm{a}}_0\cdot {\mathrm{Z}}^4+{\mathrm{a}}_1\cdot {\mathrm{Z}}^3+{\mathrm{a}}_2\cdot {\mathrm{Z}}^2+{\mathrm{a}}_3\cdot \mathrm{Z}+\mathrm{c}$, as in Elazar et al. (21). All other amino acid polynomial fits were left as in ref. 21. Polynomial fit for the insertion profiles of amino acids that were modified relative to the dsTβL measurements ref. 21.

^*Maximal difference between adjusted profiles and experimental data.

^†Modified to be slightly negative at the cytoplasmic side.

^‡Symmetrized.

We represent subsequences in the query and their apparent insertion energies as a graph, where nodes N stand for each subsequence (Fig. 1A). Nodes N_i and N_j are connected with a directed edge N_i→N_j if and only if N_i precedes and does not overlap with N_j in the query sequence and the two segments are inverted with respect to one another; that is, one segment’s N terminus is cytoplasmic, and the other’s C terminus is cytoplasmic. In addition, a virtual source node is connected to all other nodes, and every edge is weighted according to its successor node’s $\mathrm{\Delta }{G}_{insertion}^{app}$ (Eq. 2); that is, the weight of edge N_i→N_j is the insertion energy of the segment represented by N_j plus the contributions from positive residues (Lys, Arg, and His) within a five amino acid stretch C terminal to N_i, and similarly, five amino acids N terminal to N_j (SI Methods). In this graphical representation, the minimum-energy path starting from the source predicts not only the location of membrane-spanning segments, as in previous predictors, but also the orientation of the protein with respect to the membrane and the length of each inserted segment. To search for the minimum-energy path we use the Bellman–Ford algorithm (28), which takes under 10 s to find minimal paths on a representative 265 amino acid protein using a standard CPU.

Fig. 1.

Schematic representation of the graphical topology-prediction algorithm TopGraph. (A) Cylinders represent sequence segments (nodes in the graph) in either insertion orientation. Curved gray arrows represent edges connecting nodes; curved black arrows denote the minimum-energy path. Faded cylinders represent nodes not in the minimum-energy path. (B) A constraint (dashed lines) eliminates all edges bypassing it, guaranteeing, by construction, that only segments satisfying the constraint are chosen. Insets show final predicted topology.

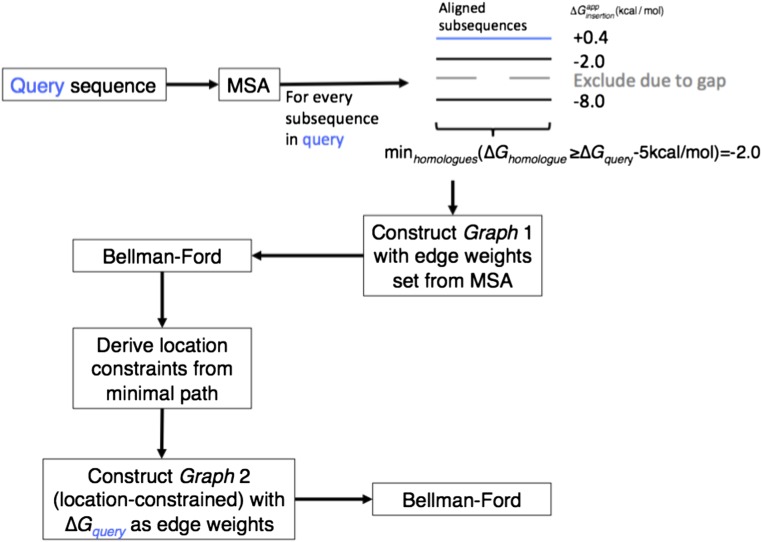
Constraints on the locations of membrane-spanning segments within the query can improve prediction accuracy. In the benchmark below we test the unconstrained prediction as well as two types of constraints: from multiple-sequence alignments (MSA) of homologous sequences, and from the TOPCONS predictor (13). To maintain the validity of the apparent insertion energies we do not use information other than from the query sequence itself to assign segment energies; rather, we use the information from MSAs or from TOPCONS only to determine where membrane spans are likely to be located, and compute the query’s insertion energy by optimizing the inserted segments’ precise locations and orientations within a stretch that includes five positions on either side of the segment determined using the MSA or TOPCONS. TopGraph^MSA conducts the search in two steps: it first predicts membrane-spanning locations using the MSA, and subsequently uses this information as location constraints in a search for minimum-energy paths in the query sequence (Fig. S2). In TopGraph^TOPCONS, by contrast, the locations of membrane-spanning segments are predicted using TOPCONS (13), and are then used to constrain the locations of membrane-spanning segments in a search for minimum-energy paths in the query (Fig. 1B). Alternative predictors could be used to constrain the locations of membrane-spanning segments with no loss in generality.

Fig. S2.

TopGraph^MSA algorithm flowchart. (A) Nonredundant MSA is generated for a query sequence using BLAST, CD-HIT clustering, and MUSCLE alignment. For every possible segment $\mathrm{\Delta }{G}_{insertion}^{app}$ is calculated. Values different from the query’s $\mathrm{\Delta }{G}_{insertion}^{app}$ by more than 5 kcal/mol are discarded. The minimal value found is used as the weight for all edges leading to the segment’s node. The Bellman–Ford algorithm is applied to find the minimum energy topology. Using the minimal topology, constraints are derived for every chosen segment. A graph is rebuilt such that every segment found in the MSA is a constraint, and weights are assigned as the $\mathrm{\Delta }{G}_{insertion}^{app}$ of the corresponding query sequence. The Bellman–Ford algorithm (28) is used again to find the minimal energy topology.

All three TopGraph variants predict the locations, lengths, orientations, and insertion energies of the query sequence. We note, additionally, that the graphical representation lends itself to imposing other types of constraints, which may be inferred from experimental or computational data; for instance, if a certain segment N_k is known to span the membrane, all edges N_i→N_j that bypass N_k may be eliminated (Fig. 1B). Conversely, nodes representing segments that are known not to cross the membrane may be eliminated, and prior data regarding the orientation of the protein in the membrane can be used to select the lowest-energy path through the graph in the known orientation. The ability to define a variety of topological constraints could aid the study of membrane proteins with incomplete structural data, such as on probe accessibility or proteolysis resistance (29), and we implemented a webserver providing free access to TopGraph including such manually constrained prediction (topgraph.weizmann.ac.il).

Prediction Accuracy Increases with Use of Prior Data.

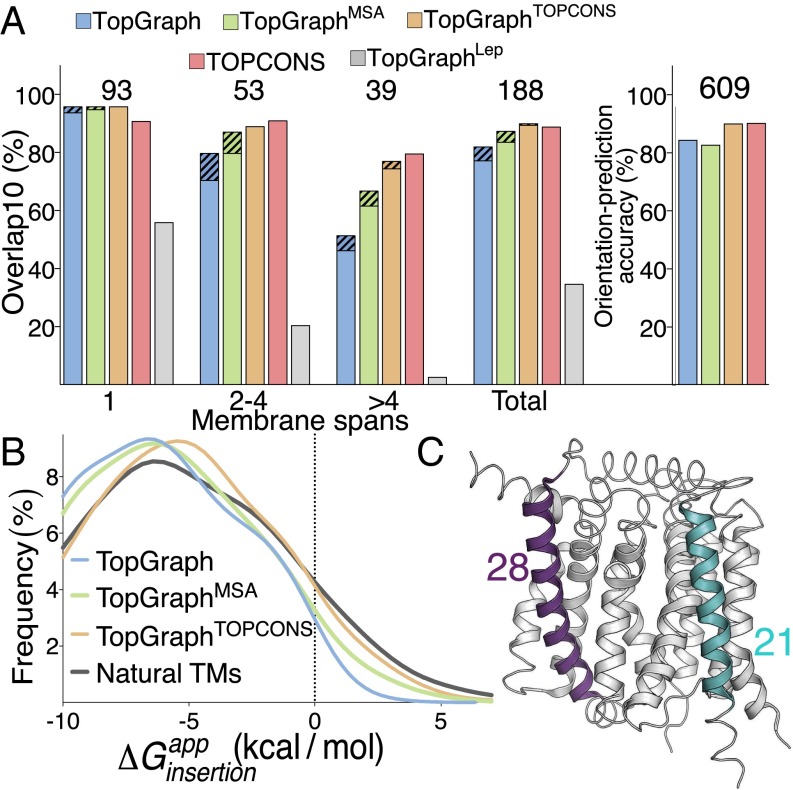
The purist TopGraph predictor, with no use of prior data predicts the locations of membrane segments in single-span proteins with high accuracy (94%; Fig. 2A). This high accuracy is not surprising given that the dsTβL scale is based on experimental data on a single-span membrane protein (21). Multispan membrane proteins are accordingly predicted less accurately, and above four segments prediction accuracy drops to 46%; the overall prediction accuracy across the entire set is 78%. When either of the two lowest-energy predicted paths is compared with the known topology, prediction accuracy increases from 70% to 80% for proteins with two to four membrane spans, and more modestly for larger membrane domains. The preprocessing filters that remove signal peptides, highly charged and nonhelical segments make a substantial contribution to prediction accuracy by eliminating, on average, two-thirds of the segments with $\mathrm{\Delta }{G}_{\mathit{insertion}}^{\mathit{app}}$ < 5 kcal/mol in each target sequence (Fig. S3). Nevertheless, prediction accuracy is high even in proteins, in which less than 20% of the sequence is eliminated by these filters; specifically, all of these proteins are predicted correctly according to the overlap10 metric.

Fig. 2.

Topology-prediction benchmark. (A, Left) Fraction of proteins where all predicted membrane spans overlap with experimentally observed membrane-spanning segments over at least 10 residues (overlap10) and there are no additional predicted segments. The number of proteins in each group is noted above the bars; dashed lines represent accuracy when considering either of the two best-energy predictions. (Right) Orientation-prediction accuracy of the C-terminal position (cytoplasmic or extracellular). (B) Distribution of insertion energies in individual membrane-spanning segments. Natural TMs reports the insertion-energy distribution of membrane-spanning segments annotated by the structure-based PDBTM (31). (C) Experimentally determined structure (PDB entry: 4K1C; ref. 42) annotated according to the TopGraph^MSA prediction: thin ribbon, extramembrane; thick ribbon, membrane spanning; two membrane-spanning segments with minimal and maximal predicted lengths are colored in turquoise and purple, respectively, and their lengths are noted.

Fig. S3.

Percent of segments eliminated by the secondary-structure and polar-residues filters in sequences from all four datasets. The percent of segments with $\mathrm{\Delta }{G}_{insertion}^{app}$ < 5 kcal/mol, which pass the secondary-structure and polar-residues filters is calculated for every sequence in each dataset. Reeb dataset in red (16); experimentally determined C-terminus orientation dataset in blue (24); soluble and transmembrane datasets in yellow and green, respectively (13). The two filters prune over half of the segments, particularly in the nonredundant set of soluble proteins, where, on average >99% of each sequence is eliminated. (Inset) The distribution of $\mathrm{\Delta }{G}_{insertion}^{app}$ for every segment in the Reeb dataset that passes the PSIPRED and charges prefilters. Also 74% of the segments eliminated by the two filters also have very high apparent insertion energy $\mathrm{\Delta }{G}_{insertion}^{app}$ > 5 kcal/mol (noted by the dashed vertical line).

For comparison, we replaced the dsTβL profiles with those from the Lep study (9) and tested prediction accuracy using the same algorithm as used for dsTβL (Fig. 2A). Bernsel et al. previously noted that the average energy assigned to single-spanning domains by the Lep scales is only slightly negative (approximately −0.3 kcal/mol) and that segments in multispanning domains are assigned positive energies on average (10), TopGraph^Lep prediction accuracy is correspondingly modest (56%) for single-spanning domains; it drops to 20% for proteins with two to four membrane spans, and there are nearly no correct predictions (3%) for larger membrane domains, with 34% overall prediction accuracy. These results are consistent with previous observations that the Lep insertion energetics are small for hydrophobic residues (9, 10, 17–19, 21, 30); because single-span membrane domains are typically more hydrophobic than multispan domains (10), the Lep scale predicts location more accurately in the former than in the latter.

We hypothesized that TopGraph^MSA may improve prediction accuracy relative to the purist TopGraph. The basis for this hypothesis is that homologous proteins are likely to have the same topology. Furthermore, although any given membrane protein must encode sufficiently favorable membrane-insertion free energy, individual segments in any protein may have lower insertion propensity than aligned segments in homologs. TopGraph^MSA retains TopGraph’s high accuracy in single-pass membrane proteins (95%) and indeed improves on unconstrained TopGraph, reaching 61% accuracy for membrane proteins with more than four spans and overall prediction accuracy of 84% (Fig. 2A). Furthermore, when considering either of the two lowest-energy paths, prediction accuracy improves to 87%, on par with TOPCONS (89%). TopGraph^TOPCONS shows nearly identical performance to TopGraph^MSA with overall prediction accuracy of 89%.

Energy-Based Prediction of Protein Orientation with Respect to the Membrane Plane.

The dsTβL scale differs from other scales in showing large asymmetries for the localization of the positively charged residues, Arg, Lys, and His, in the cytoplasm compared with the extracellular space (21); this asymmetry is a prerequisite for energy-based prediction of membrane-protein orientation. Indeed, TopGraph correctly predicts orientation in 84% of the proteins in a benchmark of 609 bacterial proteins of experimentally determined orientation (24); overall accuracy is 82% and 90%, for TopGraph^MSA and TopGraph^TOPCONS, respectively, compared with 90% for TOPCONS (Fig. 2A).

The three TopGraph variants output apparent insertion free energies that are based on the dsTβL scale (21). Applied to the Reeb dataset (16), nearly all segments (99%) predicted using the purist TopGraph exhibit negative apparent insertion energies with a mean of −6.9 kcal/mol (Fig. 2B). Using the more accurate predictors TopGraph^MSA and TopGraph^TOPCONS the mean shifts to −6.4 and −5.7 kcal/mol, respectively, and 95% of segments exhibit negative insertion energies. We computed the per-segment insertion free energies of verified membrane-spanning segments, by constraining locations to those observed in membrane–protein structures (31), and derived a very similar distribution of insertion energies (Fig. 2B), and further found that 98% of the membrane spans had apparent insertion energies below +5 kcal/mol. Our analysis suggests that individual membrane spans, even in large domains in which intersegment interactions can drive insertion, must encode sufficiently high insertion propensity. These insertion energies are in agreement with theoretical treatments, which predict an average of approximately −5 kcal/mol for membrane insertion of a single segment (1, 32). The values stand, furthermore, in contrast to the analysis of membrane segments using the Lep insertion scale (9), which computes average insertion energy of +0.8 kcal/mol (10).

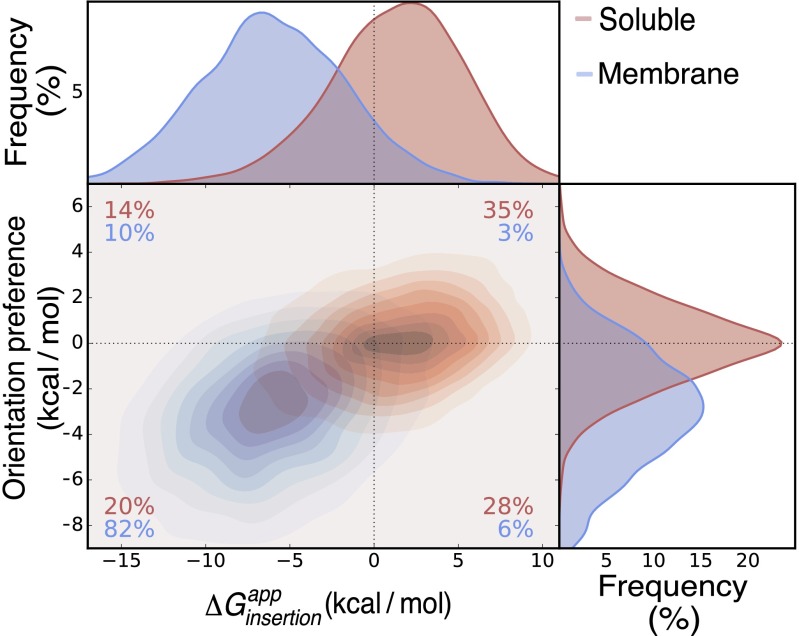
The relatively large magnitude of per-helix insertion energies predicted by TopGraph implies that it may discriminate soluble from membrane-spanning proteins. Indeed, in a set of 3,400 proteins (13), we find that a cutoff of $\mathrm{\Delta }{G}_{insertion}^{app}$ = −3 kcal/mol correctly discriminates membrane from soluble proteins with sensitivity of 96% and specificity of 93% (Table S2), comparable to other predictors (10, 33). We note that on average 99% of the sequence in soluble proteins is eliminated by the secondary-structure and polar-residues filters (Fig. S3), drastically simplifying prediction. We further find that individual membrane-spanning segments differ from segments in soluble proteins in that a large majority encode both hydrophobicity and orientation preference (the positive-inside rule; Fig. S4).

Table S2.

Discrimination of membrane from extra membrane proteins in a set of 3,710 annotated proteins ref. 13

Energy threshold (kcal/mol)	Sensitivity* (%)	Specificity† (%)
−5	91	96
−4	93	95
−3	96	93
−2	97	90
−1	99	87
0	100	85

^*$\text{Sensitivity}=\frac{TP}{\left(TP+FN\right)}$ TP = true positive, FN = false negative.

^†$\text{Specificity}=\frac{TN}{\left(TN+FP\right)}$, N = true negative, FP = false positive.

Fig. S4.

Membrane-spanning segments encode both hydrophobicity and orientation preference. 66,282 segments from soluble (13) and 4,179 segments from membrane proteins (24), for which the C-terminal position was correctly predicted, are shown in red and blue, respectively. Orientation preference is defined as the difference between the $\mathrm{\Delta }{G}_{insertion}^{app}$ of a given segment and the same segment with inverse orientation. Compared with soluble segments, membrane spans exhibit more negative insertion energies and a higher orientational preference.

Most previous membrane-topology predictors search the sequence with a fixed-length window (typically ∼21 amino acid positions); TopGraph, by contrast, optimizes the lengths of the inserted segments. Fig. 2C and Fig. S5 show several TopGraph^MSA predictions for large membrane domains plotted on their molecular structures, demonstrating that TopGraph^MSA accurately locates membrane spans even in proteins with large extramembrane domains. Furthermore, the predictor correctly assigns long and short membrane-spanning segments within the same protein. Accurate length assignment could in the future aid ab initio structure prediction in membrane domains (34–36).

Fig. S5.

Additional examples of membrane-protein structures annotated according to TopGraph^MSA predictions. Predicted membrane-spanning helices colored as a function of length (color bar in middle). PDB entries are noted above molecular representations. Segments in gray are predicted not to cross the membrane. Color bar signifies the length of the predicted membrane-spanning segments.

The Positive-Inside Rule Can Drive Insertion of Polar Segments in Large Membrane Domains.

Many transporters and receptors have membrane-embedded polar and charged residues, suggesting that a purely energy-based predictor, such as TopGraph, might not assign membrane topology correctly in these cases. We nevertheless found that TopGraph^MSA correctly predicted the locations of experimentally validated membrane-spanning segments, even if they were assigned positive insertion energies. Indeed, out of 20 proteins of 6 or more membrane-spanning segments in the Reeb dataset (16), for which TopGraph^MSA produced correct predictions, 13 had at least one segment of marginal hydrophobicity ($\mathrm{\Delta }{G}_{insertion}^{app}$ > −1.5 kcal/mol), and of these, 8 had at least one polar segment ($\mathrm{\Delta }{G}_{insertion}^{app}$ > 0 kcal/mol). Furthermore, in nine cases at least 20% of the polar segment was exposed to the membrane environment; therefore, in many cases polar segments are not fully shielded from the surrounding hydrophobic lipid in the native structure (Table S3).

Table S3.

Insertion of polar segments may be driven by the positive-inside rule

UNIPROT	TM (#TM)*	Sequence†	$\mathrm{\Delta }{G}_{insertion}^{app}$	Membrane-exposed surface area (%)	$\mathrm{\Delta \Delta }{G}_{insertion}^{app}$‡	$\mathrm{\Delta \Delta }{G}_{insertion\left(KRH\right)}^{app}$§	PDB entry	Molecular function
P11551	11 (12)	SSFIVMTIIGGGIVTPVMGFV	2.3	25.9	−0.3	3.9	3O7Q	Transporter
O29285	7 (11)	VAINAVVVTNTSAAVAGFVWMVI	1.9	27.7	8.5	13.7	2B2F	Transporter
P56874	4 (6)	RPYSWYSLFVAINTVPAAILS	0.5	22.4	0.5	6.8	3UX4	Channel
P44741	5 (10)	SFYLPAVAANFTSASSLALLGY	0.1	35.5	6.8	8.6	3M73	Channel
P02920	4 (12)	NILVGSIVGGIYLGFCFNAGA	0.0	27.4	3.3	12.0	2CFP	Permease
E8SM44	8 (12)	ISLSGILYMIPQSVGSAGTVRIGFSL	−0.2	20.0	8.2	7.5	4HUM	Transporter
Q9K0A9	2 (10)	KWAGPYIPWLLGIIMFGMGLT	−0.4	30.6	−1.8	0.1	3ZUY	Symporter
Q8DIF8	4 (6)	HIWIGLICIAGGIWHILTTPF	−0.6	31.6	2.6	1.0	3KZI	Photosystem
P02920	10 (12)	VILKTLHMFEVPFLLVGCFKYIT	−0.7	23.5	4.8	−2.7	2CFP	Permease
P69380	5 (6)	QSDVMMNGAILLALGLSWYGW	−0.7	43.4	2.0	0.9	2QFI	Transporter
P05311	3 (11)	LSGLFGVSSLAWAGHLVHVAI	−1.1	35.7	3.7	4.7	3LW5	Photosystem

^*Helix location, total TMH number in parentheses.

^†Amino acid sequence.

^‡Energy difference when marginally hydrophobic segment is forced out of the membrane.

^§Same as previous footnote but energy calculated only for Arg, Lys, and His.

To investigate how TopGraph^MSA correctly predicts topology even in these challenging cases we compared its lowest-energy prediction to a simulated topology, in which the polar segment was computationally constrained to be excluded from the membrane and the lowest-energy topology was recalculated (Table S3). In 63% of the cases we found that the exclusion of a polar segment led to significant worsening in the total apparent insertion energy (increase of 2.6–8.5 kcal/mol relative to the unconstrained topology). We therefore looked for sequence features outside the polar segment that would explain this gap, and found that by excluding the polar segment from the membrane, the distribution of Lys and Arg residues across the entire protein became roughly balanced between cytoplasm and extracellular space; in the unconstrained TopGraph^MSA prediction, by contrast, the majority of Lys and Arg residues were near the cytoplasm, where they would be favored by the positive-inside rule (ref. 2; Fig. S6). Accordingly, most of the energy gap between the correct prediction from TopGraph^MSA and the simulated topology, where the marginally hydrophobic segment is excluded from the membrane, was due to contributions from Lys and Arg residues.

Fig. S6.

Additional cases of insertion of polar segments favored by the positive-inside rule. In all cases shown, the marginally hydrophobic (or polar) segment is inserted due to a contribution from the positioning of Lys, Arg, and His residues in the cytoplasm. Polar segments in red, positive charges in cyan.

A representative example is provided by the homotrimeric 11-transmembrane (TM) archaeal ammonium transporter (PDB entry: 2B2F; ref. 37). In this protein, forcing the polar segment TM7 ($\mathrm{\Delta }{G}_{insertion}^{app}$ = +1.9 kcal/mol) out of the membrane increases the total apparent insertion energy by 8.5 kcal/mol (Fig. 3). Visual inspection shows that the correct topology positions 14 positive charges in the cytoplasm and 3 in the extracellular space, whereas the topology that excludes TM7 has a more balanced distribution of positive charges (9 and 8, respectively). Indeed, Lys and Arg residues make a large contribution (13.7 kcal/mol) to the difference in insertion energy between the correct and simulated topology. We conclude that the distribution of charges across the entire membrane domain may drive membrane insertion of weakly hydrophobic or polar segments.

Fig. 3.

Case study demonstrating that the positive-inside rule may favor membrane-insertion of polar segments. (A) The insertion of the marginally hydrophobic segment TM7 (red) positions a greater number of positive charges (turquoise) inside the cell compared with a hypothetical situation where the segment is forced out of the membrane (bottom). KR_extra and KR_intra denote the number of extra- and intracellular Lys and Arg residues. (B) Molecular structure (PDB entry: 2B2F; 37) annotated according to insertion prediction: TM7 in red; positive charges in turquoise.

Topology Prediction in a Transporter Family of Unknown Structure: Na⁺/H⁺ Exchanger as a Case Study.

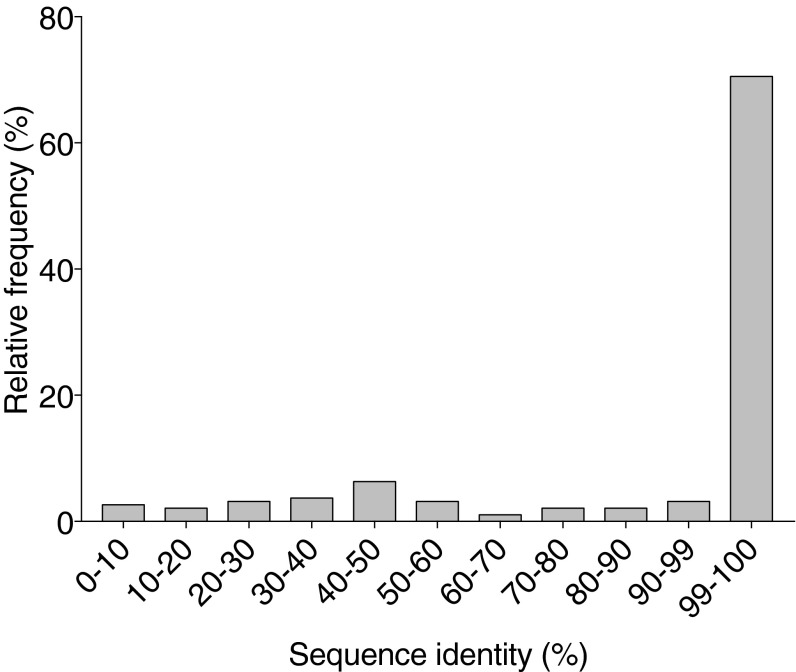
Current topology predictors are trained on known membrane protein structures. We find, for instance, that most sequences (88%) in the Reeb dataset (16) exhibit >40% sequence identity to sequences used for training at least one of the predictors used by TOPCONS (Fig. S7). To analyze a case, on which these predictors had no opportunity to train, we compared TOPCONS and TopGraph^MSA predictions for sequences belonging to the mammalian Na⁺/H⁺ exchanger (NHE) family. Several structures of functionally related proteins to NHE family members are available; the most homologous is the bacterial antiporter NhaA (PDB entry: 1ZCD; ref. 38), which is, however, of only ∼10% sequence identity to NHE family members (38, 39), and NHE family members are indeed of low homology relative to any of the sequences in the TOPCONS training sets. Due to the importance of the NHE family in pH regulation and the implication of NHE mutants in human disease (40), advanced structure–bioinformatics tools together with expert supervision were used to suggest the topology and 3D models for two members: NHE1 and NHE9 (39, 40) on the basis of the NhaA structure. These studies agreed on key topological features: all NHE family members place the C terminus in the cytoplasm and comprise 12 membrane-spanning segments in the region excluding the first 50 amino acid residues (thereby excluding the posttranslationally cleaved N-terminal signal peptide and possibly an additional membrane-spanning segment predicted in some NHE family members).

Fig. S7.

The predictors used by TOPCONS were trained on the vast majority of sequences in the Reeb topology dataset (16). The training sets from all predictors used by TOPCONS were pooled into a single set. For each entry in the Reeb dataset (16) a BLAST search was conducted against this set.

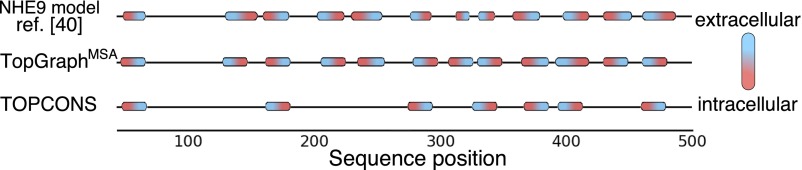
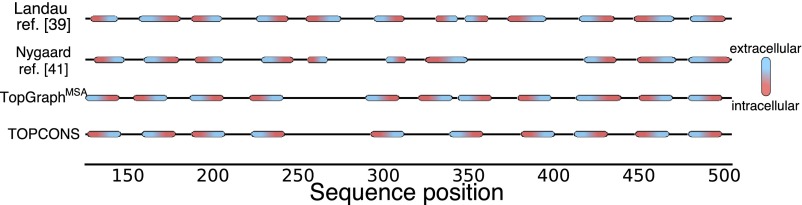
TopGraph^MSA predicts NHE9’s topology correctly relative to the NHE9 model structure, finding all 12 membrane spans and placing the C terminus in the cytoplasm (ref. 40; Fig. 4). TOPCONS, by contrast, fails to recognize five NHE9 membrane spans, and incorrectly predicts that the C terminus lies outside the cytoplasm. NHE1 presents a more difficult case for TopGraph^MSA and although the C terminus is positioned correctly and 11 of the 12 membrane spans are accurately predicted, TM5, which is buried within the core of the NHE1 model structure (39), is missed. Although this segment is assigned marginally favorable insertion energy ($\mathrm{\Delta }{G}_{insertion}^{app}$ = −0.8 kcal/mol), the secondary-structure prediction algorithm used by TopGraph mistakes TM5 for being nonhelical. TOPCONS also misses TM5 and additionally misses TM7 (Fig. S8). Our analysis is restricted to only two proteins, and we note that an alternative topology and a 3D model for NHE1 were put forward (41); we nevertheless find it encouraging that TopGraph can predict topology more accurately and largely in agreement with expert-guided modeling in these challenging cases of low sequence homology to known structures; improvements in secondary-structure prediction algorithms would further improve TopGraph accuracy. In specific cases, such as NHE1, that lack high-homology structures, but where a large body of experimental data are available, for instance on probe accessibility, topology prediction may be constrained with these data to improve accuracy.

Fig. 4.

NHE9 topology prediction. NHE9’s topology was predicted using TopGraph^MSA and TOPCONS, and compared with an experimentally constrained model (40). Red/blue ellipses represent membrane-spanning segments within the sequences. TopGraph finds all membrane spans, and correctly assigns orientation, whereas TOPCONS misses five segments, and the C-terminal position. Only positions 43–500 are shown. See Fig. S8 for a similar analysis of NHE1.

Fig. S8.

Topology predictions of NHE1. Both TopGraph^MSA and TOPCONS were used to predict the topology of NHE1, and compared with experimentally constrained models (39, 41). Red/blue ellipses represent membrane-spanning segments within the sequences. TopGraph^MSA correctly assigns 11 of the 12 segments and the C-terminal positioning, but misses TM5. TOPCONS misses both TMs 5 and 7. See Fig 4 for a similar analysis of NHE9.

SI Methods

Removing Signal Peptide, Highly Charged, and Nonhelical Segments.

Signal peptides as predicted according to the TOPCONS algorithm (provided as part of the TOPCONS output) (13) were eliminated before calculation. To reduce computational complexity, segments were also eliminated if they were either highly charged or predicted to be nonhelical. A sequence segment was considered highly charged if either of the two following conditions applies: the central 12.5 Å (relative to the presumed membrane midplane; Eq. 1) contained three or more charged or polar residues (Arg, Lys, Glu, Asp, His, Gln, and Asn); or the entire segment contained five or more charged or polar residues. A segment is deemed as nonhelical if six consecutive residues anywhere in the segment, or five consecutive residues at either end are predicted by Psi-blast based secondary structure prediction (PSIPRED) (27) to be nonhelical (PSIPRED output indicating coil or strand probability of over 50%, and helix probability under 10%).

N- and C-Terminal Sequence Contributions.

Each subsequence is assigned a $\mathrm{\Delta }{G}_{insertion}^{app}$ including contributions from Lys, Arg, and His residues in the subsequent five residue tails.

Multiple-Sequence Alignments.

For each query protein, homologous sequences were collected either by Basic Local Alignment Search Tool (BLAST) (43) search over the nonredundant sequence database, or by BLASTPGP (an integral part of PSIPRED; ref. 27), fetched from the National Center for Biotechnology Information (NCBI) database, and filtered by e-value cutoff of 10⁻⁴. All resulting sequences were clustered using Cluster Database at High Identity with Tolerance (CD-HIT) (44) with an identity threshold of 97%, and the consensus sequences were aligned using Multiple Sequence Comparison by Log-Expectation (MUSCLE) (45).

Topology Prediction Using MSA-Based Location Constraints.

TopGraph^MSA works in two stages (Fig. S2): first, to every segment in the query we assign the lowest $\mathrm{\Delta }{G}_{insertion}^{app}$ (according to Eq. 2) calculated for all aligned segments, and eliminate segments with energies different by more than 5 kcal/mol of the query segment’s $\mathrm{\Delta }{G}_{insertion}^{app}$. The Bellman–Ford algorithm then finds the minimum-energy path through this MSA-based graph, and records the locations of membrane-spanning segments. In the second step we construct a new graph for the query sequence, where edges are pruned if they bypass segments that were predicted to span the membrane in the first step (Fig. 1B), in this way constraining the locations of membrane spans according to the first step. In this second graph the edges are weighted strictly with $\mathrm{\Delta }{G}_{insertion}^{app}$ values calculated for the query sequence, and not from its homologs. We then conduct a second Bellman–Ford (28) search for minimum-energy paths.

Source Code.

The code was written in Python 2.7 using the modules numpy, networkx, and BioPython. The source code is available at https://github.com/FleishmanLab/membrane_prediction. Topology representation in the webserver and Fig. 3 and Fig. S5 were made by Protter (46).

TOPCONS and Lep-Based Predictions.

The TOPCONS server was queried using batch API at topcons.cbr.su.se/pred/help-wsdl-api/. The Lep-based insertion profiles were taken from Hessa et al. (9), table S2, and implemented within the TopGraph algorithm. For fair comparison with TopGraph results, before running the Lep-based predictions, nonhelical segments, signal peptides, and highly charged segments were removed from the subsequences used in topology prediction, as done for the TopGraph dsTβL predictions.

Data Acquisition.

All data regarding the Reeb dataset (16) including sequences, and Protein Data Bank of Transmembrane proteins (PDBTM) and Orientations of Proteins in Membranes (OPM) database topology assignments were obtained from Reeb et al. (16) supplemental information, available at: https://rostlab.org/resources/tmh_eval. We disregarded two entries (UNIPROT entries Q9QUG3 and Q9X4B7), both were predicted to consist of signal-peptides alone, with no additional membrane spanning segments by the TOPCONS server.

Discussion

Despite four decades of research on membrane-protein energetics, experimental insertion scales lacked sufficient accuracy to predict membrane-protein topology directly from sequence. Instead, predictors have been dominated by statistical models fitted to experimental data. Although statistical predictors are accurate, the use of statistics raises two objections: first, given the low counts and high redundancy among membrane proteins of known structure, training and testing sets often cannot be satisfactorily segregated (16), and such studies might overestimate the expected prediction accuracy for proteins with no homology to known structures. Although this concern may be alleviated with future accumulation of experimental data, the second objection is more fundamental: statistics-based methods cannot be used to tease apart the different energy contributions to topology and have limited use in 3D structure prediction and design—modeling tasks that require accurate energetics. Our recent experimental measurement of apparent insertion energetics using the dsTβL assay quantified the positive-inside rule and agreed with hydrophobicity measurements (21); this higher accuracy allowed us to formulate a prediction algorithm without relying on statistics derived from known membrane-protein structures. The TopGraph analysis shows that prediction accuracy is on par with the consensus predictor TOPCONS. Furthermore, the NHE case study suggests that TopGraph^MSA has an advantage over statistical predictors in large membrane domains of low homology to known structures, where the statistical predictors have had no opportunity to train. Additionally, we noted several cases in which the lengths of the predicted segments agreed with experimental structures, a property which may aid 3D structure prediction.

TopGraph allowed us to quantitatively examine aspects of membrane-protein topology. We found that the majority of membrane spans in experimental structures were assigned negative apparent insertion energies and favorable orientation preferences (the positive-inside rule), suggesting that even in large membrane domains, spans must individually encode sufficiently favorable interactions with the membrane for insertion and orientation (Fig. S4). We additionally noticed that more than a third of large membrane domains have polar segments away from their termini that are nevertheless inserted to locate a greater number of positive charges in the cytoplasm. To be sure, a relationship between insertion and the positive-inside rule was recently noted by von Heijne, Elofsson, and coworkers, who showed that positive charges could drive the insertion of proximal segments (3, 4). Our results generalize this observation and suggest that the distribution of charges across the entire protein, rather than only in the proximity of polar segments, may drive the insertion of polar segments located away from the protein’s termini. Whereas the orientation bias from a single positive charge (∼2 kcal/mol) (21) is smaller than the average net contribution from the insertion of a typical membrane-spanning segment (5–7 kcal/mol), the fact that a large membrane domain may have a dozen or more positive charges distributed across the entire protein provides a large and previously unnoted driving force for inserting polar segments. Although polar residues in membrane proteins are often linked to crucial functional features, such as oligomerization, substrate binding, and conformational change, high polarity undermines membrane insertion. We therefore speculate that the positive-inside rule has an important role in determining the architectures that underlie membrane-protein function. This insight may in the future help design altered or new membrane-protein functional sites. TopGraph may be used to test hypotheses on the relative insertion propensities of natural and engineered proteins. Furthermore, our observations of high prediction accuracy recommend the dsTβL scale as the implicit-solvent term in structure prediction, design, and dynamics of membrane proteins.

Methods

Removing Signal Peptide, Highly Charged, and Nonhelical Segments.

Signal peptides, nonhelical segments, and polar/charged subsequences were prefiltered as described in SI Methods.

N- and C-Terminal Sequence Contributions.

The $\mathrm{\Delta }{G}_{insertion}^{app}$ for every subsequence is supplemented by the contribution of Arg, Lys, and His in subsequent five residues, as described in SI Methods.

Multiple-Sequence Alignments.

Multiple-sequence alignments are generated as described in SI Methods.

Topology Prediction Using MSA-Based Location Constraints.

The use of MSA-based constraints is described in Fig. S2 and SI Methods.

Source Code.

The source code is available at https://github.com/FleishmanLab/membrane_prediction. See SI Methods for more details.

TOPCONS and Lep-Based Predictions.

The acquisition of data from the TOPCONS server and the Lep insertion scales is described in SI Methods.

Data Acquisition.

The acquisition of the dataset is described in SI Methods.