An AT-barrier mechanically controls DNA reannealing under tension

L Bongini; C Pongor; G Falorsi; I Pertici; M Kellermayer; V Lombardi; P Bianco

doi:10.1093/nar/gkw604

. 2016 Jul 4;44(16):7954–7962. doi: 10.1093/nar/gkw604

An AT-barrier mechanically controls DNA reannealing under tension

L Bongini ¹, C Pongor ², G Falorsi ¹, I Pertici ¹, M Kellermayer ², V Lombardi ^1,^*, P Bianco ¹

PMCID: PMC5027502 PMID: 27378772

Abstract

Regulation of genomic activity occurs through the manipulation of DNA by competent mechanoenzymes. Force-clamp optical tweezers that allow the structural dynamics of the DNA molecule to be measured were used here to investigate the kinetics of mechanically-driven strand reannealing. When the force on the torsionally unconstrained λ-phage DNA is decreased stepwise from above to below the overstretching transition, reannealing occurs via discrete shortening steps separated by exponentially distributed time intervals. Kinetic analysis reveals a transition barrier 0.58 nm along the reaction coordinate and an average reannealing-step size of ∼750 bp, consistent with the average bp interval separating segments of more than 10 consecutive AT bases. In an AT-rich DNA construct, in which the distance between segments of more than 10 consecutive AT is reduced to ∼210 bps, the reannealing step reduces accordingly without changes in the position of the transition barrier. Thus, the transition barrier for reannealing is determined by the presence of segments of more than 10 consecutive AT bps independent of changes in sequence composition, while the length of the reannealing strand changes according to the distance between poly-AT segments at least 10 bps long.

INTRODUCTION

Force spectroscopy is a uniquely powerful approach for revealing the structural dynamics of DNA. The first studies focused on the phenomenon of dsDNA overstretching, the inelastic elongation of DNA at forces of 60–70 pN (1–4). The phenomenon has drawn considerable attention because of the contentious interpretation of its complex phenomenology (5–7). DNA overstretching might take place either in a smooth and reversible way signaling the transition from the basic B-form to an extended S-form of ds-DNA, or in a rugged and irreversible way that reveals melting and strand separation. The concurrent occurrence of these distinct transitions has been fully explained only recently with the proposal of reliable models for both phenomena and the characterization of the related control parameters (7–16).

In the meantime, studies aimed at understanding the changes that the DNA molecule undergoes under the control of the protein machinery during replication, transcription, recombination and repair started to appear. In this context DNA unzipping and reannealing has attracted great attention. Unzipping experiments have been extensively performed on hairpins, leading to very detailed sequence-dependent thermodynamic models capable of reproducing the correct sequence of cooperatively unzipping and re-zipping regions (17) and locating the corresponding transition states that were found to correspond to the beginning of blocks of consecutive CG base pairs (bp) (18). Due to its detailed understanding, DNA unzipping was also used as a prototype mesoscale system to investigate thermodynamic properties of systems away from equilibrium such as Jarzinski inequality that relates irreversible work and free energy (19). For the same reason DNA unzipping experiments have even been used as a tool to refine the thermodynamic parameterization of bp binding free energies (20). The conventional protocol for hairpin unzipping, however, implies symmetrically distributed forces on both strands, raising the question whether it is represents the appropriate experimental model for the biologically relevant processes. In replication, for instance, the directionality of motion of DNA polymerases leads to different mechanical loads on the lagging and leading strands. DNA reannealing under asymmetric load is investigated here by recording the shortening transient following stepwise reduction in force imposed on a previously overstretched dsDNA molecule. During the high-force period the molecule has undergone different degrees of melting and strand separation (11). Stretch-release cycles were imposed on the molecule by subsequent step-wise change of the pulling force using a Dual Laser Optical Tweezers (DLOT) with a fast force feedback (11,12). The protocol was applied to either the whole λ-DNA molecule or a specifically made 3852 bp-long AT-rich DNA construct. We find that when the force on the whole λ-phage DNA molecule is abruptly dropped from above to below the overstretching transition region, reannealing of the molecule at constant force occurs in a sequence of shortening steps separated by time intervals that display exponential distribution. The statistics of the waiting times and their dependence on the force provide information on the transition kinetics, while the size of the subsequent shortening steps measures the extension of the portion of the molecule that undergoes reannealing. The kinetic analysis points at the presence of a transition barrier of 0.58 nm along the reaction coordinate. The average lengths of the reannealing strands are ∼750 and 210 bps for the whole λ-DNA and the AT-rich construct, respectively. Sequence analysis shows that, in λ-DNA, 750 bps corresponds to the number of bps separating segments of more than 10 consecutive AT bps, and that this number drops to 210 bps in the AT-rich construct. Thus, the transition barrier is determined by the presence of segments of more than 10 consecutive AT bp, independent of changes in sequence composition, while the length of the reannealing strand changes according to the value predicted by sequence analysis for the distance between poly-AT segments at least 10 bps long. The 0.58 nm length of the transition barrier suggests a mechanism by which the 10-AT-barrier is overcome, based on base pairing of the CG bases immediately following the AT-barrier.

MATERIALS AND METHODS

Samples preparation and mechanical apparatus

Mechanical measurements on the DNA molecules were performed by means of a Dual Laser Optical Tweezers with two counter-propagating 808 nm laser beams (12). Double-stranded λ-DNA (48 500 bp, New England Biolabs, Ipswich, MA, USA) was held between two streptavidin-coated polystyrene beads (Spherotech, Libertyville, IL, USA) of 3 μm diameter by means of biotinylated 3′ ends free to rotate, as previously described (21). While the bead at one end was trapped in the focus of the lasers, acting as a force transducer, the other one was attached to a micropipette integral with the microfluidic chamber carried by a piezoelectric stage (PDQ375, Mad City Lab, Madison, WI, USA), providing movements with subnanometer precision. For labeling dsDNA at both ends but on opposite strands, bio-11-dCTP, dATP, dGTP and dUTP were polymerized opposite the λ-DNA's 12-bp sticky ends using Klenow enzyme. The experiments were done at 25°C in solution with the following composition: 150 mM NaCl, 10 mM Tris, 1 mM EDTA, pH 8.0.

The AT-rich construct was a 3852-bp-long portion of the λ-phage DNA selected based on its high AT content (64% versus 50% of the λ-DNA). The sample was prepared with standard PCR employing DreamTaq polymerase (Fermentas, Vilnius, Lithuania). Primers (3′-biotin-CAGCTGCATAACGCCAAA and 3′-NH₂-C6-GCATGGTGAAAAATGCGATA) were designed with the www primer3 tool (22) using the entire λ-phage genome sequence available in the GeneBank database (23) (for further details, see Supplementary Data). The resulting reaction mixtures were purified with agarose-gel electrophoresis (1%, Tris-acetate-EDTA buffer, 10 V/cm). The final product was isolated with a Quiagen Miniprep kit and eluted into ultrapure Milli-Q water (Millipore, Billerica, MA, USA). DNA concentration was determined by measuring absorbance at 260 nm (Nanodrop 1000). Concentration was typically around 30 ng/μl. Purity, according to the 260/280 nm absorbance ratio, was approximately 1.8 in all cases. The AT-rich construct was held between two beads with one end covalently linked to a 2.5 μm carboxylated latex bead (Kisker Biotech GmbH, Steinfurt, Germany) via the amino group attached to the PCR primer. The other end of the molecule was attached to a 3 μm streptavidin-coated latex bead via the biotinyl group on the other primer. The experiments were made at 25°C in solution with the following composition: 150 mM NaCl, 10 mM Tris, 1 mM EDTA, pH 8.0. Ionic strength was modulated by changing NaCl concentration as reported in the text.

The stiffness of the trap was 0.25 pN/nm. The update frequency of the signal controlling the mechanical apparatus (and the sampling frequency of the recorded signals) was set to 2.5 and 1 kHz in length- and force-clamp mode, respectively. In force clamp mode the actual rise time (10–90%) of the force step depends on the stiffness of the molecule, increasing from 2 ms in the region of the intrinsic elasticity (below and above to overstretching region) to ≤20 ms in the region of the overstretching transition (12). The DNA molecule was first stretched in length control (feedback signal from the position of the piezoelectric stage) at constant pulling velocity (1 μm/s for full length λ-phage dsDNA and 0.5 μm/s for the AT-rich construct) from the starting unstressed length until a preset force level above the overstretching transition was reached, then the control was switched to force. The gain of direct amplifier was adjusted according to the actual stiffness of the molecule which, because of non-linearity due to the structural dynamics of DNA, depends on the region of forces explored (11,24). In order to identify the zero-extension position in the displacement data, the micropipette-bead was pressed gently against the trapped bead either prior to or following the experiment. Molecular extension (x) was calculated by correcting displacement (z) according to force (F) and trap stiffness (k) as

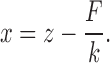Data were processed with LabView and IgorPro (WaveMetrics, Lake Oswego, OR, USA).

RESULTS

Dynamics of melting and reannealing measured under force feedback

It has previously been shown that in torsionally unconstrained λ-DNA in solution with physiological salt concentration the S-form of DNA gradually converts to melted DNA as force is kept above the overstretching transition (8,11,25,26) Under force clamp this occurs without a significant increase in length (see Figure 5 in (11)) because, even though S-DNA and ssDNA are characterized by different force-extension relations, they have a very similar extension in the region of forces of the overstretching transition ((5,7); and see Supplementary Figure S1 in Supplementary Data). The degree of melting in the overstretched molecule can be estimated from the amplitude of the slow phase of the shortening transient elicited by a stepwise force drop below the overstretching region (see also (11)). This is made evident by the experiment shown in Figure 1A. First, a stretch at constant velocity (V = 1 μm/s) is imposed on the double-stranded λ-DNA molecule to attain a force just above the overstretching force (72 pN), then the control is switched to force feedback (time marked by the dashed line) and a sequence of 25-pN stepwise force drops alternating with identical size stepwise force pulls is imposed on the molecule. The time during which force is kept at the high level (t_h) is varied at random from 1 s to 20 s, while the time at low force is kept constant at 10 s, long enough for complete reannealing and recovery of the equilibrium length of dsDNA (see Figure 1E in (11)). In the record of Figure 1A, t_h is 10 s (red), 1 s (green) and 5 s (blue). The corresponding force-extension curves are shown in Figure 1B. As emphasized by superimposing the shortening transients (Figure 1C), the fraction of the molecule that has undergone only the reversible B-S transition, measured by the amplitude of the stepwise shortening that appears simultaneous with the force drop (for a faster time scale see Supplementary Figure S2), progressively reduces with the increase in t_h, while the fraction that melted, measured by the amplitude of the slow component of the shortening transient (L_m), increases with t_h. When L_m is plotted against t_h (Figure 1D) it shows an almost direct proportionality. L_m is zero (and the initial stepwise shortening is 100% of the lengthening undergone by the B-S transition) if no melting has occurred during the overstretching period, that is for t_h smaller than ∼1.8 s, as shown by the abscissa intercept of the linear fit to data for t_h ≥ 2 s.

Figure 5. — Schematic drawing of the reannealing process. (A) DNA segment in which the double-stranded configuration is interrupted in correspondence of an AT-barrier followed by a portion with a dangling strand. (B) Intermediate state with formation of two single-stranded 10-AT-segments due to the pairing of the next CG bases. This causes the halving of force on the stretched poly-AT strand, so that the molecule shortens by x^‡ (yellow arrow). (C) Immediate base-pairing of the poly-AT segment and of the dangling strand until, after ∼750 bp, the next AT-barrier is met. The molecule shortens by a ΔL_c of (750·0.23 nm ∼) 170 nm (green arrow).

L _m is composed of a series of shortening steps separated by pauses, indicating the presence of a rate-limiting process followed by a much faster reannealing step, almost instantaneous within the temporal resolution of the experimental apparatus. In other words, a fast re-zipping process, akin to re-zipping at 0 force (above 107 bp/s according to (27)) is episodically halted by the presence of some intermediate energetic or configurational bottleneck.

The relevant parameters describing the kinetics of reannealing are, as shown in Figure 1E, the size of the shortening step (Δx) and the waiting time (t_w) between consecutive steps.

How the kinetics of reannealing depends on force was investigated by varying the low-force level (F_L) attained by the force drop. For all the records in Figure 1F the high force level is kept at 72 pN for 10 s then force is dropped to F_L of either 44 pN (green), 46 pN (red) or 53 pN (blue). It can be seen that L_m is quite similar in all the three responses (as expected since both melting-inducing parameters, the high force level and t_h, are the same), while the time taken by the slow phase to attain the equilibrium length increases with F_L from 2 s (green) to 27 s (blue).

Kinetics of reannealing

The shortening transients recorded with the protocols described in Figure 1 are analyzed in terms of the parameters t_w and Δx (Figure 1E) to define the reannealing kinetics. The complemented cumulative probability distribution of t_w (1 − cumulative distribution, CCD in the following) for four different levels of F_L: 37 pN (blue), 42 pN (red), 47 pN (black) and 52 pN (magenta) is plotted in Figure 2A (data are from 6 molecules for each F_L value, 5 cycles per molecule). The parameter CCD is preferred over the cumulative probability distribution because the complementation favors the visualization on log scale of the exponential decay at large waiting times. The multiplicity of slopes in the log plot of CCD corresponds to a multiplicity of time constants (see Supplementary Figure S3A). It can be seen that, independently of F_L, all curves show a complex multi-exponential shape characterized by an early—almost exponential—decay followed by a smooth change in slope and ending with a much slower exponential decay. All decay rates in both the fast and the slow region of the spectrum decrease with the increase of F_L. The curves, however, remain fundamentally invariant in shape as shown in the inset, where the probabilities are shown to collapse on the same master curve following the normalization for the average waiting time at each F_L, 〈t_w〉. In other words, the spectrum of decay rates uniformly extends in all its components with the increase of F_L.

Figure 2. — Analysis of the kinetic parameters of reannealing. (A) Complemented integrated probability density (CCD, 1 - cumulative distribution) of t_w at the four F_L, defined by the color code in the inset. The gradual change in slope of the curves indicates a multiplicity of time scales, with the fastest scale accounting for at least 70% of the population at each F_L. Inset: the same distribution after normalization of t_w for 〈t_w〉, the average value at each F_L. (B) Rate constant of reannealing, k_f ( = 1/〈t_w〉), in logarithmic scale, as a function of F_L. The line is the fit with Equation (1). The estimates of the slope and ordinate intercept (In(A)) are 0.139 ± 0.001 and 8.04 ± 0.06, respectively. (C) Probability density function (PDF) of the amplitudes of the reannealing segment at the four F_L (color code as in A). The continuous lines are fits with Erlang distribution functions. Inset: Amplitudes normalized for the average amplitude at each F_L (〈ΔL_c〉). (D) Relations between ln (k_f) and F_L at different ionic strengths: magenta 25 mM NaCl, blue 150 mM (from Figure 2B), orange 300 mM.

The most relevant contribution (>50%) to the slow-phase shortening is accounted for by the fastest decay rate (k_f), which is the one taken into consideration here for further analysis. All decay rates, however, display the same dependence on force, so that similar conclusions are obtained if the analyses are made on either the entire rate population or the slowest component (see Supplementary Figure S3B). Further comments on the origin of the multi-exponential distribution are made in the last section of the SI. This demonstrates in turn that, in the range of F_L investigated, the frequency response of our mechanical system is adequate to record in the whole range of the frequency domain of the responses. Further comments on the origin of the multi-exponential distribution are made in the last section of the SI. k_f exhibits an exponential dependence on F_L as shown by the linear relation obtained when ln(k_f) is plotted versus F_L (Figure 2B), suggesting that the kinetics of the reannealing process can be explained by a two-state transition according to the Kramers–Bell theory. According to the classical two-state theory, both the forward and backward transition rate constants depend exponentially on force. In this case, however, only the backward rate constant, from the melted state (M) to a double-stranded transition state (S’), is accessible, since the forward reaction, melting, is undetectably improbable at the imposed F_L.

The corresponding equation is:

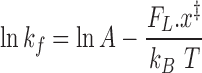(1)

where x^‡ is the distance from the melted to the transition state (that is the slope of the ln(k_f) – F_L relation), k_B is the Boltzmann constant, T is absolute temperature and A (s⁻¹) is the rate constant at zero force. The fit of Equation (1) to data in Figure 2B (blue line) gives an estimate of the slope (0.13 ± 0.02 s⁻¹ pN⁻¹) from which a distance (x^‡) of 0.58 ± 0.05 nm between M and S’ state can be calculated.

Size of the reannealing segments

Although we measure changes in molecular extension (Δx), the appropriate parameter to describe molecular shortening is the change in contour length, ΔL_c. The elastic model allowing the conversion to ΔL_c is presented in detail in the Supplementary Data. A statistical analysis of the shortening steps during the slow phase of the response to the force drop is reported in Figure 2C, where the normalized frequency histogram of ΔL_c (the probability density function, PDF) is plotted for the four F_L (colour code as in Figure 2A). Data are fit by four Erlang distributions with shape parameter 3 and rate parameters 0.012, 0.020, 0.029, 0.035 μm⁻¹ for 37, 42, 47 and 52 pN, respectively. A decrease of the observed shortening amplitude with the increase in force is evident from the reduction in ΔL_c peak frequency from 156 nm at F_L = 37 pN to 81 nm at F_L = 52 pN. Due to the skewness of the distributions, the corresponding average values (〈ΔL_c〉) are larger: 〈ΔL_c〉 ranges from 246 to 90 nm in the same range of F_L. The average value of ΔL_c for all data pooled together is 132 ± 2 nm for an average value of F_L of 45 pN. It is worth noting that, similarly to the t_w distributions in Figure 2A, the distributions of the shortening steps also rescale on the same master curve when dividing the abscissa for the average value at each F_L (inset in Figure 2C).

In these experiments λ-DNA is attached to the beads via the 3′ ends, so that melting during the high force period may have occurred starting from both 5′ ends as well as from nicks occurring in the sugar–phosphate backbone. Consequently, reannealing may occur at several points, making it impossible for a given shortening to identify which strand, and what point within the strand, is reannealing. On the other hand, in the range of F_L investigated, the kinetics of shortening events is so slow that the probability of two events to occur simultaneously is essentially zero, so that the probability distribution of ΔL_c in Figure 2C properly describes the characteristics of unitary events.

Kinetics of reannealing is independent of ionic strength

The mechanism underlying the transient kinetics has been first investigated by repeating the protocol at different ionic strengths, to modulate the strength of electrostatic interactions. The repulsion between the negatively charged sugar–phosphate backbones of the two strands decreases with the ionic strength, and this is the reason why melting probability increases upon overstretching at reduced ionic strength (28). Similarly, a reduced ionic strength could reduce the reannealing probability at the same F_L. As shown in Figure 2D, k_f is not significantly affected by either a reduction of ionic strength to 25 mM (magenta) or an increase to 300 mM (orange). Fitting the corresponding data in Figure 2D provides estimates for x^‡ of 0.49 ± 0.07 nm (magenta) and 0.53 ± 0.06 nm (orange), respectively. Both values are slightly but not significantly lower (P > 0.1) than the value 0.58 ± 0.06 nm, found with physiological ionic strength. This is in agreement with the previous results of experiments conducted in length clamp on designed constructs (7). It was shown that, following stretch-induced melting, re-hybridization occurs at a low force (∼20 pN) that, in contrast to melting, is rather insensitive to changes in ionic strength. In the absence of ionic-strength dependence it is quite likely that the reannealing process is controlled by a mechanism that provides the same structure of the transition state regardless of the strength of electrostatic interactions, most likely via a sequence-dependent mechanism.

Assessing the role of base sequence

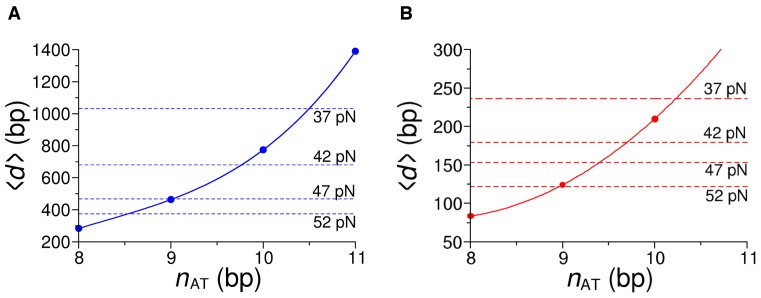
DNA reannealing in the absence of force is reported to take place sequentially at very fast rates (∼10⁷ bp/s (27)). The pauses in the slow phase of the shortening response (Figure 1B and D) show that, under the stress imposed on the molecule by our force feedback, sequential reannealing spontaneously halts and resumes. Considering that each AT base pair provides only two hydrogen bonds, and thus a smaller free energy decrease for the double strand formation, it is likely that the obstacle that stops sequential reannealing is made by a sufficiently large number of consecutive AT base pairs that constitutes a so-called ‘AT-barrier’. The average size of the stepwise shortening resumed after each pause is 132 nm, which, considering a shortening of 0.23 nm per bp, corresponds to the reannealing of (∼132/0.23) of 570 bp. Sequence analysis of λ-phage DNA (see Supplementary Data for details) allows the definition of the relation between the average distance 〈d〉 separating sequences of more than a given number of consecutive AT bases (n_AT) and n_AT (Figure 3A, blue dots). The relation shows that the number of consecutive AT bases distant at least 570 bp is 9.5; accordingly, if the barrier is constituted by a poly-AT segment of 10 or more bases, it should be followed by the reannealing of at least 750 bp, which corresponds to the average ΔL_c of 170 nm.

Figure 3. — Relation between the average distance 〈d〉 separating sequences of more than a given number of consecutive AT bases (n_AT) and n_AT. 〈d〉 and n_AT are determined with sequence analysis of the λ-DNA molecule (A, blue dots) and for the AT-rich construct (B, red dots). The continuous lines are cubic fits to the data. The dashed lines mark the average extension of the reannealing strands for each F_L, as indicated by the values next to the lines.

To test the dependence of the reannealing process on the sequence and the consistency of the AT-barrier mechanism we performed the same stretch-release experiment under force feedback on a portion of the λ-DNA molecule with an increased AT proportion. A 3582 bp-long portion of the molecule with the proportion of AT increased from 50% to 64% has been selected. Sequence analysis on this DNA construct (Figure 3B, red dots) shows that the average distance between poly-AT segments exceeding 10 bp is reduced to 210 bp, almost 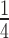Inline graphic of the values found for the whole λ-DNA (see Figure 3A). Since at ionic strengths ≤1M the AT-rich construct undergoes complete peeling during stretch and no reannealing can be observed in the same force range as that used for the whole λ-DNA molecule, these experiments were made with ionic strength increased to 1.5M. Figure 4A shows the shortening transients elicited when force is dropped from 83 pN (t_h = 2 s) to either 37 pN (green trace) or 57 pN (red trace). For the AT-rich construct, just as for λ-DNA, the time taken for the slow phase to attain the dsDNA equilibrium length (the time for the complete reannealing) increases with F_L. The analysis on t_w conducted in the AT-rich construct gives the ln(k_f) - F_L relation shown by red circles in Figure 4B. In comparison to the relation for the λ-DNA molecule (blue circles from Figure 2B), it can be seen that, even if all the points for the AT-rich construct lie above those for the λ-DNA, their dependence on force is unchanged. In fact the slope of the fit with Equation (1) gives a barrier distance of 0.58 ± 0.06 nm, which is almost identical to that of the whole λ-DNA molecule regardless the sequence composition.

The average amplitude of shortening steps 〈ΔL_c〉 for the AT-rich construct is reported in Figure 4C as a function of force (red circles) together with the corresponding λ-DNA data (blue circles). For both the AT-rich construct and the whole λ-DNA 〈ΔL_c〉 decreases by a factor of 2 in the F_L range 37–52 pN. Most importantly, at any F_L, 〈ΔL_c〉 of the AT-rich construct is ∼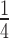 Inline graphic that of λ-DNA, as predicted by the sequence analysis (compare Figure 3A and B).

The upward shift in the k_f – F_L relation of the AT-rich construct with respect to λ-DNA (Figure 4B) should be accounted for by the influence of viscosity (see Supplementary Data). When the reannealing rates are plotted versus 〈ΔL_c〉 in double logarithmic scale (Supplementary Figure S6), data at the same force can be fit with the hyperbolic dependence k_f ∼1/ΔL_c. The few data points available at any given F_L are compatible with a power law dependence; more precisely, at any given F_L the k_f depends on the inverse of the size of the molecule. This is indicative of a viscous effect and suggests that the reannealing rates depend not only on the size of the transition barrier, but also on the length of the entire dangling strand, whose size limits the opening/closing rate of the fork at the junction between two complementary strands. In the last section of the Supplementary Data we will comment on the influence of viscosity on the multi-exponential nature of the t_w distribution.

DISCUSSION

Structural basis of the transition barrier and the mechanism to overcome it

The time course of the reannealing of torsionally unconstrained λ-DNA and its dependence on force has been determined by exploiting our fast force feedback. We found that the complex shortening transient following the force drop to a level below the overstretching region (F_L) can be explained, as previously hypothesized (11), by two processes occurring sequentially at different points along the molecule: (i) a rate-limiting reannealing of melted segments, which leads to the recovery of the double-stranded form (S’) and (ii) the subsequent abrupt (stepwise) recovery of the shorter length as expected at forces a few piconewtons below the overstretching force at which the dsDNA transition to the compact B-form takes a few milliseconds (12). As regards the nature of the transient intermediate S’ state, it cannot be identified as the double-stranded S state because, extrapolating the rate-force relation of the S to B transition (12) at the forces (F_L) considered here the S state is undetectably short-lived. On the other hand, a molecular dynamics simulation (29) shows that the free-energy barrier separating S- from B-DNA only arises at forces close to the overstretching region, questioning the existence of the S state at the F_L considered here.

The analysis of the waiting time between the shortening steps indicates that the rate of reannealing distributes exponentially with an average rate k_f that depends on F_L according to a two-state reaction kinetics that allows the estimate of the distance to the transition state x^‡. x^‡ is 0.58 nm for both the whole λ-DNA and for the AT-rich construct of 3852 bp. Since the base pair extension of ssDNA is ∼0.6 nm and that of B-DNA is 0.34 nm, the ss to B transition of two base pairs would easily account for the observed x^‡. This hypothesis, however, cannot be reconciled with the several hundreds of bp involved in the following shortening step. In fact, all possible stopping sequences of two or three base pairs are much more frequent than the average distances of hundreds of bp inferred from the shortening step.

On the other hand, statistical analysis of the sequence provides useful insights on the structural nature of the transition barrier and the mechanism to overcome it. The four times difference in the observed extension of the reannealing segments for the whole λ-DNA and the AT-rich construct (Figures 3 and 4C) can be explained if poly-AT segments ∼10 bp long act as barriers that temporary halt reannealing. How does the poly-AT barrier emerging from sequence analysis reconcile with the finding from the kinetic analysis that the distance of the M-S’ transition is 0.58 nm? The question can be solved if one assumes that the x^‡ accompanying the M to S’ transition does not arise from a ss to B transition but from the relief of tension from the strand under load, as it would happen if the S’ state is made by two uncoupled single DNA strands (2ssDNA) sharing the mechanical load. The force-extension relations of ssDNA and 2ssDNA can be predicted using two freely-jointed chain (FJC) models (see Supplementary Figure S4) and indicate that, at the level of the imposed F_L, the difference in extension per bp is ∼0.055 nm. In this case x^‡ = 0.58 nm indicates that the transition involves ∼10 bp, a conclusion converging with that from the sequence analysis applied to the size of the reannealing strand, which indicates that the barrier is a poly-AT segment 10 bp-long. This conclusion provides also the clue for describing the structural basis of the transition state and the mechanism by which a melted segment (Figure 5A) overcomes the transition barrier (red). Two single-stranded 10-AT-segments can be formed when the first few CG bases of the dangling strand following the AT barrier get close enough to their complementary partners on the strand under tension for undergoing base pairing (Figure 5B). This causes both the halving of the force on the stretched poly-AT strand (with the 0.58 nm shortening and base pairing with the complementary strand) and the rapid double strand formation/shortening of the subsequent 750 bp segment (Figure 5C). The same mechanism operates in the 3582 bp-long DNA portion that has an increased proportion of AT bases (64% instead of 50%). In this case, however, the rapid shortening following the transition state will be reduced to 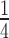Inline graphic according to the reduction of the distance between segments of more than 10 consecutive AT bases.

In principle, one might expect that also other AT-rich motifs, such as 5AT 1GC 8AT, could act as effective AT-barriers. To evaluate how strict the constrain of a pure AT-barrier is, the sequence analysis was applied to hybrid segments as that mentioned above. Consistently, the expected average distance decreases sharply and the expected shortening doesn't match any more that observed. Apparently, therefore, the presence of even a single CG base pair provides to the dangling strand an easily reachable intermediate anchor point for the efficient crossing of the AT-barrier.

Force dependence of the size of the AT-barrier

If AT barriers determine the number and extent of separate reannealing events, it is unclear why the subsequent average shortening 〈ΔL_c〉 varies by a factor of 2 in the explored force range (Figure 4C). The quantity and distribution of AT barriers along the DNA molecule is determined solely by the base sequence, which doesn't vary with force. However, slight changes in the size of the AT barriers explain the observed force dependence. Statistical analysis of the sequence of λ-DNA (see Supplementary Data) defines how the average distance between successive poly-AT segments (<d>) is related to the size in bp of the segments (n_AT) (Figure 3A, blue dots). The continuous line is a cubic fit to the data. The horizontal dashed lines intersecting the curve are drawn in correspondence of the distance calculated from the average shortening steps at each F_L (blue circles in Figure 4C). The intersection points give the expected average extension of n_AT that halts reannealing at any force level, as predicted by sequence analysis. The n_AT - F_L relation is shown by blue squares in Figure 4D. Error bars reflect the propagation of the experimental errors through the interpolation procedure and are mainly determined by the position uncertainty induced by the force feedback that amounts to ∼10 nm at each force. This analysis shows that the size of the AT-barrier actually increases with the reduction of force: in the range of force used it increases from ∼8.5 bases (at 52 pN) to ∼10.5 bases (at 37 pN). The sequence analysis applied to the AT-rich construct provides the 〈d〉 – n_AT relation shown in Figure 3B. In this case the intersection of the curve with the average extensions of reannealing strands at each F_L (red circles in Figure 4C) provides the n_AT values that are reported as red squares in Figure 4D. The n_AT – F_L relations for the AT-rich construct and the whole λ-DNA molecule coincide within the experimental error, indicating that the mechanism that defines the barrier is the same for both molecules independently of the 4 times difference in the extension of the reannealing strand. This finding is per se a demonstration of the robustness of the analysis and of the hypothesis that explains the reannealing kinetics in terms of the AT-barrier.

CONCLUSIONS

Following a force drop to values below the overstretching transition, reannealing of partially melted DNA occurs via discrete shortening steps separated by exponentially distributed time intervals. Kinetic analysis based on Kramers–Bell theory of two state transition reveals a transition barrier 0.58 nm long, while statistical analysis of the shortening steps gives an average reannealing-step size of ∼750 bp, consistent with the average bp interval separating segments of more than 10 consecutive AT bases. In an AT-rich DNA construct, in which the distance between segments of more than 10 consecutive AT is reduced to ∼210 bp, the reannealing-step size reduces accordingly without changes in the extension of the transition barrier. Thus, the transition barrier for reannealing is determined by the presence of segments of more than 10 consecutive AT bp, independent of changes in sequence composition, while the length of the reannealing strand changes according to the distance between poly-AT segments at least 10 bp long.

The size of the transition barrier suggests a mechanism for overcoming the 10-AT-barrier: base pairing of the CG bases immediately following the AT-barrier redistributes the force between the two strands of the poly-AT segment. The consequent halving of the force on either strand implies, according to the differences between the force-extension relations of ssDNA and 2ssDNA a shortening of ∼0.055 nm per bp, that is, for the 10 AT segment, of 0.55 nm, which corresponds to the length of the transition barrier obtained from the kinetic analysis.

Supplementary Material

SUPPLEMENTARY DATA

supp_44_16_7954__index.html^{(769B, html)}

Acknowledgments

The authors thank Mario Dolfi for technical assistance and Gabriella Piazzesi for comments on the manuscript.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Ente Cassa di Risparmio di Firenze [2010-1402, Italy]. Funding for open access charge: Department of Biology, University of Florence, Via Madonna del Piano 6, 50019 Sesto Fiorentino, Italy.

Conflict of interest statement. None declared.

REFERENCES

1.Smith S.B., Cui Y., Bustamante C. Overstretching B-DNA: the elastic response of individual double-stranded and single-stranded DNA molecules. Science. 1996;271:795–799. doi: 10.1126/science.271.5250.795. [DOI] [PubMed] [Google Scholar]
2.Cluzel P., Lebrun A., Heller C., Lavery R., Viovy J.L., Chatenay D., Caron F. DNA: an extensible molecule. Science. 1996;271:792–794. doi: 10.1126/science.271.5250.792. [DOI] [PubMed] [Google Scholar]
3.Léger J.F., Romano G., Sarkar A., Robert J., Bourdieu L., Chatenay D., Marko J.F. Structural transitions of a twisted and stretched DNA molecule. Phys. Rev. Lett. 1999;83:1066. [Google Scholar]
4.Sarkar A., Leger J.F., Chatenay D., Marko J.F. Structural transitions in DNA driven by external force and torque. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2001;63:051903. doi: 10.1103/PhysRevE.63.051903. [DOI] [PubMed] [Google Scholar]
5.Cocco S., Yan J., Leger J.F., Chatenay D., Marko J.F. Overstretching and force-driven strand separation of double-helix DNA. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2004;70:011910. doi: 10.1103/PhysRevE.70.011910. [DOI] [PubMed] [Google Scholar]
6.van Mameren J., Gross P., Farge G., Hooijman P., Modesti M., Falkenberg M., Wuite G.J., Peterman E.J. Unraveling the structure of DNA during overstretching by using multicolor, single-molecule fluorescence imaging. Proc. Natl. Acad. Sci. U.S.A. 2009;106:18231–18236. doi: 10.1073/pnas.0904322106. [DOI] [PMC free article] [PubMed] [Google Scholar]
7.Bosaeus N., El-Sagheer A.H., Brown T., Smith S.B., Åkerman B., Bustamante C., Nordén B. Tension induces a base-paired overstretched DNA conformation. Proc. Natl. Acad. Sci. U.S.A. 2012;109:15179–15184. doi: 10.1073/pnas.1213172109. [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Fu H., Chen H., Marko J.F., Yan J. Two distinct overstretched DNA states. Nucleic Acids Res. 2010;38:5594–5600. doi: 10.1093/nar/gkq309. [DOI] [PMC free article] [PubMed] [Google Scholar]
9.Paik D.H., Perkins T.T. Overstretching DNA at 65 pN does not require peeling from free ends or nicks. J. Am. Chem. Soc. 2011;133:3219–3221. doi: 10.1021/ja108952v. [DOI] [PubMed] [Google Scholar]
10.Zhang X., Chen H., Le S., Rouzina I., Doyle P.S., Yan J. Revealing the competition between peeled ssDNA, melting bubbles, and S-DNA during DNA overstretching by single-molecule calorimetry. Proc. Natl. Acad. Sci. U.S.A. 2013;110:3865–3870. doi: 10.1073/pnas.1213740110. [DOI] [PMC free article] [PubMed] [Google Scholar]
11.Bongini L., Melli L., Lombardi V., Bianco P. Transient kinetics measured with force steps discriminate between double-stranded DNA elongation and melting and define the reaction energetics. Nucleic Acids Res. 2014;42:3436–3449. doi: 10.1093/nar/gkt1297. [DOI] [PMC free article] [PubMed] [Google Scholar]
12.Bianco P., Bongini L., Melli L., Dolfi M., Lombardi V. Piconewton-millisecond force steps reveal the transition kinetics and mechanism of the double-stranded DNA elongation. Biophys. J. 2011;101:866–874. doi: 10.1016/j.bpj.2011.06.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
13.King G.A., Gross P., Bockelmann U., Modesti M., Wuite G.J., Peterman E.J. Revealing the competition between peeled ssDNA, melting bubbles, and S-DNA during DNA overstretching using fluorescence microscopy. Proc. Natl. Acad. Sci. U.S.A. 2013;110:3859–3864. doi: 10.1073/pnas.1213676110. [DOI] [PMC free article] [PubMed] [Google Scholar]
14.Whitelam S., Pronk S., Geissler P.L. There and (slowly) back again: entropy-driven hysteresis in a model of DNA overstretching. Biophys. J. 2008;94:2452–2469. doi: 10.1529/biophysj.107.117036. [DOI] [PMC free article] [PubMed] [Google Scholar]
15.Clausen-Schaumann H., Rief M., Tolksdorf C., Gaub H.E. Mechanical stability of single DNA molecules. Biophys. J. 2000;78:1997–2007. doi: 10.1016/S0006-3495(00)76747-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
16.Zhang X., Qu Y., Chen H., Rouzina I., Zhang S., Doyle P.S., Yan J. Interconversion between three overstretched DNA structures. J. Am. Chem. Soc. 2014;136:16073–16080. doi: 10.1021/ja5090805. [DOI] [PubMed] [Google Scholar]
17.Bockelmann U., Thomen P., Essevaz-Roulet B., Viasnoff V., Heslot F. Unzipping DNA with optical tweezers: high sequence sensitivity and force flips. Biophys. J. 2002;82:1537–1553. doi: 10.1016/S0006-3495(02)75506-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
18.Woodside M.T., Anthony P.C., Behnke-Parks W.M., Larizadeh K., Herschlag D., Block S.M. Direct measurement of the full, sequence-dependent folding landscape of a nucleic acid. Science. 2006;314:1001–1004. doi: 10.1126/science.1133601. [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Danilowicz C., Coljee V.W., Bouzigues C., Lubensky D.K., Nelson D.R., Prentiss M. DNA unzipped under a constant force exhibits multiple metastable intermediates. Proc. Natl. Acad. Sci. U.S.A. 2003;100:1694–1699. doi: 10.1073/pnas.262789199. [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Huguet J.M., Bizarro C.V., Forns N., Smith S.B., Bustamante C., Ritort F. Single-molecule derivation of salt dependent base-pair free energies in DNA. Proc. Natl. Acad. Sci. U.S.A. 2010;107:15431–15436. doi: 10.1073/pnas.1001454107. [DOI] [PMC free article] [PubMed] [Google Scholar]
21.Smith S.B., Finzi L., Bustamante C. Direct mechanical measurements of the elasticity of single DNA molecules by using magnetic beads. Science. 1992;258:1122–1126. doi: 10.1126/science.1439819. [DOI] [PubMed] [Google Scholar]
22.Rozen S., Skaletsky H. Primer3 on the WWW for general users and for biologist programmers. Methods Mol. Biol. 2000;132:365–386. doi: 10.1385/1-59259-192-2:365. [DOI] [PubMed] [Google Scholar]
23.Benson D.A., Karsch-Mizrachi I., Lipman D.J., Ostell J., Sayers E.W. GenBank. Nucleic Acids Res. 2011;39:D32–3D37. doi: 10.1093/nar/gkq1079. [DOI] [PMC free article] [PubMed] [Google Scholar]
24.Bianco P., Bongini L., Melli L., Falorsi G., Salvi L., Cojoc D., Lombardi V. Novel Approaches for Single Molecule Activation and Detection. Berlin Heidelberg: Springer; 2014. pp. 123–147. [Google Scholar]
25.Fu H., Chen H., Zhang X., Qu Y., Marko J.F., Yan J. Transition dynamics and selection of the distinct S-DNA and strand unpeeling modes of double helix overstretching. Nucleic Acids Res. 2011;39:3473–3481. doi: 10.1093/nar/gkq1278. [DOI] [PMC free article] [PubMed] [Google Scholar]
26.Bosaeus N., El-Sagheer A.H., Brown T., Akerman B., Norden B. Force-induced melting of DNA–evidence for peeling and internal melting from force spectra on short synthetic duplex sequences. Nucleic Acids Res. 2014;42:8083–8091. doi: 10.1093/nar/gku441. [DOI] [PMC free article] [PubMed] [Google Scholar]
27.Betterton M.D., Julicher F. Opening of nucleic-acid double strands by helicases: active versus passive opening. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;71:011904. doi: 10.1103/PhysRevE.71.011904. [DOI] [PubMed] [Google Scholar]
28.Wenner J.R., Williams M.C., Rouzina I., Bloomfield V.A. Salt dependence of the elasticity and overstretching transition of single DNA molecules. Biophys. J. 2002;82:3160–3169. doi: 10.1016/S0006-3495(02)75658-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
29.Bongini L., Lombardi V., Bianco P. The transition mechanism of DNA overstretching: a microscopic view using molecular dynamics. J. R. Soc. Interface. 2014;11:20140399. doi: 10.1098/rsif.2014.0399. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

SUPPLEMENTARY DATA

supp_44_16_7954__index.html^{(769B, html)}

supp_gkw604_nar-00938-f-2016-File003.pdf^{(764KB, pdf)}

[B1] 1.Smith S.B., Cui Y., Bustamante C. Overstretching B-DNA: the elastic response of individual double-stranded and single-stranded DNA molecules. Science. 1996;271:795–799. doi: 10.1126/science.271.5250.795. [DOI] [PubMed] [Google Scholar]

[B2] 2.Cluzel P., Lebrun A., Heller C., Lavery R., Viovy J.L., Chatenay D., Caron F. DNA: an extensible molecule. Science. 1996;271:792–794. doi: 10.1126/science.271.5250.792. [DOI] [PubMed] [Google Scholar]

[B3] 3.Léger J.F., Romano G., Sarkar A., Robert J., Bourdieu L., Chatenay D., Marko J.F. Structural transitions of a twisted and stretched DNA molecule. Phys. Rev. Lett. 1999;83:1066. [Google Scholar]

[B4] 4.Sarkar A., Leger J.F., Chatenay D., Marko J.F. Structural transitions in DNA driven by external force and torque. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2001;63:051903. doi: 10.1103/PhysRevE.63.051903. [DOI] [PubMed] [Google Scholar]

[B5] 5.Cocco S., Yan J., Leger J.F., Chatenay D., Marko J.F. Overstretching and force-driven strand separation of double-helix DNA. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2004;70:011910. doi: 10.1103/PhysRevE.70.011910. [DOI] [PubMed] [Google Scholar]

[B6] 6.van Mameren J., Gross P., Farge G., Hooijman P., Modesti M., Falkenberg M., Wuite G.J., Peterman E.J. Unraveling the structure of DNA during overstretching by using multicolor, single-molecule fluorescence imaging. Proc. Natl. Acad. Sci. U.S.A. 2009;106:18231–18236. doi: 10.1073/pnas.0904322106. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B7] 7.Bosaeus N., El-Sagheer A.H., Brown T., Smith S.B., Åkerman B., Bustamante C., Nordén B. Tension induces a base-paired overstretched DNA conformation. Proc. Natl. Acad. Sci. U.S.A. 2012;109:15179–15184. doi: 10.1073/pnas.1213172109. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B8] 8.Fu H., Chen H., Marko J.F., Yan J. Two distinct overstretched DNA states. Nucleic Acids Res. 2010;38:5594–5600. doi: 10.1093/nar/gkq309. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B9] 9.Paik D.H., Perkins T.T. Overstretching DNA at 65 pN does not require peeling from free ends or nicks. J. Am. Chem. Soc. 2011;133:3219–3221. doi: 10.1021/ja108952v. [DOI] [PubMed] [Google Scholar]

[B10] 10.Zhang X., Chen H., Le S., Rouzina I., Doyle P.S., Yan J. Revealing the competition between peeled ssDNA, melting bubbles, and S-DNA during DNA overstretching by single-molecule calorimetry. Proc. Natl. Acad. Sci. U.S.A. 2013;110:3865–3870. doi: 10.1073/pnas.1213740110. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B11] 11.Bongini L., Melli L., Lombardi V., Bianco P. Transient kinetics measured with force steps discriminate between double-stranded DNA elongation and melting and define the reaction energetics. Nucleic Acids Res. 2014;42:3436–3449. doi: 10.1093/nar/gkt1297. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B12] 12.Bianco P., Bongini L., Melli L., Dolfi M., Lombardi V. Piconewton-millisecond force steps reveal the transition kinetics and mechanism of the double-stranded DNA elongation. Biophys. J. 2011;101:866–874. doi: 10.1016/j.bpj.2011.06.039. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B13] 13.King G.A., Gross P., Bockelmann U., Modesti M., Wuite G.J., Peterman E.J. Revealing the competition between peeled ssDNA, melting bubbles, and S-DNA during DNA overstretching using fluorescence microscopy. Proc. Natl. Acad. Sci. U.S.A. 2013;110:3859–3864. doi: 10.1073/pnas.1213676110. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B14] 14.Whitelam S., Pronk S., Geissler P.L. There and (slowly) back again: entropy-driven hysteresis in a model of DNA overstretching. Biophys. J. 2008;94:2452–2469. doi: 10.1529/biophysj.107.117036. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B15] 15.Clausen-Schaumann H., Rief M., Tolksdorf C., Gaub H.E. Mechanical stability of single DNA molecules. Biophys. J. 2000;78:1997–2007. doi: 10.1016/S0006-3495(00)76747-6. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B16] 16.Zhang X., Qu Y., Chen H., Rouzina I., Zhang S., Doyle P.S., Yan J. Interconversion between three overstretched DNA structures. J. Am. Chem. Soc. 2014;136:16073–16080. doi: 10.1021/ja5090805. [DOI] [PubMed] [Google Scholar]

[B17] 17.Bockelmann U., Thomen P., Essevaz-Roulet B., Viasnoff V., Heslot F. Unzipping DNA with optical tweezers: high sequence sensitivity and force flips. Biophys. J. 2002;82:1537–1553. doi: 10.1016/S0006-3495(02)75506-9. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B18] 18.Woodside M.T., Anthony P.C., Behnke-Parks W.M., Larizadeh K., Herschlag D., Block S.M. Direct measurement of the full, sequence-dependent folding landscape of a nucleic acid. Science. 2006;314:1001–1004. doi: 10.1126/science.1133601. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B19] 19.Danilowicz C., Coljee V.W., Bouzigues C., Lubensky D.K., Nelson D.R., Prentiss M. DNA unzipped under a constant force exhibits multiple metastable intermediates. Proc. Natl. Acad. Sci. U.S.A. 2003;100:1694–1699. doi: 10.1073/pnas.262789199. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B20] 20.Huguet J.M., Bizarro C.V., Forns N., Smith S.B., Bustamante C., Ritort F. Single-molecule derivation of salt dependent base-pair free energies in DNA. Proc. Natl. Acad. Sci. U.S.A. 2010;107:15431–15436. doi: 10.1073/pnas.1001454107. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B21] 21.Smith S.B., Finzi L., Bustamante C. Direct mechanical measurements of the elasticity of single DNA molecules by using magnetic beads. Science. 1992;258:1122–1126. doi: 10.1126/science.1439819. [DOI] [PubMed] [Google Scholar]

[B22] 22.Rozen S., Skaletsky H. Primer3 on the WWW for general users and for biologist programmers. Methods Mol. Biol. 2000;132:365–386. doi: 10.1385/1-59259-192-2:365. [DOI] [PubMed] [Google Scholar]

[B23] 23.Benson D.A., Karsch-Mizrachi I., Lipman D.J., Ostell J., Sayers E.W. GenBank. Nucleic Acids Res. 2011;39:D32–3D37. doi: 10.1093/nar/gkq1079. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B24] 24.Bianco P., Bongini L., Melli L., Falorsi G., Salvi L., Cojoc D., Lombardi V. Novel Approaches for Single Molecule Activation and Detection. Berlin Heidelberg: Springer; 2014. pp. 123–147. [Google Scholar]

[B25] 25.Fu H., Chen H., Zhang X., Qu Y., Marko J.F., Yan J. Transition dynamics and selection of the distinct S-DNA and strand unpeeling modes of double helix overstretching. Nucleic Acids Res. 2011;39:3473–3481. doi: 10.1093/nar/gkq1278. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B26] 26.Bosaeus N., El-Sagheer A.H., Brown T., Akerman B., Norden B. Force-induced melting of DNA–evidence for peeling and internal melting from force spectra on short synthetic duplex sequences. Nucleic Acids Res. 2014;42:8083–8091. doi: 10.1093/nar/gku441. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B27] 27.Betterton M.D., Julicher F. Opening of nucleic-acid double strands by helicases: active versus passive opening. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;71:011904. doi: 10.1103/PhysRevE.71.011904. [DOI] [PubMed] [Google Scholar]

[B28] 28.Wenner J.R., Williams M.C., Rouzina I., Bloomfield V.A. Salt dependence of the elasticity and overstretching transition of single DNA molecules. Biophys. J. 2002;82:3160–3169. doi: 10.1016/S0006-3495(02)75658-0. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B29] 29.Bongini L., Lombardi V., Bianco P. The transition mechanism of DNA overstretching: a microscopic view using molecular dynamics. J. R. Soc. Interface. 2014;11:20140399. doi: 10.1098/rsif.2014.0399. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

An AT-barrier mechanically controls DNA reannealing under tension

L Bongini

C Pongor

G Falorsi

I Pertici

M Kellermayer

V Lombardi

P Bianco

Abstract

INTRODUCTION

MATERIALS AND METHODS

Samples preparation and mechanical apparatus

RESULTS