Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Sep 20;6:33733. doi: 10.1038/srep33733

Room-Temperature All-solid-state Rechargeable Sodium-ion Batteries with a Cl-doped Na3PS4 Superionic Conductor

Iek-Heng Chu 1,*, Christopher S Kompella 1,*, Han Nguyen 1,*, Zhuoying Zhu 1, Sunny Hy 1, Zhi Deng 1, Ying Shirley Meng 1,a, Shyue Ping Ong 1,b
PMCID: PMC5028709  PMID: 27645565

Abstract

All-solid-state sodium-ion batteries are promising candidates for large-scale energy storage applications. The key enabler for an all-solid-state architecture is a sodium solid electrolyte that exhibits high Na+ conductivity at ambient temperatures, as well as excellent phase and electrochemical stability. In this work, we present a first-principles-guided discovery and synthesis of a novel Cl-doped tetragonal Na3PS4 (t-Na3−xPS4−xClx) solid electrolyte with a room-temperature Na+ conductivity exceeding 1 mS cm−1. We demonstrate that an all-solid-state TiS2/t-Na3−xPS4−xClx/Na cell utilizing this solid electrolyte can be cycled at room-temperature at a rate of C/10 with a capacity of about 80 mAh g−1 over 10 cycles. We provide evidence from density functional theory calculations that this excellent electrochemical performance is not only due to the high Na+ conductivity of the solid electrolyte, but also due to the effect that “salting” Na3PS4 has on the formation of an electronically insulating, ionically conducting solid electrolyte interphase.

Rechargeable all-solid-state sodium-ion batteries (ss-SIBs), which utilize ubiquitous sodium sources, are a promising low-cost, high-safety alternative to today’s lithium-ion batteries, especially for large-scale energy storage applications1,2,3,4,5. However, a critical challenge in the development of ss-SIBs is the lack of a sodium solid electrolyte with high ionic conductivity at ambient temperatures and a wide electrochemical window. Although oxide solid electrolytes such as β-alumina and NAtrium (or sodium) SuperIonic CONductors (NASICON) are well known, they exhibit reasonable ionic conductivities only at higher temperatures1,6,7,8,9,10. Moreover, their synthesis requires high-temperature processing to reduce the grain-boundary resistance, which is incompatible with traditional cathode materials and thus requires special fabrication procedures1.

Chalcogenide-based (S, Se) chemistries offer the potential for higher ionic conductivities than oxides11,12,13,14,15,16,17,18,19,20. Though it is likely that sulfide and selenide-based solid electrolytes may exhibit lower intrinsic electrochemical stability, the formation of passivating phases at the electrode-solid electrolyte interface can potentially mitigate further reactions21,22,23. Sulfide electrolytes, particularly sodium sulfides, also tend to be softer than oxides24, which allows intimate contact between electrode and solid electrolyte to be achieved via cold pressing instead of high-temperature sintering.

In recent years, several sodium superionic conductors with ionic conductivities approaching that of traditional organic electrolytes have been identified. For example, the cubic phase of Na3PS4 (c-Na3PS4) was first reported by Hayashi and co-workers in 2012 with a measured Na+ conductivity of 0.2 mS cm−1 25. The crystal structure of c-Na3PS4 has the 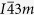Inline graphic space group and is the high-temperature26, disordered polymorph of tetragonal Na3PS4 (t-Na3PS4) with space group 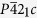Inline graphic27. Since the discovery of c-Na3PS4, there have been a number of successful efforts at further enhancing the room temperature conductivity of Na3PS4 systems26,28,29, with the highest value thus far of 0.74 mS cm−1 achieved within the (1-x)c-Na3PS4-xNa4SiS4 pseudo-binary system at x around 0.0629. A recent first principles investigation by some of the authors of this work proposed that Na-excess-induced Na disorder is the reason for the high conductivity observed in c-Na3PS4, and that Sn4+ cation doping (for P5+) may yield greater improvement in conductivity than Si4+ doping but at the expense of higher dopant formation energy30.

The introduction of defects via aliovalent doping is a common strategy to improve the ionic conductivity of materials. For Na3PS4, previous efforts have mainly focused on the cubic phase and the introduction of Na excess interstitials via substitution of P5+. An alternative strategy of aliovalent doping is to introduce Na+ vacancies in Na3PS4. Halide (X−) anion doping (for S2−) is a potential strategy for Na+ vacancy creation31. However, previous experimental efforts with (1-x)c-Na3PS4-xNaI glass-ceramics achieved a Na+ conductivity of ~0.1 mS cm−1 32, which is lower than that of the undoped and Si-doped c-Na3PS4. Furthermore, an unknown phase was found as the major precipitant when NaI was introduced at x ≥ 0.1, suggesting an intrinsic incompatibility of I− ions with the S2− host at such high doping levels.

In this work, we demonstrate the stable cycling of a TiS2/t-Na3−xPS4−xClx/Na ss-SIB at room temperature, with a capacity of about 80 mAh g−1 at a rate of C/10 over 10 cycles for the first time. The key enabler to this outstanding cell performance is a novel Cl-doped t-Na3PS4 solid electrolyte with formula Na2.9375PS3.9375Cl0.0625, which was developed using a tightly integrated combination of density functional theory (DFT) calculations, synthesis and characterization. From DFT calculations, we show that Cl− exhibits good chemical compatibility with the S2− host, with low dopant formation energy and similar ionic radius. The concomitant introduction of Na vacancies results in a predicted room-temperature Na+ conductivity exceeding 1 mS cm−1. These predictions are confirmed through experimental synthesis of tetragonal Na2.9375PS3.9375Cl0.0625, and its demonstration in a ss-SIB architecture. We will also present evidence from DFT computations that suggest that the superior performance achieved in this cell is not only the result of the high Na+ conductivity of the solid electrolyte, but also the formation of electronically-insulating, ionically-conducting passivation layers at the electrode-solid electrolyte interface due to the presence of the Cl− anion.

Results

Using DFT calculations, we first performed a systematic investigation of the dopability of potential halide X− (X = F, Cl, Br and I) into both the tetragonal and cubic phases of Na3PS4. As the DFT predictions for both phases are extremely similar, we will henceforth present only the results of the more stable tetragonal phase for brevity, and interested readers are referred to the Supplemental Information for the results on the cubic phase.

Dopability of Na3PS4

Figure 1 shows the crystal structure of t-Na3PS4. There are two symmetrically distinct Na sites in t-Na3PS4, Na1 (4d) and Na2 (2a), and the PS4 tetrahedra are centered at the 2b positions27. The symmetrically distinct Na sites in c-Na3PS4 are labeled similarly as cubic Na1 (6b) and Na2 (12d). The Na1 (4d) and Na2 (2a) sites in t-Na3PS4 essentially occupy the same positions as the Na1 (6b) sites in c-Na3PS431.

Figure 1. Crystal structure of pristine t-Na3PS4.

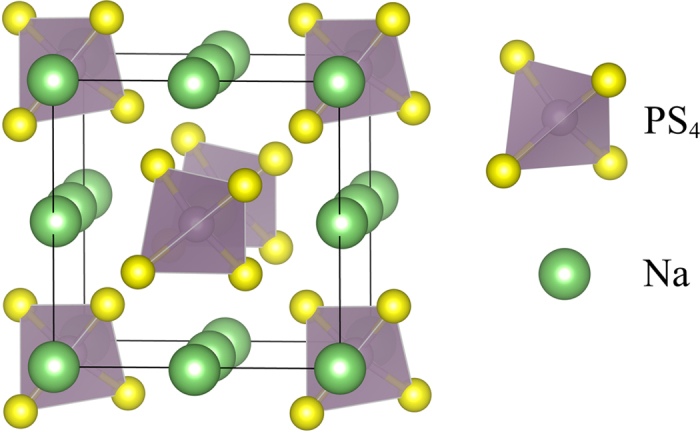
Figure 1

Open in a new tab

The tetragonal polymorph of the Na3PS4 crystal. There are symmetrically distinct Na sites in t-Na3PS4, Na1 (4d) and Na2 (2a), and the PS4 tetrahedra are centered at the 2b positions.

A single halide dopant was introduced into a 2 × 2 × 2 supercell of t-Na3PS4 by replacing one of the S atoms with X, and simultaneously a Na vacancy was introduced to form Na47P16S63X, or t-Na3−xPS4−xXx with x = 0.0625. All symmetrically distinct Inline graphic configurations (Kröger–Vink notation is adopted) were evaluated, and the lowest energy configuration was used for subsequent analyses.

Table 1 summarizes the halide dopant formation energies. We find that all halides (F, Cl, Br and I) are predicted to have relatively low formation energies at a doping level of x = 0.0625. Fluoride doping is predicted to be the most favorable (Ef = 0.76 eV/F−), followed by chloride (Ef = 0.96 eV/Cl−) and iodide (Ef = 0.99 eV/I−). Bromide doping is by far the least favorable with Ef = 1.11 eV/Br−. Higher doping levels result in a significantly higher dopant formation energy, e.g., Ef = 1.77 eV when doping Cl− in the same supercell size at x = 0.125. For all doped structures, the lowest energy structure has the X− anion substituted in the S2− (8e) site with a vacancy on the Na2 site. Nevertheless, the energy differences between different Inline graphic orderings are generally small (<10 meV/atom), which suggest that the dopants and vacancies are likely to be disordered at room temperature.

Table 1. Formation energies of anion dopants in t-Na3PS4.

Dopant RX/RS x (%) Ef (eV/dopant)
F 0.70 6.25 0.76
Cl 0.98 6.25 0.96
Br 1.07 6.25 1.11
I 1.21 6.25 0.99
Open in a new tab

Dopant formation energies Ef and ratio of halide to sulfide ionic radii (RX/RS) of the t-Na3−xPS4−xXx (X = F, Cl, Br and I) at x = 6.25%.

Despite the fact that F− doping is predicted to be the most favorable, we have selected Cl− doping for further investigation due to several considerations. First, NaCl, aka table salt, is by far a more commonly available precursor than NaF. Second, fluoride chemistry inherently comes the possibility of HF exposure. Finally, the Cl− anion has an ionic radius that is closest to S2−, which would minimize the local structural distortion introduced at the substituted site. The doping concentration of Cl is fixed at x = 0.0625, given that previous work in doping I− (which has a similar dopant formation energy at the same concentration) into c-Na3PS4 at x > 0.1 resulted in formation of unknown phases32.

Ionic conductivity of Cl-doped t-Na3PS4

As demonstrated in recent work by some of the co-authors30, pristine c-Na3PS4, i.e., without interstitial or vacancy defects, is predicted to be an extremely poor ionic conductor in AIMD simulations. Using AIMD simulations (see Methods section), a similar result is obtained with t-Na3PS4 in this work, which is not surprising given that the small differences in lattice parameters and atomic positions between the cubic and tetragonal polymorphs.

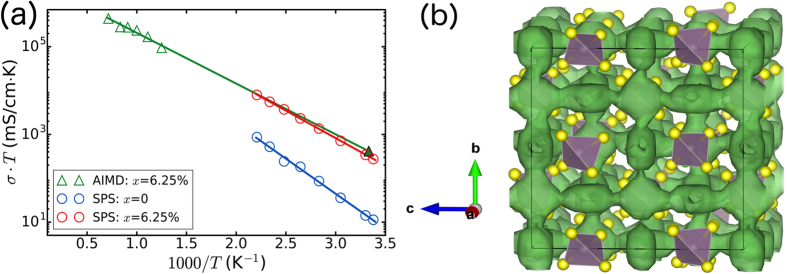
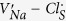Figure 2a shows the Arrhenius plot of the log of the conductivity-temperature product (Inline graphic) versus 1/T for t-Na2.9375PS3.9375Cl0.0625 obtained from AIMD simulations. With the introduction of a Inline graphic defect pair, the Na+ conductivity at 300 K is predicted to be 1.38 mS cm−1 with an activation barrier of 232 meV (see Table 2). During the preparation of this article, it has come to our attention that Klerk et al. has also performed AIMD simulations on halide doping in t- and c-Na3PS431. Though the qualitative conclusions of vacancy-induced conductivity are similar, we note that Klerk et al. only performed relatively short AIMD simulations at a single temperature of 525 K; room-temperature Na+ conductivities and activation energies were therefore not obtained.

Figure 2. Ionic conductivity and Li+ probability density distribution of t-Na3−xPS4−xClx.

Figure 2

Open in a new tab

(a) Arrhenius plots of the t-Na3−xPS4−xClx with x = 0 (blue) and 6.25% (red) obtained from SPS measurements, and x = 6.25% (green) from AIMD simulations. The filled green triangle indicates the extrapolated ionic conductivity at 300 K from AIMD simulations. (b) Isosurface of the Na+ probability density distribution (P, in green) in the t-Na3−xPS4−xClx (x = 6.25%) at 800 K, with P = 0.0001 a0−3 (a0 is the Bohr radius).

Table 2. Room temperature ionic conductivity and activation energy of t-Na3−x PS4−x Cl x .

x (%) AIMD simulations Experiment
  σ300K (mS cm−1) Ea (meV) σ303K (mS cm−1) Ea (meV)
0 N/A N/A 0.05 317
6.25 1.38 [1.04, 1.82] 232 1.14 249
Open in a new tab

Calculated AIMD and experimental Na+ conductivity and activation energy of the t-Na3−xPS4−xClx superionic conductor. Values in the square brackets indicate the error range of the calculated ionic conductivity.

From the Na+ probability density distribution (Fig. 2b), we may observe that t-Na2.9375PS3.9375Cl0.0625 is predicted to be a 3D diffuser comprising of chains of Na1 sites along the c direction interconnected via the Na2 sites, which form a body-centered cubic sublattice. Such a 3D diffusion network is expected to be highly robust against the potential introduction of blocking defects33.

Electrochemical stability of t-Na3−x PS4−x Cl x

Besides high ionic conductivity, an effective solid electrolyte candidate should also exhibit good electrochemical stability against the electrodes. Electrochemical stability may be achieved in two ways. First, the solid electrolyte can be intrinsically inert against any reaction with the electrodes. However, due to the high reactivity of Na metal and the highly oxidizing nature of the most charged high-voltage cathodes, it is difficult to find a material that is intrinsically stable over such a wide range of sodium chemical potential17,23. A second, more achievable option is to optimize the electrode-solid electrolyte chemistry as a whole such that good passivation layers are formed at the electrode-solid electrolyte interfaces that act as a barrier against further reaction. A good passivation layer should have a reasonable Na+ conductivity, and low electronic conductivity.

Figure 3 shows the Na grand potential phase stability plot of the t-Na2.9375PS3.9375Cl0.0625 solid electrolyte as a function of Na chemical potential. We find that at the Na metal anode (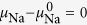Inline graphic eV), the predicted phase equilibria comprises Na2S, NaCl and Na3P in the ratio of 63:1:16. The dominant phase Na2S is a good electronic insulator with PBE band gap of 2.4 eV, and NaCl has a PBE band gap of 5.0 eV34. Na3P has a small PBE band gap of 0.4 eV (the screened hybrid HSE functional35,36 gives a band gap of 0.76 eV), but is not expected to dominate the conductivity characteristics of the anode/electrolyte interface. The predicted phase equilibria are very similar to those of pristine t-Na3PS4 that consists of Na2S and Na3P in the ratio of 4:1. It should be noted that the PBE functional tends to severely underestimate band gaps, and the true band gaps are likely to be even higher. These phases are expected to exhibit moderate Na+ conductivity, particularly in an amorphous solid-electrolyte interphase (SEI) layer.

Figure 3. Electrochemical decomposition products of doped Na3PS4 compounds.

Figure 3

Open in a new tab

Plots of Na uptake per formula unit (f.u.) of t-Na2.9375PS3.9375Cl0.0625 (red solid), c-Na3.0625Sn0.0625P0.9375S4 (blue dashed) and c-Na3.0625Si0.0625P0.9375S4 (green dashed) solid electrolytes against voltage vs Na/Na+. At low voltage (high Na chemical potential), each solid electrolyte undergoes reduction and uptakes Na, while at high voltage (low Na chemical potential), each solid electrolyte is oxidized and loses Na. Text indicates the predicted phase equilibria at corresponding regions of the profile. Only selected regions are annotated for brevity.

At voltages above 2.4 V versus Na/Na+, we find that the t-Na2.9375PS3.9375Cl0.0625 solid electrolyte is predicted to be unstable against Na extraction to form NaPS3 + S + NaCl. However, if the operating voltage is kept below 2.4 V, the predicted phase equilibria at the charged cathode-solid electrolyte interface retains t-Na3PS4 + NaCl as the primary component.

Synthesis and characterization of t-Na3−x PS4−x Cl x

Pure t-Na3PS4 was synthesized from Na2S and P2S5 precursors. The Cl− dopant was introduced by adding NaCl following the chemical reaction (1.5 − x)Na2S + 0.5P2S5 + xNaCl → Na3−xPS4−xClx. The resulting pellets were then densified via spark plasma sintering (SPS) to minimize porosity of the solid electrolyte. The synthesis details are given in the Methods section, and the dimensions and density of the pristine and doped pellets are provided in Supplementary Information (see Table S1).

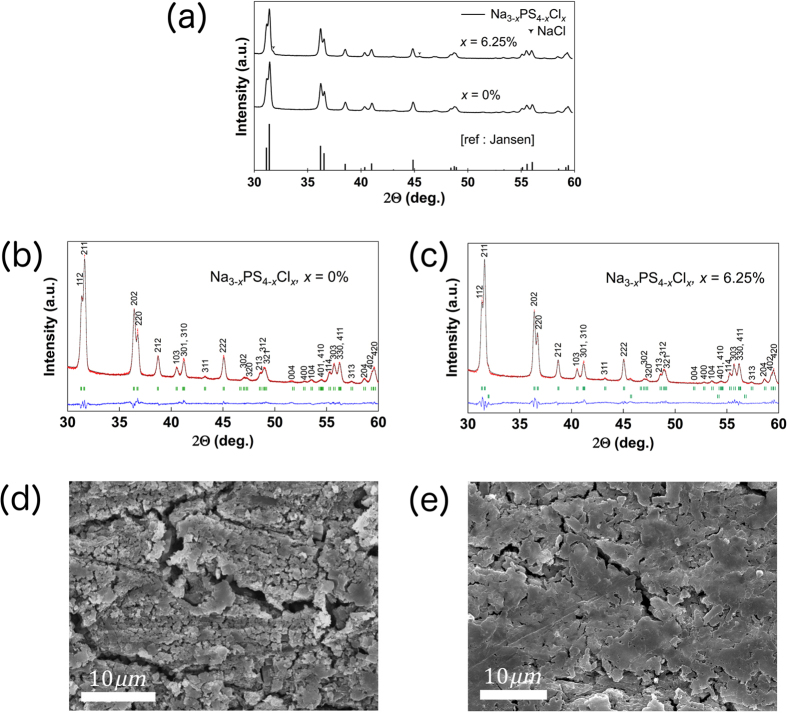
Figure 4a shows the XRD data for the two compositions, t-Na3−xPS4−xClx with x = 0% and 6.25%. At x = 0%, we identify the crystalline phase formed to be t-Na3PS4, and the XRD pattern is in excellent agreement with the previous study by Jansen et al27. With the addition of chloride via NaCl at x = 6.25%, the tetragonal phase is retained with trace amounts of unreacted NaCl, and no reflections from unknown crystals are present in the spectra. Additionally, we observe a slight increase in the peak intensities of all the XRD reflections, with the most significant change occurring in the high index peaks, (112) and (211), at about 31°. This observation is the first indication that aliovalent substitution of S2− by Cl− was successful, because the halogen has a higher scattering factor than sulfur.

Figure 4. Characterization and morphology of t-Na3−xPS4−xClx.

Figure 4

Open in a new tab

(a) XRD patterns for t-Na3−xPS4−xClx with x = 0% and 6.25%, and previous study in ref. 27. (b) Refinement plot of the pristine t-Na3PS4. (c) Refinement plot of Cl-doped t-Na3PS4. Solid red and black lines denote the observed and calculated XRD patterns, while the green ticks mark the position of the reflections allowed by the space groups of t-Na3PS4 (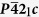Inline graphic) and NaCl (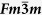Inline graphic). The difference between the observed and calculated patterns is signified by the blue line. (d) SEM image of pristine t-Na3PS4 SPS sample, and (e) SEM image of SPS sample of doped t-Na3−xPS4−xClx (x = 6.25%). Scale bar is 10 μm.

Rietveld refinement calculations were first conducted for t-Na3−xPS4−xClx. To obtain a baseline of the crystal parameters, a refinement calculation was performed on the pristine (x = 0%) structure. The refined XRD pattern of the pristine structure is shown in Fig. 4b. The refined lattice constants for the pristine structure are in excellent agreement with the previously reported values27. These parameters were then used as an initial model to study the aliovalent substitution of S2− by Cl−. Figure 4c shows the refined pattern of doped t-Na2.9375PS3.9375Cl0.0625. No unknown phase was detected in the crystal, and no side reactions were observed during the synthesis. Although a trace amount of NaCl was detected in the spectrum, our refinement results show that it comprises less than 1 at%.

Table 3 summarizes the crystallographic parameters (lattice constants, thermal factors, and atomic occupancies) of the pristine and doped solid electrolyte from the Rietveld refinement and DFT calculations, which are in excellent agreement. From the refinement calculations, we estimated an increase in the lattice volume associated with the substitution of S2− by Cl−. This volumetric change is very small and also agrees well with the DFT values. With the introduction of Cl−, there is a corresponding decrease in sodium and sulfur occupancies and increase in their respective isotropic thermal factors (Biso). These observations can be attributed to the formation of the Na+ vacancy. In summary, the Rietveld refinement supports the successful incorporation of Cl− into the S2− sublattice, with the concomitant introduction of Na+ vacancies. More advanced characterization techniques such as solid-state nuclear magnetic resonance (NMR) may be employed to confirm the success of the doping in future work.

Table 3. Rietveld refinement of t-Na3−xPS4−xClx.

Pristine (x = 0%), Space Group 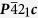Inline graphic
a = b = 6.956 (5) Å, c = 7.088 (6) Å, V = 342.9 (5) Å3
Rb = 3.86%, Rwp = 4.97%
  x y z Occ. Biso (Å2)
Na1 (4d) 0 0.5 0.426 (4) 2.00 2.54 (9)
Na2 (2a) 0 0 0 1.00 3.2 (1)
P (2b) 0 0 0.5 1.00 0.5 (6)
S (8e) 0.315 (3) 0.345 (2) 0.167 (2) 4.00 1.1 (6)
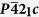
Doped (x = 6.25%), Space Group Inline graphic
a = b = 6.970 (4) Å, c = 7.092 (5) Å, V = 344.5 (4) Å3
Rb = 4.29%, Rwp = 5.31%
  x y z Occ. Biso (Å2)
Na1 (4d) 0 0.5 0.428 (6) 1.99 (4) 3.0 (2)
Na2 (2a) 0 0 0 0.99 (4) 3.4 (3)
P (2b) 0 0 0.5 1.00 0.1 (1)
S (8e) 0.316 (4) 0.344 (3) 0.165 (3) 3.94 (4) 1.19 (9)
Cl (8e) 0.316 (4) 0.344 (3) 0.165 (3) 0.02 (4) 1.19 (9)
Open in a new tab

Rietveld refinement results of t-Na3−xPS4−xClx systems, where a, b and c are lattice constants, and V, Occ., and Biso are normalized cell volume, site occupation numbers, and isotropic atomic displacement parameters, respectively. Residual factors, Rb and Rwp, for the pristine (x = 0%) composition are 3.86% and 4.97%, respectively; and for the doped (x = 6.25%) are 4.29% and 5.31%. For the pristine t-Na3PS4, the DFT calculated cell parameters are a = b = 6.99 Å, c = 7.12 Å, V = 348 Å3, in excellent agreement with the refinement results as well as those by Jansen et al. (ref. 27): a = b = 6.952 Å, c = 7.076 Å, V = 341.97 Å3.

Cross-sectional SEM images of the pristine t-Na3PS4 and doped t-Na2.9375PS3.9375Cl0.0625 SPS samples under identical processing conditions are shown in Fig. 4d,e, respectively. We note that the Cl− doping does not lead to any significant morphology changes. The images show that the local morphology of the pellets is densely formed due to SPS processing in both compounds. An EDX measurement was collected from the doped sample (see Figure S1 in Supplementary Information). From the EDX measurement, we determined that sulfur and chlorine are uniformly distributed throughout the sample, with no noticeable aggregation of element-rich domains. In conjunction with the refinement results, the majority of the chloride dopant is found to be integrated into the host crystal lattice.

Conductivity measurements of t-Na3−x PS4−x Cl x

The experimental measurement of pristine t-Na3PS4 shows a low ionic conductivity of 0.05 mS cm−1 at 303 K, with an activation energy value of 317 meV (see Fig. 2a and Table 2). The t-Na2.9375PS3.9375Cl0.0625 solid electrolyte, on the other hand, shows an extremely high conductivity of 1.14 mS cm−1 at 303 K and a low activation barrier of 249 meV. The measured conductivity and activation barrier are in excellent agreement with the calculated values (see Table 2). The room temperature Nyquist plots for the pristine t-Na3PS4 and doped t-Na2.9375PS3.9375Cl0.0625 are given in Figure S2, where the total impedance in each structure was used to calculate the room temperature conductivities of each material. A significantly larger semi-circle is observed for the pristine t-Na3PS4 compared to doped t-Na2.9375PS3.9375Cl0.0625, indicating a much larger total resistance in the pristine t-Na3PS4.

Electrochemical performance

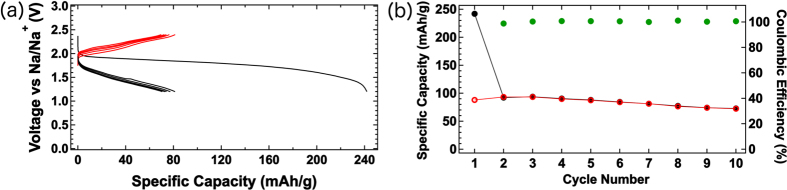
A full cell was constructed using a TiS2 charged cathode and a Na metallic anode. The choice of the TiS2 cathode is motivated by its suitable operating voltage (~1.7 V versus Na/Na+), which is well within the limits of the DFT predicted stability window of the t-Na2.9375PS3.9375Cl0.0625 solid electrolyte, as well as its fast kinetics for Na+ intercalation37. The cell was galvanostatically cycled from 1.2 V to 2.4 V. The cell was held for two minutes between switching from charging to discharging. A current density of 0.149 mA cm−2 was applied, corresponding to a C/10 rate. The theoretical capacity of the NaTiS2 active material is 198 mAh g−1. The discharge and charge capacity of the first cycle were ~240 mAh g−1 and 80 mAh g−1, respectively. The source of the excess capacity as well as the large irreversible capacity of the first cycle is currently under investigation, and will be the evaluated in a subsequent study of the interface stability and its effects on cyclability and longevity. Currently, impedance measurements during the first cycle clearly indicate the formation of stable interfacial phases at the solid-electrolyte/electrode interfaces (see Figure S3 in the Supplementary Information). The subsequent charge and discharge capacities of the cell over 10 cycles were ~80 mAh g−1, with a coulombic efficiency above 98% (see Fig. 5). Such a stable performance is consistent with the cyclic voltammetry results (see Figure S3 in the Supplementary Information) in which Cl-doped t-Na3PS4 is found electrochemically stable against the Na anode for up to 5 V. Strong polarization, common in Na-ion cells, was also observed at the point of switching from charging to discharging, and vice versa.

Figure 5. Electrochemical performance of TiS2/t-Na2.9375PS3.9375Cl0.0625/Na all-solid-state full cell.

Figure 5

Open in a new tab

Charge-discharge profile of TiS2/t-Na2.9375PS3.9375Cl0.0625/Na full cell at room-temperature. Cell was cycled under constant current conditions with a current density of 0.149 mA cm−2 (C/10 rate) from 1.2 V to 2.4 V. The cell was able to routinely deliver 80 mAh g−1 over 10 cycles. Red and black lines in the charge-discharge profile denote charging and discharging, respectively. Similarly, red and black markers signify charge and discharge capacities, while the green circles mark the coulombic efficiency by cycle.

Discussion

The design of an all-solid-state rechargeable battery is a multi-component, multi-property optimization effort; it is therefore insufficient to merely focus on bulk ionic conductivity of the solid electrolyte as the only target parameter. In this work, we have demonstrated how an integrated computational and experimental effort can significantly accelerate such multi-component, multi-property optimization, resulting in a promising new t-Na2.9375PS3.9375Cl0.0625 solid electrolyte that has been demonstrated in a full ss-SIB cell with good cyclability and capacity.

Aliovalent doping is a common strategy to introduce defects (vacancies or interstitials) into a solid electrolyte candidate to further enhance its conductivity. Surprisingly, we find halide doping in Na3PS4 to be somewhat more favorable than cation (Si4+, Ge4+ and Sn4+) doping, with slightly lower dopant formation energies of 0.76–1.11 eV vs 1.04–1.32 eV for cation30. Though dopant formation energies of 0.76–1.11 eV might appear at first glance to be relatively high, it should be noted that these values depend strongly on the chemical potential references used. At the elevated temperatures during synthesis, Na2S loss is likely to lower the chemical potentials of Na and S, significantly promoting 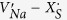Inline graphicformation.

Both the cation + interstitials and anion + vacancies doping strategies are predicted to be effective in enhancing the ionic conductivity of Na3PS4. In fact, we find no evidence of any significant difference in the predicted bulk Na+ conductivities between the cubic and tetragonal Na3PS4, which is not surprising given the very small differences in lattice parameters between the two polymorphs38. We speculate that the nature of the defects present would promote the formation of one polymorph over another. Excess Na interstitials would need to occupy the cubic Na2 (12d) sites, promoting the formation of the disordered cubic phase, while Na vacancies with halide substitution would result in slight lattice expansion (due to reduced electrostatic attraction) and promote the formation of the tetragonal phase. Indeed, our attempts at synthesizing a phase-pure Cl-doped c-Na3PS4 phase has been unsuccessful, while the Cl-doped t-Na3PS4 was readily obtained.

The fundamental difference between cation M4+ and anion X− doping is in the interfacial products that are predicted to form at the Na anode. For Si or Sn-doped Na3PS4, small-gap compounds such as Na4Si4 (space group of C2/c; PBE band gap of ~1.2 eV) and Na15Sn4 (space group of 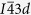Inline graphic; PBE band gap of ~0 eV) as well as Na2S and Na3P are predicted to form at the anode/solid electrolyte interface (see Fig. 3). For Cl-doped Na3PS4, on the other hand, the anode/solid electrolyte interface comprises predominantly Na2S with smaller amounts of NaCl and Na3P. Alkali halides are well-known components in the solid-electrolyte interphase (SEI) of rechargeable lithium-ion batteries, where LiF is formed from the reaction between the LiPF6 salt and the electrodes. Indeed, the “salting” of the SEI is likely to improve its ionic conductivity as Cl− dopants will similarly be introduced to the amorphous Na3P + Na2S SEI. It should be noted that in all cases (undoped, cation-doped, and halide-doped), the small-gap compound Na3P (PBE band gap of ~0.4 eV) is also predicted to form at the Na anode, though it is not the dominant phase. Based on the achieved cycling performance in this work as well as in previous works on c-Na3PS425, we would surmise that the effect of Na3P on the interfacial stability is small.

Ultimately, the total conductivity of a solid electrolyte depends not only on its bulk conductivity, but also the grain boundary contributions. In this respect, the specifics of the synthesis procedure are critically important. In this work, spark-plasma sintering was used to achieve a fully-dense solid electrolyte with reduced grain boundary resistance, and an overall conductivity exceeding 1 mS cm−1 that is very close to the DFT predicted bulk conductivity (see Fig. 2). This overall conductivity is higher than that of Si-doped c-Na3PS4 (0.74 mS cm−1)29 and is the highest value for sodium thiophosphates achieved thus far. Although the recently reported Na3PSe4 and Na3SbS4 have higher conductivities, the more expensive and less stable Se2− anion is utilized in Na3PSe414, while Na3SbS4 requires a more complicated electrolyte bilayer approach using c-Na3PS4 to stabilize the interface at the Na anode20.

We have demonstrated the potential of the t-Na2.9375PS3.9375Cl0.0625 solid electrolyte by integrating it in a ss-SIB full cell. In a full cell, the choice of the cathode and anode must be given careful consideration, as well as their interactions with the solid electrolyte. From the DFT grand potential analysis, we find that the t-Na2.9375PS3.9375Cl0.0625 electrolyte is predicted to be relatively stable up to ~2.4 V vs Na/Na+, while passivation is predicted to occur at the Na anode. Therefore, TiS2 was chosen as the cathode. At a current density of 0.149 mA cm−2, a cell capacity of ~80 mAh g−1 was achieved over 10 cycles of the TiS2/t-Na2.9375PS3.9375Cl0.0625/Na full cell. The increase in internal cell resistance, leading to capacity decay after subsequent cycling, is common when forming a SEI layer. Though the reversible capacity reported by Hayashi et al. for the c-Na3PS4 solid electrolyte is similar25, that performance was achieved with a much lower current density (0.013 mA cm−2) against a Na-Sn alloy as the anode. Though the Si-doped c-Na3PS4 and Na3PSe4 solid electrolytes have higher measured conductivities than c-Na3PS4, their room-temperature performance in a full ss-SIB cell has not yet been demonstrated14,29. To our knowledge, this is the first time that cycling at a rate as high as C/10 has been demonstrated in a full ss-SIB with a Na metal anode at room temperature.

Conclusion

In conclusion, we have demonstrated the prediction and synthesis of a novel Cl-doped tetragonal Na3PS4 solid electrolyte, or t-Na2.9375PS3.9375Cl0.0625, and its good cycling performance in a full all-solid-state rechargeable sodium-ion cell at a rate of C/10. The predicted bulk and measured total conductivities of the t-Na2.9375PS3.9375Cl0.0625 solid electrolyte exceed 1 mS cm−1, which is one of the highest conductivity reported for any sodium superionic conductor thus far. More importantly, the “salting” of Na3PS4 is predicted to improve the characteristics of the interfacial phase equilibria at the anode/solid electrolyte interface, forming an electronically insulating and ionically conducting solid-electrolyte interphase. We also demonstrate the potential of spark-plasma sintering as a technique for achieving a dense sulfide electrolyte with reduced grain boundary resistance.

Methods

Density functional theory calculations

All DFT calculations were performed using similar methodologies as previous works by the authors30,39. For the sake of brevity, we refer interested readers to those works and only briefly summarize the key parameters here.

All calculations were performed with the Vienna Ab initio Simulation Package (VASP)40, within the projector augmented wave (PAW) approach41. The Python Materials Genomics (pymatgen) materials analysis library was used for all analyses42. All structural relaxations and total energy calculations were carried out using parameters similar to those used in the Materials Project34. The key parameters are the use of the Perdew-Burke-Ernzerhof (PBE) generalized-gradient approximation (GGA)43 exchange correlation functional, an energy cutoff of 520 eV and a k-point mesh of at least 1000/atom. For the doped structures, an enumeration of all symmetrically distinct halide-vacancy orderings in a 2 × 2 × 2 supercell of Na3PS4 was carried out44, and the lowest energy configuration was used for all subsequent calculations and analyses, including ab initio molecular dynamics (AIMD) simulations. For phase diagram construction45, the pre-calculated energies of all phases in the Na-P-S-X systems (X = F, Cl, Br and I) other than those of primary interest in this work were obtained from the Materials Project database via the Materials Application Programming Interface46.

Dopability analysis

To assess the likelihood of halide doping into Na3PS4, we estimated the neutral dopant formation energy using the formalism originally presented by Wei and co-workers30,47, 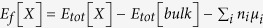Inline graphic, where Etot[X] and Etot[bulk] are the total energies of the structure with and without the neutral dopant X, respectively. μi is the atomic chemical potential of specie i that varies based on different experimental conditions; ni indicates the number of atoms of specie i being added (ni > 0) or removed (ni < 0) from the pristine structure. In this work, the lower bound of the dopant formation energy was calculated, which is equal to the difference of decomposition energies between the doped and host materials30.

Electrochemical analyses

The electrochemical stability of the solid electrolytes in contact with the electrodes was estimated using the grand potential approach proposed by Ong et al.45 which assumes that Na is the main mobile species. Under such conditions, the solid electrolyte-electrode interface is modeled as an open system with respect to Na. The relevant thermodynamic potential is then the grand potential, given as 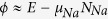Inline graphic, where E is approximated as the DFT total energy. 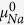It should be noted that the chemical potential of Na is related to the voltage vs Na/Na+ (V) via the following relation, with Inline graphic) where Inline graphic is the reference chemical potential of bulk Na metal.

Ionic conductivity calculations

The diffusivity and conductivity of the Cl-doped t-Na3PS4 structure were calculated using AIMD simulations. Non-spin-polarized AIMD simulations were conducted in the NVT ensemble at 800–1400 K with a Nose-Hoover thermostat48,49. A smaller plane-wave energy cutoff of 280 eV and a minimal Γ-centered 1 × 1 × 1 k-point mesh were adopted. The time step of the simulations was 2 fs. The initial structure was fully relaxed at 0 K, and the volume was fixed for AIMD at elevated temperatures until the diffusivity was converged. No framework melting was observed in all simulations. All calculations were automated using an automated in-house AIMD workflow software50,51. The Na+ diffusivity (D) and conductivity (σ) can be extracted from the AIMD simulations using the following expressions: 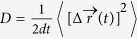Inline graphic where d is the dimensionality of diffusion ( = 3 for t-Na3PS4 structures); 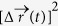Inline graphic is the average mean square displacement (MSD) over a time duration t. The diffusivity was obtained by performing a linear fitting of the MSD vs. 2dt. Arrhenius plots were constructed to determine the activation energies and obtain extrapolated room-temperature diffusivities D300K. The room temperature Na ion conductivity σ300K can then be derived from the Nernst-Einstein equation, 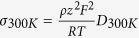Inline graphic where ρ is the molar density of diffusing Na ions in the unit cell; z = 1 is the charge of Na ions; and F and R are the Faraday’s constant and the gas constant respectively. T = 300 K was used in the above equation.

Synthesis

Pure t-Na3PS4 was synthesized from reagent-grade Na2S (Alfa Aesar, 99%) and P2S5 (Sigma Aldrich, 99%). The precursors were ground in agate mortar and pestle in a molar ratio of 75:25, respectively. To introduce the chloride dopant, NaCl (Alfa Aesar, 99.99%) was mixed into the previous precursors following the chemical reaction (1.5 − x)Na2S + 0.5P2S5 + xNaCl → Na3−xPS4−xClx. The resulting mixtures were then sealed under vacuum in a quartz tube, heated to 1073 K (800 °C) for 4 hours, and then quenched in ice water. Subsequently, the sample was ground in a mortar and pestle and sealed in an ampoule to be heat treated at 693 K (420 °C) for 2 hours to stabilize the tetragonal phase. The samples were ground back into a powder with mortar and pestle, and re-pelletized. These pellets were then processed via spark plasma sintering (SPS). To prepare the sample, a 10 mm tungsten-carbide circular die was lined with graphite foil and the powder was placed in between two tungsten-carbide plungers, also coated with graphite. The entire setup was placed in the SPS chamber, and the sample was pressed to 100 MPa (100 MPa min−1), heated to 573 K (100 K min−1), and then allowed to dwell under these processing conditions for 5 minutes to reach a densified state. All synthesis steps were performed in a dry, inert (Ar) environment, unless otherwise stated.

Characterization of solid electrolytes

The structural characterization was performed via X-ray diffraction (XRD). The data was collected by a Rigaku diffractometer over a 2Θ range of 30–60°, with a step size of 0.02° and a dwell time of 2 seconds. The beam was generated by a Cu-Kα source (40 kV, 100 mA). The sample was sealed under Kapton tape to prevent degradation or side-reactions during measurements.

Cross-sectional images of the SPS pellets were obtained using a Phillips XL30 scanning electron microscope (SEM). Pristine and doped pellets were suspended in an acrylic matrix that was polished for imaging. Iridium was sputtered onto the surface of the sample using an Emitech sputter chamber operating at 85 mA for 7 seconds. The sample was imaged using a 10 kV beam. Additionally, an elemental mapping analysis was conducted using an energy dispersive X-ray spectroscopy (EDX) aperture in the SEM. SEM and EDX were conducted under high vacuum.

Electrochemical characterization

The electrochemical performance was evaluated via electrochemical impedance spectroscopy (EIS). The data was collected using a Solartron 1260 impedance analyzer operating from 1 MHz to 1 Hz with a DC bias of 0 V and an applied AC voltage of 25 mV. Carbon was used as blocking electrodes. The pellet was held between two titanium plungers serving as current collectors. The temperature dependence of conductivity was obtained by placing the cell in an electric furnace. The cell was ramped to 453 K (180 °C) from room temperature in 25 K increments. Prior to each measurement, the cell was held at the temperature for one hour to allow the system to reach thermal equilibrium. The sodium ion-migration activation energy was calculated from the slope of the Arrhenius plot. All measurements were taken in a dry, inert (Ar) atmosphere.

A full cell was assembled using a TiS2 composite cathode against a Na metal anode. TiS2 was mixed with t-Na3−xPS4−xClx, x = 6.25% in a 1:2 weight ratio. The doped (x = 6.25%) solid electrolyte (200 mg) was cold-pressed at 360 MPa in a 13 mm polyetheretherketone (PEEK) die. The cathode blende (10 mg) was cold-pressed at 360 MPa on top of the electrolyte layer. Pure Na metal was attached to a titanium current collector and cold-pressed into the die at approximately 30 MPa. The cell was cycled using Arbin battery cycler at room temperature. Cycling was performed at a C/10 rate for 10 cycles over a voltage window from 1.2 V to 2.4 V. The cell was cycled inside an Ar glovebox.

Additional Information

How to cite this article: Chu, I.-H. et al. Room-Temperature All-solid-state Rechargeable Sodium-ion Batteries with a Cl-doped Na3PS4 Superionic Conductor. Sci. Rep. 6, 33733; doi: 10.1038/srep33733 (2016).

Supplementary Material

Supplementary Information
srep33733-s1.pdf (809.9KB, pdf)

Acknowledgments

This work was supported by the National Science Foundation’s Designing Materials to Revolutionize and Engineer our Future (DMREF) program under Grant No. 1436976. Some of the computations in this work were performed using the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1053575. This work was also performed in part at the San Diego Nanotechnology Infrastructure (SDNI), a member of the National Nanotechnology Coordinated Infrastructure, which is supported by the National Science Foundation (Grant ECCS-1542148).

Footnotes

Author Contributions S.P.O. and I.-H.C. designed the computational study. I.-H.C. performed and analyzed the calculations. Z.Z. performed the AIMD simulations. Y.S.M., H.N. and C.K. designed and performed the experimental measurements. I.-H.C., H.N. and C.K. prepared the initial manuscript. All authors discussed results and commented on the manuscript.

References

  1. Hueso K. B., Armand M. & Rojo T. High temperature sodium batteries: status, challenges and future trends. Energy Environ. Sci. 6, 734 (2013). [Google Scholar]
  2. Ellis B. L. & Nazar L. F. Sodium and sodium-ion energy storage batteries. Curr. Opin. Solid State Mater. Sci. 16, 168–177 (2012). [Google Scholar]
  3. Larcher D. & Tarascon J. Towards greener and more sustainable batteries for electrical energy storage. Nat. Chem. 7, 19–29 (2014). [DOI] [PubMed] [Google Scholar]
  4. Ong S. P. et al. Voltage, stability and diffusion barrier differences between sodium-ion and lithium-ion intercalation materials. Energy Environ. Sci. 4, 3680 (2011). [Google Scholar]
  5. Tarascon J.-M. & Armand M. Issues and challenges facing rechargeable lithium batteries. Nature 414, 359–367 (2001). [DOI] [PubMed] [Google Scholar]
  6. Deng Z., Mo Y. & Ong S. P. Computational studies of solid-state alkali conduction in rechargeable alkali-ion batteries. NPG Asia Mater. 8, e254 (2016). [Google Scholar]
  7. Tatsumisago M. & Hayashi A. Sulfide glass-ceramic electrolytes for all-solid-state lithium and sodium batteries. Int. J. Appl. Glas. Sci. 5, 226–235 (2014). [Google Scholar]
  8. Pan H., Hu Y.-S. & Chen L. Room-temperature stationary sodium-ion batteries for large-scale electric energy storage. Energy Environ. Sci. 6, 2338 (2013). [Google Scholar]
  9. Hooper a. A study of the electrical properties of single-crystal and polycrystalline β-alumina using complex plane analysis. J. Phys. D. Appl. Phys. 10, 1487–1496 (1977). [Google Scholar]
  10. Anantharamulu N. et al. A wide-ranging review on Nasicon type materials. J. Mater. Sci. 46, 2821–2837 (2011). [Google Scholar]
  11. Chu I.-H. et al. Insights into the performance limits of the Li7P3S11 superionic conductor: a combined first-principles and experimental study. ACS Appl. Mater. Interfaces 8, 7843–7853 (2016). [DOI] [PubMed] [Google Scholar]
  12. Zhang L. et al. Vacancy-contained tetragonal Na3SbS4 superionic conductor. Adv. Sci. 1600089; doi: 10.1002/advs.201600089 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Kandagal V. S., Bharadwaj M. D. & Waghmare U. V. Theoretical prediction of a highly conducting solid electrolyte for sodium batteries: Na10GeP2S12. J. Mater. Chem. A 3, 1–8 (2015). [Google Scholar]
  14. Zhang L. et al. Na3PSe4: A novel chalcogenide solid electrolyte with high ionic conductivity. Adv. Energy Mater. 5, 1501294 (2015). [Google Scholar]
  15. Kuhn A. et al. A new ultrafast superionic Li-conductor: ion dynamics in Li11Si2PS12 and comparison with other tetragonal LGPS-type electrolytes. Phys. Chem. Chem. Phys. 16, 14669–14674 (2014). [DOI] [PubMed] [Google Scholar]
  16. Bron P. et al. Li10SnP2S12: an affordable lithium superionic conductor. J. Am. Chem. Soc. 135, 15694–15697 (2013). [DOI] [PubMed] [Google Scholar]
  17. Mo Y., Ong S. P. & Ceder G. First principles study of the Li10GeP2S12 lithium super ionic conductor material. Chem. Mater. 24, 15–17 (2012). [Google Scholar]
  18. Kamaya N. et al. A lithium superionic conductor. Nat. Mater. 10, 682–686 (2011). [DOI] [PubMed] [Google Scholar]
  19. Seino Y., Ota T., Takada K., Hayashi A. & Tatsumisago M. A sulphide lithium super ion conductor is superior to liquid ion conductors for use in rechargeable batteries. Energy Environ. Sci. 7, 627–631 (2014). [Google Scholar]
  20. Banerjee A. et al. Na3SbS4: A solution processable sodium superionic conductor for all-solid-state sodium-ion batteries. Angew. Chemie 42988, 9786–9790 (2016). [DOI] [PubMed] [Google Scholar]
  21. Zhu Y., He X. & Mo Y. Origin of outstanding stability in the lithium solid electrolyte materials: insights from thermodynamic analyses based on first-principles calculations. ACS Appl. Mater. Interfaces 7, 23685–23693 (2015). [DOI] [PubMed] [Google Scholar]
  22. Richards W. D., Miara L. J., Wang Y., Kim J. C. & Ceder G. Interface stability in solid-state batteries. Chem. Mater. 28, 266–273 (2015). [Google Scholar]
  23. Ong S. P. et al. Phase stability, electrochemical stability and ionic conductivity of the Li 10±1MP2X12 (M = Ge, Si, Sn, Al or P, and X = O, S or Se) family of superionic conductors. Energy Environ. Sci. 6, 148–156 (2013). [Google Scholar]
  24. Deng Z., Wang Z., Chu I.-H., Luo J. & Ong S. P. Elastic properties of alkali superionic conductor electrolytes from first principles calculations. J. Electrochem. Soc. 163, A67–A74 (2016). [Google Scholar]
  25. Hayashi A., Noi K., Sakuda A. & Tatsumisago M. Superionic glass-ceramic electrolytes for room-temperature rechargeable sodium batteries. Nat. Commun. 3, 856 (2012). [DOI] [PubMed] [Google Scholar]
  26. Tanibata N. et al. X-ray crystal structure analysis of sodium-ion conductivity in 94Na3PS4•6Na4SiS4 glass-ceramic electrolytes. Chem Electro Chem 1, 1130–1132 (2014). [Google Scholar]
  27. Jansen M. & Henseler U. Synthesis, structure determination, and ionic conductivity of sodium tetrathiophosphate. J. Solid State Chem. 99, 110–119 (1992). [Google Scholar]
  28. Hayashi A., Noi K., Tanibata N., Nagao M. & Tatsumisago M. High sodium ion conductivity of glass–ceramic electrolytes with cubic Na3PS4. J. Power Sources 258, 420–423 (2014). [Google Scholar]
  29. Tanibata N., Noi K., Hayashi A. & Tatsumisago M. Preparation and characterization of highly sodium ion conducting Na3PS4–Na4SiS4 solid electrolytes. RSC Adv. 4, 17120 (2014). [Google Scholar]
  30. Zhu Z., Chu I.-H., Deng Z. & Ong S. P. Role of Na+ interstitials and dopants in enhancing the Na+ conductivity of the cubic Na3PS4 superionic conductor. Chem. Mater. 27, 8318–8325 (2015). [Google Scholar]
  31. de Klerk N. J. J. & Wagemaker M. Diffusion mechanism of the sodium-ion solid electrolyte Na3PS4 and potential improvements of halogen doping. Chem. Mater. 28, 3122–3130 (2016). [Google Scholar]
  32. Hibi Y., Tanibata N., Hayashi A. & Tatsumisago M. Preparation of sodium ion conducting Na3PS4-NaI glasses by a mechanochemical technique. Solid State Ionics 270, 6–9 (2015). [Google Scholar]
  33. Malik R., Burch D., Bazant M. & Ceder G. Particle size dependence of the ionic diffusivity. Nano Lett. 10, 4123–4127 (2010). [DOI] [PubMed] [Google Scholar]
  34. Jain A. et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 1, 011002 (2013). [Google Scholar]
  35. Heyd J., Scuseria G. E. & Ernzerhof M. Erratum: ‘Hybrid functionals based on a screened Coulomb potential’ [J. Chem. Phys. 118, 8207 (2003)]. J. Chem. Phys. 124, 219906 (2006). [Google Scholar]
  36. Heyd J., Scuseria G. E. & Ernzerhof M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207 (2003). [Google Scholar]
  37. Whittingham M. S. Chemistry of intercalation compounds: Metal guests in chalcogenide hosts. Prog. Solid State Chem. 12, 41–99 (1978). [Google Scholar]
  38. Bo S.-H., Wang Y. & Ceder G. Structural and Na-ion conduction characteristics of Na3PSxSe4−x. J. Mater. Chem. A 4, 9044–9053 (2016). [Google Scholar]
  39. Chu I.-H. et al. Insights into the performance limits of the Li7P3S11 superionic conductor: A combined first-principles and experimental study. ACS Appl. Mater. Interfaces 8, 7843–7853 (2016). [DOI] [PubMed] [Google Scholar]
  40. Kresse G. & Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996). [DOI] [PubMed] [Google Scholar]
  41. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994). [DOI] [PubMed] [Google Scholar]
  42. Ong S. P. et al. Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis. Comput. Mater. Sci. 68, 314–319 (2013). [Google Scholar]
  43. Perdew J. P., Burke K. & Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996). [DOI] [PubMed] [Google Scholar]
  44. Hart G. L. W. & Forcade R. W. Algorithm for generating derivative structures. Phys. Rev. B 77, 224115 (2008). [Google Scholar]
  45. Ong S. P., Wang L., Kang B. & Ceder G. Li-Fe-P-O2 phase diagram from first principles calculations. Chem. Mater. 20, 1798–1807 (2008). [Google Scholar]
  46. Ong S. P. et al. The materials Application Programming Interface (API): A simple, flexible and efficient API for materials data based on REpresentational State Transfer (REST) principles. Comput. Mater. Sci. 97, 209–215 (2015). [Google Scholar]
  47. Wei S.-H. & Zhang S. Chemical trends of defect formation and doping limit in II–VI semiconductors: The case of CdTe. Phys. Rev. B 66, 1–10 (2002). [Google Scholar]
  48. Hoover W. G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 31, 1695–1697 (1985). [DOI] [PubMed] [Google Scholar]
  49. Nose S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 81, 511 (1984). [Google Scholar]
  50. Jain A. et al. FireWorks: a dynamic workflow system designed for highthroughput applications. Concurr. Comput. Pract. Exp. 27, 5037–5059 (2015). [Google Scholar]
  51. Deng Z., Radhakrishnan B. & Ong S. P. Rational composition optimization of the lithium-rich Li3OCl1−x Brx anti-perovskite superionic conductors. Chem. Mater. 27, 3749–3755 (2015). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep33733-s1.pdf (809.9KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES