Genome‐wide tests for introgression between cactophilic Drosophila implicate a role of inversions during speciation

Abstract

Models of speciation‐with‐gene‐flow have shown that the reduction in recombination between alternative chromosome arrangements can facilitate the fixation of locally adaptive genes in the face of gene flow and contribute to speciation. However, it has proven frustratingly difficult to show empirically that inversions have reduced gene flow and arose during or shortly after the onset of species divergence rather than represent ancestral polymorphisms. Here, we present an analysis of whole genome data from a pair of cactophilic fruit flies, Drosophila mojavensis and D. arizonae, which are reproductively isolated in the wild and differ by several large inversions on three chromosomes. We found an increase in divergence at rearranged compared to colinear chromosomes. Using the density of divergent sites in short sequence blocks we fit a series of explicit models of species divergence in which gene flow is restricted to an initial period after divergence and may differ between colinear and rearranged parts of the genome. These analyses show that D. mojavensis and D. arizonae have experienced postdivergence gene flow that ceased around 270 KY ago and was significantly reduced in chromosomes with fixed inversions. Moreover, we show that these inversions most likely originated around the time of species divergence which is compatible with theoretical models that posit a role of inversions in speciation with gene flow.

Introduction

There has been much interest in understanding if and how chromosomal inversions influence the speciation process. While early verbal models (White 1973; Rieseberg 2001) focused on the consequences of fitness underdominance of inversions, a more convincing role of inversions in speciation stems from the fact that they reduce recombination across a large swathe of the chromosome (Navarro and Barton 2003). Kirkpatrick and Barton (2006) have shown that an inversion arising in a structured population can spread if it captures locally beneficial alleles. By allowing locally adapted genes to accumulate in linkage, inversions may overcome the homogenising effect of gene flow and tip the balance toward increasing divergence in the embryonic stages of speciation (Rieseberg 2001; Navarro and Barton 2003). The current flood of genome sequence data has made it possible to test two key predictions of these models empirically.

Firstly, loci differentiating species should be concentrated in or around inversions. This has been shown to be the case for genes involved in hybrid sterility (Noor et al. 2001; Khadem et al. 2011; Fishman et al. 2013) and host‐associated life cycle differences (Feder et al. 2003). Secondly, neutral divergence within and around inversions should be increased relative to colinear parts of the genomes as a consequence of reduced gene flow. A signature of elevated divergence around inversion breakpoints has been found not only in the sister species D. pseudoobscura and D. persimilis, a classic model of speciation (Noor et al. 2007; Kulathinal et al. 2009), but also in mosquitoes (Besansky et al. 2003; Michel et al. 2006), sunflowers (Rieseberg et al. 1999), shrews (Yannic et al. 2009), and Heliconius butterflies (Joron et al. 2011).

However, Noor and Bennett (2009) have cautioned against simply equating an increase in divergence within and around inversions with a reduction in gene flow, especially if this is measured in terms of $F_{st}$. Such a signature on its own does not reveal if and how inversions were involved in species divergence for several reasons. Firstly, if chromosomal inversions are fixed by positive selection, the likely inversion‐wide hitch‐hiking event will decrease diversity around the inversion and hence increase $F_{st}$, regardless of whether there has been any postdivergence gene flow (Noor and Bennett 2009). This problem can be overcome by using absolute measures of divergence, and a recent reanalysis of several datasets (Cruickshank and Hahn 2014) suggests that previous studies of species divergence have suffered from this problem. Secondly, under a history of divergence with gene flow, the population divergence time of an inversion that predates the species split because it existed as a polymorphism in the ancestral population, represents the origin of the inversion and so should be older than the species divergence time estimated from the colinear genomic background (Noor and Bennett 2009). In contrast, an inversion that arose during (or shortly after) the onset of species divergence (and so is more likely to be associated with the build up of reproductive isolation) should share the same species divergence time as the colinear background regardless of any reduction in gene flow. Finally, given the considerable variance in coalescence times, gene divergence is expected to vary widely across the genome simply by chance. Thus, demonstrating that postdivergence gene flow has been reduced by a particular inversion (or set of inversions) requires estimating the magnitude and timing of both population divergence and postdivergence gene flow separately for rearranged and colinear regions of the genome.

The sibling species D. mojavensis and D. arizonae provide an excellent opportunity for studying the effects of inversions on species divergence. They are members of the mulleri subgroup within the large D. repleta group (> 100 species) endemic to North and South America (Wasserman 1982, 1992; Durando et al. 2000; Oliveira et al. 2012). While D. mojavensis is endemic to the Sonoran and Mojave Deserts in North America, the native range of D. arizonae includes the arid lands from Arizona, USA to southern Mexico and Guatemala, but not Baja California (Wasserman 1982) (although some recent collections have shown that D. arizonae is now present in Baja California presumably due to human activity). Both species share a common mainland ancestor that diverged into D. mojavensis in Baja California and D. arizonae on the mainland (Wasserman 1992). The reinvasion of mainland Mexico from Baja California by D. mojavensis ca 250 KYA (Smith et al. 2012) involved switching host plants and resulted in the current sympatric distribution of both species on the mainland (Heed 1982; Etges et al. 1999). Although D. arizonae and D. mojavensis can produce viable offspring in the lab (Mettler 1957) and sympatric populations in mainland Sonora and Sinaloa, Mexico sometimes share breeding and feeding sites, that is the same cactus rots (Markow et al. 1983; Ruiz and Heed 1988), there is no evidence for hybridisation between these species in the wild (Wasserman 1982; Etges et al. 1999; Counterman and Noor 2006; Machado et al. 2007). D. mojavensis and D. arizonae differ by several large, fixed inversions on three chromosomes (Wasserman 1962): there are three overlapping inversions (2q, 2r, 2s) on chromosome 2 that are fixed in D. mojavensis and together cover 70 % of the chromosome, two inversions on chromosome 3 (3d fixed in D. mojavensis and 3p2 fixed in D. arizonae) and one inversion on the X (Xe, fixed in D. mojavensis) (Runcie and Noor 2009; Guillen and Ruiz 2012). Chromosomes 4 and 5 are colinear. This provides an outstanding opportunity (including replication) to test the role of inversions on gene flow in speciation.

Previous studies on the divergence history of D. mojavensis and D. arizonae are equivocal: Counterman and Noor (2006) compared gene divergence at 19 autosomal loci and found no evidence for postdivergence gene flow or any significant difference in gene divergence between loci on rearranged and colinear chromosomes. In contrast, Machado et al. (2007) in an analysis of 10 autosomal loci found that allopatric D. mojavensis and D. arizonae had significantly more fixed nucleotide differences in rearranged than colinear chromosomes, a pattern that is consistent with differential historical introgression. However, like Counterman and Noor (2006) they were unable to reject a model of strict isolation without gene flow. Given the small number of loci examined by these studies and hence their limited power, it remains unclear whether D. arizonae and D. mojavensis have experienced postdivergence gene flow at all and, if so, whether this has been reduced in rearranged chromosomes.

Here, we revisit the evolutionary history of D. arizonae and D. mojavensis using whole genome data and address the following questions:

• (1)Has there been post divergence gene flow between D. arizonae and D. mojavensis?
• (2)Is gene flow greater in sympatry suggesting that it is recent or ongoing?
• (3)Is gene flow at rearranged chromosomes reduced?
• (4)Does the origin of inversions predate the species divergence time estimated for the colinear background or did inversions arise around the time of species divergence?

Materials and Methods

SAMPLES, SEQUENCING, AND MAPPING

We sequenced genomes from five highly inbred lines; two lines of D. mojavensis collected in Sonora (LB09, PO88), two D. mojavensis lines from Baja California, (A975, A976), and one D. arizonae (Dariz) line from Ejido Puerto Arturo, Sonora (Table S1 and Methods). Because Sonoran populations of D. mojavensis and D. arizonae are considered to be sympatric (Wasserman and Koepfer 1977; Markow et al. 1983), whereas D. arizonae is not known to occur in Baja California, we refer to the comparison between D. arizonae and D. mojavensis in Sonora as “sympatric” and that between D. arizonae and D. mojavensis in Baja as “allopatric” throughout.

Lines were collected in nature, returned to the lab, and maintained on banana food at room temperature at the University of Arkansas (Table S1). To minimize heterozygosity, each line was sibmated for 10 generations prior to sequencing. DNA from 12 female flies per line was extracted using DNeasy mini‐kits (Qiagen, Valencia, California, USA). A single TruSeq library with a 180 base insert size was prepared for each D. mojavensis line. Libraries were prepared and sequenced by the NERC genepool facility in Edinburgh on an Illumina HighSeq machine to 24–29‐fold coverage per line using 100 bp paired‐end reads (Table S1).

For the D. arizonae line we generated three TruSeq libraries with different insert sizes; 180, 300, and 500 bp, each of which was sequenced on an Illumina MiSeq machine to a combined mean coverage of 49.1‐fold. Raw read data and BAM files have been deposited at the Sequence Read Archive (SRA, accession PRJNA278716).

Raw reads were filtered and adapter‐trimmed using Scythe (https://github.com/vsbuffalo/scythe) and Sickle (https://github.com/najoshi/sickle) and mapped to the D. mojavensis reference genome v.16. (based on an inbred line from Santa Catalina Island) using Stampy v.1.0.21 (Lunter and Goodson 2011). We set the expected divergence to 4 %, based on previous estimates (Machado et al. 2007). The three D. arizonae libraries were combined after mapping. We marked duplicate reads using Picard (http://picard.sourceforge.net) and performed a local realignment around indels in GATK v.2.4 (McKenna et al. 2010) using reads from all lines and default settings.

The resulting BAM files were used to generate all‐sites Variant (VCF) files using mpileup (Li et al. 2009), which were filtered using VCFtools (Danecek et al. 2011) and custom pyVCF scripts (available upon request) for mapping quality, base call quality, and coverage depth. For the X, we included the four largest scaffolds (Schaeffer et al. 2008). For the autosomes all assigned scaffolds were used (Schaeffer et al. 2008) (Table S2) with two exceptions: We did not include the dot chromosome (because of its reduced recombination rate) and a small scaffold (6654, 2.6 Mb) assigned to chromosome 4 (because there is some doubt about its assignment and orientation). We analyzed a total of 147.4 Mb, 92.6% of the euchromatic assigned sequence of the D. mojavensis genome (Table S2).

We chose a Phred‐scaled threshold of 30 for both mapping quality and base call quality. To remove putative paralogous sequences that were misaligned and regions with low coverage, we filtered out sites with more than 125‐fold or less than 10‐fold coverage in any one individual. Applying these filters, a total of 26% of sites in the reference genome were excluded from the analysis (Table S2). Exploring a range of filtering thresholds confirmed that neither per site divergence nor the difference between rearranged and colinear autosomes were greatly affected by coverage filters (Fig. S6).

GENE DIVERGENCE

Given that rearranged regions make up the majority of the 2nd and 3rd chromosome scaffold (Fig. 2), we followed Counterman and Noor (2006) and contrasted divergence between rearranged and colinear autosomes. Comparing entire chromosomes avoids making potentially arbitrary assumptions about how far recombination is reduced beyond inversion breakpoints which seems particularly problematic for the complex, overlapping rearrangements on chromosome 2 and 3. It is also conservative because colinear regions on chromosomes with inversions will reduce any inversion effect.

Figure 2.

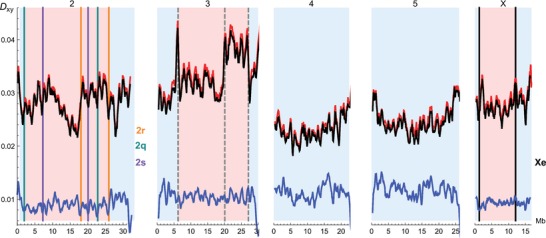
Mean per site divergence in 500 kb sliding windows. Divergence between D. arizonae and D. mojavensis is nearly identical for allopatric (black) and sympatric (red) comparisons. Divergence between the two D. mojavensis lines is shown in blue. Known inversion breakpoints on chromosome 2 (Guillen and Ruiz 2012) and the X (Runcie and Noor 2009) are indicated by solid, vertical lines, the position of the unmapped breakpoints on chromosome 3 by dashed, gray lines. All scaffolds are oriented with the centromere to the left (origin).

We computed mean pairwise divergence between D. arizonae and D. mojavensis lines from sympatric and allopatric populations separately for each chromosome and for exons, introns, and intergenic regions. Positions of these regions were extracted from the FlyBase General Feature File (GFF) for D. mojavensis (Marygold et al. 2012).

We assumed throughout that the effect of linkage disequilibrium can be ignored at distances >100 kb, which is extremely conservative given the range of recombination rates measured in Drosophila (Caceres et al. 1999; Comeron et al. 2012) and the fact that recombination rates in D. mojavensis appear to be higher than those in D. melanogaster (Ortiz‐Barrientos et al. 2006). To test for the significance of chromosome‐wide differences in divergence, we divided each chromosome into 100 kb nonoverlapping sections and compared the mean divergence across sections.

We confirmed known inversion breakpoints on chromosome 2 and the X visually by checking the orientation and insert size of D. arizonae read pairs mapped to the D. mojavensis reference genome around each breakpoint in the Integrative Genomics Viewer (Thorvaldsdottir et al. 2012). As expected, the orientation of reads was reversed around the 2r, 2s, and Xe breakpoints (Fig. S2). Because of the complex overlap of the three inversions on chromosome 2 (Guillen and Ruiz 2012), read orientation around both breakpoints of inversion 2q (the oldest inversion) is not reversed (Fig. 5).

Figure 5.

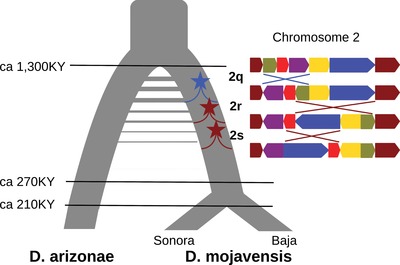
Schematic of the speciation history of D. arizonae and D. mojavensis. The onset of divergence around 1.3 MY was followed by a prolonged period of gene flow that ceased before the divergence of the different populations of D. mojavensis. Inversion 2q arose in D. mojavensis during the onset of divergence (blue star) and is the first in a cascade of three overlapping inversions on chromosome 2 that became fixed in D. mojavensis (adapted from Guillen and Ruiz (2012)).

MODELING DIVERGENCE AND GENE FLOW

To assess the support for postdivergence gene flow between D. mojavensis and D. arizonae, we compared three models: (i) isolation in allopatry, that is an instantaneous split of a single ancestral population at time τ₀ without gene flow, (ii) isolation with a constant rate of symmetric migration of $M=4N_{e}m$ migrants per generation between τ₀ and the present (i.e., the isolation with migration (IM) model) and (iii) a more realistic model where gene flow is restricted to an initial period after divergence and ceases at time τ₁ (the isolation with initial migration (IIM) model) (Fig. 1). This 4‐parameter model (τ₀, τ₁, $\theta =4N_e\mu$, M) captures the fact that diverging species may eventually become completely reproductively isolated. The models make the standard population genetic assumptions of large, randomly mating populations of constant size.

Figure 1.

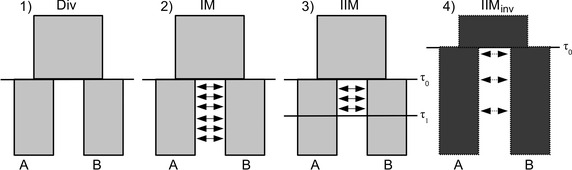
Alternative scenarios of species divergence: (1) strict divergence without gene flow, (2) isolation with migration (IM), and (3) isolation with initial migration (IIM). (4) An inversion that predates the species split should be associated with an older population divergence time τ₀.

A number of methods have been developed to fit these models either to multilocus data (Hey and Nielsen 2004) or continuous genomes (Mailund et al. 2012). For minimal samples (one or two sequences per species) and assuming an infinite sites mutation model, it is possible to compute analytically the probability of mutational configurations in a short, nonrecombining block of sequence (Wang and Hey 2010; Lohse et al. 2011; Wilkinson‐Herbots 2012). In particular, Wilkinson‐Herbots (2012, eq. 29) has derived an expression for the distribution of pairwise differences (k) under the IIM model. Given a large number of sequence blocks, this distribution can be used to estimate parameters under the IIM model. Postdivergence gene flow results in an excess of blocks with no or few divergent sites, and for sufficiently long blocks, the distribution becomes bimodal. The analytic solution of Wilkinson‐Herbots (2012) allows for efficient maximum likelihood estimation from arbitrary numbers of sequence blocks of any length. We implemented this likelihood computation in Mathematica (notebook available upon request, for an analogous implementation in R, see Wilkison‐Herbots in press, MBE) and maximised the joint logarithm of the likelihood ($lnL$) given a list of pairwise differences in sequence blocks of equal length (and assuming a constant mutation rate per block) for all three alternative models using the FindMaximum function.

To minimize the confounding effect of selection and to maximise the density of variable sites per block, we limited the likelihood analysis to intergenic sequences (Wang and Hey 2010). Although lines were highly inbred, there was some residual heterozygosity (on average 0.3 % per site per line) and blocks with any heterozygous sites were excluded. Choosing a block length of 250 bp (we later explore the effect of block length, see Sensitivity analyses) gave a total of 18,268 and 20,404 intergenic blocks for sympatric and allopatric comparisons of D. mojavensis and D. arizonae, respectively, with an average of 6.2 mutations per block (data available from the Dryad Digital repository, doi:10.5061/dryad.5jq6p).

To test for postdivergence gene flow, we first compared the relative support for different models of species divergence. We limited this initial analysis to the colinear chromosomes, as support for the divergence with gene‐flow in inverted regions may be reflective of arrangement polymorphism in the ancestor. Since the isolation model is nested within the IM model, which in turn is nested within the IIM model, we used likelihood ratio tests (assuming $2\Delta lnL$, the difference in logarithm of the likelihood between models follows a χ² distribution) to assess the relative support of models. This requires accounting for the statistical effect of linkage disequilibrium between neighbouring blocks. Assuming that blocks >100 kb apart are unlinked (see previous section), the difference in $lnL$ between models obtained from analyzing all the data can be rescaled by a factor $1/x$, where x is the mean number of 250 bp blocks in each 100 kb section of the genome included in the analysis. This is equivalent to randomly subsampling a single block per 100 kb section of the genome and averaging the inference across many such subsampled datasets. Plotting the correlation coefficient of the number of divergent sites between successively more distant pairs of blocks (Fig. S3) confirmed that linkage disequilibrium is indeed negligible at distances >100 kb.

For inversions that arose before the species split, the time of population divergence under the IIM model (τ₀) should represent the origin of the inversion. To test whether inversions are associated with older τ₀, we conducted a hierarchical set of model comparisons allowing individual parameters to differ between the colinear chromosomes and each rearranged chromosome. Given that one expects the history of the X to differ from that of the autosomes in a number of potentially counfounding ways (Charlesworth et al. 1987), we restricted this analysis to the four major autosomes. We partitioned the autosomal data into three sets: chromosome 2, chromosome 3, and chromosome 4 and 5 combined. Our rationale was that one expects the two colinear autosomes to share the same divergence and gene flow history, whereas those parameters may differ between chromosome 2 and 3 depending on the ages and combined effects of the inversions on each chromosome. Thus, under the most complex model, τ₀, τ₁, and M were free to vary between the three data partitions (this is equivalent to running independent IIM analyses on each data partition). We then tested different model simplifications in a step‐wise manner. Simplifications consisted of constraining one parameter at a time to be shared across data partitions and were accepted if this did not significantly reduce model fit relative to the unconstrained model.

Results

We first investigated gene divergence between D. mojavensis and D. arizonae, contrasting rearranged and colinear chromosomes and populations in allopatry and sympatry. We then examined divergence along the chromosome and, particularly, around inversion breakpoints. Finally, we used the distribution of divergent sites in short blocks of intergenic sequence sampled across the genome to fit explicit models of species divergence with gene flow and tested how speciation history differs between colinear and rearranged regions of the genome. Below, we present analyses based on a single D. mojavensis line from each the Baja California (A976) and Sonora (LB09) population (analyses based on replicate lines from these populations are discussed in “Sensitivity analyses”).

GENE DIVERGENCE

Pairwise divergence between D. arizonae and D. mojavensis was significantly higher for rearranged than colinear chromosomes (Fig. 2). This was the case for both sympatric and allopatric comparisons and regardless of whether we considered all sites combined (Table 1) or exons, introns, or intergenic sequence separately (Table S4). For example, divergence in sympatry across all sites was 2.9%, 3.4%, and 2.9 % for chromosomes 2, 3, and the X, but only 2.4% and 2.5% for chromosomes 4 and 5 respectively (Mann–Whitney U, $P<{10}^{-5}$). In contrast, divergence between the two D. mojavensis lines was significantly (Mann–Whitney U, $P<{10}^{-5}$) smaller for chromosomes 2 and 3 than chromosomes 4 and 5 (Table 1).

Table 1.

Mean chromosome‐wide divergence between D. mojavensis and D. arizonae in sympatry and allopatry and between D. mojavensis populations in Baja and mainland Sonora

Chrom.	Dariz/Dmoj‐LB09, sym	Dariz/Dmoj‐A975, allo	Dmoj‐LB09/Dmoj‐A975
2*	0.0289 (0.0041)	0.0282 (0.0039)	0.0089 (0.0019)
3*	0.0340 (0.0056)	0.0329 (0.0053)	0.0100 (0.0024)
4	0.0238 (0.0042)	0.0232 (0.0041)	0.0108 (0.0027)
5	0.0253 (0.0034)	0.0246 (0.0034)	0.0116 (0.0024)
X*	0.0286 (0.0037)	0.0276 (0.0035)	0.0099 (0.0020)

Standard deviation across 100 kb sections are given in brackets.

*Chromosomes with fixed inversion differences between D. arizonae and D. mojavensis.

If introgression between D. mojavensis and D. arizonae is ongoing or recent, it should be stronger in areas of sympatry, that is mainland Mexico. Contrary to this, we found no reduction in pairwise divergence between D. arizonae and D. mojavensis in sympatry (Table 1). The sliding window plots for divergence in sympatry and allopatry were virtually identical (see red and black lines in Fig. 2). Likewise, we found no excess of mutations shared between D. arizonae and D. mojavensis in sympatry but not in allopatry (Dariz=Dmoj‐LB09 ≠ Dmoj‐A975) compared to mutations shared between D. arizonae and D. mojavensis in allopatry but not in sympatry (Dariz=Dmoj‐A975 ≠ Dmoj‐LB09) (Kulathinal et al. 2009) (Table S5). This is essentially an unpolarised version of the D‐statistic recently used to test for introgression from Neanderthals into modern humans (Green et al. 2010). In fact, considering the total counts of both types of sites (so not accounting for the effect of physical linkage, see Methods), we observed a slight excess of Dariz=Dmoj‐A975 ≠ Dmoj‐LB09 sites, a pattern opposite to that expected. However, when we randomly subsampled sites with a minimum distance of 100 kb (or indeed 10 kb) to account for the non‐independence of nearby sites due to linkage, this difference was not significant (257 vs 259, Binomial sign test, $P=0.48$ (Table S5)).

Plotting pairwise divergence in 500 kb sliding windows (Fig. 2) revealed a marked increase in divergence in a large region (18–26 Mb) in the center of chromosome 2 that contains four inversion breakpoints. We also found pronounced peaks in divergence near the proximal breakpoints of inversions 2r and 2s (Fig. 2). Likewise, there were clear peaks in divergence centered on the breakpoints of inversion Xe (Runcie and Noor 2009) and 3d (6.2 and 27.1 Mb) that were recently mapped in a comparison between the genomes of D. buzattii and D. mojavensis (Delprat et al. 2015) (Fig. 2). Although the breakpoints of inversion 3p2 have not yet been characterized, we hypothesize based on cytological maps (Ruiz et al. 1990), that the observed peak in divergence at 21 Mb coincides with the proximal breakpoint of this inversion.

MODELING DIVERGENCE AND GENE FLOW

For both allopatric and sympatric comparisons of D. arizonae and D. mojavensis the IIM model gave a significantly better fit to the colinear data (as measured by $\Delta lnL$) than the IM model, which in turn fit better than a null model of strict divergence without gene flow (Table 2). In contrast, we could not reject the IM model (in favor of IIM) for the much more recent split between the two D. mojavensis populations (Table 2).

Table 2.

Support for the isolation with migration (IM) and strict divergence (Div) model of species divergence ($\Delta lnL$ relative to the IIM model) estimated from 250 bp blocks

Comparison	Div	IM
Dariz/Dmoj‐LB09 sym	−2.95	−2.05
Dariz/Dmoj‐A975 allo	−2.98	−2.23
Dmoj‐LB09/Dmoj‐A975	−1.62	−0.0093

For comparisons between D. arizonae and D. mojavensis only colinear chromosomes were used.

We initially examined parameter estimates under the most complex variant of the IIM model in which all parameters were allowed to differ between the two rearranged autosomes and colinear autosomes (Table S6). Assuming that inversions arose at or after the time of species divergence (i.e., that τ₀ is shared between colinear and rearranged autosomes) only resulted in a very minor (and non‐significant) reduction in model fit (Table 3). Likewise, allowing the cessation of gene flow (τ₁) to be shared across all three data partitions did not significantly reduce model fit. Thus, the simplest supported scenario was an IIM history in which both time parameters were shared between data partitions but colinear autosomes and chromosome 2 and 3 had different rates of gene flow (Table 3). Under this model, the effective rate of gene flow M at colinear autosomes was estimated to be more than twice that at chromosome 2, which in turn was almost twice that at chomosome 3 (Table 4, Fig. 4). No other parameter better explained the difference in the block‐wise distribution of divergent sites between rearranged and colinear autosomes (Fig. 3). The fact that there was no evidence for an older τ₀ at rearranged chromosomes (Table S6) can also be seen from the broad overlap in the marginal support for this parameter under an unconstrained analysis (Fig. S4). Interestingly, the best‐supported model in which two parameters differed between rearranged and colinear autosomes included an earlier (100–200 KY) cessation of gene flow (τ₁) at rearranged autosomes (Table 3). However, given our (conservative) correction for the effect of physical linkage (see Methods), this model did not fit significantly better than the simpler scenario where only M differed between rearranged and colinear autosomes (Table 3).

Table 3.

Support ($\Delta lnL$ relative to a completely unconstrained model) for hierarchical model simplifications

data	(τ0)	(τ1)	(τ0, τ1)	(τ0, M)	(τ0, τ1, M)
Dariz/Dmoj‐LB09 sym	−0.32	−1.6	−1.6*	−2.6	−20.5
Dariz/Dmoj‐A975 allo	−0.31	−1.9	−2.0*	−2.5	−24.7

Constraining particular parameters (in brackets) to be shared across all autosomes reduces model fit. However, the reduction in model fit is not significant for τ₀ and τ₁, that is the simplest, supported model (*) assumes that τ₀ and τ₁ are shared across all autosomes.

Table 4.

Maximum likelihood estimates of parameters under the simplest, supported model of speciation estimated from 250 bp intergenic blocks

Comparison	θ ($N_e$)	M 2	M 3	$M_{4\&5}$	τ1	τ0
Dariz/Dmoj‐LB09, sym	1.29 (0.65 × 106)	0.47	0.25	0.89	1.26 (272 KY)	5.96 (1,290 KY)
Dariz/Dmoj‐A975, allo	1.33 (0.66 × 106)	0.45	0.25	0.98	1.17 (260 KY)	5.57 (1,240 KY)
Dmoj‐LB09/Dmoj‐A975	0.72 (0.36 × 106)	0.40	0.40	0.40	0	1.76 (213 KY)

Scaled time parameters are given in brackets.

Figure 4.

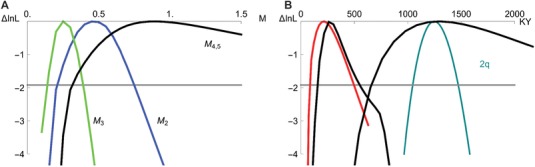
(A) Marginal support ($\Delta lnL$ relative to the maximum likelihood solution) for the rates of gene flow (M) between D. arizonae and D. mojavensis (sympatric comparison) estimated in colinear (black) and rearranged (chromosome 2, blue; chromosome 3, green) autosomes under the IIM model. (B) Marginal support for the onset of species divergence (τ₀) and the cessation of gene flow (τ₁) (black) and the divergence time between D. mojavensis populations in Baja California and Sonora (red). The age of the inversion 2q falls within the estimated onset of divergence between D. arizonae and D. mojavensis (turquoise). The horizontal line defines 95% confidence intervals of parameter estimates.

Figure 3.

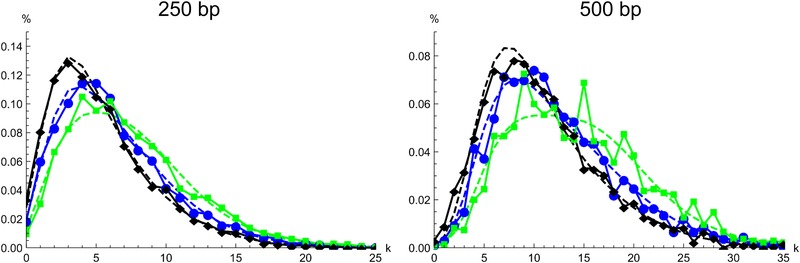
The distribution of divergent sites (k) between D. arizonae and sympatric D. mojavensis in 250 bp (left) and 500 bp (right) intergenic blocks. Colinear chromosomes 4 and 5 are shown in black, the inverted chromosomes 2 and 3 in blue and green, respectively. Points are joined for clarity. The expected distributions under the best supported model inferred from the data (Table 3) are shown as dashed lines.

The ranking of alternative models was identical for allopatric and sympatric comparisons (Table 3). Likewise, parameter estimates under the simplest supported model (IIM with different M) were very similar for D. arizonae and D. mojavensis in sympatry and allopatry (Table S8).

MOLECULAR CLOCK CALIBRATION

To convert divergence time estimates (which are scaled in units of $2N_e$ generations) into absolute values, we applied a genome‐wide, direct mutation rate estimate for D. melanogaster of $3.46\times {10}^{-9}$ (Keightley et al. 2009) and assumed six generations per year. Given the uncertainty associated with these assumptions, the aim of this calibration was merely to obtain an approximate date of events that can be compared to previous studies based on the same molecular clock.

Smith et al. (2012) analyzed data from 15 introns to study the history of three of the four geographically diverged D. mojavensis populations (including Baja California and mainland Sonora) that are partially reproductively isolated from each other by host plant, mating behavior, and geography (Mettler 1957; Markow 1991; Etges et al. 2007). While the assumption of neutrality (and hence the application of the spontaneous mutation rate) may be reasonable for intronic sequence, the intergenic regions analyzed here were less diverged between D. arizonae and D. mojavensis (0.025 across all autosomes compared to 0.043 for the introns analyzed by Smith et al. (2012)). This presumably reflects the greater selective constraint on intergenic regions (Halligan et al. 2004). To account for this, we corrected the mutation rate by a factor $0.025/0.043=0.58$. With this calibration, our θ estimates corresponds to an ancestral $N_e$ of around 6.5 × 10⁵ (Table 4), divergence between D. arizonae and D. mojavensis is estimated at ca 1.3 MYA and the cessation of gene flow ca 270 KYA (Table 4).

Reassuringly, our estimate for the divergence between Baja and the mainland populations of D. mojavensis (ca 220 KY under the IM model, Table S7, Fig. 3) roughly matches that of Smith et al. (2012) (ca 250 KYA). We stress however that there is considerable uncertainty in these estimates (Fig. 4) even when we ignore the uncertainty in the mutation rate estimate and generation time of D. mojavensis in the wild.

THE AGE OF INVERSION 2q

A duplication associated with the breakpoints of inversion 2q allows a unique and independent estimate for the age of this inversions (Guillen and Ruiz 2012). Because this 4.3 kb duplication likely arose with the inversion, one can use the gene divergence between the two duplicates in D. mojavensis to date the origin of the inversion. Applying the D. melanogaster mutation rate to the divergence between the 2q duplicates in the D. mojavensis reference genome and assuming that the non‐functional duplicate accumulates mutations at the neutral rate, gives a date of 1.25 MY (note that Guillen and Ruiz (2012) estimated a divergence of 1.4 MY based on a lower mutation rate of 0.0111 per MY). Assuming that the number of differences between the two duplicates is Poisson distributed, we can plot the support for the estimated inversion age (Fig. 4B, turquoise line). This overlaps very broadly with the maximum likelihood estimate for the onset of species divergence around 1.3 MY and suggests that inversion 2q arose around the same time. Given the overlap of the three inversions on chromosome 2, we know that inversion 2q must have arisen first (Fig. 5) (Guillen and Ruiz 2012). Thus, the estimated time of the duplication event is an upper bound for the age of all three inversions on chromosome 2.

SENSITIVITY ANALYSES AND MODEL FIT

We investigated whether other factors could explain the greater divergence at rearranged compared to colinear autosomes. For example, a greater gene density on a chromosome may be associated with stronger purifying selection, which in turn could lead to a decrease in divergence. However, gene density in D. mojavensis (as measured by the proportion of exonic sequence) does not differ systematically between colinear and rearranged chromosomes (Table S2). Noor and Bennett (2009) have argued that apparent differences in divergence between inverted and colinear chromosomes could simply reflect a bias in mapping quality, which is expected to be lower in the presence of rearrangements. While we found mean mapping quality to be slightly lower at rearranged autosomes as expected (Table S2), this could not explain the observed difference in divergence. Any effect of mapping quality must be restricted to the vicinity of the inversion breakpoints. Removing 100 kb around each of the known inversion breakpoints on chromosome 2 did not reduce chromosome‐wide divergence. Likewise, filtering with higher (or lower) coverage thresholds had almost no effect on the observed difference in divergence between colinear and rearranged autosomes (Fig. S1). In general, any systematic difference in the mapping properties of colinear and rearranged autosomes should also lead to an increase in divergence in the comparison of the two D. mojavensis populations, which we did not observe. On the contrary, their divergence was slightly lower at rearranged chromosomes (Table 1).

Although the divergence between any pair of genomes is determined by many independent coalescent events involving a very large number of ancestors (Wakeley 2009), it may seem risky intuitively to reconstruct speciation history from just a single sample per population. For example, D. mojavensis may have complex and potentially old population structure within Sonora, in which case signatures of gene‐flow from D. arizonae could be specific to particular subpopulations (Slatkin and Pollack 2008). We repeated the likelihood analyses using different replicate lines from both the Baja and the Sonora populations of D. mojavensis; A976 and PO88, respectively (Table S1). Reassuringly, these replicate analyses gave very similar parameter estimates (see Tables S8 and S9). The only exception to this was the M estimate for chromosome 2 for P088 (Table S8) that is most likely a result of the excessive residual heterozygosity of this line on chromosome 2, which meant that only half as many chromosome 2 blocks could be included in the analysis.

To investigate the impact of recombination within blocks on our inference, we repeated the likelihood analyses with longer blocks (500 bp). This resulted in a slight decrease in estimates of M and an increase in estimates of τ₀ (Table S7). Both are well known biases arising from the fact that our approach ignores recombination within blocks, which becomes increasingly problematic for longer blocks (Wall 2003). Importantly however, the influence of block length on parameter estimates was small and the ranking of models was unaffected. We stress the fact that ignoring recombination within blocks slightly underestimates migration and so renders our inferences of significant postdivergence gene flow conservative (Table S7).

Discussion

Several conclusions emerge from our genome‐wide analyses of divergence between D. arizonae and D. mojavensis:

First, our analysis of the colinear data shows that this speciation history involved a prolonged period of gene flow after the onset of divergence (Fig. 5). This is in contrast to earlier studies based on smaller sets of loci and simpler models that lacked the power to detect gene flow (Machado et al. 2007; Counterman and Noor 2006).

Second, and in contrast to the situation in D. persimilis and D. pseudoobscura (Kulathinal et al. 2009), we did not find any difference in divergence in sympatry versus allopatry, suggesting that introgression between these species is historical rather than recent or ongoing. This conclusion is also supported by the better fit of the IIM model compared to a scenario of isolation and migration until the present (IM) and the fact that the estimated cessation of gene flow between D. arizonae and D. mojavensis predates the divergence between D. mojavensis populations in Baja California and Sonora (Table 4, Fig. 5).

Third, all three chromosomes harboring fixed paracentric inversions (chromosomes 2, 3, and the X) showed greater gene divergence than the colinear autosomes 4 and 5. While we see a classic signature of increased divergence around inversion breakpoints on chromosome 3 and the X (Kulathinal et al. 2009), the picture is less clear‐cut for chromosome 2. Instead, it seems that the complex overlap of these inversions eliminated crossing‐over across most of the chromosome, and the pattern of decreased divergence inside inversions due to double‐crossover events does not apply (Dobzhansky 1937, Fig. 3, p. 111).

Finally, our hierarchical comparison of models showed that the increase in gene divergence at rearranged chromosomes is best explained by a reduction in gene flow. Importantly, our model comparison suggests that it is unlikely that the autosomal inversions arose and became fixed long after the onset of species divergence (Noor and Bennett 2009). However, we emphasize that because of the long period of gene flow, there is limited information about τ₀ in the data. Assuming gene flow at rate $M=0.47$ for a period of ${\tau }_0-{\tau }_1=4.7$ ($2N_e$ generations) implies that only a fraction of $e^{-\left(4.7\right)0.47}=0.11$ of lineages are unaffected by migration and so contribute information about τ₀. Perhaps stronger support for the conclusion that the fixed inversions do not predate species divergence comes from the gene divergence between the two duplicates generated by the 2q inversion breakpoint. This provides an upper bound for the age of all three inversions on chromosome 2 that is independent of the likelihood estimate for τ₀, but nevertheless agrees surprisingly well with it. We emphasize that the comparison between estimates for τ₀ and the age of inversion 2q does not rely on any molecular clock calibration.

MODELLING DIVERGENCE AND GENE FLOW

Using explicit models to reconstruct past speciation histories clearly has the potential to disentangle the processes involved in speciation and test how parameters such as gene flow differ between different parts of the genome. Our hierarchical framework is general and can be used to contrast historical parameters between any partition of the genome. Sousa et al. (2013) have recently developed a similar method based on IMa (Hey and Nielsen 2004). However, this approach is computationally intensive and does not scale to genomic data. In contrast, the analytic likelihood computation of Wilkinson‐Herbots (2012) provides an efficient way to fit simple divergence and gene‐flow models to whole genome data. It also does not suffer from an inflated rate of false positives (i.e., detecting migration when there is none) (Wilkinson‐Herbots, in press), which has recently been reported for IMa (Cruickshank and Hahn 2014).

Basing inferences on absolute pairwise divergence clearly involves a trade‐off: One the one hand, sampling just a single individual per population circumvents the well‐known problems of $F_{st}$‐based analyses (Charlesworth 1998; Noor and Bennett 2009) and allows for efficient analytic likelihood computations. On the other hand, such minimal sampling necessarily comes at the expense of statistical power and limits the complexity of historical models that can be explored. For example, one might bemoan the fact that we have ignored changes in $N_e$ and instead assumed that the common ancestral population of D. mojavensis and D. arizonae split into two daughter species of the same effective size. Furthermore, if speciation involves a gradual build‐up of reproductive isolation, one would ideally like to fit models of decreasing gene flow rather than assume that both divergence and the cessation of gene flow are instantaneous events. However, the tight fit between the observed distribution of pairwise differences and that predicted under the IIM model we infer (Fig. 3), suggests that there is little additional information in the distribution of pairwise differences to distinguish such more realistic scenarios. In general, the IIM model is an important extension of the IM model, because it makes the inferences of postdivergence gene flow independent of the age of a particular species pair, an important prerequisite for comparative analyses of speciation histories.

A ROLE OF INVERSIONS IN SPECIATION?

Taken together our results are compatible with a scenario where multiple inversions originated and became fixed as D. mojavensis and D. arizonae began to diverge, as envisioned by models of speciation in the face of gene flow (Navarro and Barton 2003; Kirkpatrick and Barton 2006). These models show that inversions can accelerate the build up of reproductive isolation (Navarro and Barton 2003) and, in turn, are able to spread if they trap multiple locally beneficial loci in the early stages of divergence (Kirkpatrick and Barton 2006).

However, we stress that our results do not allow us to draw any conclusions as to whether there has been direct selection against introgression at an inversion, or whether the reduction in gene flow we detect simply reflects reduced recombination. Likewise, we do not know whether inversions became established because of selection on genes inside them or due to some other (potentially neutral) mechanism. Under the Kirkpatrick–Barton model, the selective advantage of an initially rare inversion trapping locally beneficial alleles due to the migration load is proportional to the migration rate (m) and the number of beneficial alleles (Kirkpatrick and Barton 2006, eq. 2). Thus, given our estimates for $N_e$ and the number of migrants $M_{4\&5}$ (Table 4), the benefit due to the migration load of an inversion would be extremely weak (on the order of 10⁻⁴) even if it trapped hundreds of beneficial alleles. However, we emphasize that the strong and potentially short‐lived migration required for the initial establishment of an inversion under the Kirkpatrick–Barton model is far beyond the resolution of coalescent‐based inferences that can only detect weak and long‐term (on the time‐scales of drift and the per locus mutation rate) postdivergence gene‐flow. Short‐term gene flow at much higher rates would be indistinguishable from a panmictic ancestral population.

An important aim of future genomic studies on species with fixed inversion differences is to explore the link with phenotypic evolution and, specifically test whether loci involved in adaptation or isolating barriers are concentrated in rearranged chromosomes. This would be further evidence for a role of inversions in speciation. Studies of other species have suggested that isolating traits (such as floral traits in plants (Fishman et al. 2013)) map to rearrangements. So far, mapping studies for traits involved in mating behavior (song and cuticular hydrocarbons) in D. mojavensis have not found a greater concentration of quantitative trait loci on chromosomes 2 and 3 (Etges et al. 2009).

Perhaps a more promising avenue to detecting evidence of past selection on inversions is to look for selective sweep signatures of decreased diversity around more recent inversions. Intriguingly, the pairwise diversity of the two D. mojavensis lines shows small but noticeable troughs around some of the inversion breakpoints (blue line in Fig. 2). For example, the mean pairwise diversity in the 100 kb regions on either side of each of the six inversion breakpoints on chromosome 2 is reduced (0.76 %) compared to the chromosome‐wide average (0.90 %, Table 1)). This difference is significant in a permutation test ($P<0.02$). Given the age of D. mojavensis and D. arizonae, selective events at the time of species divergence should have a small effect on pairwise diversity in D. mojavensis. For example, a hard selective sweep at the time of species divergence would truncate the distribution of pairwise coalescence times at $T={\tau }_0-{\tau }_1$. Thus, the average coalescence time for a pair of lineages sampled from Baja and mainland Sonora would be reduced by a factor of $1-e^T(1+T)=0.95$ (assuming, $T=4.7$, Table 4). The fact that the observed reduction in diversity around breakpoints on chromosome 2 is slightly larger could either be due to chance or more recent selective events. Future studies on the genome wide diversity in D. mojavensis in larger samples should be able to reveal whether the inversions fixed between D. arizonae and D. mojavensis have been under strong directional selection, and how the timing of the potential sweeps involved fits into the speciation history we have inferred here.

Supporting information

Table S1: Origins of the three populations of Drosophila mojavensis and D. arizonae in this study and numbers of flies used to establish laboratory populations.

Table S2: Summary of scaffolds analysed: Composition (% exon), total length of mapped reads before and after filtering and average mapping quality (MQ) of D. arizonae reads mapped against the D. mojavensis reference genome.

Table S3: Breakpoint coordinates of inversions fixed between D. mojavensis and D. arizonae.

Table S4: Mean pairwise divergence for exons, introns and intergenic regions.

Table S5: Counts of sites uniquely shared between D. mojavensis and D. arizonae in sympatry or allopatry at colinear autosomes.

Table S6: Maximum likelihood estimates of parameters under the IIM model estimated from 250 base intergenic blocks without constraints, i.e. M and τ parameters are free to vary between colinear autosomes, chromosome 2 and chromosome 3.

Table S7: Maximum likelihood estimates of parameters under the simplest, supported model of speciation estimated from 500bp intergenic blocks.

Table S8: Maximum likelihood estimates of parameters under a model of isolation with initial migration (IIM) which differs between rearranged and colinear autosomes.

Table S9: Mean chromosome‐wide divergence between D. mojavensis and D. arizonae in sympatry (Sonora) and allopatry (Baja) for replicate lines PO88 and A976.

Figure S1: The effect of filtering on mean chromosome‐wide divergence between D. arizonae and (allopatric) D. mojavensis; the filtering thresholds used are shown as dashed lines.

Figure S2: Example IGV screenshot of D. arizonae reads mapped to the D. mojavensis reference genome.

Figure S3: Mean correlation coefficient for the number of divergent sites between D. mojavensis (LB09) and D. arizonae for pairs of 250 bp intergenic blocks plotted against distance (i.e. # of successive blocks apart).

Figure S4: Marginal support ($\Delta lnL$) for τ₀ estimated independently for chromosome 2 (blue), 3 (green) and 4& 5 combined (black) (point estimates in Table S6).