Voltammetric Mechanism of Multiion Detection with Thin Ionophore-Based Polymeric Membrane

Abstract

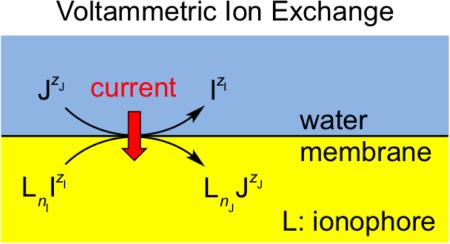
The capability to detect multianalyte ions in their mixed solution is an important advantage of voltammetry with an ionophore-based polymeric membrane against the potentiometric and optical counterparts. This advanced capability is highly attractive for the analysis of physiological ions at millimolar concentrations in biological and biomedical samples. Herein, we report on the comprehensive response mechanisms based on the voltammetric exchange and transfer of millimolar multiions at a thin polymeric membrane, where an ionophore is exhaustively depleted upon the transfer of the most favorable primary ion, I^z_I. With a new volt-ammetric ion-exchange mechanism, the primary ion is exchanged with the secondary favorable ion, J^z_J, at more extreme potentials to transfer a net charge of |z_J|/n_J – |z_I|/n_I for each ionophore molecule, which forms 1:n_I and 1:n_J complexes with the respective ions. Alternatively, an ion-transfer mechanism utilizes the second ionophore that independently transfers the secondary ion without ion exchange. Experimentally, a membrane is doped with a Na⁺- or Li⁺-selective ionophore to detect not only the primary ion, but also the secondary alkaline earth ion based on the ion-exchange mechanism, where both ions form 1:1 complexes with the ionophores to transfer a net charge of +1. Interestingly, the resultant peak potentials of the secondary divalent ion vary with its sample activity to yield an apparently super-Nernstian slope as predicted theoretically. By contrast, the voltammetric exchange of calcium ion (n_I = 3) with lithium ion (n_J = 1) by a Ca²⁺-selective ionophore is thermodynamically unfavorable, thereby requiring a Li⁺-selective ionophore for the ion-transfer mechanism.

Graphical abstract

The voltammetric operation^1,2 of an ionophore-based polymeric membrane is a powerful approach that enables the detection of multianalyte ions in contrast to the potentiometric and optical counterparts.^3,4 Voltammetric multiion detection was demonstrated by using an ionophore-free membrane,⁵ and can be facilitated by doping a membrane with a selective ionophore, which can mediate the transfer of different ions at widely separated potentials within a potential window.^6,7 Voltammetrically, the potential across the membrane/water interface is controlled externally to transfer not only the most favorable primary analyte ion, but also less favorable analyte ions at more extreme potentials as far as an ionophore is available in the membrane to form complexes with the analyte ions. Advantageously, multiple analyte ions can be preconcentrated together into a thin membrane and successively stripped into the sample solution to enable highly sensitive stripping voltammetry as demonstrated for sub-micromolar lead and zinc ions⁶ as well as low-nanomolar potassium ion and sub-micromolar ammonium ion.⁷

Voltammetric multiion detection is highly attractive for the analysis of physiological ions in biological and biomedical samples, but has been challenging owing to their millimolar concentrations. For instance, Bond and co-workers employed a thin ionophore-doped polymeric membrane⁸ to determine the millimolar concentration of a primary ion (e.g., Na⁺, K⁺, and Ca²⁺) in plasma and whole blood samples from the peak potential of a thin-layer voltammogram.⁹ The successive detection of a less favorable ion, however, was prevented by the depletion of an ionophore in the thin membrane upon complexation with the millimolar primary ion. Recently, Bakker and co-workers doped a thin polymeric membrane with multiple ionophores¹⁰ to volt-ammetrically detect multiple analyte ions (e.g., Li⁺ and K⁺) at millimolar concentrations in undiluted human plasma.¹¹ With their approach, ionophores were initially present as their analyte complexes in the membrane to obtain separate voltammetric peaks by successively stripping up to three ions.¹¹ This approach, however, required the addition of a carefully controlled amount of an ionic site to a membrane to obtain voltammetric responses to multiions.

In this work, we report on the comprehensive response mechanisms based on voltammetric ion-exchange (IE) or ion-transfer (IT) reactions to enable the detection of millimolar multianalyte ions with an ionophore-based polymeric membrane. In either mechanism, an ionophore, L, is depleted by the formation of a 1:n_I complex with the primary ion, I^z_I, upon its transfer from an aqueous sample into a thin membrane

$$n_{\mathrm{I}}\mathrm{L}\left(\mathrm{m}\right)+{\mathrm{I}}^{z_{\mathrm{I}}}\left(\mathrm{w}\right)\rightleftharpoons {\mathrm{L}}_{n_{\mathrm{I}}}{\mathrm{I}}^{z_{\mathrm{I}}}\left(\mathrm{m}\right)$$ (1)

With the new IE mechanism, the same ionophore drives the exchange of the primary ion with the secondary ion, J^z_J, at more extreme potentials to form a 1:n_J complex

$$n_{\mathrm{J}}{\mathrm{L}}_{n_{\mathrm{I}}}{\mathrm{I}}^{z_{\mathrm{I}}}\left(\mathrm{m}\right)+n_{\mathrm{I}}{\mathrm{J}}^{z_{\mathrm{J}}}\left(\mathrm{w}\right)\rightleftharpoons n_{\mathrm{I}}{\mathrm{L}}_{n_{\mathrm{J}}}{\mathrm{J}}^{z_{\mathrm{J}}}\left(\mathrm{m}\right)+n_{\mathrm{J}}{\mathrm{I}}^{z_{\mathrm{I}}}\left(\mathrm{w}\right)$$ (2)

where the charges of both ions are positive or negative. Interestingly, this voltammetric IE reaction gives a current response when the net charge transferred by each ionophore molecule is not zero, i.e.,

$$\mid z_{\mathrm{J}}\mid ∕n_{\mathrm{J}}-\mid z_{\mathrm{I}}\mid ∕n_{\mathrm{I}}>0$$ (3)

Alternatively, the IT mechanism utilizes the second ionophore, L′, to independently transfer the secondary ion without ion exchange

$$n_{\mathrm{J}}{\mathrm{L}}^{\prime }\left(\mathrm{m}\right)+{\mathrm{J}}^{z_{\mathrm{J}}}\left(\mathrm{w}\right)\rightleftharpoons {\mathrm{L}}_{n_{\mathrm{J}}}^{\prime }{\mathrm{J}}^{z_{\mathrm{J}}}\left(\mathrm{m}\right)$$ (4)

thereby eliminating the requirement of eq 3. Advantageously, our approach does not require the addition of an ionic site to a membrane in contrast to the Bakker's approach,^10,11 where an analyte ion must be initially present in the membrane phase.

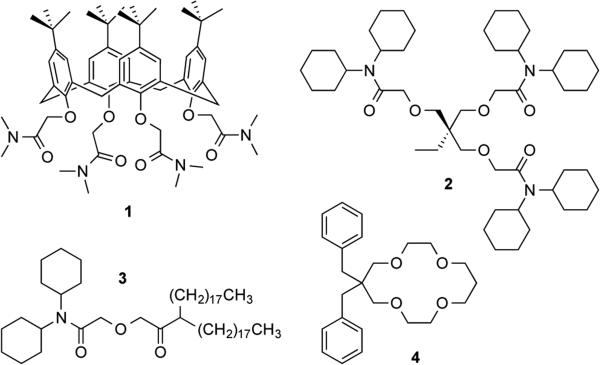
Experimentally, we demonstrate the detection of primary and secondary ions based on IE and IT mechanisms by using single and double ionophores, respectively. Specifically, a thin PVC membrane is doped with Na⁺-selective ionophore 1¹² or Li⁺-selective ionophore 2¹³ (Figure 1) to yield voltammetric responses not only to the primary ion, but also to the secondary alkaline earth ion based on the IE mechanism. The ratio of peak currents for the respective ions is assessed theoretically to confirm the formation of 1:1 complexes with both ions, which yields a net transferred charge, |z_J|/n_J–|z_I|/n_I, of +1. Interestingly, we predict theoretically and confirm experimentally that the peak potential based on the IE mechanism depends on the logarithmic sample activity of the secondary ion to yield an apparently super-Nernstian slope. By contrast, a membrane is doped with both Ca²⁺-selective ionophore 3¹⁴ and Li⁺-selective ionophore 4¹⁵ to detect the primary calcium ion and the secondary lithium ion based on the IT mechanism. The IE mechanism based on the formation of 1:3 and 1:1 complexes of ionophore 3 with the respective ions is not thermodynamically favorable, whereas a net transferred charge of +1/3 is expected.

Figure 1.

Structures of ionophores 1–4 used in this study.

THEORY

Global Model

Here, we define a global model for the IE mechanism to simulate voltammograms at a thin polymeric membrane doped with a single ionophore.¹⁶ The generalized model is applicable to any potential applied across the interface between the membrane and the aqueous solution that contains primary and secondary ions with any charges and complexation stoichiometries. Our model assumes reversible ion transfer across the membrane/water interface as characterized by the Nernst equation

$${\Delta }_{\mathrm{w}}^{\mathrm{m}}\varphi ={\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{X}}^{0^{\prime }}+\frac{RT}{z_{\mathrm{X}}F}\ln \frac{{\left[{\mathrm{X}}^{z_{\mathrm{X}}}\right]}_{\mathrm{w}}}{{\left[{\mathrm{X}}^{z_{\mathrm{X}}}\right]}_{\mathrm{m}}}$$ (5)

where ${\Delta }_{\mathrm{w}}^{\mathrm{m}}\varphi$ is the potential of the membrane phase with respect to the aqueous phase, ${\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{X}}^{0^{\prime }}$ is the formal potential of simple transfer¹⁷ of an analyte ion, X^z_x (= I^z_I or J^z_J), and [X^z_X]_w and [X^z_X]_m are its concentrations in the bulk aqueous and membrane phases, respectively. The bulk concentrations are maintained near the interface during the voltammetric transfer of an analyte ion, because the aqueous phase contains excess amounts of primary and secondary ions¹⁶ and because the membrane is sufficiently thin.^5,7,18-20 Accordingly, the bulk concentrations of the ionophore in its free and complex forms, [L] and [L_nx X^z_x], respectively, can be used to define an overall formation constant, β_nx, as

$${\beta }_{n_{\mathrm{X}}}=\frac{\left[{\mathrm{L}}_{n_{\mathrm{X}}}{\mathrm{X}}^{z_{\mathrm{X}}}\right]}{{\left[\mathrm{L}\right]}^{n_{\mathrm{x}}}{\left[{\mathrm{X}}^{z_{\mathrm{X}}}\right]}_{\mathrm{m}}}$$ (6)

The mass balance of the ionophore is also given by using the bulk concentrations as

$$L_{\mathrm{T}}=\left[\mathrm{L}\right]+n_{\mathrm{I}}\left[{\mathrm{L}}_{n_{\mathrm{I}}}{\mathrm{I}}^{z_{\mathrm{I}}}\right]+n_{\mathrm{J}}\left[{\mathrm{L}}_{n_{\mathrm{J}}}{\mathrm{J}}^{z_{\mathrm{J}}}\right]$$ (7)

where L_T is the total concentration of the ionophore. The membrane composition depends on the phase boundary potential across the membrane/water interface, which is externally controlled to drive the interfacial transfer of primary and secondary ions. The resultant current response, i, is given by

$$i=FAl\frac{d}{dt}\left(z_{\mathrm{I}}{\left[{\mathrm{I}}^{z_{\mathrm{I}}}\right]}_{\mathrm{m}}+z_{\mathrm{I}}\left[{\mathrm{L}}_{n_{\mathrm{I}}}{\mathrm{I}}^{z_{\mathrm{I}}}\right]+z_{\mathrm{J}}{\left[{\mathrm{J}}^{z_{\mathrm{J}}}\right]}_{\mathrm{m}}+z_{\mathrm{J}}\left[{\mathrm{L}}_{n_{\mathrm{J}}}{\mathrm{J}}^{z_{\mathrm{J}}}\right]\right)$$ (8)

where A and l are the area and thickness of the membrane, respectively.

Eqs 5–8 are combined and numerically solved by using Mathematica 10 (Wolfram Research, Champaign, IL) to calculate the normalized current as defined by

$$I=\frac{iRT}{F^{2}Alv{L}_{\mathrm{T}}}$$ (9)

where v is the sweep rate of the phase boundary potential. This theory section presents only the forward scan of a reversible voltammogram, which is a mirror image of the reverse scan voltammogram with respect to the horizontal axis.¹⁶ The phase boundary potential is swept from a positive potential to a negative potential to yield a positive current response based on cation transfer from the aqueous solution into the membrane.

Local Models

We also develop local models to obtain analytical expressions for peak currents and peak potentials based on IE and IT mechanisms. In the IT mechanism, the secondary ion may possess any charge and complexation stoichiometry, whereas the charge and stoichiometry of the secondary ion must satisfy eq 3 for the IE mechanism. We ensure that peak currents and peak potentials of local models agree with those of the global models developed for the IT mechanism in the previous work¹⁶ as well as for the IE mechanism in this work.

The local model for the IE mechanism gives the normalized peak current, $I_{\mathrm{p},\mathrm{J}}^{\mathrm{IE}}$, and the peak potential, ${\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{p},\mathrm{J}}^{\mathrm{IE}}$, as given by (see Supporting Information)

$$I_{\mathrm{p},\mathrm{J}}^{\mathrm{IE}}=\frac{{\left(n_{\mathrm{I}}{z}_{\mathrm{J}}-n_{\mathrm{J}}{z}_{\mathrm{I}}\right)}^2}{n_{\mathrm{I}}{n}_{\mathrm{J}}{\left(\sqrt{n_{\mathrm{I}}}+\sqrt{n_{\mathrm{J}}}\right)}^2}$$ (10)

$${\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{p},\mathrm{J}}^{\mathrm{IE}}=\frac{n_{\mathrm{I}}{z}_{\mathrm{J}}{\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LJ}}^{0^{\prime }}-n_{\mathrm{J}}{z}_{\mathrm{I}}{\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LI}}^{0^{\prime }}}{n_{\mathrm{I}}{z}_{\mathrm{J}}-n_{\mathrm{J}}{z}_{\mathrm{I}}}+\frac{RT}{\left(n_{\mathrm{I}}{z}_{\mathrm{J}}-n_{\mathrm{J}}{z}_{\mathrm{I}}\right)F}\ln \frac{L_{\mathrm{T}}^{(n_{\mathrm{J}}-n_{\mathrm{I}})n_{\mathrm{J}}}{n}_{\mathrm{J}}^{(2n_{\mathrm{I}}+n_{\mathrm{J}})∕2}}{n_{\mathrm{I}}^{2n_{\mathrm{I}}+n_{\mathrm{J}}}{\left(\sqrt{n_{\mathrm{I}}}+\sqrt{n_{\mathrm{J}}}\right)}^{n_{\mathrm{J}}-n_{\mathrm{I}}}}$$ (11)

with

$${\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LX}}^{0^{\prime }}={\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{X}}^{0^{\prime }}+\frac{RT}{z_{\mathrm{X}}F}\ln {\left[{\mathrm{X}}^{z_{\mathrm{X}}}\right]}_{\mathrm{W}}{\beta }_{n_{\mathrm{X}}}{L}_{\mathrm{T}}^{n_{\mathrm{X}}-1}$$ (12)

The peak current is not zero and the peak potential is finite, because eq 3 is satisfied as a prerequisite for the IE mechanism (i.e., n_iz_j–n_jz_i ≠ 0). Interestingly, the peak potential depends on the aqueous activity of the secondary ion, a_J, to yield an apparently super-Nernstian slope from eqs 11 and 12 as

$$\frac{d{\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{p},\mathrm{J}}^{\mathrm{IE}}}{d\log a_{\mathrm{J}}}=\frac{2.303n_{\mathrm{I}}RT}{\left(n_{\mathrm{I}}{z}_{\mathrm{J}}-n_{\mathrm{J}}{z}_{\mathrm{I}}\right)F}$$ (13)

The right-hand side of eq 13 exceeds a Nernstian slope of 2.303RT/z_JF when eq 3 is satisfied. Apparently super-Nernstian slopes have been reported for zero-current potentiometry and explained on the basis of thermodynamic equilibria,^21-23 but not reported for voltammetry.^8-11

The IT mechanism yields normalized peak current, $I_{\mathrm{p},\mathrm{X}}^{\mathrm{IT}}$, and peak potential, ${\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{p},\mathrm{X}}^{\mathrm{IT}}$, for any analyte ion¹⁶ as given by

$$I_{\mathrm{p},\mathrm{X}}^{\mathrm{IT}}=\frac{z_{\mathrm{X}}^2}{n_{\mathrm{X}}{(\sqrt{n_{\mathrm{X}}}+1)}^2}$$ (14)

$${\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{p},\mathrm{X}}^{\mathrm{IT}}={\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LX}}^{0^{\prime }}+\frac{RT}{z_{\mathrm{X}}F}\ln \frac{{\left(\sqrt{n_{\mathrm{X}}}\right)}^{n_{\mathrm{X}}+2}}{{\left(\sqrt{n_{\mathrm{X}}}+1\right)}^{n_{\mathrm{X}}-1}}$$ (15)

The peak potential is very close to ${\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LX}}^{0^{\prime }}$ and depends on the aqueous activity of an analyte ion to yield a Nernstian slope as demonstrated experimentally by others.^8-11

Noticeably, the peak potential of the secondary ion based on the IE mechanism is shifted with respect to that based on the IT mechanism when the same ionophore is employed. This potential shift is given by a combination of eq 11 with eq 15 as

$${\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{p},\mathrm{J}}^{\mathrm{IE}}-{\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{p},\mathrm{J}}^{\mathrm{IT}}\approx \frac{n_{\mathrm{J}}{z}_{\mathrm{I}}\left({\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LJ}}^{0^{\prime }}-{\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LI}}^{0^{\prime }}\right)}{n_{\mathrm{I}}{z}_{\mathrm{J}}-n_{\mathrm{J}}{z}_{\mathrm{I}}}$$ (16)

The right-hand side of eq 16 is negative for cations (because ${\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LJ}}^{0^{\prime }}<{\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LI}}^{0^{\prime }}$) and positive for anions (because ${\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LJ}}^{0^{\prime }}>{\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LI}}^{0^{\prime }}$). This result indicates that the transfer of the secondary ion is thermodynamically less favorable in the IE mechanism, where the complexes of the primary ion must dissociate to form the complexes of the secondary ion (eq 2).

Effect of Analyte Charge

We employ the global model to demonstrate the voltammetric detection of primary and secondary ions with different charges (z_I = +1 and z_J = +2) when both ions form 1:1 complexes (n_I = n_J = 1) to transfer a net charge of +1 based on the IE mechanism (eq 3). We selected these analyte charges and complexation stoichiometries, which are consistent with those used for the experimental demonstration of the IE mechanism (see below). In this case, a more negative potential facilitates the transfer of the divalent secondary cation than that of the monovalent primary cation (see eq 5), thereby shifting the following IE reaction from the left-hand side to the right-hand side

$${\mathrm{LI}}^{+}\left(\mathrm{m}\right)+{\mathrm{J}}^{2+}\left(\mathrm{w}\right)\rightleftharpoons {\mathrm{LJ}}^{2+}\left(\mathrm{m}\right)+{\mathrm{I}}^{+}\left(\mathrm{w}\right)$$ (17)

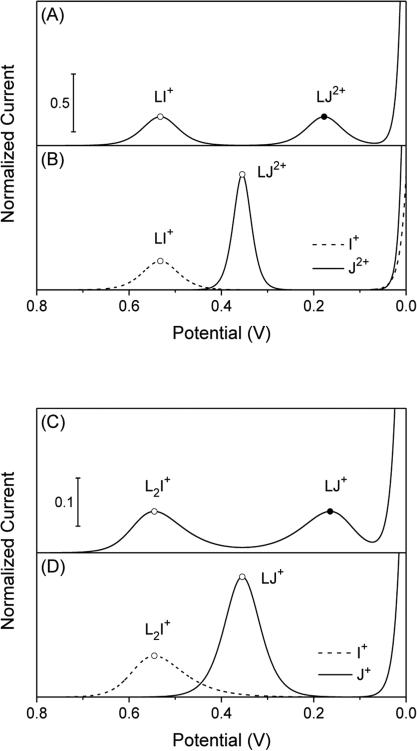
In fact, Figure 2A shows two separate voltammetric peaks for the mixed solution of primary and secondary ions, which confirms the IE mechanism. Specifically, the transfer of the primary ion at ^~0.55 V is based on the formation of its 1:1 complex, LI⁺, and is followed by voltammetric ion exchange with the secondary ion at ^~0.18 V based on the formation of its 1:1 complex, LJ²⁺. The respective peak potentials are consistent with the peak potentials predicted by eqs 15 and 11 based on local models. In addition, both global and local models give a normalized peak current of 0.25 for both primary and secondary ions, which transfer a net charge of +1per ionophore molecule as given by z_I/n_I = +1 and z_J/n_J – z_I/n_I = +1, respectively.

Figure 2.

Thin-layer voltammograms (solid and dashed lines) as simulated by using (A and B) β₁ = 10⁹ for I⁺ and β₁ = 10¹² for J⁺ and (C and D) β₂ = 10⁹ for I⁺ and β₁ = 10⁶ for J²⁺ in addition to [I^z_I]_W =[J^z_I]_W = L_T = 1 M for simplicity. The potential is defined against ${\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{I}}^{0^{\prime }}(={\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{J}}^{0^{\prime }})$. Closed circles represent the current and potential of a voltammetric peak based on the IE mechanism as calculated by using eq 10 and 11, respectively. Closed circles are based on the IT mechanism and obtained by using eqs 14 and 15.

We also employ the global model reported in the previous work¹⁶ to simulate the voltammograms of primary and secondary ions in separate solutions (Figure 2B). Voltammetric responses to the primary ion are identical in the presence and absence of the secondary ion. By contrast, a voltammetric response to the secondary ion based on the IE mechanism is obtained at much more negative potentials than in the absence of the primary ion as predicted also by eq 16 based on the local model. The extra negative potentials are required in the IE mechanism to dissociate the ionophore complexes of the primary ion upon the formation of the complexes of the secondary ion. The exchange of a secondary ion with the primary ion is thermodynamically less favorable than the transfer of the secondary ion without ion exchange. In addition, the normalized peak current based on the transfer of a net charge of z_J/n_J = +2 by the secondary ion without the primary ion is much higher than the peak current based on the IE mechanism, where each ionophore molecule transfers a net charge of z_J/n_J – z_I/n_I = +1. Noticeably, all voltammetric peaks in Figure 2A are symmetric with respective to the peak potential as expected for the formation of 1:1 complexes.¹⁶

Effect of Complexation Stoichiometry

We also employ the global model to demonstrate successive voltammetric responses to monovalent primary and secondary ions that form 1:2 and 1:1 complexes, respectively. In this case, the formation of 1:1 complexes becomes more favorable than the formation of 1:2 complex at more negative potentials, where more cations are transferred into the membrane phase (see eq 5). Accordingly, the following IE reaction is facilitated at more negative potentials

$${\mathrm{L}}_2{\mathrm{I}}^{+}\left(\mathrm{m}\right)+2{\mathrm{J}}^{+}\left(\mathrm{w}\right)\rightleftharpoons 2{\mathrm{LJ}}^{+}\left(\mathrm{m}\right)+{\mathrm{I}}^{+}\left(\mathrm{w}\right)$$ (18)

In fact, the global model shows that a voltammetric response to the primary ion is followed by a voltammetric response to the secondary ion based on the IE mechanism in their mixed solution (Figure 2C). The voltammetric response to the secondary ion is lowered and shifted to more negative potentials in the presence of the primary ion than in the absence of the primary ion (Figure 2D). The negative potential shift is due to a thermodynamic effect, whereas the lower peak current is due to a lower net charge of +1/2 (= z_J/n_J – z_I/n_I) transferred by each ionophore molecule in the IE mechanism in comparison with the transfer of the secondary ion without ion exchange (i.e., z_J/n_J = +1). The net charge transferred in the IE mechanism is identical to the net charge transferred by the primary ion (i.e., z_I/n_I = +1/2), thereby yielding the identical peak current for primary and secondary ions in their mixed solution (Figure 2C).

Noticeably, a voltammetric response to the secondary ion based on the IE mechanism (Figure 2C) is broader at the positive side of the peak potential. This asymmetry is ascribed to the 2:1 stoichiometry of the voltammetric IE reaction (eq 18), where one of L₂I¹⁺ apparently serves as an ionophore for two of J²⁺ By contrast, voltammetric peaks for the primary ion (Figures 2C and D) are broader at the negative side of the peak potential owing to the formation of 1:2 complexes.¹⁶

Zero-Current Ion Exchange

The voltammetric IE reaction (eq 2) yields a current response in contrast to a conventional zero-current IE reaction, where no net charge is transferred across the membrane/water interface as given by

$$\mid z_{\mathrm{I}}\mid {\mathrm{J}}^{z_{\mathrm{J}}}\left(\mathrm{w}\right)+\mid z_{\mathrm{J}}\mid {\mathrm{L}}_{n_{\mathrm{I}}}{\mathrm{I}}^{z_{\mathrm{I}}}\left(\mathrm{m}\right)\rightleftharpoons \mid z_{\mathrm{I}}\mid {\mathrm{L}}_{n_{\mathrm{J}}}{\mathrm{J}}^{z_{\mathrm{J}}}\left(\mathrm{m}\right)+\mid z_{\mathrm{J}}\mid {\mathrm{I}}^{z_{\mathrm{I}}}\left(\mathrm{w}\right)+(n_{\mathrm{I}}\mid z_{\mathrm{J}}\mid -n_{\mathrm{J}}\mid z_{\mathrm{I}}\mid )\mathrm{L}\left(\mathrm{m}\right)$$ (19)

Eq 19 shows that the zero-current IE reaction produces free ionophores when eq 3 is satisfied for the voltammetric IE reaction $(n_{\mathrm{I}}\mid z_{\mathrm{J}}\mid -n_{\mathrm{J}}\mid z_{\mathrm{I}}\mid >0)$. Thus, the zero-current IE reaction is unfavorable in the presence of excess amounts of the primary and secondary ions that satisfy eq 3. By contrast, no free ionophore is produced in the zero-current IE reaction when

$$n_{\mathrm{i}}\mid z_{\mathrm{j}}\mid =n_{\mathrm{j}}\mid z_{\mathrm{i}}\mid$$ (20)

In this case, no voltammetric IE reaction is expected.

EXPERIMENTAL SECTION

Chemicals

Tert-butylcalix[4]arene-tetrakis(N,N-dimethylacetamide), 1, lithium ionophore VIII (2; N,N,N′,N′,N″,N″-hexacyclohexyl-4,4′,4″-propylidynetris(3-oxabutyramide)), calcium ionophore IV (3; ETH 5234¹⁴), lithium ionophore VI (4; 6,6-dibenzyl-14-crown-4), tetradodecylammonium (TDDA) bromide, PVC (high molecular weight), 2-nitrophenyl octyl ether (oNPOE), bis(2-ethylhexyl) sebacate (DOS) were obtained from Aldrich (Milwaukee, WI). Potassium tetrakis(pentafluorophenyl)borate (TFAB) was purchased from Boulder Scientific Company (Mead, CO). All reagents were used as received. TDDATFAB was prepared by metathesis²⁴ and used as organic supporting electrolytes in the membranes. All sample solutions were prepared by using ultrapure water (18.2 MΩ·cm and TOC of 3 ppb) from the Milli-Q Advantage A10 system equipped with Q-Gard T1 pack and Quantum TEX cartridge (EMD Millipore, Billerica, MA).¹⁹ The Milli-Q system was fed with the water (15.0 MΩ·cm) purified from tap water by using Elix 3 Advantage (EMD Millipore).

Electrode Modification

A bare 5 mm-diameter gold disk was cleaned, electrochemically modified with an oxidatively doped film of decyl-substituted poly(3,4-ethylenedioxythiophene) (PEDOT-C₁₀), and spin-coated with a thin plasticized PVC membrane as reported elsewhere.¹⁶ A 2 μL THF solution of membrane components (ionophore, 4.0 mg PVC, 16.0 mg oNPOE or DOS, and 2.2 mg TDDATFAB in 1 mL THF) contained a low PVC content to ensures a negligible ohmic potential drop across the spin-coated membrane.⁵ An amount of an ionophore in the THF solution was selected to yield an ionophore concentration of 5.0 mM, otherwise mentioned, in the PVC membrane with a density of 1 g/mL.

Electrochemical Measurement

Electrochemical workstations (CHI 600A and 660B, CH Instruments, Austin, TX) were used for voltammetric measurements. A Pt-wire counter electrode was employed in the following three-electrode cell

$$\mathrm{Ag}\mid \mathrm{AgCl}\mid 3\mathrm{M}\mathrm{KCl}\mid \text{sample solution}\mid \text{PVC membrane}\mid {\text{PEDOT-C}}_{10}\mid \mathrm{Au}$$ (cell 1)

The compositions of sample solutions are given in figure captions. The positive current is carried by the transfer of a cation from the aqueous phase to the PVC membrane. A peak potential was determined from the first derivative of a voltammogram.²⁵ All electrochemical experiments were performed at 22 ± 3 °C.

RESULTS AND DISCUSSIONS

Thin-Layer Cyclic Voltammetry (CV)

In this work, we employed thin-layer CV¹⁶ to experimentally demonstrate IE and IT mechanisms for the secondary ion in the presence of the primary ion by using single and double ionophores, respectively. The characteristic features of a thin-layer CV without diffusional effects were ensured by using double-polymer-modified electrodes²⁶ in the presence of excess amounts of target ions.¹⁶ Specifically, a thin PVC membrane was spin-coated onto a gold electrode modified with the oxidized form of a conducting polymer membrane, PEDOT-C₁₀, as an efficient voltammetric ionto-electron transducer for aqueous cations.^{7,16,19,27,28} The PVC membrane was doped with single or double ionophores and hydrophobic supporting electrolytes, TDDATFAB, to obtain negligibly small ohmic potential drop across the thin membrane without introducing ion-exchange sites, i.e., ionic sites. Our thin-layer voltammetric approach is simpler than that of Bakker and co-workers, who supported a thin ionophore-doped PVC membrane by the reduced form of a poly(3-octylthiophene) membrane as a voltammetric ion-to-electron transducer for membranous cations.²⁹ Accordingly, their approach required the initial presence of an analyte cation in the PVC membrane, which must be doped with anionic sites as counter ions. Moreover, an amount of anionic sites had to be controlled carefully to obtain voltammetric responses to multiple cations.^10,11 By contrast, we confirmed experimentally in this work and our previous work¹⁶ that no ionic site is needed for voltammetric cation detection when the oxidatively doped PEDOT-C₁₀ membrane is employed for ion-to-electron transduction.

Noticeably, we considered the polarization of a conducting polymer film in our previous work¹⁶ to theoretically analyze the whole experimental voltammogram with background correction, which enabled us to determine complexation stoichiometry from the shape of the voltammogram. Advantageously, the analysis of the whole voltammogram was not needed in this work, where complexation stoichiometry was determined simply from a voltammetric peak current even without background correction (see below).

Ba²⁺ and Sr²⁺ Responses Based on the IE Mechanism

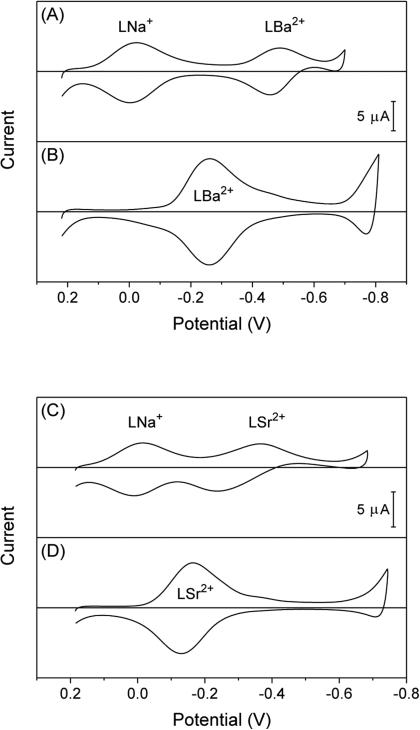
We employed Na⁺-selective ionophore 1¹² to demonstrate voltam-metric responses to secondary barium and strontium ions based on the IE mechanism. Thin-layer CVs with the mixed solution of sodium and barium ions showed two pairs of nearly reversible peaks (Figure 3A). The peak potentials of Na⁺ transfer were not affected by the presence of barium ion as expected from eqs 12 and 15. By contrast, the presence of sodium ion shifted the peak potentials of Ba²⁺ transfer from −0.26 V to −0.49 V (Figure 3B) as expected for the IE mechanism, where ionophores must dissociate from Na⁺ complexes to form Ba²⁺ complexes. Similarly, ionophore 1 gave voltammetric responses to both sodium and strontium ions in their mixed solution (Figure 3C). Volt-ammetric Sr²⁺ responses in the presence of sodium ion were based on the IE mechanism and were seen at more negative potentials than those in the absence of sodium ion (Figure 3D). In addition, voltammetric Sr²⁺ responses in the presence of sodium ion were kinetically limited as shown by a wide separation of 0.13 V between forward and reverse peak potentials. This kinetic effect also evidences the IE mechanism, because voltammetric Sr²⁺ responses in the absence of sodium ion yielded a much narrower peak separation of 0.03 V (Figure 3D).

Figure 3.

Thin-layer CVs of oNPOE/PVC membranes doped with 5 mM ionophore 1, L, in the presence of (A) 5 mM sodium acetate and 5 mM barium acetate, (B) 5 mM barium acetate, (C) 5 mM sodium acetate and 5 mM strontium acetate, or (D) 5 mM strontium acetate. Potentials are defined against the average peak potential of Na⁺ transfer. Potential sweep rate, 0.05 V/s.

Na⁺-selective ionophore 1 satisfies the requirement of eq 3 for the IE mechanism with secondary barium and strontium ions, which form 1:1 complexes to yield $\mid z_{\mathrm{J}}\mid ∕n_{\mathrm{J}}-\mid z_{\mathrm{I}}\mid ∕n_{\mathrm{I}}=+1$. Conveniently, 1:1 complexation stoichiometry was determinable from the ratio of a peak current for the secondary ion with respect to that for the primary ion in their mixed solutions (Figures 3A and C). Specifically, the peak current ratio, $I_{\mathrm{p},\mathrm{J}}^{\mathrm{IE}}∕I_{\mathrm{p},\mathrm{I}}^{\mathrm{IT}}$, was calculated by combining eq 10 for the secondary ion with eq 14 for the primary ion to yield

$$\frac{I_{\mathrm{p},\mathrm{J}}^{\mathrm{IE}}}{I_{\mathrm{p},\mathrm{I}}^{\mathrm{IT}}}=\frac{{\left(n_{\mathrm{I}}{z}_{\mathrm{J}}-n_{\mathrm{J}}{z}_{\mathrm{I}}\right)}^2{\left(\sqrt{n_{\mathrm{I}}}+1\right)}^2}{z_{\mathrm{I}}^2{n}_{\mathrm{J}}{\left(\sqrt{n_{\mathrm{I}}}+\sqrt{n_{\mathrm{J}}}\right)}^2}$$ (21)

Table 1 lists unique peak current ratios, $I_{\mathrm{p},\mathrm{J}}^{\mathrm{IE}}∕I_{\mathrm{p},\mathrm{I}}^{\mathrm{IT}}$, as expected from eq 21 for monovalent primary ions and divalent secondary ions with various complexation stoichiometries. Experimentally, we obtained ratios of 0.89 ± 0.09 (N = 5) for the forward peak current of the secondary barium ion with respect to that of the primary sodium ion (e.g., Figure 3A). This ratio is closest to a theoretical ratio of 1 with 1:1 complexation stoichiometry for both ions (n_I = n_J = 1). Similarly, peak current ratios of 0.96 ± 0.01 (N = 3) for primary sodium and secondary strontium ions (e.g., Figure 3C) confirm the formation of 1:1 complexes for both ions. Noticeably, ionophore 1 also forms 1:1 complexes with lithium ion, which does not give a voltammetric response in the presence of sodium ion (Figure S-1A), because $\mid z_{\mathrm{J}}\mid ∕n_{\mathrm{J}}-\mid z_{\mathrm{I}}\mid ∕n_{\mathrm{I}}=0$.

Table 1.

Peak Current Ratio, $I_{\mathrm{p},\mathrm{J}}^{\mathrm{IE}}∕I_{\mathrm{p},\mathrm{I}}^{\mathrm{IT}}$, with z_I = +1 and z_J = +2.

	n J
n I	1	2	3
1	1	0	0.18
2	9	1.5	0.20
3	25	6.0	1.9

We confirmed the IE mechanism for secondary barium and strontium ions more quantitatively by assessing the negative shift of their peak potentials in the presence of the primary sodium ion. Specifically, peak potentials of the secondary barium ion in the absence of sodium ion (Figures 3B) were very close to its peak potentials in the presence of sodium ion and peak potentials of sodium ion (Figure 3A). This observation is confirmed theoretically by eq 16, which can be rearranged to

$${\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{p},\mathrm{J}}^{\mathrm{IT}}\approx \frac{\left(z_{\mathrm{J}}∕n_{\mathrm{J}}-z_{\mathrm{I}}∕n_{\mathrm{I}}\right){\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{p},\mathrm{J}}^{\mathrm{IE}}+\left(z_{\mathrm{I}}∕n_{\mathrm{I}}\right){\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{p},\mathrm{I}}^{\mathrm{IT}}}{z_{\mathrm{J}}∕n_{\mathrm{J}}}$$ (22)

where z_J/n_J – z_I/n_I = z_I/n_I = +1 and z_J/n_J = +2 for sodium and barium ions. Eq 22 was also confirmed for the secondary strontium ion (Figures 3C and D), where ${\Delta }_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{p},\mathrm{Sr}}^{\mathrm{IE}}$ was estimated more accurately from the average of forward and reverse peak potentials by eliminating kinetic effects on them.

Super-Nernstian Slope Based on the IE Mechanism

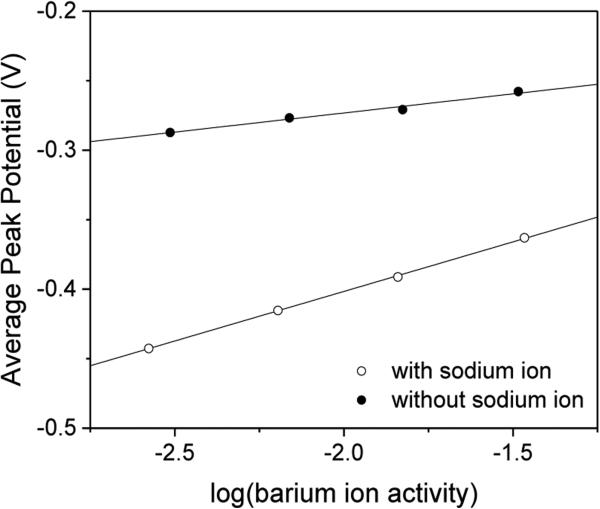
Interestingly, our theory for the IE mechanism predicted an apparently super-Nernstian slope for the peak potential of the secondary ion with respect to the logarithm of its sample activity. Specifically, a slope of 2.303RT/F per decade was predicted by eq 16 for the divalent secondary ion in the presence of the monovalent primary ion when both ions form 1:1 complexes with an ionophore. This theoretical prediction was confirmed experimentally by using Na⁺-selective ionophore 1 for the secondary barium ion. In fact, super-Nernstian slopes of 67 ± 5 mV/decade (N = 4) were obtained when averages of forward and reverse peak potentials were plotted against the logarithm of aqueous activities of barium ion (Figure 4). These slopes were apparently twice larger than a Nernstian slope of 29 mV/decade as expected for a divalent ion and were closer to a value of 59 mV/decade as predicted for the IE mechanism by eq 16 with z_I = +1, z_J = +2, and n_I = n_J = 1, thereby quantitatively confirming the IE mechanism. Moreover, this is the first voltammetric demonstration of apparently super-Nernstian slopes, which were reported for the primary ion in the presence of the secondary ion in zero-current potentiometry.^21-23 By contrast, nearly Nernstian slopes of 28 ± 2 mV/decade (N = 4) were obtained for barium ion in the absence of sodium ion as expected from eqs 12 and 15(Figure 4).

Figure 4.

Averages of peak potentials based on Ba²⁺ responses with oNPOE/PVC membranes doped with 5.0 mM ionophore 1 in the (open circles) presence and (closed circles) absence of 5.0 mM sodium acetate. Potentials are defined against the average peak potential of Na⁺ transfer. Potential sweep rate, 0.05 V/s.

Noticeably, the intercept of super-Nernstian responses to barium ion in the presence of sodium ion (−0.29 ± 0.02 V for N = 4) was more negative than that of Nernstian responses to barium ion in the absence of sodium ion (−0.19 ± 0.02 V for N = 4). This result confirms that the IE mechanism is thermodynamically less favorable owing to competition between sodium and barium ions for complexation with the ionophore.

Ca²⁺ Response Based on the IE Mechanism

Here, we demonstrate the effect of complexation stoichiometry on the IE mechanism by using Li⁺-selective ionophore 2¹³ for the secondary calcium ion. In this work, we not only confirmed the formation of 1:1 complexes between ionophore 2 and lithium ion,³⁰ but also revealed the formation of both 1:1 and 1:2 complexes with calcium ion when an ionophore concentration was relatively high. A sufficiently low concentration of ionophore 2 resulted in the dominant formation of 1:1 complexes with calcium ion. We confirmed the theoretical prediction that a voltammetric response to the secondary calcium ion in the presence of lithium ion was due to the formation of 1:1 complexes based on the IE mechanism.

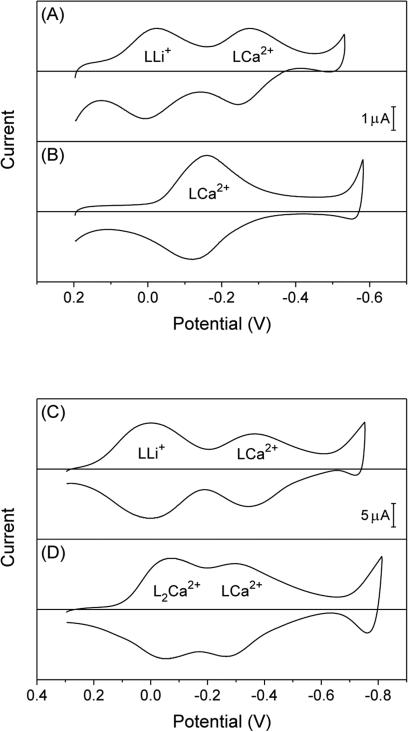
We employed a low concentration (2.0 mM) of ionophore 2 to yield a voltammetric response to the secondary calcium ion based on the IE mechanism, which was preceded by a Li⁺ response (Figure 5A). With this low ionophore concentration, only 1:1 complexes were formed between calcium ion and ionophore 2 in the membrane as confirmed by the single pair of voltammetric Ca²⁺ peaks in the absence of lithium ion (Figure 5B). A comparison of voltammograms with and without lithium ion confirmed the IE mechanism for calcium ion in the presence of lithium ion. While the voltammetric Li⁺ response was not affected by calcium ion, the voltammetric Ca²⁺ response was lowered and shifted toward more negative potentials in the presence of lithium ion. The lower peak current of the Ca²⁺ response was very similar to the peak current of the preceding Li⁺ response, which yielded peak current ratios of 0.98 ± 0.01 (N = 3). These peak current ratios agree with a theoretical ratio, $I_{\mathrm{p},{\mathrm{Ca}}^{2+}}^{\mathrm{IE}}∕I_{\mathrm{p},{\mathrm{Li}}^{+}}^{\mathrm{IT}}$, of 1 as expected for the formation of 1:1 complexes with both ions (Table 1), where the same net charge of +1 is transferred by each ionophore molecule for the Ca²⁺ response based on the IE mechanism ($\mid z_{\mathrm{J}}\mid ∕n_{\mathrm{J}}-\mid z_{\mathrm{I}}\mid ∕n_{\mathrm{I}}=+1$) and for the Li⁺ response ($\mid z_{\mathrm{I}}\mid ∕n_{\mathrm{I}}=+1$). Noticeably, ionophore 2 did not give a voltammetric response to sodium ion in the presence of lithium ion (Figure S-1C), because both ions form 1:1 complexes to yield $\mid z_{\mathrm{J}}\mid ∕n_{\mathrm{J}}-\mid z_{\mathrm{I}}\mid ∕n_{\mathrm{I}}=0$.

Figure 5.

Thin-layer CVs of oNPOE/PVC membranes doped with (A and B) 2.0 or (C and D) 5.0 mM ionophore 2, L, in the presence of (A and C) 50 mM lithium acetate and 5 mM calcium acetate or (B and D) 5 mM calcium acetate. Potentials are defined against the average peak potential of Li⁺ transfer. Potential sweep rate, 0.05 V/s.

A higher concentration (12.5 mM) of ionophore 2 gave two pairs of voltammetric peaks not only with the mixed solution of lithium and calcium ions (Figure 5C), but also with the separate solution of calcium ion (Figure 5D). In the latter case, two pairs of voltammetric peaks are ascribed to the formation of 1:2 and 1:1 Ca²⁺–ionophore complexes.¹⁶ In fact, ratios of 0.94 ± 0.02 (N = 6) for peak currents around −0.28 V with respect to peak currents around −0.06 V (Figure 5D) agree with a theoretical value of 1 for the successive formation of 1:2 and 1:1 complexes.¹⁶ Less negative potentials were required for the formation of 1:2 complexes, which was thermodynamically more favorable not only because they had higher stoichiometry, but also because the formation of 1:1 complexes required the dissociation of 1:2 complexes as given by

$${\mathrm{L}}_2{\mathrm{Ca}}^{2+}\left(\mathrm{m}\right)+{\mathrm{Ca}}^{2+}\left(\mathrm{w}\right)\rightleftharpoons 2{\mathrm{LCa}}^{2+}\left(\mathrm{m}\right)$$ (23)

Nevertheless, a voltammetric response to the secondary calcium ion in the presence of the primary lithium ion (Figure 5C) was not based on the formation of 1:2 Ca²⁺–ionophore complexes, which yields no net charge transfer across the membrane/water interface, i.e., $\mid z_{\mathrm{J}}\mid ∕n_{\mathrm{J}}-\mid z_{\mathrm{I}}\mid ∕n_{\mathrm{I}}=0$, as given by

$$2{\mathrm{LLi}}^{+}\left(\mathrm{m}\right)+{\mathrm{Ca}}^{2+}\left(\mathrm{w}\right)\rightleftharpoons {\mathrm{L}}_2{\mathrm{Ca}}^{2+}\left(\mathrm{m}\right)+2{\mathrm{Li}}^{+}\left(\mathrm{w}\right)$$ (24)

Overall, a voltammetric Li⁺ response (Figure 5C) was followed by a voltammetric Ca²⁺ response based the formation of 1:1 Ca²⁺–ionophore complexes in the IE mechanism. Noticeably, ratios of the peak current of the Ca²⁺ response with respect to that of the Li⁺ response, 0.77 ± 0.02 (N = 5), were lower than a theoretical value of 1 expected for n_I = n_J = 1, but were much closer to the expected value than theoretical values with other complexation stoichiometries (Table 1).

Ca²⁺ and Li⁺ Responses Based on Double Ionophores

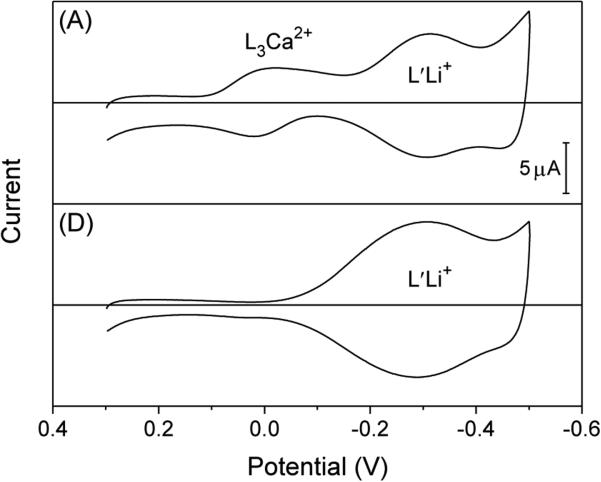
We studied a DOS/PVC membrane doped with Ca²⁺-selective ionophore 3 and Li⁺-selective ionophore 4 to demonstrate that a voltammetric response to the secondary lithium ion in the presence of the primary calcium ion was based on the IT mechanism by ionophore 4 not the IE mechanism by ionophore 3. Specifically, the peak potentials of lithium ion were nearly identical in the presence and absence of calcium ion (Figure 6A and B, respectively) as expected from eqs 12 and 15 for the IT mechanism. This result excludes the IE mechanism by ionophore 3 for the voltammetric Li⁺ response in the presence of calcium ion, which must be observed at more negative potentials than a voltammetric Li⁺ response in the absence of calcium ion. Moreover, no Li⁺ response was observed in the presence of calcium ion when a membrane was doped only with ionophore 3 (Figure S-2A). It, however, should be pointed out that a prerequisite of eq 3 for the IE mechanism was satisfied by ionophore 3, which forms 1:3 complexes with calcium ion³⁰ and 1:1 complexes with lithium ion to yield $\mid z_{\mathrm{J}}\mid ∕n_{\mathrm{J}}-\mid z_{\mathrm{I}}\mid ∕n_{\mathrm{I}}=+1∕3$ (see Supporting Information). Overall, the voltammetric IE reaction between calcium and lithium ions by ionophore 3 was thermodynamically unfavorable owing to their competition and was not seen within the potential window.

Figure 6.

Thin-layer CVs of a DOS/PVC membrane doped with 5.0 mM ionophore 3, L, and 5.0 mM ionophore 4, L′, in the presence of (A) 50 mM lithium acetate and 5 mM calcium acetate or (B) 50 mM lithium acetate. Potentials are defined against the average peak potential of Li⁺ transfer. Potential sweep rate, 0.05 V/s.

Noticeably, the IE mechanism was not considered in the previous voltammetric studies of multiple-ionophore systems,^10,11 which also employed ionophores 3 and 4. Thus, these previous studies did not unambiguously evidence by themselves that each ionophore really contributed to a voltammetric response to the corresponding analyte ion.

CONCLUSIONS

In this work, we reported comprehensive mechanisms to enable the voltammetric detection of multiple analyte ions at millimolar concentrations, which are high enough to deplete ionophores in thin polymeric membranes.^9,10,16 Significantly, this work lays the foundation for various applications of voltammetric multiion detection including the detection of millimolar physiological ions in biological and biomedical samples.^9,11 Specifically, the IE and IT mechanisms based on single and multiple ionophores, respectively, were assessed theoretically and demonstrated experimentally. Interestingly, we found that a voltammetric IE reaction yields a net current response in contrast to a conventional zero-current IE reaction in the potentiometric and optical counterparts.^3,4 Moreover, the sensitivity of the new IE mechanism is enhanced by a super-Nernstian slope in contrast to a Nernstian slope of the IT mechanism.^8-11 The IE mechanism, however, is enabled only when the charges and complexation stoichiometries of primary and secondary ions satisfy eq 3. In addition, the voltammetric IE process is less favorable thermodynamically (see eq 16 and Figures 3 and 5) and possibly kinetically (Figure 3B) than in the absence of the primary ion. By contrast, the IT mechanism with a dedicated second ionophore is more versatile without the requirement of eq 3 and is less amenable to unfavorable competition between primary and secondary ions, because a selective ionophore is employed for each ion.

Our voltammetric approach based on a thin ionophore-based polymeric membrane is useful to detect multiple analyte ions not only at a range between low-nanomolar and sub-micromolar concentrations,⁷ but also at millimolar concentrations as demonstrated in this work. On one hand, the extremely low detection limits were achieved by employing stripping voltammetry, where preconcentrated analyte ions were exhaustively stripped to maximize the peak current that vary with analyte concentrations. The multiple-ionophore approach based on the IT mechanism will be applicable to stripping voltammetry. On the other hand, millimolar concentrations of multianalyte ions can be determined from their peak potentials, which vary with the logarithm of analyte activities to yield either Nernstian^8-11 or super-Nernstian slope. We envision that the voltammetric detection of millimolar multianalyte ions will be useful to simplify the long-standing practice of the potentiometric counterpart for clinical blood analyzers,³¹ in-vivo applications,³² and wearable sweat sensing,³³ which require the ion-selective electrode dedicated for each analyte ion.