Abstract
Longitudinal blood flow during murine bone graft healing was monitored non-invasively using diffuse correlation tomography. The system utilized spatially dense data from a scanning set-up, non-linear reconstruction, and micro-CT anatomical information. Weekly in vivo measurements were performed. Blood flow changes in autografts, which heal successfully, were localized to graft regions and consistent across mice. Poor healing allografts showed heterogeneous blood flow elevation and high inter-subject variabilities. Allografts with tissue-engineered periosteum showed responses intermediate to both autografts and allografts, consistent with healing observed. These findings suggest that spatiotemporal blood flow changes can be utilized to differentiate the degree of bone graft healing.
OCIS codes: (170.0110) Imaging systems, (170.6960) Tomography, (170.3660) Light propagation in tissues
1. Introduction
Critical-sized bone defects cannot heal without intervention [1]. Annually, more than 500,000 U.S. and 2.2 million global orthopedic procedures are carried out to treat critical-sized bone defects [2, 3]. Among those procedures, autograft transplantation utilizes healthy endogenous bone and soft tissue from a non-load bearing region of the skeleton. Autografts often achieve complete healing; however, the procedure is limited by tissue availability and associated donor site morbidity [2, 3]. Alternatively, allograft transplantation, the “gold-standard” treatment for critical-sized bone defects [2, 4, 5], utilizes processed cadaveric bone to repair bone defects. To reduce immunogenicity, allografts are completely devitalized, during which the periosteum, a thin tissue layer covering the outer bone surface, which is important for complete bone healing [6], is lost. As a result, allografts exhibit poor host osteointegration with a 60%, 10-year post-implantation failure rate [7–9]. To improve allograft integration and healing, tissue engineered (T.E.) allografts have been developed and studied. The T.E. approaches deliver periosteum mimicking cells and/or growth factors to the graft site, which include the use of bone morphogenetic proteins, mesenchymal stem cells (MSCs), and/or osteoprogenitor cells [10–13]. To assess the effectiveness of allografts augmented with tissue engineered periostea, a murine segmental femoral defect model (graft model) is often used in pre-clinical studies. In the graft model, the healing outcome and the physiological changes during healing are assessed, such as graft vascularization, bone callus formation and bone strength [5].
Vascularization is recognized as an especially critical process in bone healing, as blood supplies the necessary nutrients, circulating cells, growth factors, and oxygen to the graft site [14]. Overall blood supply to grafts depends both on intravascular volume and blood flow. Blood flow can change rapidly in existing vasculature of native bones and tissues surrounding grafts due to inflammation and metabolic demands in the early phase of healing [14]. Characterization of longitudinal blood flow changes, as an important step to study graft vascularization, has the potential not only to advance our understanding of graft healing, but to establish a standard to compare the healing process in different graft types. However, the measurement of blood flow in bone is often confounded by high bone density as well as the heterogeneity of the intraosseous blood supply [15]. A few methods to measure bone blood flow are available, such as radioactive or fluorescent microsphere techniques [16, 17], magnetic resonance imaging (MRI), positron emission tomography (PET) [15], and laser Doppler flowmetry [18, 19]. Nevertheless, the application of these techniques for longitudinal studies of blood flow in bone has proven difficult due to invasiveness (microspheres), limited penetration depth (laser Doppler) or cost (MRI and PET) [15, 19, 20]. As a result, systematic comparison of spatial and temporal blood flow changes in different graft types has not yet been performed.
Diffuse correlation spectroscopy (DCS) and tomography (DCT) are deep-tissue, non-invasive techniques that can quantify blood flow index, which is sensitive to microvasculature [21]. DCS and DCT are developed by expanding the theory of dynamic light scattering, which mainly accounts for a single scattering event, to the domain where multiple scattering dominates, which is the case after near-infrared light (650 nm – 950 nm) propagates more than a few millimeters within highly scattering tissue [22, 23]. With DCS/DCT, the fluctuation of collected light signal, quantified by the intensity auto-correlation function, is linked to the motion of scatterers (i.e., red blood cells) [21].The measurements are non-invasive, inexpensive and easy to perform. The measurement method to infer average flow index from the diffuse light intensity auto-correlation function is referred to as DCS and the 3-dimensional (3D) imaging method is called DCT.
DCS has been widely applied to monitor the blood flow in tumors, brain and skeletal muscle in animals and humans in vivo [24–30]. Moreover, it has been validated by comparison with laser Doppler flowmetry [31, 32], Doppler ultrasound [25, 33–36], arterial-spin labeled MRI [37–40], xenon computed tomography (CT) [41], and fluorescent microsphere measurements [29, 42]. In most cases, the relative change of blood flow with respect to the baseline has been validated. However, careful calibration studies can be performed to convert the blood flow index to a quantitative measure of perfusion [43]. DCT, which provides 3D relative blood flow images, has been applied to monitor 3D blood flow in rat brain [44, 45] and human breasts [46]. Previously, we reported a non-contact scanning DCT system designed for murine graft study and showed its capability to capture localized flow changes between before and 1 week after graft transplantation in mice with allografts [47].
In this study, we report improvement on the DCT system as well as the results of longitudinal blood flow changes in mice with three different graft types; i.e., autograft, allograft and T.E. allograft with MSCs. The paper is structured as follows: In Section 2, methods regarding the instrumentation, a nonlinear DCT reconstruction, simulation set-up to compare a linear and a non-linear DCT reconstruction method, in vivo mouse measurement protocol and generation of mesh from micro-CT images are presented. In Section 3, we show the performance comparison between linear and non-linear DCT reconstruction methods, a representative example of the longitudinal 3D blood flow changes in a mouse with an autograft, comparison of blood flow changes in three representative mice from different groups and the averaged blood flow changes in the graft region. Finally, a discussion of the results is presented in Section 4.
2. Methods
2.1 Instrumentation
A typical diffuse correlation instrument consists of a light source, photon-counting avalanche photodiodes (APDs) and a correlator, as shown on the left side of Fig. 1. The long-coherence-length laser source at 785 nm is delivered to the tissue using a multi-mode fiber. Multiple-scattered light signals are collected using single-mode fibers at several millimeters away from the source. Photon-counting avalanche photodiodes (SPCM-AQ4C, Excelitas Technologies, Waltham, MA) are utilized to detect the light intensity and relay the data to a correlator (Flex030EM, Correlator.com, Bridgewater, NJ), which outputs the intensity temporal auto-correlation function g2.
Fig. 1.
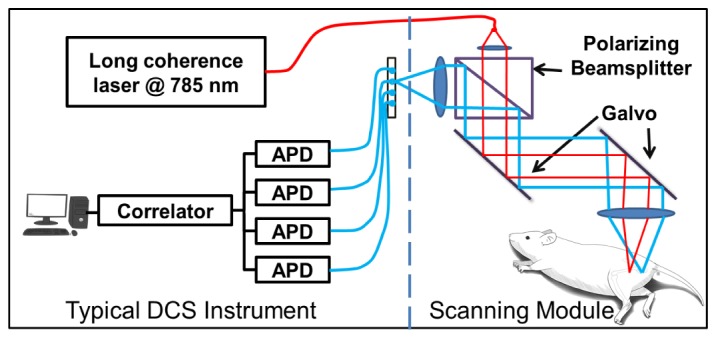
Non-contact scanning system set-up. The system consists of a 785 nm laser source, 4 avalanche photodiodes (APDs), a correlator and a scanning module to image the source and detectors on the tissue surface. The source-detector separations were kept constant while galvo mirrors scan the source-detector pattern in 2 dimensions.
To collect spatially dense data for DCT, a non-contact scanning module was added to the typical DCS instrument as shown on the right of Fig. 1. A fiber collimator is employed to collimate the beam coming out of the source fiber. Then, the collimated beam goes through one arm of a polarizing beamsplitter (CM1-PBS252, Thorlabs, Newton, NJ), is redirected by two galvanometer mirrors and projected on the tissue surface using a 50 mm doublet lens (AC254-050-B, Thorlabs, Newton, NJ). The typical beam spot size and the light power on the tissue is 0.3 mm and less than 1 mW, respectively. For the data collection, the detection fibers are imaged onto the tissue surface at known separations from the source through the other arm of the polarizing beamsplitter using two identical lenses. With this design, the source-detector separations are maintained while the galvanometer mirrors scan the source-detector pattern in two dimensions. The current design is improved upon our previous system [47], and it has better light throughput. The scanning module is similar to the scanning module design of the laminar optical tomography (LOT) system [48]; however, this particular non-contact scanning module enables measurements at much larger source-detector separations and has a bigger field of view than the LOT system.
2.2 Non-linear image reconstruction
Using the diffuse correlation instrument, the normalized intensity auto-correlation function g2(r,τ) ≡ <I(r,t)·I(r,t + τ)>/<I(r,t)>2 is measured, where τ is the delay time, I(r,t) in the measured intensity over time t at position r, and I(r,t) = |E(r,t)|2 with E(r,t) representing the electric field vector. The fundamental quantity under investigation in optical coherence theory is the electric field temporal auto-correlation function, G1(r,τ) ≡ <E*(r,t)·E(r,t + τ)>, where * denotes complex conjugate and < > denotes integration over time. The Siegert relation provides the connection between the normalized intensity auto-correlation and the normalized electric field auto-correlation functions [49],
| (1) |
where the normalized electric field temporal auto-correlation is g1(τ) ≡ G1(r,τ)/ G1(r,0). In Eq. (1), β is a parameter primarily determined by the optical set-up of the system, and is inversely proportional to the number of speckles in the detection area [49].
In highly scattering media (e.g., tissue), the correlation diffusion equation provides the theoretical model to describe the propagation of electric field temporal auto-correlation, G1(r,τ), as follows:
| (2) |
where μa and are the absorption and reduced scattering coefficient respectively, ν is the speed of light in the medium, D ≡ ν/(3(μa + )) is the photon diffusion coefficient, κ0 = 2π/λ is the wave vector of the photon where λ is the wavelength in the tissue, α is the fraction of moving scatterers and <Δr2(r,τ)> is the mean–squared displacement of scatterers, Sδ3(r-rs) is a point source located at rs with the source strength S. In Eq. (2), flow is characterized using <Δr2(r,τ)>. To simplify this expression, a Brownian motion model is usually utilized [21], which gives <Δr2> = 6Dbτ and Db is the Brownian diffusion coefficient. As a result, the parameter, αDb, is referred to as the blood flow index.
To solve for G1(r,τ) in Eq. (2), the following partial-flux boundary condition is used [21, 50]:
| (3) |
where is the unit vector pointing away from the scattering media boundary and zb = 2(1 + Reff) / [3 (1-Reff)], where Reff ≈ -1.440n−2 + 0.710n−1 + 0.668 + 0.0636n is the effective reflection coefficient to account for the index mismatch between the tissue and air boundary, and n is the refraction index ratio of tissue and air.
Analytical solutions to the correlation diffusion equation in a simple geometry, for example infinite, semi-infinite, or layered geometry, have been derived and widely used in various studies [21]. In more general cases, the correlation diffusion equation needs to be solved numerically using finite difference method (FDM) or finite element method (FEM).
With the experimental measurements, g2 is obtained for multiple source-detector pairs and the corresponding g1,m can be calculated using Eq. (1). DCT utilizes the experimentally obtained g1,m to reconstruct the flow distribution, αDb(r): this process is called solving the inverse problem. The inverse problem is constructed to minimize a cost function of the Rytov fashion [51], as follows:
| (4) |
In Eq. (4), Nsd is the total number of source-detector pairs utilized in the measurements, i represents one of the source-detector pairs, rsi is the corresponding source position, rdi is the detector position, g1,m (rsi,rdi,τ) is the measured auto-correlation function with source located at rsi and detector at rdi, and g1,c(rsi,rdi,τ) is the calculated auto-correlation function based on an estimate of flow distribution using Eq. (2). As the auto-correlation function spans over a wide range of τ values, for computational simplicity, one representative τ0 is chosen. A simple method is to choose the same τ for all source-detector pairs [52]. We use a τ0 value in which g1,c(rs,rd,τ) decays to e−1 for each source-detector pair, since it yields the optimal data sets [45].
The steps to solve the inverse problem with a non-linear solver are illustrated in Fig. 2. First, a finite element mesh is utilized to define the geometry. Then, an initial guess of the flow distribution is made and the optimal data set is selected. The iteration to update flow estimate starts with the calculation of g1,c(rs,rd,τ) based on the flow estimate and is followed by obtaining the difference between g1,c and g1,m, ϕi = ln(g1,m (rsi,rdi,τ) / g1,c(rs,rd,τ)). After that, the stopping criteria are evaluated. The stopping criteria are set such that when the decrease in χ2 is less than 2% for two successive reconstructions, the iteration stops. However, the final result is not selected as the result from the last iteration. More detailed discussions on selection of optimal results using L-curve analysis are presented at the end of this section. If the stopping criteria are not met, a Jacobian matrix, W, is built, which satisfies the equation ϕi = W • Δ(αDb(r)), where Δ(αDb(r)) is the difference between flow estimate and true flow distribution. Note that W is built in the same way as been described in our previous publication [47]. After W is constructed, Δ(αDb(r)) is obtained by
| (5) |
where T indicates a matrix transpose and η is a regularization parameter which is decreased with each iteration. The formulation includes Tikhonov regularization to stabilize matrix inversion [53], which is especially effective for solving the ill-posed equations (i.e., the number of unknowns is much larger than that of linear independent equations). As the final step in each iteration, Δ(αDb(r))(n) is added to the flow estimate, yielding αDb(r)(n). The iterative update of the flow is carried out until the stopping criteria are met.
Fig. 2.
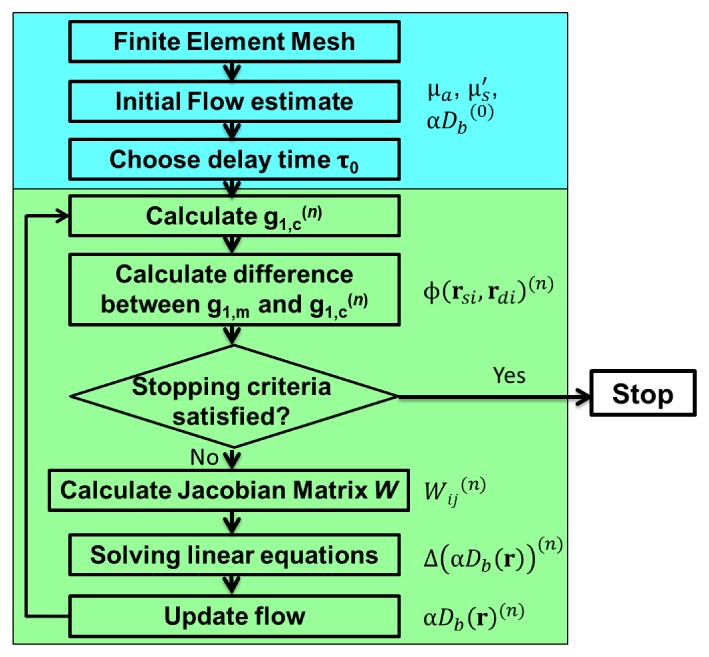
Flow chart of a non-linear DCT reconstruction method. The initialization steps are shown in the upper box (in blue) and the iterative steps are shown in the lower box (in green).
An inverse problem solver generally needs to minimize χ2. However, with the existence of noise in the measured data and the ill-posedness of the inverse problem, iterative minimization of χ2 may amplify noise into image artifacts such as a flow estimate with unreasonably high values (e.g., more than 50 times the background flow) at some positions. Thus, the final iteration of the iterative reconstructions may not necessarily provide physiologically reasonable flow images although it gives the smallest χ2. To identify the occurrence of this problem and to choose the optimal reconstruction results, an L-curve analysis is performed and served as the final criteria to select the optimal reconstruction result [54].
With each iteration in the reconstruction, a total flow perturbation from the initial guess can be calculated as δ(αDb)(n) = αDb(r)(n)- αDb(r)(0). The norm ||δ(αDb)(n)|| provides a measure of the fluctuation in the reconstructed flow estimate. On the other hand, the χ2(n) calculated at each iteration, as defined in Eq. (4), measures the difference between g1,c and g1,m and quantifies the quality of the flow estimate αDb(r)(n). For the L-curve analysis, the cost function χ2(n) at each iteration is plotted against the norm of the total flow perturbation ||δ(αDb)(n)||, which gives an “L” shape curve. To account for the different orders of magnitude between the two axes, both parameters are normalized to their respective maximum values. Then, the curvature of the L-curve at each data point is calculated. Finally, the iteration which generates the data point with the maximum curvature in the “L” curve is selected as the optimal iteration and the corresponding αDb(r) is taken as the final reconstructed flow distribution. An example of the typical L-curve from reconstruction on mouse data is shown in Fig. 3.
Fig. 3.
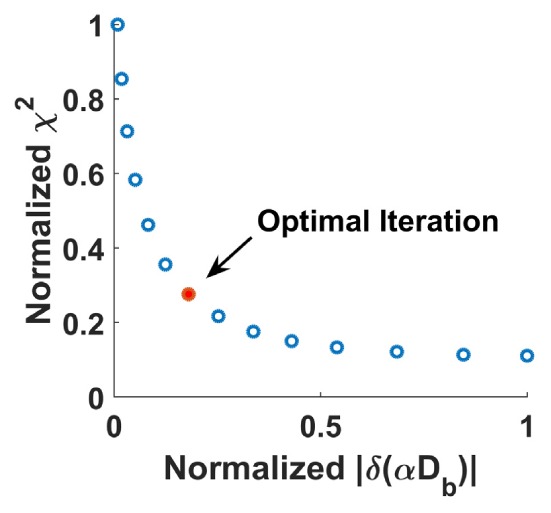
A L-curve obtained from the iterative image reconstructions of mouse data. L-curve analysis is employed to choose the optimal results from image reconstructions, which is the iteration with the maximum curvature on the L-curve as shown in red dot.
2.3 Numerical simulation to compare a linear and a non-linear reconstruction method
To compare the non-linear inverse problem solver with a linear solver that we reported previously [47], reconstructions based on simulated data were carried out. g1 of multiple source-detector pairs over a region of heterogeneous flow distribution was calculated using a FEM based solver of Eq. (2) modified from Near Infrared Fluorescence and Spectral Tomography (NIRFAST), a software package for diffuse optical tomography [55]. The simulation geometry consists of a cylindrical region with higher flow and a surrounding homogeneous background, as shown in Fig. 4(a). It is discretized using a finite element mesh (x: −8.0 mm to 8.0 mm, y: −13.5 mm to 13.5 mm, z: 0 mm to 8.0 mm, total number of nodes: 201791, total number of elements: 1031591). The higher flow region has a diameter of 1.5 mm and a length of 15 mm, and it is submerged 2 mm deep into the background. The cylindrical region has αDb = 2.0x10−6 mm2/s, and the background region has αDb = 1.0x10−6 mm2/s. Figure 4(b) shows the pattern of the source and detectors utilized to scan over the region for data collection, which has source-detector separations of 3.0, 4.5, 6.0 and 7.5 mm. The pattern was scanned in both x and y directions, with step sizes Δx = 0.35 mm and Δy = 0.70 mm. The scan coverage is shown in Fig. 4(c), which only includes source and detector positions inside the rectangular region of −3.5 mm < x < 3.5 mm and −10 mm < y < 10 mm in order to speed up the calculation. The original pattern consists of 1764 source-detector pairs and the final pattern includes 1272 pairs.
Fig. 4.
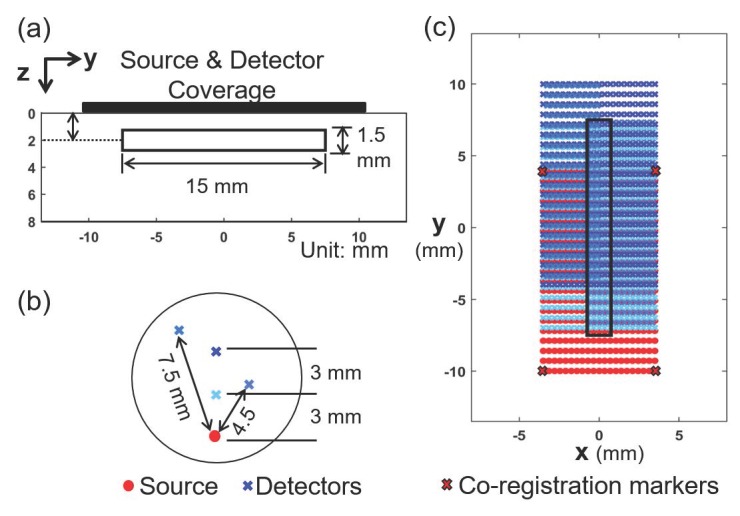
Set-up of the simulation to compare a linear and a non-linear reconstruction method. (a) A cylinder of 1.5 mm diameter and 15 mm length was embedded in a homogeneous background. (b) The source-detector pattern consists of 1 source and 4 detectors with separation of 3.0, 4.5, 6.0 and 7.5 mm, respectively. (c) Two dimensional scan of the pattern cover a rectangular area over the cylindrical anomaly region on the surface of the simulation geometry. This is similar to the typical coverage of an in vivo measurement on a mouse.
To compare the reconstruction results, a coarse mesh (x: −8.0 mm to 8.0 mm, y: −13.5 mm to 13.5 mm, z: 0 mm to 8.0 mm, total number of nodes: 94826, total number of elements: 462047) was used for both the linear reconstruction method and the non-linear reconstruction method. No noise was added to the simulated data.
2.4 In vivo mouse measurement protocol
For the in vivo bone graft measurements, three groups of mice were used for DCT imaging: the autograft group, the allograft group and the T.E. allograft group. The animal study was conducted according to a protocol approved by the University Committee on Animal Resources (UCAR) at the University of Rochester. The details of the graft surgical procedures can be found in the literature [56, 57]. Briefly, a 4 mm segment of the left femur of a BABL/c mouse is removed and replaced with a graft. For the autograft, the removed segment was transplanted back. For the allograft group, decellularized bone segments from C57BL/6 mice (different strain than BALB/c) were utilized for the grafts. For the T.E. allograft group, decellularized bone segments from C57BL/6 mice were seeded with MSCs using hydrogel [57], and then transplanted into the femoral defect. For each group, 5 mice were initially planned for the study, since the purpose of the study was to identify the spatiotemporal characteristics of the blood flow index of different groups and provide information needed to calculate sample size for future studies. However, one mouse in the allograft group and one mouse in the autograft group died due to the adverse effects associated with ketamine, anesthetic for the surgery, before the start of any post-surgery DCT measurements, and thus were excluded from the study.
As illustrated in Fig. 5(a), DCT scans were performed before the graft surgery (denoted as week 0), and then every week after surgery for 9 weeks. For each scan, the mouse was placed on a warming pad and anesthetized with continuous isoflurane administration (1 - 2.5%). Isoflurane was chosen for minimal interference with microcirculation, fast anesthetic effect and reliability [58–60]. Fur was removed from the scanning site using electric clippers. Then, the source-detector pattern shown in Fig. 4(b) was scanned over the tissue surface with a step size of 0.35 mm in the direction perpendicular to the length of the femur and 0.70 mm in the direction parallel to the length of the femur. The scan region covered the entire femur with the graft, with the femur located at the center, similar to the simulation geometry shown in Fig. 4(c). The four corner positions of the rectangular scan area covered by the source were marked using a skin-compatible surgical marker during the first measurements (i.e., pre-surgical measurements) and maintained throughout the longitudinal measurements. Alignment of the scanning pattern with the co-registration markers was performed before each DCT scan thereafter. At week 11 after surgery, an additional DCT scan was performed and then followed by micro-CT imaging of the mouse leg at the Center for Musculoskeletal Research at the University of Rochester. To co-register DCT scans with micro-CT, barium sulfate markers were applied on the mouse skin on top of the DCT scan markers and served as reference points in the micro-CT images. After the micro-CT scan, standard Digital Imaging and Communications in Medicine (DICOM) format medical images of left hindlimbs were obtained.
Fig. 5.
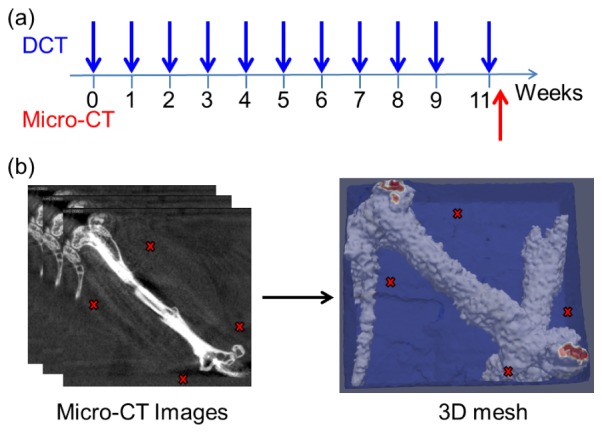
Experimental measurements and mesh generation. (a) Timeline showing weekly DCT measurements and final micro-CT imaging; (b) 3D FEM mesh generated from micro-CT images. (red X: co-registration markers)
2.5 Generation of FEM mesh based on anatomical information from micro-CT
The micro-CT images were processed with NIRFAST Slicer [61], a free software package which can view medical images, perform de-noising and image-segmentation, and export segmented medical images into Matlab (Mathworks, Natick, MA) for 3D finite element mesh generation. After the images were imported into NIRFAST Slicer, de-noise algorithm with median filter was performed and then the images were segmented using a built-in K-means and Markov random field algorithm [61], and divided into the region of bone, soft tissue and air. The segmentation was fine-tuned manually using the paintbrush tool. The reference points for the DCT scan region were marked on the segmented images. Finally, segmentation results were sent to Matlab, by which 3D finite meshes of the legs were generated. The generated mesh had the region of the transplanted graft, the remaining host femur and the surrounding soft tissue labeled as different regions and typically consisted of more than 100,000 nodes in total, as is shown in Fig. 5(b).
After the 3D mesh was generated in Matlab, the source-detector pattern from DCT scan was registered on the mesh by overlaying the co-registration markers with the corresponding source positions and linearly interpolating the other sources and detectors on the tissue surface. The tissue surface curvature was not accounted for in current study as it was usually small. In addition, the sources and detectors within 1 mm of the mesh boundaries, where the tissue curvature was big, were excluded. The same absorption coefficient μa = 0.01 mm−1 was assumed for both soft tissues and bone throughout the measurements. Previous results have shown that ignoring the difference in the reduced scattering coefficients between the soft tissues and the bone results in significant errors in the reconstructed absolute blood flow values [47]. To account for this effect, reduced scattering coefficient from literature was used, with = 0.8 mm−1 for soft tissues and = 2.0 mm−1 for bone [62]. In addition, the relative blood flow change (rBF), which was αDb(r,t) normalized with the pre-surgical measurement at week 0, was reported in the results section as it can mitigate the possible error in αDb introduced by inaccurate [47].
2.6 Statistical analysis
To determine the existence of statistical significance, Shapiro-Wilk test was utilized to test the normality of the data distribution for each group. One-way ANOVA or non-parametric Kruskal-Wallis test was utilized based on the result of the normality test. When the null hypothesis (i.e., three groups have the same mean) was rejected (p < 0.05), Tukey’s honestly significant difference procedure was used for multiple comparisons to identify the pair of groups which demonstrated statistical significance.
3. Results
3.1 Comparison of a linear and a non-linear reconstruction method
Reconstruction results from a linear DCT reconstruction method and a non-linear reconstruction method are shown in Fig. 6. To compare the results, we define the region that has the final flow change larger than 1/e of the maximum change as the recovered anomaly region. The expected center of the anomaly region is (0.0, 0.0, 2.0) mm. For the linear solver, the reconstructed anomaly region centers at (−0.2, −0.5, 1.4) mm; for the non-linear solver, the recovered anomaly region centers at (0.2, −0.9, 1.8) mm. Compared with the linear solver, the non-linear solver gives a much better depth localization of the reconstructed anomaly. However, results from the non-linear reconstruction still need improvement. For example, the average αDb value within the anomaly from the non-linear reconstruction is lower than the expected value and the high αDb region disperses beyond the expected z range (1.25 – 2.75 mm).
Fig. 6.

DCT reconstruction results obtained with a linear reconstruction method and a non-linear reconstruction method. z slices at different depths of expected results, results from a linear reconstruction method and results from a non-linear reconstruction method are shown in the three rows. The expected background αDb is 1.0x10−6 mm2/s and the anomaly region αDb is 2.0x10−6 mm2/s. Same colorbar is used for all plots.
3.2 Relative blood flow changes in a mouse with an autograft
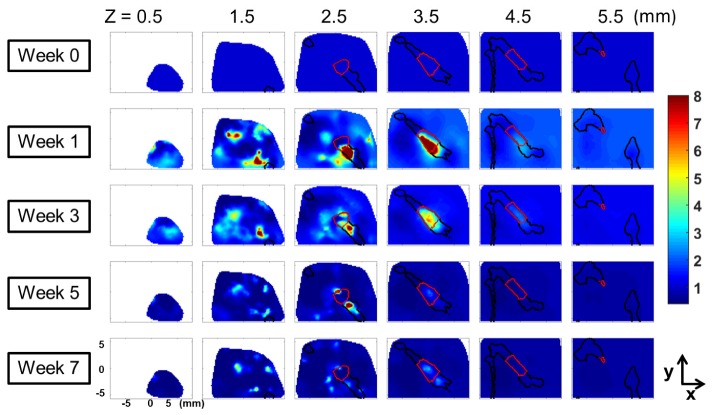
The longitudinal changes in 3D rBF of a mouse with an autograft were shown in Fig. 7 as an example of DCT reconstructed flow changes. In Fig. 7, the rows show the rBF distribution in weeks 0, 1, 3, 5 and 7. The columns show the rBF at the tissue depths equal to 0.5, 1.5, 2.5, 3.5, 4.5 and 5.5 mm. The profile of the bones, including the femur, the tibia and the coxal bone are outlined using black lines and the graft region is shown with red lines. The same colorbar was used for all plots.
Fig. 7.
Longitudinal rBF changes in an autograft mouse at selected weeks and tissue depths. rBF is obtained by normalizing the reconstruction results from each week to the results of week 0. The rows show the results at weeks 0, 1, 3, 5 and 7, respectively and the columns show the results at tissue depths z = 0.5 mm, 1.5 mm, 2.5 mm, 3.5 mm 4.5 mm and 5.5 mm, respectively. (Black lines: outline of the bones; red lines: outline of the graft)
From the results, it can be seen that the blood flow in an autograft mouse peaked at week 1 and gradually decreased as healing progressed. At the final stage of healing, blood flow returned to the pre-transplantation baseline level. Moreover, blood flow increase was mainly localized in the graft region for the autograft mouse, as shown in the tissue depth of 3.5 mm. At shallow depths (as shown in slices for z ≤ 1.5 mm), a few regions of high blood flow were observed in the soft tissue region. On the contrary, at deeper region with the graft, the changes in soft tissue blood flow were much smaller compared to those in the graft region (as shown in slices for z ≥ 3.5 mm).
3.3 Comparison of blood flow changes between different groups
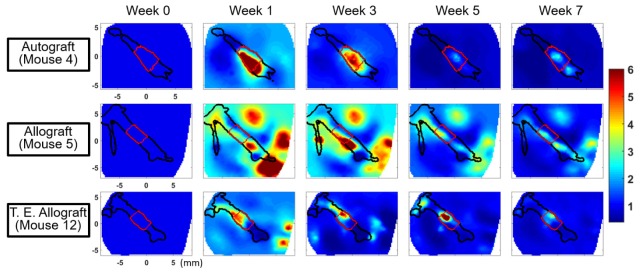
To compare the difference in blood flow changes among the three different groups, images from one representative mouse in each group at the tissue depth passing through the center of the femur were shown in Fig. 8. The three rows show the results from the autograft group, the allograft group and the T.E. allograft group, respectively, and the columns show different time points at weeks 0, 1, 3, 5 and 7, respectively. The outlines of the bones and the grafts are shown in black and red lines, respectively. The same colorbar was used for all plots.
Fig. 8.
Comparison of blood flow changes in different graft types with varying degree of healing potential. One representative mouse from each group is selected and only the z slice which includes the center of the femur is shown: autograft (z = 3.5 mm), allograft (3.2 mm) and T. E. allograft (3.2 mm). The columns show the results at weeks 0, 1, 3, 5 and 7, respectively. (Black lines: outline of the bones; red lines: outline of the grafts)
Compared to the blood flow distribution in the autograft mouse (Fig. 8 top) that showed a well-localized blood flow elevation within the bone primarily in the graft region at week 1 and 3, blood flow in the allograft mouse (Fig. 8 middle) exhibited multiple regions in soft tissues with higher blood flow than that in the graft. At week 5 and 7, blood flow in these multiple regions decreased and more localized blood flow elevation was found within the allograft.
The blood flow in the T.E. allograft mouse (Fig. 8 bottom) exhibited spatial and temporal features similar to both autografts and allografts. At week 1, blood flow elevations were found within the graft as well as in multiple regions in soft tissue. The level of blood flow elevations was similar between the graft and the soft tissue at week 1, but the elevation within the graft became more prominent compared to soft tissues as healing progressed.
3.4 Average rBF changes in graft region for different groups
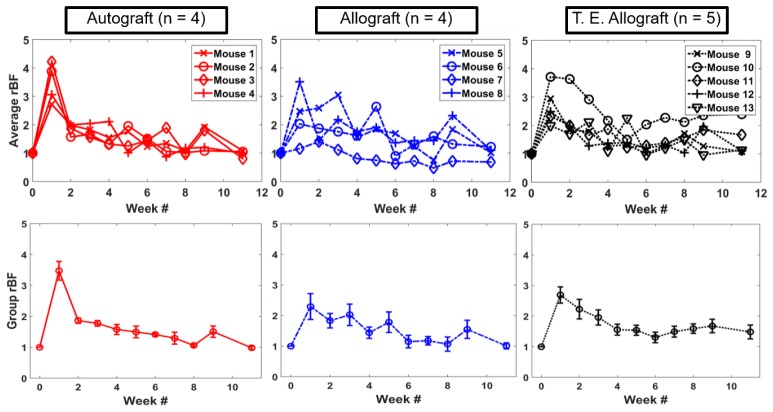
The longitudinal changes of the average blood flow in the graft region for an individual mouse were shown in top row of Fig. 9. As mentioned previously in Section 2.4, there were 4 mice in the autograft group, 4 in the allograft group and 5 in the T.E. allograft group.
Fig. 9.
Average relative blood flow changes in the graft region for mice in the three different groups. Each curve shows the longitudinal changes of one mouse and each plot includes the mice from the same group. Top row shows longitudinal changes of individual mice and bottom row shows group averaged longitudinal changes of each group. The error bar is the standard error of the mean for the group averaged rBF.
In the autograft group, graft blood flow increased significantly from the baseline level 1 week after the graft transplantation and decreased more than half of the initial elevation at the 2-week time point. After that, blood flow decreased gradually towards the baseline level. This pattern was consistent in every autograft mouse. For the allograft group, more variations between the mice within the group were observed. The time to peak ranged from week 1 to week 5. The average graft rBF returned to the baseline at a slower pace than that of the autograft group. For the T.E allograft group, the blood flow peaked at week 1, similar to that of the autograft. However, the trend in blood flow decrease was not as consistent as that of the autograft group. Overall, the changes in the T.E. allograft group were more similar to the autograft group compared to the allograft group in that 4 out of 5 mice demonstrated a similar temporal pattern to the autograft.
The bottom row of Fig. 9 shows the group averaged rBF within the graft. Even though different groups showed varying degrees of averaged rBF at week 1, it was not statistically significant partly due to the limited sample size. On the other hand, observations made for individual mouse strongly suggest that whether the rBF peaks at week 1 can be a potential criterion to distinguish the degree of healing. To quantify this, we defined Percentage of Peak (POP) at week 1 for each mouse, as the following:
| (6) |
where max(rBF(t)) is the maximum rBF from the longitudinal curve spanning the monitoring period as shown in the top row of Fig. 9. The group averaged POP at week 1 are shown in Fig. 10, along with the standard error of the mean as error bars. The statistical test on POP revealed that the autograft group is significantly different from the allograft group, but not from the T.E. allograft group.
Fig. 10.
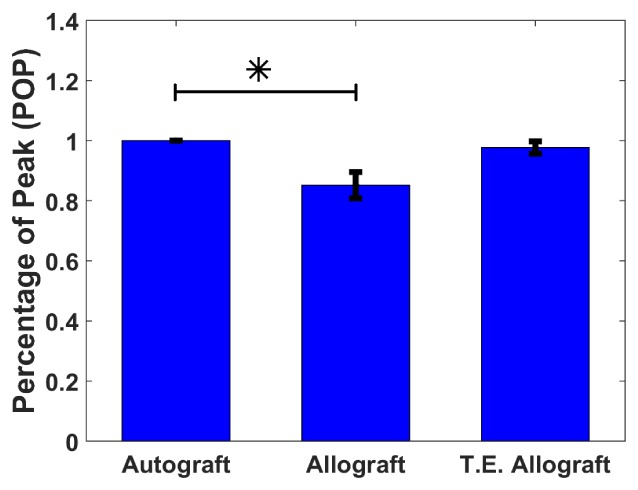
Group-averaged Percentage of Peak (POP) at week 1 for the three graft groups. The error bar is the standard error of the mean. The asterisk (*) indicates that the allograft group is significantly different from the autograft group.
4. Discussion
In this study, we used an improved version of the DCT system from our previous publication [47], to monitor the longitudinal blood flow changes in mice with femoral grafts. Using the non-contact scanning system and a non-linear reconstruction method, we showed spatial and temporal differences in blood flow among three groups of mice with different graft types over 11 weeks of healing. The study is unique in that: (1) the non-invasive nature of the DCT instrument enabled frequent longitudinal blood flow monitoring of the same mouse throughout the experiment; (2) DCT based on spatially dense data and non-linear reconstruction algorithm provides comprehensive spatial and temporal blood flow changes throughout the healing process, which was not available in previous studies due to limitations of other imaging modalities; (3) the study revealed different spatial and temporal blood flow changes in autografts, allografts and T.E. allografts with MSCs, strongly suggesting blood flow changes in early stages of healing (< 5 weeks) may be utilized to predict bone healing outcome of different graft types.
4.1 Longitudinal blood flow changes in grafts
The longitudinal rBF changes show a general trend of blood flow elevation after the graft transplantation and subsequent return to the pre-surgery baseline level. However, the autografts, the allografts and the T.E. allografts show different temporal patterns. The autograft group consistently displayed a peak in graft blood flow at 1 week after the transplantation. From the tomographical results, the flow changes in autografts were also well localized in the graft region. The allograft group, on the other hand, exhibited more variations in the change of blood flow within the group, with blood flow peaking from 1 week to 5 weeks after the transplantation and the elevation returned to the baseline at a much slower rate. In the 3D results, more elevations in the tissue surrounding the graft were observed compared to the autograft group. The T.E. allograft group showed intermediate changes between the autograft group and the allograft group, with blood flow peaking at week 1, similar to the autograft group: however, the rate of blood flow decrease was slower. The blood flow changes were better localized at the graft region compared to the allograft group.
The trend in blood flow changes in autografts, which showed a sharp blood flow increase followed by a return to the baseline level, agrees with previous studies in bone graft/fracture blood flow monitoring, including studies using radio-active microsphere [63], laser Doppler flowmetry [18], and DCS [56]. The increase in blood flow at week 1 is likely due to several factors including inflammatory response to surgical insult, hyperemia, and angiogenesis associated with tissue regeneration [64]. It is worthwhile to note that, since our measurements were conducted on a weekly basis, the immediate drop of blood flow (within 3 days after the surgery) in the graft following the surgery reported by other techniques was not captured in the current study. In addition, the observation that the allograft group exhibited a longer period of blood flow elevation is consistent with previous results observed by DCS [56]. The elongated blood flow elevation may be an indicator for delayed healing in allografts, which has been observed in other studies evaluating the bone callus formation and vasculature formation [13, 57].
With the rich spatial and temporal information provided by the non-invasive DCT, differences in blood flow changes in autografts, allografts, and T.E. allografts with MSCs were clearly captured, as shown in Fig. 9. Autografts exhibited consistent blood flow elevation at week 1 which subsequently decreases, consistent with good healing. Although not identical to autografts, the T.E. allograft group showed a similar blood flow pattern to autografts compared to the untreated allograft group, demonstrating improvements in bone graft healing using this tissue engineering approach. Hoffman et al. demonstrated that a mixture of unaltered MSCs and osteoprogenitor cells can further improve the bone callus formation, bridging endochondral bone formation and bone bio-mechanical stability [13]. In the future, DCT may play a valuable role in assessing the healing potential of T.E. allografts with different compositions of cell populations, soluble cues, and/or matrices to guide the optimization of tissue engineering approaches.
4.2 Development of methods
In the methods and the results sections, the improvement on instrumentation and image reconstruction method are presented, which includes: (1) increased light throughput in the non-contact scanning system, enabling the collection of spatially dense data at multiple source-detector separations (up to 7.5 mm); (2) a non-linear reconstruction method that gives better depth localization, as opposed to the previous linear reconstruction program; (3) use of micro-CT derived 3D mesh and assignment of optical properties based on anatomical information, compared to semi-infinite mesh assumption used previously [47]. With the current methods, longitudinal blood flow changes during graft healing were successfully monitored non-invasively and the spatial and temporal differences among three graft types were revealed. The versatility of the current system also enables direct application in other studies, such as monitoring tumor blood flow change after chemotherapy in rats [65]. Despite the improvements, several limitations remain to be addressed in future studies.
First, the non-linear reconstruction method has limitations. The simulation results show image artifacts in the shallow depth (<1.5 mm) and error in the reconstruction position and contrast. To suppress the image artifacts, spatially variant regularization to account for the sensitivity difference at different tissue depths might be used [45]. The reconstruction may be further improved by better utilization of the anatomical information. To this end, reconstruction with soft-priors will be implemented in the future as it has been shown to be more robust to noise and give better reconstruction results [66]. In addition, in the average rBF results (Fig. 9), mouse 7 exhibited much smaller changes compared to other mice. Inspection of the anatomical structure revealed that the femur of mouse 7 (centered at z = 5.5 mm) was much deeper than the others (typically centered at z = 3.5 mm). Considering the maximum source-detector separation used is 7.5 mm, the changes in the graft may not be detected as well as other mice with shallower bones. This may imply the need for a more rigorous study on the depth sensitivity of the current system and the necessity of criteria for correction or exclusion based on the bone depth.
Second, the influence of the tissue surface curvature on the non-contact data collection was not accounted for. The non-contact scanning system projects a planar pattern for data collection. However, in the image co-registration, the source and detectors are interpolated to the tissue surface and their heights followed the profile of the tissue, which is not planar. To partially account for this inconsistency, the sources and detectors within 1 mm of the mesh boundaries, where the height changes are big, were excluded from the reconstruction. Despite the exclusion of those data, the influences of tissue curvature on image reconstruction were not systematically investigated in the current study. A potential solution is to account for the propagation of the auto-correlation function in free space, similar to a method proposed for diffuse optical tomography [67].
Third, the image co-registration scheme is not ideal. To record the DCT scan region and co-register it with the micro-CT images, DCT scan markers and barium sulfate markers were used. The size of the markers, especially the Barium Sulfate markers, which are typically 1 mm in diameter, is comparable to the scanning step size. Although only the center of each marker was used, possible mismatch is expected. To study the effect of the mismatch in image co-registration, a reconstruction on the autograft mouse data as shown in Fig. 7 with a 0.5 mm displacement of the source-detector pattern was carried out. The results showed the displacement in source-detector pattern mainly introduced a spatial shift of the high blood flow region for about 0.5 mm in the reconstructed results. The general distribution and the temporal trends did not change. In the future, a more accurate image co-registration scheme may be needed and a more rigorous study needs to be designed to study the stability of the reconstruction with image co-registration mismatch.
Finally, the assignment of optical properties from literature is not ideal. Optical properties, especially reduced scattering coefficients can greatly influence the accuracy of reconstructed αDb values [47]. To account for the difference in scattering in soft tissue and bone, from literature was assigned in the current study. In the future, better optical property assignment may be achieved by combining the current DCT system with a diffuse optical tomography system that can provide 3D absorption coefficients and reduced scattering coefficients of each mouse.
Additionally, there is a potential concern related to the use of the Siegert relation in our analysis. It has been reported in the literature that the signals from adult human bone may not satisfy all the assumptions of the Siegert relation under certain conditions [68]. In our case, the necessary conditions to satisfy the assumptions are provided by the presence of a thick muscle layer over the bone and natural ensemble averaging through breathing-induced motion [22, 56]. In the future, the limits of the approximations in small animal models could be explicitly checked.
In spite of the limitations, the current DCT study provided previously unavailable information on the 3D longitudinal blood flow changes in three different graft types. Recently, there has been an increased research interest in the development of DCT scanning system and application of DCT in different studies. He et al. used a motorized stage to move the source and detectors over the scan region and used this system to capture the blood flow contrast in patients with breast tumors [46]. Johansson et al. constructed a scanning system that used a motorized stage to move the subject rather than the source-detector pattern and combined diffuse correlation measurements with broadband diffuse optical measurements to study the hemodynamics of mouse tumor [69]. However, in general, DCT is still a technology that has not been widely applied. To this end, we plan to compare our DCT measurements with more established methods, such as fluorescent microspheres or dynamic contrast enhanced MRI in the future.
5. Summary
In summary, we have utilized a DCT system to study the longitudinal blood flow changes in three groups of mice with different graft types; i.e., autografts, allografts and T.E. allografts. Our system enabled the collection of spatially dense data with multiple source-detector separations for 3D imaging reconstruction, utilized a non-linear reconstruction approach to improve the accuracy in the reconstruction and leveraged the anatomical structure of each mouse obtained with micro-CT to define the geometry and optical properties. The DCT results show that after the graft surgery, blood flow increased in grafts for all groups and then returned to the pre-transplantation baseline level. The autograft group exhibited consistent trends in blood flow changes in the graft region, with the blood flow peaking 1 week after surgery. The allografts showed more temporal variations in blood flow within the group. The T.E. allografts exhibited blood flow changes that were more similar to the autografts. The results monitored by our DCT system strongly suggest that 3D longitudinal blood flow changes may serve as surrogate markers for assessing the success of bone healing at relatively early time points.
Acknowledgements
We thank Michael Thullen and Dr. Hani Awad for their help in micro-CT imaging, Rejune Choe for the illustration, Jingxuan Ren and Gabriel Ramirez for their general support and discussion throughout the experiments. We also thank Turgut Durduran for providing valuable discussions. Portions of this work were presented at the OSA Biomedical meeting in 2016, paper number: OTh1D. 2.
Funding
National Science Foundation (NSF) (CBET 1507384); AAFPRS Leslie Bernstein Resident Research Grant (352604); National Institute of Health (NIH) (R01 AR064200); NYSTEM IDEA (C028099).
References and links
- 1.Spicer P. P., Kretlow J. D., Young S., Jansen J. A., Kasper F. K., Mikos A. G., “Evaluation of bone regeneration using the rat critical size calvarial defect,” Nat. Protoc. 7(10), 1918–1929 (2012). 10.1038/nprot.2012.113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Greenwald A. S., Boden S. D., Goldberg V. M., Khan Y., Laurencin C. T., Rosier R. N., American Academy of Orthopaedic Surgeons. The Committee on Biological Implants , “Bone-graft substitutes: facts, fictions, and applications,” J. Bone Joint Surg. Am. 83-A(Suppl 2 Pt 2), 98–103 (2001). [DOI] [PubMed] [Google Scholar]
- 3.Giannoudis P. V., Dinopoulos H., Tsiridis E., “Bone substitutes: an update,” Injury 36(Suppl 3), S20–S27 (2005). 10.1016/j.injury.2005.07.029 [DOI] [PubMed] [Google Scholar]
- 4.Hoffman M. D., Van Hove A. H., Benoit D. S. W., “Degradable hydrogels for spatiotemporal control of mesenchymal stem cells localized at decellularized bone allografts,” Acta Biomater. 10(8), 3431–3441 (2014). 10.1016/j.actbio.2014.04.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Xie C., Reynolds D., Awad H., Rubery P. T., Pelled G., Gazit D., Guldberg R. E., Schwarz E. M., O’Keefe R. J., Zhang X., “Structural bone allograft combined with genetically engineered mesenchymal stem cells as a novel platform for bone tissue engineering,” Tissue Eng. 13(3), 435–445 (2007). 10.1089/ten.2006.0182 [DOI] [PubMed] [Google Scholar]
- 6.Zhang X., Awad H. A., O’Keefe R. J., Guldberg R. E., Schwarz E. M., “A perspective: engineering periosteum for structural bone graft healing,” Clin. Orthop. Relat. Res. 466(8), 1777–1787 (2008). 10.1007/s11999-008-0312-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hornicek F. J., Gebhardt M. C., Tomford W. W., Sorger J. I., Zavatta M., Menzner J. P., Mankin H. J., “Factors affecting nonunion of the allograft-host junction,” Clin. Orthop. Relat. Res. 382, 87–98 (2001). 10.1097/00003086-200101000-00014 [DOI] [PubMed] [Google Scholar]
- 8.Wheeler D. L., Enneking W. F., “Allograft bone decreases in strength in vivo over time,” Clin. Orthop. Relat. Res. 435, 36–42 (2005). 10.1097/01.blo.0000165850.58583.50 [DOI] [PubMed] [Google Scholar]
- 9.Mankin H. J., Hornicek F. J., Raskin K. A., “Infection in massive bone allografts,” Clin. Orthop. Relat. Res. 432, 210–216 (2005). 10.1097/01.blo.0000150371.77314.52 [DOI] [PubMed] [Google Scholar]
- 10.Devescovi V., Leonardi E., Ciapetti G., Cenni E., “Growth factors in bone repair,” Chir. Organi Mov. 92(3), 161–168 (2008). 10.1007/s12306-008-0064-1 [DOI] [PubMed] [Google Scholar]
- 11.Chang H., Knothe Tate M. L., “Concise review: the periosteum: tapping into a reservoir of clinically useful progenitor cells,” Stem Cells Transl. Med. 1(6), 480–491 (2012). 10.5966/sctm.2011-0056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Evans S. F., Chang H., Knothe Tate M. L., “Elucidating multiscale periosteal mechanobiology: a key to unlocking the smart properties and regenerative capacity of the periosteum?” Tissue Eng. Part B Rev. 19(2), 147–159 (2013). 10.1089/ten.teb.2012.0216 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hoffman M. D., Benoit D. S. W., “Emulating native periosteum cell population and subsequent paracrine factor production to promote tissue engineered periosteum-mediated allograft healing,” Biomaterials 52, 426–440 (2015). 10.1016/j.biomaterials.2015.02.064 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Tomlinson R. E., Silva M. J., “Skeletal blood flow in bone repair and maintenance,” Bone Res. 1(4), 311–322 (2013). 10.4248/BR201304002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Dyke J. P., Aaron R. K., “Noninvasive methods of measuring bone blood perfusion,” Ann. N. Y. Acad. Sci. 1192(1), 95–102 (2010). 10.1111/j.1749-6632.2009.05376.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tu Y. K., Bishop A. T., Kato T., Adams M. L., Wood M. B., “Experimental carpal reverse-flow pedicle vascularized bone grafts. Part II: bone blood flow measurement by radioactive-labeled microspheres in a canine model,” J. Hand Surg. Am. 25(1), 46–54 (2000). 10.1053/jhsu.2000.jhsu025a0046 [DOI] [PubMed] [Google Scholar]
- 17.Serrat M. A., “Measuring bone blood supply in mice using fluorescent microspheres,” Nat. Protoc. 4(12), 1749–1758 (2009). 10.1038/nprot.2009.190 [DOI] [PubMed] [Google Scholar]
- 18.Melnyk M., Henke T., Claes L., Augat P., “Revascularisation during fracture healing with soft tissue injury,” Arch. Orthop. Trauma Surg. 128(10), 1159–1165 (2008). 10.1007/s00402-007-0543-0 [DOI] [PubMed] [Google Scholar]
- 19.Koo H., Hupel T., Zdero R., Tov A., Schemitsch E. H., “The effect of muscle contusion on cortical bone and muscle perfusion following reamed, intramedullary nailing: a novel canine tibia fracture model,” J. Orthop. Surg. 5(1), 89 (2010). 10.1186/1749-799X-5-89 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.McCarthy I., “The physiology of bone blood flow: a review,” J. Bone Joint Surg. Am. 88(Suppl 3), 4–9 (2006). 10.2106/JBJS.F.00890 [DOI] [PubMed] [Google Scholar]
- 21.Durduran T., Choe R., Baker W. B., Yodh A. G., “Diffuse optics for tissue monitoring and tomography,” Rep. Prog. Phys. 73(7), 076701 (2010). 10.1088/0034-4885/73/7/076701 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Boas D. A., Diffuse Photon Probes of Structural and Dynamical Properties of Turbid Media: Theory and Biomedical Applications (University of Pennsylvania, 1996). [Google Scholar]
- 23.Dougherty R. L., Ackerson B. J., Reguigui N. M., Dorri-Nowkoorani F., Nobbmann U., “Correlation transfer: Development and application,” J. Quant. Spectrosc. Radiat. Transf. 52(6), 713–727 (1994). 10.1016/0022-4073(94)90037-X [DOI] [Google Scholar]
- 24.Cheung C., Culver J. P., Takahashi K., Greenberg J. H., Yodh A. G., “In vivo cerebrovascular measurement combining diffuse near-infrared absorption and correlation spectroscopies,” Phys. Med. Biol. 46(8), 2053–2065 (2001). 10.1088/0031-9155/46/8/302 [DOI] [PubMed] [Google Scholar]
- 25.Yu G., Durduran T., Zhou C., Wang H. W., Putt M. E., Saunders H. M., Sehgal C. M., Glatstein E., Yodh A. G., Busch T. M., “Noninvasive monitoring of murine tumor blood flow during and after photodynamic therapy provides early assessment of therapeutic efficacy,” Clin. Cancer Res. 11(9), 3543–3552 (2005). 10.1158/1078-0432.CCR-04-2582 [DOI] [PubMed] [Google Scholar]
- 26.Yu G., Durduran T., Lech G., Zhou C., Chance B., Mohler E. R., 3rd, Yodh A. G., “Time-dependent blood flow and oxygenation in human skeletal muscles measured with noninvasive near-infrared diffuse optical spectroscopies,” J. Biomed. Opt. 10(2), 024027 (2005). 10.1117/1.1884603 [DOI] [PubMed] [Google Scholar]
- 27.Sunar U., Quon H., Durduran T., Zhang J., Du J., Zhou C., Yu G., Choe R., Kilger A., Lustig R., Loevner L., Nioka S., Chance B., Yodh A. G., “Noninvasive diffuse optical measurement of blood flow and blood oxygenation for monitoring radiation therapy in patients with head and neck tumors: a pilot study,” J. Biomed. Opt. 11(6), 064021 (2006). 10.1117/1.2397548 [DOI] [PubMed] [Google Scholar]
- 28.Zhou C., Choe R., Shah N., Durduran T., Yu G., Durkin A., Hsiang D., Mehta R., Butler J., Cerussi A., Tromberg B. J., Yodh A. G., “Diffuse optical monitoring of blood flow and oxygenation in human breast cancer during early stages of neoadjuvant chemotherapy,” J. Biomed. Opt. 12(5), 051903 (2007). 10.1117/1.2798595 [DOI] [PubMed] [Google Scholar]
- 29.Zhou C., Eucker S. A., Durduran T., Yu G., Ralston J., Friess S. H., Ichord R. N., Margulies S. S., Yodh A. G., “Diffuse optical monitoring of hemodynamic changes in piglet brain with closed head injury,” J. Biomed. Opt. 14(3), 034015 (2009). 10.1117/1.3146814 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Durduran T., Yodh A. G., “Diffuse correlation spectroscopy for non-invasive, micro-vascular cerebral blood flow measurement,” Neuroimage 85(Pt 1), 51–63 (2014). 10.1016/j.neuroimage.2013.06.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Durduran T., Non-Invasive Measurements of Tissue Hemodynamics with Hybrid Diffuse Optical Methods (University of Pennsylvania, 2004). [Google Scholar]
- 32.Mesquita R. C., Skuli N., Kim M. N., Liang J., Schenkel S., Majmundar A. J., Simon M. C., Yodh A. G., “Hemodynamic and metabolic diffuse optical monitoring in a mouse model of hindlimb ischemia,” Biomed. Opt. Express 1(4), 1173–1187 (2010). 10.1364/BOE.1.001173 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Menon C., Polin G. M., Prabakaran I., Hsi A., Cheung C., Culver J. P., Pingpank J. F., Sehgal C. S., Yodh A. G., Buerk D. G., Fraker D. L., “An integrated approach to measuring tumor oxygen status using human melanoma xenografts as a model,” Cancer Res. 63(21), 7232–7240 (2003). [PubMed] [Google Scholar]
- 34.Buckley E. M., Cook N. M., Durduran T., Kim M. N., Zhou C., Choe R., Yu G., Schultz S., Sehgal C. M., Licht D. J., Arger P. H., Putt M. E., Hurt H. H., Yodh A. G., “Cerebral hemodynamics in preterm infants during positional intervention measured with diffuse correlation spectroscopy and transcranial Doppler ultrasound,” Opt. Express 17(15), 12571–12581 (2009). 10.1364/OE.17.012571 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Roche-Labarbe N., Carp S. A., Surova A., Patel M., Boas D. A., Grant P. E., Franceschini M. A., “Noninvasive optical measures of CBV, StO(2), CBF index, and rCMRO(2) in human premature neonates’ brains in the first six weeks of life,” Hum. Brain Mapp. 31(3), 341–352 (2010). 10.1002/hbm.20868 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zirak P., Delgado-Mederos R., Martí-Fàbregas J., Durduran T., “Effects of acetazolamide on the micro- and macro-vascular cerebral hemodynamics: a diffuse optical and transcranial doppler ultrasound study,” Biomed. Opt. Express 1(5), 1443–1459 (2010). 10.1364/BOE.1.001443 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Durduran T., Yu G., Burnett M. G., Detre J. A., Greenberg J. H., Wang J., Zhou C., Yodh A. G., “Diffuse optical measurement of blood flow, blood oxygenation, and metabolism in a human brain during sensorimotor cortex activation,” Opt. Lett. 29(15), 1766–1768 (2004). 10.1364/OL.29.001766 [DOI] [PubMed] [Google Scholar]
- 38.Yu G., Floyd T. F., Durduran T., Zhou C., Wang J., Detre J. A., Yodh A. G., “Validation of diffuse correlation spectroscopy for muscle blood flow with concurrent arterial spin labeled perfusion MRI,” Opt. Express 15(3), 1064–1075 (2007). 10.1364/OE.15.001064 [DOI] [PubMed] [Google Scholar]
- 39.Durduran T., Zhou C., Buckley E. M., Kim M. N., Yu G., Choe R., Gaynor J. W., Spray T. L., Durning S. M., Mason S. E., Montenegro L. M., Nicolson S. C., Zimmerman R. A., Putt M. E., Wang J., Greenberg J. H., Detre J. A., Yodh A. G., Licht D. J., “Optical measurement of cerebral hemodynamics and oxygen metabolism in neonates with congenital heart defects,” J. Biomed. Opt. 15(3), 037004 (2010). 10.1117/1.3425884 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Carp S. A., Dai G. P., Boas D. A., Franceschini M. A., Kim Y. R., “Validation of diffuse correlation spectroscopy measurements of rodent cerebral blood flow with simultaneous arterial spin labeling MRI; towards MRI-optical continuous cerebral metabolic monitoring,” Biomed. Opt. Express 1(2), 553–565 (2010). 10.1364/BOE.1.000553 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kim M. N., Durduran T., Frangos S., Edlow B. L., Buckley E. M., Moss H. E., Zhou C., Yu G., Choe R., Maloney-Wilensky E., Wolf R. L., Grady M. S., Greenberg J. H., Levine J. M., Yodh A. G., Detre J. A., Kofke W. A., “Noninvasive measurement of cerebral blood flow and blood oxygenation using near-infrared and diffuse correlation spectroscopies in critically brain-injured adults,” Neurocrit. Care 12(2), 173–180 (2010). 10.1007/s12028-009-9305-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Mesquita R. C., D’Souza A., Bilfinger T. V., Galler R. M., Emanuel A., Schenkel S. S., Yodh A. G., Floyd T. F., “Optical monitoring and detection of spinal cord ischemia,” PLoS One 8(12), e83370 (2013). 10.1371/journal.pone.0083370 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Diop M., Verdecchia K., Lee T.-Y., St Lawrence K., “Calibration of diffuse correlation spectroscopy with a time-resolved near-infrared technique to yield absolute cerebral blood flow measurements,” Biomed. Opt. Express 2(7), 2068–2081 (2011). 10.1364/BOE.2.002068 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Culver J. P., Durduran T., Furuya D., Cheung C., Greenberg J. H., Yodh A. G., “Diffuse optical tomography of cerebral blood flow, oxygenation, and metabolism in rat during focal ischemia,” J. Cereb. Blood Flow Metab. 23(8), 911–924 (2003). 10.1097/01.WCB.0000076703.71231.BB [DOI] [PubMed] [Google Scholar]
- 45.Zhou C., Yu G., Furuya D., Greenberg J., Yodh A., Durduran T., “Diffuse optical correlation tomography of cerebral blood flow during cortical spreading depression in rat brain,” Opt. Express 14(3), 1125–1144 (2006). 10.1364/OE.14.001125 [DOI] [PubMed] [Google Scholar]
- 46.He L., Lin Y., Huang C., Irwin D., Szabunio M. M., Yu G., “Noncontact diffuse correlation tomography of human breast tumor,” J. Biomed. Opt. 20(8), 086003 (2015). 10.1117/1.JBO.20.8.086003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Han S., Johansson J., Mireles M., Proctor A. R., Hoffman M. D., Vella J. B., Benoit D. S. W., Durduran T., Choe R., “Non-contact scanning diffuse correlation tomography system for three-dimensional blood flow imaging in a murine bone graft model,” Biomed. Opt. Express 6(7), 2695–2712 (2015). 10.1364/BOE.6.002695 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Hillman E. M. C., Boas D. A., Dale A. M., Dunn A. K., “Laminar optical tomography: demonstration of millimeter-scale depth-resolved imaging in turbid media,” Opt. Lett. 29(14), 1650–1652 (2004). 10.1364/OL.29.001650 [DOI] [PubMed] [Google Scholar]
- 49.Lemieux P. A., Durian D. J., “Investigating non-Gaussian scattering processes by using nth-order intensity correlation functions,” J. Opt. Soc. Am. A 16(7), 1651–1664 (1999). 10.1364/JOSAA.16.001651 [DOI] [Google Scholar]
- 50.Haskell R. C., Svaasand L. O., Tsay T.-T., Feng T.-C., McAdams M. S., Tromberg B. J., “Boundary conditions for the diffusion equation in radiative transfer,” J. Opt. Soc. Am. A 11(10), 2727–2741 (1994). 10.1364/JOSAA.11.002727 [DOI] [PubMed] [Google Scholar]
- 51.Boas D. A., Yodh A. G., “Spatially varying dynamical properties of turbid media probed with diffusing temporal light correlation,” J. Opt. Soc. Am. A 14(1), 192–215 (1997). 10.1364/JOSAA.14.000192 [DOI] [Google Scholar]
- 52.Lin Y., Huang C., Irwin D., He L., Shang Y., Yu G., “Three-dimensional flow contrast imaging of deep tissue using noncontact diffuse correlation tomography,” Appl. Phys. Lett. 104(12), 121103 (2014). 10.1063/1.4869469 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Arridge S. R., “Optical tomography in medical imaging,” Inverse Probl. 15(2), R41–R93 (1999). 10.1088/0266-5611/15/2/022 [DOI] [Google Scholar]
- 54.Hansen P. C., “Analysis of Discrete Ill-Posed Problems by Means of the L-Curve,” SIAM Rev. 34(4), 561–580 (1992). 10.1137/1034115 [DOI] [Google Scholar]
- 55.Dehghani H., Eames M. E., Yalavarthy P. K., Davis S. C., Srinivasan S., Carpenter C. M., Pogue B. W., Paulsen K. D., “Near infrared optical tomography using NIRFAST: Algorithm for numerical model and image reconstruction,” Commun. Numer. Methods Eng. 25(6), 711–732 (2009). 10.1002/cnm.1162 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Han S., Hoffman M. D., Proctor A. R., Vella J. B., Mannoh E. A., Barber N. E., Kim H. J., Jung K. W., Benoit D. S. W., Choe R., “Non-Invasive Monitoring of Temporal and Spatial Blood Flow during Bone Graft Healing Using Diffuse Correlation Spectroscopy,” PLoS One 10(12), e0143891 (2015). 10.1371/journal.pone.0143891 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Hoffman M. D., Xie C., Zhang X., Benoit D. S., “The effect of mesenchymal stem cells delivered via hydrogel-based tissue engineered periosteum on bone allograft healing,” Biomaterials 34(35), 8887–8898 (2013). 10.1016/j.biomaterials.2013.08.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Gargiulo S., Greco A., Gramanzini M., Esposito S., Affuso A., Brunetti A., Vesce G., “Mice anesthesia, analgesia, and care, Part I: anesthetic considerations in preclinical research,” ILAR journal / National Research Council, Institute of Laboratory Animal Resources 53(1), E55–E69 (2012). 10.1093/ilar.53.1.55 [DOI] [PubMed] [Google Scholar]
- 59.Gargiulo S., Greco A., Gramanzini M., Esposito S., Affuso A., Brunetti A., Vesce G., “Mice anesthesia, analgesia, and care, Part II: anesthetic considerations in preclinical imaging studies,” ILAR journal / National Research Council, Institute of Laboratory Animal Resources 53(1), E70–E81 (2012). 10.1093/ilar.53.1.70 [DOI] [PubMed] [Google Scholar]
- 60.Gargiulo S., Gramanzini M., Liuzzi R., Greco A., Brunetti A., Vesce G., “Effects of some anesthetic agents on skin microcirculation evaluated by laser Doppler perfusion imaging in mice,” BMC Vet. Res. 9(1), 255 (2013). 10.1186/1746-6148-9-255 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Jermyn M., Ghadyani H., Mastanduno M. A., Turner W., Davis S. C., Dehghani H., Pogue B. W., “Fast segmentation and high-quality three-dimensional volume mesh creation from medical images for diffuse optical tomography,” J. Biomed. Opt. 18(8), 086007 (2013). 10.1117/1.JBO.18.8.086007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Jacques S. L., “Optical properties of biological tissues: a review,” Phys. Med. Biol. 58(11), R37–R61 (2013). 10.1088/0031-9155/58/11/R37 [DOI] [PubMed] [Google Scholar]
- 63.Brueton R. N., Revell W. J., Brookes M., “Haemodynamics of Bone Healing in a Model Stable Fracture,” in Bone Circulation and Vascularization in Normal and Pathological Conditions, Schoutens A., Arlet J., Gardeniers J. W. M., Hughes S. P. F., eds. (Springer US, 1993), pp. 121–128. [Google Scholar]
- 64.Kalfas I. H., “Principles of bone healing,” Neurosurg. Focus 10(4), E1 (2001). 10.3171/foc.2001.10.4.2 [DOI] [PubMed] [Google Scholar]
- 65.Choe R., Ramirez G., Proctor A. R., Han S., Durduran T., Brown E. B., “Diffuse correlation spectroscopy and tomography for longitudinal monitoring of blood flow changes induced by chemotherapy in breast cancer xenografts,” in Biomedical Optics 2016 (Optical Society of America, Fort Lauderdale, Florida, 2016), p. CTu4A.4. [Google Scholar]
- 66.Yalavarthy P. K., Pogue B. W., Dehghani H., Paulsen K. D., “Weight-matrix structured regularization provides optimal generalized least-squares estimate in diffuse optical tomography,” Med. Phys. 34(6), 2085–2098 (2007). 10.1118/1.2733803 [DOI] [PubMed] [Google Scholar]
- 67.Ripoll J., Schulz R. B., Ntziachristos V., “Free-space propagation of diffuse light: theory and experiments,” Phys. Rev. Lett. 91(10), 103901 (2003). 10.1103/PhysRevLett.91.103901 [DOI] [PubMed] [Google Scholar]
- 68.Binzoni T., Sanguinetti B., Van de Ville D., Zbinden H., Martelli F., “Probability density function of the electric field in diffuse correlation spectroscopy of human bone in vivo,” Appl. Opt. 55(4), 757–762 (2016). 10.1364/AO.55.000757 [DOI] [PubMed] [Google Scholar]
- 69.Johansson J. D., Mireles M., Morales-Dalmau J., Farzam P., Martínez-Lozano M., Casanovas O., Durduran T., “Scanning, non-contact, hybrid broadband diffuse optical spectroscopy and diffuse correlation spectroscopy system,” Biomed. Opt. Express 7(2), 481–498 (2016). 10.1364/BOE.7.000481 [DOI] [PMC free article] [PubMed] [Google Scholar]