Multi-spectral photoacoustic elasticity tomography

Abstract

The goal of this work was to develop and validate a spectrally resolved photoacoustic imaging method, namely multi-spectral photoacoustic elasticity tomography (PAET) for quantifying the physiological parameters and elastic modulus of biological tissues. We theoretically and experimentally examined the PAET imaging method using simulations and in vitro experimental tests. Our simulation and in vitro experimental results indicated that the reconstructions were quantitatively accurate in terms of sizes, the physiological and elastic properties of the targets.

1. Introduction

Photoacoustic tomography (PAT) is a robust biomedical imaging method that can offer the structural and functional information of biological tissues with excellent resolution and high contrast [1–7]. PAT imaging techniques have been successfully applied to the early detection of cancer, probing the brain function and examining vascular and skin diseases [8–11]. More importantly, recent work also shows that PAT can reconstruct the tissue mechanical properties including the acoustic velocity, the elastic modulus and the temperature [12–15], and optical and physiological properties such as the optical absorption and scattering coefficients, the deoxyhemoglobin (HbR) and oxyhemoglobin (HbO₂) concentrations by using spectrally resolved photoacoustic (PA) measurements [6,16–19]. In particular, the uniqueness regarding simultaneous reconstruction of different chromophore concentrations and acoustic velocity has been resolved for multi-spectral PAT [18], which can reveal spatially resolved quantitative physiological and molecular information by exploiting the known spectral characteristics of specific chromophores. The generated physiological properties of biological tissues including the concentrations of HbR and HbO₂ and water (H2O) content are essential for an accurate diagnostic decision-making in lesion detection and image-guided cancer treatment.

Interestingly, the bulk elastic modulus of normal and diseased tissues have been explored by ultrasonography, where the ranges of the elastic moduli from soft tissues span over as much as four orders of the magnitudes [20,21]. Recently, PAT has been implemented to characterize the elastic moduli of phantoms or biological tissues using single-wavelength measurements. However, most of work conducted can only reconstruct the elastic moduli-related parameters, which cannot achieve the truly quantitative and spectrally resolved PA elasticity tomography (PAET) [14]. In this study, multi-spectral PAET is proposed to directly reconstruct the chromophore concentrations and quantitative elastic modulus of biological tissues simultaneously. The capability of reconstructing the physiology and elastic properties by using multi-spectral PAET, paves a new avenue for better differentiating benign from malignant lesions since the elastic contrast between diseased and healthy tissues is very high [21].

2. Methods and materials

2.1 The multi-spectral PAET reconstruction method

To formulate the reconstruction model for multi-spectral PAET, the PA wave generation and propagation in an acoustic coupling media are described by the basic Newton’s law of motion Eq. (1), equation of continuity (2) and the thermal elastic Eq. (3) in terms of thermal confinement [1],

$$\rho (r)\frac{\partial }{\partial t}V(r,t)=-\nabla p(r,t).$$ (1)

$$\nabla ·V(r,t)=-\frac{1}{\rho (r)v_s^2(r)}\frac{\partial }{\partial t}p(r,t)+\beta \frac{\partial }{\partial t}T(r,t).$$ (2)

$$\rho (r)C_p\frac{\partial }{\partial t}T(r,t)=H(r,t).$$ (3)

where V is particle velocity, v_s is the acoustic velocity, t is time, r is the spatial location, $\rho$ is the density of the media, T and p are the temperature and pressure, H is the source term which can be written as $H=\Psi I(t)$, C_p is the specific heat, $\Psi$is the light absorbed energy density, and I(t) is the temporal illumination function. Considering Eqs. (1)-(3) and eliminating V, we get

$$\rho (r)\nabla ·(\frac{1}{\rho (r)}\nabla p(r,t))-\frac{1}{v_s^2(r)}\frac{{\partial }^2}{\partial t^2}p(r,t)=-\frac{\beta }{C_p}\frac{\partial }{\partial t}H(r,t).$$ (4)

If the bulk elastic modulus K is denoted as $K=\rho v_s^2$, Eq. (4) is written,

$$\nabla (\frac{1}{\rho (r)}\nabla p(r,t))-\frac{1}{K}\frac{{\partial }^2}{\partial t^2}p(r,t)=-\frac{\beta }{\rho C_p}\frac{\partial }{\partial t}H(r,t).$$ (5)

If a homogeneous elastic reference medium is assumed with density $\rho ={\rho }_0$, Eq. (5) is written,

$${\nabla }^{2}p(r,t)-\frac{{\rho }_0}{K}\frac{{\partial }^2}{\partial t^2}p(r,t)=-\frac{\beta }{C_p}\frac{\partial }{\partial t}H(r,t).$$ (6)

Denoting the following Fourier transform form for acoustic pressure,

$$P(r,\omega )={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}p(r,t)\exp (-i\omega t)dt}.$$ (7)

And taking the Fourier transform on variable t of Eq. (7), we obtain,

$${\nabla }^{2}p(r,\omega )+\frac{K_0}{K}{k}_0^{2}p(r,\omega )=i\frac{k_0\beta }{C_p}{v}_0\Psi \left(r\right).$$ (8)

where $k_0=\omega /v_0$ is the wave number described by the angular frequency $\omega$and the speed of acoustic wave v₀ in a reference medium, K₀ is the bulk elastic modulus of the reference medium and the light absorbed energy density $\Psi$ is equal to the product of the optical absorption coefficient ${\mu }_a$ and photon density $\Phi$. Equation (8) can be further written as

$${\nabla }^{2}p(r,\omega )+O{k}_0^{2}p(r,\omega )=i\frac{k_0\beta }{C_p}{v}_0\Psi \left(r\right).$$ (9)

where O is a coefficient that depends on the bulk modulus K and $O=K_0/K$ .

In multi-spectral PAT, the frequency-domain Helmholtz wave equation is expresses as

$${\nabla }^{2}p(r,\omega ,\lambda )+O{k}_0^{2}p(r,\omega ,\lambda )=i\frac{k_0\beta }{C_p}{v}_0\mu (r,\omega )\Phi (r,\lambda )$$ (10)

where λ is the wavelength of the incident light. According to the Beer’s law, the wavelength-dependent tissue absorption coefficient is written [16,18],

$${\mu }_a(\lambda )={\displaystyle \sum _{i=1}^{}{\epsilon }_i}(\lambda )c_i.$$ (11)

in which $c_i$ is the concentration and ${\epsilon }_i(\lambda )$is the extinction coefficient of the ith chromophore at wavelength λ . Consequently, Eq. (10) is rewritten,

$${\nabla }^{2}p(r,\omega ,\lambda )+O{k}_0^{2}p(r,\omega ,\lambda )=i\frac{k_0\beta }{C_p}{v}_0{\displaystyle \sum _{i=1}{\epsilon }_i\left(\lambda \right)}{c}_i\Phi \left(r,\lambda \right).$$ (12)

Equation (12) is the forward equation for multi-spectral PAET and the finite element discretization form of Eq. (12) is [16,18],

$$Ap=B$$ (13)

The inverse solution can be obtained by solving the following inverse equation:

$$(J^{T}J+\xi I)\Delta \chi =J^T(p^o-p^c).$$ (14)

in which$\Delta \chi ={\left(\begin{array}{cccccccc}\Delta c_{l,1}& \Delta c_{l,2}& \mathrm{...}& \Delta c_{l,n}& \Delta O_1& \Delta O_2& \mathrm{...}& \Delta O_n\end{array}\right)}^T$is the update vector for l chromophores, elasticity modulus-related parameter O and N is the node number of the finite element mesh;$\xi$ is the regularization parameter determined by combined Marquardt and Tikhonov regularization schemes [16]; $p_i^o$ and $p_i^c$ are measured and calculated data for i = 1,2,…M boundary locations and are written as for each acoustic frequency ω within each incident optical wavelength λ,

$$p^o={(p_1^o,p_2^o,\cdots ,p_M^o)}^T|(\omega ,\lambda ), p^c={(p_1^c,p_2^c,\cdots ,p_M^c)}^T|(\omega ,\lambda ).$$ (15)

The Jacobian matrix, J is denoted as $J=[{\tilde{J}}_{O,\lambda ,\omega },{\tilde{J}}_{c_i,\lambda ,\omega }]$, where ${\tilde{J}}_{O,\lambda ,\omega }$ and ${\tilde{J}}_{c_i,\lambda ,\omega }$ represents the Jacobian submatrix for the elastic modulus and different chromophores, respectively [15]. In consideration of $\Psi ={\mu }_a\Phi$, the elements in Jacobian matrix ${\tilde{J}}_{c_i,\lambda ,\omega }$ are determined by

$$\frac{\partial p_i\left(\omega ,\lambda \right)}{\partial {(c_l)}_{,j}}={\displaystyle \sum _{k=1}^N(}\frac{\partial p_i\left(\omega ,\lambda \right)}{\partial {\Psi }_k\left(\lambda \right)}\frac{\partial {\Psi }_k\left(\lambda \right)}{\partial {\mu }_{a,j}\left(\lambda \right)}{\epsilon }_l\left(\lambda \right)\begin{array}{cc})& (i=1,\mathrm{2...}M;j=1,\mathrm{2...}N;l=1,\mathrm{2...}Chrom)\end{array}.$$ (16)

in which Chrom is the number of chromophores and the derivatives $\partial \Psi /\partial {\mu }_a$ in Eq. (3) are further denoted as

$$\frac{\partial {\Psi }_k\left(\lambda \right)}{\partial {\mu }_{a j} \left(\lambda \right)}=(\begin{array}{cc}{\Phi }_j+{\mu }_{a,j}(\partial {\Phi }_j/\partial {\mu }_{a,j})& if\begin{array}{c}\begin{array}{cc}& (k=j)\end{array}\end{array}\\ {\mu }_{a,k}(\partial {\Phi }_k/\partial {\mu }_{a,j})& if\begin{array}{cc}& (k\ne j)\end{array}\end{array}|\left(\lambda \right).$$ (17)

The sensitivity of $\partial p(\omega ,\lambda )/\partial \Psi (\lambda )$ and $\partial \Phi /\partial {\mu }_a$ in each iteration can be calculated from Eq. (10) and the following photon diffusion equation for each wavelength, respectively,

$$\nabla ·D(r,\lambda )\nabla \Phi (r,\lambda )-{\mu }_a(r,\lambda )\Phi \left(r,\lambda \right)=-S(r,\lambda ).$$ (18)

in which S(r) is the light source term and D(r) is the optical diffusion coefficient and assumed as a constant in this study.

Likewise, the elements in Jacobian submatrix ${\tilde{J}}_{O,\lambda ,\omega }$ are determined by [22],

$$\left[A\right]\left\{\frac{\partial p\left(\omega ,\lambda \right)}{\partial O_j}\right\}=-\left[\frac{\partial A}{\partial O_j}\right]\left\{p\left(\omega ,\lambda \right)\right\}.$$ (19)

The Jacobian matrix can be calculated through the following steps using the adjoint method:

First, we define a MxN matrix $\Psi$, and let $\Psi$satisfy the following relationship:

$$[\Psi ]\left[A\right]=[{\Delta }_d].$$ (20)

where the vector ${\Delta }_d$ has the unit value at the measurement sites/nodes and zero at other nodes. Then we left multiply Eq. (19) by $\Psi$, which yields

$$[\Psi ]\left[A\right]\left\{\frac{\partial p\left(\lambda \right)}{\partial O_j}\right\}=-[\Psi ]\left[\frac{\partial A}{\partial O_j}\right]\left\{p\left(\lambda \right)\right\}.$$ (21)

Inspecting Eq. (20) into Eq. (21), we can immediately find that the left hand side of Eq. (21) actually gives the corresponding elements in the Jacobian submatrix ${\tilde{J}}_{O,\lambda ,\omega }$.

As such, in multi-spectral PAET, the image formation task is to update chromophores concentration and bulk elastic modulus distributions via the iterative solution of Eqs. (13), (14) and (18) so that a weighted sum of the squared difference between computed and measured acoustic pressures can be minimized.

2.2 The multi-spectral PAET imaging systems

For our home-made PAT imaging system at the Faculty of Health Sciences of the University of Macau, a pulsed light from an Nd:YAG laser with OPO based on the multi-wavelength excitation (wavelength range from 680 to 1064 nm; pulse duration: 5-10 ns; frequency rate: 20 Hz; Surelite I-10, Continuum) was used to illuminate the phantom/biological tissues via an optical subsystem and generate acoustic signals. A transducer (1MHz central frequency; OLYMPUS NDT) and the phantom were immersed into a water tank. A rotary stage rotated the transducer relative to the center of the tank as shown in Fig. 1. The incident optical fluence was controlled at 10 mJ/cm², and the diameter of the incident laser beam was 2.0 cm. The complex wavefield signal was amplified by a Pulser/Receiver (5073R, OLYMPUS).

Fig. 1.

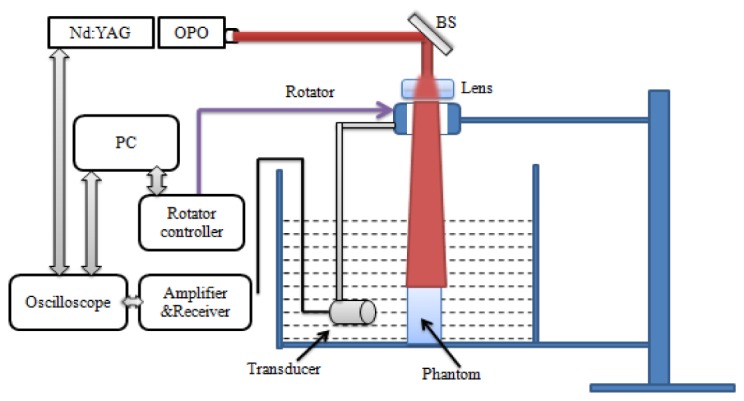
Schematic of the PAT system. BS: beam splitter; PC: personal computer.

2.3 Simulation and in vitro experimental tests

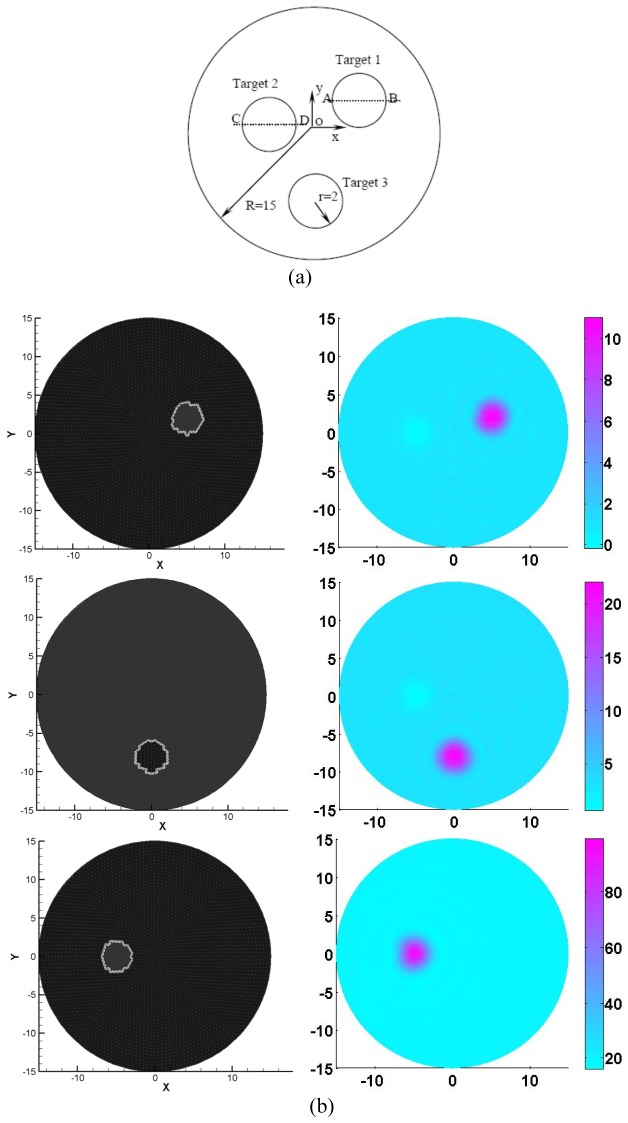
For simulation test 1, a circular background with the diameter of 3cm contained three circular targets (2mm in radius each as shown in Fig. 2(a)), where each target had different contrasts in physiological properties (Hb, HbO₂, and H₂O) and bulk elastic modulus (K). The chromophore concentrations and K used were provided in Table 1 and six optical wavelengths (633, 670, 723, 805, 854and 896nm) were utilized to generate the measurements for the multi-spectral PAET. A total of 120 detectors were equally distributed along the boundary of the circular background. The extinction coefficient for each chromophore was adopted from the website at http://omlc.ogi.edu/spectra/index.html [23].

Fig. 2.

(a) Test geometry. The dimension units are in millimeters. (b) The exact (left column) and recovered (right column) images using 6 optical wavelengths. The first to the third rows of Fig. 2(b) denote the Hb, HBO₂ and H₂O, respectively. The axes (left and bottom) illustrate the spatial scale, in mm, whereas the color scale (right) denote HbO₂ and HbR in μM, and H₂O in percentage.

Table 1. Chromophore Concentrations and K for the targets in simulation test 1.

Objects position	HbO2 (μM)	HbR (μM)	H2O (%)	K (GPa)
Background	6	2	20	2.2
Top right	6	10	20	2.2
Top left	6	2	70	2.8
Bottom middle	20	2	20	2.8

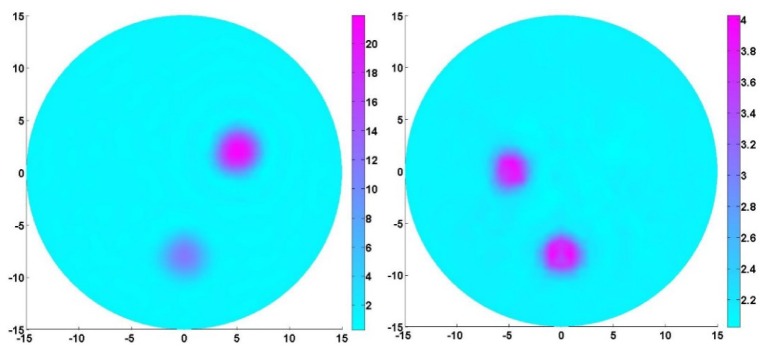
The test geometry for the second simulation was the same as simulation test 1, in which we assumed the chromophore of the targets only consisted of HbR. Two inclusions (top right and middle bottom targets) had different HbR contrast levels while two inclusions (top left and middle bottom targets) had the same contrast level for K. The HbR concentrations and K used for the second simulation test were given in Table 2. The measurements from two wavelengths (670nm and 896nm) were used for the multi-wavelength PAET reconstruction and the extinction coefficients were also taken from the website at http://omlc.ogi.edu/spectra/index.html [23]. In this study, the constant Gruneisen function $\Gamma ={c_0}^2\beta /C_p$ ($c_0$ = 1495 m/s), ${{\mu }^{\prime }}_s$ = 1.0 mm^-1, and K₀ = 2.23GPa were used for all the tests.

Table 2. HbR concentration and K of the targets in simulation test 2.

Objects position	HbR (μM)	K(GPa)
Background	2	2.2
Top right	20	2.2
Top left	2	4.0
Bottom middle	10	4.0

In addition, for the first in vitro experiment, we embedded a square chicken breast (length: 3mm; width:2mm) into a 3.5-cm-diameter solid cylindrical phantom. We then immersed the chicken breast-bearing solid phantom into the water tank. Two optical wavelengths (532 and 680nm) were used for the measurements. The phantom materials used consisted of Intralipid as scatterer and India ink as absorber with Agar powder (1-2%) for solidifying the Intralipid and India ink solution.

For the second in vitro experiment, we placed a phantom that contained the porcine liver tissue into the water. The solid cylindrical phantom with the diameter of 3.5cm consisted of Intralipid as the scatterer and India ink as the absorber with Agar powder (1-2%) for solidifying the Intralipid and India ink solution. In this test, we used the dual-wavelength of 700nm and 750nm for the measurements and the molar extinction coefficients of porcine liver were adopted from reference [24].

3. Results and discussion

In the following sections we show the reconstruction results that demonstrate the feasibility of the multi-spectral PAET reconstruction method. The multi-spectral PAET approach is examined using several simulations and in vitro experiments based on the reconstruction model and imaging systems mentioned above.

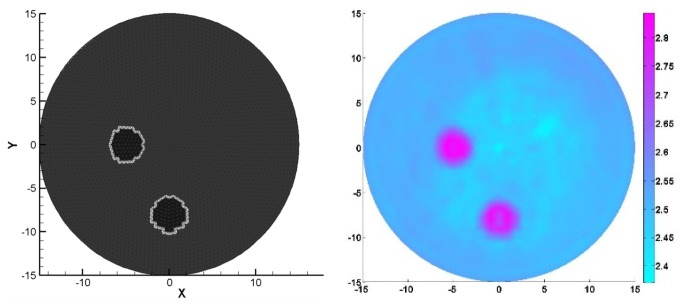
Figures 2 and 3 showed the recovered results for simulation case 1, in which the figures on the left column of Fig. 2 displayed the exact locations of the targets including HbO₂, HbR, H₂O and K whereas the recovered images were presented on the right Figs. 2(b) and 3 corresponding to HbO₂, HbR, H₂O and K, respectively. It was discovered from the recovered results in Figs. 2 and 3 that the crosstalk errors between the chromophore concentrations and bulk elastic modulus were effectively resolved by using our multi-spectral PAET reconstruction method. Meanwhile, the sizes and the quantitative physiological and elastic properties of the targets were quantified by estimating the full width half maximum of the recovered quantitative properties, which were provided in Table 3. Interestingly, for the reconstructed sizes, we discovered that the errors ranged from 5% to 7% whereas for the recovered quantitative elastic or physiology properties, the errors were less than 12.5%.

Fig. 3.

The exact (left side) and recovered (right side) K images using 6 optical wavelengths for the simulation test 1 based on the test geometry in Fig. 2(a). The axes (left and bottom) illustrate the spatial scale, in mm, whereas the color scale (right) denotes K in GPa.

Table 3. The reconstructed chromophore concentrations and K for the targets in simulation test 1.

Targets	HbO2 (μM)	HbR (μM)	H2O (%)	K (GPa)	Sizes errors (%)
Top right	5	11	22	2.4	5
Top left	5	2	80	2.9	7
Bottom middle	21	2	22	2.9	5

For the second simulation test, the aim was to examine if the targets that had different HbR and elastic modulus contrast levels can be effectively recovered in terms of the position, size and quantitative physiology and elastic properties. The reconstruction results in Fig. 4 indicated that the multi-spectral PAET algorithm was very robust for simultaneous recoveries of tissue physiological and elastic properties. In particular, multi-spectral PAET can effectively minimize the crosstalk errors between HbR and K and improve the image quality for multi-parameter reconstructions. In addition, by estimating the full width half maximum of the recovered quantitative properties in Fig. 4, we discovered that the reconstructed errors for the target sizes as well as the quantitative HbR concentration and K were less than 10%.

Fig. 4.

Quantitative HbR (left) and K (right) images recovered by our multi-spectral PAET. The axes (left and bottom) illustrate the spatial scale, in mm, whereas the color scale (right) denote HbR in μM and K in GPa.

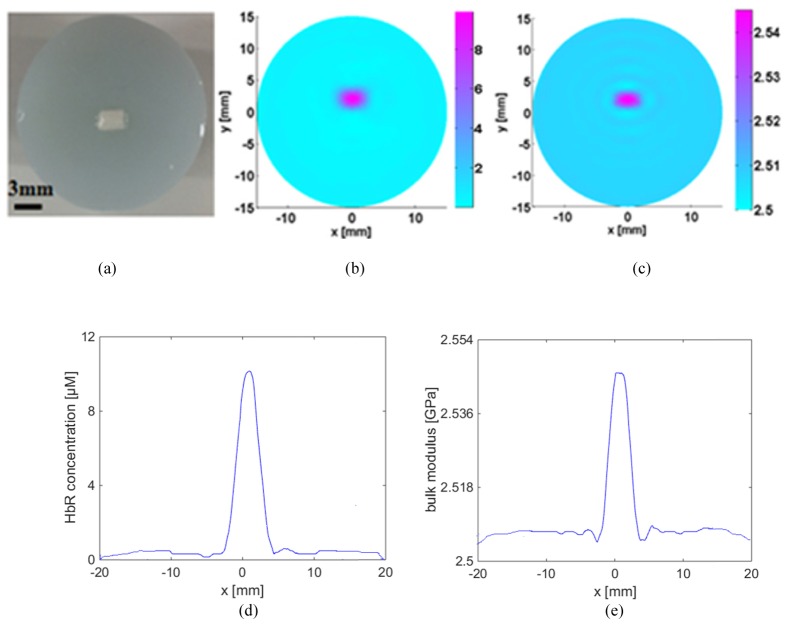
The first in vitro test was performed to explore the merits of the developed multi-spectral PAET reconstruction method. For this experiment, we used the chicken breast as the target, as plotted in Fig. 5(a). In addition, the optical properties and molar extinction coefficients of the chicken breast were provided in Table 4. In particular, we used balance scales to measure the mass of a piece of chicken breast, and then placed the chicken breast inside the water to measure its volume. The measured mass density of the chicken breast was 1045kg/m³. The imaging results were provided in Fig. 5, in which Figs. 5(b) and 5(c) showed the recovered HbR concentration and bulk elastic modulus K, respectively. Likewise, by estimating the full width half maximum of the quantitative properties profiles in Fig. 5, we found the reconstructed HbR concentration of the chicken breast was nearly 10 μM while the corresponding peak value of K was 2.5GPa. In particular, the reconstructed size of the chicken breast in length was 3.1mm, which was in good agreement with its true size of 3.0mm.

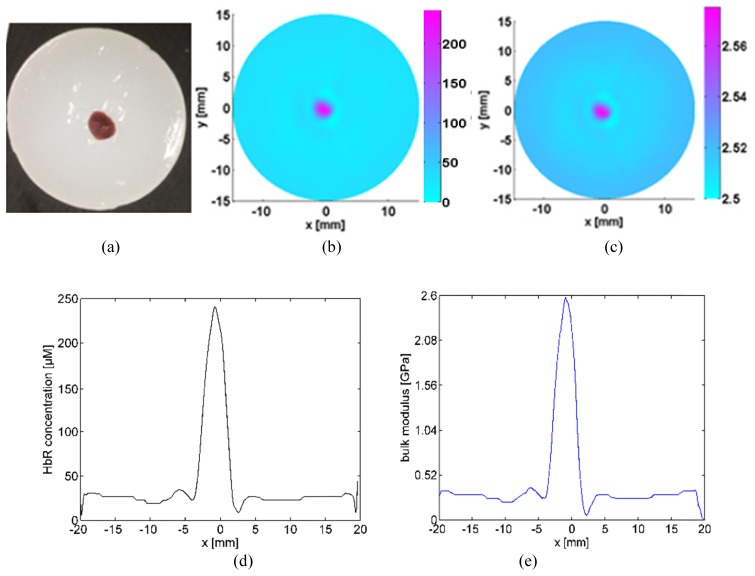
Fig. 5.

The Photograph of the chicken breast used for the first in vitro experimental test (a), the recovered HbR concentration image (b), the recovered K image (c), the HbR profile plotted along the center of the target (d), and the K profile plotted along the center of the target (e). The axes (left and bottom) illustrate the spatial scale, in mm, whereas the color scale (right) denote HbR in μM and K in GPa.

Table 4. Optical properties and extinction coefficients of the chicken breast.

Wavelengths (nm)	Target positions	Molar extinction coefficient (cm−1/M)	Absorptioncoefficient (cm−1)
532	Background Chicken breast	40580	0.01 0.8
680	Background Chicken breast	2407	0.01 0.046

For the second in vitro experimental test, the liver samples were imaged by using our PAT imaging system and the recovered K and HbR concentration were presented in Fig. 6. By estimating the full width half maximum of the quantitative properties profiles in Fig. 6, the reconstructed HbR concentration of subovate porcine liver was around 241.7 μM while the recovered bulk elasticity modulus K was about 2.6 GPa.

Fig. 6.

The Photograph of the porcine liver tissue used for the second in vitro experimental test (a), the recovered HbR concentrations image (b), the recovered K (c), the HbR profile plotted along the center of the target (d), and the K profile plotted along the center of the target (e). The axes (left and bottom) illustrate the spatial scale, in mm, whereas the color scale (right) denote HbR in μM and K in GPa.

In addition, it should be pointed out that to access the recovered quantitative properties of the targets by using the full width half maximum method, six profiles plotted along the center of the target were extracted and used for further analysis. For each profile, the quantitative property at the center of the target was considered as the reconstructed result. Then we calculated the mean value of the reconstructed results from the six profiles, which was considered as the recovered value for the target. It should also be pointed out that for the in vivo case, it may be very challenging to recover the quantitative elastic and physiological properties due to the highly heterogeneous distributions of optical properties from different biological tissues. In particular, for the in vivo test, the absorption spectra are very hard to be accurately determined. However, it is possible to recover the quantitative parameters if the reconstruction regions are focused on the tumor or lesion areas.

Further, to experimentally examine the reconstruction accuracy of the developed reconstruction method, it is essential to compare the recovered elastic moduli with the actual ones from different tissues (Table 5). It is noted that the actual bulk elastic modulus K was determined as $K=\rho v_s^2$. Because the density $\rho$ was measured in this study for different experimental tests, the actual bulk elastic modulus can easily be calculated by using the following longitudinal velocities for the different tissues [21]. We found the reconstruction error between the recovered bulk elastic modulus and actual one was less than 15%.

Table 5. Average longitudinal velocities for the different phantoms [21].

Velocity	Agar	Porcine	Fat Turkey Breast	Bovine Liver
vs (m/s)	1489.3	1501.6	1576.3	1590.0

In summary, our reconstruction results indicated that the quantification of chromophore concentrations and elastic bulk modulus is feasible by using the developed PAET imaging method when spectral priors are incorporated into the inverse reconstruction. In particular, images that are generated from simulated and in vitro data are presented, in which both the physiological and K properties images can be reconstructed based on our multi-spectral PAET reconstruction algorithm. Consequently, the spectrally resolved PAET approach provides an efficient means of concurrent reconstruction of multiple parameters including different chromophore concentrations and K. More importantly, it is clear from the reconstructed results that the crosstalk issue for recovery of multiple parameters are successfully resolved by using multi-spectral PA measurements. Specifically, multi-spectral PAET can effectively minimize the crosstalk error and improve the image quality for all the test cases.

According to the previous work, we know that the ranges of the elastic moduli of soft tissues span over as much as four orders of magnitudes [21]. Consequently, the recovered elastic property by using PAET can be applied to the diagnosis and therapeutic treatment of diseases that are characterized by changes in the elastic property of biological tissues. In addition, we discovered that the PAET image reconstruction methods are also able to quantitatively reconstruct absorbing objects of different sizes and different elastic modulus contrast levels. Nonetheless, the ability of reconstructing the elastic property image by using PA measurements may provide us a novel tool to quantify physiological function, disease progression, or response to intervention.