Estimation of Jones matrix, birefringence and entropy using Cloude-Pottier decomposition in polarization-sensitive optical coherence tomography

Abstract

Estimation of polarimetric parameters has been a fundamental issue to assess biological tissues that have form birefringence or polarization scrambling in polarization-sensitive optical coherence tomography (PS-OCT). We present a mathematical framework to provide a maximum likelihood estimation of the target covariance matrix and its incoherent target decomposition to estimate a Jones matrix of a dominant scattering mechanism, called Cloude-Pottier decomposition, thereby deriving the phase retardation and the optic axis of the sample. In addition, we introduce entropy that shows the randomness of the polarization property. Underestimation of the entropy at a low sampling number is mitigated by asymptotic quasi maximum likelihood estimator. A bias of the entropy from random noises is corrected to show only the polarization property inherent in the sample. The theory is validated with experimental measurements of a glass plate and waveplates, and applied to the imaging of a healthy human eye anterior segment as an image filter.

1. Introduction

Polarization-sensitive optical coherence tomography (PS-OCT) has been developed as an extension to conventional OCT [1] to observe the depth-resolved polarization property of a sample by measuring the state of a polarized electromagnetic (EM) field [2–6] or the linear map of the polarized EM fields [7–9]. Since everything about PS-OCT is more complicated than conventional OCT, it still has plenty of room left for improvement of PS-OCT in aspects of both the hardware and the software. Among them, Makita et al. raised one of the fundamental issues in PS-OCT that the mean of the phase retardation is significantly biased from the true value because of asymmetric distribution [10]. Various methods have been developed to apply averaging to such polarimetric parameters [11–19]. In another approach, an estimator of the phase retardation based on the likelihood of the distribution was also developed [20]. However, these approaches are limited to estimating only a partial aspect of the polarization property, because they have focused on one or some of parameters, for example, the phase retardation, the optic axis, Stokes parameters, Jones matrix or degree of polarization uniformity [21]. Lack of a sophisticated and unified method of the estimation is our motivation for this study to develop a new approach that resolves the estimation issue in PS-OCT.

Although the Jones matrix is an operator to characterize the sample’s coherent property that changes the state of polarized light [22], it is also a subject of the measurement that inherently involves a stochastic process. In the measurement, the observed quantities need to be evaluated statistically. The most common approach to this may be Stokes-Mueller formalism [23]. Although Stokes-Mueller formalism has advantages consisting of only observable quantities and a capability of geometric treatment as an orthogonal group, it does not provide a clear perspective on statistical correlation between the field variables.

It has been known that the Jones and Stokes-Mueller formalisms can be understood abstractly using group theory [24,25]. In 1986, Cloude extended the polarisation algebra to the special unitary group of degree 4, SU(4), and showed that the positive semidefinite Hermitian matrix in SU(4) was useful in estimating the Jones matrix in SU(2) [26]. This theory has been advanced in the field of polarimetric radar imaging to detect and classify natural and artificial terrain objects from airborne and satellite radar systems [27]. Although there are some variations in how to call this incoherent decomposition method, we call it Cloude-Pottier decomposition after the book in [28]. There are only a few reports that used it for biomedical applications [29–32], and no reports in OCT to the best of our knowledge.

In this study, we develop a novel method to estimate a 4 × 4 covariance matrix that is converted from the measured Jones matrix. Applying Cloude-Pottier decomposition to the 4 × 4 covariance matrix, we estimate the Jones matrix and entropy that shows a randomness of the Jones matrix, and obtain the phase retardation and the optic axis of the sample from the estimated Jones matrix. To the best of our knowledge, this is the first time to apply the entropy for PS-OCT to show the randomness of the polarization properties. In addition, an underestimation of the entropy at a low sampling number in the ensemble average is mitigated by an estimator for the eigenvalues of the 4 × 4 covariance matrix [33]. Moreover, a bias in the entropy by random noises is estimated and corrected. Specifically, we derive equations that show relationships between the bias and noises for both an accumulated Jones matrix along the depth and a local Jones matrix that cancels the axial accumulation. Section 2 describes the details of the theory, and Section 3 shows experimental results to validate the theory and demonstrates image filtering by Cloude-Pottier decomposition for the anterior eye segment. Section 4 describes discussions about some topics that are relevant to our results, including other methods for parameterizing the depolarization.

2. Theory

2.1 Statistical description of the Jones matrix using the target covariance matrix

We write measured Jones matrix of the sample as

$$J=\left[\begin{array}{cc}\underset{¯}{E_1}& \underset{¯}{E_2}\end{array}\right]=\left[\begin{array}{cc}{J}_{1\text{H}}& J_{2\text{H}}\\ J_{1\text{V}}& J_{2\text{V}}\end{array}\right],$$ (1)

where the first and second columns are measured Jones vectors in response to orthogonally polarized incident electromagnetic fields with each other. As the first step for the statistical analysis of the Jones matrix, it is rearranged to 1 × 4 target vector that is defined as

$$\underset{¯}{\kappa }=\frac{1}{2}\mathrm{Tr}\left(J\Psi \right),$$ (2)

where Tr(X) denotes a trace of the matrix X, and Ψ is an arbitrary complete basis set. All bases of the Ψ are used to create the target vector κ in Eq. (2). The symbol κ is used here instead of k that is commonly used in the literature of polarimetric radar imaging to avoid confusion with a wavenumber. A Pauli basis set and a lexicographic ordering basis set are often used as the Ψ [27]. In this paper, we use the lexicographic ordering basis set to simplify the calculation and the representation. The lexicographic ordering basis set is defined as

$$\left\{{\Psi }_{\text{L}}\right\}=\left\{\begin{array}{cccc}2\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]& 2\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]& 2\left[\begin{array}{cc}0& 0\\ 1& 0\end{array}\right]& 2\left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right]\end{array}\right\}.$$ (3)

Using Eqs. (1)-(3), the target vector is given as

$$\underset{¯}{{\kappa }_{\text{L}}}={\left[\begin{array}{cccc}{J}_{\text{1H}}& J_{\text{2H}}& J_{\text{1V}}& J_{\text{2V}}\end{array}\right]}^{\text{T}},$$ (4)

where the superscripted T denotes a transpose operation to the vector.

Assuming that κ can be modeled as multivariate complex Gaussian distribution, the probability density function (pdf) of κ is described as [27,33–36]

$$p(\underset{¯}{\kappa })=\frac{1}{{\pi }^m\det (C)}\exp \left(-{\underset{¯}{\kappa }}^{\text{†}}{C}^{-1}\underset{¯}{\kappa }\right),$$ (5)

where det(X) denotes a determinant of X, m is the dimension of κ. In the case of Eq. (4), m = 4. The superscripted dagger denotes complex transpose. C is a positive semidefinite covariance matrix that is defined as C = E{κκ^†}, where E{X} denotes the expectation of X. C can be estimated by

$$Z=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\underset{¯}{\kappa }}_i{\underset{¯}{\kappa }}_i^{\text{†}}},$$ (6)

which is known as the maximum likelihood estimator of C [34], and where n is a sampled number, κ_i denotes the i-th target vector in the n averaged samples. It is also known that Z has a complex Wishart distribution as [27,33–36]

$$p(Z)=\frac{n^{mn}{[\det (Z)]}^{n-m}}{{[\det (C)]}^n{\tilde{\Gamma }}_m(n)}\exp \left[-n\mathrm{Tr}\left(C^{-1}Z\right)\right],$$ (7)

$${\tilde{\Gamma }}_m(n)={\pi }^{m(m-1)/2}{\displaystyle \prod _{i=1}^m\Gamma (n-i+1)},$$ (8)

where Γ(X) is a gamma function.

In the case of {Ψ_L}, we use a new symbol T instead of Z for clarity, and define T as [27]

$$T\equiv \overline{\underset{¯}{{\kappa }_{\text{L}}}\underset{¯}{{\kappa }_{\text{L}}^{\text{†}}}}=\left[\begin{array}{cccc}\overline{{\left|J_{\text{1H}}\right|}^2}& \overline{J_{\text{1H}}{J}_{\text{2H}}^{*}}& \overline{J_{\text{1H}}{J}_{\text{1V}}^{*}}& \overline{J_{\text{1H}}{J}_{\text{2V}}^{*}}\\ \overline{J_{\text{2H}}{J}_{\text{1H}}^{*}}& \overline{{\left|J_{\text{2H}}\right|}^2}& \overline{J_{\text{2H}}{J}_{\text{1V}}^{*}}& \overline{J_{\text{2H}}{J}_{\text{2V}}^{*}}\\ \overline{J_{\text{1V}}{J}_{\text{1H}}^{*}}& \overline{J_{\text{1V}}{J}_{\text{2H}}^{*}}& \overline{{\left|J_{\text{1V}}\right|}^2}& \overline{J_{\text{1V}}{J}_{\text{2V}}^{*}}\\ \overline{J_{\text{2V}}{J}_{\text{1H}}^{*}}& \overline{J_{\text{2V}}{J}_{\text{2H}}^{*}}& \overline{J_{\text{2V}}{J}_{\text{1V}}^{*}}& \overline{{\left|J_{\text{2V}}\right|}^2}\end{array}\right],$$ (9)

where the overline denotes ensemble average, assuming that the sample is wide-sense stationary and ergodic in the region of interest. By definition, T is a positive semidefinite Hermitian matrix as well as C and Z.

2.2 Cloude-Pottier decomposition

In Cloude-Pottier decomposition [26–28], T is rearranged by matrix diagonalization as

$$\begin{array}{l}T=UA{U}^{\text{†}},\\ A=\mathrm{diag}[{\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4],{\lambda }_1\ge {\lambda }_2\ge {\lambda }_3\ge {\lambda }_4\ge 0,\\ U=[\begin{array}{cccc}\underset{¯}{e_1}& \underset{¯}{e_2}& \underset{¯}{e_3}& \underset{¯}{e_4}\end{array}],\end{array}$$ (10)

where A is a diagonal matrix with elements of four eigenvalues, and U is a unitary matrix that consists of four 1 × 4 eigenvectors. The inequalities of the eigenvalues is given because T is a positive semidefinite Hermitian matrix. The eigenvalues in Eq. (10) are normalized as

$${\lambda }_i^{\prime }=\frac{{\lambda }_i}{{\displaystyle \sum _j^4{\lambda }_j}},i=1,2,3,4,$$ (11)

so that 0 ≤ λ_iʹ ≤ 1. The eigenvalue λ_iʹ can be regarded as a probability that the corresponding eigenvector e_i occurs in a sense of multinomial process [37]. In the case of {Ψ_L}, the eigenvector e_i is rearranged to a Jones matrix L_i as

$$\begin{array}{l}\underset{¯}{e_i}:={\left[\begin{array}{cccc}{a}_i& b_i& c_i& d_i\end{array}\right]}^{\text{T}},\\ L_i=\left[\begin{array}{cc}{a}_i& b_i\\ c_i& d_i\end{array}\right].\end{array}$$ (12)

As described above, this incoherent approach to derive L_i by Cloude-Pottier decomposition is applicable for the measured Jones matrix in Eq. (1). However, it does not show the local polarization property of the sample, because all influence before and after the backscattering at the sample is accumulated in Eq. (1) along the depth. The cumulative attribute can be eliminated by calculating a local Jones matrix [10,38,39]. Instead of the cumulative Jones matrix in Eq. (1), we use Eq. (19) in [40] as the local Jones matrix, where we also processed the data by k-dependence correction. Since a product of two multivariate Gaussian distributions is also a multivariate Gaussian distribution [41], the statistical description in the above also holds for the local Jones matrix. In the case of the local Jones matrix, it was weighed as

$$\frac{\sqrt{{\Vert {\stackrel{⌢}{\mathbf{E}}}_{sample}^{\prime }(z-\frac{\delta z}{2})\Vert }_2{\Vert {\stackrel{⌢}{\mathbf{E}}}_{sample}^{\prime }(z+\frac{\delta z}{2})\Vert }_2}}{{\Vert {\stackrel{⌢}{\mathbf{E}}}_{sample}^{\prime -1}(z-\frac{\delta z}{2}){\stackrel{⌢}{\mathbf{E}}}_{sample}^{\prime }(z+\frac{\delta z}{2})\Vert }_2}{\stackrel{⌢}{\mathbf{E}}}_{sample}^{\prime -1}(z-\frac{\delta z}{2}){\stackrel{⌢}{\mathbf{E}}}_{sample}^{\prime }(z+\frac{\delta z}{2}),$$ (13)

where the same notations in [40] are used in Eq. (13); ${\stackrel{⌢}{\mathbf{E}}}_{sample}^{\prime }$ is a measured Jones matrix of the sample with k-dependence correction, and two Jones matrices that are axially separated for δz centered at a depth z are used. ‖X‖₂ denotes an operator norm. The Cloude-Pottier decomposition is then used to estimate the local Jones matrix. A local phase retardation R_i of L_i is derived as

$$R_i=\arg ({\xi }_1^{(i)}{\xi }_2^{(i)*}),$$ (14)

where ${\xi }_1^{(i)}$ and ${\xi }_2^{(i)}$ are the eigenvalues of L_i, and arg(x) denotes the argument of the complex value x. Assuming that the sample has a dominant scattering mechanism, L₁ and R₁ that are paired up with the largest eigenvalue λ₁ can be regarded as the Jones matrix and the local phase retardation of the dominant scattering mechanism, respectively [26]. In addition, when the sample is modeled as multinomial process [37], an expected value of the phase retardation can be defined as

$$\mathrm{E}(R)={\displaystyle \sum _i{\lambda }_i^{\prime }{R}_i}.$$ (15)

In addition, optic axis of L_i is derived from an eigenvector that is paired to ${\xi }_1^{(i)}$. The eigenvector is converted to Stokes vector, and the angle relative to a reference can be calculated.

To show a degree of randomness of the Jones matrix in a region of interest, an entropy, which was originally developed for quantum mechanics [42] and has been applied to statistical optics [23,43,44], is derived in the von Neumann sense as [26,37,45]

$$H={\displaystyle \sum _i-{\lambda }_i^{\prime }{\log }_4{\lambda }_i^{\prime }},$$ (16)

where the logarithmic base is set to be m = 4 so that 0 ≤ H ≤ 1. When H = 0, the sample has completely homogeneous Jones matrix. When H = 1, the sample has a completely random Jones matrix. In practice, the measured entropy is between them.

2.3 Asymptotic quasi maximum likelihood estimator (AQ-MLE) of the eigenvalues

It is known that the entropy is underestimated if the number of samples for ensemble average of the covariance matrix is low [33,46,47]. To mitigate the underestimation of the entropy, we use AQ-MLE of the eigenvalues [33]. Since the probability density function of the eigenvalues is too complicated and is not an analytical expression, López-Martínez et al. introduced some approximations to derive the estimator in [33].

The eigenvalues of the ensemble averaged covariance matrix are estimated by the AQ-MLE as

$${\stackrel{⌢}{l}}_i={\lambda }_i-\frac{{\lambda }_i}{n}{\displaystyle \sum _{j=1,j\ne i}^m\frac{{\lambda }_j}{{\lambda }_i-{\lambda }_j}-O(n^{-1}),i=1,2,\dots ,m},$$ (17)

where ${\stackrel{⌢}{l}}_i$ is is the estimated i-th eigenvalue, λ_i is the i-th eigenvalue calculated by a finite number of samples in the ensemble average, n is the number of samples, and m = 4 because of the dimension of our covariance matrix. The term O(n⁻¹) indicates an approximation order, and is ignored in the practical calculation. The estimated eigenvalues are normalized and used to estimate the entropy as

$$\hat{H}={\displaystyle \sum _{i=1}^4-{\stackrel{⌢}{l}}_i^{\prime }}{\log }_4{\stackrel{⌢}{l}}_i^{\prime },{\stackrel{⌢}{l}}_i^{\prime }=\frac{{\stackrel{⌢}{l}}_i}{{\displaystyle \sum _{i=1}^4{\stackrel{⌢}{l}}_i}},$$ (18)

where Ĥ is the estimated entropy.

2.4 Correction of the bias in the entropy induced by noise for the non-localized cumulative Jones matrix

Since the entropy shows randomness of the measured Jones matrix, it includes both polarization property of the subject and influence of the noise. When the signal-to-noise ratio (SNR) is low, the bias to the entropy would be high, resulting in unreliable quantitative evaluation of the polarization property of the subject. Compared to polarimetric radar imaging, this influence may be more prominent in PS-OCT, where we are often interested in an axially deep position whose signal fades exponentially. We therefore develop a correction method to remove the bias of the entropy induced by the noise. As the first step, we develop the bias correction for the non-localized cumulative Jones matrix shown in Eq. (1).

Since the random noise and the polarization property of the subject are independent, the following additivity is satisfied;

$$H_{\text{measured}}=H_{\text{subject}}+H_{\text{noise}},$$ (19)

where H_measured, H_subject and H_noise are the entropies of the measured data, the subject and the noise, respectively. In this section, we focus on the estimation of H_noise to remove the bias in H_measured.

The 4 × 4 covariance matrix can be divided to two subspaces that are related to E₁ and E₂. The entropy satisfies the following inequality called subadditivity [48];

$$H_{noise}\left(\underset{¯}{E_1},\underset{¯}{E_2}\right)\le H_{noise}\left(\underset{¯}{E_1}\right)+H_{noise}\left(\underset{¯}{E_2}\right),$$ (20)

where H_noise(E₁) and H_noise (E₂) are the subspace entropies, and H_noise (E₁,E₂) is the explicit expression as a joint entropy of the noise in the covariance matrix. Assuming that the noises in the subspaces of E₁ and E₂ are independent, Eq. (20) holds equality as

$$H_{noise}\left(\underset{¯}{E_1},\underset{¯}{E_2}\right)=H_{noise}\left(\underset{¯}{E_1}\right)+H_{noise}\left(\underset{¯}{E_2}\right).$$ (21)

Equation (21) shows that the entropy of the noise in 4 × 4 covariance matrix can be derived from the summation of the entropies of the noises in the subspaces, namely, 2 × 2 covariance matrices. Nevertheless, it may be still difficult to utilize the pdfs of the covariance matrix and the eigenvalue [27,33,46] to derive H_noise. Hence, we suggest yet another approach in the following.

H_noise(E₁) and H_noise (E₂) can be derived from the eigenvalues as

$$H_{noise}\left(\underset{¯}{E_i}\right)={\displaystyle \sum _{j=1}^2{\zeta }_j^{(i)}\log \left({\zeta }_j^{(i)}\right)},$$ (22)

where ${\zeta }_j^{(i)}$ is the j-th eigenvalue of the subspace composed of E_i. The eigenvalue has the following relationship [23] with a degree of polarization (DOP) or a degree of polarization uniformity (DOPU) in the case of OCT [21];

$${\zeta }_j^{(i)}=\frac{1\pm P^{(i)}}{2},$$ (23)

where P⁽ⁱ⁾ is the DOPU of the subspace composed of E_i. Consequently, it turns out that H_noise(E₁,E₂) can be derived if a relationship between the DOPU and the noise is derived.

Assuming that the measured Jones matrix has an independent complex additive white Gaussian noise in each matrix element, the Jones matrix can be described as [49]

$$J_{\text{measured}}=\left[\begin{array}{cc}\underset{¯}{E_1}+\underset{¯}{n_1}& \underset{¯}{E_2}+\underset{¯}{n_2}\end{array}\right]=\left[\begin{array}{cc}{E}_{\text{1H}}+n_{\text{1H}}& E_{\text{2H}}+n_{\text{2H}}\\ E_{\text{1V}}+n_{\text{1V}}& E_{\text{2V}}+n_{\text{2V}}\end{array}\right]=\left[\begin{array}{cc}{g}_{\text{1H}}& g_{\text{2H}}\\ g_{\text{1V}}& g_{\text{2V}}\end{array}\right].$$ (24)

Note that Eq. (24) is a cumulative Jones matrix along the depth that is characteristic to PS-OCT as described above. Stokes parameters of [g_1H g_1V]^T are defined as

$$\left[\begin{array}{c}{s}_0^{(1)}\\ s_1^{(1)}\\ s_2^{(1)}\\ s_3^{(1)}\end{array}\right]=\left[\begin{array}{c}{\left|g_{\text{1H}}\right|}^2+{\left|g_{\text{1V}}\right|}^2\\ {\left|g_{\text{1H}}\right|}^2-{\left|g_{\text{1V}}\right|}^2\\ 2 \mathrm{Re}\left[g_{\text{1H}}{g}_{\text{1V}}^{\text{*}}\right]\\ 2 \mathrm{Im}\left[g_{\text{1H}}{g}_{\text{1V}}^{\text{*}}\right]\end{array}\right],$$ (25)

and Stokes parameters of [g_2H g_2V]^T are also defined similarly. In [49], biases in s₀⁽¹⁾ and s₁⁽¹⁾ by the noise variance were canceled, and ensemble average of the Stokes parameters were used to calculate the DOPU. In contrast, since we would like to derive only the bias component in DOPU, we take a different approach in the following.

The Stokes parameters without the noise components are derived as

$$\left[\begin{array}{c}{s^{\prime }}_0^{(1)}\\ {s^{\prime }}_1^{(1)}\\ {s^{\prime }}_2^{(1)}\\ {s^{\prime }}_3^{(1)}\end{array}\right]:=\left[\begin{array}{c}{\left|E_{\text{1H}}\right|}^2+{\left|E_{\text{1V}}\right|}^2\\ {\left|E_{\text{1H}}\right|}^2-{\left|E_{\text{1V}}\right|}^2\\ 2 \mathrm{Re}\left[E_{\text{1H}}{E}_{\text{1V}}^{\text{*}}\right]\\ 2 \mathrm{Im}\left[E_{\text{1H}}{E}_{\text{1V}}^{\text{*}}\right]\end{array}\right]=\left[\begin{array}{c}{\left|E_{\text{1H}}\right|}^2+{\left|E_{\text{1V}}\right|}^2\\ {\left|E_{\text{1H}}\right|}^2-{\left|E_{\text{1V}}\right|}^2\\ 2\left|E_{\text{1H}}\right|\left|E_{\text{1V}}\right|\cos \delta \\ 2\left|E_{\text{1H}}\right|\left|E_{\text{1V}}\right|\sin \delta \end{array}\right],$$ (26)

where δ = arg[E_1HE_1V*]. δ is influenced by polarization property of the subject but not by the signal intensity. In addition, it is eventually cancelled in P⁽ⁱ⁾ as seen later. We then define other Stokes parameters using ensemble averaged signal intensities as

$$\left[\begin{array}{c}{s}_0^{″(1)}\\ s_1^{″(1)}\\ s_2^{″(1)}\\ s_3^{″(1)}\end{array}\right]:=\left[\begin{array}{c}\overline{{\left|E_{\text{1H}}\right|}^2}+\overline{{\left|E_{\text{1V}}\right|}^2}\\ \overline{{\left|E_{\text{1H}}\right|}^2}-\overline{{\left|E_{\text{1V}}\right|}^2}\\ 2\overline{\left|E_{\text{1H}}\right|}\overline{\left|E_{\text{1V}}\right|}\cos \delta \\ 2\overline{\left|E_{\text{1H}}\right|}\overline{\left|E_{\text{1V}}\right|}\sin \delta \end{array}\right]=\left[\begin{array}{c}\overline{{\left|g_{\text{1H}}\right|}^2}+\overline{{\left|g_{\text{1V}}\right|}^2}-\left(\overline{{\left|n_{\text{1H}}\right|}^2}+\overline{{\left|n_{\text{1V}}\right|}^2}\right)\\ \overline{{\left|g_{\text{1H}}\right|}^2}-\overline{{\left|g_{\text{1V}}\right|}^2}-\left(\overline{{\left|n_{\text{1H}}\right|}^2}-\overline{{\left|n_{\text{1V}}\right|}^2}\right)\\ 2\sqrt{\overline{{\left|g_{\text{1H}}\right|}^2}-\overline{{\left|n_{\text{1H}}\right|}^2}}\sqrt{\overline{{\left|g_{\text{1V}}\right|}^2}-\overline{{\left|n_{\text{1V}}\right|}^2}}\cos \delta \\ 2\sqrt{\overline{{\left|g_{\text{1H}}\right|}^2}-\overline{{\left|n_{\text{1H}}\right|}^2}}\sqrt{\overline{{\left|g_{\text{1V}}\right|}^2}-\overline{{\left|n_{\text{1V}}\right|}^2}}\sin \delta \end{array}\right],$$ (27)

where we implicitly assume that the signal amplitude is much higher than the noise amplitude for each element of the Jones matrix so that distributions of the measured amplitudes are Gaussian [50] and that the polarization property of the subject has a symmetric pdf of the signal intensity so that it does not bias the ensemble average in Eq. (27). DOPU that shows the bias by the relative relationship between the signal intensity and noise power is derived as

$$\begin{array}{ll}{P}^{(1)}& =\frac{\sqrt{{\left\{s_1^{″(1)}\right\}}^2+{\left\{s_2^{″(1)}\right\}}^2+{\left\{s_3^{″(1)}\right\}}^2}}{s_0^{″(1)}}\\ & =\frac{\sqrt{{\left[\overline{{\left|g_{\text{1H}}\right|}^2}-\overline{{\left|g_{\text{1V}}\right|}^2}-\left(\overline{{\left|n_{\text{1H}}\right|}^2}-\overline{{\left|n_{\text{1V}}\right|}^2}\right)\right]}^2+4\left(\overline{{\left|g_{\text{1H}}\right|}^2}-\overline{{\left|n_{\text{1H}}\right|}^2}\right)\left(\overline{{\left|g_{\text{1V}}\right|}^2}-\overline{{\left|n_{\text{1V}}\right|}^2}\right)}}{\overline{{\left|g_{\text{1H}}\right|}^2}+\overline{{\left|g_{\text{1V}}\right|}^2}-\left(\overline{{\left|n_{\text{1H}}\right|}^2}+\overline{{\left|n_{\text{1V}}\right|}^2}\right)}.\end{array}$$ (28)

P⁽²⁾ is also derived similarly. Using Eqs. (21)-(23), (27) and (28), H_noise is calculated from the measured signal intensities and noise powers. Note that Eq. (28) used ensemble averaged signal intensities but not ensemble averaged Stokes parameters, which enabled us to derive the DOPU of the bias rather than a bias-corrected DOPU of the sample. The additivity of the entropy shown in Eqs. (19) and (21) ensures our approach to separate the individual contributions.

2.5 Correction of the bias in the entropy induced by noise for local Jones matrix

Although the equations in Section 2.4 are effective for a certain axial depth, we have not considered cumulative attributes of the Jones matrix along the axial depth in PS-OCT. If a region of interest is set spatially including the axial direction, the resultant DOPU and entropy may have an artifact by high birefringence that changes the Jones matrices rapidly in the axial direction. Hence, we derive H_noise of the local Jones matrix in this section.

To calculate the local Jones matrix, two Jones matrices that are axially separated for δz centered at a depth z are used as described in [40] and Eq. (13). Using the same notations in [40] and Eq. (13), we write all matrix elements down as

$${\stackrel{⌢}{\mathbf{E}}}_{sample}^{\prime }(z+\frac{\delta z}{2})=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right],{\stackrel{⌢}{\mathbf{E}}}_{sample}^{\prime }(z-\frac{\delta z}{2})=\left[\begin{array}{cc}e& f\\ g& h\end{array}\right].$$ (29)

The local Jones matrix is derived as

$${\stackrel{⌢}{\mathbf{E}}}_{sample}^{\prime -1}(z-\frac{\delta z}{2}){\stackrel{⌢}{\mathbf{E}}}_{sample}^{\prime }(z+\frac{\delta z}{2})={\left[\det \left({\stackrel{⌢}{\mathbf{E}}}_{sample}^{\prime }(z-\frac{\delta z}{2})\right)\right]}^{-1}\left[\begin{array}{cc}ha-fc& hb-fd\\ -ga+ec& -gb+ed\end{array}\right].$$ (30)

Since the determinant in Eq. (30) has the effect of distorting the noise floor of the matrix, it complicates the estimation of the entropy. We therefore use the following equation instead;

$$\begin{array}{r}\det \left({\stackrel{⌢}{\mathbf{E}}}_{sample}^{\prime -1}(z-\frac{\delta z}{2})\right){\stackrel{⌢}{\mathbf{E}}}_{sample}^{\prime -1}(z-\frac{\delta z}{2}){\stackrel{⌢}{\mathbf{E}}}_{sample}^{\prime }(z+\frac{\delta z}{2})=\left[\begin{array}{cc}ha-fc& hb-fd\\ -ga+ec& -gb+ed\end{array}\right]\\ \equiv \left[\begin{array}{cc}\underset{¯}{{\epsilon }_1}& \underset{¯}{{\epsilon }_2}\end{array}\right]=\left[\begin{array}{cc}{\epsilon }_{\text{1H}}& {\epsilon }_{\text{2H}}\\ {\epsilon }_{\text{1V}}& {\epsilon }_{\text{2V}}\end{array}\right].\end{array}$$ (31)

To calculate H_noise of the local Jones matrix, we use Eq. (31) instead of Eq. (24) and follow the same procedure to calculate P⁽¹⁾ and P⁽²⁾. Unlike Eq. (24), however, Eq. (31) does not satisfy the additivity in Eq. (21), because the first and second column vectors in Eq. (31) are dependent. In this case, Eq. (21) can be modified as

$$H_{noise}\left(\underset{¯}{{\epsilon }_1},\underset{¯}{{\epsilon }_2}\right)=H_{noise}\left(\underset{¯}{{\epsilon }_1}\right)+H_{noise}\left(\underset{¯}{{\epsilon }_2}\right)-H_{noise}\left(\underset{¯}{{\epsilon }_1}:\underset{¯}{{\epsilon }_2}\right),$$ (32)

where the third term in the right side is mutual information of ε₁ and ε₂ [48]. It can be rearranged using a conditional entropy as

$$\begin{array}{cc}{H}_{noise}\left(\underset{¯}{{\epsilon }_1}:\underset{¯}{{\epsilon }_2}\right)& =H_{noise}\left(\underset{¯}{{\epsilon }_1}\right)-H_{noise}\left(\underset{¯}{{\epsilon }_1}|\underset{¯}{{\epsilon }_2}\right)\\ & =H_{noise}\left(\underset{¯}{{\epsilon }_2}\right)-H_{noise}\left(\underset{¯}{{\epsilon }_2}|\underset{¯}{{\epsilon }_1}\right),\end{array}$$ (33)

where H(Y|X) denotes the entropy of Y conditioned on X. Using Eq. (32) and Eq. (33), the joint entropy is rearranged as

$$\begin{array}{cc}{H}_{noise}\left(\underset{¯}{{\epsilon }_1},\underset{¯}{{\epsilon }_2}\right)& =H_{noise}\left(\underset{¯}{{\epsilon }_2}\right)+H_{noise}\left(\underset{¯}{{\epsilon }_1}|\underset{¯}{{\epsilon }_2}\right)\\ & =H_{noise}\left(\underset{¯}{{\epsilon }_1}\right)+H_{noise}\left(\underset{¯}{{\epsilon }_2}|\underset{¯}{{\epsilon }_1}\right).\end{array}$$ (34)

To calculate Eq. (34), the variance of each element in Eq. (31) is required. Assuming strong constant phasor plus a weak random phasor sum [50] for each matrix element, the variances are derived as

$$\begin{array}{r}\mathrm{Var}({\epsilon }_{\text{1H}})=\mathrm{Var}(ha-fc)=\mathrm{Var}(h)\mathrm{Var}(a)+\mathrm{Var}(h){\left\{E(a)\right\}}^2+{\left\{E(h)\right\}}^2\mathrm{Var}(a)\\ +\mathrm{Var}(f)\mathrm{Var}(c)+\mathrm{Var}(f){\left\{E(c)\right\}}^2+{\left\{E(f)\right\}}^2 \mathrm{Var}(c),\end{array}$$ (35)

$$\begin{array}{r}\mathrm{Var}({\epsilon }_{\text{1V}})=\mathrm{Var}(-ga+ec)=\mathrm{Var}(g)\mathrm{Var}(a)+\mathrm{Var}(g){\left\{E(a)\right\}}^2+{\left\{E(g)\right\}}^2 \mathrm{Var}(a)\\ +\mathrm{Var}(e)\mathrm{Var}(c)+\mathrm{Var}(e){\left\{E(c)\right\}}^2+{\left\{E(e)\right\}}^2 \mathrm{Var}(c),\end{array}$$ (36)

$$\begin{array}{r}\mathrm{Var}({\epsilon }_{\text{2H}})=\mathrm{Var}(hb-fd)=\mathrm{Var}(h)\mathrm{Var}(b)+\mathrm{Var}(h){\left\{E(b)\right\}}^2+{\left\{E(h)\right\}}^2 \mathrm{Var}(b)\\ +\mathrm{Var}(f)\mathrm{Var}(d)+\mathrm{Var}(f){\left\{E(d)\right\}}^2+{\left\{E(f)\right\}}^2 \mathrm{Var}(d),\end{array}$$ (37)

$$\begin{array}{r}\mathrm{Var}({\epsilon }_{\text{2V}})=\mathrm{Var}(-gb+ed)=\mathrm{Var}(g)\mathrm{Var}(b)+\mathrm{Var}(g){\left\{E(b)\right\}}^2+{\left\{E(g)\right\}}^2 \mathrm{Var}(b)\\ +\mathrm{Var}(e)\mathrm{Var}(d)+\mathrm{Var}(e){\left\{E(d)\right\}}^2+{\left\{E(e)\right\}}^2 \mathrm{Var}(d),\end{array}$$ (38)

where Var(X) and E(X) denote variance and an expected value of X, respectively. Conditional variances that are necessary to calculate Eq. (34) are derived as

$$\mathrm{Var}({\epsilon }_{\text{1H}}|\underset{¯}{{\epsilon }_2})={\left\{E(h)\right\}}^2\mathrm{Var}(a)+{\left\{E(f)\right\}}^2\mathrm{Var}(c),$$ (39)

$$\mathrm{Var}({\epsilon }_{\text{1V}}|\underset{¯}{{\epsilon }_2})={\left\{E(g)\right\}}^2\mathrm{Var}(a)+{\left\{E(e)\right\}}^2\mathrm{Var}(c),$$ (40)

$$\mathrm{Var}({\epsilon }_{\text{2H}}|\underset{¯}{{\epsilon }_1})={\left\{E(h)\right\}}^2\mathrm{Var}(b)+{\left\{E(f)\right\}}^2\mathrm{Var}(d),$$ (41)

$$\mathrm{Var}({\epsilon }_{\text{2V}}|\underset{¯}{{\epsilon }_1})={\left\{E(g)\right\}}^2\mathrm{Var}(b)+{\left\{E(e)\right\}}^2\mathrm{Var}(d).$$ (42)

Using the ensemble average of the absolute square of individual elements in Eq. (31) and the variances in Eqs. (35)-(42), we derive

$$P^{(\underset{¯}{{\epsilon }_1})}=\frac{\sqrt{{\left[\overline{{\left|{\epsilon }_{\text{1H}}\right|}^2}-\overline{{\left|{\epsilon }_{\text{1V}}\right|}^2}-\left(\mathrm{Var}({\epsilon }_{\text{1H}})-\mathrm{Var}({\epsilon }_{\text{1V}})\right)\right]}^2+4\left(\overline{{\left|{\epsilon }_{\text{1H}}\right|}^2}-\mathrm{Var}({\epsilon }_{\text{1H}})\right)\left(\overline{{\left|{\epsilon }_{\text{1V}}\right|}^2}-\mathrm{Var}({\epsilon }_{\text{1V}})\right)}}{\overline{{\left|{\epsilon }_{\text{1H}}\right|}^2}+\overline{{\left|{\epsilon }_{\text{1V}}\right|}^2}-\left(\mathrm{Var}({\epsilon }_{\text{1H}})+\mathrm{Var}({\epsilon }_{\text{1V}})\right)},$$ (43)

$$P^{(\underset{¯}{{\epsilon }_2})}=\frac{\sqrt{{\left[\overline{{\left|{\epsilon }_{\text{2H}}\right|}^2}-\overline{{\left|{\epsilon }_{\text{2V}}\right|}^2}-\left(\mathrm{Var}({\epsilon }_{\text{2H}})-\mathrm{Var}({\epsilon }_{\text{2V}})\right)\right]}^2+4\left(\overline{{\left|{\epsilon }_{\text{2H}}\right|}^2}-\mathrm{Var}({\epsilon }_{\text{2H}})\right)\left(\overline{{\left|{\epsilon }_{\text{2V}}\right|}^2}-\mathrm{Var}({\epsilon }_{\text{2V}})\right)}}{\overline{{\left|{\epsilon }_{\text{2H}}\right|}^2}+\overline{{\left|{\epsilon }_{\text{2V}}\right|}^2}-\left(\mathrm{Var}({\epsilon }_{\text{2H}})+\mathrm{Var}({\epsilon }_{\text{2V}})\right)},$$ (44)

$$P^{(\underset{¯}{{\epsilon }_1}|\underset{¯}{{\epsilon }_2})}=\frac{\sqrt{{\left[\overline{{\left|{\epsilon }_{\text{1H}}\right|}^2}-\overline{{\left|{\epsilon }_{\text{1V}}\right|}^2}-\left(\mathrm{Var}({\epsilon }_{\text{1H}}|\underset{¯}{{\epsilon }_2})-\mathrm{Var}({\epsilon }_{\text{1V}}|\underset{¯}{{\epsilon }_2})\right)\right]}^2+4\left(\overline{{\left|{\epsilon }_{\text{1H}}\right|}^2}-\mathrm{Var}({\epsilon }_{\text{1H}}|\underset{¯}{{\epsilon }_2})\right)\left(\overline{{\left|{\epsilon }_{\text{1V}}\right|}^2}-\mathrm{Var}({\epsilon }_{\text{1V}}|\underset{¯}{{\epsilon }_2})\right)}}{\overline{{\left|{\epsilon }_{\text{1H}}\right|}^2}+\overline{{\left|{\epsilon }_{\text{1V}}\right|}^2}-\left(\mathrm{Var}({\epsilon }_{\text{1H}}|\underset{¯}{{\epsilon }_2})+\mathrm{Var}({\epsilon }_{\text{1V}}|\underset{¯}{{\epsilon }_2})\right)},$$ (45)

$$P^{(\underset{¯}{{\epsilon }_2}|\underset{¯}{{\epsilon }_1})}=\frac{\sqrt{{\left[\overline{{\left|{\epsilon }_{\text{2H}}\right|}^2}-\overline{{\left|{\epsilon }_{\text{2V}}\right|}^2}-\left(\mathrm{Var}({\epsilon }_{\text{2H}}|\underset{¯}{{\epsilon }_1})-\mathrm{Var}({\epsilon }_{\text{2V}}|\underset{¯}{{\epsilon }_1})\right)\right]}^2+4\left(\overline{{\left|{\epsilon }_{\text{2H}}\right|}^2}-\mathrm{Var}({\epsilon }_{\text{2H}}|\underset{¯}{{\epsilon }_1})\right)\left(\overline{{\left|{\epsilon }_{\text{2V}}\right|}^2}-\mathrm{Var}({\epsilon }_{\text{2V}}|\underset{¯}{{\epsilon }_1})\right)}}{\overline{{\left|{\epsilon }_{\text{2H}}\right|}^2}+\overline{{\left|{\epsilon }_{\text{2V}}\right|}^2}-\left(\mathrm{Var}({\epsilon }_{\text{2H}}|\underset{¯}{{\epsilon }_1})+\mathrm{Var}({\epsilon }_{\text{2V}}|\underset{¯}{{\epsilon }_1})\right)}.$$ (46)

Equation (34) is calculated using Eq. (22), (23) and Eq. (43)-(46).

In the experiments, depth-dependent noise variance of each matrix element is calculated applying third-order polynomial fit to the averaged noise power of A-scans without placing a scattering sample. The absolute-squared expected values of the matrix elements in Eq. (24) or (29) that are used in Eqs. (35)-(42) are calculated as $\overline{{\left|g_{\text{1H}}\right|}^2}-\overline{{\left|n_{\text{1H}}\right|}^2}$ and similarly for all other elements.

3. Experimental results

To validate the theory experimentally, we show measurement results of three static samples; a glass plate (WG11010, Thorlabs, Newton, New Jersey, USA), quarter waveplates (QWP) at 633 nm (WPQ10ME-633, Thorlabs) and at 1310 nm (WPQ10ME-1310, Thorlabs). The QWP at 633 nm has a single-pass phase retardation of 141 nm at 1310 nm wavelength according to the manufacturer, which is converted to a double-pass phase retardation of 1.35 rad. Although it is not exactly a double-pass phase retardation of one eighth waveplate (EWP), we call it EWP for expedience.

The PS-OCT system used for the experiment, which had a center wavelength of 1297 nm, was described in [40]. In the case of the measurements of the static samples, the axial separation δz that corresponds to a thickness of the sample is too long to ignore nonlinear frequency response of the signals between the OCT channels (cf [51].). To create correction parameters, we measured 2% intralipid as an axially-distributed non-birefringent scattering sample. Equations (9) and (10) of [40] were calculated for the axial depth domain, namely, q_HV(z) and q₁₂(z), but not for k-dependence in this case. They were averaged for 800 × 128 A-scans, and the depth-dependent signal amplitudes and phases were smoothed by 11th-order polynomial fit. Inverse matrices of the resultant Q_HV(z) and Q₁₂(z) were multiplied to the Jones matrix as shown in Eq. (15) of [40] to the axial depth domain.

For the analysis of the static samples, we extracted each single pixel of the front and back surfaces, respectively, to apply the ensemble averaging. We note that we did not use axially neighboring pixels around the front and back surfaces for the ensemble averaging in the case of the static samples.

3.1 Estimation of the phase retardation

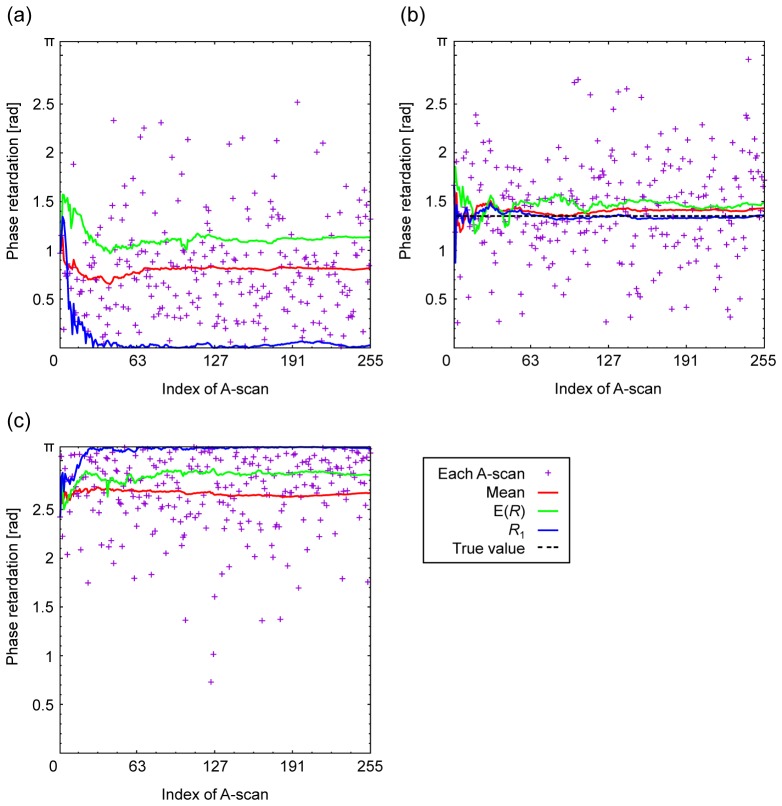
To evaluate the estimation performance of Cloude-Pottier decomposition at high-entropy condition, the local Jones matrix between the front and back surfaces of the static samples were measured, and the phase retardation was estimated by mean, E(R) in Eq. (15) and R₁ in Eq. (14). The results of the glass plate, the EWP and the QWP are plotted in Fig. 1(a), 1(b) and 1(c), respectively. In Fig. 1, the plot of each A-scan shows the phase retardation calculated by each single A-scan. The plots of mean, E(R) and R₁ were calculated using all 0 to n-th A-scans for the estimation. The entropies of (a), (b) and (c) were 0.74, 0.62 and 0.66, respectively. The effective SNRs (ESNRs) [10,52] of (a), (b) and (c) were 3.50, 5.27 and 4.88 dB, respectively.

Fig. 1.

Plots of phase retardations of the glass plate (a), the EWP (b) and the QWP (c). The horizontal axes show the index of A-scan. For the plots of mean, E(R) and R₁, all A-scans from 0 to n-th indices are used for the estimation. Since it is clear that the true values of (a) and (c) are on the sides of the measurable range, true values are not shown for them.

The mean and E(R) were biased when the true value is close to the sides of the measurable range as shown in Fig. 1(a) and 1(c). The biases of the mean and E(R) were because of the asymmetric distribution and noise components in R_i (i ≥ 2), respectively. The biases of the mean and E(R) in Fig. 1(b) were smaller than (a) and (c), because the distribution was nearly symmetric. In contrast, R₁ converged on the true value in all of Fig. 1(a), 1(b) and 1(c) with less than ~32 A-scans. Hence, R₁ would be the most effective way of unbiased estimation even if the SNR is low.

3.2 Estimation of the optic axis

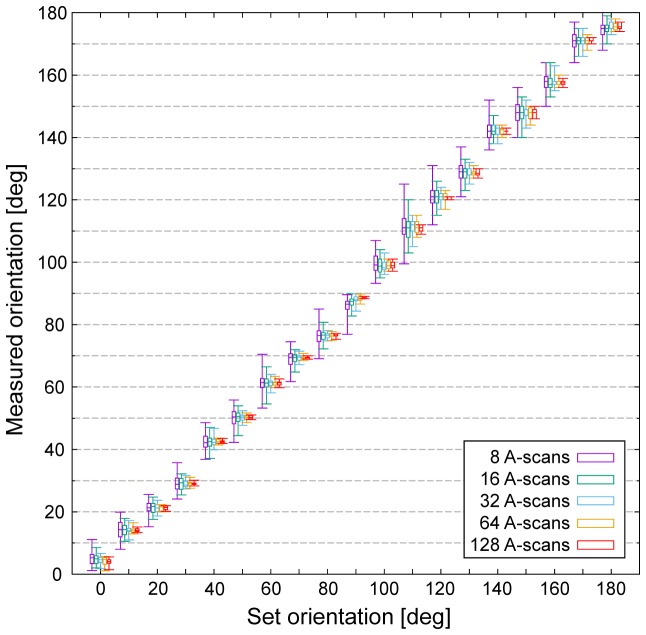
Since the optic axis is wrapped when the phase retardation is exactly π [38], the EWP was measured to evaluate the estimation of the optic axis. The orientation was set from 0 to 180 degrees with a 10-degree step, and the orientation was estimated by the eigenvector of L₁ in Cloude-Pottier decomposition. The eigenvector was converted to the Stokes parameters, and a relative orientation to 0 degree that used 800 A-scans for the ensemble average of T was calculated. A wrapping over 90-degree orientation was unwrapped manually. The estimated optic axis orientation is shown in Fig. 2. To see the influence of the number of samples, the ensemble average of T was calculated using 8, 16, 32, 64 or 128 A-scans. This calculation was repeated in 800 A-scans to see the distributions of the estimation results. The entropy and the ESNR were 0.25 and 12.42 dB in average, respectively.

Fig. 2.

Box plots of the optic axis estimated by Cloude-Pottier decomposition. The sample was the EWP. Different number of A-scans were used for the ensemble average of (T) as indicated by the figure legend, and the distributions of the estimated optic axes were shown. The plots of the different number of A-scans were displaced horizontally from the true set orientation only for the purpose of visualization. An interquartile range, a median and 100% fraction range of the distribution are indicated by the box, the bar in the box and the whiskers, respectively.

Figure 2 clearly shows that by increasing the number of A-scans for the ensemble average of T in Cloude-Pottier decomposition, it gives a better estimation of the orientation with narrower distribution close to the set orientation. Consequently, Fig. 1 and Fig. 2 showed that the Jones matrix could be estimated by L₁ in Cloude-Pottier decomposition without the bias.

3.3 Estimation of the entropy by AQ-MLE

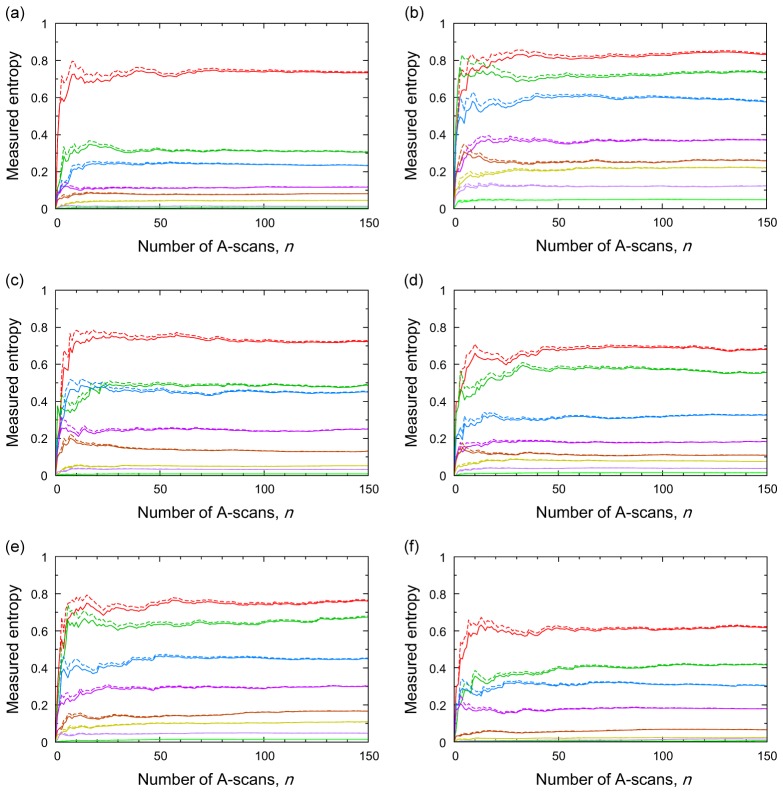
To evaluate the AQ-MLE shown in Eqs. (17) and (18), we measured the glass plate, the EWP and the QWP with settings of balanced and unbalanced SNRs. The settings are summarized in Table 1, where signal intensities relative to the maximum Jones-matrix element are shown. Note that the terminologies of the balanced- and unbalanced-SNR settings indicate relative relationships of the signal intensities between the Jones-matrix elements, but these are not related to balanced photoreceivers of the photodetection system. Since it is impossible to evaluate whole of SU(2) space experimentally, we only use these settings in Table 1 to confirm that the entropies H, Ĥ, and H_noise follow our theory experimentally in Sections 3.3, 3.4 and 3.5. In addition, the signals were attenuated arbitrarily to see the convergence of the entropy in various conditions. The results are shown in Fig. 3. In this evaluation of AQ-MLE, only the local Jones matrix were used to calculate the entropies.

Table 1. Relative signal intensities between the Jones-matrix elements used for the test target analysis.

Sample	Balanced-SNR setting			Unbalanced-SNR setting
	Front surface [dB]	Back surface [dB]		Front surface [dB]	Back surface [dB]
Glass plate	Setting (a)			Setting (b)
	$\left[\begin{array}{cc}-0.8& -0.5\\ -1.2& 0\end{array}\right]$	$\left[\begin{array}{cc}-0.2& -0.1\\ -0.9& 0\end{array}\right]$		$\left[\begin{array}{cc}-0.8& -21.6\\ -22.6& 0\end{array}\right]$	$\left[\begin{array}{cc}-0.3& -20.9\\ -21.7& 0\end{array}\right]$
EWP	Setting (c)			Setting (d)
	$\left[\begin{array}{cc}0& -2.7\\ -2.3& -2.4\end{array}\right]$	$\left[\begin{array}{cc}-1.7& -0.3\\ 0& -2.7\end{array}\right]$		$\left[\begin{array}{cc}-0.8& -3.9\\ -4.7& 0\end{array}\right]$	$\left[\begin{array}{cc}0& -24.9\\ -23.7& -0.8\end{array}\right]$
QWP	Setting (e)			Setting (f)
	$\left[\begin{array}{cc}-1.3& -0.3\\ 0& -1.7\end{array}\right]$	$\left[\begin{array}{cc}-1.2& -1.9\\ 0& -4.1\end{array}\right]$		$\left[\begin{array}{cc}0& -4.7\\ -4.3& -0.4\end{array}\right]$	$\left[\begin{array}{cc}-22.2& -0.4\\ 0& -21.7\end{array}\right]$

Fig. 3.

Measured entropy without (solid line) or with (dashed line) AQ-MLE. The horizontal axis indicates the number of A-scans n used for the ensemble average of (T). The raw OCT data were measured at different signal intensities, and the results were plotted with different colors. The samples and the measurement settings are shown in Table 1.

In Fig. 3, the entropy without AQ-MLE, H, was generally underestimated at small numbers of A-scans, n ≤ ~20. The signals with high H had high variance and required more n till they converged. The underestimation was mitigated in the entropy with AQ-MLE, Ĥ, at the small n, although the Ĥ still had remaining variance before the convergence. Both H and Ĥ converged to the same entropy at high n as expected in Eq. (17). As the signal attenuation was lower, H was lower and the difference between H and Ĥ was small even at small n. These observations were common in all of the samples and settings in Table 1, indicating that AQ-MLE was a robust and effective method to mitigate the underestimation of the entropy.

3.4 Estimation of H_noise at a single depth

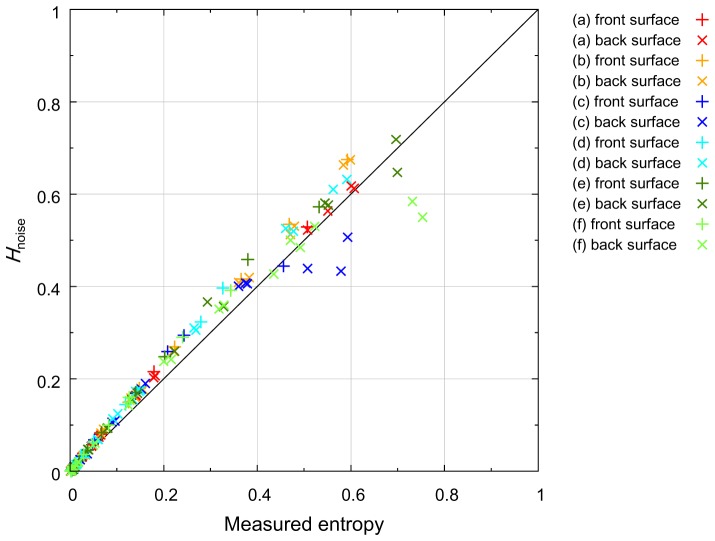
Since H_subject of a static sample is 0 temporally, H_measured of the static sample should equal H_noise in Eq. (19). To validate the theory in Section 2.4 under this simple condition, H_noise of the measured cumulative Jones matrix at a certain depth is calculated from the measured data with the same settings shown in Table 1. Using the equations in Section 2.4, H_noise is estimated and plotted with the entropy Ĥ in Fig. 4.

Fig. 4.

Estimation results of H_noise at a single depth. The settings (a)-(f) in the figure legend correspond to Table 1. The black solid line shows ideal estimation where the measured entropy equals H_noise.

In Fig. 4, H_noise mostly corresponded to Ĥ with no dependence on the samples and the signal settings. Looking at the plots closely, however, H_noise slightly overestimated Ĥ. Although the reason of the overestimation is unclear, we speculate that a portion of the noise in the OCT channels might be correlated because of the depth-encoded configuration. When the entropy Ĥ is higher than 0.4, some plots showed the underestimation of Ĥ by H_noise. It would be because the assumption of strong constant phasor plus a weak random phasor sum [50] was not valid.

3.5 Estimation of H_noise for the local Jones matrix

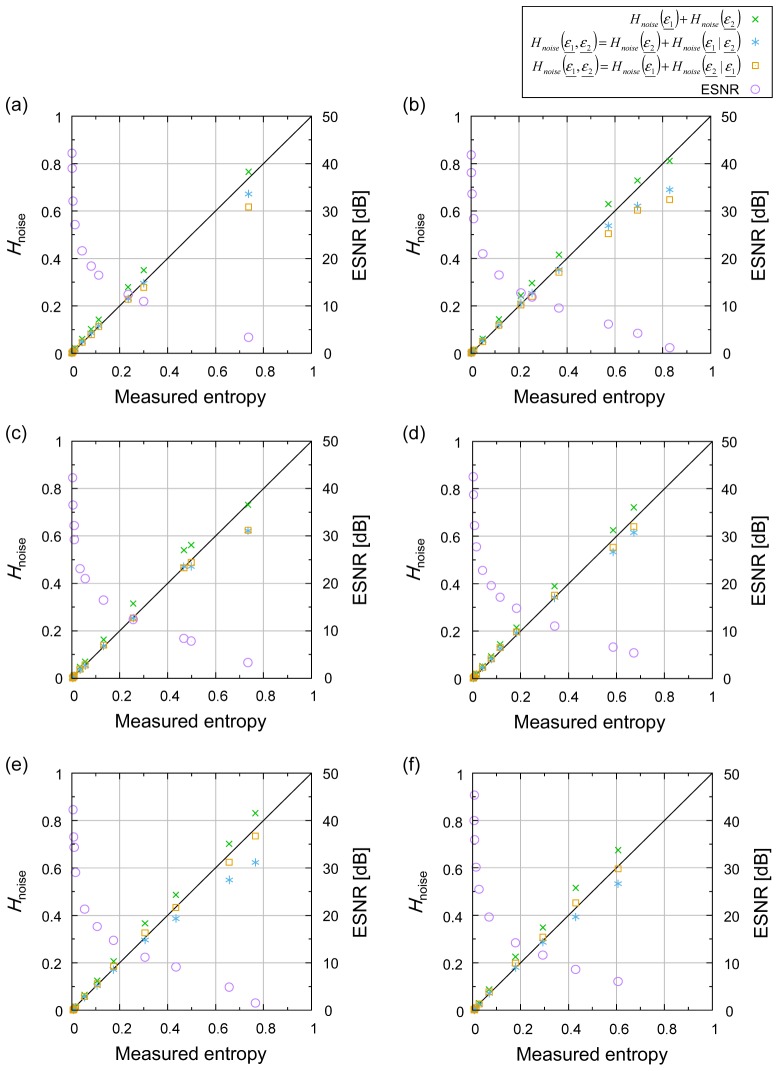
To validate the theory for the local Jones matrix in Section 2.5 under the simple condition of H_subject = 0 as well as Section 3.4, H_noise of the local Jones matrix is also calculated from the measured data with the same settings shown in Table 1. Using the equations in Section 2.5, H_noise is estimated and plotted with the entropy Ĥ in Fig. 5. For comparison, $H_{\text{noise}}(\underset{¯}{{\epsilon }_1})+H_{\text{noise}}(\underset{¯}{{\epsilon }_2})$, two equivalent calculation methods of H_noise shown in Eq. (33) and ENSR are plotted.

Fig. 5.

Estimation results of H_noise for the local Jones matrix. The samples and settings of (a)-(f) correspond to Table 1. The black solid line shows ideal estimation where the measured entropy equals H_noise.

In Fig. 5, $H_{\text{noise}}(\underset{¯}{{\epsilon }_1})+H_{\text{noise}}(\underset{¯}{{\epsilon }_2})$ overestimated the entropy except high Ĥ in (b) and (c). The overestimation of Ĥ by $H_{\text{noise}}(\underset{¯}{{\epsilon }_1})+H_{\text{noise}}(\underset{¯}{{\epsilon }_2})$ was because it did not exclude the mutual information as indicated in Eq. (32). In contrast, both two methods of H_noise in Eq. (33) matched well with Ĥ. The exception was at high Ĥ over ~0.5, where H_noise underestimated Ĥ. This would be also because the assumption of strong constant phasor plus a weak random phasor sum [50] was not valid. Again, the estimation in Fig. 5 was successful with no dependence on the samples and the signal settings as well as Fig. 4.

In Fig. 5, the ESNR plots would be effective to understand the relation between the SNR and the entropy intuitively. However, although the ESNR and the entropy would have a restricted relation, it requires further studies to clarify how the ENSR is related to the entropy and other polarimetric parameters theoretically.

3.6 Image filtering by Cloude-Pottier decomposition for the anterior eye segment

The Cloude-Pottier decomposition is applied for image filtering. A single B-scan with a lateral scanning range of 12 mm consisting of 800 A-scans was used for the demonstration. A superior region of the anterior segment of a healthy right eye was scanned in a vertical direction. The study protocol adhered to the tenets of the Declaration of Helsinki and was approved by the institutional review board of Tohoku University Graduate School of Medicine. First, a coherent Jones-matrix filter [40] was applied to the measured cumulative Jones matrix with a kernel size of 3 × 1 pixels (axial × lateral), which corresponds to 20.6 × 15 µm² in tissue. The local Jones matrix was then calculated with the axial separation of 2 pixels (13.6 µm in tissue). The spatially moving filter of Cloude-Pottier decomposition was applied to the local Jones matrix with a kernel size of 7 × 11 pixels (axial × lateral), which corresponds to 48.1 × 165 µm² in tissue. These spatial kernel sizes were determined by taking a trade-off between the sampling number and the loss of spatial resolution into consideration. A threshold was applied to the pixels by polarization-insensitive signal intensity [40] to exclude the noise area from the ensemble average of T.

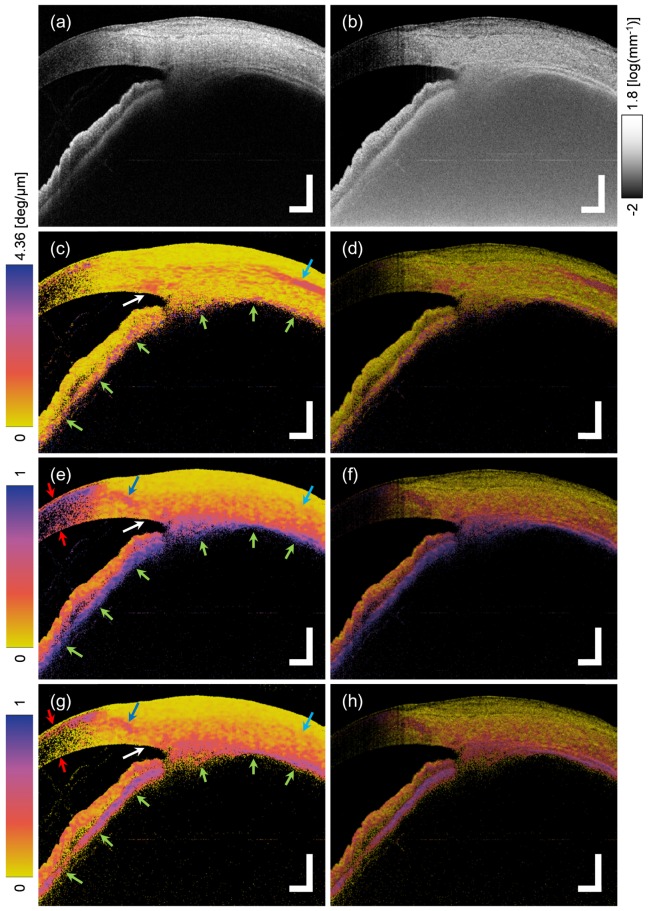
Figure 6 shows the images of the polarization-insensitive intensity (a), the local retardation R₁ (c), the entropy H without any correction (e) and Ĥ with the AQ-MLE and the correction of the bias H_noise (g), respectively. An intensity threshold was applied to Fig. 6(c), 6(e) and 6(g) to color the noise area black. An attenuation coefficient image [53] that was created using the raw data of Fig. 6(a) is shown in Fig. 6(b). Composite images of Fig. 6(c), 6(e) and 6(g) with 6(b) were created by multiplying normalized Fig. 6(b) to individual RGB values of Fig. 6(c), 6(e) and 6(g), respectively.

Fig. 6.

Images of the anterior eye segment around the angle at the superior region. Polarization-diverse signal intensity (a), the attenuation coefficient (b), the local retardation R₁ (c), the entropy without the correction methods (e), the entropy with AQ-MLE and the bias correction of H_noise (g). Figures (d), (f) and (h) are the composite images of (c), (e) and (g) with (b), respectively. The scale bars indicate 1 mm in air. Ametrine color map [66] was used for (c)-(h).

In Fig. 6(c), trabecular meshwork and the peripheral sclera showed high local retardation as indicated by a white arrow. The contrast of the local retardation between conjunctiva and sclera was visible in Fig. 6(c) and 6(d). The sclera had more organized fibrous tissue at the anterior stroma around the equatorial region as indicated by a light-blue arrow in Fig. 6(c). Although pigmented tissues, such as the posterior region of the iris and ciliary body indicated by light-green arrows, showed high local retardation, these seems to be artificial as discussed in the results of the entropy.

In Fig. 6(e)-6(h), the entropy bias by H_noise can be identified at low signal intensity regions. Although the posterior region of the iris and the ciliary body showed high entropy close to 1 in Fig. 6(e), the entropy with the bias correction in Fig. 6(g) showed moderately high entropy as indicated by the light-green arrows. This result is because of melanin in the pigmented tissues, which is common in the retinal pigment epithelium (RPE) [21,54–59]. High entropy of the cornea indicated by red arrows in Fig. 6(e) was corrected in Fig. 6(g) except a part of the anterior corneal stroma, where polarization scrambling effect is seen if the probing beam illuminates the corneal lamellae in a nearly perpendicular direction [40]. The sclera showed inhomogeneous and moderately high entropy in all of the imaged area as shown in Fig. 6(g) and 6(h).

Another interesting region was indicated by a blue arrow in Fig. 6(e) and 6(g), which showed high entropy but low local retardation. Since this region corresponds to the corneoscleral limbus, where the corneal and scleral laminar tissues change transitionally with fibrovascular ridges [60,61], the anisotropic fibrous structure might have anisotropic optic axes in the kernel window and have resulted in the high entropy. It is known that such anisotropic fibrous structure can be found at various biological tissues [62–64]. Since the entropy is sensitive to both the phase retardation and the optic axis, the entropy is effective to find any type of anisotropic birefringence except for a special case with a combination of diattenuation and depolarization [65]. As shown in the corneoscleral limbus, the visualization of both the local retardation and the entropy was important to characterize the tissue. In addition, the optic axis imaging will provide more comprehensive understanding of the tissue birefringence [62–64], and remains for future studies.

4. Discussion

The experimental results in Section 3 validated the theory in Section 2. The phase retardation and the optic axis were estimated correctly without the bias. The underestimation of the entropy was mitigated by AQ-MLE. The influence of the noise to the entropy was estimated as H_noise from the signal intensities and noise powers, and removed from the images in Fig. 6(g) and 6(h) to show only H_subject.

Although we created the composite images in Fig. 6(d), 6(f) and 6(h) by linearly multiplying the logarithmic attenuation coefficient image to preserve the original contrast in Fig. 6(b), this operation resulted in decreased brightness in most regions of the images. When subjective viewability matters more than the linearity of the operation, it may be effective to apply nonlinear image processing for contrast enhancement such as adjustment of dynamic range, gamma correction and adaptive methods [67,68].

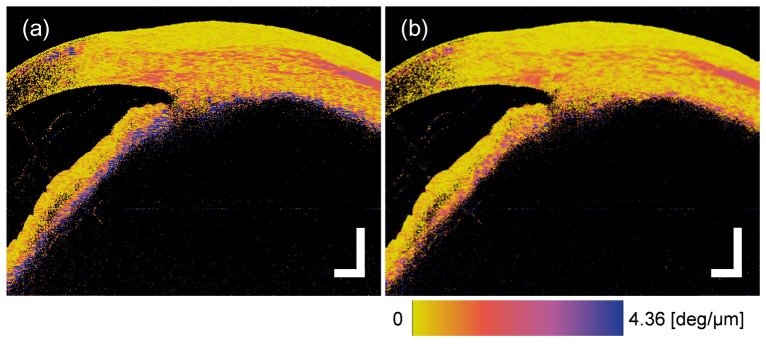
Since our previous method of Jones-matrix averaging, coherent Gaussian spatial filter [40], was a coherent averaging process, it could not show the statistical property of the signals. In contrast, Cloude-Pottier decomposition enabled to show the statistical property using the entropy. Although these methods have different attributes that make a comparison in such aspect unavailable, both can calculate the local retardation. Using the same raw data of Fig. 6, the local retardation images of the anterior eye segment were calculated and shown in Fig. 7 to compare these processing methods. The kernel sizes of these filtering methods in Fig. 7(a) and 7(b) followed Ref [40]. for the coherent Gaussian spatial filter and Section 3.6 for Cloude-Pottier decomposition, respectively. Although both methods were effective to reduce the speckle noise, some differences were found qualitatively. First, the scleral local retardation in Fig. 7(a) was higher than Fig. 7(b). The coherent averaging in Fig. 7(a) might make the anisotropic birefringence look as high birefringence with speckle noise remained, while the incoherent averaging of Cloude-Pottier decomposition in Fig. 7(b) might make it depolarized and result in lower birefringence relatively. Second, the influence of the polarization scrambling at the ciliary body and the posterior region of the iris was high in Fig. 7(a) but was low in Fig. 7(b). This result indicated that the statistical treatment of the data by Cloude-Pottier decomposition could reduce the artifact in the local retardation caused by the polarization scrambling.

Fig. 7.

Local retardation images of the anterior eye segment processed by the coherent Gaussian spatial filter (a) and Cloude-Pottier decomposition (b). The image (b) is exactly same as Fig. 6(c). The scale bars indicate 1 mm in air.

Cloude-Pottier decomposition relies on the mathematical theorems that the covariance matrix C follows the complex Wishart distribution and that Z and T are the MLE of C [34]. Together with various parameters calculated from L_i and λ_i, this multivariate distribution has also been utilized for the segmentation and classification of geographic objects [27,37,69–74]. These successful applications in radar polarimetry encourage us to adapt their approaches for PS-OCT in future.

To visualize the polarization scrambling, DOPU was developed and applied to the identification of the RPE [21,55–59,75,76]. In addition, the bias correction of DOPU was suggested [49]. DOPU and entropy are associated through Eq. (23) [23], which we used to derive H_noise. Although DOPU is a parameter to characterize the uniformity of the state of EM fields, the entropy is a naturally scalable parameter to characterize the randomness not only of the state of EM field but also of the linear map of EM fields. Another parameter, depolarization index, was also suggested by Lippok et al. [77]. Since it is known that the depolarization index and the entropy have a restricted relationship [78], they would show similar properties. In addition, differential depolarization index was recently suggested by Ortega-Quijano et al., and was shown to be effective for enhancing the depolarization contrast [79] and insensitive to an artifact by the diattenuation [80] like Lorentz depolarization indices [65]. It would be interesting to compare these parameters, and remains for future studies.

Uniqueness of the Cloude-Pottier decomposition has been discussed [81,82]. On the one hand, however, there could be arbitrary ways of the matrix decomposition, as various approaches of the decomposition have been suggested in Mueller formalism [83,84]. On the other hand, a controversial argument was raised about the physical meaning of the decomposed components in the Cloude-Pottier decomposition [85], partly because the relationship between the coherence and the polarization is not fully understood yet. In another perspective, it is known that the concept of the target covariance matrix is mathematically related to the density matrix developed in quantum mechanics [86]. As such, understanding of PS-OCT may progress along with the related research areas.

5. Summary

In summary, we developed the theory on the unbiased estimation of Jones matrix, birefringence and entropy using Cloude-Pottier decomposition for PS-OCT. The experimental results of the glass plate, the waveplates and the anterior segment of the healthy eye proved the effectiveness of the estimation. Despite the complexity of the theory at a glance, the basic procedure of the calculation is simple; ensemble average of the target covariance matrix, eigendecomposition and some rearrangement. Our approach would be useful in assessing the statistical properties of the Jones matrix measured from biological subjects by PS-OCT and to evaluate the polarization properties of the subjects quantitatively, and additionally could have potential to help clinical examinations with further development.

Disclosures

MY: Tomey Corporation (E,P), TN: Tomey Corporation (F).

Funding

This study was supported in part by Tomey Corporation. The funder had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.