Assessment of a multi-layered diffuse correlation spectroscopy method for monitoring cerebral blood flow in adults

Abstract

Diffuse correlation spectroscopy (DCS) is a promising technique for brain monitoring as it can provide a continuous signal that is directly related to cerebral blood flow (CBF); however, signal contamination from extracerebral tissue can cause flow underestimations. The goal of this study was to investigate whether a multi-layered (ML) model that accounts for light propagation through the different tissue layers could successfully separate scalp and brain flow when applied to DCS data acquired at multiple source-detector distances. The method was first validated with phantom experiments. Next, experiments were conducted in a pig model of the adult head with a mean extracerebral tissue thickness of 9.8 ± 0.4 mm. Reductions in CBF were measured by ML DCS and computed tomography perfusion for validation; excellent agreement was observed by a mean difference of 1.2 ± 4.6% (CI_95%: −31.1 and 28.6) between the two modalities, which was not significantly different.

1. Introduction

Patients requiring intensive care due to life-threatening neurological emergencies, such as ischemic stroke, traumatic brain injury and subarachnoid hemorrhage, are at high risk of secondary brain injury [1–3]. Although multiple factors contribute to poor outcome, a major focus is preventing delayed cerebral ischemia. For example, approximately one-third of patients with subarachnoid hemorrhage will develop secondary brain injury within two weeks of the initial event primarily due to cerebral vasospasm [4]. Consequently, a major focus of neurointensive care is maintaining adequate cerebral blood flow (CBF) through treatments such as administering nimodipine, inducing hypertension, and intervening with surgical or pharmacological angioplasty [5]. A key component of patient management is the use of monitoring techniques to detect signs of impaired CBF, such as elevated flow velocities in cerebral arteries as measured by transcranial Doppler. However, this is not a direct measure of CBF and cerebral ischemia can occur without evidence of arterial narrowing [6]. Cerebral blood flow can be monitored directly by thermal diffusion and laser Doppler flowmetry [7,8], but these are invasive methods, which has hindered their wider applicability. To date, there remains no established bedside technique capable of monitoring CBF.

Near-infrared spectroscopy (NIRS) is a portable, non-invasive technology that can be used to monitor cerebral oxygenation at the bedside of critical-care patients [9,10]. Cerebral blood flow can be measured directly using the optical dye indocyanine green as an intravascular contrast agent [11–13]. With the application of light propagation models to account for absorption in extracerebral tissues, this contrast-enhanced approach can also provide quantitative CBF measurements [14], but it is limited to single time point measurements. An alternative approach is diffuse correlation spectroscopy (DCS) that monitors changes in CBF by detecting speckle patterns caused by the motion of red blood cells [15–17]. A normalized intensity autocorrelation curve is determined from the measured temporal speckle pattern, and a blood flow index is obtained by fitting the autocorrelation curve with an analytical solution to the correlation diffusion equation for a semi-infinite homogeneous medium [18]. A number of validation studies involving alternative methods of measuring blood flow have shown that DCS can track perfusion changes in the brain accurately [15,19]. Modeling DCS data in this manner is reasonable if contributions from extracerebral tissues are small such as for neonates and certain animal models [15,20,21]. However in the adult head, reflected light measured on the scalp must travel through more substantial extracerebral layers (i.e. scalp and skull), leading to partial volume errors and underestimations of CBF.

A number of approaches have been proposed to account for tissue heterogeneity when applying DCS to monitor CBF in adults, starting with the use of a correction factor based on partial volumes estimates [22]. Another approach is to weight the model fit to shorter correlation times since these represent longer photon pathlengths (i.e. photons that have a greater chance of having propagated deeper into tissue) [23,24]. However, these methods can only enhance the sensitivity to CBF but do not completely separate the effects of light propagation and blood flow in the various tissues. A more direct approach is to adapt a multi-layered solution to the diffusion approximation that accounts for the contribution of the extracerebral layers. Using Monte Carlo simulations and layered tissue phantom, this approach has been shown to improve the sensitivity to CBF [25], and it has been used to analyze DCS data acquired from participants performing a functional task [26]. These studies highlight the importance of using a theoretical model that accounts for extracerebral tissue layers to improve sensitivity to cerebral tissue when analyzing DCS data acquired on the adult head.

The current study investigates the application of a multi-layered (ML) DCS model to data acquired at multiple source-detector distances with the aim of separating brain and scalp blood flow (SBF). Two sets of experiments were conducted to assess the improved depth sensitivity of the ML modeling approach. First, a two-layered tissue-mimicking phantom was constructed in which the pseudo-flow property of each layer could be independently altered. Data were acquired at two source-detector distances while the diffusion coefficient in the deeper layer was gradually increased. Second, the approach was applied to measuring CBF in a juvenile swine model, which was chosen because the thickness of the extracerebral layers is similar to that of the adult human head. Cerebral blood flow was reduced by altering blood CO₂ tension from normocapnia to hypocapnia. For validation, CBF was independently measured by computed tomography perfusion (CTP) [14,27].

2. Theory

With DCS, the measured temporal intensity fluctuations are used to compute the normalized intensity autocorrelation function, g₂(ρ,τ) [18]:

$${\text{g}}_2\left(\text{ρ},\text{τ}\right)\equiv \frac{\text{I}\left(\text{ρ},\text{t}\right)\text{I}\left(\text{ρ},\text{t}+\text{τ}\right)}{\text{I}{\left(\text{ρ},\text{t}\right)}^2}$$ (1)

where, <I(ρ,t)> is the light intensity measured by a detector located at a distance ρ from the source at time t, and τ is the correlation time. Equation (1) is related to the electric field autocorrelation function, G₁(ρ,z,τ) ≡ <E(ρ,z,τ) • E*(ρ,z,t + τ)>, by the Siegert relation [28]:

$${\text{g}}_2\left(\text{ρ},\text{τ}\right)=1+\text{β}\frac{{\left|{\text{G}}_1\left(\text{ρ},\text{z},\text{τ}\right)\right|}^2}{\text{I}{\left(\text{ρ},\text{t}\right)}^2}$$ (2)

where, β is the coherence factor of the detection system. It has been shown for a high scattering, low-absorbing medium, such as tissue, that G₁(ρ,z,τ) can be modeled by the correlation diffusion equation at a depth z in the medium [16,29]. By modeling the medium as a series of parallel slabs over a semi-infinite medium, the diffusion equation is given by [16,29]:

$${\text{P}}_{\text{i}}\left[{\nabla }^2-{{\text{μ}}_{\text{Pi}}}^2\left(\text{τ}\right)\right]{\text{G}}_1\left(\text{ρ},\text{z},\text{τ}\right)=-v\text{Sδ}\left(z-z_0\right)$$ (3)

where, P_i = v/(3µ_ai + ${\mu }_{\mathrm{si}}^{\prime }$) is the photon diffusion coefficient in layer i, v is the speed of light, µ_ai is the absorption coefficient and ${\mu }_{\mathrm{si}}^{\prime }$ is the reduced scattering coefficient. S is the light source defined at an effective depth z₀ ( = 1/${\mu }_{\mathrm{s}1}^{\prime }$) by the delta function $\text{δ}\left(z-z_0\right)$. Finally, μ_Pi accounts for the loss of correlation due to dynamical processes (i.e. the motion of scatterers) and is given by:

$${\text{μ}}_{\text{Pi}}^2\left(\text{τ}\right)=\frac{3\nu }{{\text{P}}_{\text{i}}}\left({\text{μ}}_{\text{ai}}+2{\text{μ}}_{\text{si}}^{\text{'}}{\text{k}}_0^2{\text{αD}}_{\text{i}}\text{τ}\right)$$ (4)

where, k₀ = 2πn/λ is the wavenumber of light (λ is wavelength and n is the refractive index, which is set to 1.4 for all tissues), α represents the fraction of scattering events related to motion, which in tissue represents the fractional blood volume, and D_i is the diffusion coefficient of the i^th layer. If blood flow is modeled as a pseudo-Brownian process [18], which is valid for brain [30], then the blood flow index, F_i, is given by αD_i.

Modeling tissue as a semi-infinite homogeneous medium, the analytical solution to Eq. (3) is given as [16,18]:

$${\text{G}}_1\left(\text{ρ},\text{z},\text{τ}\right)=\frac{3{\text{μ}}_{\text{si}}^{\text{'}}}{4\text{π}}\left[\frac{\text{exp}\left(-{\text{μ}}_{\text{P}1}{\text{r}}_1\right)}{{\text{r}}_1}-\frac{\exp \left(-{\text{μ}}_{\text{P}1}{\text{r}}_1\right)}{{\text{r}}_2}\right]$$ (5)

where, r₁ = [ρ² + z₀²]^½, r₂ = [ρ² + (z₀ + 2z_b)²]^½, and z_b is the extrapolated boundary defined by 2P₁(1 + R_eff)(1 – R_eff)⁻¹ [31]. The effective reflection coefficient, R_eff, is given by 0.493 for the refraction indices of tissue and air [32]. In the general case consisting of parallel slabs on a semi-infinite medium, the field autocorrelation function at the surface (i = 0), ${\tilde{G}}_1^0\left(\text{s},\text{z},\tau \right)$, can be determined by solving Eq. (3) in the Fourier domain [26]:

$${\tilde{G}}_1^0\left(\text{s},\text{z},\tau \right)={\displaystyle \int }{\text{G}}_1^0\left(\text{ρ},\text{z},\text{τ}\right){\text{e}}^{\text{isρ}}{\text{d}}^2\text{ρ}$$ (6)

Similar to Li et al., the appropriate boundary conditions were applied to ${\text{G}}_1^0\left(\text{ρ},\text{z},\text{τ}\right)$, which is obtained by numerically computing the inverse Fourier transform of ${\tilde{G}}_1^0\left(\text{s},\text{z},\tau \right)$ at the surface [25,26]:

$${\text{G}}_1^0\left(\text{ρ},\text{z},\text{τ}\right)=\frac{1}{2\text{π}}\underset{0}{\overset{\infty }{{\displaystyle \int }}}{\tilde{G}}_1^0\left(\text{s},\text{z}=0,\text{τ}\right){\text{sJ}}_0(\text{sρ})\text{ds}$$ (7)

where s is the radial spatial frequency, J₀ is the Bessel function of zeroth order computed by the MATLAB function besselj and the solution of ${\tilde{G}}_1^0\left(\text{s},\text{z},\tau \right)$. The Hankel transform in Eq. (7) was computed numerically by rearranging the solution for a three-layered model to the form of the Gauss-Laguerre quadrature in MATLAB:

$${\tilde{G}}_1^0\left(\text{s},\text{z},\tau \right)=\frac{\text{numerator}}{\text{denominator}}$$ (8)

$$\begin{array}{ll}\text{numerator}=& \text{S}\left(0,\text{z}-{\text{z}}_{\text{b}}\right)\\ & \times {\text{z}}_0\{{\tilde{\mu }}_{{\text{P}}_1}{\text{P}}_1\text{cos h}\left({\tilde{\mu }}_{\text{D}}\left({\text{L}}_1-{\text{z}}_{\text{b}}\right)\right)[{\tilde{\mu }}_{{\text{P}}_2}{\text{P}}_2\text{cos h}\left({\tilde{\mu }}_{{\text{P}}_2}{\text{L}}_2\right)\\ & +{\tilde{\mu }}_3{\text{P}}_3\text{sin h}\left({\tilde{\mu }}_2{\text{L}}_2\right)]\\ & +{\tilde{\mu }}_{{\text{P}}_2}{\text{P}}_2\text{sin h}\left({\tilde{\mu }}_{{\text{P}}_1}\left({\text{L}}_1-{\text{z}}_{\text{b}}\right)\right)\left[{\tilde{\mu }}_{{\text{P}}_3}{\text{P}}_3\text{cos h}\left({\tilde{\mu }}_{{\text{P}}_2}{\text{L}}_2\right)+{\tilde{\mu }}_{{\text{P}}_2}{\text{P}}_2\text{sin h}\left({\tilde{\mu }}_{{\text{P}}_2}{\text{L}}_2\right)\right]\}\end{array}$$

$$\begin{array}{ll}\text{denominator}=& {\tilde{\mu }}_{{\text{P}}_2}{\text{P}}_2\text{cos h}\left({\tilde{\mu }}_{{\text{P}}_2}{\text{L}}_2\right)[{\tilde{\mu }}_{{\text{P}}_1}\text{cos h}\left({\tilde{\mu }}_{{\text{P}}_1}{\text{L}}_1\right)\left({\text{P}}_1+{\tilde{\mu }}_{{\text{P}}_3}{\text{P}}_3{\text{z}}_0\right)\\ & +\text{sin h}\left({\tilde{\mu }}_{{\text{P}}_1}{\text{L}}_1\right)\left({\tilde{\mu }}_{{\text{P}}_3}{\text{P}}_3+{\tilde{\mu }}_{{\text{P}}_1}^2{\text{P}}_1{\text{z}}_0\right)]\\ & +\text{sin h}\left({\tilde{\mu }}_{{\text{P}}_2}{\text{L}}_2\right)[{\tilde{\mu }}_{{\text{P}}_1}\cosh \left({\tilde{\mu }}_{\text{P}}{\text{L}}_1\left({\tilde{\mu }}_{{\text{P}}_3}{\text{P}}_1{\text{P}}_3+{\tilde{\mu }}_{{\text{P}}_2}^2{\text{P}}_2^2{\text{z}}_0\right)\right)\\ & +\sinh \left({\tilde{\mu }}_{{\text{P}}_1}{\text{L}}_1\right)\left({\tilde{\mu }}_{{\text{P}}_2}^2{\text{P}}_2^2+{\tilde{\mu }}_{{\text{P}}_1}^2{\tilde{\mu }}_{P_3}{\text{P}}_1{\text{P}}_3{\text{z}}_0\right)]\end{array}$$

where, μ̃_Pi²(s,τ) = μ_Pi²(τ) + s² for the i^th layer, and L₁ and L₂ are the thicknesses of the first and second tissue layers (i.e. scalp and skull, respectively); the third layer is brain, which is assumed to be infinitely thick.

3. Methods

3.1 Instrumentation

3.1.1 Hybrid optical imaging system

The light source of the DCS instrument was a continuous-wave laser (DL785-100-S, CrystalLaser, Nevada) emitting at 785 nm with a maximum output power of 100 mW and a coherence length >5 m. The emitted light was attenuated by electronically controlled variable neutral density filters and coupled to a multimode emission fiber (N.A. = 0.22, core = 400 µm; Fiberoptics Technology, Pomfret, CT). Twelve single-mode fibers (SMF-28e + , N.A. = 0.14, length = 4 m, core = 8.2 µm, single-mode cutoff wavelength at 1260 nm) were split into separate fiber bundles located at source-detector distances (SDDs) of 20 and 27 mm. Due to the considerable drop in light intensity with distance, one fiber was placed at 20 mm and the remaining 11 were placed at 27 mm. Each fiber was coupled to the input of a single photon counting module (SPCM-AQ4C, Excelitas Canada Inc). The output of each SPCM was sent to a 16-channel photon correlator board (DPC-230, Beker & Hickl) that computed the normalized intensity autocorrelation functions, g₂(ρ,τ).

Tissue optical properties (i.e. μ_a and ${\mu }_{\mathrm{s}}^{\prime }$) were measured by a TR NIRS system described in detail elsewhere [30,33]. Briefly, the instrument consisted of a picoseconds pulsed diode laser (LDH-P-C 764, PicoQuant, Germany) emitting at 764 nm with an average output power and pulse repetition rate of 1.4 mW and 80 MHz, respectively. The light was guided by the same type of optical fiber as the DCS emission probe; the two probes were bundled together to emit light at the same location. The pulsed light was detected by 121 optical fibers (core = 200 µm, cladding = 220 µm, N.A. = 0.22, length = 0.5 m), which were bundled together with the 11 DCS single-mode detection fibers located at the SDD of 27 mm. Collected photons were guided to a fast hybrid photomultiplier detector (PMA Hybrid, PicoQuant, Germany) whose output was sent to a time-correlated single-photon counting (TCSPC) module (HydraHarp 400, PicoQuant, Germany). At the end of the study, the instrument response function (IRF) was measured to account for instrument-related temporal dispersion [34].

3.1.2 Computed tomography perfusion

All CT imaging was performed with a Revolution CT scanner (General Electric Company, Waukesha, WI). Perfusion images were acquired by performing a dynamic contrast-enhanced protocol, which involved serial acquisition of image volumes, one acquired every second, for 40 seconds (200 mA, 80 kVp, 2.5-mm slice thickness, and a FOV of 140 x 140 x 40 mm). Each volume consisted of 32 coronal slices, which encompassed the entire head. The beginning of the dynamic scanning was immediately followed by a bolus injection of 1.0 mL/kg of iodine-based contrast agent (iopamidol [370-Isovue®], Bracco S.p.A., Milan, Italy) at a rate of 3 mL/s into the cephalic vein.

3.2 Experimental procedure

3.2.1 Two-layered diffusion phantom experiments

A two-layered phantom was designed using computer-aided 3D drawing software (Rhinoceros 5; Robert McNeel & Associates, North America). It was constructed from dark polyvinyl chloride (12 mm thick) and had internal dimensions of 180 x 140 x 110 mm. Two layers were created by inserting a polyester Mylar sheet (polyethylene terephthalate; McMaster-Carr) with a thickness of 25.4 µm (Fig. 1). One side of the box remained open which enabled a Mylar sheet framed by a clear polycarbonate to be positioned at a depth of either 5 or 10 mm from the top of the box. Three holes were drilled into the top of the box to hold the probes in place: one emission fiber and two detection fibers at SDDs of 20 and 30 mm. Both layers (i.e.top and bottom) were filled with a 0.8% Intralipid solution (Fresenius Kabi, Germany) to mimic the light scattering properties of tissue. The viscosity in the bottom layer was increased by adding methyl cellulose (4000 cP; Sigma-Aldrich, St. Louis, MO) [18].

Fig. 1.

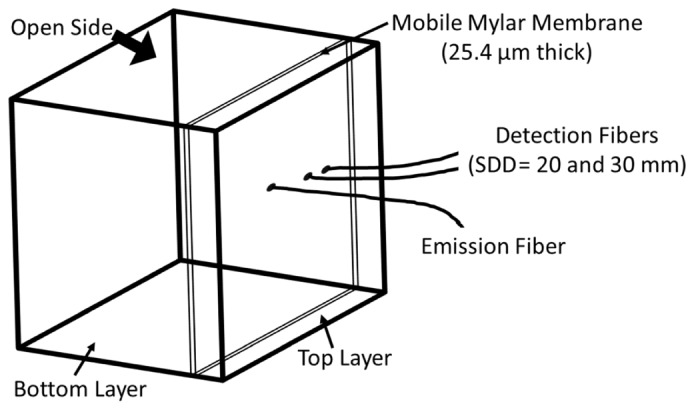
A wire diagram of the constructed two-layered phantom. With the box tipped on its side, cellulose could be added to either layer layer via the open side. The mobile Mylar membrane could be removed by the open side or inserted into slots at 5 or 10 mm relative to the surface that included the optical fibers.

To replicate the homogeneous condition, DCS data were first acquired at a SDD of 30 mm and multiple cellulose concentrations (0, 0.05, 0.1, 0.15, and 0.2%), but without the mobile Mylar membrane. In addition to acquiring DCS data, μ_a and ${\mu }_{\mathrm{s}}^{\prime }$ were measured by TR NIRS at each cellulose concentration. Next, the mobile membrane was inserted in one set of slots to create a ‘top’ layer. DCS data were acquired at 20 and 30 mm while replacing the solution in the ‘bottom’ layer with a mixture of intralipid and cellulose of various concentrations between 0 and 0.2%, but maintaining the top-layer concentration at 0%. Data acquired with the homogeneous phantom were analyzed by the analytical solution Eq. (5) for the homogeneous model (DCS_HM). Data acquired with the two-layered phantom were analyzed with DCS_HM (SDD = 30 mm) and ML DCS method using data from both separations.

3.2.2 Animal experiments

Experiments were conducted under the guidelines of the Canadian Council of Animal Care (CCAC) and approved by the Animal Use Sub-Committee at Western University. Experiments were conducted on seven pigs (all female) with an average weight of 15.5 ± 0.4 kg and average scalp and skull thicknesses of 3.5 ± 0.2 mm and 6.4 ± 0.4 mm, respectively. The animals were obtained from a local supplier on the day of the experiment. Following anesthetic induction with 5% isoflurane, the animals were tracheotomized and mechanically ventilated on a mixture of oxygen and medical air. A catheter was inserted into a femoral artery for blood gas analysis. After surgery, isoflurane was reduced to 3-4% and the animal was transported to the CT suite where the experiments were conducted.

Before data collection, CT scout images were acquired to determine the best location for the probe holder on the head (i.e. the position corresponding to the largest brain diameter). During the experiment, arterial oxygen saturation, heart rate (HR), respiratory rate, mean arterial pressure (MAP), and rectal temperature were continuously monitored. Arterial blood samples were obtained to measure arterial pH, the arterial partial pressure of carbon dioxide (paCO₂), the arterial partial pressure of oxygen (paO₂), the concentration of blood glucose (BG), and the total blood hemoglobin concentration (ctHb). Samples were acquired before and after each set of measurements to assess physiological stability during data acquisition. The order for the three modalities was CTP, TR NIRS, and DCS at normocapnia (paCO₂ between 38 and 42 mmHg) and reversed at hypocapnia (paCO₂ betw*een 20 and 25 mmHg) to avoid removing the DCS probes from the head between measurements. The DCS data were acquired by maximizing the count rate without oversaturating the correlator board. Following a CTP measurement, at least ten minutes transpired before acquiring any data to ensure complete clearance of the injected contrast agent. Each capnic level was maintained by adjusting the ventilation volume and rate. To investigate if the multi-distance DCS measurements were affected by SBF, the acquisition protocol was repeated after creating incisions in the scalp around three lateral sides of the probe holder to reduce SBF [14]. The time course of a typical experiment is illustrated in Fig. 2.

Fig. 2.

A diagram of the time course for a typical experiment. Blood gas analysis (BGA) was performed to confirm capnia level, where normo and hypo represent normocapnia and hypocapnia, respectively. Data acquisitions (DA) are listed in sequential order; TR NIRS (not shown in the diagram) is always acquired between CTP and DCS.

3.3 Data analysis

3.3.1 Computed tomography perfusion

Maps of CBF were calculated using the CT perfusion software package PERFUSION 5 (GE Healthcare Worldwide), which was developed and validated in-house [35]. Region-of-interest (ROI) analysis was performed using in-house developed software that performed pixel thresholding to remove signal contributions from large vessels that can lead to CBF overestimations [36]. For each slice, three ROI’s (~5 cm²) were manually drawn on the scalp, skull, and cerebral cortex, as seen in Fig. 3. The location of the scalp ROI was located laterally to the actual positions of the DCS probes. This was done to avoid motion artifacts near tissue interfaces such as bone and scalp caused by breathing. The brain ROI was drawn on the cerebral cortex since the NIRS signal is more sensitive to superficial brain tissue than deeper white matter. Absolute blood flow values for each of the three tissues (scalp, skull and brain) were obtained by averaging ROIs across ten to twelve sequential slices. Finally, the thicknesses of the scalp and the skull (i.e. L₁ and L₂, respectively) were measured by image-viewing software (AW VolumeShare 4, GE Healthcare).

Fig. 3.

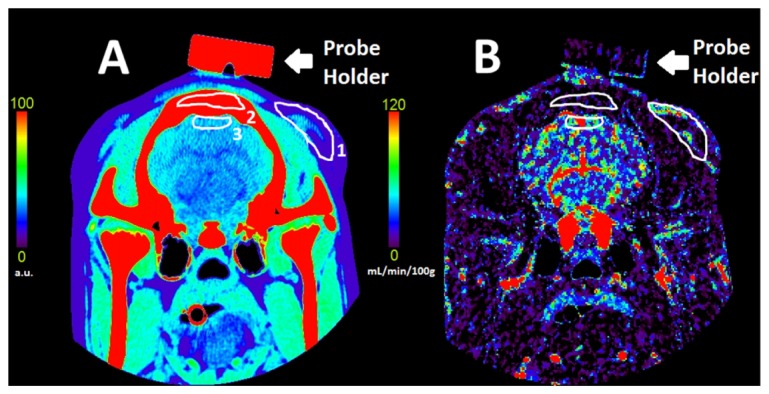
Coronal CT image of a pig’s head (A) and the corresponding blood flow map (B). The scalp (1), skull (2) and brain (3) ROIs are shown in white. Bar codes are given to illustrate relative x-ray attenuation (A) and blood flow in mL/min/100g (B).

3.3.2 Diffuse correlation spectroscopy

All intensity autocorrelation functions were acquired over an integration time between 30 and 90 s depending on the achieved count rate. Measured g₂(ρ,τ) functions were converted to the field autocorrelation function by Eq. (2). Data were analyzed using both solutions to the diffusion approximation: the semi-infinite homogeneous model Eq. (5) and the ML model (Eqs. (6) and (7)). Estimates of the diffusion coefficients were determined using a non-linear least squares fitting routine (MATLAB^© function fminsearchbnd with D_i values constrained to be positive) to fit an analytical model to g₂(ρ,τ). For the homogeneous model, data from one SDD were analyzed to generate a diffusion coefficient for the tissue-mimicking phantom or a blood flow index denoted F_HM for the in vivo data. These values were derived using the values of μ_a and ${\mu }_{\mathrm{s}}^{\prime }$ measured by TR NIRS, which were also determined by the solution to the diffusion approximation for a semi-infinite homogeneous medium [37]. The fitting was performed for correlation times from 1 µs up to times corresponding to g₂(ρ,τ) > 0.5, since focusing the fit of the autocorrelation function to short correlation times increases the sensitivity to deeper propagating photons [23]. For the animal experiments the g₂(ρ,τ) functions acquired at 20 and 27 mm were analyzed separately and denoted F_HM,1 and F_HM,2, respectively.

For the ML DCS model, the g₂(ρ,τ) functions acquired at the two SDDs were analyzed simultaneously. The µ_a and ${\mu }_{\mathrm{s}}^{\prime }$ values for all three layers were set to the values obtained from TR NIRS using the homogeneous model, and L₁ and L₂ values were obtained from the CT images. For each animal, the coherence factor (β) was estimated prior to the fitting by averaging the first five points of each autocorrelation function. To focus on deeper propagating photons, the fitting was performed between correlation times defined by g₂(ρ,τ) < 0.8 to 0.1 s for the shorter SDD (20 mm), and 1 µs to g₂(ρ,τ) > 0.5 for the longer SDD (27 mm). For the flow phantom, the two fitting parameters were the diffusion coefficients in the top and bottom layers (D_T and D_B, respectively). Similarly, the fitting parameters for the analysis of the in vivo data were the blood flow indices in scalp and brain (denoted F_S and F_B, respectively), assuming negligible flow in the middle (skull) layer (i.e. F_skull = 0).

3.4 Statistical analysis

Uncertainties are given as the standard error of the mean unless otherwise stated. All statistics were computed with the IBM SPSS Statistics 20 software package. For the phantom experiments, linear regression analysis was conducted to identify a significant relationship between increasing viscosity in the bottom layer and the measured diffusion coefficients (D_T and D_B).

For the animal experiments, possible changes in the measured physiological parameters and optical properties due to altering paCO₂ or the scalp incisions were tested by a repeated measures analysis of variance (ANOVA). The same test was conducted on all measured flow parameters, which include the blood flow estimates for scalp, skull and brain measured by CTP, and for the blood flow indices measured by DCS techniques: F_S and F_B from the ML DCS analysis, and F_HM,1 and F_HM,2 from the homogeneous model. Relative blood flow changes measured by CTP and ML DCS when paCO₂ was altered from normocapnia to hypocapina were compared by a paired t-test. Finally, Bland-Altman analysis was conducted to compare the reductions in CBF and F_B obtained by CTP and ML DCS, respectively. This included a one-sample t-test to identify differences between the two modalities and linear regression to determine proportionality bias.

4. Results

4.1 Phantom experiments

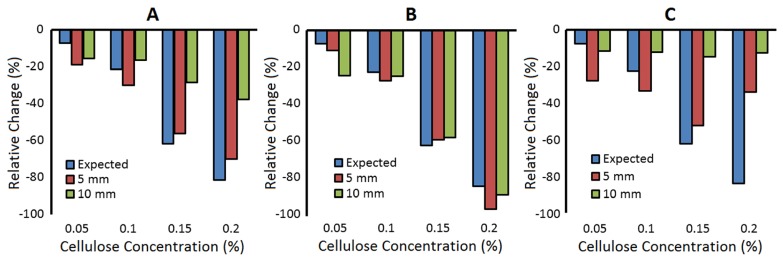
Figure 4 illustrates the relative change (i.e. from 0% cellulose) in the estimated diffusion coefficient from the homogeneous model (A) and the ML DCS model (B) as the viscosity in the bottom layer of the phantom was increased by adding cellulose. In the latter case, the diffusion coefficient from the bottom layer (D_B) is shown. For comparison, each graph also includes the measured change in the diffusion coefficient for the homogeneous phantom.

Fig. 4.

Relative change in the measured diffusion coefficient as the viscosity of the tissue-mimicking phantom was increased. The label ‘expected’ refers to the homogeneous case (blue bars), and the labels ‘5 mm’ and ‘10 mm’ refer to thickness of the top layer for the two-layered case (red and green bars, respectively). For the two-layered experiments, cellulose was only added to the bottom layer. (A) Diffusion coefficient determined by analyzing the two-layered data with the homogeneous model (SDD = 30 mm). Diffusion coefficients for the bottom (B) and top (C) layers of a two-layered model applied to the same data used in (A). This analysis used data acquired at SDD of 20 and 30 mm.

The results in Fig. 4(A) were obtained using the HM DCS model to characterize the g₂(ρ,τ) curves acquired at a SDD of 30 mm, and as expected the magnitude of the error was larger as the top layer thickness increased. The results in Fig. 4(B) were obtained using the ML DCS model to characterize g₂(ρ,τ) acquired at SDDs of 20 and 30 mm. Linear regression analysis indicated that increasing the viscosity in the bottom layer significantly reduced D_B, but had no effect on D_T for either a 5 or 10 mm thick top layer. The optical properties measured by TR NIRS in the homogeneous phantom were µ_a = 0.033 ± 0.003 cm⁻¹ and ${\mu }_{\mathrm{s}}^{\prime }$ = 8.5 ± 0.2 cm⁻¹.

4.2 Animal experiments

4.2.1 Physiological parameters

For all physiological parameters, significant differences were observed pre- and post-scalp incision, except for pH, paCO₂ and paO₂. As expected, significant differences between normocapnia and hypocapnia were observed for pH and paCO₂ [p<0.001, partial-η² > 0.98, Power = 1]; however, significant changes in paO₂ and MAP were also observed [p<0.05, partial-η² > 0.69, Power > 0.85] (see Table 1), where partial-η² is an estimate measure of effect size. Changes were not observed for any of the other measured physiological parameters. Their mean values were 38.4 ± 0.1 °C (temperature), 120 ± 2 beats per minute (HR), 5.3 ± 0.2 mmol/L (BG) and 9.2 ± 0.1 g/dL (ctHb). Lastly, no differences were observed in μ_a (0.168 ± 0.008 cm⁻¹) and ${\mu }_{\mathrm{s}}^{\prime }$ (9.0 ± 0.8 cm⁻¹) between capnic conditions.

Table 1. Average values at normocapnia and hypocapnia for the arterial partial pressure of carbon dioxide (paCO₂,) and oxygen (paO₂). * p<0.05 and ** p<0.001 between conditions. Data are presented as average ± SEM.

Condition	**pH	**paCO2 (mmHg)	*paO2 (mmHg)	*MAP (mmHg)
Normocapnia	7.473 ± 0.006	39.5 ± 0.4	173 ± 10	41 ± 1
Hypocapnia	7.658 ± 0.006	22.2 ± 0.4	210 ± 10	38 ± 1

4.2.2 Absolute blood flow

Five blood flow index sets (F_S and F_B) measured by ML DCS out of a total of 28 were removed due to either a large residue (i.e. > 0.01) in the optimization procedure (two cases) or an F_B value that approached zero (i.e. < 10⁻⁹) (one case). Lastly, both sets of g₂(ρ,τ) curves (i.e. during normocapnia and hypocapnia) from one experiment were removed due to poor coupling between the optical probes and skin.

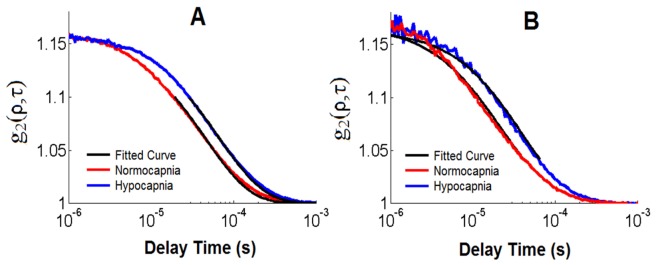
Normalized intensity autocorrelation curves from one experiment are plotted in Fig. 5. This set was chosen as the F_B values at normo- and hypo-capnia were similar to the average values across all animals. The shift to longer correlations times from normocapnia to hypocapnia evident in Fig. 5 represents a −38.7% flow change measured by ML DCS.

Fig. 5.

Normalized intensity autocorrelation functions acquired during normocapnia (red curve) and hypocapnia (blue curve) at SDD of 20 mm (A) and 27 mm (B) with count rates of ~465 and ~55 kHz, respectively. The fit of the ML DCS model is illustrated by the black curve.

No significant changes in any of the blood flow indices (i.e. F_S and F_B values from the ML DCS analysis and F_HM from the HM DCS analysis) were found by comparing values pre and post scalp incisions. This unexpected finding was likely due to increased variability in the DCS signal due to probe pressure effects since it was necessary to remove the fibers to perform the incisions [38]. Consequently, capnic data before and after scalp incision were grouped together in all subsequent analysis. Note, SBF measured by CTP did not change with scalp incisions since the scalp ROI (Fig. 3) was lateral to probe location to avoid breathing-related motion artifacts.

Figure 6 plots the blood flow estimates obtained by CTP and DCS for the two paCO₂ conditions. Significant differences between normocapnia and hypocapnia were found for CBF measured by CTP [p<0.001, partial-η² = 0.984, Power = 1] and F_B measured by ML DCS [p<0.05, partial-η² = 0.816, Power = 0.685]. Significant differences were also found for F_HM at a SDD of 20 mm [p<0.05, partial-η² > 0.876, Power > 0.852] and a SDD of 27 mm [p<0.05, partial-η² > 0.826, Power > 0.710]. In contrast, no significant differences between capnic conditions were found for SBF measured by CTP, and F_S measured by ML DCS. Finally, skull flow measured by CTP (8.9 ± 0.7 mL/min/100g) and the coherence factors β (0.158 ± 0.001 and 0.168 ± 0.002, for SDD of 20 and 27 mm, respectively) did not change significantly with paCO₂ (data not shown).

Fig. 6.

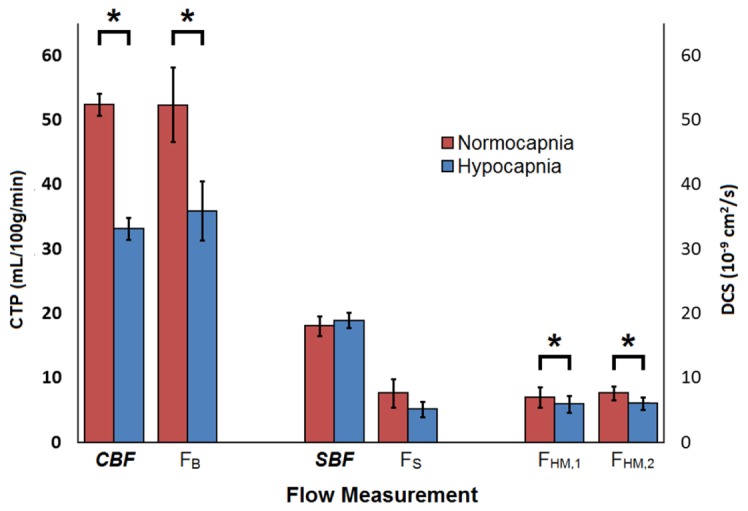
Scalp blood flow (SBF) and cerebral blood flow (CBF) measured by CT, and the corresponding blood flow indices measured by DCS during normocapnia (red bars) and hypocapnia (blue bars). All values were averaged over their pre- and post- scalp incision measurements. F_S and F_B were obtained from the ML model analysis of DCS data acquired at SDDs of 20 and 27 mm. F_HM was obtained by analyzing data from each SDD separately with the HM model (F_HM,1 refers to 20 mm and F_HM,2 refers to 27 mm). Significant differences observed between capnic conditions are represented by *.

A significant Pearson correlation (R = 0.538) was observed between CBF and F_B; however, no significant correlation was observed between CBF and either F_HM,1 (R = 0.351) or F_HM,2 (R = 0.387). Significant correlations were observed between F_S and both F_HM,1 (R = 0.972) and F_HM,2 (R = 0.881).

4.2.3 Relative blood flow

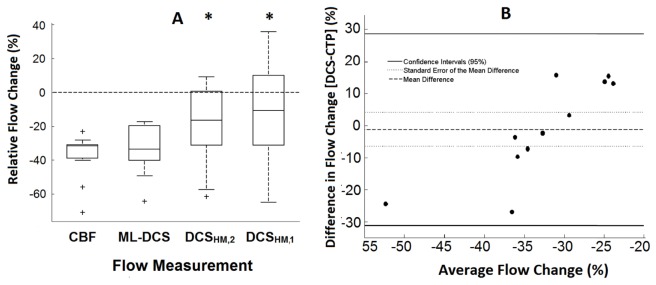
The relative change in CBF and DCS indices when reducing paCO₂ from normocapnia to hypocapnia are presented in Fig. 7.

Fig. 7.

(A) Box plot of relative flow change caused by reducing paCO₂ from normocapnia to hypocapnia. Flow values of CBF, F_B, F_HM,1 and F_HM,2 measured by CTP (N = 14), ML DCS (N = 11), DCS_HM,1 (N = 14) and DCS_HM,2 (N = 14), respectively. The center line, box edges, error bars, and the cross represent the median, 1st and 3rd quartiles, CI_95%, and outliers, respectively. Significant changes compared to CBF are represented by *. (B) Bland-Altman plot comparing reductions in CBF and F_B measured by CTP and ML DCS (N = 11). The mean difference between the two modalities, the standard error of the mean, and the CI_95% are indicated by the solid line, the dotted line and the dashed line, respectively.

Mean CBF reduction measured by CTP (−36.4 ± 3.3%) was not significantly different from the corresponding F_B change (−33.5 ± 4.5%). In contrast, the F_HM,1 change (−13.2 ± 7.5%) was significantly different from both the CTP and ML DCS results. Similarly, the change in F_HM,2 (−19.1 ± 6.0%) was significantly different from CTP results and a trend was observed when compared to F_B (p = 0.054). A Bland-Altman analysis comparing relative CBF changes measured by CTP and ML DCS is shown in Fig. 7(B). The mean difference between the two modalities was −1.2 ± 4.6% (CI_95%: −31.1 and 28.6). Linear regression analysis of the Bland-Altman plot indicted a significant proportional bias (p<0.001, R = 0.837).

4.2.4 Real-time flow monitoring

To demonstrate the ability of ML DCS to resolve dynamic differences in scalp and brain blood flow, a series of g₂(ρ,τ) curves acquired during the transition from normocapnia to hypocapnia, which is illustrated by the solid black vertical line in Fig. 8, from one experiment were analyzed. In this example, the flow change calculated by the difference between means of the first and last minutes was −42.9% in the brain and 5.2% in the scalp. The coefficients of variation for the baseline scalp and brain time series were 9.8% and 8.4%, respectively.

Fig. 8.

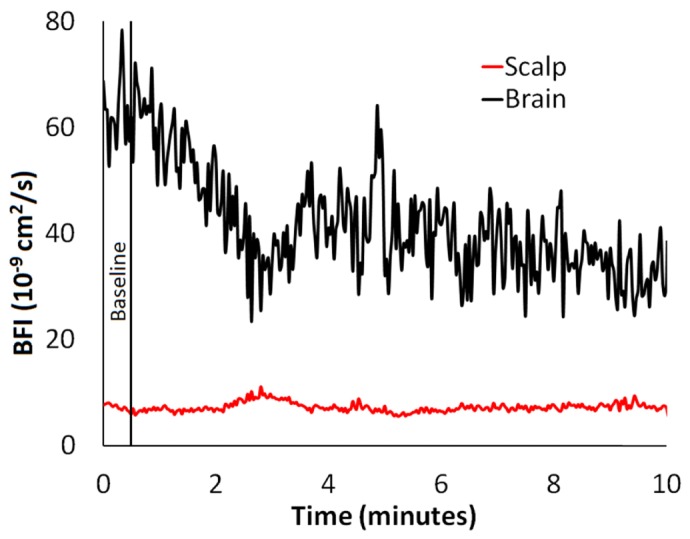
Blood flow dynamics during the transition from normocapnia to hypocapnia, which is illustrated by the solid black vertical line, from one experiment. Each g₂(ρ,τ) curve was acquired for two seconds and analyzed separately by the ML DCS model to obtain time series of F_B and F_S. Data were acquired at a count rate of 554.3 ± 0.4 kHz and 101.5 ± 0.2 kHz at SDDs of 20 mm and 27 mm, respectively. The thickness of the scalp and the skull were 3.7 ± 0.4 mm and 6.0 ± 0.4 mm, respectively; F_skull = 0.

5. Discussion

The aim of this work was to test the ability of a depth-sensitive DCS approach to retrieve the blood flow index from the brain despite the presence of a substantial superficial tissue layer. The approach was based on obtaining two autocorrelation functions with varying depth sensitivities by placing detectors at distances from the source of 20 and 27 mm. The multi-distance data were then analyzed with a three-layered solution to the correlation diffusion equation to account for light propagation through scalp, skull and brain, and the different blood flows in scalp and brain [26]. Rather than fitting a complete autocorrelation curve, different ranges of correlation times were used to fit the curves obtained at the two source-detector distances in order to alter the weighting to shorter or longer photon pathlengths [23,39]. More specifically, the range for the longer SDD (27 mm) was restricted to early correlation times, while longer correlation times were selected for the shorter SDD (20 mm). Similar flow percent changes were found by entire curve fit of multiple distances by the ML DCS analysis, but weighting towards longer and shorter photon pathlengths improved variance of the measured brain blood flow indices. Further work to optimize the technique setup (i.e. determine optimal SDDs, autocorrelation fit ranges, measured count rates, and SNR) is required prior to clinic implementation.

The feasibility of the ML DCS approach was first verified using a two-layer tissue-mimicking phantom in which the diffusion property of the bottom layer was altered by adding four different cellulose concentrations [18]. The change in the measured diffusion coefficient of the bottom layer, which varied from 20% to 80% by increasing the cellulose concentration, was in good agreement with the change observed in the homogeneous phantom over the same concentration range (Fig. 4). In contrast, as expected, the diffusion coefficient of the 10-mm thick top layer did not change when cellulose was added to the bottom compartment (data not shown). In agreement with Gagnon et al. [25], these results highlight the ability of a multi-layered model to resolve differences in flow rates in different layers with minimal crosstalk between the measured diffusion coefficients.

The second aim of the study was to apply the same ML DCS approach to an animal model in which CBF was independently measured by CT perfusion. Juvenile pigs were selected as the total thickness of their extracerebral tissues was expected to be similar to that of adult humans. The mean values of scalp and skull thicknesses were 3.5 ± 0.2 and 6.4 ± 0.4 mm, respectively, which are within the expected range for humans, although larger values can be found depending on the location on the head [40]. Global CBF was reduced by lowering paCO₂ from normocapnia to hypocapnia. Overall, good agreement was found between the average CBF reductions measured by CTP (36.4 ± 3.3%) and ML DCS (33.5 ± 4.5%). The corresponding estimates of cerebrovascular reactivity (CVR), defined as the change in CBF per unit change in paCO₂, were −1.9 ± 0.2% per mmHg and −1.7 ± 0.2% per mmHg for CTP and ML DCS, respectively. These estimates are in good agreement with our previous studies involving this animal model: −2.3% per mmHg from CTP and −2.3% per mmHg from DCS probes placed directly on the exposed cerebral cortex [14,30]. In addition, good agreement was also found between the absolute blood flow index determined from ML DCS (Table 2) and our previous values derived from autocorrelation functions measured directly on the brain, (~48x10⁻⁹ cm²/s at normocapnia and ~28x10⁻⁹ cm²/s at hypocapnia) [30]. This agreement suggests that F_B could be used as a marker to track longitudinal changes in CBF, similar to previous DCS studies involving infants [41]. However, this would require careful assessment of the reproducibility of F_B considering the added complexity of the analysis. Intriguingly, the group-wise variability in F_B (~40%) was in good agreement with previous studies in which the blood flow index was derived from the semi-infinite homogeneous model [30,37]. This is despite the addition of a scalp blood flow index (i.e. F_s) in the fitting routine. Recently, Boas et al. demonstrated DCS blood flow indices provide a direct measure of tissue perfusion but this relationship depends on hematocrit and average vessel diameter, which are difficult to measure noninvasively [42]. Another possibility to quantify blood flow indices measured by DCS is direct calibration by an all-optical modality [37].

Table 2. Average flow values (CBF and SBF, F_B and F_S) measured by CTP and ML DCS, respectively, for normocapnic and hypocapnic conditions. Significant differences between capnic conditions are indicated by *.

Capnic Condition	*CBF (mL/min/100g)	*FB (10−9 cm2/s)	SBF (mL/min/100g)	FS (10−9 cm2/s)	*FHM,1 (10−9 cm2/s)	*FHM,2 (10−9 cm2/s)
Normocapnia	52.4 ± 1.7	52.3 ± 6.9	18.1 ± 1.5	7.3 ± 2.1	7.1 ± 1.3	7.7 ± 1.1
Hypocapnia	33.2 ± 1.7	36.3 ± 4.2	19.0 ± 1.2	5.0 ± 1.2	6.0 ± 1.3	6.1 ± 1.0

Although the results of this study demonstrate that a multi-layered modeling approach can account for the effects of extracerebral tissue, the accuracy of F_B will be affected by errors in the additional model input parameters (i.e. the thicknesses of scalp and skull, and tissue optical properties). To assess the sensitivity to uncertainties in the thickness measurements, the g₂(ρ,τ) curves from the tissue-mimicking phantom with a 10-mm top layer were re-analyzed with the top layer thickness varied by ± 20%. The resulting error in the diffusion coefficient for the bottom layer was less than 10%, similar to that reported by Gagnon et al. (2008). For each pig, an average standard deviation of 2 mm is estimated for the thickness of the extracerebral tissue, and therefore, a similar error less than 10% can be expected for the multi-layer analysis. In clinical practice, the thicknesses of the scalp and skull could be obtained from medical images or possibly measured directly using ultrasound. Alternately, the total scalp/skull thickness could be included as an additional fitting parameter, similar to an approach proposed for measuring cerebral oxygenation by multi-distance frequency-domain NIRS [43]. This would likely require more SDDs than used in the current study and careful attention to the shortest SDD in order to avoid violating the Siegert relationship [44]. Regarding the optical properties, all three tissue layers were set to the single µ_a and ${\mu }_{\mathrm{s}}^{\prime }$ values measured by TR NIRS since the primary focus was assessing the ability of DCS to measure changes in CBF, which is fairly insensitive to uncertainties in absolute µ_a and ${\mu }_{\mathrm{s}}^{\prime }$ [37,44]. Separate values of µ_a and ${\mu }_{\mathrm{s}}^{\prime }$ for each tissue layer could be obtained using a multi-layer solution to analyze the TR NIRS data [45,46].

An alternative and simpler approach to account for partial volume errors is to multiply the change in the blood flow index obtained from the homogeneous model by a correction factor based on the partial pathlength through brain [22,23,25]. Durduran et al. (2004a) initially used a value of 5 based on modeling the head as a two-layered medium. More recently, Selb et al. proposed a factor of 3 by restricting the fitting to early correlation times. In the current study, correction factors of 2.4 and 1.8 were found for SDDs of 20 and 27 mm, respectively, by comparing the mean change in F_HM to the CBF change measured by CTP. Similarly, a factor of 1.5 was determined from the tissue phantom experiments with a 10-mm thick top layer and a SDD of 30 mm. The smaller values at larger separations (27 and 30 mm) would be expected given the improvement in depth sensitivity as the SDD is increased. Although applying a correction factor is simpler than using a multi-layered model, high variability across experiments was found. In this study, the correction factor varied by ± 60% across animals. Furthermore, the similarity between mean F_HM and F_S values in Table 2 indicates that the DCS signal is heavily weighted by extracerebral tissue. This sensitivity could lead to erroneous CBF estimates if SBF changed due to systemic effects or variations in surface probe pressure, highlighting the value of a multi-layered model to uncouple brain and scalp blood flow. Interestingly, the disagreement between perfusion changes determined by CT and the DCS flow index obtained with the homogeneous model contradicts a previous study in which DCS was compared to CBF measurements obtained with Xenon CT [48]. Possible reasons for this discrepancy could include differences between species – the extracerebral layer of the pig has a more substantial muscle contribution, the extracerebral thickness, which was not reported by Kim et al, and possibly the effects of probe pressure, which can reduce the effects of scalp contamination [38]. Although it should be noted that the sensitivity of the homogeneous model to superficial tissues found in the current study is in agreement with others [24,25,38].

An unexpected finding was the proportional bias revealed by regression analysis in the Bland-Altman plot (Fig. 7(B)) despite similar flow changes measured by CTP and ML DCS (mean difference = −1.2 ± 4.6%). This bias remained even after removing the outlier that had a mean CBF change greater than 50%. One explanation is the accuracy of the ML DCS approach could be affected by variations in the thickness of the extracerebral layer; however, no correlation with F_B was found. Considering the range of CBF reductions was limited to between 20 to 40%, this bias should be viewed with caution. A wider range of flow changes, for instance by including hypercapnia experiments to increase CBF, would help to assess the validity of the observed bias. Another unexpected finding was an average perfusion signal in skull of 9 mL/min/100g measured by CTP. This would appear to contradict the assumption of the ML DCS method that skull has negligible blood flow. However, this value is likely artificial considering a similar ‘perfusion’ signal (10 mL/min/100g) was found in the probe holder (see Fig. 3(B)). Likely this artifact is related to greater variability in flow estimates in areas of extremely low contrast enhancement. It should be noted that there was no change in skull blood flow between capnic levels.

6. Conclusion

In summary, this study demonstrates that DCS has the ability to separate scalp and brain blood flow, as demonstrated in Fig. 8, despite the presence of a relatively thick extracerebral layer (of the order of 1 cm). The ML DCS technique could be further optimized by incorporating optical property measurements for the different tissue layers and by improving the SNR through the use of a software correlator to measure only relevant correlations times [49]. Recent improvements for monitoring CBF were demonstrated in the adult head by a pressure modulation algorithm, without requiring a priori anatomical information [24]. The approach taken by Baker et al. can be combined with the multi-layered model presented in this study to isolate cerebral signals detected by DCS when estimating extracerebral tissue thickness by imaging methods is unavailable. Future work will implement a multi-layered DCS/TR-NIRS hybrid to demonstrate a means of quantifying the cerebral metabolic rate of oxygen in adults [14,50].

Funding

This work was supported by grants from the Canadian Institutes of Health Research, and the National Science and Engineering Council of Canada and a personnel award to K. St. Lawrence from the Heart and Stroke Foundation, Ontario Provincial Office. K. Verdecchia was supported by a scholarship from a Queen Elisabeth II Graduate Scholarship in Science and Technology (QEII-GSST).