Assessing methods for generalizing experimental impact estimates to target populations

Abstract

Randomized experiments are considered the gold standard for causal inference, as they can provide unbiased estimates of treatment effects for the experimental participants. However, researchers and policymakers are often interested in using a specific experiment to inform decisions about other target populations. In education research, increasing attention is being paid to the potential lack of generalizability of randomized experiments, as the experimental participants may be unrepresentative of the target population of interest. This paper examines whether generalization may be assisted by statistical methods that adjust for observed differences between the experimental participants and members of a target population. The methods examined include approaches that reweight the experimental data so that participants more closely resemble the target population and methods that utilize models of the outcome. Two simulation studies and one empirical analysis investigate and compare the methods’ performance. One simulation uses purely simulated data while the other utilizes data from an evaluation of a school-based dropout prevention program. Our simulations suggest that machine learning methods outperform regression-based methods when the required structural (ignorability) assumptions are satisfied. When these assumptions are violated, all of the methods examined perform poorly. Our empirical analysis uses data from a multi-site experiment to assess how well results from a given site predict impacts in other sites. Using a variety of extrapolation methods, predicted effects for each site are compared to actual benchmarks. Flexible modeling approaches perform best, although linear regression is not far behind. Taken together, these results suggest that flexible modeling techniques can aid generalization while underscoring the fact that even state-of-the-art statistical techniques still rely on strong assumptions.

I. Introduction

The rapid growth of experimentation in disciplines such as sociology, economics, political science, education, and criminology reflects increasing scholarly emphasis on causal inference in the social sciences. By allocating subjects randomly to treatment and control groups, experimental researchers strive to overcome problems of self-selection and unmeasured confounders. When certain core assumptions are met (e.g., subjects respond only to their own treatment assignments and not the assignments of others and outcome data are observed for all subjects), randomized experiments generate unbiased estimates of the average treatment effect among the experimental subjects (Fisher 1935 [1971]).

The ability to make unbiased inferences about the average treatment effect among the participants in an experiment can be enormously valuable, but experimental researchers often strive to illuminate other causal parameters, such as the average treatment effect among people in other locations or points in time. The term generalization refers to the process by which inferences about the average treatment effect (ATE) from a specific experiment are applied to a target population, a group of subjects who would potentially receive the treatment in a different time, place, or manner. Intuitively, researchers sense that generalization is susceptible to error when the target population differs from the experimental subject pool, although intuitions differ as to the severity of this problem. The adequacy of generalizations based on experimental data is a common source of controversy, for example, in the interpretation of laboratory experiments involving undergraduate subjects.¹ This topic is also receiving increasing attention in education research (e.g., Olsen et al. 2013; Tipton 2013; Tipton et al. 2014).

One way to grapple with the challenge of generalization is to enhance the experimental design. The impetus behind field experimentation, for example, is to narrow the distance between the experimental setting and the real world setting to which experimenters hope to generalize. Another important design idea is to select experimental subjects at random from some broader population so that the experimental results provide unbiased estimates of the ATE in both the sample and the larger population from which the sample was drawn. This strategy has been used in education research in large federal evaluations of Upward Bound, Head Start, and others; a variation of this idea has been proposed in education research by Tipton et al. (2014). A third design idea is to replicate experiments in different settings using a variety of treatments and outcome measures in order to learn about the conditions under which treatment effects vary. Each of these design-based approaches is valuable, but as a practical matter, researchers often encounter practical constraints that limit the range of experiments that may be conducted and the manner in which subjects may be sampled. For example, the extensive experimental literature on police responses to domestic violence (Sherman 1992; Sherman et al. 1992) involves research at multiple sites that were chosen in part because police in those locations were willing to participate in an experiment. Our point is not to find fault with these studies but rather to note that even well-developed research literatures in the social sciences have important gaps, and extrapolation from one setting to another inevitably involves a fair amount of guesswork.

The purpose of this paper is to explore the extent to which generalization may be assisted by statistical techniques that adjust for observed differences between the experimental subject pool and a target population. The problem of generalization we envision grows out of the following scenario. A researcher conducts an experiment and wants to use the results in order to learn about the average treatment effect among a different group of people, the target population. Imagine that the researcher has access to some background information about the experimental subjects (e.g., their age, social class, etc.) and that the same information is available for members of the target population. In some cases, this background information may include untreated outcomes in the target population. The statistical challenge is to use the experimental data to accurately estimate the average treatment effect in the target population.

This scenario has attracted increased scholarly attention, and our work builds on a series of attempts to develop statistical procedures to aid generalization. For example, Hotz, Imbens, and Mortimer (2005) use a bias-corrected matching estimator to forecast the impact of an active-labor market program in a new location based on experimental results from other locations. Cole and Stuart (2010) and Stuart et al. (2010) propose the use of propensity score weighting, and Tipton (2014) suggests propensity score subclassification, all in the context of clinical trials or educational interventions. Hartman, Grieve, and Sekhon (2010), also in the context of a medical trial, use genetic matching in combination with maximum entropy weighting to generalize results beyond the experimental subject pool.

The present paper assesses the performance of a range of statistical approaches to generalizing experimental results and contributes to the literature in the following ways. First, we examine several different propensity-score-based approaches. Second, we evaluate the performance of a relatively new approach based on Bayesian Additive Regression Trees (BART; Chipman et al. 2007; Hill 2012). Third, we extend previous work by looking more closely at how the accuracy of various methods of generalization varies according to the differences between the experimental subject pool and the target population and the way in which observed and unobserved factors moderate the relationship between treatment and outcome. Fourth, we compare the relative bias and efficiency of the approaches using a simulation that is closely calibrated to the “real world” because it is based on data from an actual multi-site field experiment. Fifth, we use data from a multi-site randomized experiment to assess how well an evaluation carried out in just one site would predict the ATE in each of the other sites.

The paper begins by formalizing ideas about treatment effect heterogeneity and spelling out the identifying assumptions under which it is possible to generalize experimental results to a target population. We then discuss the issue of the “alignment” of the covariates— whether covariates important for sample selection are also important contributors to the response surface—and present results from simulations that illustrate the implications for estimation. The remainder of the paper explores the relative efficacy of the methods considered in the context of our calibrated simulations and an actual multi-site experiment.

The results suggest that estimation approaches vary in terms of the accuracy of their forecasts, with the Bayesian nonparametric methods outperforming regression in simulations where generalization is designed to be relatively easy. In simulations where generalization is designed to be challenging (that is, when observed covariates are not sufficient to explain treatment effect heterogeneity across samples), all of the proposed methods perform poorly. In the study with actual experimental benchmarks, some methods perform relatively well, suggesting that actual applications may be more tractable than worst-case scenarios.

II. Notation and Assumptions

This section introduces the statistical notation that will be used throughout the paper. This framework will be useful when contrasting the assumptions required for each of the estimators that we will evaluate.

We follow what has become standard practice in the study of causal inference in statistics and define causal effects as comparisons between potential outcomes, the outcome that manifests if treatment is received, Y (1), and the outcome that manifests if treatment is not received, Y (0). Thus an individual-level causal effect can be defined as the difference between these potential outcomes for the i^th individual, Y_i(1)−Y_i(0). The challenge at the heart of all causal inference is that we can only observe one of these potential outcomes for any given individual.

It is common therefore to focus on causal estimands that average over these individual-level causal effects either across the sample or population. For instance, for a sample of size n, the Sample Average Treatment Effect (SATE) can be defined as ${\mathrm{E}}_S[Y_i(1)-Y_i(0)]=\frac{1}{n}{\sum }_{i=1}^n{Y}_i(1)-Y_i(0)$. Design strategies such as randomized experiments create independence between the potential outcomes and the treatment assignment, Z_i; formally, Y_i(0), Y_i(1) ⊥ Z_i. This property allows us to identify SATE because it implies E_S[Y_i | Z_i = 1] = E_S[Y_i(1) | Z_i = 1] = E_S[Y_i(1)] and E_S[Y_i | Z_i = 0] = E_S[Y_i(0) | Z_i = 0] = E_S[Y_i(0)]. The same argument holds for the identification of the population ATE (PATE), assuming the sample for which we have data is representative of the population.²

A common challenge in causal inference is to identify causal effects in the absence of randomization. In this case researchers often assume that, conditional on a vector of observed covariates X_i, assignment is as good as random: Y_i(0), Y_i(1) ⊥ Z_i | X_i. If this so-called igorability assumption (Rubin 1978) holds, SATE can be identified using similar arguments as above, such as E_S[Y_i | Z_i = 1, X_i] = E_S[Y_i(1) | Z_i = 1, X_i] = E_S[Y_i(1) | X_i], with the added requirement of averaging over the distribution of X, as in E[Y_i(1)] = E_X[E_S[Y_i(1) | X_i]]. Whether ignorability is plausible in any given application is often controversial, since it depends on conjectures about the relationship between treatment assignment and unobserved factors that affect outcomes.

In this paper we address the related challenge of generalizing treatment effect estimates from an experimental sample to a distinct target population with M members indexed by j. We refer to the corresponding causal estimand as the Target Average Treatment Effect, or TATE, defined as ${\mathrm{E}}_T[Y_j(1)-Y_j(0)]=\frac{1}{M}{\sum }_{j=1}^M{Y}_j(1)-Y_j(0)$.³

What assumptions need to hold in order to identify TATE? First, we require the proper implementation of random assignment, such that Y_i(0), Y_i(1) ⊥ Z_i holds. We assume that we have measured a common vector of covariates, X_k, for each individual k across both experimental and target datasets. We further assume that no members of the target population have received the treatment; therefore Z_j = 0 for all j. We will consider two scenarios with regard to the outcomes, one in which Y_j = Y_j(0) is observed for all members of the target population, and one in which it is not observed for any.

First consider the scenario in which Y_j is observed. In this case, since Y_j = Y_j(0) ∀j, the challenge is entirely in estimating E_T [Y_j(1)]. To make inferences about Y_j(1) in the target population, we need to leverage what we know about the relationship between Y_i(1)and X_i in the experimental sample. Defining S_k as the indicator for sample membership— experimental versus target (S_k = 1 for the target population, S_k = 0 for the experimental sample)—and switching to a common index k across members of both, we define the necessary assumption as Y_k(1) ⊥ S_k | X_k. We will refer to this assumption as sample ignorability for treatment potential outcomes. In essence this assumption implies that observations with the same values of X_k would be expected to have the same distribution of Y_k(1) regardless of whether they belong to the experimental sample or target population. In terms of estimation this assumption implies that the information in X_k about Y_k(1) is sufficient to recover the “missing” Y_k(1) given the observed X_k in the target population. See Stuart et al. (2011) for diagnostics that can be used to assess this assumption by comparing Y_k(0) in the experimental and target data sets.

The task is slightly different when Y_j is not observed in the target population. In this case our estimation challenge reduces to using the apparent relationship between X_i and Y_i(1)−Y_i(0) in the experimental data to infer treatment effects in the target population. The required assumption can be expressed as Y_k(1) − Y_k(0) ⊥ S_k | X_k. That is, for those with the same values of X_k, we need the distribution of Y_k(1) − Y_k(0) to be the same in the experimental subject pool and target population. We will refer to this assumption as sample ignorability for treatment effects. One implication of this assumption is that the covariates we need to be concerned about in practice are those that are predictive of sample selection and the treatment effect. It is not clear which of the two sample ignorability assumptions is stronger a priori.

III. Estimators

When the required assumptions from Section II hold, performance differences between estimators will revolve around their ability to appropriately condition on X_k. Strategies that are able to either recover treatment effect moderation in the experimental sample or create balance across experimental and target datasets with respect to those moderators will give the most accurate estimates of the TATE.

A. Linear Regression

One approach to generalization is to build a model for E[Y_k | Z_k, X_k]. Perhaps the simplest approach is to fit a linear regression model of the outcome given treatment assignment and the observed covariates, including treatment by covariate interactions to allow for systematic treatment effect heterogeneity: $\mathrm{E}[Y_k\mid Z_k,X_k]={\beta }_0+{\gamma }_0{Z}_k+{\sum }_{p=1}^P{\beta }_p{X}_{pk}+{\sum }_{p=1}^P{\gamma }_p{X}_{pk}{Z}_k$. When the outcome Y is observed in the target population, this model is fit using both experimental and target data; when Y is not observed in the target population, the model is fit using only the experimental data. The estimated impact in the target population is obtained by generating predicted outcomes under control and treatment for each individual in the target population, taking their differences, and then averaging over these individual-level predicted treatment effects. The downside of this approach is that it relies on relatively strict assumptions about additivity and linearity and can further depend on extrapolation if the covariate distribution in the experimental sample differs markedly from that in the target population.

B. Propensity Score Strategies

The next set of strategies applies propensity score methods for treatment effect estimation in observational studies to the current setting of generalizing treatment effects. In standard applications, the propensity score reflects the probability of being in the treatment group. The treatment and control groups are made similar with respect to the observed covariates (Rosenbaum and Rubin 1983; Stuart 2010) by matching observations in each group based on the propensity score or by weighting each observation by the inverse of its estimated probabilty of receiving treatment.

In our adaptation of this method for generalization, the propensity score models membership in the target (versus experimental) sample (S_k) and the propensity scores are used to make the experimental subjects “look like” the target population. In this approach, target data are used only to model the probability of being in the target population (instead of the experimental sample); this method does not make use of outcome data in the target population, even when they are available. We expect that this approach will work well (1) when the covariates strongly predict membership in the target population and (2) when these predictors are also the moderators of treatment effects.

In particular, we use a form of propensity score weighting that weights the experimental data so that they closely resemble data in the target population, similar in spirit to Horvitz-Thompson weighting in sample surveys (Horvitz and Thompson 1952). An analogous approach was used to account for non-representative samples in Haneuse et al. (2009), Pan and Schaubel (2009), Cole and Stuart (2010), and Stuart et al. (2011). Our weighting method involves three steps: (1) Fit a model of membership in the target dataset (S_k = 1); (2) Construct weights w_k as follows:

$$w_k=\left\{\begin{array}{ll}\hfill 0& \text{if}{S}_k=1\hfill \\ \hfill \frac{{\widehat{e}}_k}{1-{\widehat{e}}_k}& \text{if}{S}_k=0\hfill \end{array}\right\},$$

where ê_k is the estimated propensity score for subject k (the probability of being in the target population); and (3) Using the experimental sample, fit a weighted least squares regression model of the outcome given treatment assignment and the covariates using the weights w_k. The coefficient on the treatment indicator in this outcome model is the estimated TATE.

The weights for all members of the target population are set to zero, since those subjects are not used in the subsequent outcome model. For the experimental sample, the weights serve to make the experimental observations similar to observations in the target population. This is analogous to “weighting by the odds” in the propensity score literature, whereby the control group is weighted to look like the treatment group in order to estimate the average treatment effect on the treated (Harder, Stuart, and Anthony 2010; Hirano, Imbens, and Ridder 2003). Note that the weights w_k are slightly different from those used in Stuart et al. (2010), since in that context the experimental sample was a subsample of the target population. In the context considered here the experimental subjects and target population are disjoint sets, with the propensity score estimated using a stacked dataset of experimental and target observations.

We investigate three methods for estimating propensity scores. First, we use logistic regression that includes a set of covariates as main effects. Second, we use random forests (RF), as implemented using the default settings of the randomForest package for R (Liaw and Wiener 2002). Third, we use generalized boosted regression models (GBM), as implemented using the default settings of the gbm package for R (Ridgeway 2012). While logistic regression is arguably the most common method for estimating propensity scores, recent work has shown that more flexible machine learning methods such as random forests and GBM often work better, especially for propensity score weighting (e.g., Lee, Lessler, and Stuart 2009). RF and GBM both allow for complex, non-linear associations between the predictors and the outcome (membership in the target population, in our application).

For each of these three propensity score estimation approaches, we specify the outcome models in two ways. First, we simply include the covariates in the weighted outcome models. Second, we fit weighted outcome models that allow treatment effects to vary as a function of the covariates; i.e., we include treatment by covariate interactions.⁴ This implementation is closer to the spirit of “double robustness” (Robins and Rotnitzky 2001; van der Laan and Robins 2003) in the sense that we allow the covariates to predict both the selection process and treatment effects. Note that these interactions represent an extension of traditional implementations of doubly robust models. To understand the rationale behind this approach, recall that extrapolation from an experimental sample to a target population will only be biased if two conditions are met: (1) one or more covariates have distributions that differ between experimental sample and target population and (2) these covariates moderate the treatment effect. The inclusion of treatment by covariate interactions allows weighting estimators to address both of these conditions. We refer to these two approaches as IPSW, for “inverse probability of selection weighting,” and DR, for “double robustness.”

C. BART

Propensity score strategies provide one alternative to the often restrictive modeling assumptions of linear regression; another alternative is to directly model E[Y_k | X_k] using a more flexible modeling approach.⁵ In addition to avoiding strict linearity and additivity assumptions, machine learning algorithms automate the detection of treatment by covariate interactions, which may be useful for applications where theory offers little guidance about treatment effect heterogeneity.

Bayesian Additive Regression Trees (BART, Chipman, George, and McCulloch 2007, 2010) is an algorithm that satisfies both requirements. BART previously has been proposed for use in causal inference settings by Hill (2011); its ability to detect heterogeneity in treatment effects has been demonstrated both in that article and by Green and Kern (2012). BART relies on a “sum-of-trees” model that allows for a flexible combination of additive and multivariate features. In particular we let Y_k = E[Y_k | Z_k, X_k] + ε_k, where

$$\begin{array}{l}\mathrm{E}[Y_k\mid Z_k=z_k,X_k=x_k]=f(z_k,x_k)\\ =g(z_k,x_k;T_1,M_1)+g(z_k,x_k;T_2,M_2)+\cdots +g(z_k,x_k;T_V,M_V).\end{array}$$

Here each g(T_v, M_v) denotes the fit from a single small regression tree model, ε_k ~ N (0, σ²), V is typically allowed to be large (the default value in the R dbarts package is 200), and prior distributions are used to avoid overfitting. In particular the prior (probabilistically) constrains the size of each tree to be relatively small (most often 2 to 4 terminal nodes). Additionally, the fit from each tree is shrunk so that its contribution to the total fit is small. The default choices of hyperparameters for this prior appear to work well in practice (see Chipman, George, and McCulloch 2007, 2010). We fit the BART model using a Markov Chain Monte Carlo (MCMC) algorithm and then obtain draws of the random variables f(z, x) and σ from their posterior distributions.

To estimate TATE in the scenario with observed outcome data for the target population, we begin by fitting BART to the combined experimental and target datasets. We then draw from the posterior distributions for f(1, x_j) and f (0, x_j) for each observation in the target population. We combine these draws to create draws from the posterior distribution of the causal effect for each person, d(x_j) = f (1, x_j) − f(0, x_j) and then average these distributions across the target dataset to obtain a Monte Carlo estimate of the posterior distribution of the TATE. The estimation approach in the scenario without observed outcome data is analogous except that BART is fit only to the experimental dataset.

IV. Alignment simulations

The ways in which covariates influence BART and OLS can be quite different from the ways in which they affect propensity score-based estimators. BART and OLS model only the response surface, so the covariates that are most strongly associated with the outcome play the most important roles. Propensity scores are, by definition, determined most strongly by the covariates most associated with sample selection. Modeling selection is helpful in reducing bias in treatment effect estimation only to the extent to which these same covariates are also predictive of the outcome variable. Hill and Su (2013) refer to the degree of symmetry between the covariates’ strength of prediction of treatment selection and strength of prediction of the outcome variable as “alignment.” When the goal is to extrapolate the average treatment effect from an experiment to a target population, alignment takes on a slightly more specialized meaning. Alignment in the context of this inferential goal has to do with the concordance between the covariates’ strength of prediction of the selection mechanism (between experiment and target) and the strength of prediction of the treatment by covariate interactions in the response surface.

A. Simulation set-up

We first test the properties of our estimators using simulations that distinguish between “positively aligned” and “negatively aligned” scenarios. These simulations are not designed as a comprehensive evaluation of the methods; they instead serve a pedagogic purpose, illustrating the implications of parameters (such as alignment) that are examined in more detail in subsequent analyses. We expect the IPSW and DR estimators to perform better in the positively aligned setting than the negatively aligned setting. We also expect the OLS and BART estimators that make use of observed outcomes in the target dataset to perform better than the respective OLS and BART estimators that do not use this information. It is unclear from the outset, however, whether the BART, IPSW, or DR estimators will dominate overall.

In both simulation scenarios two pre-treatment covariates, X₁ and X₂, were generated as independent normal random variables with mean and standard deviation equal to 1. The indicator for selection into experimental versus target datasets, S, was generated using independent random draws from a Bernoulli distribution with the probability of S = 1 given by

$$Pr(S=1)=\frac{1}{1+e^{-({\gamma }_1{X}_1+{\gamma }_2{X}_2)}}.$$

The experimental and target samples comprise a total of 2000 observations. Given the values of γ₁ and γ₂ used (detailed below), the selection model places roughly 500 of the 2,000 observations in the experimental sample.

The response surface is reasonably simple, allowing for effect modification and non-linearity (through a squared term). Presented in potential outcomes notation, the surface can be expressed as

$$\begin{array}{l}\widehat{Y(1)}={\beta }_1{X}_1+{\beta }_2{X}_2+{\varphi }_1{X}_1^2+{\varphi }_2{X}_2+2\\ \widehat{Y(0)}={\beta }_1{X}_1+{\beta }_2{X}_2,\end{array}$$

where ϕ₁ and ϕ₂ reflect the degree of effect modification. For both scenarios, β₁ = β₂ = 1.

We can conceive of positive and negative alignment in this simple setting as the degree of correspondence between the γ coefficients and the ϕ coefficients.⁶ In our positively aligned scenario, X₂ is more important than X₁ both for sample selection and treatment effect heterogeneity (γ₁ = 0.45, γ₂ = .60, ϕ₁ = 0.74, ϕ₂ = 1.20). In our negatively aligned scenario, X₂ plays a stronger role for sample selection than X₁, with γ₁ = .25 and γ₂ = .80, but X₁ is more important for treatment effect heterogeneity, with ϕ₁ = 2 and ϕ₂ = .50. In order to equalize the amount of potential bias across the two scenarios, the average distance between SATE and TATE was forced to be approximately the same across the two settings (about 1.20 in each case).

We evaluate the methods by comparing their standardized bias and root standardized mean square error. Standardized bias is calculated as the average (across simulations) of the estimated effect minus the true effect, divided by the standard deviation of the outcome variable in the target population. The root standardized mean square error (RSMSE) is calculated in an analogous way, as the square root of the average squared standardized bias.

B. Results

Table 1 displays the results from these simulations. OLS (T) and BART (T) refer to the situation in which we observe untreated outcomes in the target population. The IPSW and DR prefixes denote inverse probability of treatment weighted methods and approximately doubly robust methods, respectively. The LR, RF, and GBM suffixes denote logistic regression, random forests, and generalized boosted models, respectively.

Table 1.

Alignment Simulations: Standardized bias and RSMSE

	Standardized bias		RSMSE
Alignment	Positive	Negative	Positive	Negative
OLS (T)	−0.034	−0.020	0.050	0.050
BART (T)	−0.027	−0.017	0.036	0.025
OLS	−0.033	−0.020	0.051	0.051
BART	−0.037	−0.024	0.049	0.034
IPSW-LR	−0.024	−0.019	0.051	0.060
IPSW-RF	−0.214	−0.141	0.217	0.148
IPSW-GBM	−0.032	−0.026	0.050	0.053
DR-LR	−0.006	−0.006	0.038	0.047
DR-RF	−0.021	−0.015	0.043	0.046
DR-GBM	−0.010	−0.014	0.036	0.041

Note: The table shows standardized bias and RSMSE averaged over 10,000 simulated datasets for the alignment simulations discussed in the text. Standardized Bias refers to bias divided by the standard deviation of the outcome in the target dataset. RSMSE refers to Root Standardized Mean Square Error. (T) refers to simulations in which control outcomes are available in the target dataset. OLS denotes linear regression; BART denotes Bayesian Additive Regression Trees; IPSW-LR (IPSW-RF/IPSW-GBM) denotes inverse propensity score weighting with propensity scores estimated using logistic regression (random forests/boosting); DR-LR (DR-RF/DR-GBM) refers to double robust weighted linear regression models with propensity scores estimated using logistic regression (random forests/boosting).

From Table 1, we see that the standardized bias of all methods other than IPSW-RF is relatively small across both scenarios. We therefore focus our discussion on RSMSE. As expected, the IPSW and DR estimators typically perform better in the positively aligned scenario than in the negatively aligned scenario. Also as expected, the OLS estimator has similar performance across the positively and negatively aligned scenarios; since it is based on models of the outcome, the alignment of the predictors in the sample selection and outcome models is less important for OLS than it is for IPSW-based methods, which rely more heavily on models of sample selection. Surprisingly, BART performs better in the negatively aligned case.

When comparing performance across estimators, we find that in the positively aligned scenario BART (T), DR-GBM, and DR-LR have the lowest RSMSE. In the negatively aligned scenario BART and BART (T) perform quite a bit better than any other estimator, with BART (T) having RSMSE at least 60% smaller than that of any other estimator. This was expected given that BART does not privilege covariates that strongly predict the treatment assignment. The second best performing method in the negatively aligned scenario is BART without the target population information, followed by DR-GBM.⁷

IPSW-RF performs surprisingly poorly in both the positively and negatively aligned scenarios, especially in comparison with the other IPSW-based estimators. This seems to be in part due to inaccurate estimation of the probabilities of membership in the target population. RF works well with high-dimensional data that do not follow a true parametric model; our setting, in contrast, is characterized by low-dimensional data following a relatively simple parametric model. In particular, RF works best when the number of variables used to form a decision at each node is quite a bit smaller than the total number of variables in the model; with only two variables in our model our setup is poorly suited for RF. DR-RF in contrast performs reasonably well, which highlights the advantages of double robustness. Although the selection model estimated by RF is very poor (as reflected in the poor performance of IPSW-RF), the outcome model is able to compensate, so that the performance of DR-RF is close to the performance of the other DR estimators.

V. Calibrated Simulations

We further explore the performance of these estimators in a setting that is more closely calibrated to a realistic application. We crafted a simulation that uses real data from the evaluation of the School Dropout Demonstration Assistance Program (SDDAP) (Dynarski at al. 1998). Specifically, we use the pre-treatment covariates, the randomized treatment indicator (for the experimental sample), and the observed selection mechanism between experimental sample and target population. We then simulate outcome data calibrated to closely match the empirical response surface for one of the outcomes from the experimental evaluation. The SDDAP dataset, which has been used in other methodological work on causal inference (e.g., Agodini and Dynarski 2004; Stuart and Rubin 2008), contains a rich mix of continuous and binary covariates that are theoretically predictive of the outcome, making it well suited for the kind of simulation exercise we conduct here.

A. Data and selection mechanisms

The SDDAP was an initiative carried out by the U.S. Department of Education from 1991 to 1996 with the goal of reducing high school dropout. The initiative was carried out in 85 middle and high schools. SDDAP was a combination of “restructuring” efforts that treated entire schools, putting in place programs and policies designed to reduce dropout, and “targeted” efforts, which involved targeting individual at-risk students for intervention. The specific entry criteria for the targeted programs varied across schools, but all were designed for students deemed to be at high risk of dropping out of school. Services offered by the targeted programs included intensive instruction, attendance monitoring, and counseling. An evaluation of the SDDAP program was carried out by Mathematica Policy Research, Inc. and consisted of two components: (1) a non-experimental study comparing schools with school-wide restructuring efforts to comparison schools in the same geographic area and (2) a randomized experiment with at-risk students randomized to the dropout prevention programs or a control condition. The evaluation collected baseline data and 2 to 3 years of follow-up data for each student based on student questionnaires and administrative records. In this study we will use data from the randomized trial, which was carried out in 8 middle and 8 high schools across the country. We will focus on the middle schools, for which there was more evidence of intervention effects (Dynarski et al. 1998). See Dynarski et al. (1998) for more details on the programs under study and the evaluation itself.

For our simulations, we restrict the SDDAP dataset to 5 of the 8 original middle school experimental sites (Flint, Newark, Rockford, Sweetwater, Miami; total n = 2,118) for which there are sufficient baseline and post-treatment outcome measures. (The covariates and outcomes measured varied across sites). As we will describe next, we divide these 5 sites into “experimental samples” and “target populations” so as to maximize the overall difference between the experimental and target sites with respect to covariates that moderate the treatment effect. We start by selecting 35 covariates—10 continuous and 25 binary— plausibly related to treatment effect heterogeneity (see Table 2 for a list of covariates). All continuous covariates are standardized to have mean 0 and standard deviation 1. We also use the randomly assigned treatment indicator from the SDDAP evaluation and one of the quasi-continuous post-treatment outcomes, Year 1 math test scores. We impute missing data once using iterative regression imputation (Su et al. 2011).

Table 2.

Descriptive statistics for Calibration Simulations

Covariate	Sample Mean		|Standardized Difference|
	Experimental	Target
Cohort†	0.76	0.50	0.52
Age	12.34	13.43	1.51
Number of schools attended since 1st grade	3.02	3.31	0.16
Female	0.45	0.51	0.14
Number of siblings†	2.87	2.79	0.05
Educational aspirations	2.63	2.71	0.13
Educational expectations	2.30	2.37	0.10
Sure of graduating from high school	0.60	0.68	0.16
Homework	0.84	0.72	0.26
Talk about school with parents	0.95	0.96	0.08
Sibling dropped out	0.29	0.22	0.17
Ever skip school	0.18	0.12	0.18
Ever late for school	0.54	0.53	0.02
Extracurricular activities†	0.70	0.74	0.10
Reading more than 2 hrs/wk	0.32	0.32	0.00
TV more than 2 hrs/day†	0.74	0.73	0.01
Mother employed	0.53	0.63	0.22
Mother has BA or higher	0.29	0.21	0.21
Father employed†	0.71	0.81	0.25
Father has BA or higher	0.28	0.25	0.08
Not living with both parents†	0.37	0.44	0.16
Family receives public assistance	0.58	0.35	0.48
Primary language not English	0.07	0.08	0.03
Overage for grade	0.83	0.46	0.73
Low grades	0.15	0.23	0.18
Discipline problems at school	0.68	0.52	0.32
External locus of control	0.65	0.45	0.40
Self-esteem	−0.08	0.01	0.14
School climate†	0.14	0.14	0.00
Baseline math test score†	28.16	39.17	0.58
Baseline reading test score†	26.06	37.25	0.63
% days absent (log)	−1.78	−1.87	0.27
Black	0.02	0.17	0.40
White	0.34	0.20	0.34
Hispanic	0.48	0.44	0.08

Note: The table shows experimental sample and target population means for all 35 covariates used in the Calibration Simulations. The last column shows absolute standardized differences, i.e., the absolute value of the difference between experimental and target means divided by the standard deviation in the target population.

^†denotes covariates that moderate the treatment effect at at least 3 out of 5 sites (see text).

We examine how often each covariate moderates the treatment effect on Year 1 math test scores across the 5 sites using a series of linear regression models (not shown). For 9 of the 35 covariates, there is evidence of significant treatment effect heterogeneity for at least 3 sites. We then use these 9 covariates to compute a Mahalanobis distance between experimental and target sites for each of the $\left(\begin{array}{c}5\\ 2\end{array}\right)=10$ possible divisions of the 5 sites into groups of 2 and 3. Based on the largest of these Mahalanobis distances, we select Newark, Rockford, and Sweetwater as our experimental sites (n = 382) and Flint and Miami for our target populations (n = 1,736).⁸ This procedure leads to experimental and target sites that are relatively far apart in terms of covariates that moderate the treatment effect (Table 2 lists the means and standardized differences), making generalization from the experimental sample to the target population more challenging.⁹

B. Simulation design factors

Recall that we simulate exclusively the outcome variable and consider covariates to be fixed. Our simulations vary three distinct design factors. The first design factor varies whether the outcome models differ across target and experimental sites (factor levels labeled either “ignorable” or “non-ignorable” sample selection). The second design factor varies whether covariates enter the model for simulated outcomes linearly or non-linearly (factor levels labeled as “linearity” or “non-linearity”). The third design factor varies the relationship between sample selection and treatment effect heterogeneity. Similar to the alignment simulations above, positive (negative) alignment indicates that covariates that are important for sample selection are important (unimportant) for treatment effect heterogeneity.

C. Simulating outcome data for the baseline case of ignorable sample selection and linear response surface

We discuss our strategy for simulating outcome data that closely match the observed outcomes first for the baseline case of ignorable sample selection and linearity. We start by regressing the observed outcome variable (Year 1 math test scores) on the covariates listed in Table 2, the randomly assigned treatment indicator, and a set of two-way interaction terms between the treatment indicator and each covariate. The inclusion of these interaction terms allows us to capture systematic treatment effect heterogeneity (Djebbari and Smith 2008). Note that this regression model for the outcome variable is fit to the pooled experimental and target data. Based on the model fit, we simulate a new vector of regression coefficients as described in Gelman and Hill (2006: 142–143).¹⁰ Each of these simulated vectors of regression coefficients is then multiplied by two versions of the design matrix from the regression model, that is, the matrix containing the covariates, the treatment indicator, and their interactions (plus a constant). One version of the design matrix sets the treatment indicator to 1 for all observations (adjusting the interaction terms accordingly); this yields simulated treated outcomes. The other version of the design matrix sets the treatment indicator to 0 for all observations; this yields simulated control outcomes. Finally, we add independent, identically distributed normal noise to each simulated outcome, where the variance of the noise distribution is the same as the residual variance from the regression model.¹¹ This process yields simulated outcomes both under control and treatment for observations in the experimental sample as well as the target population.

Our simulation procedure ensures that the distribution of simulated outcomes closely matches the distribution of observed Year 1 math test scores. Moreover, the simulation procedure preserves the systematic treatment effect heterogeneity present in the observed data, so that the magnitude of systematic treatment effect heterogeneity in our simulations mirrors the level of systematic treatment effect heterogeneity that researchers can expect when analyzing “real” datasets (or at least the SDDAP data). This is important since, ceteris paribus, the greater the amount of systematic treatment effect heterogeneity, the more challenging it is to generalize experimental results to target populations. In this sense our simulations provide a realistic challenge that is informative about the difficulty of generalizing experimental impact estimates beyond our specific set of simulations. Finally, since we simulate outcomes but retain the original covariates, our data resemble the data that experimentalists typically encounter.

D. Modifications to reflect other levels of the design factors

We modify this basic approach to simulating outcome data in three ways to create scenarios that differ in how challenging it is to infer TATE from the experimental results. Recall that our first design factor varies whether response surfaces are the same for the experiment and target. In order to mimic the situation in which response surfaces differ, we fit separate regression models for observed Year 1 math test scores in the experimental and target datasets. Since the parameters governing the data generating process for our simulated response surfaces are now different, both ignorability assumptions will be violated; we therefore refer to the levels of this design factor as ignorable and non-ignorable sample selection.

The second design factor is linearity/non-linearity of the model for simulated outcomes. In the non-linear setting, we additionally include squared terms for the 10 continuous covariates (also interacted with the treatment indicator) in the regression model that is fit to the observed Year 1 math test scores and then used to generate simulated outcomes. This makes modeling the relationship between simulated outcomes and covariates more difficult, since estimators will be unaware that the data generating process includes squared terms. In other words, response surface models that fail to include these squared terms will be misspecified. Estimators that estimate TATE by correcting for sample selection instead of directly modeling the response surface will be unaffected by this modification if they are able to correctly model the sample selection process.

Our third design factor (positive or negative alignment) varies the relationship between sample selection and treatment effect heterogeneity. This design factor is motivated by the property discussed in Section II. Conceptually, even if a covariate is strongly predictive of sample selection but does not modify the treatment effect, it is not necessary to adjust for it in order to obtain an unbiased estimate of the treatment effect in the target population. We are thus most concerned about covariates that strongly predict both sample selection and treatment effect heterogeneity. We consider two settings in which covariates that influence sample selection are either strong or weak moderators of the treatment effect. We do this by regressing sample selection (i.e., membership in the target dataset) on the covariates using a linear probability model. We then align the importance of the interaction term coefficients from the regression model for observed Year 1 math test scores with the coefficients from this sample selection model. In particular, separately for binary and continuous covariates, we rank order the coefficients in the sample selection model based on their absolute value. We then use these two rank orderings to reshuffle interaction term coefficients for binary and continuous covariates from the regression model for observed Year 1 math test scores.

To pin down ideas, imagine that in the sample selection model age has the largest coefficient among all continuous covariates (recall that continuous covariates are standardized so coefficients are directly comparable). When simulating new coefficient vectors based on the regression model for observed Year 1 math test scores in the positive alignment setting, we assign the largest coefficient (in absolute value) among the 10 interaction term coefficients for continuous covariates to age. In this way sample selection and treatment effect heterogeneity are positively aligned: age is an important predictor both of whether a subject is in the experimental or target dataset and of this subject’s treatment effect.

Conversely, we also generate a negatively aligned setting in which covariates that are important for sample selection are unimportant for treatment effect heterogeneity. We do this by reversing the rank orderings before reassigning interaction term coefficients. All else equal, when ignorability holds, the positively aligned setting should pose a more difficult challenge for all estimators. On the other hand, the negatively aligned setting should yield a relative advantage for estimators that model the response surface since they will tend to give more weight to the strongest effect moderators. Estimators that model only the sample selection process should benefit from the positively aligned setting.

Our three design factors yield 8 distinct simulation scenarios: ignorable/non-ignorable sample selection × linearity/non-linearity × positive/negative alignment. For each scenario, we create 10,000 sets of simulated outcomes. The results reported below refer to the performance of our estimators across these sets of simulated outcomes.

E. Results

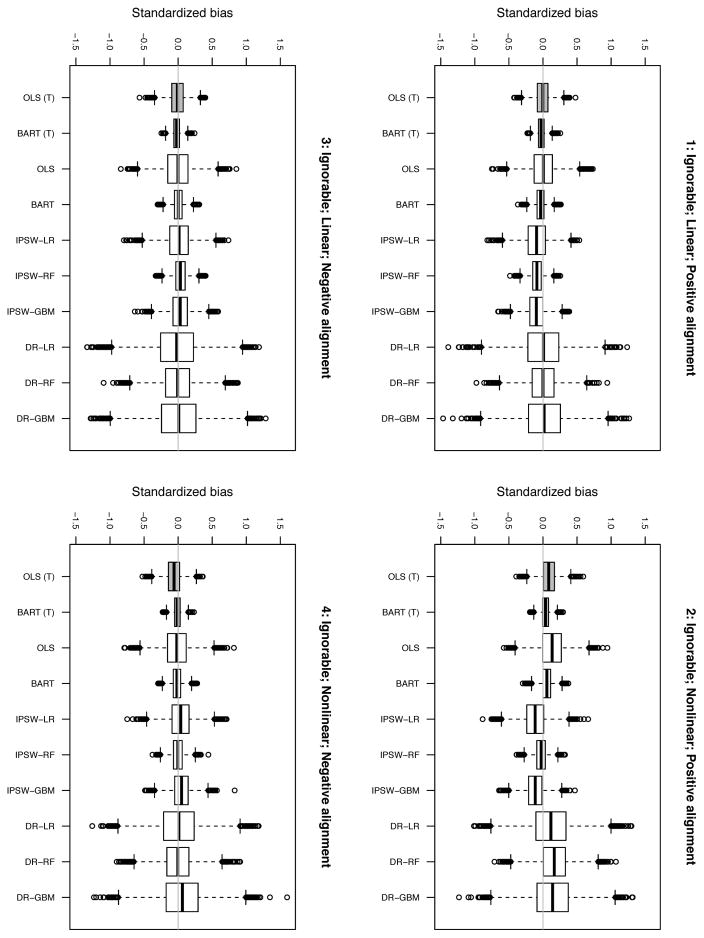
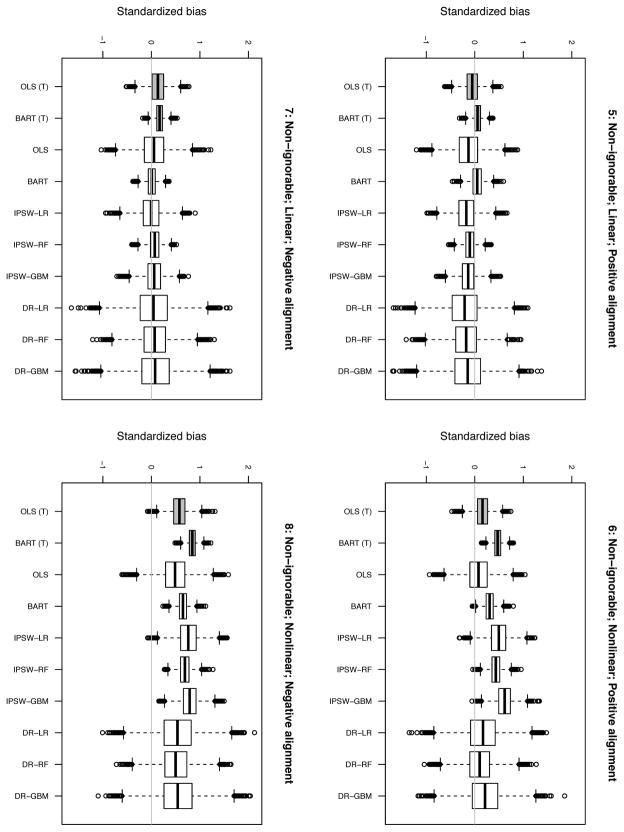
Figures 1 and 2 display results. Estimator labels are the same as in Table 1.

Figure 1.

Results for ignorable scenarios 1–4

Figure 2.

Results for non-ignorable scenarios 5–8

E.1. Ignorable setting

We begin by discussing the results for simulations in which the ignorability of sample selection assumption is satisfied, displayed in Figure 1. For linear response surfaces, regardless of whether alignment is positive or negative (scenarios 1 and 3), all of the estimators are either unbiased or nearly so (within 0.1 standard deviations; see Table 3). OLS and the DR estimators show the smallest bias across both of these settings. The primary difference between estimators is the variability of their estimates (see Table 4 for RSMSE estimates). OLS (T) and BART (T), which take advantage of the target outcomes, have lower RSMSE than OLS and BART, which ignore this information. Among the estimators that ignore the target outcomes, BART and IPSW-RF have the lowest RSMSE by a wide margin, with IPSW-RF and IPSW-GBM achieving the next best RSMSEs. The DR estimators perform worst with regard to RSMSE (although the random forests version is noticeably better than the other two).

Table 3.

Calibration Simulations: Standardized bias

Scenario	1	2	3	4	5	6	7	8	avg bias	avg bias
	Ignorable				Non-ignorable				Ignorable	Non-ignorable
OLS (T)	0.00	0.09	−0.01	−0.06	−0.05	0.16	0.13	0.58	0.00	0.20
BART (T)	−0.02	0.04	−0.02	−0.01	0.06	0.47	0.17	0.84	0.00	0.39
OLS	0.00	0.13	0.00	−0.02	−0.13	0.08	0.05	0.49	0.03	0.12
BART	−0.04	0.06	0.00	−0.02	0.05	0.31	0.01	0.65	0.00	0.25
IPSW-LR	−0.09	−0.11	0.01	0.04	−0.17	0.49	−0.01	0.76	−0.04	0.27
IPSW-RF	−0.09	−0.03	0.03	0.00	−0.10	0.43	0.07	0.69	−0.02	0.27
IPSW-GBM	−0.10	−0.11	0.03	0.05	−0.14	0.61	0.06	0.79	−0.03	0.33
DR-LR	0.01	0.12	−0.02	0.01	−0.21	0.16	0.05	0.54	0.03	0.14
DR-RF	0.00	0.17	−0.01	0.00	−0.18	0.10	0.07	0.50	0.04	0.12
DR-GBM	0.02	0.14	0.01	0.06	−0.15	0.21	0.08	0.55	0.06	0.17

Note: All results reported here average over 10,000 simulated datasets. See Figures 1 and 2 for a description of the scenarios. Standardized Bias refers to bias divided by the standard deviation of the outcome in the target population. (T) refers to simulations in which control outcomes are available in the target dataset. OLS denotes linear regression; BART denotes Bayesian Additive Regression Trees; IPSW-LR (IPSW-RF/IPSW-GBM) denotes inverse propensity score weighting with propensity scores estimated using logistic regression (random forests/boosting); DR-LR (DR-RF/DR-GBM) refers to double robust weighted linear regression models with propensity scores estimated using logistic regression (random forests/boosting). The last two columns show the average standardized bias for the ignorable (1–4) and non-ignorable (5–8) scenarios.

Table 4.

Calibration Simulations: RSMSE

Scenario	1	2	3	4	5	6	7	8	avg RSMSE	avg RSMSE
	Ignorable				Non-ignorable				Ignorable	Non-ignorable
OLS (T)	0.11	0.15	0.13	0.14	0.17	0.22	0.22	0.60	0.13	0.30
BART (T)	0.06	0.08	0.07	0.06	0.11	0.48	0.19	0.85	0.07	0.41
OLS	0.20	0.24	0.22	0.21	0.31	0.28	0.30	0.57	0.22	0.37
BART	0.08	0.10	0.08	0.08	0.14	0.33	0.11	0.66	0.09	0.31
IPSW-LR	0.21	0.22	0.20	0.19	0.28	0.54	0.24	0.80	0.20	0.47
IPSW-RF	0.13	0.10	0.11	0.10	0.16	0.45	0.14	0.70	0.11	0.36
IPSW-GBM	0.17	0.18	0.16	0.16	0.23	0.64	0.20	0.81	0.17	0.47
DR-LR	0.33	0.35	0.36	0.34	0.44	0.41	0.42	0.68	0.34	0.48
DR-RF	0.24	0.29	0.26	0.24	0.36	0.32	0.34	0.60	0.26	0.40
DR-GBM	0.34	0.37	0.37	0.35	0.42	0.44	0.43	0.69	0.36	0.50

Note: All results reported here average over 10,000 simulated datasets. See Figures 1 and 2 for a description of the scenarios. RSMSE refers to Root Standardized Mean Square Error. (T) refers to simulations in which control outcomes are available in the target dataset. OLS denotes linear regression; BART denotes Bayesian Additive Regression Trees; IPSW-LR (IPSW-RF/IPSW-GBM) denotes inverse propensity score weighting with propensity scores estimated using logistic regression (random forests/boosting); DR-LR (DR-RF/DR-GBM) refers to double robust weighted linear regression models with propensity scores estimated using logistic regression (random forests/boosting). The last two columns show the average RSMSE for the ignorable (1–4) and non-ignorable (5–8) scenarios.

The relative performance of the estimators in the nonlinear, negative alignment setting (4) closely follows that of the linear settings. BART (T) and BART once again lead with regard to RSMSE, followed closely by IPSW-RF. Once again the DR estimators (particularly LR and GBM) perform worst with regard to RSMSE.

The nonlinear positive alignment setting (2) is more challenging for all estimators. IPSW-RF, BART (T), and BART show the smallest standardized bias (absolute values range from .03 to .06). The other estimators demonstrate substantially more bias (with absolute values ranging from .09 to .17). Similar but stronger patterns exist with regard to RSMSE. BART (T), BART, and IPSW-RF perform best in terms of RSMSE while the DR estimators perform particularly poorly.

In sharp contrast to the results of the earlier alignment simulations, IPSW-RF performs exceptionally well in these 4 scenarios. This lends weight to the argument that its poor performance in prior simulations was at least partially due to the very small number of covariates. In contrast, the performance of IPSW-GBM is much less impressive here.

Finally, it is interesting to note the contrast between the IPSW and DR estimators. The DR estimators, as we would predict, yield estimates with much greater variability than the IPSW estimators. On the other hand, the bias of the DR estimators is typically quite small and often somewhat smaller than the bias of the IPSW estimators. The exception is scenario 2. Here we know that the outcome model is misspecified; it appears that the selection models are not close enough to the truth for the double robust properties to kick in.

E.2. Non-ignorable scenarios

The results from the four non-ignorable scenarios (5–8) are displayed in Figure 2. In these settings, none of the estimators has sufficient information to accurately recover the TATE because the response surfaces are different in the experimental and target datasets.

Results for the linear, negative alignment scenario (7) are the most similar to the results for the ignorable scenarios. The estimators that ignore the target outcomes are virtually unbiased and follow the same pattern as in the ignorable setting with regard to RSMSE.

Interestingly, the methods that use the target outcomes perform slightly worse than before; these methods are able to capture Y (0) well but have a hard time with Y (1). Methods that do not exploit information about Y (0) in the target dataset seem to benefit from the fact that their bias in estimating Y (0) cancels out some of the bias in estimating Y (1).

The results from the linear, positive alignment setting (5) follow a slightly different pattern with all but OLS (T) and the BART estimators exhibiting noticeable bias; IPSW-LR, IPSW-GBM, and the DR estimators are the worst offenders. RSMSEs follow the usual pattern.

The nonlinear, positive alignment scenario (6) exhibits a vastly different pattern with regard to bias. Here OLS and the DR estimators outperform all the others (standardized bias ranging from .08 to .21, with BART next (.31). OLS (T), OLS, and DR-RF perform the best with respect to RSMSE. IPSW-LR and IPSW-GBM exhibit by far the worst RSMSEs. The nonlinear, negative alignment setting (8) results are similar to the comparable positive alignment setting (6) except that in (8) none of the estimators are able to eliminate the bias.

VI. Comparison of methods using real data with experimental benchmarks

In this section we move from simulations to a test of the methods based on real data, where the ignorability assumption may or may not be satisfied. This allows us to assess the potential efficacy of the methods we are considering in a situation similar to what a researcher might genuinely encounter.

We use data from the Infant Health and Development Program (IHDP). This study targeted 985 infants in eight sites across the United States who were born preterm with low birth weight. Approximately one third of the infants were then randomly assigned (within site) to receive an intervention consisting of intensive, high quality center-based child care in years two and three of life as well as home visits and parenting support groups in years one through three (Brooks-Gunn et al. 1994). The effect on the average score for the Peabody Picture Vocabulary Test (PPVT) at age three (across all sites) was 6.8 points with standard error of .9; since the PPVT is scaled similarly to an IQ measure (with a standard deviation of 15), this is a large effect size.

A. Benchmarking set-up

Given that random assignment took place within site, we can consider each site to be a separate randomized experiment. Importantly for our purposes, the average treatment effect also varied substantially across sites with estimates (from separate regressions of the outcome on the treatment assignment and the covariates discussed below) ranging from 3.1 to 11.6.¹² Thus, a reasonable test of the comparative efficacy of the methods considered in this paper is to evaluate the accuracy of estimates when generalizing the results from one site to another. The mother-specific covariates available to support this prediction (measured at time of birth) are her age, educational attainment, ethnicity (black, white, Hispanic), marital status, receipt of prenatal care, and whether she worked, drank alcohol, or used drugs while pregnant. Child-specific covariates are sex, birth weight (plus an indicator for less than 2500 grams), weeks born preterm, first-born status, and age at time of test. Father’s ethnicity and household income as well as income-to-needs ratio are also available.¹³

We examine all possible (8 × 7) pairs of distinct sites. Specifically, for each site, we generalize the experimental results from that site to each of the seven other target sites and then compare the projected estimates in any given target site with the experimental benchmark for that site. We move to this IHDP example and away from the SDDAP in part to illustrate the methods in another setting (child care) and also because the intervention is more standardized than the interventions implemented in the SDDAP schools; it is thus more plausible that the effects will be stable across sites and thus a better example to use for this benchmarking exercise.

B. Results

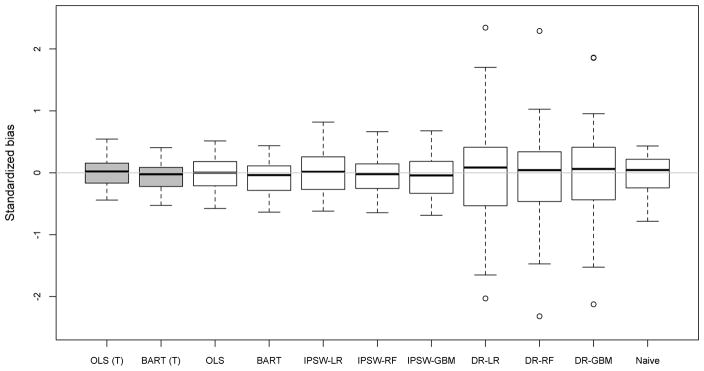
Table 5 and Figure 3 summarize the results from generalizing impacts from each IHDP site to each of the other sites (all 8 × 7 possible pairings of “source” and “target”) using each of the generalization methods. In these results we see substantial variation across methods with respect to RSMSE but less variation with respect to standardized bias.¹⁴

Table 5.

Projection of Site-Specific Impacts: Standardized Bias and RSMSE

	Standardized bias	RSMSE
OLS (T)	0.008	0.230
BART (T)	−0.058	0.224
OLS	−0.006	0.267
BART	−0.067	0.265
IPSW-LR	0.014	0.368
IPSW-RF	−0.025	0.297
IPSW-GBM	−0.054	0.345
DR-LR	0.102	1.212
DR-RF	−0.075	0.729
DR-GBM	−0.056	0.747
Naive	−0.010	0.280

Note: All results reported here average over the 8 × 7 = 56 combinations of experimental and target sites. Standardized Bias refers to bias divided by the standard deviation of the outcome in the target dataset. RSMSE refers to Root Standardized Mean Square Error. (T) refers to simulations in which control outcomes are available in the target dataset. Naive denotes no adjustment; OLS denotes linear regression; BART denotes Bayesian Additive Regression Trees; IPSW-LR (IPSW-RF/IPSW-GBM) denotes inverse propensity score weighting with propensity scores estimated using logistic regression (random forests/boosting); DR-LR (DR-RF/DR-GBM) refers to double robust weighted linear regression models with propensity scores estimated using logistic regression (random forests/boosting). Naive refers to the simple difference in means in the experimental sample.

Figure 3.

Results for Projection of Site-Specific Impacts

The method that shows the least standardized bias (.006) when predicting site-specific impacts is OLS. Next best with respect to standardized bias are OLS (T), IPSW-LR, and IPSW-RF (all with absolute standardized biases of less than 0.03). Arguably, however, all of the standardized bias numbers are quite small in terms of practical significance given that they are all less than .11 in standard deviation units.

The methods show far more substantial variation as well as different rankings with respect to RSMSE. BART (T) and OLS (T) show the smallest RSMSE, which is in part attributable to the additional data used by those estimators. However, even with respect to the estimators that do not utilize outcomes in the target group, BART and OLS remain the best, with the naive estimator and the IPSW approaches relatively close behind. The methods with by far the worst performance with regard to RSMSE are the Doubly Robust (DR) approaches, whose RSMSE is two or three times as large as the RSMSE for the other estimators.

VII. Conclusion

This paper considers a special case of the generalization problem: using data from an experiment to make inferences about a distinct target population when a common set of covariates is available. We employed a variety of approaches to shed light on this problem: Monte Carlo simulations, simulations carefully calibrated to actual data, and empirical benchmarking. Our assessment of different estimators suggests that there is no universally dominant approach that performs well across a range of different scenarios.

When sample ignorability holds, some of the methods considered here do an adequate job of forecasting average treatment effects in the target population. In this setting the advice appears to be reasonably simple: use BART or IPSW-RF. At the same time, we cannot recommend the use of approximately doubly robust estimators. Even though they sometimes have a slight edge in standardized bias, their poor performance in terms of RSMSE severely limits their usefulness. Utilizing target outcomes when they are available often makes sense, although it is possible to construct scenarios in which this additional information fails to improve accuracy.

One surprising result from our simulations is that, overall, linear regression performed better than expected; this leads one to wonder if it is worthwhile for researchers to adopt more sophisticated methodological strategies. Two caveats should be stressed. The first is that since we generated our simulated data using a linear regression (albeit with many quadratic terms but otherwise respecting the OLS assumptions), we may have tilted the playing field in favor of linear regression; it should be the best fitting line to the non-linear response surface that we created. The second caveat is that linear regression tends to fall apart when the covariate distribution in the experimental dataset does not overlap with the covariate distribution in the target dataset (see for example, Hill 2011). This situation is not present in our calibration simulation scenarios. By using data from a real evaluation, we sought to craft simulations that are representative of the type of overlap that would occur in practice, but it is not hard to imagine scenarios in which the lack of overlap would be much more extreme (e.g., extrapolation from education experiments conducted on American undergraduates to primary school students in developing countries).

While most papers investigating the efficacy of methodological strategies in non-experimental studies tend to assume that the appropriate form of ignorability holds, our work also explores the implications when ignorability fails. In the scenarios explored by our SDDAP simulations, none of the methods performs reliably. Although the SDDAP simulations cover only a small range of possible data generating processes, the fact that we can so easily construct simulations that thwart accurate generalization tempers some of the enthusiasm for sophisticated estimation methods. Although such methods tend to perform better than naive extrapolation, their inadequacy when ignorability fails suggests that researchers must attend first and foremost to ensuring that ignorability is satisfied through clever designs or comprehensive and intelligent data collection.

Relatedly, if sample ignorability is doubtful, it may be helpful to investigate the extent of non-linearity in the experimental data. Although experimental results may not reflect relationships in the target population, it seems reasonable to believe that strong evidence of nonlinearity in the experimental data implies some degree of nonlinearity in the target, even if the actual model coefficients predicting the response surfaces differ. If substantial non-linearity exists and ignorability is in question, it is probably unwise to proceed with the analysis.

Our IHDP example provides a reassuring counterpoint to our SDDAP simulation results. Although there is no guarantee that ignorability is satisfied in this setting, all of the methods tested demonstrate low standardized bias. The fact that BART and OLS perform best with regard to RSMSE in this setting reinforces some of the lessons learned from our SDDAP simulations.

While the IHDP results are encouraging, this multi-site experiment represents something of a best-case scenario in terms of data requirements. A rich set of individual-level covariates was available across the sites we studied, whereas when extrapolating to a target population, researchers are often limited to a small set of variables that are measured only at the aggregate level (see, for example, Cole and Stuart 2010). This constraint may prevent researchers from extrapolating based on the results from multivariate models of treatment effect moderation, since the multivariate distribution of the covariates in the target population is only partially observed. One might circumvent this problem by making assumptions about the covariate distribution in the target population, but that adds another layer of uncertainty to the problem of generalization. The current paper also raises many open questions for future work, including covariate selection and the role of sample size (of both the experimental sample and the target population) in the performance of the approaches.

The challenges of generalization go much deeper than the lack of comparable individual-level measures across sites. Generalization presents formidable problems of inference because researchers typically have no direct way to ascertain whether sample ignorability holds. Researchers may have theoretically-grounded conjectures about ignorability, but testing them is difficult, ironically, because it is hard to construct a research design that is sufficiently general to convincingly assess when generalization is likely to be successful. That said, one potentially fruitful line of research would be to gather a wide array of multi-site experiments (i.e., studies in different locations that employ similar treatments, outcomes, and covariates) and compare the forecasting accuracy of various statistical approaches. This type of investigation would not only shed light on the relative merits of different statistical approaches but could also suggest features of cross-site comparisons that are conducive or unconducive to generalization.