Electrostatic component of binding energy: Interpreting predictions from Poisson-Boltzmann equation and modelling protocols

Abstract

Macromolecular interactions are essential for understanding numerous biological processes and are typically characterized by the binding free energy. Important component of the binding free energy is the electrostatics, which is frequently modeled via the solutions of the Poisson-Boltzmann Equations (PBE). However, numerous works have shown that the electrostatic component (ΔΔG_elec) of binding free energy is very sensitive to the parameters used and modeling protocol. This prompted some researchers to question the robustness of PBE in predicting ΔΔG_elec. We argue that the sensitivity of the absolute ΔΔG_elec calculated with PBE using different input parameters and definitions does not indicate PBE deficiency, rather this is what should be expected. We show how the apparent sensitivity should be interpreted in terms of the underlying changes in several numerous and physical parameters. We demonstrate that PBE approach is robust within each considered force field (CHARMM-27, AMBER-94 and OPLS-AA) once the corresponding structures are energy minimized. This observation holds despite of using two different molecular surface definitions, pointing again that PBE delivers consistent results within particular force field. The fact that PBE delivered ΔΔG_elec values may differ if calculated with different modeling protocols is not a deficiency of PBE, but natural results of the differences of the force field parameters and potential functions for energy minimization. In addition, while the absolute ΔΔG_elec values calculated with different force field differ, their ordering remains practically the same allowing for consistent ranking despite of the force field used.

GRAPHICAL ABSTRACT

Poisson –Boltzmann framework for implicit solvent models deliver results that are sensitive to various physical and numerical input parameters. This should not, however, be interpreted as its weakness. Emphasis is given on what these variations indicate when one considers different force fields, extents of minimization and method of dielectric assignment. All these interpretations are made in terms of the electrostatic component of binding energy ΔΔG_elec of binary protein complexes.

Introduction

Interactions of biomolecules, namely proteins and nucleic acids, are essential for many biological activities in a living cell. These interactions are typically characterized via the binding free energy^1–3. The binding free energy is a complex quantity composed of various energy terms and many methods have been developed to predict it^4,5, including approaches for modeling the binding free energy changes caused by mutations^6–8. Among the various energy terms contributing to the binding free energy, the electrostatics plays prominent role due to its long-range nature^9–11. Simultaneously, its importance is substantiated by the fact that the biological macromolecules are, in general, ubiquitously charged.

From computational stand-point the electrostatics in molecular biology is modeled via various approaches roughly classified as explicit and implicit approaches^12–18. A particular case of implicit modeling is utilizing Poisson-Boltzmann equation (PBE) to deliver the potential distribution and the corresponding electrostatic energy components^11,19,20. A number of computational packages devoted exclusively for solving the PBE have been developed such as DelPhi²¹, MIBPB²², PBSA²³ and APBS²⁴. The continuum approaches have been successfully used for pH-dependent simulations^25–27, end-point free energy calculations²⁸, calculation of electrostatic components of interaction energy of molecules¹¹ and effects of mutations⁸, determination of protein pKa values^29,30, solving electrostatics of nucleic acids³¹ and numerous other examples^19,32.

Despite abovementioned successes, the applicability PBE to model electrostatic energies in molecular biology has been discussed especially with regards to sensitivity of obtained solutions to the input parameters of the system and the modeling protocol^16,33–38. It was demonstrated that PBE approach is accurate in predicting solvation free energy^39–42, folding free energy change caused by mutations⁴³ and salt dependence of the binding free energy^44,45 as compared with either experimental quantities or results from explicit water calculations. However, there is no consensus on the applicability of PBE to model the electrostatic component of binding free energy^34,37,39. Perhaps the main reason is that there is no experimental data for the electrostatic component of binding free energy, since there is no mean of decoupling electrostatic term from the combination of all the other interaction energy terms via experiments. Computationally, one can evaluate the performance of PBE of modeling macromolecular interactions by comparing with the results obtained via explicit water modeling of hydration energies of the complex and unbound monomers ^46–48. However, such a benchmarking is dependent on the force field and modeling protocol⁴⁶. In parallel, PBE is frequently used within Molecular Mechanics Poisson-Boltzmann Surface Area (MMPB/SA) approach^49–53, and thus the calculated electrostatic component of the energy depends on the applied force field parameters and 3D structures used in MMPB/SA analysis⁵⁴. The abovementioned examples and the lack of experimental data indicate that there is no absolute value of the “correct” magnitude of electrostatic component of binding free energy. Rather it is force field dependent.

Not surprisingly, attempts at developing protocols for PBE based implicit modeling have been a significant topic of research and discussion. The literature has several publications that list suggestions for modeling in PBE framework by acknowledging many different parameters (and their combinations) that must be considered prior to drawing affirmative conclusions from the PBE solver outputs ³⁷. As has been discussed by Sorensen et. al.³⁵, these parameters could be of physical importance as well as bear computational significance. The physical parameters to PBE include the solute-solvent dielectric, charge/radius combination for atoms (force field parameters), concentration of salt in the solution and several others. The computational parameters include the grid resolution (quintessential to the finite difference method employed for solving PBE by the solvers), description of solute-solvent interface, corrections to the energies due to discretization of 3D space, placement of solute in the box and the volume occupied by it and many others ³⁵.

In this paper, we specifically chose to discuss the electrostatic component of binding energy of proteins (ΔΔG_elec) as predicted by PBE. This stems from considering previously published works by Harris et. al.³⁶, Talley at. al.³⁷, Izadi et. al.¹⁶ and others ⁵⁵ which have extensively discussed computation of ΔΔG_elec. The assortment of such works provokes the idea that besides investigating the sensitivity of ΔΔG_elec to various modeling protocols, it is utterly important to consider the limits of those protocols and relate it with the questions being asked.

As noted earlier, both Talley et. al.³⁷ and Harris et. al.³⁶ study ΔΔG_elec. Both demonstrate that ΔΔG_elec is sensitive to the force field (charge/radius parameters to describe the solute). Further on, Talley et. al.³⁷ provide a comprehensive analysis of factors like probe-radius (to draw the solute-solvent interface) and inner dielectric constant and their combination to show how ΔΔG_elec must be interpreted. On the other hand, Harris et.al. show that ΔΔG_elec is highly sensitive to the definition of the solute-solvent surface (or protein-solvent interface). Yet both acknowledge the unfortunate fact that ΔΔG_elec cannot be experimentally obtained, making it difficult to set standards for PBE protocols or cherish the success of predictions. A major difference between the two is that Talley et. al. recommends structural refinement via energy minimization using the force field being used to assign charges and radii to the solute atoms. In fact, they clarify the effect that minimization can have on the ΔΔG_elec values. The justifications are physically valid and have also been used by Sorensen et. al.³⁵. Harris et. al. in turn use unaltered X-ray structures (protonation is implied) of the protein complexes to describe the problems with predictions made by PBE. Specifically, they state that the electrostatic component of the solvation energy (ΔΔG_elec) is less sensitive to either the choice of force field or definition of protein-solvent interface, which is contrary to ΔΔG_elec. Demonstrating the eventual unpredictability of ΔΔG_elec based on these two parameters, they conclude that PBE methods lack robustness and hence are not suitable techniques for computer aided drug discoveries. On the same ground, Talley et.al. suggest that ΔΔG_elec is meaningless without deriving an optimized combination of probe radius and inner dielectric constant for either homo- or hereto-complexes. They further describe that the absolute value of ΔΔG_elec is misleading and hence, one should correctly evaluate results based on the nature of the objective question being asked. The observation that PBE delivered ΔΔG_elec are sensitive to various input parameters does not indicate that PBE approach is not robust, but prompts that results are evaluated within the scope of the question being asked. It is, therefore, vital to look at the trend of ΔΔG_elec values obtained from using different modeling protocols to answer the question of reliability of predictions from PBE.

This prompted us to conduct our investigation along these lines by computing ΔΔG_elec with three different force fields – CHARMM-27⁵⁶, AMBER-94⁵⁷ and OPLS-AA^58,59 using energy minimized and non-minimized sets of structures. At the same time, we examine the effect on ΔΔG_elec due to two different dielectric assignment methods – homogeneous 2-dielectric model and Gaussian-based smooth dielectric distribution model⁴². We appreciate the reasons to challenge the robustness of PBE methods based on its inability to render or reproduce exact numbers for ΔΔG_elec, but we emphasize that absolute values of ΔG_elec could be misleading and that conclusions about PBE results must be drawn keeping in mind the methodology used. The use of more than 600 protein complexes (including homo- and hetero- complexes) provides reliability to our results from statistical point of view.

Methods

Preparation of 3D structures of protein complexes

A total of 621 protein complexes used in this work were taken from the database created by Ray Luo’s group at UCI (http://rayl0.bio.uci.edu/rayl). For our purposes, we extracted dimers out of complexes that had more than a pair of chains in their 3D structure from Protein Data Bank (PDB)^60,61. Furthermore, some of these complexes contained modified residues, which were mutated back to their parent residues as described in the PDB file header. The chains with missing terminal residues were intentionally left untreated as no part of this work involved comparison of results obtained on incomplete structures. Complexes, which contained duplicate residues, were obliterated off the set eventually leaving 603 complexes with each complex rendering two chains and its dimeric structure (3 in total) making a total of 1809 molecules referred to as the “RAWSET” henceforth. It was ensured that these structures had no atoms/molecules that were not parts of the protein so as to provide identical and unbiased inputs to the three force fields chosen for this work – CHARMM-27, AMBER-94 and OPLS-AA. A common protocol was followed in order to prepare the initial structures compatible with packages that incorporate energy minimization modules through these force fields. The PDB IDs for the molecules used are presented as supplementary information.

CHARMM-27

The RAWSET structures were protonated using the PSFGEN plugin available with VMD⁶² to obtain the initial structures for minimization using CHARMM-27. This was called the CHARMM-NONMIN set. The histidine residue in any structure was taken to be in its neutral state (HSE in CHARMM nomenclature) and the other ionizable residues were retained in their charged states. The ends of the chains were capped with appropriate N/C terminal moieties.

AMBER-94

The same RAWSET structures were protonated using the xLEAP tool (of the AmberTools package^23,63) for simulations using AMBER-94. The resulting set of initial structures was called the AMBER-NONMIN set. The histidines, the ionizable residues and the chain ends were treated identically as done for CHARMM-27 set (Histidines present as HIE in the AMBER nomenclature). The procedure rendered respective AMBER format coordinate and parameter files.

OPLS-AA

The OPLS - All Atom force field was incorporated through the GROMACS⁶⁴ simulation package which was used to generate the respective topology, coordinate and other auxiliary files for minimization. The histidines were protonated in their neutral states (HISE in the OPLS nomenclature); the ionizable residues and chain ends were treated as stated previously. These made the OPLSAA-NONMIN set of structures.

All of the respective initial structures were void of any explicit water molecules or ions as the minimizations were to be carried out using implicit solvent Generalized Born model (GB), for which the theory is well explained by Ref.⁶⁵.

Energy Minimizations

All the minimizations were performed using the Generalized Born (GB) solvent models. For each force field, the complex and the component chains were minimized separately. However, a set for each of the force field was created which only had the complexes minimized and the component chain structures were merely extracted out of it. This was done in order to assess the sensitivity of ΔΔG_elec on the conformations of the component chains with respect to the complex.

NAMDv2.9 ⁶⁶ was used for the CHARMM-27 and AMBER-94 sets; for the latter the AMBER module embedded in NAMD was used. To execute the GB model based minimization, the respective module in NAMD was turned on in conjunction with zero ion concentration. A value of 12 Å for the cutoff was used to calculate the Born radius based on the extent of desired descreening (called alphaCutoff) based on the Bashford-Case model employed by NAMD^67–69. Simultaneously, the cut-off for non-bonded forces was set at 14 Å with switching made to occur at 13 Å. Conjugate gradient (CG) method of minimization was executed in all the cases and all the other requisite parameters were kept at their default values.

For minimization of the OPLS-AA set, GROMACSv5.0.5 was used. To maintain consistency, the conjugate gradient integrator was used for minimization. In order to execute GB model minimization, GROMACS requires infinite cut-off values for non-bonded forces and a “group” cut-off scheme, which were all accordingly taken into account. To determine the Born radii of the component atoms, the Hawkins-Cramer-Truhlar method (HCT) incorporated by GROMACS was used ⁷⁰ which is primitive to the Bashford-Case model used by NAMD. The salt concentration was set at 0. The minimization was halted before the total number of steps if the maximum force value converged to less than 10 KJ/mol/nm. All the other required parameters were set to values that were identical to the NAMD minimization parameters.

The process of minimization produced two supersets of structures called the MIN-500 and MIN-5000 which comprised of structures minimized for 500 and 5000 steps respectively. Each of the three force fields had their own MIN-500/MIN-5000 structure sets. In the next section, we introduce two daughter sets for each of the above sets based on the definition of the dielectric boundary of the protein molecules and the continuum solvent.

Calculation of Electrostatic Components of the Binding Energy

The electrostatic component of binding energy for a complex (ΔΔG_elec), with two chains (say ‘A’ and ‘B’) is given by combining the electrostatic components of the binding free energies of the individual molecules in the following manner:

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{elec}}}=\mathrm{\Delta }{G}_{\mathit{\text{complex}}}-\mathrm{\Delta }{G}_A-\mathrm{\Delta }{G}_B$$ (1)

Here ΔG_complex, ΔG_A and ΔG_B are the free energies of the complex and the individual monomers, respectively.

The electrostatic components of the binding energies (ΔΔG_elec) of the complexes were calculated using DelPhi²¹. However, two different approaches were taken into account based on the definition of the dielectric boundaries in the system and the distribution of the internal dielectric constant. Consequently, two different methods of determining ΔΔG_elec were invoked.

The first set of values was calculated using the traditional two-dielectric model (uniform dielectric constants for the proteins and water phase, respectively) and solvent accessible surface (SAS) as the interface between the protein and the solvent. Hence, they have been referred to as the traditional calculations (TRADITIONAL) hereafter. The solvent probe radius used in those calculations was 1.4 Å to emulate water. For those cases, the solvation energy of a given molecule was calculated from the coulomb energy and the corrected reaction field energy terms that DelPhi outputs^21,71 (Eq. 2). This combination of the two energy terms is justified for use only when the solute and the solvent are homogeneous dielectric media and there is the dielectric boundary between them (typically referred as molecular surface where induced charges are positioned⁷¹),

$$\mathrm{\Delta }{G}_x=G_{\mathit{\text{coulomb}},x}+G_{\mathit{\text{self}}-\mathit{\text{reaction}},x}$$ (2)

Here ‘x’ is the complex or either chains. Note that it is naturally assumed that the state in vacuum is identical to the one in solution for any chosen ‘x’.

The second set of calculations was done using recently developed method of Gaussian-based smooth dielectric function⁷² encoded in DelPhi. The variance for the Gaussian distribution (SIGMA) was set at 0.93, based on our previous works^30,41,72. This set of calculations hereafter is referred to as the GAUSSIAN set. Since, the dielectric “constant” throughout the entire space of the macromolecule and its surface varies, the method of induced charges cannot be applied to determine the reaction field energy (the electrostatic component of the solvation energy). Because of that, the total electrostatic energy (the sum of coulombic and polar solvation energies) was calculated as the difference of the grid energy of the complex and separated molecules (being taken from the complex, i.e. having identical bound/unbound conformation of the chains), The complex and individual chains were kept at the same position and the same grid center and resolution to cancel grid effects:

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{elec}}}=G_{\mathit{\text{complex}}}-G_A-G_B$$ (3)

where G_x is the grid energy for any x = complex, A and B.

This approach resulted in two set of calculations: One set comprised of minimized complexes as well as individually minimized component chains which implies difference in the conformation of a chain in its bounded and unbounded states. For those cases, only the traditional solvent accessible surface based calculations (TRADITIONAL) were used for DelPhi calculations (eq. 1 and 2).

The second set comprised of chains with conformers extracted directly out from the minimized structure of the corresponding complex. This implies total identity of a chain’s bounded and unbounded state conformations. For those cases, both TRADITIONAL and GAUSSIAN protocols were used.

For the CHARMM and AMBER sets, the coordinate file (.pdb) was fed in, along with atomic charge (.crg) and radii (.siz) parameters for the respective force fields, while for the OPLS-AA set of structures, (handled via GROMACS) the respective coordinate-charge-radii (.pqr) files were directly fed in as arguments for the respective electrostatic calculations. With the internal and external dielectric constants set to 2 and 80, for protein and water respectively, a resolution of 2 grids/Å was imposed for the calculations using DelPhi (it was shown before that DelPhi is quite insensitive to grid spacing/resolution^21,72). The size of the cuboidal box containing the complex was customized such so the complex filled approximately 70% of its total volume. At the same time, the center of the box was placed at its geometric center and the same box center and dimensions were used for the calculations of the component chains to ensure identical boundary conditions for the chains and the complex, and to cancel the grid effects in case of GAUSSIAN sets. The boundary condition for the potential in all the calculations was set at the “dipolar” mode wherein the boundary potentials are approximated by the Debye-Huckel potential of the dipole resulting from the molecular charge distribution. Furthermore, the salt concentration of the solvent continuum was set to 0.0.

Analysis of the Results of Comparison of Binding Energy

The similarities of the electrostatic component of the binding energy values from different sets treated in this study were quantified based on the statistical measures. This involved fitting a linear model to the scatter plot obtained from plotting these values for each protein complex treated according to the sets they belonged to. The slope of the linear model was indicative of the similarity of the values from the two sets being compared while the Pearson’s correlation (r) denoted the quality of the linear fit. To describe the trends of comparison, we use the word ‘ranking’. Any particular calculation of ΔΔG_elecon the set of complexes, when sorted in some order, gives the ranking of ΔΔG_elec If the order, or what we define ranking, were identical, the correlation of the linear model would be ‘1’ if the two sets of ΔΔG_elec were plotted against each other. It would be ‘-1’ if the sorted order were exactly reversed. Thus, correlation signifies the comparative ranking of ΔΔG_elec from two different calculations. In parallel, we carry root mean square difference (RMSD) analysis of the obtained values of electrostatic component of the binding energy. The RMSD between any two set of ΔΔG_elec values was obtained using the following:

$$\mathit{\text{RMSD}}(\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{elec}}})=\sqrt{\sum \frac{{(\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{elec}},i}-\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{elec}},i}^{\prime })}^2}{N}}$$ (4)

For N ΔΔG_elec values being compared between two sets, the non-primed values indicate one set and the primed ones indicate the other set.

Results and Discussions

As it was mentioned above, the electrostatic component of the binding energy as modeled via PBE is expected to be a function of force field and modeling protocol, either because of the specificity of force field parameters (different partial charges and radii) or differences in the 3D structures resulting from hydrogen placement and subsequent minimization procedure. Here we aim at assessing the force field dependence of ΔΔG_elec in statistical manner by conducting the following investigations: (a) what is the effect of force field parameters on ΔΔG_elec provided the experimentally determined 3D structures are not altered? (b) What is the effect on ΔΔG_elec within the same force field if the 3D structures are energy minimized? (c) What is the effect on ΔΔG_elec across different force fields in conjunction with energy minimization? (d) How the dielectric constant assignments affect the conclusions (the standard 2-dielectic model vs Gaussian-based smooth dielectric function)? And (e) how further structural relaxation (bound vs unbound protocol) impacts the results.

(a) The effect of force field parameters on ΔΔG_elec

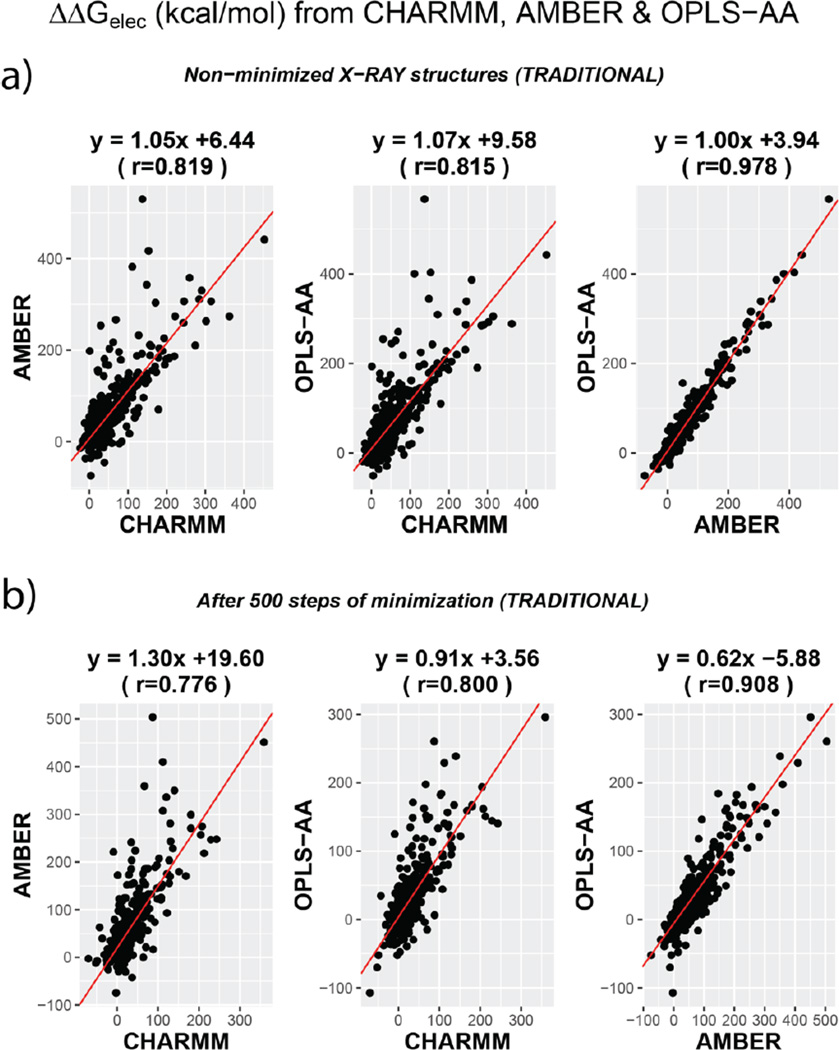
We first compare the ranking of ΔΔG_elec across different force fields without altering the conformation of the 3D X-ray structures of the proteins (protonation is implied). Figure 1 shows the comparison of the various combinations of force-fields and the equations represent the linear model fit to the data. For this section, we will focus on panel ‘a’ of the figure. Panel ‘b’ illustrates the comparisons after minimization for 500 steps (discussed in later sections). Fig S1 illustrates the comparison for all the cases including structures after 5000 steps of minimization.

Figure 1.

Comparison of ΔΔG_elec across the three force fields presented as scatter plots. TOP panel (a) compares values from non-minimized structures. BOTTOM Panel (b) compares them for structures obtained after 500 steps of CG minimization. The RED line indicates the straight line of best fit and the equations corresponding to each fit is mentioned on the top of the plots. All cases shown in Figure S1.

The correlation coefficients for the various pairs are 0.819 (CHARMM vs AMBER), 0.815 (CHARMM vs OPLS-AA) and 0.978 (AMBER vs OPLS-AA). Besides, the respective slopes of the linear model fits are 1.05, 1.07 and 1.00. The slope-correlation pairs indicate appreciable similarity amongst ΔΔG_elec calculated with different force-field parameters. The high similarity of AMBER vs OPLS-AA is also corroborated by the fact that the latter force-field is an improvement of AMBER with due modification embedded in it to account for the behavior of atoms in liquid phase media and amidst different water models ⁵⁹. The ΔΔG_elec calculated using CHARMM parameters are also statistically correlated with AMBER or OPLS-AA ΔΔG_elec ranking, but the correlation coefficient is relatively lower (~0.81). For some (~ 1.5%) cases in CHARMM vs AMBER and CHARMM vs OPLS-AA comparisons, the absolute difference of the calculated ΔΔG_elec is more than 150 kcal/mol even when the backbone is identical, indicating that hydrogen placement and difference in partial charges and atomic radii could significantly impact ΔΔG_elec. For comparison, the range of absolute difference of ΔΔG_elec between AMBER and OPLS-AA is 0.00 – 106.02 kcal/mol (~0.16% differed by more than 100 kcal/mol).

Hence, we see that force-field differences are capable of rendering significant differences in the calculated ΔΔG_elec of a molecule. The outliers and non-ideal correlation coefficients indicate that modeling ΔΔG_elec with non-minimized structures perhaps might not be very insightful. Most of the outliers in Figure 1a are due to difference in the hydrogen placement involving interfacial residues, determined using different modeling packages (e.g. VMD⁶² for CHARMM, AmberTools-15^23,63 for AMBER and GROMACS⁶⁴ for OPLS-AA). In part this is also due to the fact that force field parameters are developed for energy calculations using structures which are structurally relaxed. Such structures can be computationally obtained via energy minimization. A good review of the methods of force field development comprising of these details can be found elsewhere^73,74. Therefore, this necessitates relaxation of hydrogen positions (minimization), especially those at the interface and without these adjustments one can obtain significantly altered ΔΔG_elec with change in force field as described above. In the next section, we discuss the convergence of ΔΔG_elec attained after minimizing the structures to different extents.

(b) The effect of minimization on the ΔΔG_elec within the same force field

Here we compare the ΔΔG_elec values obtained with the same force field but with structures of complexes that were subjected to different extents of energy minimization (500 and 5000 steps of conjugate gradient energy minimization).

A trend is consistently observed in all the force fields calculations with subtle variations across them. In comparing the structures that have been minimized (MIN-500 vs. MIN-5000), the similarity of the ΔΔG_elec values increase (significant in the case of CHARMM and OPLS-AA) against when ΔΔG_elec values from non-minimized X-ray structures (NONMIN) are taken into account. The comparisons are shown in Figure S2. This points out that relaxation can have noticeable impact on the ΔΔG_elec value. Such effects have also been observed by other authors³⁷. Furthermore, extensive minimization (5000 steps) does not drastically alter the ΔΔG_elec obtained after 500 steps of minimization. This hints at convergence of ΔΔG_elec on account of convergence of the structures as they find an energy minimum (local/global) and are “trapped” therein. Table 1 lists the structural RMSD values for the various sets of structures (RMSDs of protein Cα atoms of complexes only). In all the cases, the structural RMSD is significantly smaller between MIN-500 and MIN-5000 sets.

Table 1.

Table showing the average structural RMSD value of the 603 structures from each set. The values are for C-α atoms of the complexes only.

Structural RMSD Values. All values are in Å. (±) indicate standard deviations
		NONMIN	MIN-500	MIN-5000
CHARMM	NONMIN	0.0	0.3087 ± 0.2380	0.5880 ± 0.2552
	MIN-500		0.0	0.4294 ± 0.1437
	MIN-5000			0.0
		NONMIN	MIN-500	MIN-5000
AMBER	NONMIN	0.0	0.2267 ± 0.2412	0.2452 ± 0.2988
	MIN-500		0.0	0.0544 ± 0.1528
	MIN-5000			0.0
		NONMIN	MIN-500	MIN-5000
OPLS-AA	NONMIN	0.0	0.3101 ± 0.1952	0.3321 ± 0.2086
	MIN-500		0.0	0.0578 ± 0.1222
	MIN-5000			0.0

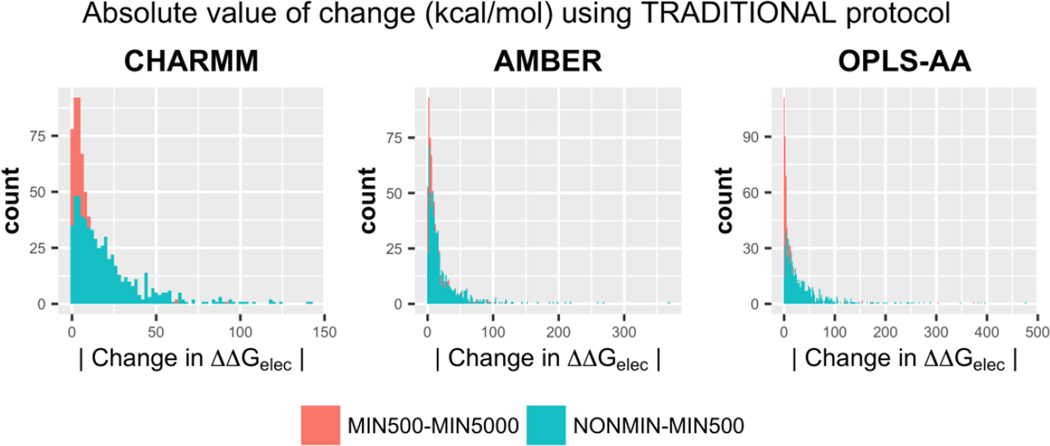
To quantify the absolute change in ΔΔG_elec values due to minimization, RMSD from respective sets were calculated alongside analyzing the histograms for the absolute value of the change in ΔΔG_elec. Figure 2 shows the histograms. The histograms are a clear indicator that changes upon extended minimization are contained within < 25 kcal/mol (comparing MIN500 – MIN5000 sets). On the contrary, the changes in ΔΔG_elec are larger and might even exceed 200 kcal/mol, when comparing NONMIN and MIN500 sets. The trend is corroborated by the ΔΔG_elec RMSD values (Table 2). On correlating the structural RMSD with RMSD of ΔΔG_elec one can see that the two are proportional, i.e. extended minimization causes minor structural changes (mostly for the lighter hydrogen atoms) and hence exhibit little changes in ΔΔG_elec.

Figure 2.

Histograms depicting the frequencies of finding a certain value for the absolute change in ΔΔG_elec upon initial minimization (NON-MIN500) and extended minimization (MIN500 – MIN5000). The comparisons are shown for all the three force fields. These results pertain to the TRADITIONAL 2-dielectric distribution.

Table 2.

Table listing the root-mean-square difference (RMSD) of ΔΔG_elec for each force field between the various pairs of differently minimized structures. NONMIN – protonated X-ray structures; MIN-500 – structures minimized for 500 CG steps and MIN-5000 – structures minimized for 5000 CG steps.

COMPARISON WITHIN SAME FORCE-FIELD (TRADITIONAL)
		NONMIN	MIN-500	MIN-5000
CHARMM	NONMIN	0	28.59	38.54
	MIN-500		0	12.88
	MIN-5000			0
		NONMIN	MIN-500	MIN-5000
AMBER	NONMIN	0	10.16	10.57
	MIN-500		0	2.94
	MIN-5000			0
		NONMIN	MIN-500	MIN-5000
OPLS-AA	NONMIN	0	46.62	48.21
	MIN-500		0	4.47
	MIN-5000			0

All values are in kcal/mol.

To summarize the above observations and inferences, we note that comparing the ΔΔG_elec after 500 and 5000 minimization steps for each force field calculations results in extremely good correlation coefficients (> 0.97). This indicates that in vast majority of the cases a short minimization of 500 steps is enough to make PBE calculations robust (almost minimization independent) within a particular force field. The odds, therefore, that a longer minimization would cause drastic changes in the ΔΔG_elec values are fairly low. Moreover, PBE solutions are able to capture the minor structural deviations of the structures minimized to different extents (500 and 5000 steps), thus, hinting at convergence of both - ΔΔG_elec and structural geometries.

(c) The effect of minimization on ΔΔG_elec across different force fields

Here we compare the ΔΔG_elec values across the force fields for structures of complexes after 500 steps of conjugate gradient energy minimization (due to convergence the results from 5000 steps of minimization are presented in the Suppl. Information; Table S1 (extension of Table 3), Fig S1). Since the minimization protocol and subsequent ΔΔG_elec calculations were done along the lines adopted by Talley et. al.³⁷, i.e. the monomeric chains of the complexes were not minimized separately but were extracted directly out of the minimized complex’s structure, their results carry the tag of ‘Only Complex Minimized’.

Table 3.

Table listing the Pearson’s correlation coefficient (r) and root-mean-square difference for the various pairs of force fields, before and after minimization. Since MIN-500 and MIN-5000 the results are very similar, the ones from former are only shown. NONMIN – protonated X-ray structures; MIN-500 – structures minimized for 500 CG steps. Full information in Table S1.

	Correlation		RMSD (kcal/mol)
	Non minimized (NONMIN)	Minimized (MIN-500)	Non minimized (NONMIN)	Minimized (MIN-500)
CHARMM vs. AMBER	0.819	0.776	40.71	50.81
CHARMM vs. OPLS-AA	0.815	0.800	43.18	27.06
AMBER vs. OPLS-AA	0.978	0.908	15.47	40.51

Figure 1b shows the comparison of ΔΔG_elec values after minimization across the three force fields. The changes in the correlations of ΔΔG_elec post minimization and associated RMSD changes of ΔΔG_elec are shown in Table 3. One can notice that the effect of minimization is not consistently observed in all the pairs. For instance, the ratio of correlation for CHARMM vs AMBER before and after minimization is not the same as that of CHARMM vs OPLS-AA or AMBER vs OPLS-AA. This is not surprising. Since minimization by a force field implies being treated by its potential energy function, initially identical structures could be driven to different conformations with lower energies. Moreover, a minimization of total energy by different force fields does not necessarily mean that the electrostatic component of it would be altered by the same factors³⁷.

Another lack of consistency is seen in the RMSD values. It is unpredictable how differences in the 3D conformation affect the differences in the ΔΔG_elec values. For example, ΔΔG_elec from CHARMM and OPLS-AA differ by 43.18 kcal/mol (RMSD) before minimization and the difference drops down to just 27.06 kcal/mol after minimization. However, this change is associated by a drop in the correlation value (0.815 – 0.800). On the contrary, the ΔΔG_elec from AMBER vs OPLS-AA comparison sees a significant increase in their RMSD (accompanied by a subtle drop in the correlation) after minimization. Yet, the two force fields feature very similar values of ΔΔG_elec over other pairs.

One can appreciate the ability of PBE to capture these differences. These differences, therefore, should not be inferred as valid reasons to show that PB models fail to generate identical solutions upon varying certain numerical parameters. It is clear that despite significant structural deviations incurred upon minimization, the rankings across the force fields do not change significantly.

(d) Effect of changing the dielectric assignment method

Two different dielectric models were used to reveal the sensitivity of the ranking of ΔΔG_elec to the spatial distribution of dielectrics. It was a major conclusion made by Harris et. al.³⁶ that the fragility of PBE is revealed when different solute surface definitions are employed. This was demonstrated in terms of poor correlation (R² < 0.3) when ΔΔG_elec from using different surface definitions were compared. At the same time, they clearly showed that the electrostatic component of solvation energy (ΔG_elec) is not much sensitive to this change.

In our work, we have used two different dielectric distribution models. The 2-dielectric model (piecewise dielectric distribution) draws a sharp dielectric interface between the molecule and the solvent continuum. This method has been in traditional usage and hence is referred to as TRADITIONAL protocol. The other model, based on Gaussian-based smooth dielectric distribution (referred to as the GAUSSIAN model), involves smoothing of this protein-solvent interface besides assigning smooth dielectrics for protein interiors based on atom packing. For instance, regions in the protein that are very loosely packed have enough room to orient their dipoles when exposed to an external field, making them suitable candidates for higher dielectric values (as high as that of the solvent)⁷². With number of atoms ranging from 650 to 27,500 in the 603 proteins considered in our study, the resulting dielectric distributions are significantly different for the two approaches. Therefore, it is expected that the absolute values of ΔΔG_elec (solvation) and ΔΔG_elec (binding) would differ significantly. For purposes of comparing the two by taking into account the effect of minimization, we only discuss the results obtained after 500 steps of minimization (MIN-500 set). All the aforementioned results pertain to the TRADITIONAL protocol. We perform the same analysis on the results from using the GAUSSIAN protocol and interpret them accordingly.

The GAUSSIAN protocol renders very similar correlations for the rankings (with respect to TRADITIONAL protocol) of ΔΔG_elec for non-miniminzed protonated structures across different force fields. The absolute numbers of ΔΔG_elec are, however, very different for the two. Table 4 lists the slopes, correlation and ΔΔG_elec RMSD values for the two protocols. The data is illustrated in Figure S3, S4 in SI.

Table 4.

Table listing the slopes and correlation coefficient (r) as well as the ΔΔG_elec RMSD for the various pairs of force fields. The values pertain to calculations without any minimization (TOP panel) as well as after 500 steps of minimization (BOTTOM panel). In each panel, the corresponding values are listed for the two dielectric assignment methods – TRADITIONAL (2-dielectric model) and GAUSSIAN.

Before Minimization
	Slopes		Correlations		RMSD (kcal/mol)
	TRADITIONAL	GAUSSIAN	TRADITIONAL	GAUSSIAN	TRADITIONAL	GAUSSIAN
CHARMM vs. AMBER	1.05	0.78	0.819	0.729	40.71	88.89
CHARMM vs. OPLSAA	1.07	0.43	0.815	0.731	43.18	92.93
AMBER vs. OPLSAA	1.00	0.54	0.978	0.988	15.47	81.10
After Minimization for 500 steps
	Slopes		Correlations		RMSD (kcal/mol)
	TRADITIONAL	GAUSSIAN	TRADITIONAL	GAUSSIAN	TRADITIONAL	GAUSSIAN
CHARMM vs. AMBER	1.30	0.76	0.776	0.737	50.81	78.28
CHARMM vs. OPLSAA	0.91	0.53	0.800	0.736	27.06	77.07
AMBER vs. OPLSAA	0.62	0.69	0.908	0.983	40.51	49.66

Table 4 provides several inferences. First, the slopes of the linear model fits are significantly different. The slopes from GAUSSIAN are 0.5–0.7 times that from TRADITIONAL values except when ΔΔG_elec for AMBER and OPLS-AA are compared after minimization (slope increased by 11%). This reflects the difference in the absolute values of ΔΔG_elec obtained from the two protocols. The difference is also corroborated by the corresponding RMSD values. In all the cases, GAUSSIAN protocol causes the ΔΔG_elec values from force fields to differ by a larger value than TRADITIONAL (increased RMSD for GAUSSIAN).

However, the correlation values are fairly similar, both, before and after minimization. Thus, the trend of similarity is inherited. Moreover, the inherent similarity of AMBER and OPLS-AA force field parameters are also reflected in the results. As was shown previously, the TRADITIONAL approach also maintains this ranking of ΔΔG_elec despite minimization. This indicates that some of the vital features of the ranking of ΔΔG_elec are preserved across both kinds of dielectric models.

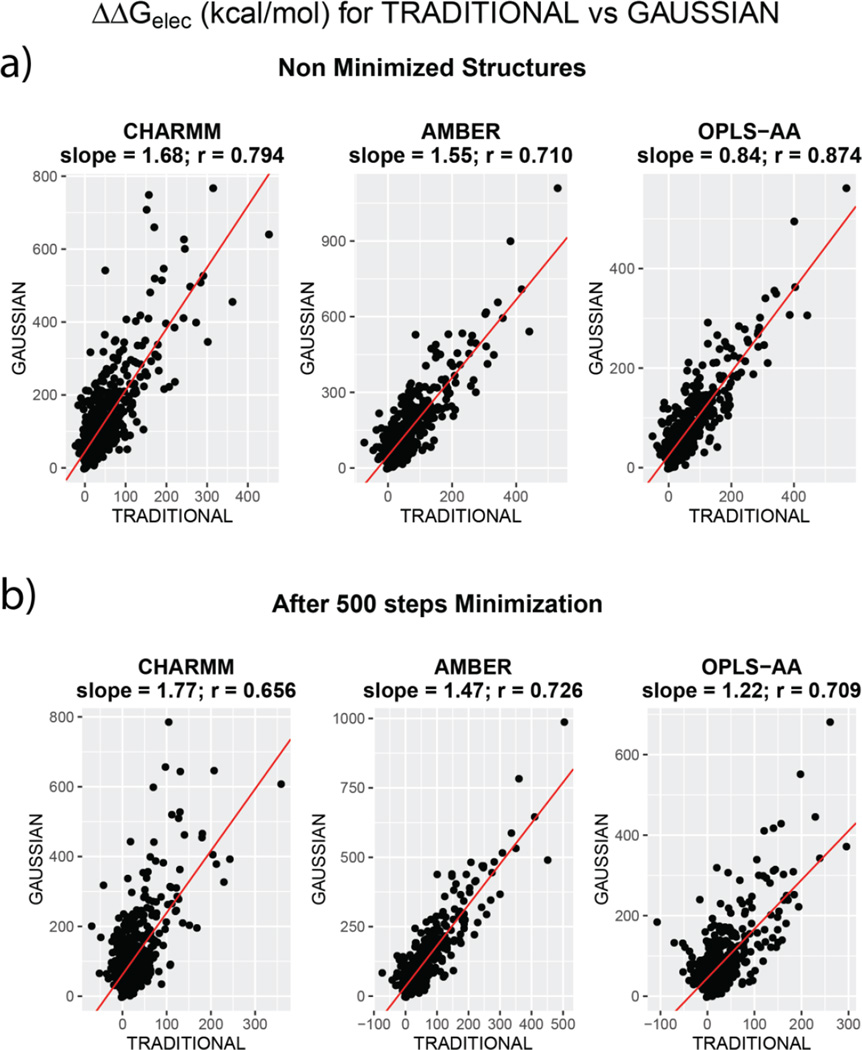
We now address the question of the ranking of the absolute values of ΔΔG_elec when adjudged in terms of the two dielectric models, i.e. what is the correlation when ΔΔG_elec from TRADITIONAL and GAUSSIAN approaches are compared. It is reminded that the severely low correlations (0.1 < R² < 0.3) were reported by Harris et al.³⁶ for ΔΔG_elec comparisons using different surface definitions. Our results show otherwise. When ranking of ΔΔG_elec is compared (TRADITIONAL vs GAUSSIAN), the correlations are appreciably higher, regardless of the extent of minimization. Figure 3 plots ΔΔG_elec computed by these methods for each force field. Panel ‘a’ and ‘b’ illustrate the cases before and after minimization respectively.

Figure 3.

Comparison of ΔΔG_elec obtained by using different dielectric assignment methods – TRADITIONAL and GAUSSIAN. Comparison is illustrated for all the three force fields. TOP panel (a) compares values from non-minimized structures. BOTTOM Panel (b) compares them for structures obtained after 500 steps of CG minimization. The RED line indicates the straight line of best fit and the equations corresponding to each fit is mentioned on the top of the plots

As one can see, the correlation is as low as 0.656 for CHARMM (after minimization) and as high as 0.874 for OPLS-AA (before minimization). Certainly, the correlations are force field dependent but fairly high correlation values provide a different ground for drawing conclusions about the robustness of PBE as opposed to Harris et al.³⁶. But the discrepancy between our observations and theirs could stem from two major sources:

1. Harris et. al. use only 14 different protein complexes in their study using two different force fields (AMBER and CHARMM). With such a small sample set, drawing statistical inferences about the similarity of ranking is not very reliable. For our work, we use 603 binary complexes with available crystal structures. This renders our observations more reliable, from statistical perspectives.

2. Their comparison of the ranking of ΔΔG_elec was based on exploring different protein-solvent surface definitions resulting in altered surfaces. This impacts the exposure of charges to the water phase which has a significant contribution to the polar component of solvation energy. In fact, Talley et al³⁷ show that ΔΔG_elec is dependent on the probe radius used for drawing the interfacial surfaces. In our case, the inclusion of GAUSSIAN method of dielectric distribution, which does not draw sharp interfacial surfaces, provides an alternative where sensitivity to probe radius is totally eliminated.

To verify our hypothesis, we performed the following analysis. Of the 603 protein complexes from each set, we randomly chose 15 (to mimic the sample set of Harris et. al.) and compared their ΔΔG_elec values obtained using the TRADITIONAL and GAUSSIAN approaches. This sampling of 15 complexes from the entire pool was repeated 100 times and the average of the correlation (over 100 trials) were calculated.

The standard deviation was also computed over the 100 trials. This analysis was performed for all the three force fields. The results are tabulated in Table 5.

Table 5.

Table listing the average correlation coefficient and the std. deviation over 100 trials when for each trial, 15 random samples of ΔΔG_elec values computed using TRADITIONAL and GAUSSIAN approaches, were compared. The average and std. deviation of correlations are shown for all the three force fields. The TOP panel lists the values for non-minimized structures, the BOTTOM one is for structures minimized for 500 CG steps.

Sample Size = 15; Number of Trials = 100
With non-minimized structures
	Average correlation	Std. Deviation
CHARMM	0.7	0.1
AMBER	0.8	0.2
OPLS-AA	0.8	0.1
With minimized structures (500 steps)
	Average correlation	Std. Deviation
CHARMM	0.6	0.3
AMBER	0.8	0.1
OPLS-AA	0.6	0.3

Table 5 contains the results from one of the many attempts. All the attempts rendered very similar results. In no case did the average correlation drop below 0.7 and was always less than 0.85 for non-minimized structures (collectively for all the force fields). In case of ΔΔG_elec obtained after minimization, the lower limit dropped to 0.5.

Very certainly, altering the method of dielectric assignment by drawing different interfacial surfaces would render different ΔΔG_elec but that is due to the change in the exposure level of the solute charges to the solvent. This should not be answered in terms of PBE’s failure to be robust. However, we appreciate the issue of a suitable protein-solvent dielectric surface raised by Harris et. al. Our results, using Gaussian-based smoothing, can prove to be a suitable candidate for the appropriate description of spatial dielectric distribution in the PBE framework.

However, the lack of any experimental data for ΔΔG_elec provides no ground of justification of the advantage of one method over the other (TRADITIONAL vs GAUSSIAN). Yet, considering the validity on physical grounds, it appears that the GAUSSIAN protocol imparts a more meaningful description of the charge configuration endowed with some flexibility when immersed in a high dielectric solvent media^{30,35,41,72,75}. Furthermore, the GAUSSIAN approach has also been shown to perform well against the experimental values of solvation free energies of small molecules of which ΔΔG_elec (binding) is a component^30,72.

(e) The effect of separately minimizing monomers vs. leaving them intact

This section focuses on determining the effects of minimization of individual chains on the ΔΔG_elec values and comparisons within the force fields and across them. Thus, we separately minimized the monomeric chains of the complexes. The results discussed till this point comprise of monomers extracted exactly out of the minimized complex structure. This ensured identical bound/unbound states for the monomeric chains. The monomers, when separately minimized for the same number of steps as their parent complex, render non-identical bound/unbound conformations. The results from this set are labeled with ‘Complex + Monomers Minimized’. The effect of executing these two protocols was examined in our course of identifying other factors that could characterize a modeling protocol.

Tables 6, 7 lists the correlation and RMSD values of ΔΔG_elec for the two approaches - bound and unbound protocols. Two comparisons are included – comparison within same force field (Table 6) and across different force fields (7). These values were not calculated for GAUSSIAN method as it requires exact cancellation of the grid energies while calculating ΔΔG_elec of the complex using Equation-3 and hence separate minimization of monomers would not allow that.

Table 6.

For each force field, the ΔΔG_elec RMSD for the various pairs of differently minimized structures are shown. The LEFT panels present the RMSD when bound/unbound states of monomeric chains were identical (‘Complex Minimized Only’) and the RIGHT panel presents the RMSD when monomers and their complexes were all individually minimized (non-identical bound/unbound state; ‘Complex + Chain Minimized’). NONMIN – protonated X-ray structures; MIN-500 – structures minimized for 500 CG steps and MIN-5000 – structures minimized for 5000 CG steps.

Comparison Within Same Force-Field using ΔΔGelec Pearson correlation and (RMSD) (TRADITIONAL) | All RMSD values are in kcal/mol
Identical Bound/Unbound states					Non-Identical Bound/Unbound states
		NONMIN	MIN-500	MIN-5000		NONMIN	MIN-500	MIN-5000
CHARMM	NONMIN	0	0.95 (28.59)	0.91 (38.54)	NONMIN	0	0.91 (30.73)	0.91 (35.63)
	MIN-500		0	0.97 (12.88)	MIN-500		0	0.94 (15.51)
	MIN-5000			0	MIN-5000			0
		NONMIN	MIN-500	MIN-5000		NONMIN	MIN-500	MIN-5000
AMBER	NONMIN	0	0.99 (10.16)	0.98 (10.57)	NONMIN	0	0.79 (42.59)	0.79 (42.53)
	MIN-500		0	0.99 (2.94)	MIN-500		0	0.93 (19.95)
	MIN-5000			0	MIN-5000			0
		NONMIN	MIN-500	MIN-5000		NONMIN	MIN-500	MIN-5000
OPLS-AA	NONMIN	0	0.92 (46.62)	0.91 (48.21)	NONMIN	0	0.51 (68.33)	0.47 (71.85)
	MIN-500		0	0.99 (4.47)	MIN-500		0	0.79 (35.38)
	MIN-5000			0	MIN-5000			0

Table 7.

For differently minimized structures, the ΔΔG_elec RMSD values are listed when corresponding sets across force fields are compared. The LEFT panels present the RMSD when bound/unbound states of monomeric chains were identical (‘Complex Minimized Only’) and the RIGHT panel presents the RMSD when monomers and their complexes were all individually minimized (non-identical bound/unbound state; ‘Complex + Chain Minimized’). NONMIN – protonated X-ray structures; MIN-500 – structures minimized for 500 CG steps and MIN-5000 – structures minimized for 5000 CG steps.

Comparison Within Same Force-Field using ΔΔGelec Pearson correlation and (RMSD) (TRADITIONAL) | All RMSD values are in kcal/mol
Identical Bound/Unbound states					Non-Identical Bound/Unbound states
		CHARMM	AMBER	OPLS-AA		CHARMM	AMBER	OPLS-AA
NONMIN	CHARMM	0	0.82 (40.71)	0.82 (43.18)	CHARMM	0	---	---
	AMBER		0	0.98 (15.47)	AMBER		0	---
	OPLS-AA			0	OPLS-AA			0
		CHARMM	AMBER	OPLS-AA		CHARMM	AMBER	OPLS-AA
MIN-500	CHARMM	0	0.78 (50.81)	0.80 (27.06)	CHARMM	0	0.85 (34.93)	0.66 (41.21)
	AMBER		0	0.91 (40.51)	AMBER		0	0.61 (49.66)
	OPLS-AA			0	OPLS-AA			0
		CHARMM	AMBER	OPLS-AA		CHARMM	AMBER	OPLS-AA
MIN-5000	CHARMM	0	0.74 (58.01)	0.77 (29.24)	CHARMM	0	0.84 (40.12)	0.58 (50.40)
	AMBER		0	0.91 (41.43)	AMBER		0	0.56 (55.88)
	OPLS-AA			0	OPLS-AA			0

^---For the NONMIN set, the Bound/Unbound states of the monomers are the same. Hence, the corresponding fields do not contain any values. The change occurs only after minimization (MIN-500/5000).

The ΔΔG_elec are not significantly altered upon minimizing the monomers individually when comparisons are made within a force field. In all the cases, the correlation values are higher or RMSD is lower or both, when comparing ΔΔG_elec of minimized structures against when ΔΔG_elec from non-minimized structures are involved (Table 6). This is identical to the results seen using the previously discussed TRADITIONAL and GAUSSIAN protocols. Yet, upon particular inspection of the ΔΔG_elec RMSD values, separate minimization of chains causes ΔΔG_elec values after a short (500 steps) and long (5000 steps) to differ noticeably. This is expected because each structure (complex and its chains) is placed in its natural minimum regardless of its bound or unbound state. Hence, the differences from each molecule accrue to cause a larger difference to occur upon extended minimization.

On the other hand, when comparisons are made across different force fields, certain drastic effects are observed. Especially, the effect is prominent with AMBER vs OPLS-AA comparisons (Table 7). While the previous approaches showed that ΔΔG_elec from these force fields preserved it’s similarity even after minimization, this approach rendered a totally different picture. Upon comparing the ΔΔG_elecof minimized structures, the correlation drops down from 0.978 (NONMIN) to 0.611 (MIN-500; for AMBER and OPLS-AA) and the RMSD increases. Furthermore, this approach also causes the CHARMM/AMBER and CHARMM/OPLS-AA RMSD to drop upon minimization (accompanied by increased correlation). This is contrary to what is observed when bound/unbound states are identical.

Conclusion

In our work, we address the issue of how certain conclusions drawn from PBE model predictions could be misleading when certain parameters are overlooked. We elect to describe this using the quantity called electrostatic component of binding free energy of complexes, or ΔΔG_elec. In this light, we consider the work published by Harris et. al.³⁶ which evaluates the sensitivity of ΔΔG_elec predictions towards differences in force field parameters and protein-solvent interfacial surface definition. Despite the robustness of predictions made for the electrostatic component of solvation energy (ΔΔG_↓elec of individual monomers, they state, the binding energy obtained from taking their difference (ΔΔG_elec) is unpredictable by PBE models and hence undermine its robustness. On the other hand, Talley et. al.³⁷ demonstrated how ΔΔG_elec should be understood as a function of modeling protocol. We opine that the observations recorded by Harris et. al. is a result of changes in the solvent exposure of solute charges when surface definition is altered and as such, is expected. But it should not be used to justify that the PB models fail to reproduce the ranking of ΔΔG_elec as surface definition is altered.

Our results address the following questions: (a) what is the effect of force field parameters on ΔΔG_elec provided the experimentally determined 3D structures are not altered? (b) What is the effect on ΔΔG_elec within the same force field if the 3D structures are energy minimized? (c) What is the effect on ΔΔG_elec across different force fields in conjunction with energy minimization? (d) How the dielectric constant assignments affect the conclusions (the standard 2-dielectic models vs. Gaussian-based smooth dielectric function)? And (e) how further structural relaxation (bound vs. unbound protocol) impacts the results.

In that order, we find the following. The absolute values of ΔΔG_elec are force field dependent. For structures that haven’t been energy minimized, the difference in ΔΔG_elec using different force fields could also result from differential placement of hydrogen atoms in the structure. Nevertheless, the ranks of ΔΔG_elec from different force fields (CHARMM27, AMBER94 and OPLS-AA in our case) are correlated. After minimization (for 500 steps), we see that correlations change but are not completely lost. Upon extended minimization for 5000 steps, any change from 500-step minimization is significantly small. This indicates convergence of ΔΔG_elec within the same force field. This correlates strongly with structural RMSD incurred after extensive minimization of an already minimized structure. We, therefore, suggest an energy minimization be performed prior to executing PB model calculations using a particular force field. Despite the fact that minimization changes the absolute values of ΔΔG_elec (also shown extensively by Talley et.al.), the correlation of ΔΔG_elec ranking from different force fields is not degraded severely. The different potential energy functions of the force fields drive initially identical 3D structures to different conformations (as a result of minimization). So the differences of ΔΔG_elec predicted from different force fields change (may increase or decrease). We see that PBE predictions are able to reveal these changes. One important observation was that the PB model captured the inherent similarity of charge/radius set from AMBER and OPLS-AA. The strong correlation was even preserved after minimization. Besides, the ranking of ΔΔG_elec was fairly preserved across force fields in general, despite changes in the absolute values. Changes in absolute values occur due to change of 3D structure (which converges after an initial minimization). However, individual minimization of monomeric chains can distort the ranking of ΔΔG_elec and hence must be undertaken with proper care.

The prominent finding of our work was that the Gaussian-based smoothing of dielectric boundaries between proteins and the solvent continuum (GAUSSIAN protocol) not only renders similar trends of ΔΔG_elec across different force fields but also predicts ΔΔG_elec values that are appreciably correlated to the ones predicted by the traditional 2-dielctric model (TRADITIONAL protocol). We also show that this correlation is present independent of the number of complexes being studied. This finding addresses two major concerns reported by Harris et al. First, sensitivity of ΔΔG_elec ranking to change in dielectric boundary definition is a result of change in solvent exposure of charges. With smoothed dielectric discontinuities (as achieved by GAUSSIAN), this problem appears to have been elevated. Thus, it is the protocol of PBE calculation that yields separate trends of ΔΔG_elec ranking and hence, it should be the primary factor under consideration when assessing the sensitivity of PB model. Secondly, and very much in line with the first case, the appreciable correlation of GAUSSIAN ranks of ΔΔG_elec with TRADITIONAL ones encourage us to state that eliminating dielectric discontinuities by applying appropriate smoothing should be considered as a non-trivial factor to PB models in the future. Smoother dielectric assignments also provide better physical meaning to the system and have been suggested equally in the past^76,77.

Overall, our work emphasizes on the interpretation of PBE delivered results. With so many possible applications, it is necessary to relate PBE predictions with the nature of investigation. As Talley et. al.³⁷ state, variation in protocol affects ΔΔG_elec values, so they either should be used in the framework of the corresponding force field (for example in the MMPB/SA investigation with a particular force field) or for ranking only. As is advocated by Sorensen et. al.³⁵ a range of numerical and physical input parameters can alter the solutions of PB equation. The absolute value of electrostatic component of ΔΔG_elec is meaningless without addressing other energy contributions. Thus in the calculations of the binding energy, as for example utilizing MMPB/SA approach, all energies must be calculated within the same force field.