Towards physics of neural processes and behavior

Abstract

Behavior of biological systems is based on basic physical laws, common across inanimate and living systems, and currently unknown physical laws that are specific for living systems. Living systems are able to unite basic laws of physics into chains and clusters leading to new stable and pervasive relations among variables (new physical laws) involving new parameters and to modify these parameters in a purposeful way. Examples of such laws are presented starting from the tonic stretch reflex. Further, the idea of control with referent coordinates is formulated and merged with the idea of hierarchical control and the principle of abundance. The notion of controlled stability of behaviors is linked to the idea of structured variability, which is a common feature across living systems and actions. The explanatory and predictive power of this approach is illustrated with respect to the control of both intentional and unintentional movements, the phenomena of equifinality and its violations, preparation to quick actions, development of motor skills, changes with aging and neurological disorders, and perception.

1. The preamble

Imagine that you place a toy frog on the top of a table in the evening, go to the bedroom, and fall asleep. Early in the morning, you may be certain that the toy is waiting for you on the table, where you left it the night before (let us assume that no other living being could take the toy and no low-probability event, such as an earthquake, happened). Now repeat the experiment with a live frog. Early in the morning, you may be certain that it will not be waiting for you where you left it. Assume also, for the purpose of this mental experiment, that the weight, shape and all other mechanical parameters of the frog and the toy have been perfectly matched, and that the external forces were the same. According to laws of physics, if you know the initial state of an object, its parameters, and the external forces, you can predict where the object will be in future. Violations of such predictions mean that some, unaccounted for, forces acted on the object; this is how some of the celestial bodies have been discovered. Why did the two experiments end up with dramatically different outcomes? An informal answer comes from the famous Harvard’s Law: “Under the most rigorously controlled conditions of pressure, temperature, volume, humidity, and other variables, the organism will do as it well damn pleases” (Bloch, 2003). I am going to try to formulate a less informal answer in this paper.

2. Basic physical laws and new physical laws

The main goal of research in natural science is to unite our experiences into a coherent, logical system (cf. Einstein, 1922; Feldman, 2015). I am going to accept this axiomatic statement without making a distinction between physics of inanimate objects and biology. In physics of inanimate nature, natural laws couple physical variables with the help of parameters. For example, the Second Newton Law links force (F) acting on a material object and change in its velocity (acceleration, a) with the help of a parameter called “mass” (m): F = ma. Hooke’s Law links a change in force (ΔF) applied to a deformable object of a particular class (a spring) to a change in its dimension (deformation, Δx) with the help of a parameter called “stiffness” (k): ΔF = −kΔx. The number of such universal physical laws is relatively small. I am going to address them as Basic Physical Laws, BPLs. As the example in the Preamble shows, living systems differ from objects in the inanimate nature in an important way: While they do not violate any of the BPLs (at least, so far we have no reasons to suspect that they do), their behavior cannot be predicted based on those laws, at least at our current level of understanding. There are many definitions of “living systems” (or simply “life”) found in books, dictionaries, and on the internet. Most of them do not define living systems but rather enumerate their features such as homeostasis, metabolism, growth, adaptation, reproduction, separation from the environment (e.g., by a membrane), and some others. Other definitions use terms such as self-organization (a vague term, not really defined itself). Let me suggest a definition, which tries to make a step toward development of an area of natural science dealing with living systems: Physics of Living Systems.

2.1. Basic definition

A living system is a system able to: (1) unite BPLs into chains and clusters leading to new stable and pervasive relations among physical variables and involving new parameters; and (2) modify these parameters in a purposeful way. In other words, new physical laws (NPLs) emerge in living systems, and then these systems modify parameters of the new laws to achieve their goals.

This definition is applicable to living systems of different complexity, from a macromolecule to an animal, and to the world economy. At this point, already, a number of obvious questions emerge. For example, what is “purposeful”? What are the processes leading to goals and purposes? What is the origin of NPLs (assuming that they exist)?

These questions may be addressed at different levels. For example, the evolutionary process and natural selection have likely played a central role in shaping NPLs, particularly those common across organisms and species (Brandon, 1990, 1997). Evolutionary biology has also been trying to explain teleological, i.e. goal-directed, aspects of biology in terms of laws (McShea and Brandon, 2010). These explanations, however, do not address the formulation of specific NPLs and their parameters; they are also not telling us what the physiological basis of specific NPLs in a given organism is. For example, the formulations of some of the laws underlying the evolutionary process claim that these laws have “no need to turn to physics.” (McShea and Brandon, 2010; p. 110). In contrast, since our goal is to move toward physics of living systems, classical physics is going to form the foundation. NPLs also may be specific to an individual organism with no obvious advantages with respect to natural selection. For example, these may include NPLs underlying special skills (see Section 8.6), like those involved in circus performance, playing musical instruments, and professional sports that give no clear evolutionary advantage and may in fact have negative impact on health and life expectancy.

In the current context, I am using the words “goals” and “purposes” as shortcuts for processes with unknown physics (and physiology) that make actions of a living system look meaningful and functional to an external observer. A detailed review of philosophical aspects related to teleology of processes in living systems can be found in McLaughlin (2001).

Mathematical modeling approaches, including optimization methods, have been used to explore possible causes of purposeful actions (for reviews see Prilutsky and Zatsiorsky, 2002; Todorov, 2004; Diedrichsen et al., 2010). Typically, such approaches assume behavioral goals (e.g., formalized as a cost function), compute salient variables, and compare them to observed behaviors. A close match between the computed and observed variables is viewed as evidence that the assumed criterion adequately reflects relevant biological processes. While these approaches may suggest important insights, they fall short of understanding, or even considering, laws of nature (physics) that lead to the emergence of goal-directed biological actions. There is an important difference between “being able to predict” and “knowing laws of nature leading to” a phenomenon; for example, a regression model may be well suited for the former, but not for the latter.

The state of neural and motor elements involved in any action changes over time. So, biological actions may be viewed as outputs of a dynamical system (for review see Kugler and Turvey, 1987; Kelso, 1995). If one wants to control behavior of a dynamical system, the only way to do this is to change parameters of that system (Glansdorf and Prigogine, 1971). For example, consider a simple mechanical pendulum consisting of a weightless rigid rod and a point mass at its end. To control motion of such a pendulum one can change its parameters (such as length and point of suspension). Of course, one can build an artificial system that would simulate motion of the pendulum with high precision by placing an actuator between the rod and the mass, computing requisite time-varying forces, and applying them to the mass, but this would not help to understand the physics of actual pendulum motion. While behaviors of living systems can be well approximated with engineering methods, these methods are based on pre-programming of performance variables, which limits their usefulness for understanding the physics of dynamical systems involved in the production of biological movements. Let me reiterate that there is a qualitative difference between discovering laws of nature in a system and using computational means to reproduce its behavior. Note that many years ago Bernstein (1935) emphasized the impossibility to pre-program performance variables by biological systems in the changing environment. So, from a physical view, changing parameters is the only natural method of producing changes in performance variables during biological motion.

In BPLs, typically it is assumed that parameters change at a much slower rate compared to variables; so, in many cases, parameters, such as mass, stiffness, electric charge, and so on, are assumed to be constant. As discussed later, this is not necessarily the case for NPLs. In fact, parameters of these laws can change at a faster rate than variables linked by those laws.

Within this paper, I am going to focus on biological movements to illustrate NPLs. This is due to both personal experience and the fact that movements are very attractive objects for exploration of NPLs. The well-developed apparatus of classical mechanics makes salient variables (such as forces, moments of forces, rotations, translations, their derivatives, etc.) measurable with reasonable accuracy and objectivity. In contrast, studies of perception are typically based on measurements that are indirect and may rely on subjective experiences. In studies of cognition, salient variables are not measurable at all (sometimes, not even defined), and researchers frequently limit themselves to ingenious experiments with outcome variables that are only indirectly related to the processes under exploration, for example, reaction time, and/or to indirect indicators of neurophysiological processes such as evoked potentials and MRI signals.

In studies of human movements, we are still at a pre-Newtonian stage. Being an optimist, I believe that we are close to formulating at least some NPLs. At this time, however, the field is dominated by computational models that describe regularities of behavior expressed in mechanical and/or electrical (muscle activations) performance variables. These models are useful because they present in a compact way large bodies of experimental observations. They may be compared to the Kepler Laws, which later formed the foundation of Newton’s Law of Gravity. One has to understand the limitations of computational modeling, however: Such models may provide hints, but not answers. Also, assuming computational processes within the object of study (e.g., the brain) is not acceptable to a physicist; this would be similar to assuming computations performed on planets and stars that display movements obeying the Kepler Laws.

The main idea of the approach advocated in this paper follows rather closely the principle of activity introduced by Bernstein about 50 years ago (1966, 1967). In contrast to the dominant views of Pavlov’s school, Bernstein considered living systems active rather than reactive. While Pavlov viewed all actions as combinations of inborn and conditioned reflexes, Bernstein viewed purposeful actions as initiated from within the body. The main idea is also related to the insight of Gelfand and Tsetlin (1962, 1966) that variables and parameters describing biological objects can be classified into essential and non-essential. This idea may be reformulated here as: Organisms produce actions by manipulating essential parameters of NPLs.

3. Tonic stretch reflex as a universal NPL

One of the most widespread NPLs related to movements of animals is arguably the relation between muscle force and its length mediated by the mechanism of the tonic stretch reflex (TSR, Liddell and Sherrington, 1924). Imagine that the distal tendon of a muscle is separated from its natural point of attachment and is connected to a motorized device that can stretch the muscle slowly and measure its length and force. Imagine also that the animal is unable to change descending commands from the brain to the spinal segments controlling the muscle, for example due to a cut of the neural axis at a higher spinal level (spinalized animal) or at a midbrain level (decerebrated animal). If the muscle shows no activation in the initial state, its slow stretch will lead to an increase in force due to the elastic properties of the peripheral tissues; the magnitude of this force change will be relatively small (the thin dashed line in Fig. 1). At some length, the muscle will show first signs of electrical activation–threshold of the TSR (A) – accompanied by a much steeper dependence of force on length (two thick lines in Fig. 1; cf. Matthews, 1959). Further, let us consider only the active muscle force (F) as a function of muscle length (L), i.e., the magnitude of deviation from the thin dashed line in Fig. 1. Note that muscle stretch beyond A leads to an increase in its activation level, more or less in parallel with the force increase (see the increasing font of EMG – electromyogram – in Fig. 1).

Fig. 1.

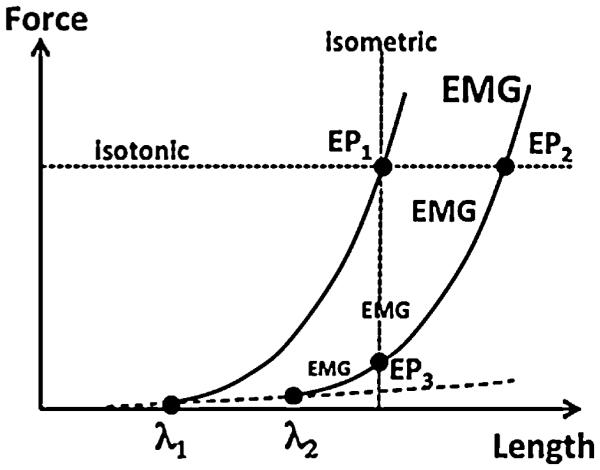
An illustration of the dependence of muscle force on length. Slow stretch of a muscle with no activation leads to a relatively slow increase in force due to the elastic properties of the peripheral tissues (the thin dashed line). At some length – tonic stretch reflex threshold (A) – the muscle will show first signs of electrical activation (EMG) accompanied by a much steeper dependence of force on length. For a given external load, the system reaches equilibrium (EP) with a certain force-length combination. A change in A can lead to a shift in EP accompanied by changes in length and/or force depending on the external loading conditions.

Different functional forms have been used to describe the F(L) relation due to the TSR. For example, in original studies by Feldman (1979): F = k₀exp(L − λ) when L > λ and F = 0 for L ≤ λ. This equation represents a NPL with two variables, F and L, and two parameters, k₀ and λ. A number of experiments on both humans and non-human animals have provided evidence that changes in descending signals can only change A for a muscle, but not k₀, which defines the shape of the F(L) dependence (Matthews, 1959; Feldman, 1966; Feldman and Orlovsky, 1972). In other words, brain structures can manipulate only one essential parameter A to control a muscle, while muscle activation and mechanical variables change as consequences of changes in A given external forces.

The TSR threshold λ can also be considered as a neurophysiological variable. Consider, for simplicity, that there are only two inputs into a neuron, descending and reflex, reflecting muscle length (the top insert in Fig. 2). Since a neuron is a threshold element, it generates action potentials at times when its membrane potential reaches the threshold value (Fig. 2, left panel). If the descending input is over the threshold, the neuron will generate action potentials at the highest possible frequency independently of the other input (Fig. 2, right panel). This would effectively eliminate the TSR. If the descending input depolarizes the neuronal membrane to a value under the threshold, neuronal activity will only be seen for a certain magnitude of the other input, i.e. at values of muscle length over the threshold value (λ). The frequency of action potential generation will increase with an increase in muscle length (illustrated in the left panel of Fig. 2 with different rates of membrane depolarization and in the right panel with the two dashed curves). The two illustrations show that the same parameter, λ, can be measured in mechanical units (meters, as in Fig. 1) and in neurophysiological units (millivolts, as in the left panel of Fig. 2). In other words, the TSR mechanism provides for a seamless translation between the languages of neural and mechanical processes without any computation.

Fig. 2.

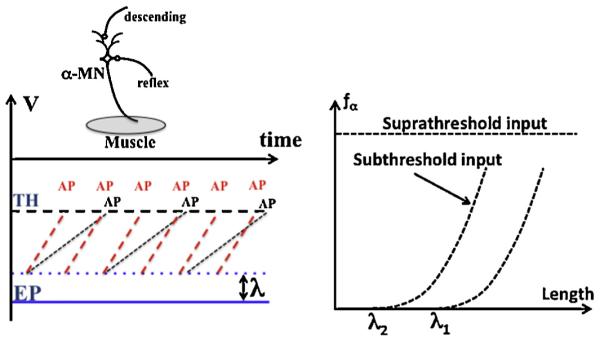
Consider two inputs into a neuron, descending and reflex (top insert). Left panel: The neuron generates action potentials (only marked as AP, not drawn) when the membrane potential reaches the threshold value (TH) (left panel). Without excitatory inputs, the membrane is at equilibrium potential (EP). Membrane subthreshold depolarization (λ) moves the membrane potential closer to TH. Reflex feedback leads to ramp-like depolarization of the membrane (black ramps and AP for a shorter muscles, red ramps and AP for a longer muscle). The frequency of AP generation depends on the reflex input. Right panel: For a suprathreshold input, the neuron would generate action potentials at the highest possible frequency. Membrane subthreshold depolarization (λ) shifts the dependence of the neuron firing frequency (fα) on muscle length (compare the two curves in the right panel). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

The NPL linking two mechanical variables, F and L, with one modifiable parameter λ uses a chain of BPLs to link the two variables. These include, in particular, BPLs that define how muscle fibers react to external force, how these changes are transmitted to sensory endings in muscle spindles, how deformation of the sensory endings leads to the generation of action potentials, how these are transmitted along afferent fibers, how they act via synapses on neurons, how motoneurons are recruited and generate action potentials, how these are transmitted to muscle fibers, how neuromuscular synapses work, and how action potentials on the muscle fiber membrane lead to cross-bridge formation and force generation. In fact, every step within this simplified chain is in itself a chain/cluster involving multiple BPLs.

Sometimes, muscle behavior is associated directly with a set of typical parameters, such as damping, stiffness, and impedance, which describe well-known BPLs (e.g., Hogan et al., 1987; Hof, 2003; reviewed in Latash and Zatsiorsky, 2015). Note, however, that, while the F(L) dependence of a muscle may resemble that of a non-linear spring, the TSR does not turn muscles into damped mass-spring systems. Unlike mass-spring systems, muscles are essentially active, and the TSR has identifiable purposes. In particular, the TSR acts to (help) stabilize equilibrium states of the body in the environment (Latash, 2010). Also a typical mass-spring system is described with constant parameters while the organism can modify parameters of NPLs in a purposeful way.

4. Referent coordinates as parameters of NPLs

According to the main idea, expressed about 50 years ago as the equilibrium-point hypothesis (Feldman, 1966, 1986; reviewed in Feldman and Levin, 1995), the control of a muscle by the central nervous system can be adequately described as a change in the tonic stretch reflex threshold λ that links the active muscle force to muscle length (see Figs. 1 and 2). Actual performance will depend on the external force (load) acting on the muscle, and the muscle is expected to come to an equilibrium state with a certain combination of F and L (equilibrium point, EP in Fig. 1) for a given λ. In particular, the same shift of λ (from λ₁ to λ₂ in Fig. 1) would lead to a change in the active force in isometric conditions (compare EP₃ and EP₁ in Fig. 1) and to a movement in isotonic conditions (compare EP₂ and EP₁ in Fig. 1).

This idea has been generalized for the control of any multi-muscle system with the help of the notion of referent coordinate (X_R). Imagine that you deal with a stubborn hungry donkey. You want the donkey to move to a new location. One method to control the donkey (suggested by the immortal Hodja Nasreddin) is to tie a carrot to the end of a stick and move the carrot in front of the donkey’s head to the desired location. The carrot will define a new X_R for the donkey, and the donkey’s motion will be driven by the difference between the actual head coordinate and X_R. The donkey will stop when its head reaches the carrot. In more formal terms, the donkey, as a physical system, moves towards a state with minimal potential energy, and this state is defined by the carrot coordinates, which represent parameters of a NPL. While we do not know the exact functional form of this NPL, is can be expressed, for example, as a dependence of donkey’s head acceleration on the vector from the head to the carrot in external space.

X_R can be defined at different levels of analysis of natural action. For a single muscle, λ is the X_R. For a natural voluntary movement, at the level of task formulation, X_R,TASK is a vector that defines referent coordinates for salient task-specific variables. We will address the question how X_R,TASK leads to X_R at lower levels down to λs for individual muscles a bit later. At this time, we do not know the neurophysiological mechanisms involved in the specification of X_R at levels higher than the single-muscle level. It is likely, however, that the basic principle of specifying subthreshold depolarization level of a neuronal pool and organizing feedback on a salient performance variable may be used at all the levels involved in natural actions.

In order to initiate a movement, corresponding parameters (X_R) have to be changed, and performance variables will change according to the involved NPLs. A time profile of X_R(t) may be viewed as a control trajectory for a movement. At each new value of X_R, there is a combination of relevant performance variables corresponding to a new equilibrium state of the system (F_EQ; X_EQ in Fig. 3). The time profile of those variables may be referred to as the equilibrium trajectory of the system. The actual trajectory of the effector (body) will depend on many other factors such as, for example, inertia of the moving system. Fig. 3 illustrates the three trajectories for a single effector (the relevant variables are its force and coordinate) assuming that the movement is very fast. Note that the control and equilibrium trajectories are faster than the actual trajectory. This is an illustration of the aforementioned fact that parameters of NPLs may change faster than corresponding variables.

Fig. 3.

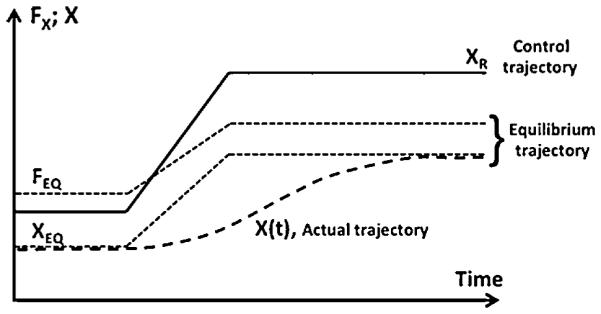
Control of an action can be adequately described as a time shift on the referent coordinate (X_R) of the effector. It leads to changes in equilibrium states (combinations of force and coordinate, F_EQ and X_EQ) that depend on the current external forces (equilibrium trajectory). Actual trajectory lags behind and reflects mechanical properties of the effector.

5. Motor redundancy and abundance

One of the problems embedded in the advocated approach is the transformation of task-specific X_R,TASK to X_R at lower levels, and ultimately, to muscle-specific X_R, i.e., λs. We assume that task formulation is relatively low-dimensional (e.g., the three coordinates for the donkey’s head). To implement this low-dimensional X_R,TASK, however, the donkey would have to move its legs, joints, and muscles. So, there have to be several few-to-many transformations leading from X_R,TASK to X_R for the limbs, joints, and muscles (λs). Such transformations are examples of problems of redundancy (Bernstein, 1967; Turvey, 1990); each transformation is equivalent to solving n equations with m unknowns, where m > n.

Traditionally, problems of motor redundancy have been approached trying to find single solutions, for example using optimization methods (reviewed in Prilutsky and Zatsiorsky, 2002). Recently, however, an alternative approach to such problems has been offered as the principle of abundance (Gelfand and Latash, 1998; Latash, 2012). According to this principle, the central nervous system does not produce single optimal solutions to typical problems of redundancy but facilitates families of solutions equally able to solve the task with acceptable accuracy (“good enough solutions”, cf. Simon, 1982; Loeb, 2012). Such families reflect both preferred sharing of the input among the apparently redundant elemental variables and desired stability of action.

Imagine that a donkey is led by the same carrot trajectory in the same conditions from the same initial state to the same desired final location in space multiple times. The principle of abundance predicts that motion of the legs, joint rotations, and muscle activation patterns will show relatively high variability across trials, while the head trajectory will remain relatively invariant. This prediction has been confirmed in many studies (reviewed in Latash, 2008), starting from the classical study of professional blacksmiths by Bernstein (1930). In that study, the trajectory of the hammer across repetitive strikes was relatively low, while the joint trajectories showed much higher variability.

The relatively high variability of the trajectories of effectors (such as joints and muscles) does not mean that all possible combinations of variables produced by the effectors are realized randomly. There are preferred patterns of sharing the salient task-specific variables among the effectors; such preferred patterns show high consistency during well-learned actions (e.g., locomotion, multi-finger hand action, etc.). They have been most commonly described using optimization methods (e.g., Alexander, 2002; Prilutsky and Zatsiorsky, 2002; Terekhov et al., 2010). So far, the physics of sharing has been unknown.

6. Structured variability as a central biological concept

Stability of any action is crucial for success in the environment characterized by unpredictable forces and changing targets. In addition, internal states of the body, including excitability of neurons, are varying all the time. As a result, a certain irreducible amount of variability is always present. Ensuring stability of salient variables in the presence of internal and environmental variability is one of the crucial features of biological systems. The concept of task-specific stability, introduced by Schöner (1995), suggests that biological systems are able to stabilize various salient variables in a task-specific way. This leads to specific signatures seen in the structure of variability across multiple attempts at solving the same problem. A method to analyze structure of variability has been developed within the framework of the uncontrolled manifold (UCM) hypothesis and used in many studies of various tasks performed by different unimpaired and impaired populations (reviewed in Latash et al., 2007; Latash, 2008).

For example, imagine that a person tries to produce a certain magnitude of total force while pressing with two fingers (Fig. 4). This task has an infinite number of solutions corresponding to the line F₁ + F₂ = F_TASK in the abundant space of finger forces. The solution space is the UCM for this task. If multiple trials are performed at this task, the cloud of data points measured in individual trials will form an ellipse elongated along the solutions space (the UCM for the total force; Scholz et al., 2002). Imagine now that the force sensors are positioned at equal distances from a pivot (the insert in Fig. 4). The subject will now have to keep the total moment of force close to zero with respect to the pivot. In such conditions, the cloud of data points may rotate and the ellipse may become elongated with respect to the line F₁ − F₂ = 0 (the UCM for the total moment of force; Latash et al., 2001). So, performance of the same explicit task may be associated with different patterns of variability depending on what the subject views as an important task feature. Such analysis may be performed with respect to different variables (Scholz and Schöner, 1999; Scholz et al., 2000; Latash, 2008) allowing researchers to explore what variables the performer sees as salient.

Fig. 4.

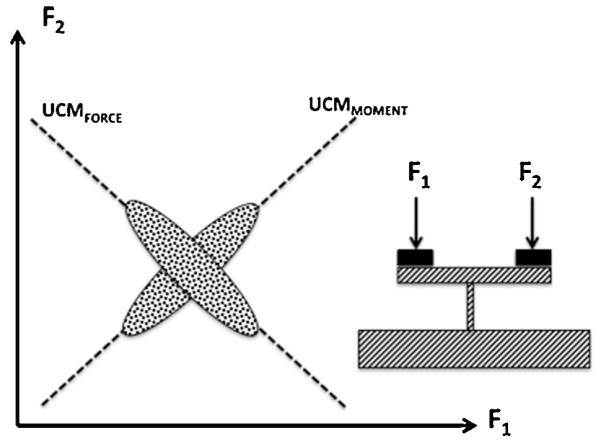
An illustration of a task to produce a certain magnitude of total force while pressing with two fingers: F₁ + F₂ = F_TASK. The solution space is shown as UCM_FORCE . If the fingers press at equal distances from a pivot (insert), the moment of force has to be kept close to zero. The solution space for this task is shown as UCM_MOMENT. Possible data distributions over multiple trials are shown as ellipses.

In general, this framework can be applied to non-motor domains (for a more detailed discussion see Latash, 2008). In particular, stability of salient percepts may be based on varying contributions from individual sensors and modalities as long as these variations are primarily confined to the corresponding UCM – a subspace corresponding to an unchanged salient percept. Stability of meaning conveyed by a spoken or written message may be based on varying sentences. Solving a problem in one’s mind may be associated with reaching a state in a space of appropriate concepts satisfying the constraints imposed by the problem; such a state may be reached by varying trajectories. So far, no experimental studies of stability beyond the motor domain have been performed.

The concept of structured variability has implications for issues of philosophy. Consider, for example, the famous Chinese Room Problem formulated by Searle (1992), related to the famous Turing test. You do not know whether there is a person who knows both English and Chinese in the room or someone who knows neither of the two languages but has access to a complete multi-volume collection of all possible phrases in English with perfect translations into Chinese. The task is to find out whether the room has an actual bilingual person or the multi-volume collection of phrases. It is only allowed to submit phrases in English and analyze translations in Chinese delivered from the room. According to Searle, there is no solution. In fact, there is a solution to the problem based on the assumed biological specificity of structured variability. Imagine that you asked for translations of tens of thousands of phrases, and had one long phrase repeated multiple times at random locations within the set. A multi-volume collection would produce identical translations for the repeated phrase. A bilingual person would generate varying translations that all preserve the meaning of the original phrase.

7. Top-down and bottom-up approaches

The general framework described so far leads to the emergence of numerous new problems. These problems have been addressed using two approaches, top-down and bottom-up. Within the first approach, analysis starts with trying to identify laws that lead to the formation of X_R,TASK. Selecting a target for an action is based on numerous factors. One of the most promising approaches is arguably the dynamical field theory developed by Schöner and colleagues (Thelen et al., 2001; Erlhagen and Schöner, 2002). It considers interactions within a neuronal network that creates a time-varying activation field with a few inputs related to both sensory information and internal body states. In particular, the relative weight of such inputs may vary leading to mistakes in performance as in the classical A-non-B errors seen in infants (Schöner and Thelen, 2006). Such errors are seen in infants between 6 and 10 months of age. A typical experiment would involve an infant sitting in his/her mother’s lap and the experimenter showing the infant a toy and then hiding it under one of the two identical non-transparent cups turned upside down. At the first trial, the infant reaches toward the cup hiding the toy. If at the second trial the toy is hidden under the other cup (the infant can see the toy manipulations at all times!), the infant first reaches to the first cup that has no toy under it and only then – to the other cup. In other words, memory on the previous reach overpowers the visual information leading to an error in target selection.

The alternative approach, bottom-up, starts with the identification of control variables for muscles, λs. Generalization of the control at the muscle level to joint control is relatively straight-forward for a single kinematic degree-of-freedom joint spanned by two opposing muscles, agonist and antagonist. The control of joint action can be described with two λs or with two variables describing reciprocal activation and coactivation of the muscles, the r-command (reciprocal command leading to unidirectional λ shifts for the agonist and antagonist muscles) and c-command (coactivation command leading to counter-directional λ shifts for the two muscles) (Feldman, 1980). The situation becomes more complicated for more realistic joints with several degrees-of-freedom spanned by redundant sets of muscles. At the joint, limb, and whole-body levels, adequate NPLs and relevant parameters are hidden; there have been only a handful of attempts at experimental measurement of those parameters (Latash and Gottlieb, 1991; Domen et al., 1999; Ambike et al., 2015b), but they have all been based on assumed mechanical models of the effectors that were likely oversimplified (cf. Gribble et al., 1998).

While the referent configuration (RC, a set of referent coordinates) at the task level has been defined with respect to salient performance variables, and the RCs at the muscle level have been associated with λs, RCs at intermediate levels are all but unknown. One of the ideas originating from the classical studies by Bernstein (1967) has been that elements are united by the central nervous system into relatively stable groups to reduce the number of parameters manipulated at task-related neural levels. Such groups have been addressed as “synergies” (d’Avella et al., 2003; Ivanenko et al., 2004; Ting and Macpherson, 2005) or “modes” (Latash et al., 2001; Krishnamoorthy et al., 2003). Modes may reflect RCs at intermediate stages of the assumed control hierarchy reflecting the person’s experience with everyday tasks.

Recently it has been suggested that another coordinate system (“control coordinates”) may be involved in the control of movements reflecting task-specific organizations of elemental RC shifts (e.g., λ shifts) that allows ensuring stability of performance using local control organized about each of these new coordinates (Akulin et al., 2015). Unlike modes, control coordinates are sensitive to task changes, particularly to changes in conditions that affect stability of performance. When a person encounters a novel task, he/she searches for an adequate set of control coordinates that would allow implementing local control rules. Local rules mean that, during quick corrective actions, a neural variable reflecting RC_i changes based on the actual and previous values of that very RC_i, whereas other variables do not affect the action. Quick corrective actions necessary to stabilize an action in the unpredictable environment are organized along axes of this new coordinate system. Overall, the organization of intermediate stages in the hierarchy with few-to-many transformations remains a matter of speculation with fragmented experimental evidence.

8. Predictive and explanatory power of the physical approach

The physical approach advocated in this paper has allowed interpreting some of the poorly understood phenomena, observing novel phenomena, introducing new concepts, and quantifying changes in relevant NPLs and parameters in persons with impaired motor function (reviewed in Latash, 2008; Latash and Huang, 2015).

8.1. Equifinality and its violations

One of the phenomena discussed as a strong prediction of the control with referent coordinate is equifinality, a property of a neuromotor system to come to an originally planned final position despite possible transient changes in external forces. A number of studies reported equifinality during fast movement performed by humans and animals (Bizzi et al., 1976; Kelso and Holt, 1980; Schmidt and McGown, 1980; Latash and Gottlieb, 1990), while other studies reported violations of equifinality (Lackner and DiZio, 1994; DiZio and Lackner, 1995; Hinder and Milner, 2003). Such violations were observed under special conditions such as moving in a rotating centrifuge or in an artificial force field simulating negative damping. These findings have been used as arguments against the main ideas of control with referent coordinates. Note, however, that the RC hypothesis (as well as equilibrium-point hypothesis) predicts equifinality only under certain conditions such as the lack of changes in the control variables (λ or RC) and in the muscle force-generating properties in response to a perturbation. Both conditions may be violated in experiments leading to violations of equifinality within the framework of the RC hypothesis. As discussed later, unintentional drifts in RC are likely to take place while peripheral muscle force-generating properties may also change in response to a brief burst of activation (the catch property of muscles, Burke et al., 1970, 1976), which may be induced by a perturbation. Overall, this experimental material resulted in productive discussions of the RC hypothesis (Feldman and Latash, 2005; Feldman, 2015).

Within the advocated scheme, equifinality is indeed expected at the task level, assuming that the subject of this mental experiment is not changing RC_TASK, but not at lower levels that can involve different combinations of RC_i matching the RC_TASK. A series of recent studies with multi-joint movements and multi-finger force production have reported violations of equifinality at abundant levels of elements in the presence of (relative) equifinality at the task level (Wilhelm et al., 2014; Zhou et al., 2014; Reschechtko et al., 2014). Note that these observations were made in natural conditions, without rotating subjects in a centrifuge or using artificial negative damping force fields. Such violations are natural consequences of the assumed lower stability of the system in directions that do not affect task-specific salient variable (within the uncontrolled manifold – UCM – for those variables, cf. Scholz and Schöner, 1999).

Evidence for equifinality at a more functional level has been obtained in experiments with long-lasting electrical stimulation applied to cortical areas (including the motor areas) of monkeys (Graziano et al., 2002, 2005). The stimulation led to complex movement patterns involving both the upper extremities and the head that resembled elements of movements from the everyday repertoire of the monkey. They could look like a defensive reaction (turning the head away and bringing a hand to the head in a defensive gesture) or a feeding behavior (bringing a hand to the mouth and turning the head towards the hand). The same stimulation applied while the monkey was in different initial postures resulted in similar final postures (equifinality) achieved with different movements of the hand and the head.

8.2. Unintentional movements

When a transient perturbation has a dwell time in-between the application and removal of a perturbing force, violations of equifinality may be observed even at the task level (Zhou et al., 2014, 2015a,b; Reschechtko et al., 2014). These violations are large, up to 50% of the effects of the perturbation. These novel phenomena show that RC_TASK can drift independently of the will of the performer, i.e. that humans can show unintentional movements. A novel concept of RC-back-coupling has been suggested to account for unintentional movements. This concept assumes that when actual body configuration is kept away from its RC by external forces, RC drifts towards the actual configuration. This drift may be viewed as a reflection of the natural tendency of all physical systems to relax toward minimum of potential energy.

This idea is illustrated in Fig. 5. Imagine an effector (the filled circle) involved in a one-dimensional task of moving along a coordinate X. When RC_X for the effector matches its coordinate X_E, the effector rests at the bottom of the potential field (top panel). Movement of the effector is produced by a shift of RC_X leading to motion of the effector shown with the arrow (middle panel). This process is fast with typical times on the order of 0.1 s reflecting neural conduction and electromechanical delays. We address it as direct coupling between RC_X and X_E. If the effector is blocked from moving toward RC_X (the black “brick” in the bottom panel of Fig. 5), the effector produces a non-zero force on the block, and RC_X starts moving towards X_E leading to an unintentional movement observed after the stop is removed. The experimental estimations of this RC-back-coupling process in experiments with perturbations have suggested an exponential drift with the time constant of about 1 s (Zhou et al., 2015a,b).

Fig. 5.

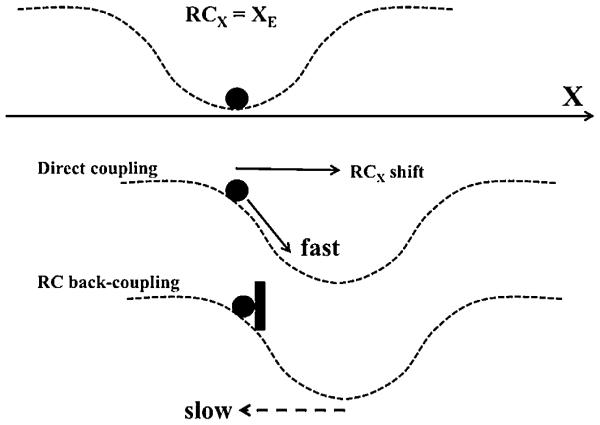
An illustration of an effector in one-dimensional tasks. When referent coordinate of the effector (RC_X) matches its actual coordinate X_E, the effector rests at the bottom of the potential field (top). A shift of RC_X leads to motion of the effector (the arrow in the middle panel). If the effector is blocked (by the black “brick”, bottom panel), RC_X starts moving towards X_E. This process is relatively slow compared to the direct coupling in the middle panel.

In fact, unintentional movements have been known for some time. If a person is asked to produce a constant force with an effector under visual feedback on the force level, and then the feedback is turned off, the force starts to drop (Slifkin et al., 2000; Vaillancourt and Russell, 2002). The subjects in such experiments are unaware of the drop in force, even when it reaches one-third of the initial force level. Within the RC-hypothesis, a drop in force is associated with a drift of the effector RC toward its actual coordinate, possibly accompanied by a drift of the apparent stiffness of the effector. In experiments with constant force production, the force drift is slow, typically with a time constant of about 10 s.

Taken together, the observations of fast and slow RC drifts suggest at least two kinds of relaxation processes within the system for movement production: Fast, triggered by perturbations; and slow that can take place in steady states. The different speeds of the two relaxation processes suggest that they happen in spaces characterized by different stability properties: Faster drifts are expected in stable spaces, while slower drifts are typical of less stable spaces. Since all movements are based on abundant sets of elements, the two types of unintentional actions have been associated with processes within the UCM (unstable sub-space with slow relaxation processes) and within the orthogonal to the UCM sub-space (stable sub-space with fast relaxation processes) (Ambike et al., 2015a). This remains a speculative interpretation in need of experimental support.

8.3. Anticipatory synergy adjustments

Another novel phenomenon described recently in human experiments is anticipatory synergy adjustments (ASAs, Olafsdottir et al., 2005; Shim et al., 2006). ASAs represent a gradual change in an index of stability of a salient performance variable in preparation for a quick action. This index was computed as the relative amount of inter-trial variance within the subspace that has no effect on that salient performance variable (the UCM). During steady-state performance, most of the inter-trial variance is typically confined to the UCM for this variable corresponding to a high stability index. Only a fraction of the variance is in the orthogonal to the UCM subspace (ORT subspace). Fig. 6 illustrates a typical data distribution for a task of producing a constant sum of two elemental variables, X₁ and X₂ (e.g., accurate total force production with two fingers). Note that the cloud of data points is elongated along the solution space (UCM) for X₁ + X₂ = C. When a person prepares for a quick, self-paced action, the amount of within-UCM variance starts to drop and/or the amount of the within-ORT variance starts to grow about 200–300 ms prior to the action initiation (compare the three ellipses in the left panel of Fig. 6). This feed-forward mechanism allows the CNS to avoid fighting its own synergies stabilizing the variables that have to be changed quickly. It has been described for a variety of actions, from multi-finger tasks to whole-body tasks (Shim et al., 2006; Klous et al., 2011; Krishnan et al., 2011).

Fig. 6.

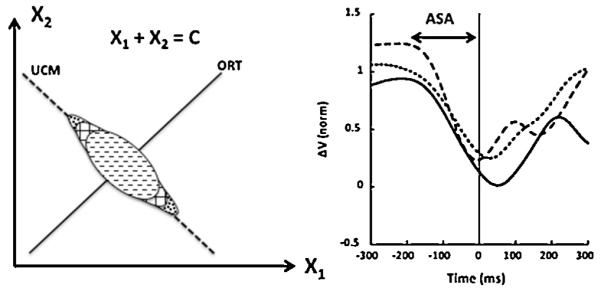
Left: An illustration of a task X₁ + X₂ = C. During steady state, data across trials form an ellipse elongated along the solution space (UCM). During preparation to a quick change in C, the amount of within-UCM variance starts to drop and/or the amount of the within-ORT variance starts to grow about 200–300 ms prior to the action initiation. Right: The time profiles of a multi-muscle synergy index (ΔV, normalized difference between within-UCM and within-ORT variances) during preparation to a quick action (at time zero) computed with three different methods (different curves). Note the anticipatory synergy adjustment (ASA). Reproduced by permission from Klous et al. (2011).

The right panel of Fig. 6 illustrates the time profile of the synergy index, computed as the normalized difference between the variances along the UCM and ORT spaces, prior to a self-paced action by a standing person. ASAs demonstrate that, in addition to changes in RC associated with an action, there is another group of variables manipulated by the CNS that ensure desired action stability. While a few suggestions on how controlled stability of action could be organized have been formulated (Latash et al., 2005; Martin et al., 2009), relevant parameters remain unknown.

8.4. Applications to and lessons from clinical studies

One of the first applications of the idea of control with referent coordinates (parameters of NPLs) addressed spasticity, a common consequence of a number of neurological disorders (such as spinal cord injury, stroke, cerebral palsy, and multiple sclerosis). Traditionally, spasticity has been viewed as a combination of impaired voluntary control (negative signs) and excessive involuntary muscle activation (positive signs) (Hughlings Jackson, 1889; Landau, 1974). However, several studies have documented beneficial effects of treatment with intrathecal baclofen on both spastic muscle contractions and residual voluntary control of the affected extremities (Latash et al., 1990; Latash and Penn, 1996). These observations are compatible with the scheme that views spasticity as a problem of control of the muscle referent coordinate (tonic stretch reflex threshold λ; Jobin and Levin, 2000). Fig. 7 illustrates this idea for a muscle with a particular biomechanical range of motion (between L_MIN and L_MAX). In a healthy muscle, λ can be shifted far beyond the biomechanical length limits; as a result, the muscle can show high activation levels when it is short and be relaxed when it is long. Imagine now that the range of λ shifts is constrained to a narrow interval limited by λ_MIN and λ_MAX. In this case, involuntary muscle activation would be seen at all length values L > λ_MIN, and it would be impossible to activate the muscle (i.e., it would be paralyzed) at length values L < λ_MAX. Voluntary muscle control would only be available within a narrow range of muscle length values shown in Fig. 7.

Fig. 7.

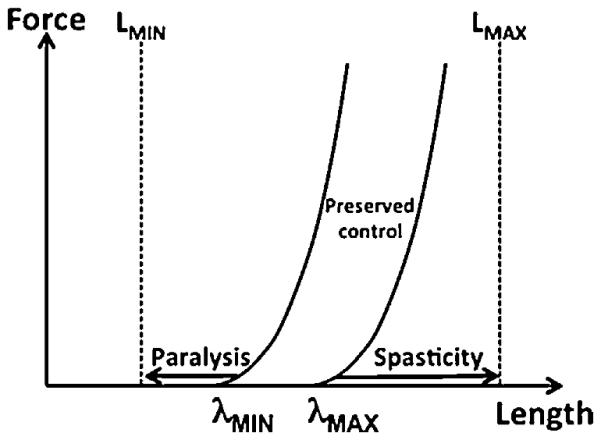
A spastic muscle is characterized by a reduced range of voluntary change of the tonic stretch reflex threshold (λ), from λ_MIN to λ_MAX. As a result, the muscle cannot generate voluntary activation at length values below λ_MIN and it shows spastic contractions at length values over λ_MAX. The total biomechanical range of muscle length is shown between L_MIN and L_MAX.

Neurophysiological mechanisms of NPLs that involve brain structures are unknown. Indirect evidence comes from studies of patients with various neurological disorders (reviewed in Latash and Huang, 2015). In particular, patients after unilateral stroke affecting one of the large hemispheres typically display major differences in the control of the contralesional arm (more impaired) and ipsilesional arm (relatively less impaired). While general patterns of motion of the two arms may differ significantly in such patients, there are no major differences in the structure of variance in the joint configuration space between the two arms (Reisman and Scholz, 2003). Similar observations were made in stroke survivors who performed multi-digit tasks: Significantly changed performance in the more affected hand was accompanied by unchanged structure of inter-trial variance (Latash and Huang, 2015).

Patients with Parkinson’s disease (PD) and multi-system atrophy (a brain disorder, formerly addressed as olivo-ponto-cerebellar atrophy, leading to a mixture of parkinsonian and cerebellar signs) show a dramatically different picture: Their overall movement patterns may be relatively unaffected, in particular in early-stage PD patients tested on their optimal medication, while there are significant differences in the structure of inter-trial variance reflecting impaired action stability (Park et al., 2012, 2013; Jo et al., 2015). ASAs are delayed and reduced in subcortical disorders. These observations promise important insights into the neurophysiology of instability (typical of PD and cerebellar disorders) and of lack of agility (bradykinesia and episodes of freezing). Given that these changes are seen at early stages of PD, sometimes even before clinical symptoms become apparent (Park et al., 2012, 2014), they also promise early biomarkers of this common neurodegenerative disease.

Taken together, these observations suggest that cortical mechanisms may be directly involved in specifying RC shifts during voluntary actions. This conclusion is corroborated by recent studies with transcranial magnetic stimulation (Raptis et al., 2010). Subcortical loops seem to be more crucial for ensuring proper, task-specific stability of actions – a conclusion corroborated by clinical observations of patients that show a combination of poor stability and poor agility (e.g., Parkinson’s disease) and those showing ataxia (cerebellar disorders). Overall, these observations are compatible with Bernstein’s idea of brain operators distributed among brain structures (Bassin et al., 1966) developed by Houk (2005) under the name of distributed processing modules.

8.5. Links of NPLs to effects of aging

NPLs developed within one’s lifetime are based on particular neural substrates. During early development, anatomical elements (e.g., muscles, joints, and digits) are likely being united into modes based on their involvement in typical everyday tasks. As in the earlier text, we imply under modes linear combinations of variables corresponding to their coupling observed during natural movements with parameters varying within a broad range (e.g., Danion et al., 2003). As suggested by the notion of “cortical piano” (Schieber, 2001), this may be accomplished by forming and strengthening neural projections within the brain. During aging, the progressive death of neurons at all levels of the central nervous system, from the cortex to segmental spinal levels (Eisen et al., 1996; Erim et al., 1999; Dinse, 2006), leads to destruction of some of those projections. As a consequence, the central nervous system has to switch to the pre-existent element-based method of movement control. This “back-to-elements” hypothesis (Kapur et al., 2010) accounts for the worse synergic control (Olafsdottir et al., 2007, 2008) and the counter-intuitive better individual control of digits in older persons (Shinohara et al., 2003).

8.6. Motor skill as a NPL

Some NPLs are common across species and across individuals: a typical aforementioned example is the tonic stretch reflex mechanism. Other NPLs are experience specific. These NPLs form the basis of what is addressed as motor skills. Within the introduced framework, a skill may be viewed as a reflection of a new NPL built as a result of practice and/or as a new rule for changes in parameters of existing NPLs. For example, to move in zero gravity or under water requires changing the rules of how RC for the effector has to be moved to perform an action with desired kinematics. It may also require changes of preferred patterns of sharing RC_TASK among RCs at lower levels. Since the number of environmental states is infinite, building an optimal solution for each and every situation is not feasible. So, an ability to use pre-existing NPLs and parametrize them to perform actions leading to “good enough success” is vital (Simon, 1956; Loeb, 1999).

Exercise may lead to emergence of NPLs of varying complexity. Some NPLs involve relatively short chains of BPLs that are commonly associated with reflex-like actions (e.g., long-latency reflexes or pre-programmed reactions, Hammond, 1955; Tatton et al., 1978; reviewed in Shemmell et al., 2010). Others involve longer chains associated with well-learned skills or “cognitive processes” – an undefined notion meaning that the chain is too complex to be deciphered.

Learning a motor skill typically requires coupling physical variables reflecting interaction with the environment with parameters that result in changes in physical variables acting on the environment. For example, riding a bicycle requires learning and implementing a rule that links spontaneous deviations of the body from the vertical to small turns of the front wheel in the direction of the deviations. After this NPL has emerged, it can be easily generalized to different bicycles. Such NPLs are indeed pervasive and very hard to modify, even if the modification may look trivial from the computational point of view. For example, a recent video on the Internet showed a gentleman who built a connector between the front frame with the handles and the front wheel, which reversed the effects of handle motion on the wheel: The wheel turned right when the handles turned left. It took this person many months to learn how not to fall down from his new bicycle, although, from the computational point of view, this required a trivial change in the sign of the relation between handle motion and front wheel turn.

Building a skill also requires creating appropriate sensory feedback. There is indirect evidence that sensory signals during everyday movements reflect information on complex variables, e.g., leg orientation in space and leg length during locomotion (Bosco and Poppele, 2002). Note that there are no peripheral receptors that change their activity with those particular physical variables. This suggests that the central nervous system is able to create higher-order sensory signals that are used to build new NPLs.

8.7. Implications for perception

Perception, as intrinsic measurement of a physical variable, has to be based on two components: To measure anything, one has to have a measuring device (e.g., a ruler) and a referent value from which the measurement is performed. The importance of these two components has been recognized since the classical observation of von Helmholtz that natural movement of the head and/or an eye leads to adequate perception of self-motion in the motionless environment, while pressing on the eye with a finger leads to an illusion of motion of the external world. Von Helmholtz drew a conclusion that signals to muscles involved in voluntary eye movements somehow affected visual perception in combination with the signals from light-sensitive receptors.

Further, a concept of efferent copy was introduced (Von Holst and Mittelstaedt, 1950) to account for the role of motor command in perception. According to this concept, a copy of the neural command to motoneurons is used to estimate an expected change in sensory signals and is sent to a neural structure that also receives signals reflecting the change of the sensory feedback produced by the action (reafference). The reafference signals are compared to the efferent copy, and, if there is a mismatch, a correction signal is sent to the motoneurons. This concept has been criticized lately, and inadequacy of its original formulation has been exposed (Feldman, 2015).

The original idea, however, remains valid: One has to use a referent coordinate to interpret sensory signals from peripheral receptors, and this referent coordinate represents a parameter in the corresponding NPL. Within this idea, peripheral receptors measure deviations of effectors from their centrally defined RCs, while percepts represent the sum of signals defined by the RC and by the sensory information (Feldman, 2009). For example, perceiving joint angle is based on its centrally defined referent position and sensory signals from various receptors (including muscle spindles, Golgi tendon organs, and articular receptors) that all reflect deviation of the joint from the referent position. This general idea is corroborated by observations of only minor effects of total joint replacement on joint position sense (Karanjia and Ferguson, 1983; Wada et al., 2002) and of kinesthetic illusions induced by muscle vibration (Craske, 1977; Lackner and Levine, 1979; Roll et al., 1989).

9. Concluding comments

Why did the toy and the frog behave differently in the mental experiment described in the Preamble? The toy behaved according to BPLs. The frog’s behavior was also guided by its personal NPLs, which, for example, could result in less predictable behaviors due to changes in some of the corresponding parameters with hunger, boredom, and other factors. Changes in internal states of the body lead to changes in parameters of NPLs resulting in apparently spontaneous movements or movements that seem to violate BPLs such as walking uphill, flying against the wind, and swimming against the current. Applications of the idea of NPLs are potentially broad, from the simplest motor acts to cognition. At this time, the latter is beyond my comprehension. But NPLs have to form the foundation of all behaviors because laws of nature have no pity and no exceptions.