Highlights
-
•
The firstever dengue vaccine, Dengvaxia®, has recently been licensed for use in several countries.
-
•
Mathematical models are valuable tools for assessing vaccination impact on dengue burden.
-
•
Model assumptions regarding dengue serotype immune interactions are inconsistent.
-
•
Our results demonstrate how model assumptions critically affect vaccine impact predictions.
Abstract
Dengue is one of the most important and wide-spread viral infections affecting human populations. The last few decades have seen a dramatic increase in the global burden of dengue, with the virus now being endemic or near-endemic in over 100 countries world-wide. A recombinant tetravalent vaccine candidate (CYD-TDV) has recently completed Phase III clinical efficacy trials in South East Asia and Latin America and has been licensed for use in several countries. The trial results showed moderate-to-high efficacies in protection against clinical symptoms and hospitalisation but with so far unknown effects on transmission and infections per se. Model-based predictions about the vaccine's short- or long-term impact on the burden of dengue are therefore subject to a considerable degree of uncertainty. Furthermore, different immune interactions between dengue's serotypes have frequently been evoked by modelling studies to underlie dengue's oscillatory dynamics in disease incidence and serotype prevalence. Here we show how model assumptions regarding immune interactions in the form of antibody-dependent enhancement, temporary cross-immunity and the number of infections required to develop full immunity can significantly affect the predicted outcome of a dengue vaccination campaign. Our results thus re-emphasise the important gap in our current knowledge concerning the effects of previous exposure on subsequent dengue infections and further suggest that intervention impact studies should be critically evaluated by their underlying assumptions about serotype immune-interactions.
1. Introduction
Dengue is a vector-borne viral illness of increasingly global importance (Kyle and Harris, 2008, Simmons et al., 2012). Traditionally associated with the tropics, the geographic expansion of its two mosquito vectors, Aedes aegypti and Aedes albobictus, together with ongoing globalization and urbanization have resulted in the invasion and establishment of dengue in much wider latitude ranges (Simmons et al., 2012, Messina et al., 2014, Lourenço and Recker, 2014). Treatment of dengue is currently limited to supportive care and alleviation of clinical symptoms; and in the absence of a population-wide vaccination campaign, control efforts against dengue virus (DENV) transmission are currently focused on the mosquito vectors, either through direct measures (e.g. application of insecticides) or through the limitation of vector breeding habitats (e.g. environmental management) (Simmons et al., 2012).
The Sanofi Pasteur live attenuated, tetravalent dengue vaccine (CYD-TDV), Dengvaxia®, the most advanced vaccine candidate to date, successfully completed Phase III clinical efficacy trials across several endemic countries in South East Asia and Latin America. The results showed moderate-to-high efficacy against virologically confirmed infections, hospitalization and severe dengue (Sabchareon et al., 2012, Capeding et al., 2014, Hadinegoro et al., 2015, Villar et al., 2015). However, there were marked variations between individual serotypes, between naive individuals and individuals with pre-existing antibodies to dengue serotypes (Dorigatti et al., 2015, Hadinegoro et al., 2015) and also between countries with different levels of transmission intensities (Hadinegoro et al., 2015). Based on available data it is further unclear whether the vaccine protects equally well against infection and/or onwards transmission as against clinical symptoms.
Besides these uncertainties regarding vaccine action it is important to note that there is currently little consensus regarding the effect of serotype immune-interactions on infection and transmission probabilities, especially within the context of dengue modelling (Ferguson and Anderson, 1999, Ferguson et al., 1999, Cummings et al., 2005, Adams et al., 2006, Wearing and Rohani, 2006, Nagao and Koelle, 2008, Aguiar et al., 2008, Recker et al., 2009, Wikramaratna et al., 2010, Lourenço and Recker, 2013, Lourenço and Recker, 2010) (also see Andraud et al. (2012) for a systematic review on the most common modelling approaches). For instance, antibody-dependent enhancement (ADE) and cross-immunity have both been proposed to underlie dengue's complex epidemiology and in driving the ubiquitous multi-annual periodicities in dengue incidence and serotype prevalence. Contrasting model assumptions further extend to the total number of infections that individuals might experience, with some models assuming full immunity after a secondary, heterologous exposure whilst others allow consecutive infections by all four serotypes. Importantly, different assumptions about immunity and serotype immune interactions have been shown to generate qualitatively similar epidemiological dynamics (Lourenço and Recker, 2013), yet their effect on the impact of vaccination, especially where the vaccine only offers partial and/or serotype-specific protection, has not yet been explored.
With Dengvaxia® already having been licensed for use in Mexico, Brazil, El Salvador and the Philippines, and other vaccine candidates currently being in the pipeline (Schwartz et al. (2015)), there has been a growing effort in modelling the population-wide application of a dengue vaccine and its potential impact on disease burden (Johansson et al., 2011, Chao et al., 2012, Beatty et al., 2012, Coudeville and Garnett, 2012, Durham et al., 2013, Ndeffo Mbah et al., 2014, Rodriguez-Barraquer et al., 2014, Thavara et al., 2014). It is therefore imperative to explore in more detail the effects of commonly used model assumptions about dengue serotype immune-interactions on the epidemiological dynamics of dengue following the implementation of a vaccination campaign. Here, using a spatially explicit, agent-based model, we demonstrate how model assumptions regarding cross-immunity and cross-enhancement critically affect qualitative and quantitative vaccine impact predictions. Our results thus re-emphasize the need for these to be carefully evaluated in future impact and cost-benefit analyses.
2. Results
We used a spatially explicit, individual-based meta-population framework (Lourenço and Recker, 2013) to simulate and quantify the short- and long-term impact of a dengue vaccination campaign under different assumptions about serotype immune-interactions (see Section 4). The model was qualitatively fitted against a hyper-endemic setting, with co-circulation of all four serotypes and seasonal dynamics driven by temporal changes in mosquito population densities (Supplementary Fig. S1). Pre-vaccination epidemiologies were quantified by averaging over a 20 year period before the start of the intervention campaign. These were then compared to the dynamics following the introduction of a vaccine over a 25-year period. The post-vaccination era was divided into relevant periods to analyse and highlight short- and long-term impacts separately (e.g. to compare the overall reduction in incidence over 25 years against the immediate effects within the first 10 years). Vaccination impact itself was then determined by the relationship between pre- and post-vaccination incidence levels and age-exposure profiles. In this framework we do not explicitly differentiate infection outcomes, such that incidence solely refers to infection counts and not (symptomatic) disease.
2.1. Vaccination impact without serotype immune-interactions
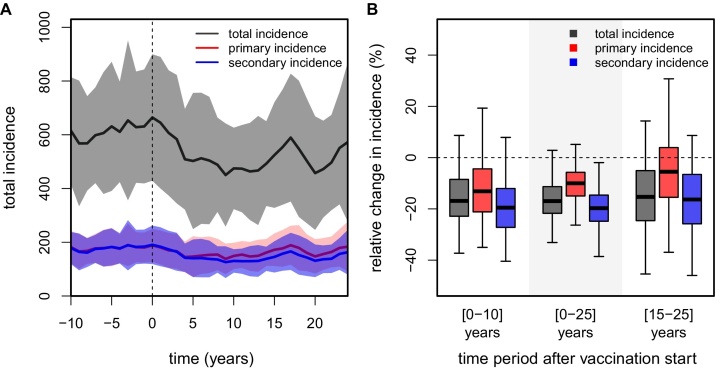
First we investigated the impact of routine vaccination with no immune interactions and four possible consecutive infections, which we here refer to as the neutral model. We assumed a vaccination coverage level of 75%, administered as a single dose at the age of 6 years (see Section 4). Vaccine efficacy levels (in terms of preventing infections) were assumed to be 30% and 70% in dengue-naive and pre-exposed individuals, respectively, in line with pooled estimates (i.e. aggregated sero-positive and sero-negative estimations) from the CYD-TDV Phase III trials (Capeding et al., 2014, Villar et al., 2015, Hadinegoro et al., 2015). For simplicity, however, and in contrast to trial data, equal efficacies for all serotypes were assumed. Under these assumptions we find that both the short- and long-term effects of vaccination in this hyper-endemic scenario lead to a moderate reduction in dengue incidence, on average by ≈15–20%, but with substantial variations between model runs (Fig. 1).
Fig. 1.
Impact of dengue vaccination without immune-interactions. Results show the outcome of a routine vaccination campaign based on 50 individual model runs, using a vaccination coverage of 75% at the age of 6 years (vaccination start at t = 0, vertical dashed lines). Solid lines in timeseries plots are the 1-year averages, with between-run variability shown as shaded areas. Incidence is presented per 100K individuals. (A) Timeseries showing changes in total, primary and secondary infections (grey, red and blue respectively). (B) Boxplots (see Section 4) showing the distribution in vaccine impact as the percent reduction in total, primary and secondary incidence (grey, red and blue, respectively) for 3 relevant periods post-vaccination. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)
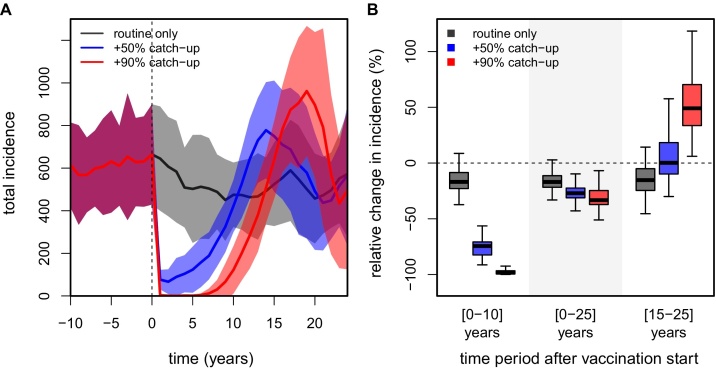
It is likely that the introduction of a dengue vaccine might be coupled with a population-wide catch-up campaign, in which individuals within a defined age range are targeted for vaccination in order to maximise the (short-term) impact on dengue burden. In our model we realised such a strategy by vaccinating a certain percentage of the population between the ages of 10 and 50 years, regardless of their prior immune status (see Section 4). We considered two catch-up scenarios, one in which the one-off campaign reached 90% coverage and one limited to 50%; the coverage for routine vaccination was kept at 75% at 6 years of age in both cases. As shown in Fig. 2A, the inclusion of a catch-up campaign has a significant and rapid impact on dengue burden, with incidence briefly dropping to near extinction levels for very high catch-up rates. Notably, even a 50% catch-up campaign can potentially reduce dengue incidence by nearly 75% over the first 10 years post-vaccination (Fig. 2B). However, and in stark contrast to a routine vaccination only programme, dengue incidence starts to rebound around five years after the start of vaccination and might even briefly surpass pre-vaccination levels before settling down to levels achieved by routine vaccination only (Fig. 2A). Nevertheless, the overall impact of vaccination over the first 25 years when combined with a population-wide catch-up campaign could be highly beneficial and, importantly, positively correlated with catch-up efforts.
Fig. 2.
Impact of dengue vaccination + catch-up without immune-interactions. Results show the outcome of a routine vaccination campaign based on 50 individual model runs, using a vaccination coverage of 75% at age of 6 years and a target age group for catch-up between 10 and 50 years (vaccination start at t = 0, vertical dashed lines). Solid lines in timeseries plots are the 1-year averages, with between-run variability shown as shaded areas. Incidence is presented per 100K individuals. (A) Timeseries showing the effect of coupling three possible catch-up campaigns with routine vaccination on total dengue incidence (grey for routine vaccination only, blue for routine + catch-up 50%, red for routine + catch-up 90%). (B) Boxplots showing the distribution in vaccine impact as the percent reduction in incidence (grey for routine vaccination only, blue for routine + catch-up 50%, red for routine + catch-up 90%), over three different periods post-vaccination. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)
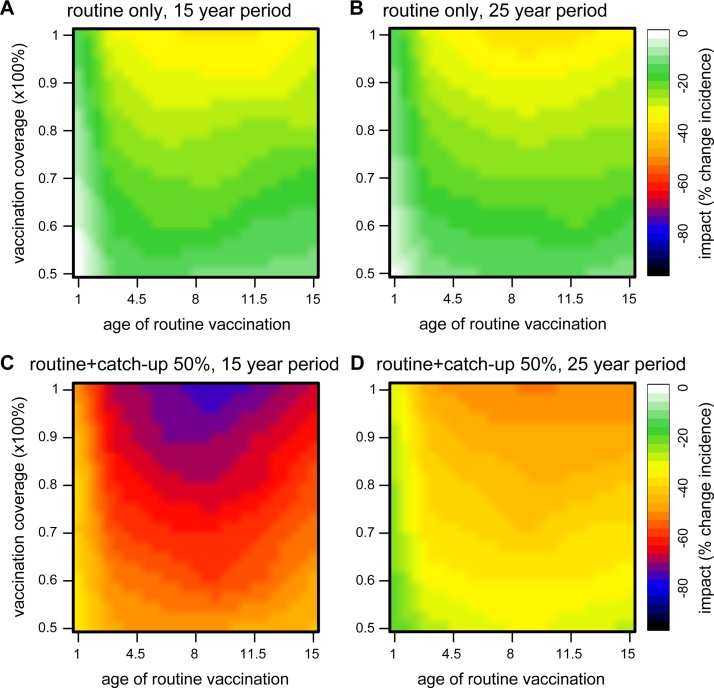
The particular nature of this vaccine in relation to differential protection between naive and pre-exposed individuals introduces a non-linear response in vaccine impact for different age groups. We addressed this by measuring impact over a wide range of vaccination ages and coverages. Fig. 3 illustrates how vaccine impact changes in response to both the age and coverage of routine vaccination, with and without a 50% catch-up, over two post-vaccination time periods. In all cases, the weakest impact was found when vaccination age was low, due to the relatively low vaccine efficacy in dengue-naive individuals. In contrast, vaccine impact could be maximised when routinely targeting the age group where individuals would, on average, have had experienced their first dengue infection (here between 6 and 12 years of age, best seen in Fig. 3C), at which point vaccine impact could nearly be doubled under high coverage levels. This age-range arises from a fine balance between maximizing the number of individuals who would acquire high vaccine-induced protection (seropositives) and minimizing the number of first infections. Accordingly, beyond this age range impact is again reduced, as the benefit of protecting individuals from first infection and boosting seropositives who could still have +2 infections would have been lost. These observations imply that the optimal age group for vaccination will be strongly dependent on the epidemiological setting, with higher transmission intensities requiring younger age groups to optimise vaccine impact.
Fig. 3.
Effect of vaccination age and coverage on vaccine impact without immune-interactions. (A) and (B) Vaccination-only impact as the percent reduction in total incidence relative to pre-vaccination levels over two time periods post-vaccination (first 15 years in A, and first 25 years in B). (C) and (D) Impact of vaccination coupled with an initial catch-up campaign over two post-vaccination time periods (first 15 years in C and first 25 years in D). In all subplots, there is a clear age-dependence in vaccine impact, introduced from the unequal vaccine efficacies between naive and seropositive individuals. The catch-up campaign has a strong effect in the short-term impact of the vaccine, which dictates its more positive outcome after 25 years. However, the 25 year period may include a strong rebound effect in incidence (see main text and Fig. 2). The target age group for catch-up was between 10 and 50 years.
2.2. Vaccination impact with serotype immune-interactions
Next we considered the effects of serotype immune-interactions on vaccination impact, where we again considered changes to dengue incidence and also shifting age patterns as measures of vaccine impact. Unless stated otherwise we assumed four possible infections with no immune-interaction other than the one under consideration. As before we assumed a coverage of 75% for routine vaccination and 50% for the one-off catch-up targeting a core age group of 10–50 years.
2.2.1. Maximum number of infections
First we considered the effect of the required number of infections for the development of full immunity. Due to the scarcity of clinically apparent tertiary and subsequent infections (Gibbons et al., 2007), many epidemiological models assume full cross-protection after a secondary, heterologous challenge (see (Johansson et al., 2011, Andraud et al., 2012) for reviews). However, data from cohort studies have been insufficient to discern whether the rarity of such events simply reflect clinical immunity, whereby third and fourth infections could indeed be common but clinically silent (Gibbons et al., 2007, Kyle and Harris, 2008, Endy et al., 2011, Burke et al., 1988, Tien et al., 2010, Lin et al., 2010, Sharp et al., 2014). A previous study has shown that the ‘twice infected – protected’ hypothesis can have significant effects on vaccine impact (Chao et al., 2012), while another has demonstrated that relaxing this hypothesis crucially affects estimates of dengue's reproductive number (R0) and age-related seroconversion rates (Wikramaratna et al., 2010). Similarly, in order to fit hyper-endemic seroprevalence rates we had to adjust the transmission rates in our model accordingly. This resulted in an increase in R0 from ≈4 in the (neutral) 4-infection model to ≈7 in the 2-infection model (see Supplementary Fig. 1 and Table 1 for examples and parameter values).
Table 1.
Parameters and values for the model.
| Parameter | Description | Value [range] | Refs. |
|---|---|---|---|
| Δ | maximum number of infections | 2 or 4 | Johansson et al., 2011, Andraud et al., 2012 |
| 1/δh | intrinsic incubation period | 2 days [2–7] | Halstead (2007) |
| 1/γh | human infectious period | 4 days [4–12] | Vaughn et al., 2000, Gubler et al., 1981 |
| 1/αh | temporary cross-immunity | 2–12 months [2–12] | Sabin (1952) |
| ϕh | enhancement, second infections | 2 [1–5] | Reich et al. (2013) |
| M | vectors per human host | 0.95–2 [0.3–20] | Focks et al. (2000) |
| vector biting rate | 0.55 per day [0.33–1] | Trpis and Hausermann (1986) | |
| extrinsic incubation period | 7 days [6–12] | Watts et al., 1987, Reich et al., 2013 | |
| vector average life-span | ≈20 days [8–42] | Trpis and Hausermann, 1986, Trpis and Hausermann, 1995, Reich et al., 2013 | |
| vector-to-human transm. prob. | per bite [0.33–1] | Sabin, 1952, Armstrong and Rico-Hesse, 2003, Reich et al., 2013 | |
| when Δ = 2 | 0.66 | – | |
| when Δ = 4 | 0.5 | – | |
| when Δ = 4, ϕh = 2 | 0.475 | – | |
| when Δ = 4, 1/αh = 12 | 0.505 | – | |
| when Δ = 4, 1/αh = 12, ϕh = 2 | 0.480 | – | |
| human-to-vector transm. prob. | equal to | Sabin, 1952, Armstrong and Rico-Hesse, 2003 | |
| μ | introduction rate (rand. serotype) | 0.03 per day | – |
| Nh | human host population size | 3.6 million | – |
| ω | daily mobility | 0.000001 per day | – |
| ah, bh | Weibull scale, shape (humans) | 0.0002, 10 | – |
| Weibull scale, shape (mosquito) | 0.007, 6 | – | |
| L | number of communities (L × L lattice) | 100 | – |
| H | number of humans cummunities | 360 | – |
| 1/νh | human average life-span | 60 years | – |
| R0 | dengue's reproduction number | Johansson et al. (2011) | |
| when Δ = 2 | ≈7.4 | – | |
| when Δ = 4 | ≈4.2 | – |
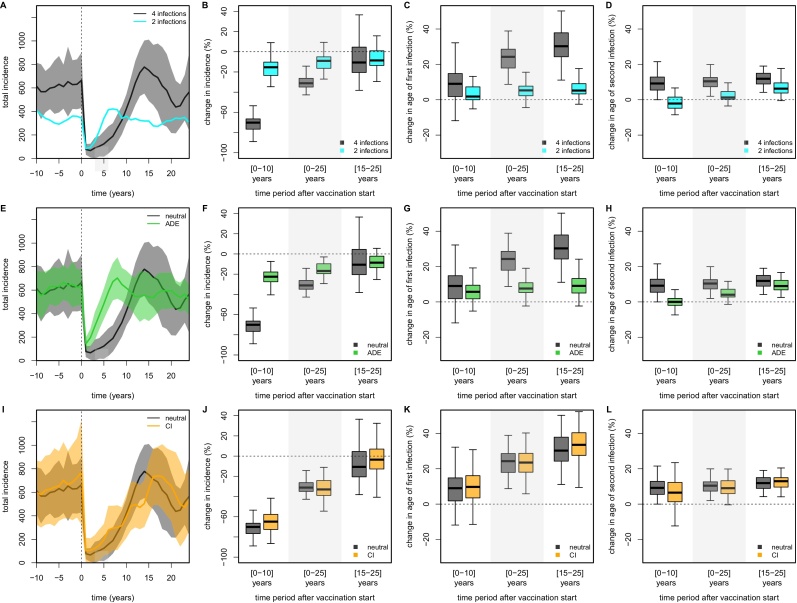
Despite the increase in R0, the limitation to only two possible infections significantly lowered total incidence rates (Fig. 4A). The predicted vaccine impact was also affected, with incidence starting to rebound almost immediately after the initial catch-up due to the higher R0, thus greatly reducing the short-term impact on dengue burden (Fig. 4A and B). Furthermore, the effect of vaccination on the average ages of first and second infection were much less pronounced in the 2-infection model compared to the neutral model (Fig. 4C and D). These observations demonstrate that detailed knowledge about the acquisition of clinical and/or sterile immunity to dengue over the course of repeated infections is crucial for model-based vaccine impact predictions.
Fig. 4.
Effect of immune-interactions on vaccination impact. Comparison of pre- and post-vaccination dynamic behaviour and vaccine impact between the neutral model (grey) and models with 2 infections (cyan, A–D), antibody-dependent enhancement (ADE, green, E–H) and temporary cross-immunity (CI, orange, I–L). All scenarios include a catch-up campaign targeting a core group of individuals between 10 and 50 years of age with coverage 50%; routine vaccination coverage was 75% of individuals at 6 years of age. Incidence is presented per 100K individuals. (First column, A,E,I) Comparative timeseries between neutral and other models, showing the dynamics of total incidence. Solid lines represent 1-year averages and shaded areas show between-run variability based on 50 individual model runs. (Second column, B,F,J) Quantitative impact of vaccination as the percent change in incidence compared to pre-vaccination levels. (Third column, C,G,K) Quantitative impact of vaccination as the percent change in the age of first infection compared to pre-vaccination levels. (Fourth column, D,H,L) Quantitative impact of vaccination as the percent change in the age of secondary infection compared to pre-vaccination levels. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)
2.2.2. Antibody-dependent enhancement
ADE has been considered in models in various forms, either by enhancing susceptibility to and/or infectivity of a secondary, heterologous infection (Wikramaratna et al., 2010, Cummings et al., 2005, Wearing and Rohani, 2006, Ferguson and Anderson, 1999, Recker et al., 2009). Here we used both, simply because the explicit but probabilistic nature of infection events in our model restricts the maximum possible level of enhancement compared to differential equation based models (for example, for a probability of transmission from human to vector of 0.5 per infectious bite, ADE can only reach a maximum factor of 2). In terms of vaccine impact, we found dengue incidence levels rebounding much quicker after the initial catch-up (Fig. 4E), more than halving the short-term impact compared to the neutral model (Fig. 4E and F). Furthermore, although the average ages of first and subsequent infections still increased as a result of vaccination, this was much less pronounced in the model assuming ADE (Fig. 4G and H). Hence, as in the case of complete cross-immunity after secondary infection (Fig. 4A–D), assumptions regarding immune enhancement after a primary infection can crucially affect the predictions of vaccination impact.
2.2.3. Temporary cross-immunity
Finally we investigated whether temporary cross-immunity, whereby individuals recovering from infection are assumed to be fully protected against infection by any serotype for a short period of time and commonly incorporated in dengue models (Wearing and Rohani, 2006, Nagao and Koelle, 2008, Lourenço and Recker, 2010, Aguiar et al., 2008, Reich et al., 2013), could affect vaccine impact predictions. As expected from previous work on our neutral model (Lourenço and Recker, 2013), we found that temporary cross-immunity only has a minimal effect on vaccination impact (Fig. 4I–L), even when considering a 12 months period of immunity. This result can be explained by the low probability that individuals get exposed to a heterotypic serotype within the short window of protection in our spatially explicit framework (Lourenço and Recker, 2013), which is also in line with cohort studies (Gibbons et al., 2007, Sharp et al., 2014) and a recent mathematical approach (Reich et al., 2013) that have robustly measured and/or estimated the time between infections to be several times above the often modelled range. Note, previous work has shown that even periods of 24 months of cross-protection do not alter the epidemiological dynamics of dengue within this spatially-explicit setting (Lourenço and Recker, 2013), such that the expected effect on vaccination impact would be equally small.
2.2.4. Comparison of serotype immune-interactions
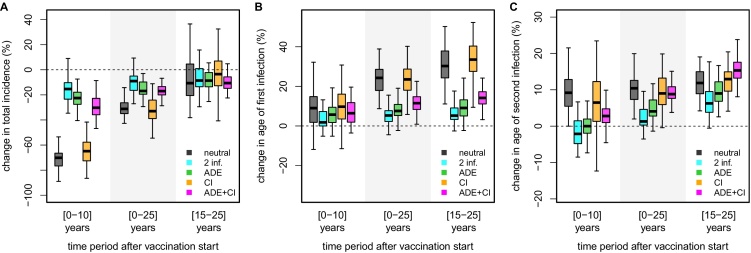
Fig. 5 summarises the comparison between the contrasting results of the neutral, 2-infections, ADE and temporary cross-immunity models. We also consider temporary cross-immunity in combination with ADE, but found the effect to be only marginal and with differences compared to the neutral model mostly driven by the effects of immune enhancement. It is important to note, however, that model discrepancies in terms of impact predictions are most pronounced in the short-term, i.e. within the first 10 years post-vaccination. Furthermore, all models agree with an overall positive effect over the 25-year period post-vaccination. The differences in the resulting age-profiles of first infection, however, appear long-lasting, which can have significant effects on further measurements of impact, such as hospitalization rates or case severity, if these are to be considered as age-dependent.
Fig. 5.
Comparison of impact predictions between immune-interactions. Boxplots summarising and comparing impact predictions of vaccination + catch-up between the neutral model (grey) and models assuming 4 types of serotype immune-interactions: full immunity after 2 infections (cyan), antibody-dependent enhancement (ADE, green), temporary cross-immunity (CI, orange) and ADE + CI (magenta). Impact predictions are based on the relative reductions in total incidence (A) and increases in average ages of primary (B) and secondary (C) infections for three relevant post-vaccination time periods. The catch-up campaign targets a core group of individuals between 10 and 50 years of age with coverage 50%; routine vaccination coverage was 75% of individuals at 6 years of age. Results are based on 50 independent simulations. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)
3. Discussion
Immunological serotype interactions are at the heart of many epidemiological investigations of dengue. The phenomenon of antibody-dependent enhancement in particular has received much attention and can be considered as one of the major obstacles in vaccine development, as it suggests that neutralizing antibodies must be raised to protective levels against all four serotypes simultaneously (Messer et al., 2014, Flipse and Smit, 2015). It also features prominently in the published modelling literature where enhancement of and/or susceptibility to secondary infections are proposed as possible drivers of dengue's multi-annual patterns in incidence and serotype prevalences. Temporary cross-protection in individuals recovering from a recent infection has also been put forward as one of the desynchronising forces underlying dengue epidemiology. Model assumptions further diverge with regards to cross-immunity in the form of permanent protection against reinfection after a secondary heterologous challenge and whether this clinically apparent protection does have an effect on subsequent infections and viral transmission or not. In fact, most model discrepancies revolve around the question whether and how previous exposures to dengue affect the probabilities and transmissibilities of subsequent infections (Andraud et al., 2012, Johansson et al., 2011).
We have previously shown that within an individual-based meta-population framework, the explicit incorporation of immune competition between serotypes is not necessary to reproduce dengue's ubiquitous epidemiological patterns (Lourenço and Recker, 2013). The unique flexibility of this framework therefore allowed us to examine how model-based predictions of dengue vaccination impact could be affected by underlying assumptions about serotype immune interactions. We focused particularly on intervention-mediated shifts in incidence and age-exposure profiles, as these may be used to define important metrics for the evaluation of health-economic benefits and risks associated with the introduction of a dengue vaccine.
Analysis of the neutral model without immune-interactions within a hyper-endemic transmission setting showed that the relatively low efficacy of CYD-TDV, particularly in naive individuals, would only result in a modest but stable ≈15–20% reduction in dengue incidence (compared to pre-vaccination levels) when using routine vaccination only at the age of 6. When vaccination was introduced around the mean age of first infection, this could potentially increase to ≈35%. When coupled with a nation-wide catch-up campaign to maximise short-term impact our results confirmed the expected and rapid reduction in incidence, which, dependent on catch-up coverage and vaccine target age, could briefly go near extinction levels. In the long-term, however, we observed a rebound in dengue incidence, driven by the incomplete vaccine-induced protection and demographic turnover in the population, that might potentially surpass pre-vaccination levels. While this undesired effect was shown to be temporary, with total long-term impacts generally being positive regardless of this rebound, there is clearly an important trade-off between maximising short-term impact and guarding against long-term repercussions, which re-emphasizes the growing awareness and support for the implementation of other control measures alongside vaccination as part of an integrated intervention programme (Johansson et al., 2011).
We further considered the effects of the three most widely used assumptions about dengue serotype immune-interactions (Andraud et al., 2012) on vaccination impact and found that two of these had a pronounced effect: ADE and the maximum number of consecutive dengue infections that an individual might experience before developing complete immunity. Although both assumptions feature frequently in the modelling literature it should be noted that these present extreme ends of a spectrum. That is, although the occurrence of third and fourth dengue infections is not contested, it is often argued that these do not contribute significantly to dengue transmission. Equally, while the susceptibility/infectivity enhancement of secondary infections is due to the observed increase in risk of severe infection outcomes in these infections, it is clear that not every secondary infection is enhanced. Therefore, our results concerning these two types of immune interactions should equally be seen as extreme points, with more realistic assumptions probably leading to somewhat less pronounced effects.
The inclusion of temporary cross-immunity did not noticeably change the post-vaccination epidemiology of dengue, with incidence rates and average ages of infection following the start of vaccination being comparable to those predicted by the neutral model without cross-immunity. This is not too surprising, however, as we have previously shown that temporary cross-immunity, at least within this spatially explicit setting, does not cause any appreciable changes in simulated epidemiologies, simply because only a small proportion of the population would ever experience a heterologous challenge within the short window of protection Lourenço and Recker (2013). In comparison, ADE and full cross-immunity after a secondary infection have a direct effect on dengue's force of infection, which in both cases can lead to an accelerated rebound following the initial catch-up campaign and with it a significant decrease in the short-term impact on dengue incidence.
An important point to note here is that in the case of assuming full protection after two infections a significant parameter recalibration was required in our framework (see Table 1). Fitting this model to match seroprevalence profiles from highly endemic settings resulted in dengue's reproductive number to increase to R0 ≈ 7, compared to R0 ≈ 4 in the 4-infection model (both values are within the wide range of R0 estimates for dengue – see Table S1 of Lourenço and Recker (2013)). We argue, however, that the differences in the qualitative behaviour between the two models are not simply due to changes in the transmission potential, as demonstrated in Supplementary Fig. S3. What this implies is that the underlying assumptions regarding serotype immune-interactions can crucially affect parameter values obtained by fitting mathematical models to epidemiological data. Here we demonstrated that this in turn can significantly affect vaccination impact predictions, potentially changing the critical vaccination fraction for disease eradication and control (Johansson et al., 2011).
The difference in vaccine impact under changes to immune interactions was particularly pronounced in the average ages of first and second infections. Whereas the neutral model showed a noticeable increase in the ages of infection over all time periods considered, this was markedly reduced when considering either immune-enhancement or full protection after two heterologous infections. Although not fully explored within this framework, it is clear that this is an important consideration under the assumption that infection outcomes are partially driven by age as well as previous exposure. Furthermore, as the CYD-TDV trials showed an increase in hospitalisation rates in young vaccine recipients, there is the possibility that vaccine efficacy might also be age- as well as exposure-dependent, potentially resulting in non-linear feed-back between maximising population-wide vaccine impact and minimising the risk for the individual.
In terms of realising vaccination in our model we made a number of simplifying assumptions. For example, we considered that vaccination was administered in a single dose. In reality, as proposed by CYD-TDV trial data, more doses might be required for optimal efficacy. In terms of vaccine-induced protection we were guided by the observations from the recent CYD-TDV vaccine trials (Capeding et al., 2014, Villar et al., 2015, Sabchareon et al., 2012) but crucially assumed that the vaccine was equally efficacious against all four serotypes, whereas the trials revealed significant heterogeneities (Dorigatti et al., 2015, Hadinegoro et al., 2015). Although not explored in any detail here, we found that relaxing this assumption can have a significant impact on long-term serotype dynamics, as viruses for which the vaccine may be less efficacious can demonstrate earlier resurgence in the post-vaccination era (see Supplementary Fig. S4 for examples). It is also relevant to mention that different modes of vaccine action have been proposed to explain the trial data, such as lower immunogenicity in younger children or waning of vaccine-induced immunity (Wilder-Smith and Massad, 2016). To what degree this would affect the results presented here will have to be subject of further research, however. A final consideration concerns the endemic setting in which the vaccine is being introduced. We restricted our analysis to a hyper-endemic setting for two reasons. First, the subjective here was to highlight the importance of serotype immune interactions for model-based predictions on dengue vaccination impact. Secondly, based on the WHO's current recommendation CYD–TDV should not be considered in settings with low transmission where the vaccine would predominantly administered to sero-negative individuals with potentially unfavourable outcomes (see e.g. http://www.who.int/wer/2016/wer9121.pdf?ua=1 and http://www.who.int/immunization/sage/meetings/2016/april/SAGE_April_2016_Meeting_Web_summary.pdf?ua=1&ua=1). Our results suggest similar expectations, as we predict that vaccination at the youngest age of 9 years, as defined by CYD-TDV's licensure, would result in insignificant vaccine impact, since the mean age of infection in low transmission areas would be significantly higher.
In summary, here we have demonstrated that commonly used hypotheses on immunological serotype interactions can significantly and differentially affect model-based predictions on measures of dengue vaccination impact. This highlights once again the important gap in our current knowledge regarding the development of immunity to dengue and its effect on the probability and transmissibility of subsequent infections. Future model-based studies should therefore present robust sensitivity analysis surrounding the assumptions on serotype immune-interactions.
4. Methods
4.1. Individual-based model
To investigate the post-vaccination dynamics of dengue we used a spatially explicit, individual-based meta-population model as previously formulated and described in Lourenço and Recker (2013). Briefly, within this framework, every human and mosquito host is defined with an unique state representing its epidemiological history. Human individuals are considered to be either susceptible, exposed, infectious or recovered with respect to each serotype, allowing up to four sequential infections. Only the susceptible, exposed and infectious states of the epidemiologically relevant adult life-stage of the mosquito are considered. The size of the human population is kept constant with deaths being replaced by births. To account for seasonal variation in vector densities, an annually driven mosquito birth rate is used. An age-dependent risk of mortality is assumed for both humans and mosquitoes, described by a continuous Weibull distribution. Mosquitoes have a per-day biting rate, and unless stated otherwise, equal probabilities in human-to-vector and vector-to-human transmission are assumed. All parameter values, ranges found in the literature and references can be found in Table 1. For comparison with the dynamical and extensive sensitivity analysis performed on the original framework (Lourenço and Recker, 2013), most of the parameters have been kept the same.
Host population structure is included by subdividing humans and mosquitoes into a spatially organised sets of communities, forming a squared and non-wrapping lattice. Individuals mix homogeneously within each community. Mosquitoes are further allowed to disperse locally, implying that each vector can bite humans belonging to its own and neighbouring communities. Long distance transmission events, driven by daily human mobility, can take place by allowing mosquitoes to bite humans of randomly chosen, distant patches with low probability.
The model includes demographic, biological and ecological stochasticities, arising from the probabilistic nature of state transitions. For simplicity, we disregard the effects of varying host-structure, human mobility or mosquito densities in this study, and refer the reader to the original publication in which the dynamic effects of these demographic factors and other ecological and biological parameters are explored in detail Lourenço and Recker (2013).
4.2. Fitting to hyper-endemic setting
To find a baseline transmission range for the model that would be in line with hyper-endemic settings, the age profile of the human population with exposure to at least one serotype was fitted against a set of empirical data found in the literature (references and examples of model fit can be found in Supplementary Fig. S1). As previously demonstrated Wikramaratna et al. (2010), considering a model assuming full immunity to all four serotypes after a secondary infection led to a substantial increase in dengue's reproductive number (R0) when fitting to the same data (see Table 1 and Supplementary Fig. S1). This difference was achieved by changing the human-to-vector and vector-to-human transmission probabilities accordingly, therefore keeping the host and vector demographic dynamics unchanged. The mathematical formulation of R0 applicable to this framework can be found in Lourenço and Recker (2013).
4.3. Immunological interactions
For comparison purposes we defined a neutral model (Lourenço and Recker (2013)), in which all immunity related assumptions were relaxed – that is, individuals were allowed to experience up to four heterotypic infections with no immunological interactions between the serotypes apart from the exclusion of co-infections. To account for immunological interactions between dengue serotypes, the following three mechanisms (as well as some combinations) are considered: (i) temporary cross-immunity (Sabin (1952)), whereby individuals recovering from infection are fully protected against re-infection for a period of time, (ii) antibody-dependent enhancement (Simmons et al., 2012, Ferguson and Anderson, 1999), which increases both susceptibility to and infectivity of secondary infections (Recker et al., 2009), and (iii) acquisition of complete immunity after two infections only (Wikramaratna et al. (2010)). Since the inclusion of these factors can change the force of infection in comparison to the neutral model, we adjusted the human-to-vector and vector-to-human transmission probabilities accordingly, in order to maintain the same transmission setting (Table 1).
4.4. Vaccination strategies
We implement vaccination in our model using both catch-up and routine strategies (alone or in combination). Routine vaccination is implemented by targeting individuals at the point they reach a certain age, according to a given coverage probability as a single dose, with vaccine-induced protection being instantaneous. Protection is assumed to prevent infections according to given vaccine efficacy levels, which differ between seropositive and seronegative individuals (70% and 30%, respectively). Catch-up campaigns, on the other hand, target a specific age group regardless of their immune status (without loss of generality we assumed this to be between 10 and 50 years), with a certain coverage rate and implemented as a one-off, single pulse event. These assumptions, discussed in the main text, may deviate from future campaigns in endemic areas but are crucial for a simple and robust analysis of the mechanistic drivers of vaccine outcome between the different model structures considered in this study. Unless otherwise stated, the target age for routine vaccination was 6 years assuming a coverage of 75%. Although not of particular relevance for the purpose of this work, these values were primarily chosen because (i) 6 marks the start of school in many countries, which could facilitate vaccine coverage, and (ii) coverage levels above 80–85% might become economically and/or logistically infeasible in many dengue endemic settings.
4.5. Measuring vaccination outcomes
To quantify vaccination impact we divided the post-vaccination era into relevant periods (short-term in 0–10 years, long-term in 0–25 years and mid-term in 15–25 years). In these time ranges, vaccine impact was determined by comparing pre- and post-vaccination incidence levels as well as age-exposure profiles. The pre-vaccination period was assumed to be the 20 years prior to vaccine introduction. This was done by measuring averages found within each time period, across 50 independently simulated populations. The distributions of vaccine impact predictions is presented by means of box and whiskers plots, in which the boxes show the interquartile ranges (lower and upper) and the median, whereas the lower and upper whiskers show the lowest datum still within 1.5 IQR of the lower quartile and the highest datum still within 1.5 IQR of the upper quartile, respectively.
Acknowledgements
This work was financially supported by the European Research Council (ERC 268904 – DIVERSITY to JL) and the Royal Society (University Research Fellowship to MR).
Footnotes
Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.epidem.2016.05.003.
Appendix A. Supplementary data
The following are the supplementary data to this article:
References
- Adams B., Holmes E.C., Zhang C., Mammen M.P., Nimmannitya S., Kalayanarooj S. Cross-protective immunity can account for the alternating epidemic pattern of dengue virus serotypes circulating in Bangkok. Proc. Natl. Acad. Sci. U. S. A. 2006;103(October (38)):14234–14239. doi: 10.1073/pnas.0602768103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aguiar M., Kooi B.W., Stollenwerk N. Epidemiology of dengue fever: a model with temporary cross-immunity and possible secondary infection shows bifurcations and chaotic behaviour in wide parameter regions. Math. Model. Nat. Phenom. 2008;3(December (4)):48–70. [Google Scholar]
- Andraud M., Hens N., Marais C., Beutels P. Dynamic epidemiological models for dengue transmission: a systematic review of structural approaches. PLoS ONE. 2012;7(January (11)):e49085. doi: 10.1371/journal.pone.0049085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armstrong P.M., Rico-Hesse R. Efficiency of dengue serotype 2 virus strains to infect and disseminate in Aedes aegypti. Am. J. Trop. Med. Hyg. 2003;68(May (5)):539–544. doi: 10.4269/ajtmh.2003.68.539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beatty M., Boni M.F., Brown S., Buathong R., Burke D., Coudeville L. Assessing the potential of a candidate dengue vaccine with mathematical modeling. PLoS Negl. Trop. Dis. 2012;6(3):e1450. doi: 10.1371/journal.pntd.0001450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burke D.S., Nisalak A., Johnson D.E., Scott R.M. A prospective study of dengue infections in Bangkok. Am. J. Trop. Med. Hyg. 1988;38(January (1)):172–180. doi: 10.4269/ajtmh.1988.38.172. [DOI] [PubMed] [Google Scholar]
- Capeding M.R., Tran N.H., Hadinegoro S.R.S., Ismail H.I.H.M., Chotpitayasunondh T., Chua M.N. Clinical efficacy and safety of a novel tetravalent dengue vaccine in healthy children in Asia: a phase 3, randomised, observer-masked, placebo-controlled trial. Lancet. 2014;384(9951):1358–1365. doi: 10.1016/S0140-6736(14)61060-6. [DOI] [PubMed] [Google Scholar]
- Chao D.L., Halstead S.B., Halloran M.E., Longini I.M. Controlling dengue with vaccines in Thailand. PLoS Negl. Trop. Dis. 2012;6(10) doi: 10.1371/journal.pntd.0001876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coudeville L., Garnett G.P. Transmission dynamics of the four dengue serotypes in southern Vietnam and the potential impact of vaccination. PLoS ONE. 2012;7(12):e51244. doi: 10.1371/journal.pone.0051244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cummings D.A.T., Schwartz I.B., Billings L., Shaw L.B., Burke D.S. Dynamic effects of antibody-dependent enhancement on the fitness of viruses. Proc. Natl. Acad. Sci. U. S. A. 2005;102(October (42)):15259–15264. doi: 10.1073/pnas.0507320102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dorigatti I., Aguas R., Donnelly C.a., Guy B., Coudeville L., Jackson N. Modelling the immunological response to a tetravalent dengue vaccine from multiple phase-2 trials in Latin America and South East Asia. Vaccine. 2015;33(31):3746–3751. doi: 10.1016/j.vaccine.2015.05.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durham D.P., Ndeffo Mbah M.L., Medlock J., Luz P.M., Meyers L.A., Paltiel A.D. Dengue dynamics and vaccine cost-effectiveness in Brazil. Vaccine. 2013;31(August (37)):3957–3961. doi: 10.1016/j.vaccine.2013.06.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Endy T.P., Anderson K.B., Nisalak A., Yoon I.K., Green S., Rothman A.L. Determinants of inapparent and symptomatic dengue infection in a prospective study of primary school children in Kamphaeng Phet, Thailand. PLoS Negl. Trop. Dis. 2011;5(January (3)):e975. doi: 10.1371/journal.pntd.0000975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferguson N., Anderson R. The effect of antibody-dependent enhancement on the transmission dynamics and persistence of multiple-strain pathogens. Proc. Natl. Acad. Sci. U. S. A. 1999;96(January):790–794. doi: 10.1073/pnas.96.2.790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferguson N.M., Donnelly C.A., Anderson R.M. Transmission dynamics and epidemiology of dengue: insights from age-stratified sero-prevalence surveys. Philos. Trans. R. Soc. Lond. Ser. B, Biol. Sci. 1999;354(April (1384)):757–768. doi: 10.1098/rstb.1999.0428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flipse J., Smit J.M. The complexity of a dengue vaccine: a review of the human antibody response. PLoS Negl. Trop. Dis. 2015;9(6):e0003749. doi: 10.1371/journal.pntd.0003749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Focks D., Brenner R.J., Hayes J., Daniels E. Transmission thresholds for dengue in terms of Aedes aegypti pupae per person with discussion of their utility in source reduction efforts. Am. J. Trop. Med. Hyg. 2000;62(January (1)):11–18. [PubMed] [Google Scholar]
- Gibbons R.V., Kalanarooj S., Jarman R.G., Nisalak A., Vaughn D.W., Endy T.P. Analysis of repeat hospital admissions for dengue to estimate the frequency of third or fourth dengue infections resulting in admissions and dengue hemorrhagic fever, and serotype sequences. Am. J. Trop. Med. Hyg. 2007;77(November (5)):910–913. [PubMed] [Google Scholar]
- Gubler D.J., Suharyono W., Tan R. Viraemia in patients with naturally acquired dengue infection. Bull. World Health Organ. 1981;59(2):623–630. [PMC free article] [PubMed] [Google Scholar]
- Hadinegoro S.R., Arredondo-García J.L., Capeding M.R., Deseda C., Chotpitayasunondh T., Dietze R. Efficacy and long-term safety of a dengue vaccine in regions of endemic disease. N. Engl. J. Med. 2015, July;373 doi: 10.1056/NEJMoa1506223. p. 150727090428004. [DOI] [PubMed] [Google Scholar]
- Halstead S.B. Dengue. Lancet. 2007;370(November (9599)):1644–1652. doi: 10.1016/S0140-6736(07)61687-0. [DOI] [PubMed] [Google Scholar]
- Johansson M., Hombach J., Cummings D.T. Models of the impact of dengue vaccines: a review of current research and potential approaches. Vaccine. 2011;29(August (35)):5860–5868. doi: 10.1016/j.vaccine.2011.06.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kyle J.L., Harris E. Global spread and persistence of dengue. Annu. Rev. Microbiol. 2008;62(January):71–92. doi: 10.1146/annurev.micro.62.081307.163005. [DOI] [PubMed] [Google Scholar]
- Lin C.C., Huang Y.H., Shu P.Y., Wu H.S., Lin Y.S., Yeh T.M. Characteristic of dengue disease in Taiwan: 2002–2007. Am. J. Trop. Med. Hyg. 2010;82(April (4)):731–739. doi: 10.4269/ajtmh.2010.09-0549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lourenço J., Recker M. Viral and epidemiological determinants of the invasion dynamics of novel dengue genotypes. PLoS Negl. Trop. Dis. 2010;4(November (11)):e894. doi: 10.1371/journal.pntd.0000894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lourenço J., Recker M. Natural persistent oscillations in a spatial multi-strain disease system with application to dengue. PLoS Comput. Biol. 2013;9(October (10)):e1003308. doi: 10.1371/journal.pcbi.1003308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lourenço J., Recker M. The 2012 Madeira dengue outbreak: epidemiological determinants and future epidemic potential. PLoS Negl. Trop. Dis. 2014;8(August (8)):e3083. doi: 10.1371/journal.pntd.0003083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Messer W.B., Alwis R.D., Yount B.L., Scott R., Huynh J.P., Smith S.A. Correction for Messer et al., Dengue virus envelope protein domain I/II hinge determines long-lived serotype-specific dengue immunity. Proc. Natl. Acad. Sci. U. S. A. 2014;111(5):1939. doi: 10.1073/pnas.1317350111. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Messina J.P., Brady O.J., Scott T.W., Zou C., Pigott D.M., Duda K.A. Global spread of dengue virus types: mapping the 70 year history. Trends Microbiol. 2014;22(January (3)) doi: 10.1016/j.tim.2013.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagao Y., Koelle K. Decreases in dengue transmission may act to increase the incidence of dengue hemorrhagic fever. Proc. Natl. Acad. Sci. U. S. A. 2008;105(March (6)):2238–2243. doi: 10.1073/pnas.0709029105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ndeffo Mbah M.L., Durham D.P., Medlock J., Galvani A.P. Country- and age-specific optimal allocation of dengue vaccines. J. Theor. Biol. 2014;342(February):15–22. doi: 10.1016/j.jtbi.2013.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Recker M., Blyuss K.B., Simmons C.P., Hien T.T., Wills B., Farrar J. Immunological serotype interactions and their effect on the epidemiological pattern of dengue. Proc. R. Soc. B. 2009;276(July (1667)):2541–2548. doi: 10.1098/rspb.2009.0331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reich N.G., Shrestha S., King A.a., Rohani P., Lessler J., Kalayanarooj S. Interactions between serotypes of dengue highlight epidemiological impact of cross-immunity. J. R. Soc. Interface. 2013;10:20130414. doi: 10.1098/rsif.2013.0414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez-Barraquer I., Mier-y Teran-Romero L., Schwartz I.B., Burke D.S., Cummings D.A. Potential opportunities and perils of imperfect dengue vaccines. Vaccine. 2014;32(January (4)):514–520. doi: 10.1016/j.vaccine.2013.11.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabchareon A., Wallace D., Sirivichayakul C., Limkittikul K., Chanthavanich P., Suvannadabba S. Protective efficacy of the recombinant, live-attenuated, CYD tetravalent dengue vaccine in Thai schoolchildren: a randomised, controlled phase 2b trial. Lancet. 2012;380(12):1559–1567. doi: 10.1016/S0140-6736(12)61428-7. [DOI] [PubMed] [Google Scholar]
- Sabin A.B. Research on dengue during World War II. Am. J. Trop. Med. Hyg. 1952;1(January (1)):30–50. doi: 10.4269/ajtmh.1952.1.30. [DOI] [PubMed] [Google Scholar]
- Schwartz L.M., Halloran M.E., Durbin A.P., Longini I.M. The dengue vaccine pipeline: implications for the future of dengue control. Vaccine. 2015;33(June (29)):3293–3298. doi: 10.1016/j.vaccine.2015.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp T.M., Hunsperger E., Mu noz Jordán J.L., Margolis H.S., Tomashek K.M. Sequential episodes of dengue-Puerto Rico, 2005–2010. Am. J. Trop. Med. Hyg. 2014;91(3):235–239. doi: 10.4269/ajtmh.13-0742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simmons C.P., Farrar J.J., Nguyen v.V., Wills B. Dengue. N. Engl. J. Med. 2012;366(April (15)):1423–1432. doi: 10.1056/NEJMra1110265. [DOI] [PubMed] [Google Scholar]
- Thavara U., Tawatsin A., Nagao Y. Simulations to compare efficacies of tetravalent dengue vaccines and mosquito vector control. Epidemiol. Infect. 2014;142(June (6)):1245–1258. doi: 10.1017/S0950268813001866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tien N.T.K., Luxemburger C., Toan N.T., Pollissard-Gadroy L., Huong V.T.Q., Van Be P. A prospective cohort study of dengue infection in schoolchildren in Long Xuyen, Viet Nam. Trans. R. Soc. Trop. Med. Hyg. 2010;104(September (9)):592–600. doi: 10.1016/j.trstmh.2010.06.003. [DOI] [PubMed] [Google Scholar]
- Trpis M., Hausermann W. Dispersal and other population parameters of Aedes aegypti in an African village and their possible significance in epidemiology of vector-borne diseases. Am. J. Trop. Med. Hyg. 1986;35(6):1263. doi: 10.4269/ajtmh.1986.35.1263. [DOI] [PubMed] [Google Scholar]
- Trpis M., Hausermann W. Population size, dispersal, and longevity of domestic Aedes aegypti aegypti (Diptera: Culicidae) by MarkReleaseRecapture in the Village of Shauri Moyo in Eastern. J. Med. Entomol. 1995;32(1):27–33. doi: 10.1093/jmedent/32.1.27. (7) [DOI] [PubMed] [Google Scholar]
- Vaughn D.W., Green S., Kalayanarooj S., Innis B.L., Nimmannitya S., Suntayakorn S. Dengue viremia titer, antibody response pattern, and virus serotype correlate with disease severity. J. Infect. Dis. 2000;181(January (1)):2–9. doi: 10.1086/315215. [DOI] [PubMed] [Google Scholar]
- Villar L., Dayan G.H., Arredondo-García J.L., Rivera D.M., Cunha R., Deseda C. Efficacy of a tetravalent dengue vaccine in children in Latin America. N. Engl. J. Med. 2015;372:113–123. doi: 10.1056/NEJMoa1411037. [DOI] [PubMed] [Google Scholar]
- Watts D.M., Burke D.S., Harrison B.A., Whitmire R.E., Nisalak A. Effect of temperature on the vector efficiency of Aedes aegypti for dengue 2 virus. Am. J. Trop. Med. Hyg. 1987;36(1):143. doi: 10.4269/ajtmh.1987.36.143. [DOI] [PubMed] [Google Scholar]
- Wearing H.J., Rohani P. Ecological and immunological determinants of dengue epidemics. Proc. Natl. Acad. Sci. U. S. A. 2006;103(August (31)):11802–11807. doi: 10.1073/pnas.0602960103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wikramaratna P.S., Simmons C.P., Gupta S., Recker M., Schneider B.S. The effects of tertiary and quaternary infections on the epidemiology of dengue. PLoS ONE. 2010;5(January (8)):172–180. doi: 10.1371/journal.pone.0012347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilder-Smith A., Massad E. Age specific differences in efficacy and safety for the CYD-tetravalent dengue vaccine. Expert Rev. Vaccines. 2016;15(April (4)):437–441. doi: 10.1586/14760584.2016.1143366. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.