Pattern Adaptation and Normalization Reweighting

Abstract

Adaptation to an oriented stimulus changes both the gain and preferred orientation of neural responses in V1. Neurons tuned near the adapted orientation are suppressed, and their preferred orientations shift away from the adapter. We propose a model in which weights of divisive normalization are dynamically adjusted to homeostatically maintain response products between pairs of neurons. We demonstrate that this adjustment can be performed by a very simple learning rule. Simulations of this model closely match existing data from visual adaptation experiments. We consider several alternative models, including variants based on homeostatic maintenance of response correlations or covariance, as well as feedforward gain-control models with multiple layers, and we demonstrate that homeostatic maintenance of response products provides the best account of the physiological data.

SIGNIFICANCE STATEMENT Adaptation is a phenomenon throughout the nervous system in which neural tuning properties change in response to changes in environmental statistics. We developed a model of adaptation that combines normalization (in which a neuron's gain is reduced by the summed responses of its neighbors) and Hebbian learning (in which synaptic strength, in this case divisive normalization, is increased by correlated firing). The model is shown to account for several properties of adaptation in primary visual cortex in response to changes in the statistics of contour orientation.

Introduction

In primary visual cortex, prolonged viewing of an oriented stimulus (the adapter) results in response suppression for neurons tuned near the adapter and a repulsive shift of orientation tuning curves away from the adapter (Müller et al., 1999; Dragoi et al., 2000, 2001; Felsen et al., 2002; Benucci et al., 2013). A standard view of adaptation is that it represents a simple fatigue-like process in highly responsive neurons (i.e., in which adaptation only adjusts the gain of individual neurons according to their recent history of responses) (Maffei et al., 1973; Carandini and Ferster, 1997). Although neuron-specific response suppression (Fig. 1C) is consistent with fatigue-based models of adaptation, the shifts in orientation tuning observed in V1 (Fig. 1D) are more difficult to explain.

Figure 1.

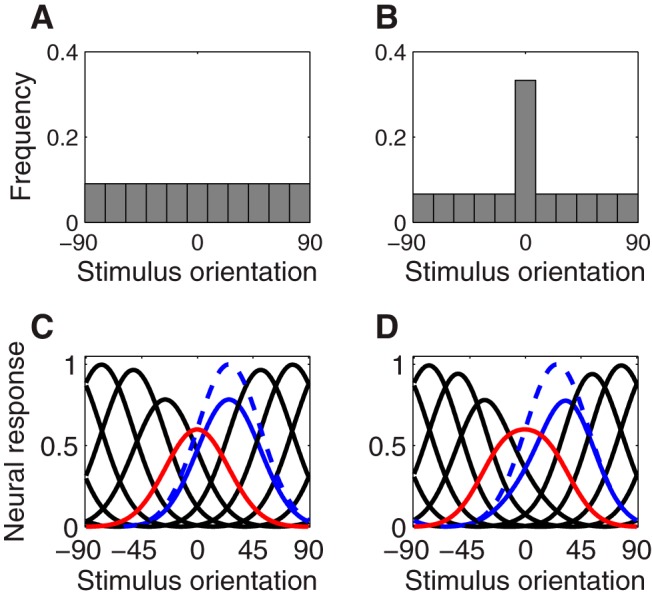
Neuron-specific adaptation and stimulus-specific adaptation. A, Unbiased distribution over 11 equally spaced stimulus orientations. B, Biased distribution over stimulus orientation in which the adapter, 0°, is overrepresented by a factor of 5. C, Neuron-specific adaptation, consistent with neural-fatigue models of adaptation. Red curve represents postadaptation tuning curve of a neuron with preferred orientation equal to the adapter. Solid black and blue curves represent postadaptation tuning curves for other neurons in the population. Dashed blue curve represents preadaptation tuning curve corresponding to the solid blue curve below it. Neural responses are suppressed near the adapter, with the magnitude of suppression falling off with difference in orientation. D, Stimulus-specific adaptation. Neural responses are again suppressed near the adapter, but the suppression is asymmetrically greater on the tuning-curve flanks overlapping the adapted orientation. Preferred orientations are repelled away from the adapter (e.g., blue curves).

Repulsive shifts in orientation preference might serve to remove dependencies arising from variations in the statistics of visual input while tolerating dependencies in the responses that arise due to tuning-curve overlap. Consider the responses of a population of orientation-tuned neurons to the following stimulus ensembles: (1) all orientations occur equally often (Fig. 1A); and (2) one orientation (the adapter) occurs with greater frequency than other orientations (Fig. 1B). The covariances of the responses to both stimulus ensembles will be large for some pairs of neurons because they have overlapping tuning curves. Without adaptation, the covariance of neural responses to the biased stimulus ensemble would be larger, relative to the unbiased ensemble, among neurons tuned to orientations near the adapter. Instead, the tuning-curve changes in cat V1 following exposure to a biased stimulus ensemble, which include response suppression and shifts in preferred orientation, almost precisely restore the covariances observed with an unbiased stimulus ensemble (Benucci et al., 2013).

In this study, we reformulate adaptation as a homeostatic control process that uses a simple Hebbian learning rule. The proposed model homeostatically maintains response products (the products of the firing rates of pairs of neurons) by adjusting the weights of divisive normalization. This removes response dependencies that arise from variations in the statistics of visual input. Divisive normalization is a neural process describing nonlinear behavior in sensory neurons in which the output of a neuron is computed as the feedforward drive of that neuron divided by (i.e., normalized by) the sum of the drives to neighboring neurons (Heeger, 1992b; Carandini and Heeger, 2011). It has been suggested that the weights of divisive normalization are optimized to improve the efficiency of sensory coding (Schwartz and Simoncelli, 2001; Wainwright et al., 2002; Sinz and Bethge, 2013). Divisive normalization (or gain control) has also been used to explain some adaptation phenomena (Ohzawa et al., 1982; Heeger, 1992b; Wainwright et al., 2002; Wissig and Kohn, 2012; Solomon and Kohn, 2014). The model that we propose updates the normalization weights between each pair of neurons based on the product of their responses and could be implemented by a simple synaptic mechanism for coincidence detection (Levy and Steward, 1983; Yao and Dan, 2001; Yao et al., 2004). The model has no free parameters determining the shape of tuning curves following adaptation. Simulation results demonstrate close agreement with physiological data, including changes in the gain of neural responses, repulsive shifts in tuning curves, and approximate maintenance of response covariances.

Materials and Methods

Simulation

Model simulations followed the experimental protocol of Benucci et al. (2013). Model neurons were presented with sequences of gratings with orientations drawn from a distribution that was either unbiased, so that each orientation occurred with equal frequency, or biased, so that one orientation was overrepresented by a constant factor (Fig. 1A,B). Stimulus contrast was 50%. One minor difference between the simulations and the actual experimental protocol was that there were no blank trials in the simulations, so increasing the probability of one orientation always involved a commensurate decrease in the probability of other orientations. Simulations were run for various amounts of orientation bias in the stimulus ensemble. Larger overrepresentation of the adapted orientation led to adaptation effects that were larger in magnitude but qualitatively similar. All figures shown here are based on simulations using 11 stimulus orientations, with the vertical orientation overrepresented by a factor of 5. All program codes used to generate the figures are available online (see Notes).

Neural responses

We simulated the responses of a population of orientation-tuned V1 neurons to sequences of gratings. Responses were obtained by first computing a feedforward drive for each neuron, and then normalizing across the neural population. We used the divisive-normalization model, which has been used to explain a variety of neurophysiological phenomena in V1, including cross-orientation and surround suppression (Heeger, 1992b; Carandini et al., 1997b; Carandini and Heeger, 2011). Specifically, the model consisted of N = 121 model neurons representing a subpopulation of neurons sharing a particular receptive-field location and preferred spatial frequency. Simulated neural responses were obtained by computing a feedforward drive for each neuron with Gaussian orientation tuning curves, then normalizing across the neural population. Tuning widths σ_b were identical across the population yielding an orientation-tuning bandwidth (half-width at half-height) of 30° following normalization. Preferred orientations of the neurons were evenly distributed over 0°–180°. Neural responses (firing rates) were obtained by normalizing the squared feedforward drive to each neuron by a weighted sum of each other neuron's feedforward drive. The model included neuron-specific weights (Carandini and Heeger, 2011), so that the normalization pool of neuron i was a weighted sum over neurons j in the population with weights W_j,i. Given a feedforward drive F_i(θ) to each neuron i with preferred orientation θ_i in the presence of stimulus orientation θ and contrast C, the normalized responses were computed as follows:

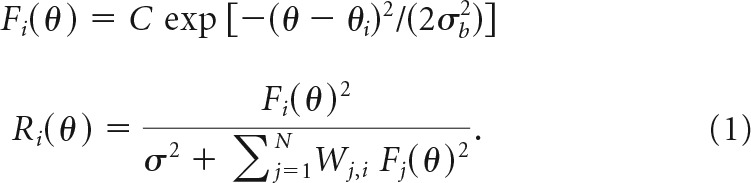The semisaturation constant σ represents the contrast at which neurons achieve half their maximal response. This constant does not require fine-tuning and can be varied over a large range of realistic values: from nearly zero to around half the stimulus contrast, without dramatically changing the predictions of the response-product model. The results shown here were generated with σ = 0.17, or one-third of the stimulus contrast of 0.5.

Response-product homeostasis model

A learning rule adjusted the normalization weights for each pair of simulated neurons, based on their responses to each stimulus. Instead of trying to minimize some form of statistical dependency (correlation, for example), the model maintained the expected response products (i.e., the pairwise product of neural responses) as close to a target level as possible. Specifically, normalization weights were adjusted after each stimulus presentation as follows:

where the C_j,i represented the homeostatic targets for the response products. For a biased stimulus ensemble, the overrepresented orientation evoked strong activity in a subpopulation of neurons tuned near that orientation, leading to elevated response products among those neurons. The normalization weight between two such neurons was consequently increased in proportion to the elevation of the product of their responses relative to the homeostatic target. The homeostatic targets for the response products, the C_j,i, were not free parameters of the model, but rather depended only on the similarity of the two neurons' tuning curves. For most of the simulations reported here, the homeostatic target was the expected product of responses to the unbiased stimulus distribution, with uniform normalization weights: C_j,i = E_unbiased (R_jR_i). For the rest of the simulations, the homeostatic target was based on natural texture images (see Learning the homeostatic target). The only free parameter was the learning rate α. We confirmed that this quantity can be adjusted to match the rate of adaptation observed empirically (∼1.5 s for the neuron tuned to the orientation of the adapter to drop halfway from its initial gain to its steady-state gain), but the value of α did not affect the shape of tuning curves at steady state.

This learning rule is an approximation of gradient descent on an objective function that favors homeostatic maintenance of the response product. Specifically, given a penalty on the sum of squared deviations from response-product homeostasis, the learning rule adjusts each weight W_j,i to reduce the component of the error associated with neurons i and j. This update rule has as its fixed point the set of weights that exactly maintains the expected product of the responses for each pair of simulated neurons. Although it is not guaranteed to converge with an arbitrary set of tuning curves, it converged very quickly in our simulations.

Feedback normalization

Although we are agnostic as to the mechanistic implementation of normalization, we recognize the need to establish that the model we describe could operate in a physiologically realistic recurrent network. The normalization model we used was implemented as a feedforward procedure, but the normalization model has also been implemented with the divisive suppression emerging through recurrent feedback (Carandini and Heeger, 2011). Recurrent processing has been shown to achieve steady-state responses that are identical under certain conditions to those achieved by feedforward divisive normalization (Heeger, 1992b). We implemented a generalization of this recurrent processing that included arbitrary normalization weights as follows:

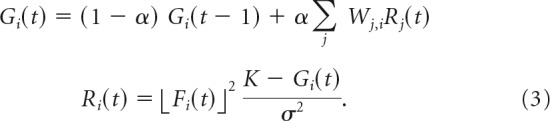At steady state,

where ⌊F_i(t)⌋² is the half-squared linear input to neuron i, σ is the semisaturation constant of normalization, and K is a constant (K > G_i(t)) that determines the response gain (i.e., the maximum-attainable firing rate). R_i denotes the steady-state response of neuron i, assuming constant input. The steady-state behavior can be derived by assuming that, at steady state, G_i(t) = G_i(t − 1), and is exactly equivalent to divisive normalization when all of the normalization weights W_j,i are equal to one another (Heeger, 1992b).

Learning the homeostatic target

The simulations were repeated using a homeostatic target based on texture images, rather than on the experimental stimulus ensemble (a sequence of gratings drawn from a uniform distribution over orientation). To approximate the homeostatic target corresponding to the natural environment, we analyzed a set of 90 natural images (Burge and Geisler, 2011) using a V1-like filter bank. Specifically, we used the steerable pyramid (Simoncelli et al., 1992; Portilla and Simoncelli, 2000), a subband image transform, to decompose each texture image into separate orientation and spatial-frequency channels. Each channel simulates the responses of a large number of linear receptive fields with the same spatial-frequency and orientation tuning. The receptive fields are defined so that they cover all orientations and spatial frequencies evenly (i.e., the sum of the squares of the tuning curves is exactly equal to 1 for all orientations and spatial frequencies). For each orientation and spatial-frequency channel, the transform includes receptive fields with two different phases, like odd- and even-phase Gabor filters. The sum of the squares of the responses of two such receptive fields computes what has been called an energy response (Adelson and Bergen, 1985; Heeger, 1992a) because it depends on the local spectral energy within a spatial region of the stimulus, for a particular orientation and spatial frequency. We computed the average of the products of the energy responses for each pair of orientations, and averaged the response products across spatial locations. Finally, we averaged rows of this response-product matrix along the diagonal (and plotted the result as a function of relative orientation) to remove influences of cardinal bias (Girshick et al., 2011). The results were similar for each spatial-frequency channel so we show results for only one channel.

Covariance homeostasis model

An alternative model maintained the response covariances of each pair of neurons, using an update rule that adjusted normalization weights based on deviation of covariance from a target. This model used a learning rule analogous to Equation 2, with covariance substituted for response product as follows:

Weight updates in this model occurred following a sequence of N stimuli, where N is assumed to be large enough to compute covariance, rather than on individual stimuli. Covariance, unlike response product, has no instantaneous definition, so a memory of recent average responses must be maintained. We simulated the covariance model by computing the neural response covariance across the entire ensemble at each weight update. The homeostatic targets C_j,i^cov were the neural response covariances for an unbiased stimulus ensemble with uniform weights.

Gain-change adaptation in one or two layers

We implemented two alternative models of adaptation in which response gain was adjusted to homeostatically maintain average neural responses. In the one-layer feedforward gain model, each neuron had a response gain g_i that multiplicatively scaled the orientation-tuning curve. The normalized response was then as follows:

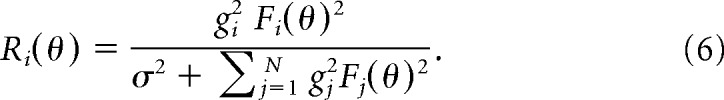This adaptation model adjusted the gains g_i to maintain mean (normalized) responses at a homeostatic target C, which was the average response of a neuron for the unbiased stimulus distribution. Gains were adjusted on each stimulus presentation according to the following:

We also implemented a two-layer model without normalization in which the response of output neuron R_i,2 was computed as a weighted sum over the orientation-tuned responses of input-layer neurons R_j,1. Both input- and output-layer neurons represented orientation-tuned neurons in V1. Each output-layer neuron computed a weighted sum over input-layer responses, with Gaussian weights centered on the preferred orientation θ_i of the output neuron (Fig. 2). The responses to a stimulus of orientation θ were as follows:

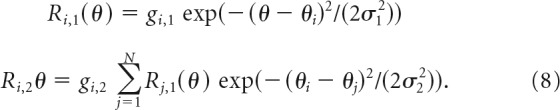In this model, σ₁ represents the bandwidth of the Gaussian defining the orientation tuning of input-layer neurons, and σ₂ represents the bandwidth of the Gaussian defining the sensitivity of each output-layer neuron to the responses of input-layer neurons with different preferred orientations. The value of σ₁ was varied across simulations, with concomitant changes to the value of σ₂ so that the output-layer orientation-tuning bandwidth was always 30° (half-width at half-height), which is typical for V1 neurons.

Figure 2.

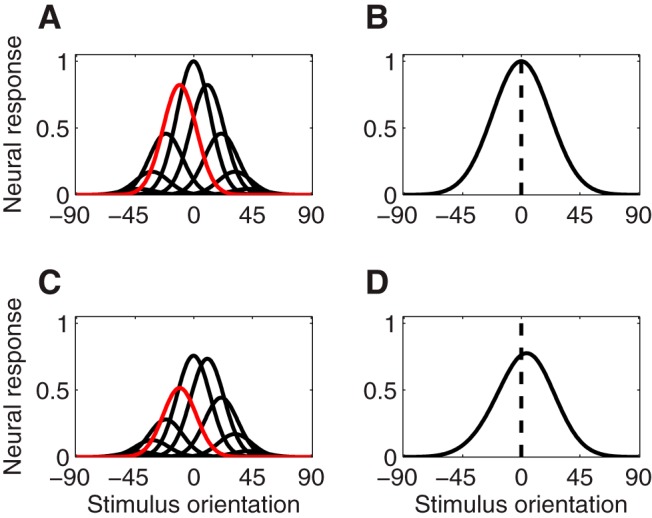
Two-layer feedforward gain-change model. A, B, Preadaptation. C, D, Postadaptation. A, C, Orientation-tuning curves of input-layer neurons, scaled according to their weight in contributing to the response of an output-layer neuron. B, D, Tuning curve of the output-layer neuron. A reduction of gain for input-layer neurons following adaptation (compare A and C) leads to a reduction of gain in the output-layer neuron, along with a shift in tuning preference (compare B and D). A, C, Red curves represent the input-layer neuron tuned to the adapter orientation (−12°). B, D, Vertical dashed line indicates the preferred orientation of the output-layer neuron before adaptation.

The gains g_i of neurons in both layers were adjusted dynamically to maintain the mean responses. Specifically, the learning rule adjusted the gains according to the following:

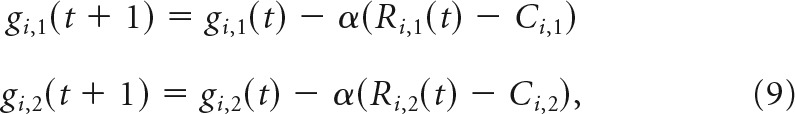where C_i,1 and C_i,2 were the expected mean responses of each neuron for the unbiased stimulus distribution, when gains are equal to 1.

Model comparison

Cross validation was used to compare the four models. The data consisted of measured population responses (13 orientations, 21 multiunit recordings) for each of 11 adaptation experiments from Benucci et al. (2013). Each experimental dataset consisted of tuning curves measured preadaptation and postadaptation. These 11 experimental conditions were averaged to obtain estimates of the postadaptation neural responses [Benucci et al. (2013), their Fig. 4D]. To assess the ability of each model to explain the observed adaptation effects, we resampled conditions to generate a bootstrapped distribution of preadaptation and postadaptation tuning curves. Each of the alternative models consisted of a large number (121) of simulated neurons. For each bootstrapped neural population and for each model, we optimized the preadapt model neural population by selecting for each real recording site the closest matching model neuron after a scaling and additive offset. That is, for each empirical tuning curve t_i^{data,pre-adapt}, we selected the scaled model tuning curve with additive offset s_i^pre + c_i^pre × t_m(i)^{model,pre-adapt} that minimized ‖t_i^{data,pre-adapt} − (s_i^pre + c_i^pre × t_m(i)^{model,pre-adapt})‖². This was necessary to account for inhomogeneity in the sampling of recording sites. We repeated this procedure for a large range of bandwidths, and selected the bandwidth that minimized overall error of the matched populations.

Figure 4.

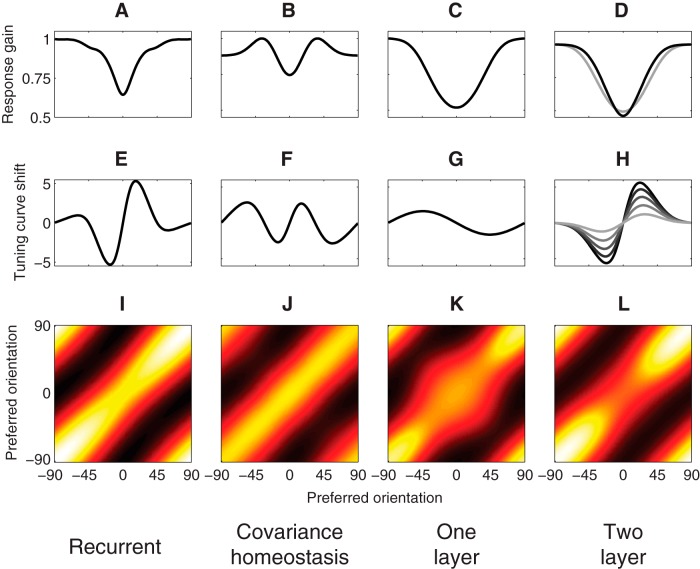
Adaptation in four alternative models. A, E, I, Response-product homeostasis with recurrent normalization. B, F, J, Covariance homeostasis model, which updates normalization weights to maintain covariance directly. C, G, K, One-layer feedforward gain-change model. D, H, L, Two-layer feedforward gain-change model. Input-layer bandwidth was 22°, which was chosen to produce large enough (>5°) shifts in preferred orientation. A–D, Postadaptation response gain, measured as the peak value of a neuron's tuning curve. E–H, Shift in preferred orientation, measured as the circular mean of its tuning curve, plotted as a function of the neurons' preadaptation preferred orientation. For the two-layer feedforward gain-change model, each curve corresponds to input-layer neurons with different orientation bandwidths (from darkest to lightest: 20°, 22°, 24°, 26°, 28°). I–L, Postadaptation response covariance for the biased stimulus distribution.

We then simulated each model on the experimental conditions described by Benucci et al. (2013). None of the models we simulated had additional free parameters beyond those used to fit the preadaptation population. Following simulation, a single scaling and additive-offset parameter were fit to the postadaptation tuning curves to account for long-term drift in gain and baseline firing rate that would otherwise dominate the model error. We then computed the mean-squared error (MSE) of each model's fit to the postadaptation neural responses. This final measure of goodness of fit is as follows:

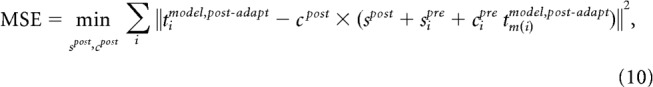and was computed for each of 8000 samples from the experimental data and for each of the four alternative models.

Results

We simulated a collection of model V1 neurons responding to a sequence of sine wave gratings. The feedforward response of each neuron was determined by a Gaussian orientation-tuning curve with 30° bandwidth. Preferred orientations spanned the full range from 0° to 180°. The output of a neuron was the feedforward response of the neuron normalized by (i.e., divided by) a weighted sum of the feedforward responses of all of the neurons. The weight by which neuron j contributed to the normalization of neuron i, W_j,i, was modifiable. In a response-product homeostasis model, the W_j,i were modified to bring the product of the responses of the two neurons, R_jR_i, closer to a target response product, C_j,i. We initially set the C_j,i to be the expected response product for a uniform distribution of gratings and all identical values for the W_j,i.

Scaling and shifting tuning curves

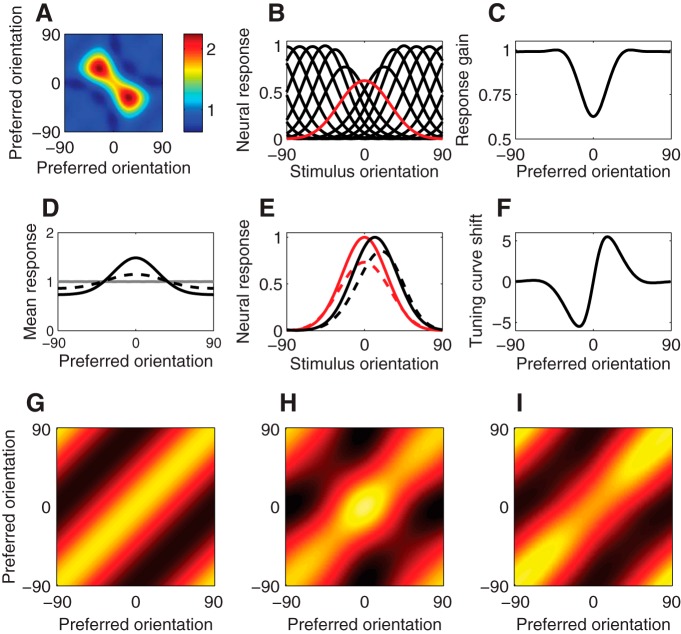
Following exposure to a biased stimulus distribution in which one orientation (0°) was overrepresented (Fig. 1B), the normalization weights adapted so as to homeostatically maintain the expected response products at the same level evoked by an unbiased stimulus distribution. The normalization weights were uniform for the unbiased stimulus ensemble (preadaptation) but exhibited a negative-diagonal structure following adaptation to the biased stimulus ensemble (postadaptation; Fig. 3A). The biased stimulus ensemble increased the average product of neural responses (averaged across the stimuli) for pairs of neurons with tuning curves that overlapped the overrepresented stimulus (the adapter) while slightly decreasing all other response products due to the reduced frequency of those neurons' preferred stimuli. The larger inhibitory weights between pairs of neurons tuned near the adapter reduced their excess correlated responses. However, neurons with very similar orientation preferences often responded together, even for the unbiased stimulus ensemble. As a result, the largest increase in response products, relative to the homeostatic target for the response products, was for neuron pairs with preferred orientations on opposite sides of the adapter (at a difference in orientation preference determined by the tuning-curve width). These neurons often responded separately for the unbiased stimulus ensemble but were jointly driven by the adapter.

Figure 3.

Adaptation in the response-product homeostasis model. A, Normalization weights following adaptation to a vertical (0°) adapter, arranged according to the preferred orientations of each pair of neurons. Preadaptation weights were initially uniform and constant. The two peaks along the diagonal represent increased normalization weights between pairs of neurons with preferred orientations on opposite sides of the adapter orientation. B, Neural tuning curves following adaptation. Red curve represents tuning curve of neuron tuned to the vertical adapter. C, Postadaptation neural response gain (peak value of the tuning curve) as a function of preadaptation preferred orientation. D, Mean responses. Gray curve represents mean responses (averaged across the unbiased stimulus distribution) for unadapted neurons, as a function of preferred orientation. Solid black curve represents mean responses for the biased stimulus distribution without adaptation. Dashed black curve represents postadaptation mean responses for the biased stimulus distribution. Adaptation partially restores imbalances in mean neural responses with the biased stimulus distribution. E, Tuning curves for two example simulated neurons. Solid curves represent preadaptation. Dashed curves represent postadaptation. Red curves represent neuron tuned to the adapter orientation. Black curves represent neuron tuned to a flanking orientation. F, Postadaptation shift of preferred orientation (measured using the circular mean of the tuning curve) as a function of preadaptation preferred orientation. G–I, Neural response covariance. G, Neural response covariance for the unbiased stimulus distribution, without adaptation. H, Neural response covariance for the biased stimulus distribution, without adaptation. I, Neural response covariance for the biased stimulus distribution postadaptation.

Adaptation to an overrepresented orientation led to orientation-tuned suppression of simulated neurons. Following adaptation, response gain was reduced for neurons tuned to the adapter (Fig. 3B,C). This decrease occurred due to an increase in the normalization weights for pairs of neurons with preferred orientations near that of the adapter (Fig. 3A). Similar changes in gain have been reported in macaque V1 (Müller et al., 1999; Wissig and Kohn, 2012; Patterson et al., 2013) and in cat V1 (Dragoi et al., 2000, 2001; Felsen et al., 2002, 2005; Benucci et al., 2013). The orientation-tuned reduction in gain largely (but incompletely) compensated for the imbalance in mean responses evoked by a biased stimulus distribution (Fig. 3D), similar to experimental results (Benucci et al., 2013). The magnitude of gain changes in the simulation results was similar to that reported by Benucci et al. (2013) under the stimulus conditions that we simulated, although the gain changes were evident over a broader range of preferred orientations in their data. This may reflect a deviation of our model from physiology, or it may reflect the experimental use of multiunit responses and averaging across recording sites with similar preferred orientations.

Adaptation resulted in a repulsive shift of simulated orientation-tuning curves (Fig. 3E,F). Repulsive shifts in preferred orientation following adaptation arose due to large increases in normalization weights between neurons tuned to opposite flanks of the adapter. Consider measuring the response of a neuron tuned to an orientation clockwise of the adapter. A stimulus at the preadaptation preferred orientation for this neuron also evoked a strong excitatory drive in a neuron tuned to an orientation on the adapter's opposite flank. Adaptation increased the weight of divisive normalization between this pair of neurons, so that they suppressed one another more strongly. A stimulus slightly more clockwise than the preadaptation preferred orientation evoked a somewhat smaller excitatory drive to the neuron being measured but also less divisive suppression from the competing anticlockwise neural population, leading on balance to larger responses for orientations further from the orientation of the adapter. For the same reason, adaptation also led to an asymmetry in the tuning curves for neurons tuned near the adapter; the flank of the tuning curve closer to the adapter orientation was shallower.

Repulsive shifts in preferred orientation in the model had a characteristic S-shape (Fig. 3F), similar to experimental data. Repulsive shifts similar to those produced by the model have been reported in cat (Dragoi et al., 2000, 2001; Felsen et al., 2002, 2005; Benucci et al., 2013) and macaque V1 (Müller et al., 1999; Wissig and Kohn, 2012; Patterson et al., 2013). The model attained a maximal shift in orientation tuning for simulated neurons with preadaptation orientation preferences ±20° relative to the orientation of the adapter. This is generally in line with experimental results, although the S-shaped curve of repulsive shifts reported by Benucci et al. (2013) was broader (peaking at ∼15°–45° relative to the adapter) than our simulation results. As with response suppression, this broadening may reflect the use of multiunit responses (although we note that tuning-curve repulsion has also been observed with single-unit recordings) (Müller et al., 1999; Dragoi et al., 2000; Felsen et al., 2002, 2005) and spike-sorted microarray recordings (Dragoi et al., 2001; Wissig and Kohn, 2012). Other studies have reported a range of values for the preferred orientations exhibiting maximal repulsion of 5°–22.5° (Dragoi et al., 2000) and 15°–75° (Patterson et al., 2013). The magnitude of the repulsive shifts in the simulation results was ∼5° when the adapter orientation was over-represented by a factor of 5 (Fig. 3F), and it depended on the degree to which the adapter was overrepresented. This closely matched the shift magnitudes reported by Benucci et al. (2013) under similar stimulus conditions. Asymmetry in the tuning curve flanks, like that predicted by the model, also appears to be evident in the Benucci et al. (2013) data, although they did not explicitly test for this.

Attractive shifts have also been reported for adaptation. These shifts occur under very different conditions than those we consider here. These include (1) very large stimuli, leading to disinhibition of neurons with receptive fields in the center of the stimulus as neurons in the suppressive surround are also adapted (Wissig and Kohn, 2012); (2) adaptation in cortical areas in which part of the adaptive effect is inherited from the inputs (e.g., MT inheriting adaptation from V1) (Kohn and Movshon, 2004); and (3) very long adaptation duration, which presumably is due to a different mechanism akin to perceptual learning (Schoups et al., 2001; Ghisovan et al., 2009). None of these effects is in the stimulation regimen we studied.

A variant of the model that computed divisive normalization from a weighted sum of neighboring neurons' outputs (feedback rather than feed-forward drives) had similar results (Fig. 4, first column). As mentioned above, when all recurrent weights are equal, this recurrent model is exactly equivalent to feed-forward normalization in steady state. In the general case, when the divisive suppression of each neuron is an arbitrarily weighted sum over responses of other neurons, we found that the behavior of the recurrent implementation diverged from feedforward divisive normalization. When normalization weights were nearly equal, however, the two models behaved very similarly. Unlike the response-product model with feedforward normalization, the recurrent implementation was sensitive to the value of the semisaturation constant σ. Values of σ smaller than one-third of the stimulus contrast produced prominent attractive shifts in orientation tuning that peaked at 45° from the adapter.

Approximate covariance homeostasis

In an unbiased stimulus ensemble, the covariance of the simulated neural responses exhibited a diagonal structure (Fig. 3G), simply reflecting the similarity of the responses for pairs of neurons with similar preferred orientations. Without adaptation, the covariance of simulated responses to the biased stimulus ensemble increased, relative to the unbiased ensemble, among neurons tuned to orientations near the orientation of the adapter (Fig. 3H, bump at 0°). Following adaptation to a biased stimulus ensemble, the diagonal structure of the response covariances was largely restored (Fig. 3I), reproducing the results reported by Benucci et al. (2013). This occurred despite the fact that covariance was not estimated by the model and was not directly under constraint. Instead, the normalization weights were adjusted according to the product of the responses of each pair of simulated neurons. As a result, the change in average response product induced by the biased stimulus ensemble was perfectly compensated. Response product is related to covariance, but the two are not identical (see Covariance-homeostasis model). Consequently, the diagonal covariance structure was not recovered perfectly. For pairs of neurons with preferred orientations near the adapter, the postadaptation covariance was slightly smaller than the preadaptation levels (compare Fig. 3G with Fig. 3I). However, this slight overshoot of equalization of covariance appears to be a feature of the model because a similar effect is also evident upon reexamination of the empirical results (Fig. 5, black dashed curve).

Figure 5.

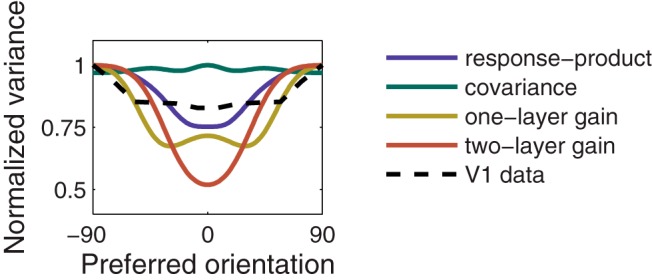
Postadaptation neural response variances for the biased stimulus distribution (corresponding to the diagonals of the covariance matrices in Figs. 3I, 4J–L). The values were normalized to a maximum of 1, separately for each curve. Black dashed curve represents experimental data of Benucci et al. (2013).

Homeostatic target

An advantage of the response-product model is that it accounts for experimental effects of adaptation with no free parameters to optimize. Instead, the behavior of the model is driven by the shape of tuning curves in V1 and by the homeostatic target. In the simulations presented so far, the target was the expected response products evoked by an unbiased distribution of grating orientations. The use of an environment that consists of single gratings flashed one at a time for defining the homeostatic target is arbitrary. We therefore verified that similar results would be obtained when the target response products were estimated from natural images analyzed by a V1-like filter bank. We used a collection of natural textures and computed the matrix of response products of the filters. The matrix was then averaged along the diagonal to remove the effects of cardinal bias (Girshick et al., 2011) from the response-product matrix. The resulting expected response products, as a function of relative orientation, are plotted in Figure 6A. The response-product model behaved similarly with this homeostatic target compared with using the unbiased-grating-ensemble target (Fig. 6B,C).

Figure 6.

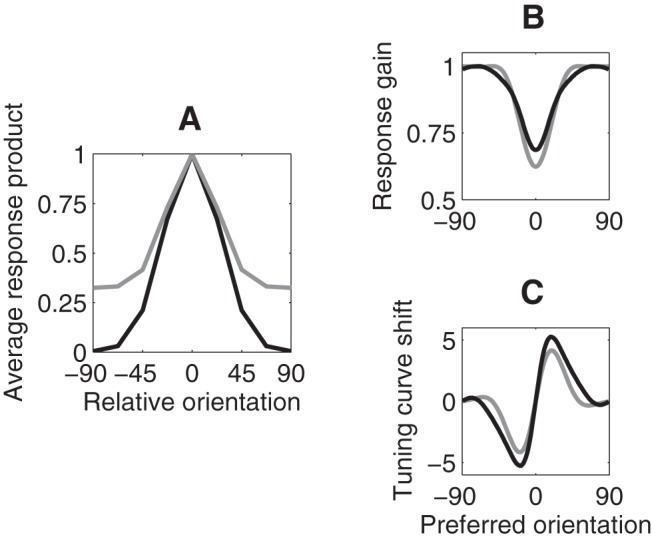
Homeostatic targets. A, Two different possible homeostatic targets, corresponding to two different environments, plotted as a function of relative orientation. Solid black curve represents response products corresponding to an unbiased ensemble of gratings. Gray curve represents response products corresponding to natural textures. B, Postadaptation neural response gain (peak value of the tuning curve) as a function of preadaptation preferred orientation. C, Postadaptation shift of preferred orientation (measured using the circular mean of the tuning curve) as a function of preadaptation preferred orientation. B, C, Black and gray curves represent results using homeostatic targets shown in the corresponding colors in A.

Conditional variance

Schwartz and Simoncelli (2001; see also Sinz and Bethge, 2013) examined the responses of a bank of orientation- and spatial-frequency-tuned linear receptive fields as a simple model of the population of V1 simple cells. They showed that, in response to natural images, the variance of the response of one such linear receptive field depends on the absolute value of the response of a neighboring receptive field (i.e., conditional-variance dependence). That is, when one linear response is large (either positive or negative), a neighboring neuron's response is likely to be large as well. An appropriate choice of normalization weights can undo this dependence. The optimal weights are commensurate with physiological measurements of surround suppression in which the strength of suppression depends systematically on the difference in orientation between center and surround (Cavanaugh et al., 2002; Shushruth et al., 2013). Such weights are also consistent with psychophysical studies of surround masking that have found larger suppressive effects with iso-orientation surrounds (Xing and Heeger, 2000; Shushruth et al., 2013). Conditional-variance dependence is a property of natural images and can vary between environments. Prior work has shown that some adaptation phenomena (including tuning-curve repulsion) can be explained by adjusting normalization weights to reduce conditional-variance dependence (Wainwright et al., 2002).

Although our model never estimates the conditional variance of neural responses and does not explicitly attempt to stabilize or remove these dependencies, homeostatically regulating the response product of normalized (as opposed to linear) responses also stabilizes this form of nonlinear dependence. This is because increasing the degree of conditional-variance dependence between two neurons increases the product of their normalized responses as long as there is a relatively diverse population of neurons constituting the normalization pool.

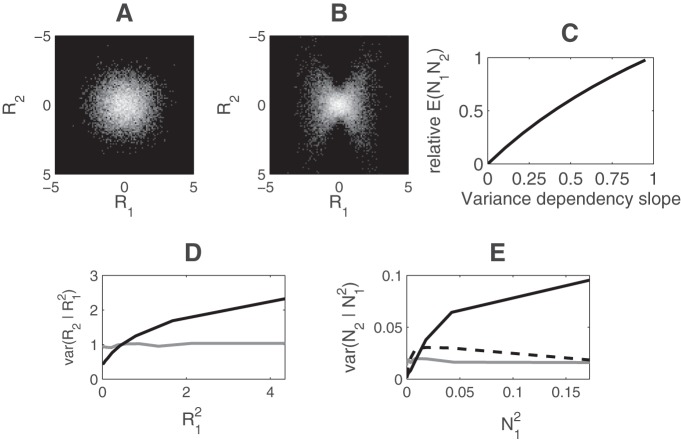
We verified with a population of simulated neurons that response-product homeostasis largely removes conditional-variance dependencies of normalized responses. We simulated a population of 40 neurons. Neural responses were assumed to be Gaussian distributed and independent of one another; the joint histogram of two such neurons, R₁ and R₂, is shown in Figure 7A. Next, we introduced a conditional-variance dependency by setting var(R₂) = 1.0 − α × var(R₁) + α × R₁² (Fig. 7D). All other linear responses were unchanged. The form of this dependency was carefully chosen so that it did not change the variance of either neuron's response. However, it did produce the bowtie dependence in the joint histogram characteristic of conditional-variance dependence (Schwartz and Simoncelli, 2001; Wainwright et al., 2002) (Fig. 7B). This form of dependence has been shown to reduce the efficiency of neural encoding of orientation (Schwartz and Simoncelli, 2001).

Figure 7.

Conditional variance. A, Joint histogram of the linear responses of two neurons, R₁ and R₂, out of a population of 40 similar neurons. Brightness indicates the frequency of a particular pair of responses. B, Joint histogram of linear responses R₁ and R₂ after the introduction of a conditional-variance dependency between R₁ and R₂. C, Expected product of normalized responses N₁ and N₂ as a function of the slope of the conditional-variance dependence relationship (α = 0.75 corresponds to B). D, Conditional variance of R₂ as a function of R₁². Gray curve represents the independent neural responses shown in A; conditional variance was constant. Black curve represents the bowtie distribution shown in B; conditional variance increased with R₁². E, Conditional variance plotted as in D, but for normalized responses instead of linear responses. Gray curve represents independent neural responses (A). Black curve represents neural responses with a bowtie conditional-variance dependence (B). Dashed black curve corresponds to conditional variance following response-product homeostasis adaptation of normalization weights.

Although both the means of the individual linear responses R₁ and R₂ and their correlation or expected product are independent of the magnitude of the conditional variance dependence between them, the product of their normalized responses does depend on this quantity. Larger values of α lead to larger expected products between normalized responses N₁ and N₂ (Fig. 7C). As a result, when the neural population underwent response-product stabilizing adaptation, changes in the magnitude of conditional-variance dependency were compensated by changes in normalization weights. Figure 7E (solid black curve) shows the conditional variance of normalized response N₂ on N₁ before adaptation. After adaptation, the conditional-variance dependence was removed from the normalized responses, restoring the relationship observed in independent neurons (Fig. 7E, dashed curve).

Conventional adaptation

The experimental protocol with a biased stimulus distribution (Benucci et al., 2013) is appealing from the perspective of testing models based on homeostasis. By staying within the regimen for which a hypothetical homeostasis process can be expected to operate effectively, no additional model parameters were required for comparing model simulations with empirical results.

We also simulated a conventional adaptation experiment, with each trial consisting of a top-up adapter followed by a test stimulus, but doing so required an additional model parameter. Because the model (as presented above) has unbounded normalization weights, it predicts unrealistically large suppressive effects following prolonged exposure to a single grating. However, a very small decay term on the normalization weights (decaying toward the initial uniform weights) allowed the model to be applied to conventional adaptation. With this decay term included, simulation results exhibited suppressive gain changes and repulsive shifts in tuning (simulations results not shown) that were similar, although larger in magnitude, to those presented above.

Perceptual learning

Theoretical results have shown that a neural population optimized to encode a nonuniform prior over orientations (i.e., some orientations occur more often than others) can account for improved orientation discrimination near the overrepresented orientations (Girshick et al., 2011; Ganguli and Simoncelli, 2014). In this optimized population, more neurons are used to encode orientations that occur more often, and these tightly packed tuning curves are also more narrowly tuned to maintain fixed tuning-curve overlap (Girshick et al., 2011; Wei and Stocker, 2012; Ganguli and Simoncelli, 2014). This population can be described as exhibiting tuning-curve attraction toward the overrepresented orientation along with reduced orientation-tuning bandwidth near that orientation.

Perceptual learning (a very large number of repeats of the same or very similar stimulus, while practicing a discrimination task), unlike adaptation, gives attraction instead of repulsion (Schoups et al., 2001). Even very long-term exposure to the stimulus without performing a task has been reported to give attraction (Ghisovan et al., 2009). It is likely that the result of long-term exposure reflects a distinct and qualitatively different process from short-term adaptation, and that both operate simultaneously on different timescales. However, any plausible adaptation process should be able to coexist with longer-term tuning-curve changes associated with optimization to a prior (i.e., the homeostasis rule should not strongly oppose changes associated with perceptual learning).

We verified that a neural population optimized to encode orientations from a nonuniform stimulus ensemble (Wei and Stocker 2012; Ganguli and Simoncelli, 2014) is at response-product homeostasis (Fig. 8). These tuning curves are attracted toward the overrepresented orientation and narrower near that orientation (Fig. 8C). The optimal tuning curves produce a diagonal covariance structure in response to this stimulus distribution (i.e., the stimulus distribution for which the neural population is optimized). These tuning curves also produce the same response products to the biased stimulus distribution as does a uniform population responding to an unbiased stimulus distribution. Response-product homeostasis thereby guarantees that these tuning curves do not change (i.e., do not adapt) when exposed to the biased stimulus distribution, so as to maintain an efficient representation. This is important because the natural environment is not uniform with respect to orientation: vertical and horizontal orientations occur more often, and there is evidence that the neural population in V1 is optimized to represent this bias (Girshick et al., 2011).

Figure 8.

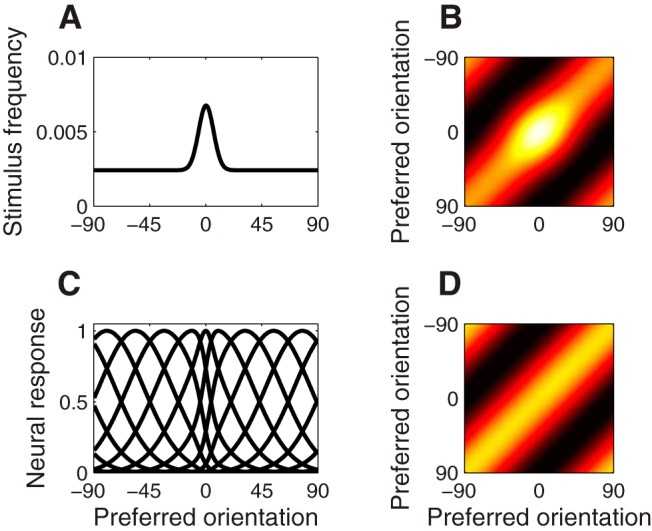
Optimal tuning curves and response-product homeostasis. A, A biased stimulus distribution, or prior, over orientations. B, The neural response covariance matrix of baseline tuning curves for this biased stimulus distribution. C, The population of tuning curves that maximizes mutual information between stimulus and neural response given the prior in A, based on Ganguli and Simoncelli (2014). D, Neural response covariance matrix of the optimal tuning curves for the biased stimulus distribution.

Covariance-homeostasis model

We also simulated a model that homeostatically maintained response covariance. Although covariance and the expected value of the response product are very similar, the only difference being that the former is mean subtracted: the two learning rules produced very different results. This model performed much worse than the model that homeostatically maintained response products. We used cross-validation to compare this and other alternative models with the response-product homeostasis model (Fig. 9). The covariance-homeostasis model was rejected (p < 0.01). Despite the apparent similarities between the two models, homeostatic maintenance of covariance led to response gain changes (Fig. 4B) that did not match experimental data (Benucci et al., 2013) and unrealistic attractive shifts in tuning curves for simulated neurons with preferred orientations that were distant from the adapter (Fig. 4F, secondary peaks beyond ±45°). This failure occurred because of how covariance depends on changes in the mean responses, which are not perfectly stabilized during adaptation. Consider a pair of neurons X and Y tuned slightly past 45° clockwise and counterclockwise of the adapter. Because these neurons rarely respond together, their covariance, equal to E(XY) − E(X)E(Y), is negative and dominated by the product of their mean responses E(X)E(Y). For a biased stimulus distribution, these neurons' preferred orientation appears less often, and they respond less on average. Because adaptation imperfectly corrects for changes in mean response, E(X)E(Y) decreases (becomes closer to 0), and covariance increases (becomes less negative). The positive error in covariance increases the normalization weights, and the tuning curves of the two simulated neurons shift away from each other. However, because the neurons have preferred orientations that are closer to one another than to the adapter, these neural-tuning shifts (away from each other) manifest as attraction toward the adapted orientation.

Figure 9.

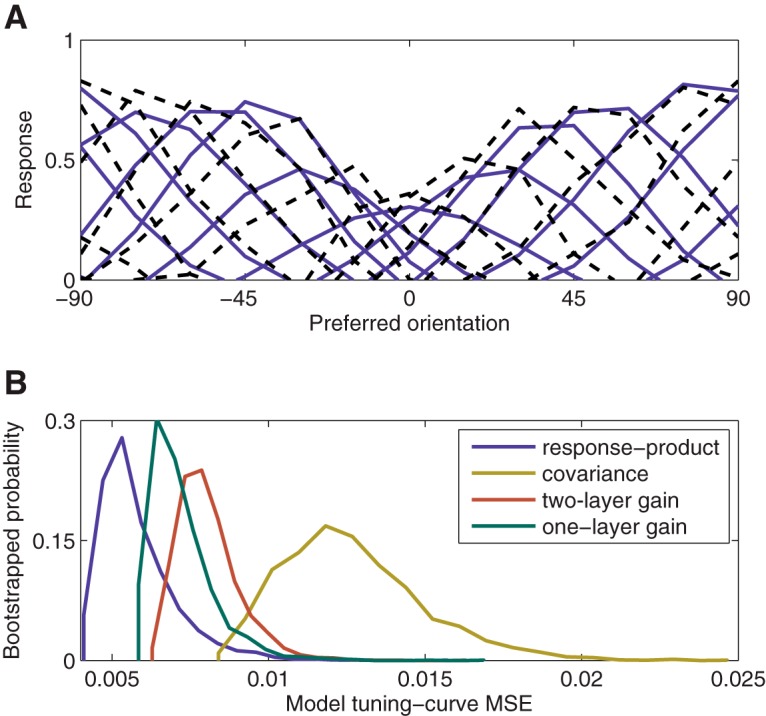
Comparison of the fit to experimental data of the response-product homeostasis model and three alternative models (covariance homeostasis, two-layer feedforward gain-change, and one-layer feedforward gain-change). A, Example resampled tuning curves (black dashed curves) and predictions from the response-product adaptation model (solid curves). The model adaptation effects are a close match to the experimental data. B, Bootstrapped distribution of errors for each of the four models under consideration. Each alternative to the response-product adaptation model had significantly higher error (p < 0.01; measured as the proportion of bootstrap iterations for which error was higher), except for the one-layer gain-change model, which was not significant (p ≈ 0.06).

In addition, the covariance-homeostasis model perfectly compensated for the change in response variances evoked by the biased stimulus distribution, incommensurate with the empirical results (Figs. 4J, 5). A model that homeostatically maintained response correlation was even worse and did not even reproduce maximal suppression at the adapted orientation. This is because correlations along the diagonal are, by definition, unity and hence are unaffected by changes in the stimulus ensemble, so that self-normalization weights of neurons tuned to the adapter did not increase when maintaining correlation.

Gain-change adaptation models

We investigated whether adaptation processes that adjust each neuron's gain individually could account for the observed effects of adaptation in V1. The simplest reasonable model of orientation-selective adaptation is a single population of neurons that reduce their gain when highly stimulated, and that reduce their gain by a greater amount when they respond more. We chose a model that dynamically adjusts response gain to maintain mean-response homeostasis. Although there are many other choices of the precise relationship between average responses and gain adjustment, mean-response homeostasis captures the stimulus specificity of adaptation and approximate homeostasis has been reported in the neural population (Benucci et al., 2013). The one-layer feedforward gain-change model that we simulated included unweighted (i.e., all weights equal one) divisive normalization between neurons tuned to different orientations, such that changes in gain affected the normalization pool. Omitting normalization in this model produced only neuron-specific adaptation (Fig. 1C) and thus no tuning-curve shifts.

When implemented in this way, adaptation failed to produce tuning-curve repulsion, although it could not be rejected statistically in our model comparison (p ≈ 0.06; Fig. 9). Indeed, adaptation led to pronounced tuning-curve attraction toward the adapter instead of repulsion from the adapter (Fig. 4G). Neurons tuned to the adapter responded less strongly, so when stimuli near the adapter appeared, there was less input to the normalization pool from those neurons, and less divisive suppression overall, leading to larger responses among flanking neurons. If normalization was omitted, or assumed to be implemented in such a way that response-gain changes in V1 do not affect the normalization pool, then there were no shifts in preferred orientation at all (simulation results not shown).

How then can gain changes produce tuning-curve repulsion? One possibility is that response suppression in an input layer leads to asymmetric suppression in an output layer (Fig. 2). This is a priori unlikely for orientation repulsion in V1 because the input layer (presumably LGN) is at most only weakly selective for orientation. Nevertheless, we also investigated a two-layer model in which the response of each output-layer cell was computed as a weighted sum over the orientation-tuned responses of input-layer cells, and in which the gains of neurons in both layers were adjusted to homeostatically control the mean response of each neuron. Normalization was omitted from this model to avoid the attractive shifts observed in the one-layer model (and we confirmed that the two-layer model failed when normalization was included; simulation results not shown). This adaptation process led to strong reduction in gain of input-layer neurons tuned to the overrepresented orientation, which was inherited by similarly tuned neurons in the output layer.

The orientation bandwidth of the input-layer neurons needed to be narrow to explain the large (∼5°) shifts in orientation tuning observed in V1 neurons for the conditions that we simulated (Benucci et al., 2013). We simulated the model with several choices of input-layer bandwidth. Half-width at half-height ranged from 20° to 28°, compared with a nominal output-layer bandwidth of 30° (Fig. 4D,H). Large shifts were observed only when the input-layer neurons had bandwidth <22° (Fig. 4H), which is on the low end of the plausible range for V1.

When input-layer bandwidth was narrow enough to explain the large shifts in orientation tuning, the two-layer model did a very poor job of explaining homeostatic regulation of covariance (Figs. 4L, 5). The two-layer model overcorrected neural covariance following adaptation, such that covariance among neurons tuned near the adapter was much lower than was observed experimentally (Benucci et al., 2013) and was rejected in our model comparison (p < 0.01; Fig. 9). While not definitively ruling out the entire class of models that adapt through changes in gain, these simulation results suggest that gain changes alone are unlikely to be explain adaptation in V1.

Discussion

A model for sensory adaptation, which extends the normalization model with a Hebbian learning rule for normalization weights, was simulated with a biased stimulus distribution similar to that used by Benucci et al. (2013), and produced similar tuning-curve shifts. The model provided a quantitatively accurate fit to those data without introducing free parameters to be optimized. Simulation results were also similar to empirical results in the broader literature on adaptation using conventional experimental protocols (with each trial consisting of a top-up adapter followed by a test stimulus), including gain changes and shifts in preferred orientation (Müller et al., 1999; Dragoi et al., 2000, 2001; Felsen et al., 2002), although the comparison was necessarily more qualitative. The model also accounted for changes in the covariance of neural responses with adaptation (Benucci et al., 2013), even though the learning rule homeostatically controls the products of each pair of neural responses. We compared this model with alternatives, to address the critical question of what quantity (if any) is under homeostatic maintenance during adaptation. A related model that homeostatically controlled the covariance of neural responses could not account for the data. Nor were we able to adequately explain adaptation with models that changed response gains (homeostatically maintaining mean responses), even when an additional orientation-tuned input layer was included.

Response-product model and efficient coding

A long-standing hypothesis is that neural coding is optimized for efficiency in transmitting information about sensory inputs (Barlow, 1961; Dan et al., 1996; Simoncelli and Olshausen, 2001; Doi et al., 2012) and that adaptation, including changes in tuning-curve properties, plays a role in maintaining efficiency despite changes in stimulus statistics (Barlow and Földiák, 1989; Wainwright et al., 2002; Felsen et al., 2005; for review, see Schwartz et al., 2007). An efficient neural representation uses the full range of activity patterns that it can produce, and the responses of different neurons are as close as possible to independent. When some stimuli are more common than others (i.e., during adaptation), a subset of possible activity patterns is overrepresented, and the encoding capacity is underutilized. The efficient-coding hypothesis states that adaptation should adjust the neural representation to maintain independence. Models of adaptation have therefore been proposed that dynamically adjust responses to decorrelate them (Barlow and Földiák, 1989; Hosoya et al., 2005). Decorrelation is theoretically appealing, but is not a realistic goal for visual cortex, where correlations are largely driven by overlapping tuning curves. Nor is decorrelation even desirable under realistic conditions; the correlations due to tuning-curve overlap improve the robustness of the neural representation when the signal-to-noise ratio is low (Atick and Redlich, 1990; Doi et al., 2012).

We propose that a more realistic goal of adaptation is to stabilize the statistical dependencies between neural responses, rather than to attempt in vain to eliminate them. Our model stabilizes the expected product of neural responses, rather than the mean-subtracted expected product (covariance). It remains to be seen whether the response-product model is equivalent to a specific formulation of efficient coding that depends on the statistics of the noise, the cost function to be optimized (e.g., mutual information) and other constraints (e.g., fixed number of neurons and/or spikes).

Because response product has an instantaneous definition based only on the current responses of neurons in the population, weight updates in our model depend only on the current responses and the long-term homeostatic target. This feature is not shared by covariance homeostasis, which requires tracking the recent mean responses, or correlation homeostasis, which requires recent means and variances. Response products (i.e., products of instantaneous firing rates) could be computed with Poisson-distributed spiking neurons by measuring the frequency of spike co-occurrence. Cellular mechanisms for spike-co-occurrence detection have been described (Levy and Steward, 1983), suggesting that the response-product computation may be particularly easy for neurons.

Other adaptation effects

There are some adaptation phenomena that we do not purport to explain. (1) We do not attempt to model adaptation effects that result from varying contrast, as opposed to orientation-specific pattern adaptation. A separate and complementary process that dynamically adjusts σ could readily be added to the model to change the overall contrast gain with changes in stimulus contrast. (2) We do not attempt to model the cellular mechanisms underlying adaptation, including somatic hyperpolarization (Carandini et al., 1998; Sanchez-Vives et al., 2000) and synaptic depression (Finlayson and Cynader, 1995; Chung et al., 2002). Multiple distinct mechanisms may be operating in parallel (Dhruv et al., 2011).

The model presumes that there is no precortical adaptation. There is evidence for what has been called “contrast gain control” in the retina (Shapley and Victor, 1978, 1979), which is analogous to normalization in the current model, with fixed normalization weights and a fixed σ value. But there is little or no evidence for precortical adaptation in the cat visual system (Movshon and Lennie, 1979; Ohzawa et al., 1985). In primates, magnocellular LGN neurons exhibit contrast adaptation at moderate to high temporal frequencies (Solomon et al., 2004). As noted in the preceding paragraph, separate and complementary contrast adaptation processes could be readily added to the model, some of which could be precortical, to fit primate data from experiments in which stimulus contrast (and not just orientation) is varied.

Relationship to previous models

Several existing models of adaptation have explained tuning-curve repulsion in terms of changes in recurrent connection strengths. Teich and Qian (2003, 2010) reported tuning-curve shifts consistent with both adaptation (tuning-curve repulsion) and perceptual learning (tuning-curve attraction), by adjusting excitatory and inhibitory weights between neurons. But they did not propose a means by which these weights could be learned. Felsen et al. (2002) explained adaptation-induced tuning shifts using a model that reduced recurrent excitatory synaptic weights in proportion to the firing rate of the presynaptic neuron. Their model required that V1 orientation tuning largely arise from these weighted, recurrent interactions, and chose initial weights accordingly.

In contrast, our model depends on responses of pairs of neurons, and the initial weight of reciprocal interactions is uniform instead of being allowed to vary arbitrarily to fit the data. The learning rule in our model differs from bottom-up gain-adaptation and recurrent gain-adaptation models (Felsen et al., 2002; Teich and Qian, 2003) in that learning is triggered by the correlated firing of pairs of neurons. This predicts that adaptation should be contingent on the coactivation of different subpopulations of neurons, each of which is selective for different stimuli. This prediction can be tested by presenting stimuli with multiple components, and determining whether adaptation is contingent on the particular combination of stimulus components. Contingent adaptation has been reported in salamander retina, where a decorrelation process analogous to our model was proposed as driving changes in synaptic weights between retinal ganglion cells and bipolar cells (Hosoya et al., 2005). Experiments comparing adaptation to gratings versus plaids (i.e., combinations of two oriented components) have tested contingent adaptation in V1 (Carandini et al., 1997a; 1998). The results of these studies, while generally consistent with our model's predictions, were not conclusive due to the small number of cells examined. We plan, in subsequent work, to test model predictions based on this requirement of contingent activity.

Adaptation-induced shifts of stimulus preference have been explained by two-layer models in which the response of each output-layer cell is a weighted sum over the input-layer cells, and in which adaptation adjusts the gains of neurons in the input layer. Such inherited-adaptation models can explain repulsive shifts in the centers of V1 receptive fields via gain changes in LGN (Dhruv and Carandini, 2014), and repulsive shifts in orientation preferences of V1 complex cells via gain changes in simple cells (Müller et al., 1999), although the invariance of repulsive shifts to the spatial phase of the adapter contradicts this latter explanation (Felsen et al., 2002). These models are appealing, most notably because they rely only on well-established changes in gain. We implemented a two-layer feedforward gain-change model in which adaptation adjusted the gains of neurons in both the input and output layers. To produce realistic shifts in preferred orientation, we had to omit normalization and assume an input layer that was more narrowly tuned than the output layer (Fig. 4H). Even with these modifications, the two-layer feedforward gain-change model did a poor job of maintaining covariance homeostasis (Fig. 5), inconsistent with the data (Benucci et al., 2013). Furthermore, if adaptation-induced shifts in orientation tuning were restricted to layers in V1 that receive input from orientation-tuned neurons from other layers in V1, one might expect a systematic dependence of shift magnitudes on recording depth, which has not been observed (Dragoi et al., 2000).

Our model's learning rule is similar to other models that have been proposed to explain stimulus-conditioning-induced changes to orientation tuning in V1, which is a phenomenon distinct from adaptation that requires precisely timed pairs of stimuli (Yao and Dan, 2001; Yao et al., 2004). These models use a spike-timing-dependent learning rule that increases the weight of excitatory synapses following a presynaptic-then-postsynaptic spike pair while decreasing it for a postsynaptic-then-presynaptic pair of spikes.

In conclusion, we posit that adaptation is a simple form of (Hebbian) learning that is contingent on joint neural activity. We have, consequently, proposed a theory of cortical learning in a tractable model system (visual adaptation in V1). To the extent that normalization proves indeed to be a canonical computation throughout cortex (Carandini and Heeger, 2011), adaptation of normalization weights may explain adaptation phenomena for other visual dimensions (location, spatial frequency, etc.) as well as for other nonvisual domains, e.g., dynamic changes in reward value and decision-making (Louie et al., 2014).

Notes

Supplemental material for this article is available at http://hdl.handle.net/2451/34764 (Matlab code to generate all figures). This material has not been peer reviewed.