Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Sep 21;6:33873. doi: 10.1038/srep33873

Critical behavior of the quasi-two-dimensional semiconducting ferromagnet CrSiTe3

Bingjie Liu 1,2, Youming Zou 1, Lei Zhang 1, Shiming Zhou 3, Zhe Wang 1,2, Weike Wang 1, Zhe Qu 1,a, Yuheng Zhang 1,3
PMCID: PMC5030636  PMID: 27649846

Abstract

The semiconducting ferromagnet CrSiTe3 is a promising candidate for two-dimensional magnet simply by exfoliating down to single layers. To understand the magnetic behavior in thin-film samples and the possible applications, it is necessary to establish the nature of the magnetism in the bulk. In this work, the critical behavior at the paramagnetic to ferromagnetic phase transition in single-crystalline CrSiTe3 is investigated by bulk magnetization measurements. We have obtained the critical exponents (β = 0.170 ± 0.008, γ = 1.532 ± 0.001, and δ = 9.917 ± 0.008) and the critical temperature TC = 31.0 K using various techniques such as modified Arrott plot, Kouvel-Fisher plot, and critical isotherm analysis. Our analysis suggests that the determined exponents match well with those calculated from the results of renormalization group approach for a two-dimensional Ising model coupled with long-range interaction.

Two-dimensional (2D) materials have attracted significant attention because of the emergence of novel physics and potential applications1,2,3,4,5. One of the primary goals in this area is to develop ferromagnetic (FM) semiconductors, which not only are eagerly needed in next-generation nano-spintronics6,7,8, but also exhibit unusual magnetism that are of great interest on its own9. Within this context, the intrinsic semiconducting ferromagnet CrSiTe3 has generated considerable interest recently because first principle calculations predict the important coexistence of ferromagnetic and semiconducting properties upon exfoliating down to single layers in this material10. More interestingly, the Curie temperature in single layers is predicted to be higher than that in bulk, and to further increase when CrSiTe3 single layers are strained10,11,12.

To understand the magnetic behavior in thin-film samples and the possible applications of this material, it is necessary to establish the nature of the magnetism in the bulk. Previous studies find that it undergoes a paramagnetic (PM) to FM phase transition around 33 K and shows a strong coupling between magnetic and lattice degrees of freedom13. Nevertheless, the nature of the PM-FM phase transition is not fully understood yet. Early neutron measurements found a critical exponent β ≈ 0.17 and a spin gap of ~6 meV14. Based on these results, they suggested CrSiTe3 to be a rare example of the quasi-2D Ising ferromagnet14. Recent neutron work observed a critical exponent β ≈ 0.151 (2) close to the value expected for a 2D phase transition15. However, based on the spin wave analysis, they argued that the spins should be Heisenberg-like15. These controversial results prompt us to perform an extensive magnetization measurement to investigate the critical behavior of CrSiTe3, expecting the universality class to which the material belongs to gives important clues for the understanding of the unusual magnetism in this material. By performing critical analysis with various techniques, we have determined the critical exponents and the critical temperature for CrSiTe3. Our analysis indicate that the obtained critical exponents are in good agreement with those calculated from the results of renormalization group approach for 2D Ising model coupled with long-range interaction.

Results and Discussion

According to the scaling hypothesis, the critical behavior of a magnetic system exhibiting a second-order magnetic phase transition near the Curie point can be characterized by a series of critical exponents16. The existence of a diverging correlation length 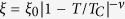Inline graphic leads to universal scaling laws for the spontaneous magnetization MS(T) and the initial susceptibility χ0(T). The spontaneous magnetization MS(T) below TC, the inverse initial susceptibility χ0−1(T) above TC and the measured magnetization M(H) at TC are characterized by a set of critical exponents β, γ, and δ, respectively. The mathematical definitions of these exponents from magnetization are described as17:

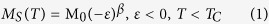graphic file with name srep33873-m2.jpg
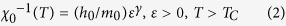graphic file with name srep33873-m3.jpg
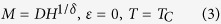graphic file with name srep33873-m4.jpg

where ε = (T − TC)/TC is the reduced temperature, and M0, h0/m0 and D are the critical amplitudes. Using scaling hypothesis, the relationship among the variables M(H, ε), H and T can be expressed as:

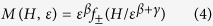graphic file with name srep33873-m5.jpg

where f+ for T > TC and f− for T < TC, respectively, are the regular functions. Furthermore, the renormalized magnetization 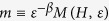Inline graphic and the renormalized field 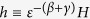Inline graphic should follow two universal rules: one for T < TC and the other for T > TC.

Figure 1(a) shows the temperature dependence of magnetization M(T) under an applied field of 1000 Oe after the zero-field-cooling sequence (left coordinate). An abrupt PM-FM transition is observed to occur around 34 K. Curie-Weiss fitting to the magnetization above 150 K yields the Curie-Weiss temperature θ = 52(6) K. This is almost twice the value of TC, suggesting strong FM interactions in CrSiTe3. The effective moment is determined to be μeff = 4.0(4) μB, which is close to the theoretical value expected for Cr3+ of 3.87 μB. Figure 1(b) displays the isothermal magnetization M(H) at 2 K, which shows a typical FM behavior with the saturation field HS ~4000 Oe. The inset to Fig. 1(b) shows the enlarged view of the M(H) at low fields. Little magnetic hysteresis is observed, which means almost zero coercive force in CrSiTe3. All these results are in good agreement with previous reports13.

Figure 1.

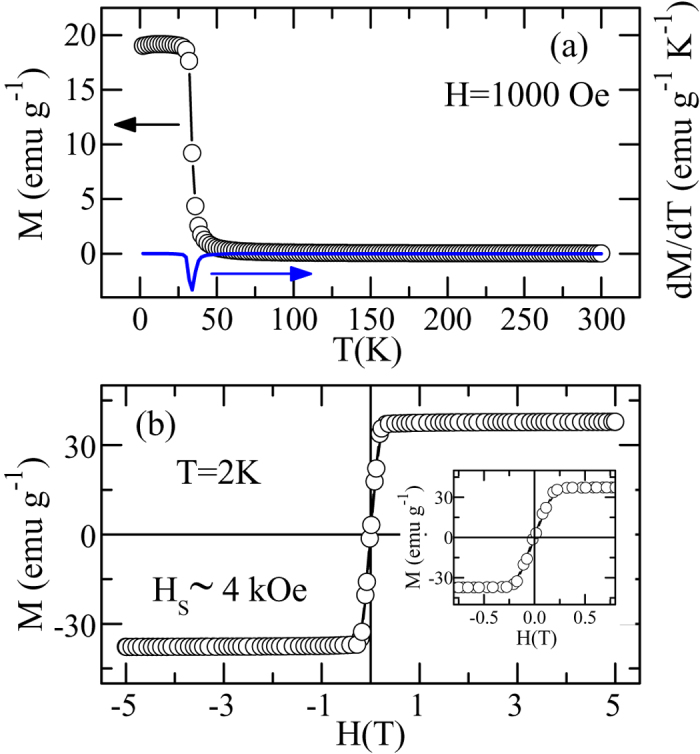
Figure 1

Open in a new tab

(a) The temperature dependence of magnetization M(T); (b) the isothermal magnetization M(H) at 2 K for CrSiTe3. The inset shows the enlarged view in the low field region.

Typical initial isotherm curves are shown in Fig. 2(a). Generally, one can obtain the critical exponents and the critical temperature by the Arrott plot analysis18. The Arrott plot assumes that the critical exponents follow the mean-field theory with the critical exponents β = 0.5 and γ = 1.0. Following this method, the M2 vs. H/M will show a set of parallel straight lines, and the isotherm at the critical temperature TC should pass through the origin. Meanwhile, it can directly give χ0−1(T) and MS(T) as the intercept on H/M axis and on positive M2 axis, respectively. Moreover, according to the Banerjee’s criterion19, one can judge the order of the magnetic transition through the slope of the straight line: the positive slope corresponding to a second-order transition and the negative slope to a first-order one. Figure 2(b) shows the Arrott plot of CrSiTe3. Obviously, the positive slope in the Arrott plot clearly indicates that the PM-FM phase transition is a second-order one. However, all curves show nonlinear behavior, indicating that the mean-field model is not valid for CrSiTe3.

Figure 2.

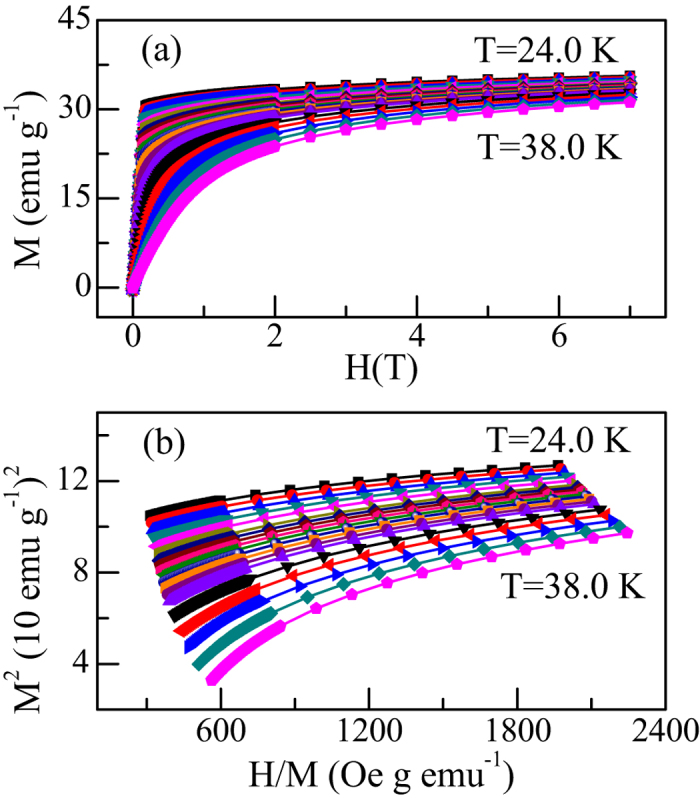
Figure 2

Open in a new tab

(a)Typical initial isotherm curves around TC for CrSiTe3; (b) the Arrott plot (M2 vs. H/M) of isotherms around TC for CrSiTe3.

We also examined other three-dimensional (3D) models, including 3D-Heisenberg, 3D-XY, 3D-Ising and tricritical mean-field models20,21. As shown in Figure S1 in Supplementary Information, all these models failed to yield parallel straight lines, suggesting the breakdown of these 3D models.

The failure of these 3D models might not be surprising, since CrSiTe3 was found to show strong 2D characteristics14,15. Hence, we further analyze the isothermal data with 2D-Ising model22, which are shown in Fig. 3(a). It can be clearly seen that there is a set of relatively parallel straight lines, indicating that the 2D-Ising model is much superior to those 3D models. However, it is noted that one still cannot find a single straight line that passes through origin, hinting that CrSiTe3 could not be rigorously described by the 2D-Ising model.

Figure 3.

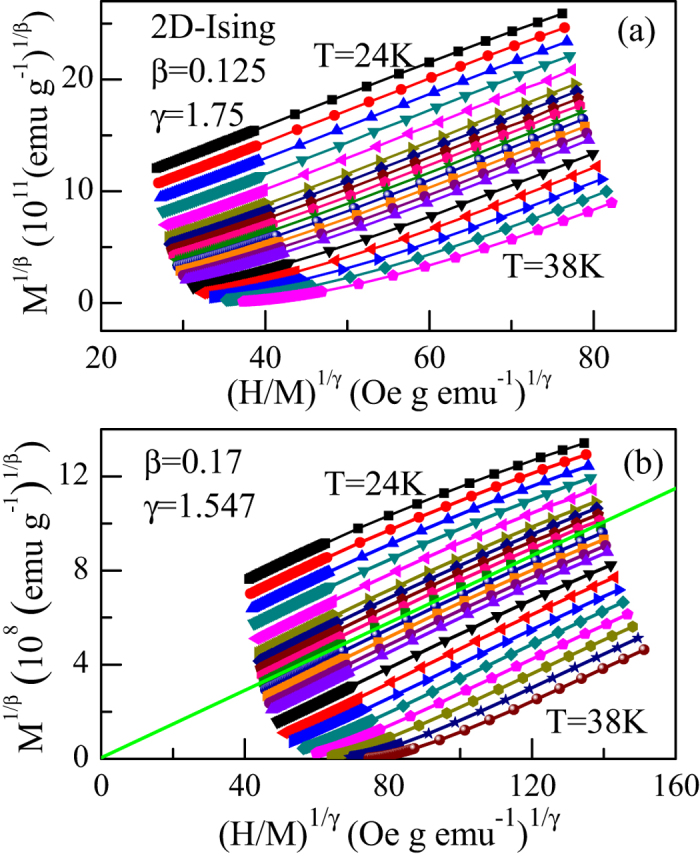
Figure 3

Open in a new tab

(a) The 2D-Ising model plot of isotherms for CrSiTe3; (b) the modified Arrott plot (M1/β vs. (H/M)1/γ) of isotherms with β = 0.17 and γ = 1.547 for CrSiTe3. The straight line is the linear fit of isotherm at 31.0 K which almost passes through origin.

To clarify the critical behavior of CrSiTe3, we have taken recourse to which is commonly known as modified Arrott plot23. The modified Arrott plot is given by the Arrott-Noaks equation of state:

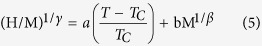graphic file with name srep33873-m8.jpg

where a and b are considered to be constants. To find out the proper values of β and γ, a rigorous iterative method has been used24. The starting values of MS(T) and 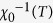Inline graphic were determined from the 2D-Ising model plot (see Fig. 3(a)) following the Eqs (1) and (2). The obtained new values of β and γ were then used to figure out new modified Arrott plot. It should be mentioned that during fitting the straight lines, the critical temperature TC is a free parameter and varied in order to get the best fitting results. This process was repeated until the iterations converge. After doing this exercise, the stable values of the critical exponents and the critical temperature have been obtained. Figure 3(b) displays the modified Arrott plot generated by using β = 0.17 and γ = 1.547. It is noted that at very low fields, the plotted isotherms are slightly curved as they represent averaging over domains magnetized in different directions25. Nevertheless, there is a set of reasonably good parallel straight lines. Moreover, the isotherm is found to pass through the origin at 31.0 K, which is the TC of CrSiTe3. 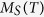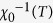The finally obtained Inline graphic and Inline graphic are plotted as a function of temperature in Fig. 4(a). Using these values of MS(T) and χ0−1(T), Eq. (1) gives β = 0.170(8), TC = 31.06(9) K for T < TC and Eq. (2) gives γ = 1.532(1), TC = 30.83(9) K for T > TC, respectively. These estimated critical exponents and TC from Eqs (1) and (2) are reasonably close to the values obtained from modified Arrott plot in Fig. 3(b).

Figure 4.

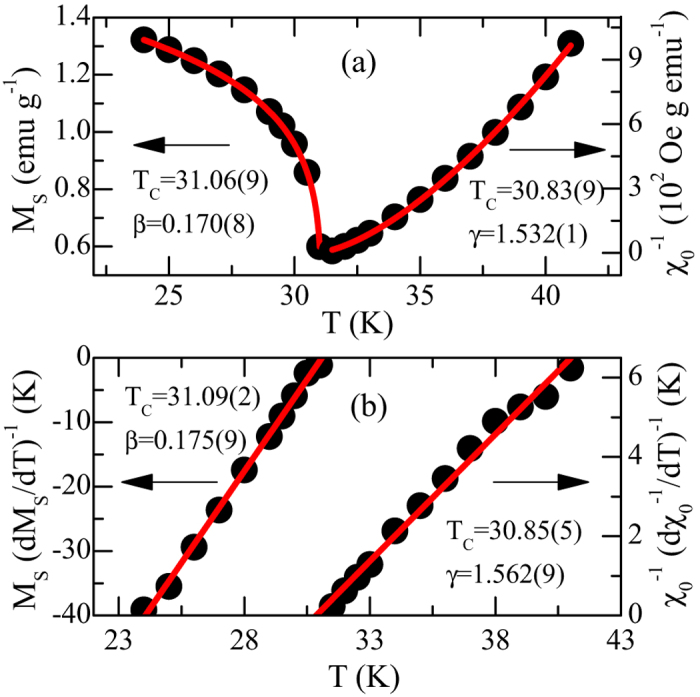
Figure 4

Open in a new tab

(a) The temperature dependence of MS and χ0−1 for CrSiTe3 with the fitting solid lines; (b) the Kouvel-Fisher plot of spontaneous magnetization MS(T) (left axis) and inverse initial susceptibility χ0−1(T) (right axis) for CrSiTe3.

To obtain more accurate values of the critical exponents as well as the critical temperature, we used the Kouvel-Fisher technique26. According to this method, MS(dMS/dT)−1 and χ0−1(dχ0−1/dT)−1 plotted against temperature should be straight lines with slopes 1/β and 1/γ, respectively. As shown in Fig. 4 (b), the linear fits to the data give β = 0.175(9), TC = 31.09(2) K for T < TC and γ = 1.562(9), TC = 30.85(5) K for T > TC, respectively. It can be mentioned that values of the critical exponents as well as the critical temperature are not sensitive to the temperature range chosen (see Figure S3 and Table SI in Supplementary Information), indicating that they are reliable and unambiguous.

The third exponent δ can be determined from the critical isotherm analysis and the Widom scaling relation. Figure 5 shows the isotherm at TC = 31.0 K and its inset shows the same plot in log-log scale. According to Eq. (3), the M(H) at the critical temperature should be a straight line in log-log scale with the slope 1/δ. Such a fitting yields δ = 9.917(8) (see the inset to Fig. 5, a logarithmic plot of all MH data near TC can be seen in Figure S2 in Supplementary Information). Using the Widom scaling relation 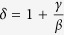Inline graphic and the values of β and γ determined from Modified Arrott plot and Kouvel-Fisher plot, we obtain δ = 10.012(47) and δ = 9.925(56), respectively, which are very close to that obtained from critical isotherm analysis. Therefore, the critical exponents and TC obtained in this work are self-consistent and accurate within the experimental precision.

Figure 5. M vs. H plot collected at TC (=31.0 K) for CrSiTe3.

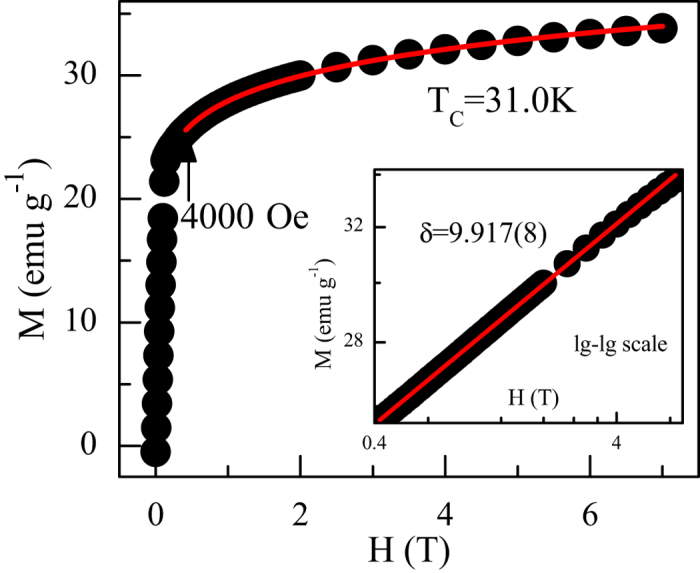
Figure 5

Open in a new tab

Inset shows the same plot in log-log scale and the straight line is the linear fit following Eq. (3). The critical exponent mentioned in graph is obtained from fitting of the data.

In order to further verify the values of the critical exponents and TC, we used Eq. (4) to check whether these critical exponents can generate a scaling equation of state for CrSiTe3. Figure 6(a) shows the plot of m vs. h. It can be clearly seen that all data collapse into two different curves: one below TC and the other above TC. Additionally, we performed m2 vs. h/m plot in Fig. 6(b), where all data also fall on two independent branches. All these results clearly indicate that the interactions get properly renormalized in critical regime following scaling equation of state.

Figure 6.

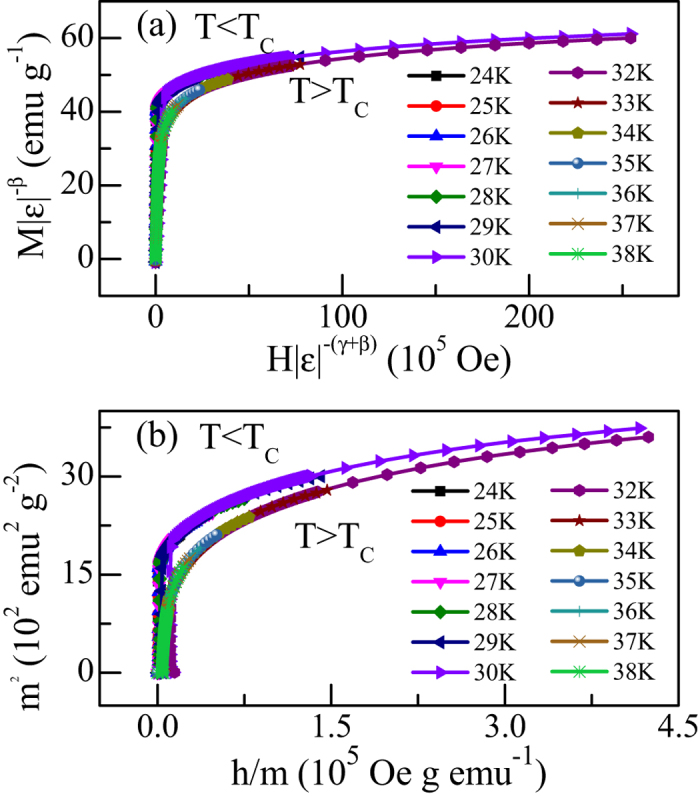
Figure 6

Open in a new tab

(a) The renormalized magnetization plotted as a function of renormalized field following Eq. (5) with TC = 31.0 (K), and β, γ from Table 1 for CrSiTe3. (b) The renormalized magnetization and field (defined in text) replotted in the form of m2 vs. h/m for CrSiTe3. The above two plots show all data collapse into two separate branches: one below TC and another above TC.

All critical exponents derived from various methods are summarized in Table 1 along with the theoretically predicted values for different models. The exponent β determined in this work is close to that reported in previous neutron scattering studies14,15. It is obvious that experimentally determined critical exponents β, γ, and δ are close to the 2D-Ising model. However, both β and γ show some deviation from the theoretical values, which might be associated with the following reasons. First, despite of strong 2D characteristics, CrSiTe3 has a 3D long-range ordering ground state owing to the non-negligible interlayer coupling14,15. Second, there is strong spin-lattice coupling in this material13. Both factors might contribute to the deviation from the prediction of the 2D Ising model.

Table 1. Comparison of critical exponents of CrSiTe3 with different theoretical models (MAP = Modified Arrott plot; KFP = Kouvel-Fisher plot; cal = Calculated).

Composition Ref. Technique β γ δ
CrSiTe3 This work MAP 0.170 ± 0.008 1.532 ± 0.001 10.012 ± 0.047cal
KFP 0.175 ± 0.009 1.562 ± 0.009 9.925 ± 0.056cal
Critical isotherm     9.917 ± 0.008
14 Neutron 0.17    
15 Neutron 0.151 ± 0.002    
2D Ising 20 Theory 0.125 1.75 15
Mean field 18 Theory 0.5 1.0 3.0
3D Heisenberg 18 Theory 0.365 1.386 4.8
3D XY 18 Theory 0.345 1.316 4.81
3D Ising 18 Theory 0.325 1.24 4.82
Tricritical mean field 19 Theory 0.25 1.0 5
Open in a new tab

The errors represent the fitting error.

Finally, we would like to discuss the nature as well as the range of interaction in CrSiTe3. For a homogeneous magnet, the universality class of the magnetic phase transition depends on the exchange interaction J(r). A renormalization group theory analysis predicts J(r) decays with distance r as27:

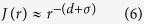graphic file with name srep33873-m13.jpg

where d is the spatial dimensionality and σ is a positive constant. According to this model, the range of the spin interaction is long for σ < 2 and is short for σ > 227. The susceptibility exponent γ is predicted as27:

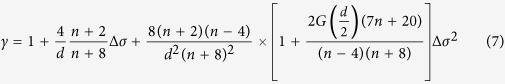graphic file with name srep33873-m14.jpg

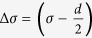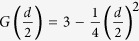where Inline graphic and Inline graphic, n is the spin dimensionality. We followed the procedure similar to ref. 28 to get the range of interaction σ as well as the dimensionality of both lattice d and spin n in this system. The parameter σ is chosen for a particular values of {d:n} so that it yields a value of γ close to the experimentally observed γ = 1.562. The remaining exponents are then calculated from the following expressions: ν = γ/σ, α = 2 − νd, β = (2 − α − γ)/2, and δ = 1 + γ/β. This exercise is repeated for different set of {d:n}, and typical results are summarized in Table 2. It should be mentioned that the obtained exponents show significant difference from the experimentally determined critical exponents, when the spin is considered to be Heisenberg-like (n = 3), regardless of 2D (d = 2) or 3D (d = 3). This fact suggests that the spin interaction should not be of Heisenberg type. Nevertheless, {d:n} = {2:1} and σ = 1.630 give the exponents (β = 0.206, γ = 1.817, and δ = 9.811) which are close to our experimentally observed values (see Table 1). The value of σ = 1.630 suggests a long-range interaction with the attractive interactive interaction between the spins decaying with distance as J(r) ≈ r−3.630. Therefore, our results indicate that the spin interaction in CrSiTe3 is of 2D Ising type ({d:n} = {2:1}) coupled with long-range (σ = 1.630) interaction.

Table 2. Critical exponents calculated following the renormalization group theory (see text).

d n σ β γ δ
2 1 1.63 0.206 1.817 9.811
2 3 1.17 0.357 1.562 5.375
3 3 2.08 0.347 1.562 5.501
Open in a new tab

Conclusion

In summary, we have reported a comprehensive study on the critical behavior of the PM-FM phase transition in the quasi-2D semiconducting ferromagnet CrSiTe3. The critical exponents (β = 0.170 ± 0.008, γ = 1.532 ± 0.001, and δ = 9.917 ± 0.008) and the critical temperature (TC = 31.0 K) are determined using various techniques such as modified Arrott plot, Kouvel-Fisher plot, and the critical isotherm analysis. The consistency in the values of the critical exponents and the critical temperature obtained from different methods and the well-obeyed scaling behavior confirm that the obtained exponents are unambiguous and purely intrinsic to the material. The exponents determined in this study match well with those given by the renormalization group calculations for a 2D Ising system ({d:n} = {2:1}) coupled with long-range attractive interactions between spins decaying as J(r) ≈ r−(d+σ) with σ = 1.630.

Methods

Single-crystal samples of CrSiTe3 were prepared by the self-flux technique13. The structure and phase purity were confirmed by single-crystal and powder X-ray diffraction measurements at room temperature. The magnetization was measured using a Quantum Design SQUID-VSM magnetometer with the magnetic field applied parallel to the c axis of the sample. Isotherms were collected at an interval of 0.5 K around TC. Care has been taken to ensure that every curve was initially magnetized. The applied magnetic field Ha has been corrected by the demagnetization of the sample following the method described in ref. 29 and the corrected H was used for the analysis of critical behavior.

Additional Information

How to cite this article: Liu, B. et al. Critical behavior of the quasi-two-dimensional semiconducting ferromagnet CrSiTe3. Sci. Rep. 6, 33873; doi: 10.1038/srep33873 (2016).

Supplementary Material

Supplementary Information
srep33873-s1.pdf (409.3KB, pdf)

Acknowledgments

This work was supported by National Natural Science Foundation of China under contract Nos U1532153 and 11574322.

Footnotes

Author Contributions Z.Q. and Y.H.Z. conceived and designed the experiments. B.L. grew the single crystal. B.L., Y.M.Z., L.Z., S.Z., Z.W. and W.W. carried out the experiments. Z.Q. and B.L. analyzed the data and wrote the paper. All the authors discussed the results and commented on the manuscript.

References

  1. Novoselov K. S. et al. Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004). [DOI] [PubMed] [Google Scholar]
  2. Novoselov K. S. et al. Two-dimensional gas of massless Dirac fermions in grapheme. Nature (London) 438, 197–200 (2005). [DOI] [PubMed] [Google Scholar]
  3. Zhang Y. et al. Experimental observation of the quantum Hall effect and Berry’s phase in grapheme. Nature (London) 438, 201–204 (2005). [DOI] [PubMed] [Google Scholar]
  4. Geim A. K. & Novoselov K. S. The rise of grapheme. Nat. Mater. 6, 183–191 (2007). [DOI] [PubMed] [Google Scholar]
  5. Castro Neto A. H. et al. The electronic properties of grapheme. Rev. Mod. Phys. 81, 109–162 (2009). [Google Scholar]
  6. MacDonald A. H. et al. Ferromagnetic semiconductors: moving beyond (Ga, Mn)As. Nat., Mater. 4, 195–202 (2005). [Google Scholar]
  7. Dietl T. A ten-tear perspective on dilute magnetic semiconductors and oxides. Nat. Mater. 9, 965–974 (2010). [DOI] [PubMed] [Google Scholar]
  8. Rogado N. S. et al. Magnetocapacitance and magnetoresistance near room temperature in a ferromagnetic semiconductor: La2NiMnO6. Adv. Mater. 17, 2225–2227 (2005). [Google Scholar]
  9. Vaz C. A. F. et al. Magnetism in ultrathin film structures. Rep. Prog. Phys. 71, 056501 (2008). [Google Scholar]
  10. Li X. X. & Yang J. L. CrXTe3 (X = Si, Ge) nanosheets: two dimensional intrinsic ferromagnetic semiconductors. J. Mater Chem. C. 2, 7071 (2014). [Google Scholar]
  11. Sivadas N. et al. Magnetic ground state of semiconducting transition-metal trichalcogenide monolayers. Phys. Rev. B 91, 235425 (2015). [Google Scholar]
  12. Chen X. F. et al. Strain-engineering of magnetic coupling in two-dimensional magnetic semiconductor CrSiTe3: Competition of direct exchange interaction and superexchange interaction. Phys. Lett. A 379, 60 (2015). [Google Scholar]
  13. Casto L. et al. Strong spin-lattice coupling in CrSiTe3. APL Mat. 3, 041515 (2015). [Google Scholar]
  14. Carteaux V. et al. 2D Ising-like ferromagnetic behavior for the lamellar Cr2Si2Te6 compound: a Neutron scattering investigation. Europhys. Lett. 29, 251 (1995). [Google Scholar]
  15. Williams T. J. et al. Magnetic correlations in the quasi-two-dimensional semiconducting ferromagnet CrSiTe3. Phys. Rev. B 92, 144404 (2015). [Google Scholar]
  16. Stanley H. E. Introduction to Phase Transitions and Critical Phenomena (Oxford University Press, London, 1971). [Google Scholar]
  17. Fisher M. E. The theory of equilibrium critical phenomenon. Rep. Prog. Phys. 30, 615–730 (1967). [Google Scholar]
  18. Arrott A. Criterion for ferromagnetism from observations of magnetic isotherms. Phys. Rev. 108, 1394–1396 (1957). [Google Scholar]
  19. Banerjee S. K. On a generalized approach to first and second order magnetic transitions. Phys. Lett. 12, 16–17 (1964). [Google Scholar]
  20. Kaul S. N. Static critical phenomenon in ferromagnets with quenched disorder. J. Magn. Magn. Mater. 53, 5–53 (1985). [Google Scholar]
  21. Huang K. Statistical Mechanics 2nd ed. (Wiley, New York, 1987). [Google Scholar]
  22. LeGuillou J. C. & Zinn-Justin J. Critical exponents from field theory. Phys. Rev. B 21, 3976–3998 (1980). [Google Scholar]
  23. Arrott A. & Noakes J. Approximate equation of state for Nickel near its critical temperature. Phys. Rev. Lett. 19, 786 (1967). [Google Scholar]
  24. Pramanik A. K. & Banerjee A. Critical behavior at paramagnetic to ferromagnetic phase transition in Pr0.5Sr0.5MnO3: a bulk magnetization study. Phys. Rev. B 79, 214426 (2009). [Google Scholar]
  25. Aharoni A. Introduction to the Theory of Ferromagnetism (Clarendon Press, Oxford, 1996). [Google Scholar]
  26. Kouvel J. S. & Fisher M. E. Detailed magnetic behavior of Nickel near its Curie point. Phys. Rev. 136, A1626–A1632 (1964). [Google Scholar]
  27. Fisher M. E., Ma S. K. & Nickel B. G. Critical exponents for long-range interactions. Phys. Rev. Lett. 29, 917–920 (1972). [Google Scholar]
  28. Fischer S. F., Kaul S. N. & Kronmuller H. Critical magnetic properties of disordered polycrystalline Cr75Fe25 and Cr70Fe30 alloys. Phys. Revl B 65, 064443 (2002). [Google Scholar]
  29. Pramanik A. K. & Banerjee A. Phase separation and the effect of quenched disorder in Pr0.5Sr0.5MnO3. J. Phys.: Condens. Matter. 20, 275207 (2008). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep33873-s1.pdf (409.3KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES