Teaching for All? Teach For America’s Effects across the Distribution of Student Achievement

Abstract

This paper examines the effect of Teach For America (TFA) on the distribution of student achievement in elementary school. It extends previous research by estimating quantile treatment effects (QTE) to examine how student achievement in TFA and non-TFA classrooms differs across the broader distribution of student achievement. It also updates prior distributional work on TFA by correcting for previously unidentified missing data and estimating unconditional, rather than conditional QTE. Consistent with previous findings, results reveal a positive impact of TFA teachers across the distribution of math achievement. In reading, however, relative to veteran non-TFA teachers, students at the bottom of the reading distribution score worse in TFA classrooms, and students in the upper half of the distribution perform better.

Teaching for All? Teach For America’s Effects across the Distribution of Student Achievement

As a result of residential segregation, low-income students have very different educational opportunities than their higher-income peers (Reardon, 2011; Reardon & Bischoff, 2011). Low-income students have fewer “high-quality” teachers, teachers are more likely to leave low-income schools, and few teachers are interested in relocating to low-income schools even when offered substantial pay increases to do so (Boyd, Lankford, Loeb, & Wyckoff, 2005; Darling-Hammond & Sykes, 2003; Glazerman, Protik, Teh, Bruch, & Max, 2013; Hanushek, Kain, & Rivkin, 2004; Isenberg et al., 2014). While school administrators have investigated a number of methods to improve teacher quality and supply in low-income schools (Ingersoll, 2004; Levin, 1968), districts increasingly rely on alternative pathways to teacher certification to recruit teachers. Of the growing numbers of alternative teacher preparation programs, Teach For America (TFA) is among the most visible and controversial (Higgins, Robison, Weiner, & Hess, 2011; Matthews, 2013; Teach For America, 2015).

TFA was founded on the simple, but unconventional premise that “good” teachers can be identified based on highly-selective background criteria, given limited amounts of training and ongoing coaching, and can be more successful in challenging, underserved schools than traditionally prepared teachers. TFA argues that its teachers can radically improve educational opportunities and achievement for low-income youth in high-poverty urban and rural communities across the US, with only a two-year commitment to teaching (Kopp, 2011). TFA’s presence expanded dramatically since its founding in 1989: In 2012, more than 10,000 TFA corps members taught 750,000 students in 46 regions across 36 states and the District of Columbia (Barahona, 2012). Although applications to the program have declined in recent years, in 2015, TFA placed over 11,000 corps members in 50 regions across the country (Rich, 2015). Lauded and critiqued for its impact in a variety of educational domains (Donaldson & Johnson, 2010, 2011; Miner, 2010; Rotherham, 2011; Veltri, 2010), TFA judges its own success and failure based on student academic outcomes in its teachers’ classrooms (Kopp, 2011).

Previous work examines the average effect of TFA on student achievement, yielding contradictory results, with some finding that TFA teachers outperform their non-TFA counterparts (Clark et al., 2013; Glazerman, Mayer, & Decker, 2006) and others finding the opposite (Darling-Hammond, Brewer, Gatlin, & Vasquez Heilig, 2005). These mixed results suggest that TFA may not have a uniform impact for all types of students in all contexts, but might instead generate heterogeneous effects. Developmental science suggests that many types of interventions affect students differently (Duncan & Vandell, 2011), and existing examinations of TFA have only begun to consider how its effects might vary across different types of students and schools (Glazerman et al., 2006; Xu, Hannaway, & Taylor, 2011).

A growing literature in economics suggests that evaluations focusing exclusively on mean impacts potentially conceal important heterogeneities in the impact of an intervention on the distribution of student outcomes (Bitler, Gelbach, & Hoynes, 2006). Given TFA’s goals related to closing achievement gaps and having students master grade-level content (Foote, 2009; Kopp, 2011; Raymond, Fletcher, & Luque, 2001; Sawchuk, 2009), TFA teachers might differentially boost achievement at different parts of the skill distribution. A distributional approach might be particularly informative in the case of TFA as its training model and organizational focus may lead its corps members to devote more or less attention to students of different skill levels in their attempts to make achievement gains for all students in their classrooms.

One prior study has examined the impact of TFA on the distribution of student achievement in elementary school, finding positive effects across the distribution in math and little impact in reading (Antecol, Eren, & Ozbeklik, 2013).¹ The present study adds to the literature on the effects of TFA by estimating distributional effects using unconditional, rather than conditional quantile treatment effects (c.f., Killeward & Bearak, 2014). It also corrects a coding error in the prior literature on TFA in which invalid scores (of 99) were treated as within the valid range, and included in previous estimates. These methodological changes yield consistent results in math, but identify policy-relevant distributional variation in reading that was previously missed. This paper thus contributes to the growing literature on the impacts of TFA, and seeks to inform larger conversations about teacher recruitment, training, and effectiveness in underserved communities by examining how the effect of TFA teachers varies across the distribution of student achievement.

Prior Research on Teach For America

The relationship between TFA and student achievement has been examined using a variety of experimental, quasi-experimental, and descriptive research designs, in many grades and contexts. Three studies used randomized experiments to isolate the causal effect of TFA on average student achievement. Glazerman et al. (2006) evaluated the effect of TFA on student achievement in grades 1–5 using a random assignment design at six TFA sites, finding that students assigned to TFA teachers outperformed students in novice and veteran non-TFA classrooms in mathematics (ES = 0.15 SD), but not reading. Clark et al. (2013) found that students randomly assigned to TFA secondary math teachers outperformed students in comparison classrooms in 11 districts in eight states (ES = 0.07 SD). TFA teachers outperformed both alternatively and traditionally certified novice and veteran comparison teachers, with larger effects in high school than middle school. Finally, Clark et al.’s (2015) recent work evaluated TFA elementary school teachers in 10 TFA sites as part of the i3 scale-up of TFA, finding that TFA corps members were as effective as more experienced same-school teachers in reading and math, and had statistically significant, positive effects on reading in grades Pre-K through 2 (ES = 0.12 SD).

The majority of the quasi-experimental evidence found that TFA teachers had a positive effect on math and science on average, and little to no impact on language arts (Boyd, Grossman, Lankford, Loeb, & Wyckoff, 2006; Henry et al., 2010; Kane, Rockoff, & Staiger, 2008; Xu et al., 2011). Most descriptive studies also found this pattern (Raymond et al., 2001; Strategic Data Project, 2012; Turner, Goodman, Adachi, Brite, & Decker, 2012; Ware et al., 2011), but there were some notable exceptions (Darling-Hammond et al., 2005; Laczko-Kerr & Berliner, 2002; Noell & Gansle, 2009; Schoeneberger, Dever, & Tingle, 2009).² Across all but one of these studies (Noell & Gansle, 2009), TFA teachers outperformed novice teachers, and in some they also outperformed veteran teachers. TFA teachers also outperform new teachers from selective undergraduate teacher preparation programs and teachers from other selective alternative preparation programs, particularly in STEM subjects and secondary grades, but they left the classroom at higher rates than both alternatively and traditionally certified teachers (Boyd, Dunlop, et al., 2012; Boyd, Grossman, et al., 2012; Clark et al., 2013; Henry, Bastian, et al., 2014; Henry, Purtell, et al., 2014). Recent evidence also suggests that there are no spillover effects of TFA on student learning into non-TFA classrooms (Hansen, Backes, Brady, & Xu, 2014).

As with every study of TFA, it is important to note that there are issues of selection inherent in the assessment of TFA’s effects. This study takes advantage of an experiment that randomized students to TFA or non-TFA classrooms, but did not randomly assign teachers to preparation pathways. TFA teachers are a select group of individuals that entered teaching through a distinctive pathway that attracted them for reasons that are not necessarily the same as for teachers who entered through traditional pathways.

There are also issues of selection that drive non-TFA teachers to work in high-poverty schools that may lead them to systematically differ from teachers in lower-poverty schools, although they do not necessarily stem from certification pathway. Given these selection issues, it is important to be clear that the results here only generalize to the kinds of high-poverty schools that employ TFA teachers in elementary grades. This is important because, from a policy perspective, one of the key questions is whether TFA teachers are more or less effective at raising student achievement than the teachers that these students would have otherwise had access to. Other work has begun to examine the selection of teachers into and away from high-poverty schools, and the results of this study should be understood within the context of these findings (Boyd, Grossman, Lankford, Loeb, & Wyckoff, 2009; Straubhaar & Gottfried, 2014).

A Distributional Perspective on Teach For America

Distributional studies show that many education policy interventions do not have a uniform effect on all intervention recipients (Arulampalam, Naylor, & Smith, 2012; Lamarche, 2007), and an extensive body of work documents heterogeneity in the effects of teachers on average student achievement (Chetty et al., 2011; Kane et al., 2008). Although tests of distributional differences in other settings have uncovered meaningful, policy-relevant variation (e.g., Bitler et al., 2006), there are still relatively few education researchers who test for these types of differences in their evaluations. Among the small number of notable exceptions is Jackson & Page (2013), who reanalyzed Project STAR data to show that that class size matters most at the top of the achievement distribution. Given TFA’s intent to promote achievement gains for all students and its expanding role in low-income districts and teacher policy, it is important to consider not just its average impact, but also the way it impacts the entire distribution of student achievement.

Although program impacts are often summarized into a single effect size representing the mean impact of a treatment, there is no guarantee of uniform impacts of TFA teachers. Consider Glazerman et al.’s (2006) finding of a positive average effect of TFA teachers on math achievement. This finding could be the result of TFA teachers being equally effective at improving student achievement at all points of the achievement distribution because the rigor of their academic preparation (Boyd, Grossman, et al., 2012; Boyd et al., 2006; Decker, Mayer, & Glazerman, 2004a) provides them with a depth of content knowledge that is strong enough to outweigh their relative lack of pedagogical experience.

However, positive average effects might also conceal meaningful variation across the distribution that is having off-setting effects. The short duration of TFA training may lead corps members to draw on their personal experiences when teaching, relying heavily on teaching strategies that they found engaging as students, which might work best for similarly higher-achieving students. However, they may lack the pedagogical content knowledge and curricular knowledge needed to effectively teach struggling students. If this were the case, the effect of having a TFA teacher might be restricted to the top of the distribution, promoting learning for some while simultaneously widening gaps in their own classrooms.

But the opposite pattern could occur as well. TFA teachers working in schools tasked with making dramatic academic improvements might feel compelled to place particular efforts on low-performing students (c. f., Carroll, 2013). This coupled with training that focuses heavily on data tracking of student performance may increase instructional support for low-performers or promote a narrower focus on basic-skills among TFA teachers relative to non-TFA teachers (Goldstein, 2013). If the intensive focus on improving test scores drives them to focus efforts on struggling students and basic skills, then the effects of TFA teachers might be largest at the bottom of the distribution.

Other work suggests that TFA’s impacts on the distribution of student achievement are not consistent across math and reading, but have little distributional variation. In keeping with research examining mean effects, Antecol et al. (2013) find positive impacts across the distribution of math achievement and little impact on the distribution of reading. Their methodological approach to distributional analysis differs from the present approach in two important ways (described in detail below). Additionally, like Glazerman et al.’s (2006) analysis of average treatment effects using these data, Antecol et al. (2013) report analyses that include data from students with invalid test scores.³ These students received raw scores of 99, which exceeds the maximum test score of approximately 50 points.⁴ These students received Normal Curve Equivalent scores of zero, which are also outside of the valid range of 1–100.

Given the policy relevance of TFA teachers in the present climate of teacher shortages, heated rhetoric, and expanding opportunity gaps between rich and poor students, we need to move beyond considering TFA’s average impact and consider how the entire distribution of student achievement is affected by having a TFA teacher. Examining variation in the impact of TFA can help to identify the relative strengths and weaknesses of the TFA program, as well as speak to larger debates about the utility of alternative certification programs that recruit teachers from selective backgrounds and provide limited training.

Data

To understand whether the effect of TFA varies across the distribution of student achievement in elementary school, this study estimates the quantile treatment effects (QTE) of being randomly assigned to a TFA versus non-TFA teacher. Mathematica Policy Research collected these data during the 2001–2002 and 2002–2003 school years, from six of the 15 active TFA regions, including Baltimore, Chicago, Los Angeles, Houston, New Orleans, and the Mississippi Delta (Decker, Mayer, & Glazerman, 2004b).⁵ These six regions were randomly selected to represent the mix of districts served by TFA (predominately black vs. Hispanic, urban vs. rural), and within each region, schools with at least one TFA and one non-TFA teacher at the same grade level were chosen at random. The final sample included 100 first through fifth grade classrooms (44 TFA, 56 non-TFA) at 17 schools, and a total of 1,969 students. While TFA has grown substantially since these data were collected, these data remain the sole experimental data with which to examine the causal impact of TFA on student achievement in elementary school that are publicly available, and thus provide valuable evidence that remains relevant in the current TFA context, particularly as TFA continues to place corps members in all of the regions included in this study.

Student achievement is measured in the fall and spring using the Iowa Test of Basic Skills (ITBS). The ITBS is a nationally normed standardized test that evaluates students’ knowledge of basic grade-level skills. The portions of the test collected in these data are the math and reading assessments, which were administered in the fall (at random assignment), and again in the spring. The ITBS is used by districts across the country to measure student progress, allowing for a direct comparison of student achievement from this sample with student achievement in a nationally representative sample of students. Given that the ITBS focuses exclusively on basic skills, this assessment is not able to provide insights about TFA’s impacts on other aspects of students’ learning or in other areas, such as behavior or socio-emotional development.

The dependent variables are the Normal Curve Equivalent (NCE) math and reading scores, which are age-adjusted and nationally normed to have a mean of 50 and a standard deviation of 21.06.⁶ Because first graders took only a portion of the reading test, they are excluded from the analysis.⁷ I further restrict my sample to students who have at least one fall and one spring test score.

In addition to the test scores that were identified as missing in the public use data, 155 of the respondents (including 9.5 percent of respondents in grades 2–5) have at least one NCE test score of 0, which correspond to raw scores of 99. ⁸ Although the total number of questions varies somewhat by level, the highest possible raw score in reading at any level is 44 and the highest possible raw score in math is 50 (Hoover, Dunbar, & Frisbie, 2013). Figure 1 presents a histogram of the raw scores from the fall math test, providing a visual depiction of these non-valid scores. These missing values were not mentioned in other work using these data, and sample sizes in each of these studies suggest that students with these scores were included in the primary analytic samples (Antecol, Eren, & Ozbeklik, 2013; Decker et al., 2004b; Glazerman et al., 2006).⁹ Fortunately, the prevalence of 99s in spring posttests is fairly balanced across TFA and non-TFA. However, there are statistically significant differences in their prevalence in both the reading and math pretests (fall tests) for the full sample and my analytic sample, with non-TFA classrooms having a higher proportion in reading and TFA classrooms having a higher proportion in math.

Figure 1. Histogram of fall raw ITBS math score (number of items answered correctly).

Notes: Figure shows histogram of the raw score (the number of math items answered correctly) on the baseline (fall) ITBS as reported in the public-use version of the data. The large point mass at 99 represents those individuals with ITBS raw math scores of 99 and associated National Percentile Ranking scores of 0, and represents a missing data code. Data from the Mathematica Policy Research Evaluation of Teach For America. Includes students in grades 2–5.

Descriptive statistics for TFA and non-TFA classrooms in the analytic sample are presented in Table 1, with additional details about missing data in Appendix Table A1.

Table 1.

Baseline characteristics of study sample and missing values¹

	Control Mean	T-C Difference	SE	P-value2
Female	0.474	0.018	0.018	0.319
Black	0.720	−0.008	0.034	0.809
Hispanic	0.238	0.016	0.021	0.459
Over age for grade	0.231	0.018	0.024	0.447
Free/reduced lunch eligible	0.975	−0.002	0.009	0.786
Did not move classes during school year (stayer)	0.928	0.018	0.014	0.195
Percent of class in research sample at end of year	0.817	−0.018	0.030	0.556
Math pretest Normal Curve Equivalent score	30.638	−0.177	0.840	0.834
Reading pretest Normal Curve Equivalent score	31.141	0.245	0.832	0.771
Math posttest Normal Curve Equivalent score	31.710	2.786	1.028	0.012
Reading posttest Normal Curve Equivalent score	31.145	0.562	0.939	0.554
Sample size:	N = 1430
Joint test for baseline child characteristics:	p = 0.224

¹Sample includes 2nd - 5th graders with at least one valid pre- and post-test

²P-values calculated after using inverse propensity score weights and clustering on randomization block

Given the arguments that TFA makes about their effectiveness relative to both experienced and inexperienced teachers trained through other pathways, I also estimate models comparing TFA teachers to only experienced non-TFA teachers, using Glazerman et al.’s (2006) experience threshold of more than 3 years. The relative characteristics of TFA versus novice and experienced non-TFA teachers are described in detail in the original report of the Mathematica study (Decker et al., 2004b). Notably, there are no differences between the groups in attrition from the sample during the course of the study, and as identified by Decker and colleagues, there are very few crossovers (less than 5 percent). However, given that there is some incidence of attrition and crossovers, the method described below is best characterized as an “intent to treat” analysis.

Method

These analyses take advantage of randomized assignment to treatment (TFA) and control (non-TFA) classrooms. The estimation of the effect of this treatment stems from the framework provided by the potential outcomes model. Each student i has two potential outcomes, Y_1i and Y_0i (in the current setting, a test score). Student i has outcome Y_1i if assigned to the treatment group and outcome Y_0i if assigned to the control group. D(i) denotes the group that student i is assigned to in a randomized experiment. If student i is assigned to the treatment group, then D(i) = 1, and if student i is assigned to the control group, D(i) = 0; the treatment effect on student i is defined as d_i=Y_1i – Y_0i.

To examine the effect of TFA on the distribution of student achievement, I estimate quantile treatment effects (QTE) (Firpo, 2007). QTE allow for unconditional comparisons of the achievement distributions of TFA and non-TFA students, and provide more information on the nature of treatment effects on the treated sample than mean differences. In the context of experimental data, QTE are estimated by calculating the difference in the two marginal distributions (cumulative distribution functions, or CDFs) and are identified at each quantile in a logic analogous to average treatment effects under the potential outcomes framework.

Let Y be a random variable with a cumulative distribution function (CDF) F(y), where F(y) = Pr[Y ≤ y]. Then, the qth quantile of the distribution F(y) is defined as the smallest value y_q such that F(y_q) is at least as large as q (e.g., y_0.5 is the median). Now consider two (marginal) distributions F₁ (the CDF for the potential outcomes if D = 1), and F₀ (the CDF for the potential outcomes if D = 0). We define the difference between the qth quantiles of these two distributions as y_q = y_q1 – y_q0, where y_qd is the qth quantile of distribution F_d.

The joint distribution of (Y_0i,Y_1i) is not identified without assumptions. However, if teacher assignment is independent of the potential outcomes, the difference in means, or average treatment effect, d = E[d_i] = E[Y₁] - E[Y₀], is identified because each expectation requires only observations from one of the two marginal distributions. Similarly, identification of the marginal distributions implies identification of the quantiles y_qd, and thus identification of the differences in their quantiles, y_q = y_q1 – y_q0. In this experimental setting, the quantile treatment effect (QTE) is the estimate of this difference in the quantiles of the two marginal distributions. Using these CDFs, I examine the difference between these two distributions at various percentiles of the outcome variable, ITBS reading or math NCE test scores. For example, I estimate the QTE at the .50 quantile by subtracting the median test score of non-TFA students from the median test score of TFA students. By comparing test scores at a number of quantiles, I am able to observe TFA’s effects on different portions of the distribution. If TFA teachers have different effects on relatively high or low-achievers, this method will identify these differences while mean comparisons with OLS regression would not.

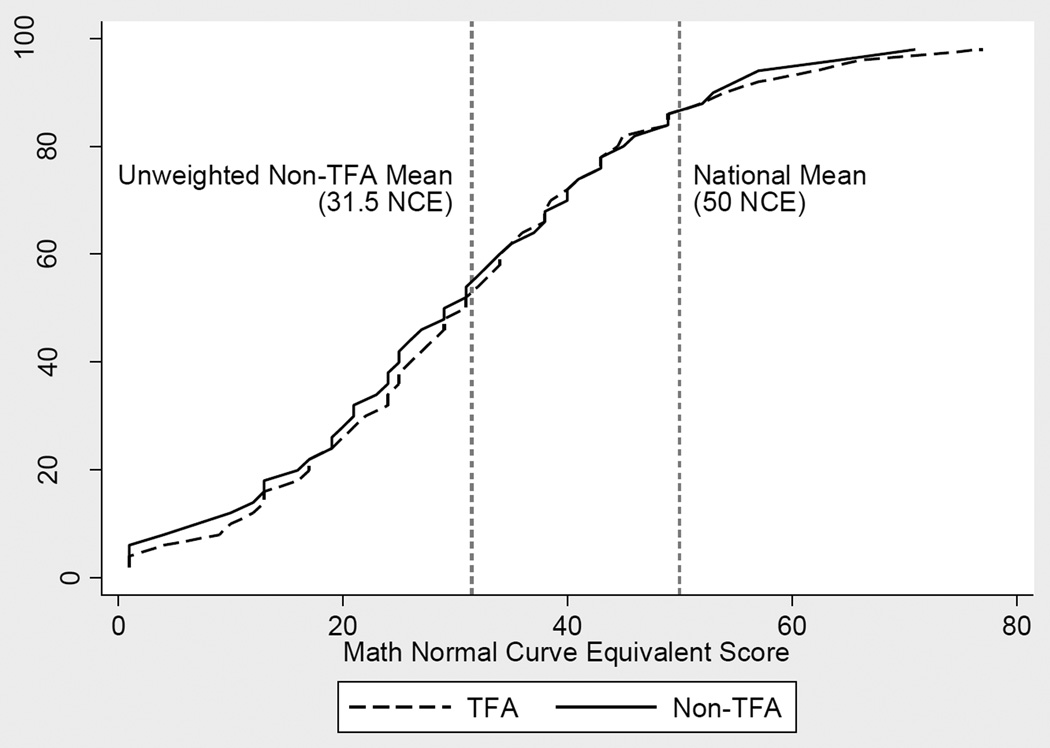
As an example, Figure 2 and Figure 3 Panel A show the CDFs and QTE for un-weighted baseline math NCE scores. Figure 2 shows the CDFs for baseline math scores in TFA and non-TFA classrooms. The CDFs present math NCE scores on the x-axis with the cumulative percent of the sample on the y-axis. The horizontal distance between these CDFs at each point in the distribution, which equals the difference in NCE scores, is the quantile treatment effect at that percentile. Included on Figure 2 (and subsequent figures) are two vertical lines indicating the ITBS national mean (at 50 NCE points) and the mean for the non-TFA classrooms (for un-weighted fall math scores this is 31.5 NCE points), which highlight that the majority of the sample scores below the national average.

Figure 2. Cumulative Density Functions (CDFs) for fall math achievement in TFA and non-TFA classrooms.

Notes: Figure shows cumulative distribution functions for baseline math Normal Curve Equivalent scores from the Iowa Test of Basic Skills separately for TFA classrooms and non-TFA classrooms. Estimates are un-weighted. Data from the Mathematica Policy Research Teach For America Evaluation.

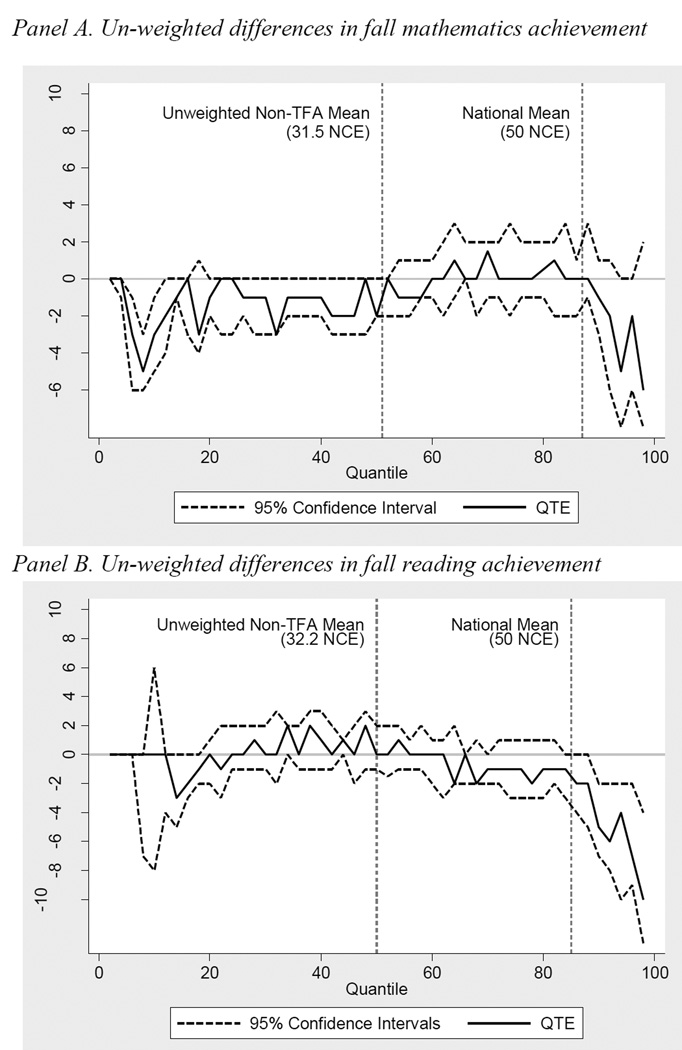
Figure 3. Un-weighted quantile treatment effect estimates of the impact of assignment to TFA classroom on reading Normal Curve Equivalent scores at baseline (fall).

Notes: Panels A & B of figure show QTE for the effect of being assigned to a TFA classroom on math and reading Normal Curve Equivalent scores from the Iowa Test of Basic Skills at baseline. Estimates are un-weighted. Data from the Mathematica Policy Research Teach For America Evaluation.

Figure 3 Panel A shows the corresponding QTE for the CDFs shown in Figure 2, where the x-axis represents the cumulative percentiles of the distribution, and the y-axis represents the difference in NCE scores between TFA and non-TFA classrooms at each percentile. The score difference (solid line) is plotted along with pointwise 95 percent confidence intervals (dashed lines), which are calculated by stratifying on block and treatment status and bootstrapping the estimates 999 times. Figure 3 Panel A shows that most of the QTE point estimates are at or near zero for baseline math scores, except at the upper and lower tails. Between the 6^th and 10^th percentiles, there is a negative and significant difference between treatment and control where the confidence intervals do not include zero, suggesting some imbalance across the distribution in random assignment.

Figure 3 Panel B mirrors Panel A, assessing the degree to which randomization successfully balanced fall scores across the distribution of reading achievement. Panel B shows that the differences between TFA and control classrooms are negative beginning above the 64^th percentile, and significant above the 90^th percentile. This suggests that randomization was even less successful for reading than math, with non-TFA classrooms having more higher-performing students at the outset.

To address the lack of balance on fall scores, I use an inverse propensity-score weighting approach as a nonparametric first step (Firpo, 2007), which allows me to balance baseline test scores across the two groups and to account for differences in the likelihood of being assigned to a TFA or non-TFA teacher in different grade levels and schools.¹⁰ This approach also allows me to adjust for differences in the presence of non-response and invalid test scores by including indicator variables for whether students had missing or invalid test scores. Inverse propensity score weighting is helpful in examining distributional differences, as it provides a semi-parametric way to adjust for many covariates while still allowing for unconditional comparisons (i.e., it allows me to account for differences in observable characteristics without examining conditional distributions). See Bitler, Gelbach, and Hoynes (2006) for a detailed discussion on the merits of inverse propensity score weighting in a distributional framework, and Powell (2014) for additional discussion on conditional versus unconditional distributions for estimating quantile treatment effects.

To estimate the inverse propensity score weights, I first use a logistic regression model to predict assignment to a TFA or non-TFA teacher as a function of randomization block, baseline test score deciles for math and reading, whether the student had valid or invalid missing values for fall or spring scores, the baseline demographic characteristics from Table 1 (including race, gender, free & reduced price lunch status, whether the student is over-age for grade, and indicators for whether the student had missing values for any of these control variables), whether the student persists to the end of the study, and what percent of the student’s class is in the research sample at spring data collection. I calculate the predicted probability of being in the treatment group, p̂, and construct weights of 1/p̂ for those in the treatment group and 1/(1 − p̂) for the control group. As shown by the p-values for mean comparisons in Table 1, these weights balance the treatment and control groups on average for these observable dimensions. Further, a test of joint significance for these characteristics is not significant, suggesting that, when using the inverse propensity score weights, there are no mean differences across random assignment groups. Propensity score weighting allows me to obtain unconditional estimates while still adjusting for any post-randomization imbalance in baseline test scores, and missing values. Inverse propensity score weight adjusted fall QTE are presented in Figure 4, and show that samples are balanced across the fall distributions in both reading and math. I thus use the inverse propensity score weights to estimate the spring QTE for reading and math.¹¹ The basic pattern of results reported below were robust to a number of different weighting equations, which are described in greater detail in the methodological appendix.

Figure 4. Inverse propensity score weighted quantile treatment effect estimates of the impact of assignment to TFA classroom on reading Normal Curve Equivalent scores at baseline (fall).

Notes: Panels A & B of figure show QTE for the effect of being assigned to a TFA classroom on math and reading Normal Curve Equivalent scores from the Iowa Test of Basic Skills at baseline. Estimates are weighted using inverse propensity score weights. Weights are 1/p̂ for treatment observations and 1/(1-p̂) for control observations, where p̂ is generated from a logistic regression of treatment status on baseline demographics, sample design variables, and baseline test score deciles. 95% CIs are obtained by bootstrapping with replacement within randomization block. Data from the Mathematica Policy Research Teach For America Evaluation.

It is also important to note that weights can only balance the two groups on observed characteristics. Given the amount of non-random sorting of students into different classrooms, due to parent, teacher, and administrator influence documented elsewhere, it is possible that sorting on unobservables might still be present at different parts of the distribution (Paufler & Amrein-Beardsley, 2014). The use of unconditional QTE in this analysis hinges on the assumption that the inverse propensity score weighting corrected for imbalance between the two groups on observed and unobserved characteristics, but this cannot be fully tested.

In addition to the missing data described above, two methodological issues differentiate the present study from Antecol et al.’s (2013) prior work examining the effect of TFA on the distribution of student achievement. This study’s methodological approach estimates unconditional QTE using inverse propensity score weights to balance groups where Antecol et al. (2013) used a fixed effects quantile treatment effects (FEQTE) method suggested by Canay (2011). Canay’s method uses a two-step additive fixed effects transformation to account for randomization block fixed effects. Several scholars have proposed alternatives to Canay’s transformation for addressing fixed effects in distributional estimators (Galvao, 2011; Koenker, 2004; Ponomareva, 2011; Powell, 2015), and some have suggested that the restrictions imposed by Canay are impractical (Arulampalam, Naylor, & Smith, 2012). Recent work also argues that additive fixed effects transformations introduce bias, even in the context of random assignment (Powell, 2014, 2015; Powell, Baker, & Smith, 2014).

In addition to introducing bias with FEQTE, Antecol and colleagues also report conditional FEQTE estimates, as opposed to unconditional QTE.¹² As noted by a number of scholars (c.f., Firpo, Fortin, & Lemieux, 2009; Frölich & Melly, 2013; Killewald & Bearak, 2014) unconditional QTE are needed in order to accurately summarize the effects of a treatment on an entire population. The inverse-propensity score weighted quantile treatment effects, which are described in more detail above, produce unconditional estimates of the impact of TFA on the distribution of student achievement, adjusting for the block randomization design, baseline control variables, previously identified missing values, and the previously unidentified missing values described above (c.f. Bitler, Domina, Penner, & Hoynes, 2015; Bitler, Gelbach, & Hoynes, 2006; Firpo et al., 2009). The process of conditioning, or including covariates, “shifts” an observation’s placement in the conditional distribution (Powell, 2010). Importantly, this can lead results from conditional and unconditional QTE to vary considerably. For example, Firpo et al (2009) note that union membership has a positive effect on wages at the conditional 90^th percentile, and a negative effect on the unconditional 90^th percentile (see also Killewald and Bearak (2014) on the motherhood wage penalty). Put differently, conditional estimates ultimately describe TFA impacts within relative distributions rather than impacts on the full distribution of students in the study sample (and by extension to the population to which this experimental sample hopes to generalize). The present study thus avoids this by using inverse propensity score weighting to estimate unconditional QTE while adjusting for differences in observable characteristics.

Results

The QTE results for spring math and reading post-tests are presented in Figure 5, Panels A and B. As with Figures 2 and 3, Figure 5 plots test score differences between students in TFA and non-TFA classrooms (y-axis), for each percentile of the distribution (x-axis). When the solid line, representing the point estimate at a given quantile, is above zero, students in TFA classrooms are scoring higher than non-TFA students, and when the solid line is below zero, students in TFA classrooms are scoring lower than those in non-TFA classrooms. These differences are statistically significant when the area between the two dashed lines (representing the 95 percent confidence intervals) does not include the horizontal line marking zero on the y-axis. In Panel A of Figure 5, the point estimates are positive across nearly the entire distribution of math, and for most of the distribution both confidence intervals are also above zero, showing that these differences are statistically significant at the 5 percent level. Although the point estimates are not the same across the distribution, and are as large as 6 NCE points at the 80^th and 88^th percentiles, tests comparing differences between various percentiles across the distribution suggest that they are not statistically different from one another at the 5 percent level. Even though we cannot rule out an effect of zero for some portions of the distribution, we can largely rule out a negative effect of TFA on math achievement, except at the very upper tail. Thus, writ large, TFA’s effect on math can be characterized as positive on average and shared throughout most of the distribution, though in a few parts of the distribution it might be more accurate to characterize it as non-negative. This is important as it shows that students are not worse off in math under TFA teachers and are likely better off. The QTE results shown visually in Figure 5 are also reported in Table 2 for each decile of the distribution.

Figure 5. Inverse propensity score weighted quantile treatment effect of assignment to TFA classrooms on posttest (spring) test scores, TFA vs. all non-TFA teachers.

Notes: Panels A & B of figure show QTE for the effect of being assigned to a TFA classroom on math and reading Normal Curve Equivalent scores from the Iowa Test of Basic Skills in the spring following random assignment. Estimates are weighted using inverse propensity score weights. Weights are 1/p̂ for treatment observations and 1/(1-p̂) for control observations, where p̂ is generated from a logistic regression of treatment status on baseline demographics, sample design variables, and baseline test score deciles. 95% CIs are obtained by bootstrapping with replacement within randomization block. Data from the Mathematica Policy Research Teach For America Evaluation.

Table 2.

Quantile treatment effect estimates on math and reading post-test NCE scores, relative to all and veteran non-TFA teachers

	q = 10	q = 20	q = 30	q = 40	q = 50	q = 60	q = 70	q = 80	q = 90
TFA vs. all non-TFA teachers
Math post-test NCE T - C difference [95% CI]	1* [1, 4]	2* [1, 6]	1 [0, 4]	2 [0, 3]	2 [0, 4]	3* [2, 4]	5* [2, 5]	6* [4, 6]	5* [1, 7]
Reading post-test NCE T - C difference [95% CI]	−3 [−5, 0]	−2 [−4, 0]	−2 [−3, 1]	1 [0, 2]	2* [1, 3]	2 [0, 3]	1 [0, 3]	1 [−1, 1]	4* [1, 5]
TFA vs. veteran non-TFA teachers
Math post-test NCE T - C difference [95% CI]	1 [0, 4]	4* [1, 6]	2 [0, 3]	2 [0, 4]	2* [1, 3]	3* [2, 3]	4* [1, 5]	5* [3, 7]	6* [5, 7]
Reading post-test NCE T - C difference [95% CI]	−4* [−5, −2]	−2 [−4, 0]	−2 [−3, 0]	1 [0, 2]	1 [0, 2]	1 [0, 2]	1* [1, 2]	0 [−1, 1]	4* [3, 6]

95% confidence intervals reported in brackets.

^*p<0.05 two-tailed test

Figure 5 Panel B shows the QTE for spring reading scores. Here the QTE plot suggests some variation in the effect of TFA across the distribution, although for most of the distribution the confidence interval includes zero, precluding a conclusion that TFA teachers are more- or less-effective than non-TFA teachers. At the lower tail, the point estimates of the effect of TFA are negative, ranging from negative 2–4 NCE points. This effect is not statistically significant at the 5 percent level, although further analyses using 90 percent confidence intervals (not shown) suggest that at a few quantiles, there are significant negative differences at the ten percent level.¹³

In contrast, above the 40^th percentile the point estimates are positive, ranging from 2–4 NCE points. These differences are significant at the five percent level at a few percentiles, and there is further suggestive evidence of this pattern when using 90 percent confidence intervals. Comparisons between percentiles at the bottom and the top of the distribution also indicate significant differences between the effects of TFA on these portions of the distribution. However, at most percentiles of the distribution the two groups are similarly effective. Combined, this mix of small positive and negative point estimates, few of which are significantly different from zero, yields an average effect that is near zero and statistically insignificant.

In addition to comparing TFA teachers to all non-TFA teachers, it is also important to determine whether TFA performance is similar to that of veteran non-TFA teachers. The results shown in Figure 6 indicate that the pattern observed when comparing TFA teachers to all non-TFA teachers is more pronounced when TFA teachers are compared with non-TFA teachers who have more than three years of experience. The QTE graphs in reading and math have the same shape as in the full-sample comparisons. For math, the pattern is nearly identical, but the confidence intervals are tighter. In reading the negative point estimates at the bottom of the distribution, which were not significantly different at the five percent level when compared to all teachers, are statistically significant for half of the percentiles examined, as is the positive effect at the top of the distribution. Additional comparisons (not shown) relative to novice non-TFA teachers are less precise, given that the overwhelming majority of the comparison teachers are experienced, however the same general pattern of effects holds.

Figure 6. Inverse propensity score weighted quantile treatment effect of assignment to TFA classrooms on spring test scores, TFA vs. veteran non-TFA teachers only.

Notes: Panels A & B of figure show QTE for the effect of being assigned to a TFA classroom on math and reading Normal Curve Equivalent scores from the Iowa Test of Basic Skills in the spring following random assignment relative to veteran teachers. Estimates are weighted using inverse propensity score weights. Weights are 1/p̂ for treatment observations and 1/(1-p̂) for control observations, where p̂ is generated from a logistic regression of treatment status on baseline demographics, sample design variables, and baseline test score deciles. 95% CIs are obtained by bootstrapping with replacement within randomization block. Data from the Mathematica Policy Research Teach For America Evaluation. Veteran teachers have 4 or more years of experience.

To rule out some alternate explanations for the observed distributional variation in reading, I estimate a series of robustness analyses. One possibility is that a particular TFA region is driving the results, possibly due to variation in language arts curricula or instructional practices. Although the original Mathematica report suggests that the impacts were relatively similar across regions and that, “overall impacts were not attributable to any particular region, school, or grade” (p. xv), it is worth confirming that the same is true in terms of the impact of TFA on the distribution. Because the sample sizes in any one region are small and would produce noisy estimates at best, instead I estimate a series of six iterated models in which one region was dropped from the analysis each time. Across the post-test results for each of the six models, the shape of the quantile treatment effect graphs remained qualitatively consistent with the models including all six regions. These robustness models rule out regional and district differences as a potential mechanism driving these patterns of effects. It is not the case that teacher practices or curricula in a particular district lead to vastly different results across the distribution.

The negative effects of TFA at the bottom of the distribution relative to veterans could also be driven by differences in the language of the test administration, which was given in Spanish to some students. Perhaps surprisingly, fewer than 10 percent of students are tested in Spanish or are in bilingual classrooms, and many of these students have relatively high scores on both the reading and math posttests. Results are consistent with and without the inclusion of an indicator for pre-test administration in Spanish. This suggests that the language of the test administration is also not the cause of the variation in effects.

Discussion

This paper extends prior research on Teach For America by examining how student achievement in TFA and non-TFA classrooms differs across the distribution of achievement. It identifies variation in effects that was previously hidden by examining only average impacts of TFA, and missed by prior distributional work. The distributional findings reported here reveal different patterns for math and reading, which have important implications for how we understand the effects of TFA teachers. The pattern of effects indicating that TFA teachers are more effective than non-TFA teachers across the distribution in math is largely consistent with prior research on TFA (Antecol et al., 2013; Boyd et al., 2006; Glazerman et al., 2006; Kane et al., 2008; Ware et al., 2011; Xu et al., 2011; but see, Clark et al., 2015), and the finding that TFA teachers help boost scores at the top of the distribution while lowering achievement at the bottom, relative to veteran non-TFA teachers, provides nuance to previous null results in reading.

In math, students assigned to TFA teachers outperform control students throughout most of the distribution. The magnitude of the differences is striking: the largest TFA effect of 6 points corresponds to .28 SD of the nationally normed sample and .34 SD of the control group’s fall score.¹⁴ This finding suggests that TFA teachers, with minimal training, are more effective than counterfactual teachers both at pushing their highest-performing students forward and at supporting students with weak, developing math skills. This is consistent with the positive mean effects of TFA on math observed in Glazerman et al. (2006) and the distributional pattern identified by Antecol et al. (2013), and evinces a fairly wide-spread effectiveness of TFA teachers in math relative to same-school comparison teachers. This effect corresponds to approximately three months of instruction, falling somewhere between the .22 SD effect observed in the Tennessee STAR class size experiment (Krueger, 1999), and the .35 SD effect of KIPP schools (Angrist, Dynarski, Kane, Pathak, & Walters, 2010).

In contrast, the conclusions drawn about reading vary depending on whether TFA teachers are compared with all non-TFA teachers or veterans only. Compared with all non-TA teachers, there are relatively few statistically significant differences across the distribution between the two groups.¹⁵ In contrast, relative to veterans only, TFA teachers have a significant positive impact on the top of the reading distribution that is as large as .19 SD. However, TFA students at the bottom of the reading achievement distribution are scoring worse when compared with peers in classrooms with experienced teachers. The null mean effect for reading found in previous research thus appears to be concealing important distributional differences.

Although I am unable to test the mechanisms that produced these patterns, differences in content knowledge and pedagogical knowledge could produce the distributional differences in TFA’s effectiveness that I observe. It is perhaps not surprising that TFA teachers have a consistent impact across the distribution in math, given work indicating that TFA teachers have more coursework in mathematics related fields than their counterparts and particularly high scores on credentialing tests in STEM subjects (Decker et al., 2004a; Xu et al., 2011). This advantage in content knowledge should be examined as a possible source of TFA’s positive impacts across the distribution of mathematics in future work.

Given that TFA teachers have a more limited background in developing literacy and the issues facing struggling readers, it is perhaps also not surprising to find that they do worse than veteran counterparts among the lowest performing readers. Because most TFA teachers do not have a background in education, while most other elementary teachers have degrees or coursework in elementary education, including some coursework in elementary literacy, non-TFA teachers likely possess a greater understanding of developing literacy and the pedagogical content knowledge needed to teach struggling readers. While TFA teachers’ academic strengths make them relatively strong in math, they appear less-well equipped to work with students who are struggling to learn to read than veteran teachers. It seems consistent with previous work that TFA teachers would struggle with low-performing readers when compared with veterans, but not less experienced teachers. However, it is less clear why TFA teachers have positive effects on higher-performing readers relative to veterans. This suggests some alternative mechanism that differs somewhat from previous work.

In interpreting these findings, it is important to consider how the achievement distributions from this sample compare relative to the national achievement distributions in math and reading, and what this means for how TFA impacts equity. As Figure 2 highlights, although some students among this sample perform above the national average, the national mean represents approximately the 87^th percentile for this sample, while the mean score of this sample is nearly one standard deviation below the national average. In other words, the distribution of achievement represented in schools with TFA teachers is highly skewed and considerably lower than the national distribution of achievement. Given that students in TFA schools are largely concentrated within the bottom half of the national achievement distribution, the positive impacts TFA is having across the sample distribution in math, and among the higher-achieving students in reading are helping TFA students to draw closer to their more affluent peers. By helping students across the distribution of mathematics achievement represented in their schools, TFA is making progress towards accomplishing its goal of helping all of its students make academic gains (Kopp, 2011). In reading, TFA teachers are successful at helping to improve achievement for the higher-performing students in their classroom relative to veteran teachers, but they do not have the same impact on the lowest-performing students. It is also important to note that while the magnitude of the positive effects is meaningful and comparable to other highly successful educational interventions, even these relatively large effects are insufficient to close the gap with higher-income students.

Analogous to thinking about where in the national distribution students in TFA classrooms fall, there is some debate over which teachers TFA teachers should be compared with. Given work by Glazerman et al. (2013) underscoring the considerable challenges in convincing teachers to move from high SES schools to the lower-SES schools that TFA teachers work in, I compare TFA teachers only to other teachers in their same schools. This means that my results cannot speak to the relative effectiveness of TFA teachers compared with teachers in high SES neighborhoods and schools. Rather, I argue that the relevant comparison is whether students who had a TFA teacher would have been better off with the teacher who they would have otherwise received. While this is the most relevant comparison in assessing the effects of TFA teachers, by design this limits the ability to compare TFA teachers to teachers in schools and districts with no TFA presence.

With these caveats in mind, this study’s findings do have important implications for policy and for practitioners. The combination of the TFA selection and training model in place during the early 2000s was more effective than the available alternative for students across the distribution of elementary mathematics. Although this study does not examine TFA teacher practices specifically, these results suggest that there are some aspects of TFA training and teacher practice in elementary math that other certification programs and school personnel could learn from. Future work that draws from observations of TFA and non-TFA classrooms could illuminate specific aspect of TFA math teaching that differ across the two groups. In addition, elements of the TFA selection model that are useful for attracting and identifying candidates with strong math skills which may also be useful for other teacher preparation programs to incorporate into their selection processes.

In contrast, TFA teachers struggled with low-performing readers when compared with veteran teachers. For administrators employing TFA teachers, this suggests that additional supports for TFA teachers helping them to work with struggling readers may be beneficial, and assistance from veteran teachers in this area may be especially helpful. This also suggests that selective backgrounds and minimal training alone are insufficient for supporting low-performing readers, and that TFA should consider ways to address literacy instruction to support such students. Previous research uses the cutoff of the 34^th percentile of the national distribution (roughly the median for students in this sample) to help identify students at-risk of special education services (Woodward & Baxter, 1997). This suggests that many of the students who are underperforming in TFA classrooms might particularly benefit from targeted reading interventions requiring specialized training or experience, and administrators should think carefully about ways to support TFA teachers as they work with struggling readers in particular. Particular attention to the specific instructional practices and use of institutional resources that non-TFA teachers employ to support their lowest-performing readers also seems warranted. Future work examining how TFA and non-TFA classrooms differ in pedagogy, classroom organization, and targeted intervention might provide valuable insights into how teachers from different backgrounds can work together to meet the needs of underserved students.

Although these findings draw from data that reflect an earlier time period in TFA’s history, they still provide valuable insights about the impacts of TFA corps members on the distribution of student achievement. The data used in these analyses are the only publicly available, experimental data with which to examine this question. They thus represent the best opportunity to examine these relationships in a causal way. Future work would also benefit from an update of this work with administrative data that would allow for an examination of distributional patterns over time which could help to examine whether these effects are similar to patterns found among more recent cohorts.

It is also important to note that these findings diverge somewhat from the recent work of Clark et al. (2015) who find positive effects of TFA on reading scores in early grades (Pre-K – 2), but none in grades 3–5. This suggests that TFA’s effects on the distribution of achievement may be somewhat different in some earlier grades that are not included in the present study. As these data become publicly available, a replication of the findings in the present study with overlapping grade levels would be useful for considering the ways in which TFA’s effects on the distribution of achievement may have changed over time. As the TFA program continues to evolve and expand, these results provide causal evidence that TFA’s impact is consistently positive across the distribution in math, but varies across the distribution in reading in elementary school, which is the best evidence we have about TFA’s effects on the distribution of achievement in elementary school.

In sum, when evaluating TFA teachers by TFA’s own rubric—student achievement— these results suggest that both proponents and detractors are partially right: TFA clearly raises math scores throughout the distribution, while in reading it appears to raise scores for high achievers and lower scores for low achievers relative to veteran teachers. Thus, TFA does improve student achievement for some students in low-income schools in some subjects, but it –together with other teacher preparation programs and current teachers – must continue to refine selection, training models, pedagogy, and practice to meet this goal for all students.