Voltammetric Ion Selectivity of Thin Ionophore-Based Polymeric Membranes: Kinetic Effect of Ion Hydrophilicity

Abstract

The high ion selectivity of potentiometric and optical sensors based on ionophore-based polymeric membranes is thermodynamically limited. Here, we report that the voltammetric selectivity of thin ionophore-based polymeric membranes can be kinetically improved by several orders of magnitude in comparison with their thermodynamic selectivity. The kinetic improvement of voltammetric selectivity is evaluated quantitatively by newly introducing a voltammetric selectivity coefficient in addition to a thermodynamic selectivity coefficient. Experimentally, both voltammetric and thermodynamic selectivity coefficients are determined from cyclic voltammograms of excess amounts of analyte and interfering ions with respect to the amount of a Na⁺ or Li⁺-selective ionophore in thin polymeric membranes. We reveal the slower ionophore-facilitated transfer of a smaller alkaline earth metal cation with higher hydrophilicity across the membrane/water interface, thereby kinetically improving voltammetric Na⁺ selectivity against calcium, strontium, and barium ions by 3, 2, and 1 order of magnitude, respectively, in separate solutions. Remarkably, voltammetric Na⁺ and Li⁺ selectivity against calcium and magnesium ions in mixed solutions is improved by 4 and >7 orders of magnitude, respectively, owing to both thermodynamic and kinetic effects in comparison with thermodynamic selectivity in separate solutions. Advantageously, the simultaneous detection of sodium and calcium ions are enabled voltammetrically in contrast to the potentiometric and optical counterparts. Mechanistically, we propose a new hypothetical model that the slower transfer of a more hydrophilic ion is controlled by its partial dehydration during the formation of the adduct with a “water finger” prior to complexation with an ionophore at the membrane/water interface.

Graphical abstract

Ionophore-doped polymeric membranes have been widely used for potentiometric and optical sensors to yield the high ion selectivity based on ion-transfer and ion-complexation equilibria.^1–3 The potentiometric selectivity of an ionophore-based polymeric membrane has been quantitatively evaluated as a selectivity coefficient in separate or mixed solutions of analyte and interfering ions.⁴ Theoretically, a potentiometric selectivity coefficient is thermodynamically dictated by the overall equilibrium exchange of an analyte ion in the membrane with an interfering ion in the aqueous sample. Experimentally, the thermodynamic control of potentiometric selectivity is ensured by Nernstian responses to both analyte and interfering ions. Otherwise, potentiometric selectivity can be biased by the mass transport of analyte and interfering ions to the membrane/sample interface during their exchange, which is fast enough to achieve local equilibrium within the response time of a potentiometric sensor. In fact, thermodynamic ion selectivity can be determined from the optical response of a thin polymeric membrane doped with an ionophore and a chromoionophore, which is thin enough to be fully equilibrated with a sample solution.⁵

Recently, we demonstrated that the voltammetric response of an ionophore-based polymeric membrane^6,7 can be controlled not only thermodynamically, but also kinetically in contrast to the potentiometric and optical counterparts.⁸ Advantageously, cyclic voltammetry (CV) enabled us to quantitatively and separately assess the thermodynamics and kinetics of ionophore-facilitated ion transfer across the membrane/sample interface, where mass transport can be simulated^8–10 or neglected.^11,12 Specifically, we obtained kinetically limited CVs of silver, potassium, calcium, and lead ions with the corresponding ionophores to determine standard rate constants of 9.0 × 10⁻³–9.7 × 10⁻⁴.cm/s.⁸ Importantly, these rate constants support the electrochemical mechanism¹³ based on ion–ionophore complexation at the membrane/sample interface, which excludes the alternative electrochemical–chemical mechanism based on simple ion transfer¹⁴ followed by ion–ionophore complexation in the bulk membrane.¹⁵ Interestingly, a thermodynamically Ca²⁺-selective ionophore mediated the faster transfer of barium ion than calcium ion, which was ascribed to the faster formation of a 1:2 complex than a 1:3 complex of the respective ions.⁸

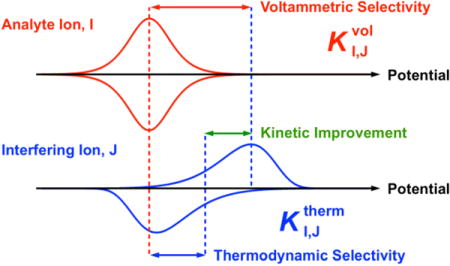
Herein, we demonstrate that the voltammetric ion selectivity of ionophore-doped polymeric membranes can be improved kinetically by several orders of magnitude in comparison with their thermodynamic selectivity as expected for the potentiometric and optical counterparts. Significantly, this work is the first to define and evaluate a voltammetric selectivity coefficient, $K_{\mathrm{I},\mathrm{J}}^{\mathrm{vol}}$, where ${\mathrm{I}}^{z_{\mathrm{I}}}$ and ${\mathrm{J}}^{{\mathrm{z}}_{\mathrm{J}}}$ represent analyte and interfering ions. We compare a voltammetric selectivity coefficient with the corresponding thermodynamic selectivity coefficient, $K_{\mathrm{I},\mathrm{J}}^{\mathrm{therm}}$, to quantitatively assess the kinetic improvement of voltammetric selectivity against thermodynamic selectivity. Conveniently, both voltammetric and thermodynamic selectivity coefficients are determined from CVs of thin ionophore-based polymeric membranes in the separate or mixed solution of an excess amount of a target ion with respect to the amount of an ionophore.^11,12 Advantageously, this approach not only eliminates mass-transport effects to simplify voltammetric theory, but also widens the potential window to observe the transfer of a highly discriminated ion, because only its salt is used as aqueous supporting electrolytes.

Experimentally, we find that the voltammetric Na⁺- or Li⁺-selectivity of ionophores 1–3 (Figure 1) is kinetically improved more against a smaller alkaline earth metal cation as a more hydrophilic interfering ion. Significantly, this work is the first to report the kinetic effect of ion hydrophilicity on ionophore-facilitated ion transfer in contrast to the well-known thermodynamic dependence of its formal potential on ion hydrophilicity.¹⁴ Specifically, Na⁺-selective ionophore 1^16,17 gives irreversible CVs of calcium, strontium, and barium ions in separate solutions to kinetically improve voltammetric selectivity by 3, 2, and 1 order of magnitude, respectively. Moreover, the voltammetric Na⁺ and Li⁺ selectivity of ionophore 2¹⁸ and 3¹⁹ is improved by 4 and >7 orders of magnitude against calcium and magnesium ions, respectively, in mixed solutions owing to both thermodynamic and kinetic effects in comparison with thermodynamic selectivity in separate solutions. Mechanistically, we propose that the slower transfer of a more hydrophilic ion is controlled by its partial dehydration upon its attachment to a “water finger” as predicted theoretically.^20–22

Figure 1.

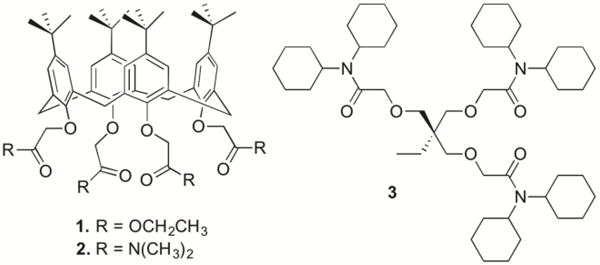
Structures of ionophores 1–3 used in this study.

THEORY

Global Model

Here, we define a global model to simulate CV of ion transfer facilitated by an ionophore doped in a thin polymeric membrane. We assume that an excess amount of an analyte or interfering ion is present in its separate aqueous solution so that the ion-transfer reaction can be treated as a first-order reaction, i.e.,

$$n_{\mathrm{X}}\mathrm{L}(\mathrm{m})\underset{k_{\mathrm{b},\mathrm{X}}}{\overset{k_{\mathrm{f},\mathrm{X}}}{\rightleftharpoons }}{\mathrm{L}}_{n_{\mathrm{X}}}{\mathrm{X}}^{z_{\mathrm{X}}}(\mathrm{m})$$ (1)

where an ion, ${\mathrm{X}}^{z_{\mathrm{X}}}(={\mathrm{I}}^{z_{\mathrm{I}}}{\mathrm{or J}}^{z_{\mathrm{j}}})$, forms 1:n_X (= n_I or n_J, respectively) complexes with an ionophore, L. This model considers the kinetics of facilitated ion transfer within a wide range from reversible cases to irreversible cases, whereas only reversible cases were considered in previous models.^11,12 The rate constants for forward and reverse reactions, k_f,X and k_b,X, respectively, are given by the Butler-Volmer type model⁸ to yield

$$k_{\mathrm{f,X}}=\frac{k_{\mathrm{X}}^0}{L_{\mathrm{T}}^{n_{\mathrm{X}}-1}}\exp \left[\frac{-{\alpha }_{\mathrm{X}}{z}_{\mathrm{X}}F\left({\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}\varphi -{\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LX}}^{0^{\prime }}\right)}{RT}\right]$$ (2)

$$k_{\mathrm{b,X}}=k_{\mathrm{X}}^0\exp \left[\frac{(1-{\alpha }_{\mathrm{X}})z_{\mathrm{X}}F\left({\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}\varphi -{\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LX}}^{0^{\prime }}\right)}{RT}\right]$$ (3)

where $k_{\mathrm{X}}^0$ is the standard ion-transfer rate constant, α_X is transfer coefficient (≈ 0.5 as determined experimentally⁸), L_T is the total concentration of the ionophore, ${\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}\varphi$ is the phase boundary potential across the membrane/water interface, and ${\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LX}}^{0^{\prime }}$ is the formal potential of facilitated ion transfer. Noticeably, $k_{\mathrm{X}}^0$ is conditional and is dependent on the aqueous concentration of the target ion, ${[{\mathrm{X}}^{z_{\mathrm{X}}}]}_{\mathrm{w}}$, and the total concentration of the ionophore as given by (see Supporting Information)

$$k_{\mathrm{X}}^0=k^0{L}_{\mathrm{T}}^{(1-\alpha )(n_{\mathrm{X}}-1)}{[{\mathrm{X}}^{z_{\mathrm{X}}}]}_{\mathrm{w}}^{(1-\alpha )}$$ (4)

where k⁰ is the concentration-independent standard rate constant. In addition, the formal potential is conditional as given by¹²

$${\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LX}}^{0^{\prime }}={\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{X}}^{0^{\prime }}+\frac{RT}{z_{\mathrm{X}}F}\ln {\beta }_{{\mathrm{n}}_{\mathrm{X}}}{L}_{\mathrm{T}}^{n_{\mathrm{X}}-1}{[{\mathrm{X}}^{z_{\mathrm{X}}}]}_{\mathrm{w}}$$ (5)

where ${\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{X}}^{0^{\prime }}$ is the formal potential of simple ion transfer that represents ion hydrophilicity,¹⁴ and ${\beta }_{n_{\mathrm{X}}}$ is an overall formation constant for the 1:n_X ion–ionophore complex in the membrane.

In thin-layer CV, the bulk concentration of any species is maintained near the interface without mass-transport effects, because the membrane is thin enough to uniformly deplete an ionophore and its complexes,^8–12 and because the aqueous phase contains an excess amount of an analyte or interfering ion.^11,12 Accordingly, the uniform membranous concentrations of an ionophore in its free and complexed forms, [L] and $[{\mathrm{L}}_{n_{\mathrm{X}}}{\mathrm{X}}^{z_{\mathrm{X}}}]$, respectively, as well as free ion, ${[{\mathrm{X}}^{z_{\mathrm{X}}}]}_{\mathrm{m}}$, are used to define the overall formation constant, i.e.,

$${\beta }_{n_{\mathrm{X}}}=\frac{[{\mathrm{L}}_{n_{\mathrm{X}}}{\mathrm{X}}^{z_{\mathrm{X}}}]}{{[\mathrm{L}]}^{n_{\mathrm{X}}}{[{\mathrm{X}}^{z_{\mathrm{X}}}]}_{\mathrm{m}}}$$ (6)

Similarly, the mass balance of the ionophore in the thin membrane is given by using the uniform membranous concentrations as

$${\mathrm{L}}_{\mathrm{T}}=[\mathrm{L}]+n_{\mathrm{X}}[{\mathrm{L}}_{n_{\mathrm{X}}}{\mathrm{I}}^{z_{\mathrm{X}}}]$$ (7)

The membrane composition depends on the phase boundary potential across the membrane/water interface, which is externally controlled to drive the interfacial transfer of a target ion. The resultant current response, i, is given by

$$\frac{i}{z_{\mathrm{X}}FA}=k_{\mathrm{f},\mathrm{X}}{[\mathrm{L}]}^{n_{\mathrm{X}}}-k_{\mathrm{b},\mathrm{X}}[{\mathrm{L}}_{n_{\mathrm{X}}}{\mathrm{X}}^{z_{\mathrm{X}}}]$$ (8)

where A is the area of the membrane phase. Moreover, the Faraday’s law yields

$$\frac{{\displaystyle {\int }_0^{t_{\mathrm{s}}}\mathit{idt}}}{z_{\mathrm{X}}\mathit{FAl}}=[{\mathrm{L}}_{n_{\mathrm{X}}}{\mathrm{X}}^{z_{\mathrm{X}}}]$$ (9)

during the forward potential sweep, and

$$\frac{{\displaystyle {\int }_{t_{\mathrm{s}}}^{t_{\mathrm{f}}}\mathit{idt}}}{z_{\mathrm{X}}\mathit{FAl}}=[{\mathrm{L}}_{n_{\mathrm{X}}}{\mathrm{X}}^{z_{\mathrm{X}}}]-\frac{L_{\mathrm{T}}}{n_{\mathrm{X}}}$$ (10)

during the reverse potential sweep, where l is the membrane thickness, and t_s and t_f are times at switching and final potentials during the potential cycle.

Eqs 6–8 are combined with eq 9 or 10 and solved numerically by using Mathematica 10 (Wolfram Research, Champaign, IL) with dimensionless parameters (see Supporting Information) to calculate the dimensionless current, I, as given by

$$I=\frac{\mathit{iRT}}{F^2{\mathit{AlvL}}_{\mathrm{T}}}$$ (11)

where v is the sweep rate of the phase boundary potential. A positive current response based on the ionophore-facilitated transfer of an aqueous cation is obtained during the forward sweep of the phase boundary potential from an initial potential to a more negative switching potential.

Local Model

In addition, we develop a local model to obtain analytical expressions for peak currents and peak potentials in irreversible cases (see Supporting Information). Peak potentials for forward and reverse potential sweeps, ${\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{pf,X}}^{\mathrm{irr}}$ and ${\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{pr,X}}^{\mathrm{irr}}$, respectively, are given by

$${\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{pf,X}}^{\mathrm{irr}}={\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LX}}^{0^{\prime }}+\frac{RT}{{\alpha }_{\mathrm{X}}{z}_{\mathrm{X}}F}\ln \frac{K_{\mathrm{X}}^0{n}_{\mathrm{X}}}{{\alpha }_{\mathrm{X}}}$$ (12)

$${\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{pr,X}}^{\mathrm{irr}}={\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LX}}^{0^{\prime }}-\frac{RT}{\left(1-{\alpha }_{\mathrm{X}}\right)z_{\mathrm{X}}F}\ln \frac{K_{\mathrm{X}}^0}{\left(1-{\alpha }_{\mathrm{X}}\right)}$$ (13)

where $K_{\mathrm{X}}^0$ is the dimensionless standard rate constant defined by

$$K_{\mathrm{X}}^0=\frac{k_{\mathrm{X}}^{0}RT}{z_{\mathrm{X}}\mathit{Fvl}}$$ (14)

Importantly, the average of forward and reverse peak potentials is equivalent to the formal potential when n_X = 1 (and α_X = 0.5 for kinetically controlled CVs), which is shown for irreversible cases by using eqs 12 and 13 to yield

$${\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LX}}^{0^{\prime }}=\frac{{\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{pf,X}}^{\mathrm{irr}}+{\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{pr,X}}^{\mathrm{irr}}}{2}-\frac{RT}{z_{\mathrm{X}}F}\ln {\left(\frac{K_{\mathrm{X}}^0{n}_{\mathrm{X}}}{{\alpha }_{\mathrm{X}}}\right)}^{{\alpha }_{\mathrm{X}}}{\left(\frac{1-{\alpha }_{\mathrm{X}}}{K_{\mathrm{X}}^0}\right)}^{1-{\alpha }_{\mathrm{X}}}$$ (15)

The forward peak current of an irreversible reaction depends on complexation stoichiometry and is given in the dimensionless form, $I_{\mathrm{pf},\mathrm{X}}^{\mathrm{irr}}$, with n_X = 1 by

$$I_{\mathrm{pf,X}}^{\mathrm{irr}}=\frac{{\alpha }_{\mathrm{X}}{z}_{\mathrm{X}}^2}{e}$$ (16)

When n_X = 2 or greater, the dimensionless forward peak current is given by

$$I_{\mathrm{pf,X}}^{\mathrm{irr}}=\frac{{\alpha }_{\mathrm{X}}{z}_{\mathrm{X}}^2}{n_{\mathrm{X}}^{(2n_{\mathrm{X}}-1)/(n_{\mathrm{X}}-1)}}$$ (17)

By contrast, the reverse peak current is given in the dimensionless form, $I_{\mathrm{pr},\mathrm{X}}^{\mathrm{irr}}$, for any complexation stoichiometry by

$$I_{\mathrm{pr,X}}^{\mathrm{irr}}=-\frac{\left(1-{\alpha }_{\mathrm{X}}\right)z_{\mathrm{X}}^2}{e{n}_{\mathrm{X}}}$$ (18)

We ensure that peak currents and peak potentials of the local model agree with those of the global model (see below).

Effect of Ion-Transfer Kinetics

We apply the global model to demonstrate the kinetic effect on thin-layer CVs of a target ion with z_X = +1 and n_X = 1 by systematically changing $K_{\mathrm{I}}^0$ from 10⁻³ to 10² (Figure 2A). CVs with $K_{\mathrm{X}}^0={10}^2$ and 10 overlap with each other, which corresponds to reversible cases. In fact, a reversible reaction with n_I = 1 yields dimensionless peak currents of 0.25 for both forward and reverse sweeps and the corresponding peak potentials that are very close to the formal potential, ${\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LX}}^{0^{\prime }}$.¹¹ By contrast, voltammetric peaks during forward and reverse potential sweeps shift toward more negative and positive potentials, respectively, as $K_{\mathrm{X}}^0$ decreases to 1 and lower values. Specifically, CVs with $K_{\mathrm{X}}^0=1$ and 10⁻¹ are quasi-reversible, where peak potentials are still close to the formal potential and peak currents are lowered with a lower $K_{\mathrm{X}}^0$ value. Irreversible voltammograms are obtained with $K_{\mathrm{X}}^0={10}^{-2}$ and 10⁻³, where normalized peak currents of 0.18 are independent of $K_{\mathrm{X}}^0$ as expected from eqs 16 and 18 with α_X = 0.5.

Figure 2.

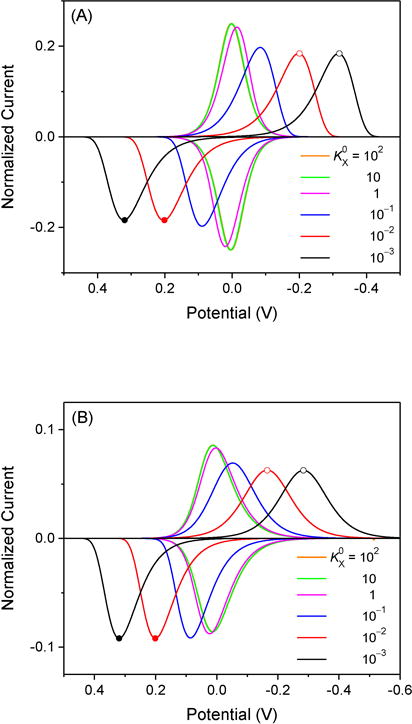
Thin-layer CVs simulated with n_X = (A) 1 and (B) 2 in addition to z_X = +1 and α_X = 0.5. The potential is defined against the formal potential, ${\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LX}}^{0^{\prime }}$. Open circles correspond to peak potentials based on eq 12 and peak currents based on eqs (A) 16 or (B) 17. Closed circles correspond to peak potentials and currents based on eqs 13 and 18, respectively.

Noticeably, the forward (or reverse) peak of quasi-reversible and irreversible CVs is asymmetric with respect to the peak potential, whereas the symmetric peak of a reversible voltammogram is expected with n_I = 1.¹¹ Specifically, the forward (or reverse) peak of a kinetically controlled CV with n_I = 1 is broader at the positive (or negative) side of the peak potential. This asymmetry contrasts to the asymmetric forward (or reverse) peak of a reversible voltammogram with n_I = 2 or greater, which is broader at the negative (or positive) side of the peak potential.¹¹

Effect of Complexation Stoichiometry

We employed the global model to find that complexation stoichiometry can be determined from its distinct effects on forward and reverse peak currents of a kinetically limited CV. When n_X = 2 (Figure 2B) or greater, the forward wave of a slower reaction with lower $K_{\mathrm{X}}^0$ becomes lower and, subsequently, broader to become more symmetric with respect to the peak potential. By contrast, the reverse wave of a slower reaction becomes higher, whereas its asymmetric peak shape is maintained. Accordingly, complexation stoichiometry can be estimated from the ratio of the reverse peak current with respect to the forward peak current, which is given for irreversible cases with n_X ≥ 2 by eqs 17 and 18 as

$$\left|\frac{I_{\mathrm{pr,X}}^{\mathrm{irr}}}{I_{\mathrm{pf,X}}^{\mathrm{irr}}}\right|=\frac{\left(1-{\alpha }_{\mathrm{X}}\right)n_{\mathrm{X}}^{n_{\mathrm{X}}/(n_{\mathrm{X}}-1)}}{{\alpha }_{\mathrm{X}}e}$$ (19)

Eq 19 with α_X = 0.5 yields a peak current ratio of 4/e for n_X = 2 and a higher ratio for higher stoichiometry. By contrast, the reverse peak current is identical to the forward peak current when n_X = 1 (see Figure 2A and also compare eq 16 with eq 18).

Noticeably, it is anomalous that the reverse peak current of a kinetically limited wave with n_X ≥ 2 is higher than that of a reversible wave (Figure 2B). This anomalous behavior is due to the lowered peak current of a reversible wave with n_X ≥ 2, which is broadened at the negative side of the peak potential¹¹ (see orange and green lines in Figure 2B). In fact, the local model predicts that the peak current of an irreversible reverse wave varies inversely with complexation stoichiometry (eq 18), but becomes higher than that of a reversible wave, which varies inversely with $n_{\mathrm{X}}{(\sqrt{n_{\mathrm{X}}}+1)}^2$.¹¹

EXPERIMENTAL SECTION

Chemicals

Sodium ionophore X^16,17 (1), tert-butylcalix[4]arene-tetrakis(N,N-dimethylacetamide) (2), lithium ionophore VIII (3; N,N,N′,N′,N″,N″-hexacyclohexyl-4,4′,4″-propylidynetris(3-oxabutyramide)), tetradodecylammonium (TDDA) bromide, PVC (high molecular weight), and 2-nitrophenyl octyl ether (oNPOE) were obtained from Aldrich (Milwaukee, WI). Potassium tetrakis(pentafluorophenyl)borate (TFAB) was purchased from Boulder Scientific Company (Mead, CO). All reagents were used as received. TDDATFAB was prepared by metathesis²³ and used as organic supporting electrolytes in PVC membranes. All sample solutions were prepared by using ultrapure water (18.2 MΩ·cm and TOC of 3 ppb) from the Milli-Q Advantage A10 system and Elix 3 Advantage (EMD Millipore, Billerica, MA).¹⁰

Electrode Modification

A bare 5 mm-diameter gold disk was cleaned, electrochemically modified with an oxidatively doped film of decyl-substituted poly(3,4-ethylenedioxythiophene) (PEDOT-C₁₀), and spin-coated with a thin plasticized PVC membrane as reported elsewhere.¹¹ A 2 μL THF solution of membrane components (ionophore, 4.0 mg PVC, 16.0 mg oNPOE, and 2.2 mg TDDATFAB in 1 mL THF) contained a low PVC content to ensures a negligible ohmic potential drop across the spin-coated membrane.²⁴ An amount of an ionophore in the THF solution was selected to yield an ionophore concentration of 5.0 mM, otherwise mentioned, in the PVC membrane with a density of 1 g/mL.

Electrochemical Measurement

Electrochemical workstations (CHI 600A and 660B, CH Instruments, Austin, TX) were used for voltammetric measurements. A Pt-wire counter electrode was employed in the following three-electrode cell

$$\mathrm{Ag}\left|\mathrm{AgCl}\right|3\mathrm{ M KCl}\left|\mathrm{sample solution}\right|\mathrm{PVC membrane}\left|{\mathrm{PEDOT}-\mathrm{C}}_{10}\right|\mathrm{Au}$$ (cell 1)

The compositions of sample solutions are given in figure captions. The positive current is carried by the transfer of a cation from the aqueous phase to the PVC membrane. A peak potential was determined from the first derivative of a voltammogram.²⁵ All electrochemical experiments were performed at 22 ± 3 °C.

RESULTS AND DISCUSSIONS

Voltammetric and Thermodynamic Selectivity Coefficients

We determine a voltammetric selectivity coefficient, $K_{\mathrm{I},\mathrm{J}}^{\mathrm{vol}}$, of a thin ionophore-based polymeric membrane for an analyte ion against an interfering ion to quantitatively estimate its kinetic improvement against the corresponding thermodynamic selectivity coefficient, $K_{\mathrm{I},\mathrm{J}}^{\mathrm{therm}}$. We can deduce from the results of the Theory section that the thermodynamic stability of ionophore complexes of analyte and interfering ions, i.e., ${\beta }_{n_{\mathrm{I}}}$ and ${\beta }_{n_{\mathrm{J}}}$, respectively, affect both voltammetric and thermodynamic selectivity. In addition, the kinetics of ionophore facilitated transfer of analyte and interfering ions, i.e., $k_{\mathrm{I}}^0$ and $k_{\mathrm{J}}^0$, respectively, contributes to voltammetric selectivity.

In this work, we apply the formula of a potentiometric selectivity coefficient⁴ to define the voltammetric counterpart by using forward peak potentials of thin-layer CV for analyte and interfering ions as

$$\log K_{\mathrm{I},\mathrm{J}}^{\mathrm{vol}}=\frac{z_{\mathrm{I}}F({\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{pf,J}}-{\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{pf,I}})}{2.303RT}$$ (20)

where ${\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{pf,I}}$ and ${\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{pf,J}}$ are the corresponding phase boundary potentials for the respective ions. We employ separate or mixed solutions containing excess amounts of analyte and interfering ions with respect to the amount of an ionophore in a thin membrane. Theoretically, a forward peak potential is obtained analytically for reversible^11,12 and irreversible (eq 12) cases and numerically for any reversibility (see Theory section). By contrast, forward peak potentials in eq 20 are replaced with formal potentials of ionophore-facilitated transfer, i.e., ${\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LI}}^{0^{\prime }}$ and ${\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LJ}}^{0^{\prime }}$, to define a thermodynamic selectivity coefficient as

$$\log K_{\mathrm{I},\mathrm{J}}^{\mathrm{therm}}=\frac{z_{\mathrm{I}}F({\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LJ}}^{0^{\prime }}-{\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LI}}^{0^{\prime }})}{2.303RT}$$ (21)

A formal potential is obtained from the average of forward and reverse peak potentials of thin-layer CV in this study, where n_I = n_J = 1 and α_X = 0.5 (see eq 15 for irreversible cases).

Experimentally, thin-layer CV is obtained by using a double-polymer-modified electrode,²⁶ where an ~1.5 μm-thick PVC membrane is doped with an ionophore and spin-coated onto a gold electrode modified with the oxidized form of a conducting polymer membrane, PEDOT-C₁₀, as an efficient voltammetric ion-to-electron transducer for aqueous cations.^8–11,27 The plasticized PVC membrane also contains hydrophobic supporting electrolytes, TDDATFAB, to obtain negligibly small ohmic potential drop across the thin membrane.

Thermodynamic Control of Voltammetric Selectivity

The voltammetric Na⁺ selectivity of a thin oNPOE/PVC membrane doped with ionophore 1^16,17 was controlled thermodynamically against potassium and lithium ions as confirmed by reversible thin-layer CVs with small separations between forward and reverse peak potentials (Figure 3). Qualitatively, voltammetric selectivity is higher for a more positive forward peak potential to follow the order of Na⁺ > K⁺ > Li⁺, which is consistent with the potentiometric ion selectivity of ionophore 1 as discussed below. Quantitatively, voltammetric selectivity coefficients were determined by using eq 20 based on forward peak potentials (Table 1). A voltammetric selectivity coefficient was nearly identical to the corresponding thermodynamic selectivity coefficient as determined by using eq 21 based on formal potentials, i.e., $\log (K_{\mathrm{Na,J}}^{\mathrm{vol}}/K_{\mathrm{Na,J}}^{\mathrm{therm}})\approx 0$. A formal potential was equivalent to the average of forward and reverse peak potentials of a reversible thin-layer CV (dashed lines in Figure 3) when an ionophore forms a 1:1 complex with a target ion.¹² The formation of a 1:1 complex with ionophore 1 was ensured for sodium ion from the symmetric peak shape of its CV¹¹ as well as lithium and potassium ions, which yielded similarly high peak currents in comparison with sodium ion (Figure 3).¹² Overall, both voltammetric and thermodynamic selectivity coefficients confirm that the Na⁺ selectivity of ionophore 1 is ~10 times higher against lithium ion than potassium ion. The superior selectivity against lithium ion is due to its hydrophilicity as confirmed by the requirement of more negative potentials to yield the current response based on simple Li⁺ transfer (<−0.5 V in Figure 3C) than simple K⁺ transfer (<−0.3 V in Figure 3B).

Figure 3.

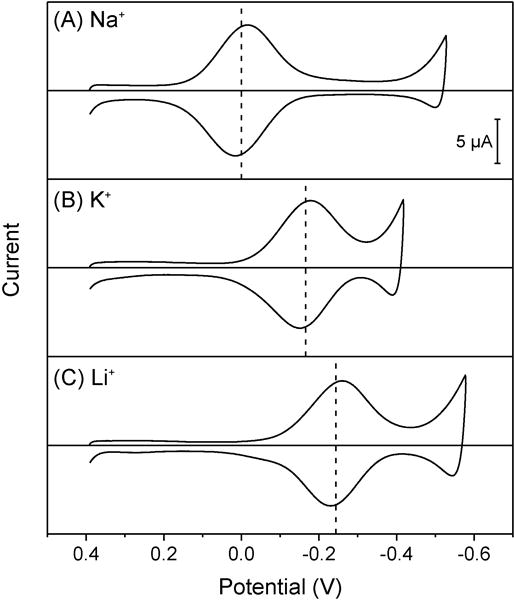
Thin-layer CVs of oNPOE/PVC membranes doped with 5 mM ionophore 1 in solutions of 5 mM (A) sodium, (B) potassium, and (C) lithium acetate. Potential sweep rate, 0.1 V/s. The potential is defined against the formal potential of sodium ion. Dashed lines represent average peak potentials.

Table 1.

Na⁺ Selectivity Coefficients of Ionophore 1

${\mathrm{J}}^{z_{\mathrm{J}}}$	$\log K_{\mathrm{Na},\mathrm{J}}^{\mathrm{vol}}$	$\log K_{\mathrm{Na},\mathrm{J}}^{\mathrm{therm}}$	$\log (K_{\mathrm{Na},\mathrm{J}}^{\mathrm{vol}}/K_{\mathrm{Na},\mathrm{J}}^{\mathrm{therm}})$
Li+a	−4.13 ± 0.04	−4.13 ± 0.02	0.00 ± 0.05
K+b	−2.9 ± 0.3	−2.9 ± 0.2	0.0 ± 0.4
Ca2+c	−8.1 ± 0.2	−5.0 ± 0.2	−3.1 ± 0.3
Sr2+c	−8.10 ± 0.05	−6.19 ± 0.09	−1.9 ± 0.1
Ba2+c	−7.70 ± 0.09	−6.89 ± 0.06	−0.8 ± 0.1

^aN = 4.

^bN = 6.

^cN = 4.

Advantageously, our voltammetric approach with an analyte-free ionophore-doped membrane allows for the determination of a thermodynamic selectivity coefficient without the bias caused by mass transport of analyte and interfering ions during their exchange across the membrane/sample interface. We speculate that potentiometric selectivity coefficients, $K_{\mathrm{I},\mathrm{J}}^{\mathrm{pot}}$, of oNPOE/PVC membranes doped with ionophore 1 ( $\log K_{\mathrm{Na,Li}}^{\mathrm{pot}}=-2.5$^16,17 and $\log K_{\mathrm{Na,K}}^{\mathrm{pot}}=-1.9$¹⁶ and −2.0¹⁷) are biased and, subsequently, inferior to the thermodynamic selectivity coefficients determined by thin-layer CV in this work. Theoretically, an unbiased equilibrium potentiometric selectivity coefficient²⁸ is equivalent to the thermodynamic selectivity coefficient based on eq 21 when z_I = z_J and ${[{\mathrm{I}}^{z_{\mathrm{I}}}]}_{\mathrm{w}}={[{\mathrm{J}}^{z_{\mathrm{J}}}]}_{\mathrm{w}}$ (see eq S-28).

Kinetic Improvement of Voltammetric Selectivity

The voltammetric Na⁺ selectivity of ionophore 1 was dramatically improved kinetically against alkaline earth metal cations, which yielded totally irreversible thin-layer CVs with wide separations between forward and reverse peak potentials (Figure 4). A peak separation was wider for a smaller cation to follow the order of Ca²⁺ > Sr²⁺ > Ba²⁺, which indicates that the transfer of a more hydrophilic ion was slower. By contrast, the transfer of a smaller cation was thermodynamically more favorable, because the formal potential (dashed lines in Figure 4) followed the order of Ca²⁺ > Sr²⁺ > Ba²⁺, which indicates that a more hydrophilic ion bound to ionophore 1 more strongly. In this assessment, the formal potential was equivalent to the average of forward and reverse peak potentials of an irreversible CV (eq 15), because ionophore 1 forms 1:1 complexes with calcium, strontium, and barium ions as confirmed by relatively similar forward and reverse peak currents (Figure 4). By contrast, the reverse peak current of an irreversible thin-layer CV is higher than its forward peak current with n_X = 2 (Figure 2B) or greater to yield a peak current ratio of 4/e or higher as given by eq 19 with α_X = 0.5.

Figure 4.

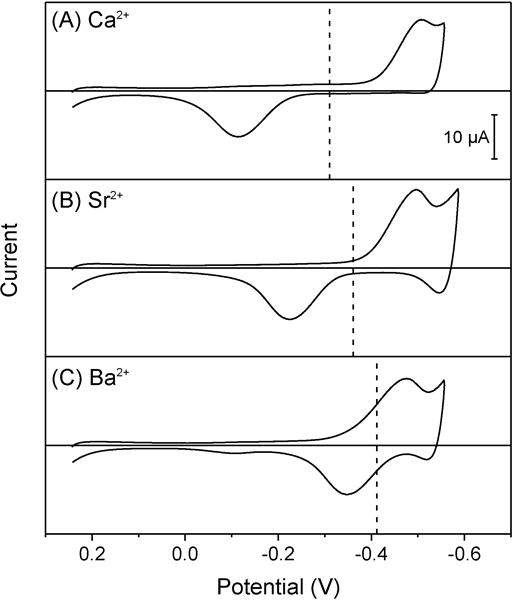
Thin-layer CVs of oNPOE/PVC membranes doped with 5 mM ionophore 1 in solutions of 5 mM (A) calcium, (B) strontium, and (C) barium acetate. The potential is defined against the formal potential of sodium ion. Potential sweep rate, 0.1 V/s. Dashed lines represent average peak potentials.

More quantitatively, we evaluated voltammetric and thermodynamic selectivity coefficients of ionophore 1 for sodium ion against calcium, strontium, and barium ions (Table 1) to reveal that voltammetric selectivity was kinetically improved by 1–3 orders of magnitude against thermodynamic selectivity as represented by $\log (K_{\mathrm{Na,J}}^{\mathrm{vol}}/K_{\mathrm{Na,J}}^{\mathrm{therm}})$. The kinetic improvement of voltammetric selectivity is theoretically given for a reversible analyte ion against an irreversible interfering ion with n_I = n_J = 1 by (see Supporting Information)

$$\log \left(\frac{K_{\mathrm{I},\mathrm{J}}^{\mathrm{vol}}}{K_{\mathrm{I},\mathrm{J}}^{\mathrm{therm}}}\right)=\frac{z_{\mathrm{I}}}{z_{\mathrm{J}}{\alpha }_{\mathrm{J}}}\log \left(\frac{K_{\mathrm{J}}^0}{{\alpha }_{\mathrm{J}}}\right)$$ (22)

Eq 22 indicates that a more negative $\log (K_{\mathrm{Na,J}}^{\mathrm{vol}}/K_{\mathrm{Na,J}}^{\mathrm{therm}})$ value for a smaller and more hydrophilic interfering ion corresponds to its slower transfer with a lower $K_{\mathrm{J}}^0$ value. Quantitatively, $K_{\mathrm{J}}^0$ values were obtained by using eq 22 with a typical α_J value of 0.5⁸ and converted to $k_{\mathrm{J}}^0$ values of (3 ± 2) × 10⁻⁷, (5 ± 1) × 10⁻⁶, and (6 ± 1) × 10⁻⁵ cm/s for calcium, strontium, and barium ions, respectively, by using eq 14 with an effective membrane thickness of 1.5 μm and a potential sweep rate of 0.065 V/s. The effective potential sweep rate was slower than an actual potential sweep rate of 0.1 V/s owing to the polarization of the PEDOT-C₁₀ membrane.¹¹

Improvement of Voltammetric Selectivity in Mixed Solution

We investigated Na⁺-selective ionophore 2¹⁸ by thin-layer CV to demonstrate that its voltammetric selectivity against calcium ion is enhanced not only kinetically in separate solutions, but also further both thermodynamically and kinetically in mixed solutions. In separate solutions, oNPOE/PVC membranes doped with ionophore 2 gave nearly reversible thin-layer CVs for sodium ion (Figure 5A), whereas nearly irreversible CVs with wide peak separations were obtained for calcium ion despite relatively similar formal potentials for both ions (dashed line in Figure 5B). These CVs yielded $\log K_{\mathrm{Na,Ca}}^{\mathrm{vol}}=-1.97\pm 0.06$ and $\log K_{\mathrm{Na,Ca}}^{\mathrm{therm}}=-0.88\pm 0.05(N=8)$. Subsequently, $\log (K_{\mathrm{Na,Ca}}^{\mathrm{vol}}/K_{\mathrm{Na,Ca}}^{\mathrm{therm}})$ values of −1.08 ± 0.08 indicate that voltammetric selectivity was kinetically improved by a factor of 12 in comparison with thermodynamic selectivity. In this analysis, $\log K_{\mathrm{Na,Ca}}^{\mathrm{therm}}$ values were obtained by using averages of forward and reverse peak potentials as formals potential in eq 21, because ionophore 2 forms 1:1 complexes with calcium ion as confirmed by similar forward and reverse peak currents (Figure 5B) as well as sodium ion, which yielded peak currents that were similar to those of calcium ion in their mixed solutions¹² (Figure 5C). Noticeably, we found that ionophore 2 gave nearly reversible voltammograms to lithium, potassium, strontium, and barium ions (Figure S-1), which are less hydrophilic than calcium ion.²⁹

Figure 5.

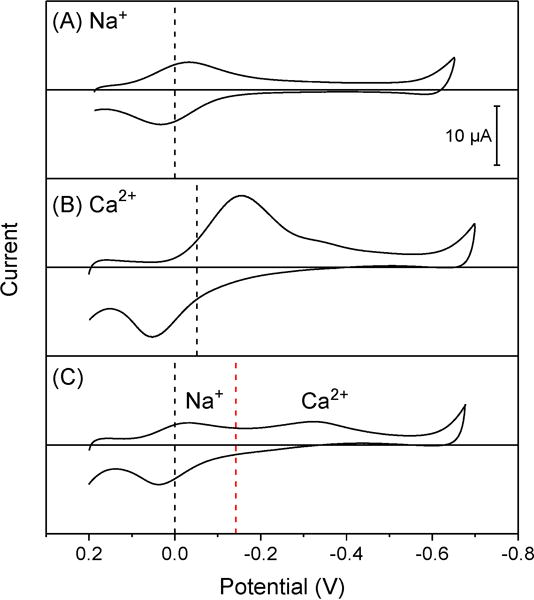
Thin-layer CVs of oNPOE/PVC membranes doped with 5 mM ionophore 2 in solutions of 5 mM acetate salts of (A) sodium ion, (B) calcium ion, and (C) sodium and calcium ions. Potential sweep rate, 0.1 V/s. The potential is defined against the formal potential of sodium ion. Dashed lines in part (A) and (B) represent average peak potentials, which are given for sodium and calcium ions by black and red dashed lines, respectively, in part (C).

A voltammetric Ca²⁺ response was observed at much more negative potentials in mixed solutions as represented by a forward peak potential of −0.32 V (Figure 5C) in comparison with that of −0.15 V in separate solutions (Figure 5B). The preceding Na⁺ response around 0 V in mixed solutions indicate that the following Ca²⁺ response was based on the voltammetric exchange of sodium ion in the membrane with calcium ion in the aqueous solution as given by¹²

$${\mathrm{LNa}}^{+}(\mathrm{m})+{\mathrm{Ca}}^{2+}(\mathrm{w})\rightleftharpoons {\mathrm{LCa}}^{2+}(\mathrm{m})+{\mathrm{Na}}^{+}(\mathrm{w})$$ (23)

By contrast, the reverse potential sweep yielded only a single voltammetric peak around 0 V, which is negative enough to drive not only the reverse reaction of eq 23, but also the dissociation of the resultant Na⁺ complex to yield

$${\mathrm{LCa}}^{2+}(\mathrm{m})+{\mathrm{Na}}^{+}(\mathrm{w})\to {\mathrm{LNa}}^{+}(\mathrm{m})+{\mathrm{Ca}}^{2+}(\mathrm{w})\to \mathrm{L}(\mathrm{m})+{\mathrm{Na}}^{+}(\mathrm{w})+{\mathrm{Ca}}^{2+}(\mathrm{w})$$ (24)

In fact, the reverse peak current based on the transfer of +2 charge per ionophore molecule (eq 24) is higher than the coupled forward peak current based on the transfer of +1 charge per ionophore molecule (eq 23). Overall, the voltammetric ion-exchange response to calcium ion is totally irreversible as indicated by a wide separation between forward and reverse peaks. The average of forward and reverse peak potentials (red dashed line in Figure 5C) is approximated to the formal potential, which is negatively shifted for the dissociation of a Na⁺ complex with respect to the formal potential of facilitated Ca²⁺ transfer by a free ionophore in separate solutions (dashed line in Figure 5B).

The kinetic improvement of voltammetric selectivity in mixed solutions was assessed quantitatively by using the corresponding voltammetric and thermodynamic selectivity coefficients. Forward peak potentials of Na⁺ and Ca²⁺ transfer in mixed solutions (Figure 5C) were used in eq 20 to yield $\log K_{\mathrm{Na,Ca}}^{\mathrm{vol}}=-5.6\pm 0.3(N=6)$. The corresponding $\log K_{\mathrm{Na,Ca}}^{\mathrm{therm}}$ values of −2.9 ± 0.3 were estimated by using averages of forward and reverse peak potentials (dashed lines) as formal potentials in eq 21. Subsequently, $\log (K_{\mathrm{Na,Ca}}^{\mathrm{vol}}/K_{\mathrm{Na,Ca}}^{\mathrm{therm}})$ values of −2.7 ± 0.4 in mixed solutions indicate that voltammetric selectivity was kinetically improved by a factor of 5.0 × 10² in comparison with thermodynamic selectivity. This kinetic improvement in mixed solutions is much more significant than in separate solutions, which indicates that the formation of a Ca²⁺ complex coupled with the dissociation of a Na⁺ complex in mixed solutions (eq 23) is much slower then the formation of a Ca²⁺ complex with a free ionophore in separate solutions. Overall, voltammetric selectivity in mixed solutions were improved both thermodynamically and kinetically by a factor of 5.2 × 10⁴ than thermodynamic selectivity in separate solutions (see above).

Kinetically Improved Selectivity of Non-Cyclic Ionophore

We found that voltammetric selectivity was improved kinetically not only by rigid cyclic ionophores 1 and 2 with slow ion-binding kinetics,^30,31 but also by flexible non-cyclic ionophore 3.¹⁹ These results suggest that the kinetics of facilitated ion transfer is not controlled by ion–ionophore complexation. Specifically, thin-layer CVs of oNPOE/PVC membranes doped with ionophore 3 were nearly reversible for lithium ion (Figure 6A) and nearly irreversible for magnesium ion (Figure 6B) in separate solutions. These CVs were used to obtain $\log K_{\mathrm{Li,Mg}}^{\mathrm{vol}}=-4.7\pm 0.3(N=7)$ from eq 20, whereas $\log K_{\mathrm{Li,Mg}}^{\mathrm{therm}}=-2.5\pm 0.5$ was determined from eq 21 using averages of peak potentials (black dashed lines) as formal potentials. Ionophore 3 forms 1:1 complexes not only with lithium ion,¹² but also with magnesium ion to yield similar forward and reverse peak currents (Figure 6B). The resultant $\log (K_{\mathrm{Li,Mg}}^{\mathrm{vol}}/K_{\mathrm{Li,Mg}}^{\mathrm{therm}})$ values of −2.2 ± 0.6 indicate that voltammetric selectivity was enhanced by a factor of ~160 in comparison with thermodynamic selectivity. Noticeably, less hydrophilic interfering ions, i.e., sodium, calcium, strontium, and barium ions,²⁹ yielded nearly reversible CVs (Figure S-2), whereas the binding of ionophore 3 with potassium ion was too weak to clearly resolve the resultant facilitated transfer from simple K⁺ transfer (data not shown).

Figure 6.

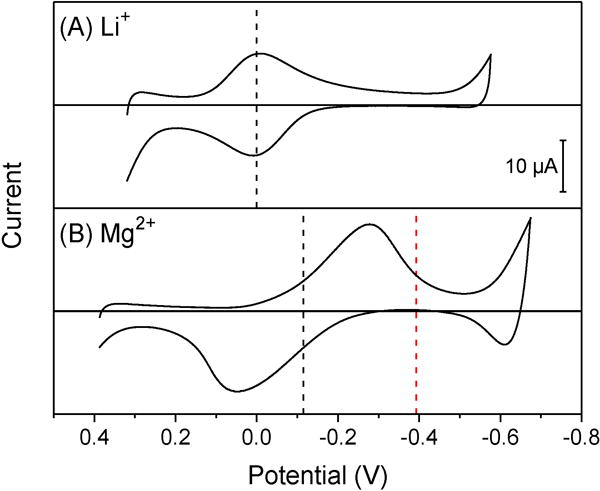
Thin-layer CVs of oNPOE/PVC membranes doped with 5 mM ionophore 3 in solutions of (A) 5 mM lithium acetate and (B) 5 mM magnesium acetate. The potential is defined against the formal potential of lithium ion. Potential sweep rate, 0.1 V/s. Black dashed lines represent average peak potentials. The red dashed line represents the potential of the thermodynamically shifted forward peak based on voltammetric Li⁺–Mg²⁺ exchange in mixed solutions of 5 mM acetate salts of lithium and magnesium ions.

A voltammetric response was observed only for lithium ion in its mixed solutions with magnesium ion (data not shown), because the voltammetric ion-exchange response to the latter was kinetically prevented. A voltammetric ion-exchange response to magnesium ion is expected for ionophore 3, which forms 1:1 complexes with both lithium and magnesium ions (see above) to yield¹²

$${\mathrm{LLi}}^{+}(\mathrm{m})+{\mathrm{Mg}}^{2+}(\mathrm{w})\rightleftharpoons {\mathrm{LMg}}^{2+}(\mathrm{m})+{\mathrm{Li}}^{+}(\mathrm{w})$$ (25)

Theoretically, the voltammogram based on eq 25 is shifted thermodynamically by ${\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LMg}}^{0^{\prime }}-{\mathrm{\Delta }}_{\mathrm{w}}^{\mathrm{m}}{\varphi }_{\mathrm{LLi}}^{0^{\prime }}$¹² in comparison with the corresponding voltammogram of facilitated Mg²⁺ transfer without lithium ion. Accordingly, the forward peak of the Mg²⁺ response based on the voltammetric ion-exchange mechanism is expected at the potential indicated by red dashed line in Figure 6B. The resultant forward peak potential is expected within the potential window, but was not observed experimentally, because voltammetric Li⁺–Mg²⁺ exchange (eq 25) was slower than the transfer of magnesium ion facilitated by a free ionophore (Figure 6B). Overall, the actual potential of the forward peak of the Mg²⁺ response in mixed solutions is <−0.6 V to yield $\log K_{\mathrm{Li,Mg}}^{\mathrm{vol}}$ < −10 in eq 20, which is improved by a factor of 3.2 × 10⁷ in comparison with thermodynamic selectivity in separate solutions (see above).

Kinetic Effect of Ion Hydrophilicity

Here, we propose a hypothetical mechanism based on the formation of a “water finger^20–22” (Figure 7) to explain the slower transfer of a smaller and more hydrophilic alkaline earth metal cation as the basis of the kinetic improvement of voltammetric selectivity. Specifically, we propose that an aqueous ion must be partially dehydrated to form the adduct with a water finger at the membrane side of the interface before complexation with an ionophore. This two-step model contrasts to the previously proposed mechanism based on the one-step formation and transfer of an ion–ionophore complex at the membrane/water interface.⁸ The rate-determining step of the two-step mechanism is likely the adduct formation, which is likely slower for a more strongly hydrated ion as observed experimentally. The kinetics of ion–ionophore complexation seems unimportant, because flexible non-cyclic ionophore 3 mediated the slow transfer of magnesium ion, which is strongly hydrated. Noticeably, this new model suggests that the facilitated transfer of barium ion was faster than that of calcium ion because of the higher hydrophilicity of the latter, which was previously ascribed to the formation of a Ca²⁺ complex with higher stoichiometry.⁸

Figure 7.

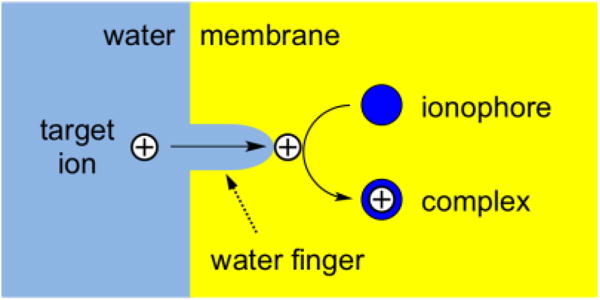
Scheme of the electrochemical mechanism based on the formation of the adduct of a target ion with a “water finger” followed by complexation with an ionophore.

CONCLUSIONS

In this work, we introduced the new concept of voltammetric ion selectivity for ionophore-based polymeric membranes to experimentally reveal its kinetic enhancement by several orders of magnitude in comparison with thermodynamic selectivity. Voltammetric ion selectivity is based on the convolution of thermodynamics and kinetics of ionophore-facilitated ion transfer at membrane/sample interfaces in contrast to the thermodynamically limited selectivity of the potentiometric and optical counterparts. Voltammetric selectivity can be improved not only kinetically in separate solutions of analyte and interfering ions, but also both thermodynamically and kinetically in their mixed solutions when an interfering ion yields a voltammetric response based on the ion-exchange mechanism.¹² Subsequently, ionophores that are not selective enough for potentiometric and optical applications may be sufficiently selective for voltammetric applications. Noticeably, voltammetric selectivity in real samples depends not only on the concentrations of analyte and interfering ions (see eqs 4 and 5), but also solution compositions including pH, neutral molecules, and macromolecules. For instance, the interfacial adsorption of lipids³² and proteins³³ results in slower ionophore-assisted ion transfer.

Experimentally, we took advantage of thin-layer CV at double-polymer-modified electrodes to determine both voltammetric and thermodynamic selectivity coefficients in the presence of excess amounts of analyte and interfering ions with respect to the amount of an ionophore. With this approach, voltammetric selectivity can be readily assessed theoretically without mass-transport effects and quantitatively determined experimentally without the need of additional aqueous supporting electrolytes, which limit the potential window to hide a voltammetric response to a highly discriminated ion. The elimination of mass-transport effects, however, requires slow potential sweep, which yielded reversible CVs for many interfering ions (see Figures 1, S-1, and S-2). Kinetic effects on voltammetric selectivity will be more important under higher mass-transport conditions, where an ionophore-doped membrane is thickened⁸ or rotated,^9,10 or an ionophore-based pipet electrode is used to form micro- and nano-interfaces.^6,7 The finite ion-transfer kinetics has been considered as a serious limitation of micropipet potentiometry.³⁴

Mechanistically, we found that the ionophore-facilitated transfer of a more hydrophilic interfering ion is slower to yield the larger kinetic improvement of voltammetric selectivity. Interestingly, this finding suggests that the rate-determining step of ionophore-facilitated ion transfer is the partial dehydration of a transferred ion for attachment to a “water finger^20–22” rather than interfacial complexation with an ionophore. This hypothetical mechanism implies that the electrochemical mechanism of ionophore-facilitated ion transfer involves not one step,^8,13 but at least two steps. In this study, interfering ions that form 1:1 complexes were studied to yield kinetically limited voltammograms without complication of different complexation stoichiometry between analyte and interfering ions as observed in the previous study.⁸ Importantly, we found that complexation stoichiometry can be determined from the ratio of the forward peak current with respect to the reverse peak current of kinetically limited thin-layer CV. This approach is complementary to the determination of complexation stoichiometry from reversible thin-layer CV in separate¹¹ and mixed¹² solutions.