Electrostatically Confined Monolayer Graphene Quantum Dots with Orbital and Valley Splittings

Abstract

The electrostatic confinement of massless charge carriers is hampered by Klein tunneling. Circumventing this problem in graphene mainly relies on carving out nanostructures or applying electric displacement fields to open a band gap in bilayer graphene. So far, these approaches suffer from edge disorder or insufficiently controlled localization of electrons. Here we realize an alternative strategy in monolayer graphene, by combining a homogeneous magnetic field and electrostatic confinement. Using the tip of a scanning tunneling microscope, we induce a confining potential in the Landau gaps of bulk graphene without the need for physical edges. Gating the localized states toward the Fermi energy leads to regular charging sequences with more than 40 Coulomb peaks exhibiting typical addition energies of 7–20 meV. Orbital splittings of 4–10 meV and a valley splitting of about 3 meV for the first orbital state can be deduced. These experimental observations are quantitatively reproduced by tight binding calculations, which include the interactions of the graphene with the aligned hexagonal boron nitride substrate. The demonstrated confinement approach appears suitable to create quantum dots with well-defined wave function properties beyond the reach of traditional techniques.

The charge carriers in graphene at low energies, described as massless Dirac quasiparticles,¹ are expected to feature long spin coherence times.²⁻⁵ Exploiting this property requires precise manipulation of individual Dirac electrons. Quantum dots (QDs) present an essential building block, yet providing tailored confinement in graphene has remained challenging. So far, e-beam lithography⁶ and various other techniques⁷⁻¹² have been used to design nanometer-sized devices. However, their performance lacks behind, for example, GaAs QDs,^13,14 as disordered sample edges of patterned graphene result in uncontrolled charge localization and scattering.^6,15−17 So far, no clear evidence for 4-fold degenerate charging sequences has been reported in transport measurements of tunable QDs. Moreover, failing to controllably lift graphene’s valley degeneracy renders spin qubits unfeasible.^2,18,19

In principle, bilayer graphene could improve the situation because an electric displacement field opens a band gap at regular AB stacking.²⁰ Indeed, electrostatically confined QDs in bilayer graphene exhibit Coulomb blockade,²¹⁻²³ yet controlling the spin or valley degree of freedom of an individual state has also not been demonstrated. Moreover, confinement is still prone to parasitic conduction channels due to residual disorder in the band gap or conducting channels along domain walls of AB- and BA-stacked areas.²⁴ Another approach exploits whispering gallery modes in electrostatically confined QDs²⁵⁻²⁷ but here the control of the wave functions by gates is difficult and dwell times are extremely short (<100 fs). On an even more intricate route, the tip of a scanning tunneling microscope (STM) is used to locally stretch a suspended monolayer graphene sheet.²⁸ The onset of charge quantization due to induced strain showcases confinement by pseudomagnetic fields. Adding a real magnetic field B leads to charging sequences with regular orbital but no valley splittings.²⁸ Creating multiple QDs in this fashion would require independent strain control for every QD on the suspended graphene. Thus, such an approach is barely scalable.

Landau quantization helps to overcome Klein tunneling by opening band gaps.²¹⁻²³ An elegant method to exploit this by combining a magnetic field and an electrostatic potential has been proposed theoretically.²⁹⁻³¹ Indeed, indications of such confinement have been found in metal contact-induced pnp junctions,³² graphene on SiO₂,^33,34 and a suspended graphene nanoribbon.³⁵ However, in these experiments the confinement potential was not tunable but was generated by electrostatic disorder.

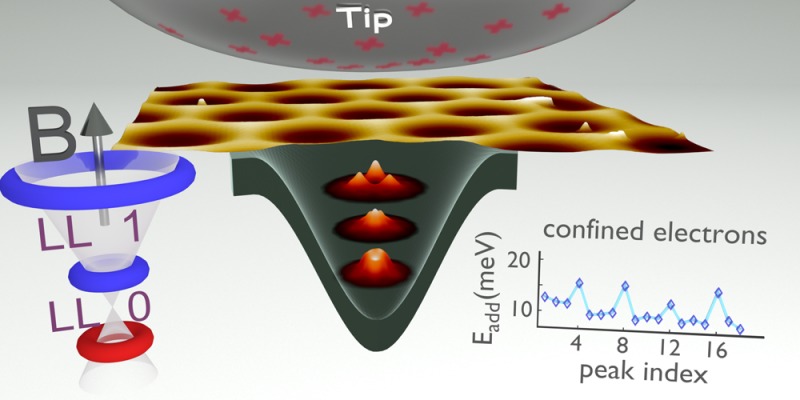
Here, we demonstrate controlled confinement by a combination of magnetic and electrostatic fields. We use the tip-induced electrostatic potential of an STM^36,37 in a B field perpendicular to the graphene plane (Figure 1a). Scanning tunneling spectroscopy (STS) reveals sequences of charging peaks by means of Coulomb staircases that appear when these confined states cross the Fermi energy E_F. The peaks systematically group in quadruplets for electrons and holes corresponding to the 4-fold (valley and spin) degeneracy in graphene (Figure 1c,d). Moreover, some quadruplets separate into doublets due to an additional valley splitting induced by the hexagonal boron nitride (BN) substrate. STS as a function of B reveals that the first confined states emerge from Landau levels (LLs) with indices ±1. A third-nearest neighbor tight binding (TB) calculation^38,39 reproduces the onset of charging events as a function of tip voltage V_tip and B as well as the magnitude of orbital and valley splittings.

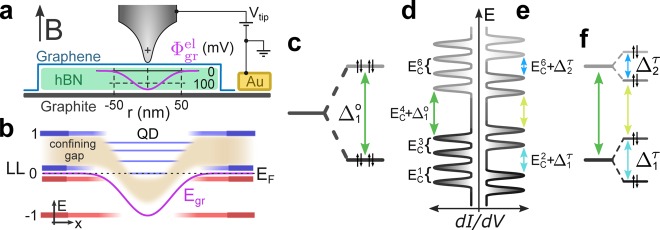
Figure 1.

(a) Sketch of the experiment. Graphene covers a 30 nm thick hexagonal boron nitride flake on graphite. The magenta line represents the tip-induced confinement potential of graphene Φ_gr^el for electrons, calculated as the numerical solution of Poisson’s equation (Supporting Information). (b) Energy diagram in real space: Fermi energy E_F, black dashed line; local band bending E_gr, magenta line; states belonging to electron (hole) LLs, blue (red); bulk LLs, 1, 0, −1. States embedded in the LL₀–LL₊₁ gap (thin blue lines) are electrostatically confined. (c) Energy level diagram for the first two orbital states of a graphene QD exhibiting an orbital splitting Δ₁. Both orbitals are 4-fold degenerate, as indicated by black arrows representing physical spin. (d,e) Charging peak sequence in the differential conductance dI/dV corresponding to the level diagrams in panels c and f, respectively. Charging peaks are separated by the addition energy E_addⁱ = E_C + Δ_i where E_Cⁱ ≈ E_C is the charging energy and Δ_i is comprised of Δ_j and/or the valley splittings Δ_k^τ. In panel d, quadruplet ordering showcases a dominant Δ₁, while Δ_k^τ become sizable in panel e, further separating quadruplets into doublets. (f) Same as panel c but including additional Δ_k. The spin splitting Δ^σ is neglected, as Δ^σ < Δ_k^τ, Δ_j, E_C in experiment.

We now sketch the principle of our experiment. A homogeneous, perpendicular B field condenses the electronic states of graphene into LLs at energies

1

where ν_F is the Fermi velocity and 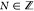is the LL index.¹ Consequently, energy gaps between the LLs emerge in the electronic spectrum. The smooth electrostatic potential Φ_gr^el (magenta line in Figure 1a) induced by the STM tip locally shifts the eigenenergies ε_i(Φ_gr) of charge carriers relative to the bulk LL energy (eq 1). Shifting ε_i into the Landau gaps creates confined states (Figure 1b).³⁰ The shape of Φ_gr^el determines the single-particle orbitals and energy levels, as in the case of artificial atoms.¹⁴ Orbital splittings Δ_j separate the energy levels (Figure 1c), which we deduce experimentally to be Δ_j^o = 4–10 meV (see below) and thus Δ_j is small compared to the first LL gap E₁ – E₀ ≈ 100 meV at 7 T. While pristine graphene exhibits a 4-fold degeneracy, varying stacking orders of graphene on top of BN induce an additional valley splitting Δ_k^τ, which turns out to be smaller than Δ_j in our experiment. The finite B field creates a small Zeeman splitting estimated as Δ^σ = gμ_BB ≈ 800 μeV at 7 T (g-factor of 2, μ_B: Bohr’s magneton). Accordingly, the orbital splittings separate quadruplets of near-degenerate QD states, which exhibit a subtle spin-valley substructure (Figure 1f).

We use the STM tip not only as source of the electrostatic potential and thus as gate for the QD states but also to sequence the energy level spectrum of the QD as the states cross E_F, that is, as the charge on the QD changes by ±e. This leads to a step in the tunneling current I(V_tip) and a corresponding charging peak in the differential conductance dI/dV_tip. In addition to the single particle energy spacings, every additional electron on the dot needs to overcome the electrostatic repulsion to the electrons already inside the QD,⁴⁰ given by the charging energy E_Cⁱ. Thus, we probe the total energetic separation of charge states i and i + 1, given by the addition energy E_add = E_Cⁱ + Δ_i, where Δ_i consists of Δ_j, Δ_k^τ, and/or Δ^σ. As we experimentally find E_C ≈ E_C ≈ 10 meV ≳ Δ_j^o (nearly independent of the charge state i, see below), the quadruplet near-degeneracy of the QD states translates to quadruplet ordering of the charging peaks (Figure 1d). Whenever either Δ_k or Δ^σ significantly exceeds the other and temperature, quadruplets separate into doublets (Figure 1e).

We prepare our sample (see Figure 1a and Supporting Information) by dry-transferring^41,42 a graphene flake onto BN.⁴³⁻⁴⁵ During this step, we align both crystal lattices with a precision better than 1° (Supporting Information). Then we place this graphene/BN stack on a large graphite flake to avoid insulating areas and simplify navigating the STM tip. Any disorder potential present in the sample will limit the confinement as long as it is larger than the Landau level gaps, thus larger gaps (e.g., the LL₀–LL_±1 gap) result in improved confinement. Moreover, the induced band bending will only be well-defined if the disorder potential is smaller than the maximum of Φ_gr^el. By using the dry-transfer technique^41,42 and a graphite/BN substrate we reduce disorder in the graphene significantly.⁴⁶⁻⁴⁸

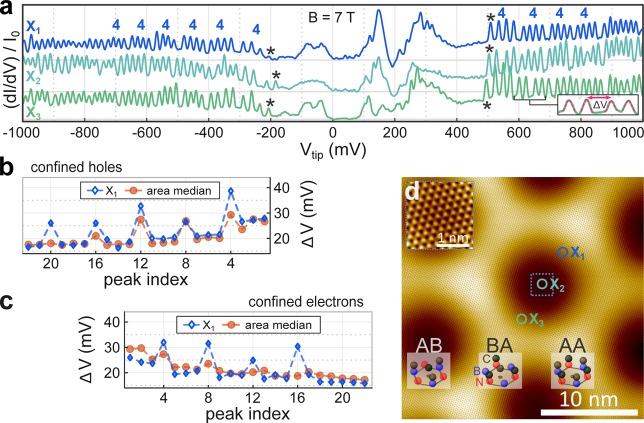
Probing the sample in our custom-build UHV-STM system⁴⁹ at T = 8 K, we observe the superstructure with a = 13.8 nm periodicity, which develops due to the small lattice mismatch of 1.8% between graphene and BN.⁴⁷ An atomically resolved STM image of this superstructure is presented in Figure 2d. Prior to measuring dI/dV spectra, the tip–sample distance is adjusted at the stabilization voltage V_stab and current I_stab and then the feedback loop is turned off (Supporting Information). Figure 2a shows exemplary dI/dV spectra, acquired at B = 7 T and adjusted to the same vertical scale by dividing dI/dV by the first value I₀ of the respective I(V) curve (Supporting Information). We observe pronounced, regularly spaced peaks for V_tip < −170 mV and V_tip > 500 mV. A closer look at the sequences reveals the expected grouping in quadruplets, which can still be distinguished up to the 20th peak. This grouping becomes even more evident by directly comparing the voltage difference between adjacent peaks ΔV in Figure 2b,c; ΔV between quadruplets is up to twice as large as ΔV within the quadruplets indicating Δ_j^o ≲ E_C while Δ_k^τ and Δ^σ are significantly smaller. To further elucidate grouping patterns, we measure 6400 dI/dV spectra at equidistant positions within a 60 nm × 60 nm area, thus probing all areas of the superstructure. The median ΔV values (orange circles in Figure 2b,c) portray the robust ordering into quadruplets on the hole side, implying Δ_j generally dominates over Δ_k^τ and Δ^σ. On the electron side of the spectra, the sequences are disturbed by a few additional charging peaks of defect states in the BN substrate⁵⁰ that are identified by their characteristic spatial development (Supporting Information). This limits the comparability of the electron and hole sector and hides possible smaller electron–hole asymmetries in the data. The dI/dV features in between the charging peaks most likely capture contributions from multiple orbital states of each LL, which are lifted in degeneracy by the tip-induced potential, but cannot be identified unambiguously (Supporting Information, Section 5).

Figure 2.

(a) Representative differential conductance spectra dI/dV(V_tip), normalized by the first value I₀ of the respective I(V_tip) curve (Supporting Information). Recording positions are X₁, between AA and AB; X₂, on AB; X₃, between AB and BA (compare panel d). Spectra on other regions (e.g., AA, BA) look similar. V_stab = 1 V, I_stab = 700 pA, V_mod = 4.2 mV_rms and B = 7 T. Quadruplets of peaks are marked by “4” and the first charging peak on either V_tip side by an asterisk. Curves are offset for clarity, while horizontal gray lines mark dI/dV = 0 S. Inset shows a zoom with Gaussian fits (dashed lines) used to extract distances between adjacent peaks ΔV as marked. (b,c) ΔV as a function of consecutive peak index for spectrum X₁ (blue, error bars smaller than symbol size) and the median values for 80 × 80 spectra recorded on 60 × 60 nm ² (orange). (d) Atomically resolved STM image (raw data) of the aligned graphene on hexagonal boron nitride (BN). V_tip = 400 mV, I = 1 nA. Differently stacked areas AB, BA, and AA marked and sketched by ball models. Inset on the upper left shows a zoom into the AB stacked area, marked by the blue square, exhibiting an obvious sublattice symmetry breaking due to the underlying BN. Positions equivalent to those where spectra in panel a were recorded are marked by circles labeled X₁, X₂, X₃.

To understand the origin of the charging peaks, we provide a detailed microscopic picture of the tip-induced gating of localized states. We will only discuss the case of positive V_tip, that is, electron confinement, because the arguments for negative V_tip are analogous. Increasing V_tip (orange arrow in Figure 3) shifts the states underneath the tip energetically down. States originating from LLs with positive index are embedded in the LL₀–LL₊₁ gap that provides electrostatic confinement (Figure 3a, see also Figure 1b). Within the bias window eV_tip = μ_gr – μ_tip, electrons tunnel from the sample into unoccupied states of the tip. One current path (dashed green arrow Figure 3a) passes through states of the QD (blue lines). The other stronger current path (solid green arrow Figure 3a) originates from the quasi-continuous LDOS at lower energies where energetically overlapping LL states strongly couple to the graphene bulk. Though increasing V_tip gates QD states down (Figure 3b), the Coulomb gap around E_F always separates the highest occupied from the lowest unoccupied state, prohibiting continuous charging of confined states. It is only when the next unoccupied level crosses μ_gr that the QD is charged by an additional electron. The electrostatic repulsion due to its charge abruptly increases the Hartree energy of all states, thereby shifting additional graphene states from below μ_tip into the bias window (Figure 3b, central transition). Consequently, the tunneling current I increases which translates to a charging peak in dI/dV_tip (Figure 3c). This mechanism is called Coulomb staircase⁴⁰ and has been observed previously, for instance, for charging of clusters within an STM experiment.⁵¹ In essence, charging peaks in dI/dV signal the coincidence of a charge level of the QD with μ_gr⁵² and thus provide a clear signature of the addition energy spectrum of the QD.

Figure 3.

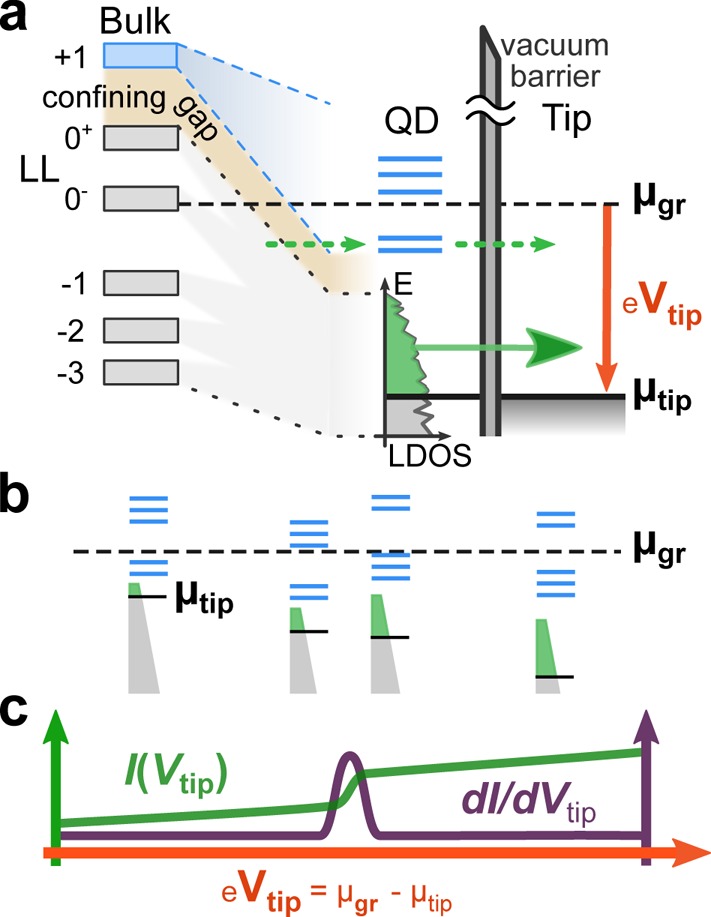
Sketch of the Coulomb staircase. (a) The chemical potentials of graphene μ_gr (black dashed line) and tip μ_tip (black solid line) define the bias window eV_tip within which graphene states tunnel into empty tip states. There are two current paths available: (i) a weak one (green dashed arrow) via quantum dot states (blue lines), (ii) a dominant one (solid green arrow) via states strongly coupled to the graphene bulk (marked LDOS). Left: bulk graphene LLs away from the tip-induced band bending. (b) Schematic diagram of change in QD energies (blue lines) and quasi-continuous LDOS underneath the tip (green and gray triangle) for increasing V_tip from left to right. Between the second and third frame, the QD changes its charge state shifting the energy of the QD states and the entire LDOS upward. (c) Tunneling current I displaying the staircase (green line) and differential conductance dI/dV (purple line) for increasing V_tip (aligned with panel b).

Because the measurement captures the QD level spacings as charging peak distances ΔV, they need to be converted to E_add via the tip lever arm α_tip. The latter relates a change of V_tip to its induced shift of the QD state energies. The lever arm is determined by the ratio of the capacitance between tip and dot C_tip, and the total capacitance of the dot C_Σ, thus α_tip = C_tip/C_Σ. C_Σ includes C_tip, the capacitance between dot and back-gate, and dot and surrounding graphene. We use a Poisson solver to estimate C_Σ = 16.5 ± 3.2 aF and C_tip = 8 ± 1.5 aF for our QD (Supporting Information). Hence, we find E_C = e²/C_Σ ≈ 10 ± 2 meV and α_tip = 0.51 ± 0.03 (close to values reported for a similar system by Jung et al.³³). Consequently charging peaks dominantly separated by E_C, that is, E_addⁱ ≈ E_C because Δ_i ≪ E_Cⁱ, should exhibit ΔV = E_C/(eα_tip) ≈ 20 mV, which is in close agreement with the values found within quadruplets at higher occupation numbers (Figure 2b,c). As expected, we also find significantly larger E_add for every fourth charging peak. In the case of clear quadruplet ordering, the orbital splittings for our QD are deduced from Δ_j^o = E_add – E_C^4j ≈ E_add – E_add^4j+1 and we find typical values of 4–10 meV for the first few orbitals (α_tip = 0.51, Figure 2b,c). For this estimate, we neglect the additional Zeeman splitting or an even smaller valley splitting.

We next provide a theoretical framework to elucidate the details of the QD level spectrum. The eigenstates of bulk graphene LLs (eq 1) feature different wave function amplitudes on sublattices¹ A and B

2

where K and K′ denote the two inequivalent K-points of the Brillouin zone associated with the two valleys. For N ≠ 0, the LL index differs by one for the two sublattices, while for N = 0 the part of the wave function with subscript |N| – 1 vanishes, resulting in polarized sublattices for each valley. The wave functions of bulk graphene (eq 2) are modified by the tip-induced potential. Assuming a radially symmetric confinement potential, the eigenstates are described by radial and angular momentum quantum numbers (n_r, m), with 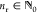and 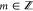. Adiabatically mapping a given LL with index N on to possible combinations of n_r and m yields⁵³

3

with 0 ≤ n_r ≤ |N| and m ≤ |N|.

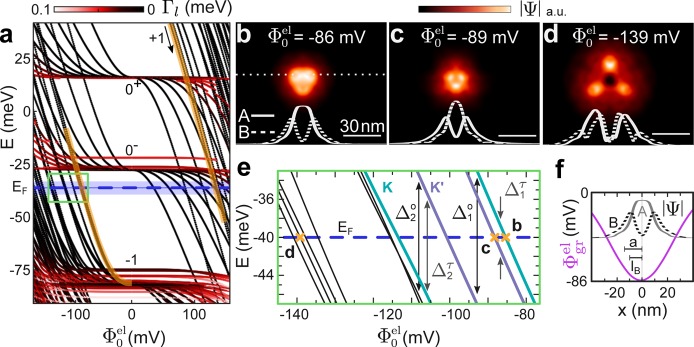
We calculate eigenstates of a 120 nm × 100 nm commensurate graphene flake on BN using third-nearest neighbor TB,³⁸ where the substrate interaction enters via a periodic superstructure potential and local strain effects,³⁹ parametrized from DFT calculations.^54,55 We approximate the amplitude Φ₀^el and shape of Φ_gr by a classic electrostatic solution of Poisson’s equation (Figure 1a, Supporting Information) with the tip radius r_tip as fit parameter. Comparing calculated charging energies to experiment yields a plausible value of r_tip ≈ 120 nm, implying a full width at half-maximum (fwhm) of the QD confinement potential of 55 nm at 7 T. We independently determine the initially free parameter E_F from the position of LL₀ in STS as E_F = −40 ± 5 meV (Supporting Information). Accordingly, the graphene is p-doped. We note that varying E_F within the stated uncertainty range (see blue horizontal bar in Figure 4a) leads to no qualitative changes in the predictions of our model. We use open boundary conditions to simulate the coupling of the flake to the surrounding graphene. Consequently, eigenstates will feature complex eigenvalues E_l = ε_l + iΓ_l/2, where the real part ε_l represents the resonant energies and the imaginary part Γ_l the coupling to the delocalized bulk states.⁵⁶ Thus, we can readily distinguish states that are spread out over the flake (large Γ_l) from those localized near the tip (small Γ_l). We color code Γ_l in Figure 4a for a calculation with the tip-induced potential centered on an AB stacked area.

Figure 4.

(a) Tight binding eigenenergies of a 120 × 100 nm ² graphene sample with open boundaries as a function of tip-induced potential amplitude Φ₀^el at B = 7 T with the tip-induced potential centered on an AB area (BA and AA yield very similar behavior, not shown). Line color encodes coupling to the boundary (imaginary part Γ_l of eigenenergies); black (red) indicates strong (weak) localization underneath the tip. States from LL_±1 and the split LL₀ are labeled by ±1 and 0, respectively. The LL₀ splitting reduces the confining gap to E_0^– – E_–1 ≈ 50 meV. First states crossing E_F from LL_±1 are highlighted in orange. Uncertainty in E_F indicated as blue horizontal bar (Supporting Information). The green rectangle marks the zoom shown in panel e. (b–d) Color plot of the wave function amplitude 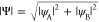of states marked by orange crosses in panel e. Φ₀ at the crossing point ε_l(Φ₀^el) = E_F is marked. Solid (dashed) white lines are line cuts along the dotted white line in panel b for contributions from sublattice A (B), as marked. All scale bars identical. (e) Zoom into area marked by a green box in panel a. Colored lines identify valley K (cyan) and K′ (purple). Orange crosses mark crossing of E_F (blue dashed line) of selected states, which are displayed in panels b–d. First two orbital Δ_j and valley Δ_k^τ splittings marked by arrows. (f) Comparison of length scales: tip-induced potential, magenta; calculated wave function amplitude |Ψ| of first state crossing E_F (same as panel b) for sublattice A (gray line) and B (dashed line); superstructure lattice constant a = 13.8 nm; magnetic length l_B (7 T) = 9.7 nm.

At B = 7 T and vanishing band bending (Φ₀^el = 0), we find only delocalized states whose eigenenergies cluster around the bulk LL energies (eq 1, Figure 4a). As we increase Φ₀, states begin to localize at the tip and shift in energy, with smaller Γ_l (darker curves) pointing to stronger localization (see Figure 4a). Comparing hole states originating from LL_–1 for negative and positive Φ₀^el, we find, as expected, stronger localization in case of negative Φ₀. The potential is always attractive to one kind of charge carriers that will localize underneath the tip. The other kind is repelled by the induced potential (see also ref (31)) which results in stronger coupling to the bulk. In order to classify our TB wave functions in terms of the quantum numbers N, n_r, and m, we consider sublattice A and B separately. Tracing the states back to their LL of origin reveals N, constraining possible n_r ≤ |N|. The value of n_r is then determined by counting radial minima in the line cuts of the wave function amplitude for each sublattice (Figure 4b–d). The distance of the first radial maximum from the center of the wave function is finally sufficient to assign the possible m quantum numbers of the LL (eq 3). Additionally, the (n_r,m) combinations need to be consistent with N differing by one on the two sublattices (eq 2). For instance, the line cuts in Figure 4b portray (0,0) and (0,1) on sublattice A and B, respectively. As expected, small angular momentum states are the first ones to localize with increasing Φ₀^el, which is in line with calculations by Giavaras et al.³⁰ Notice that the applied B naturally lifts the orbital degeneracy in QDs.⁵⁷ Delocalized states remain at bulk LL energies (red horizontal lines in Figure 4a).

We distinguish two regimes in the sequence of spin degenerate states crossing E_F for negative Φ₀^el. The first regime (Figure 4e) exhibits Δ_k ≲ Δ_j^o ≲ E_C, while the second at higher Φ₀^el is characterized by densely spaced states, thus Δ_j ≈ Δ_k^τ ≪ E_C. The sequence within the first regime corresponds to about five orbital pairs from valley K and K′, which is in line with about five quadruplets in our experimental spectra (see labels “4” in Figure 2a and ΔV sequences in Figure 2b,c). The quite uniform spacing of peaks for larger V_tip (Figure 2a) agrees with the second regime. In order to extract Δ_j^o and Δ_k within the first regime, we carefully assign the valley index to the states. Using the previously determined n_r and m in eq 3, the first state crossing E_F (Figure 4b) features LL index N_A = 0 + 1/2(0 + |0|) = 0 on sublattice A and N_B= 1 + 1/2(0 + |0|) = 1 on sublattice B, as predicted by eq 2 for a LL_|1| state in valley K. The role of the sublattices interchanges for the second state crossing E_F (Figure 4c), placing it in valley K′. Consequently, states with N_A = N_B – 1 and N_B = N_A – 1 are assigned to valleys K and K′, respectively. The calculation therefore predicts a valley splitting of about Δ₁^τ = 3 meV on the AB and BA areas (see Figure 4b,c,e). Δ₂ is comparatively large (about 12 meV) and the respective orbital splitting Δ₂^o is only larger by 1–2 meV (see Figure 4e). Consequently, additional electrons may occupy the next orbital state of one valley prior to the same orbital state of the other valley at higher occupation numbers. Hence, we limit further comparison to experiment to Δ₁. In our TB model, the strength of the valley splitting is dominated by the sublattice symmetry breaking term due to the BN substrate.³⁹ The calculations also show that the radial extent of the wave functions grows for the first couple of states crossing E_F, as expected for increasing m (compare Figure 4 panels b and c to panel d), explaining the decrease of E_Cⁱ toward higher peak indices at fixed B (see Figure 2b,c).

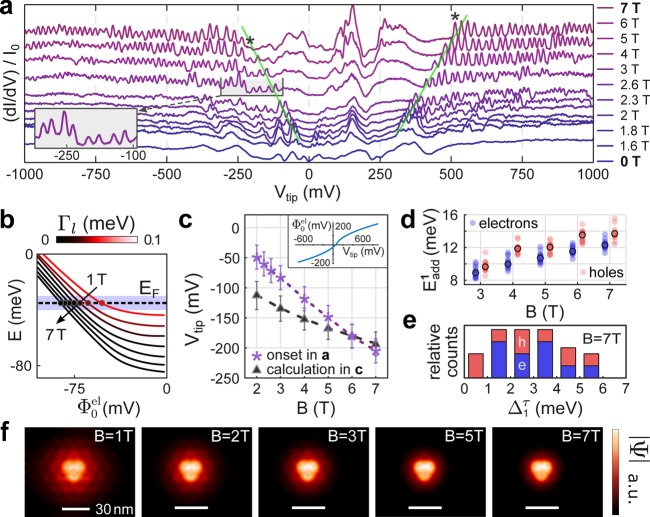
Theory and experiment can be directly compared for the B dependence of the onset voltage of charging peaks V*. Experimentally, V* shifts toward higher |V_tip| for increasing B (Figure 5a), thus gating the first state to E_F requires stronger band bending for higher B. Because the curves for B > 0 T are offset proportional to √B, the straight line connecting the first charging peaks reveals that the energy distance of the first state to E_F scales with √B. This corresponds to the increase in bulk LL energies for N ≠ 0 (eq 1), strongly suggesting those LLs as source of the confined states. This analysis is confirmed by our TB calculations, as the first crossing points of LL_±1 states with the Fermi level Φ₀^* also shift toward higher |Φ₀ | with increasing B (Figure 5b). While the evolution of states with Φ_gr^el in Figure 4a is (approximately) symmetric with respect to Φ_gr →−Φ_gr^el, the previously discussed p-doping induces an asymmetry in Φ₀ for electrons and holes (see the lines highlighted in orange in Figure 4a) and thus accounts for the observed asymmetry in V*. In Figure 5c, we compare V* and Φ₀^* by using the Φ₀(V_tip) dependence from the Poisson solver (see inset Figure 5c, Supporting Information). Care must be taken to correctly account for the work function difference between the tip and the sample: the tip’s work function (4.5–4.8 eV^36,58) exceeds that of graphene (4.5 eV), placing electric field neutrality in the positive V_tip sector. Moreover, it definitely has to lie in between the two charging peak regimes because the QD vanishes without band bending. Using a plausible work function difference of +50 meV in Figure 5c leads to satisfactory agreement between the theoretical predictions for the first state crossings and the experimental V*.

Figure 5.

(a) dI/dV spectroscopy in the vicinity of an AA stacked area at varying B, marked on the right. Four spatially adjacent spectra are averaged and the ones for B > 0 T are offset by a value proportional to √B. V_stab = 1000 mV, I_stab = 700 pA, V_mod = 4.2 mV_rms. Green lines are guides to the eye, marking the onset voltage of charging peaks V*. At 7 T, an asterisk marks the first charging peak on either side. Inset shows zoom onto marked peaks. (b) Energy of first confined hole state as a function of induced potential amplitude Φ₀^el for different B as marked. At larger B, states cross E_F at larger Φ₀, shifting V* to larger negative V_tip. Color codes imaginary part of the eigenenergy as in Figure 4a. (c) Comparison between measured and calculated V*. Inset shows the required Φ₀^el(V_tip) for conversion, taken from a Poisson-solver (Supporting Information) and including a reasonable work function difference of ΔΦ = 50 meV between graphene and tip. Error bars for measured V* reflect typical variation of V* on AA areas across a few superstructure unit cells. Error bars for calculation arise from the uncertainty in E_F. (d) Plot of the B dependence of E_add ≈ E_C¹ of 20 spectra (semitransparent dots) in the vicinity of an AA area. Data points are recorded at integer valued B fields (in Tesla) but displayed slightly shifted to the left (electrons, blue) and to the right (holes, red) for clarity. Median values are encircled in black. (e) Histogram of Δ₁ ≈ E_add² – E_add (experimental error below 0.2 meV) at B = 7 T for the same AA area used in panel d. Electron (blue bars) and hole (red bars) contributions are colored. (f) Calculated |Ψ| of the first confined hole state (see panel b) crossing E_F at different B as marked. The state originates from LL_–1, i.e., V_tip < 0 V when crossing. All scale bars identical.

Our TB simulations predict a strong reduction of Γ_l with increasing magnetic field, corresponding to the suppression of the radial tail of the wave function in Figure 5f and indicating the onset of localization between 1 and 3 T (Figure 5b). The first appearance of charging peaks in the experiment at around 2 T (Figure 5a) fits nicely. This finding is further corroborated by comparing the diameter of the LL state 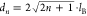, being d₁ = 89 nm (63 nm) for LL₁ at 1 T (2 T) with the fwhm of the band bending region of 55 nm, providing an independent confirmation of the estimated Φ_gr^el. At higher B, the diameter of the first QD state wave function is dominated by l_B rather than by the width of Φ_gr (Figure 4f). The compression of the wave function for increasing B (Figure 5f) also manifests itself as increase in addition energy, for instance, for E_add¹ = E_C + Δ^σ in Figure 5d, where the increase in E_add¹ with B by about 4 meV cannot be explained by that of Δ^σ, being 460 μeV between 3 and 7 T. Consequently, increased Coulomb repulsion between electrons due to stronger compression and thus larger E_C dominates E_add¹(B) . We observe a similar monotonic increase for the other E_add with odd index i, independent of the position of the QD.

Experiment and theory also provide detailed insight into the valley splitting Δ_k^τ of the first confined states. The peaks of the first quadruplets in Figures 2a and 5a (see, e.g., inset) often group in doublets, suggesting sizable values of either Δ_k or Δ^σ (Figure 1e,f). While Δ^σ is expected to be spatially homogeneous and only weakly varying between different quadruplets, the TB calculations predict strongly varying Δ_k^τ for different quadruplets (Figure 4e), which is in accordance with our observations in the experimental spectra. For a quantitative comparison, we focus on E_add, which separates the two doublets within the first quadruplet. In view of the small value of the Zeeman splitting (Δ^σ ≈ 800 μeV at 7 T), we approximate E_C² by E_add to extract the valley splitting Δ₁^τ ≈ E_add – E_add³. We record 20 spectra in the vicinity of an AA stacked area at B = 7 T to obtain a histogram of Δ₁ for electrons and holes (Figure 5e), where Δ₁^τ could be determined with an experimental error smaller than 0.2 meV. The values strikingly group around the predicted Δ₁ ≈ 3 meV found in the TB calculations (Figure 4e), with a probable offset in the QD position relative to the tunneling tip (Supporting Information, Section 5) explaining the QD probing an area adjacent to the tunneling tip. We conclude that sizable Δ_k^τ separate quadruplets into doublets, while the smaller Δ^σ contributes to the odd addition energies within the doublets. Realizing such a controlled lifting of one of the two degeneracies in graphene QDs is a key requirement for 2-qubit gate operation.² It enables Pauli blockade in exchange driven qubits as required for scalable quantum computation approaches using graphene.² Our observation of valley splittings, so far elusive, provides a stepping stone toward the exploitation of the presumably large coherence time of electron spins in graphene QDs.²⁻⁵

In summary, we have realized graphene quantum dots without physical edges via electrostatic confinement in magnetic field using low disorder graphene crystallographically aligned to a hexagonal boron nitride substrate. We observe more than 40 charging peaks in the hole and electron sector arranged in quadruplets due to orbital splittings. The first few peaks on the hole and electron side show an additional doublet structure traced back to lifting of the valley degeneracy. Note that such a lifting is key for the use of graphene quantum dots as spin qubits.² Tight binding calculations quantitatively reproduce the orbital splitting energy of 4–10 meV as well as the first orbital’s valley splitting energy of about 3 meV by assuming a tip potential deduced from an electrostatic Poisson calculation. Also the onset of confinement at about 2 T is well reproduced by the calculation. Our results demonstrate a much better controlled confinement by combining magnetic and electrostatic fields than previously found in graphene. Exploiting the present approach in transport merely requires replacing the tip by a conventional electrostatic gate with a diameter of about 100 nm. Moreover, the approach allows for straightforward tuning of (i) orbital splittings by changing the gate geometry and thus the confinement potential, (ii) valley splittings based on substrate interaction, (iii) the Zeeman splitting by altering the magnetic field, and (iv) the coupling of dot states to leads or to other quantum dots by changing the magnetic field or selecting a different quantum dot state. Finally, our novel mobile quantum dot enables a detailed investigation of structural details of graphene stacked on various substrates, by spatially mapping the quantum dot energies.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.6b02548.

• Sample preparation; STM measurement details; Poisson solver; capacitances, tip lever arm and tunnel-coupling of QD states; Landau levels and estimation of the Fermi energy; identication of defect charging peaks; assigning a valley to the TB wave functions; additional references and figures (PDF)

The authors declare no competing financial interest.