Multiscale simulations of protein-facilitated membrane remodeling

Abstract

Protein-facilitated shape and topology changes of cell membranes are crucial for many biological processes, such as cell division, protein trafficking, and cell signaling. However, the inherently multiscale nature of membrane remodeling presents a considerable challenge for understanding the mechanisms and physics that drive this process. To address this problem, a multiscale approach that makes use of a diverse set of computational and experimental techniques is required. The atomistic simulations provide high-resolution information on protein-membrane interactions. Experimental techniques, like electron microscopy, on the other hand, resolve high-order organization of proteins on the membrane. Coarse-grained (CG) and mesoscale computational techniques provide the intermediate link between the two scales and can give new insights into the underlying mechanisms. In this Review, we present the recent advances in multiscale computational approaches established in our group. We discuss various CG and mesoscale approaches in studying the protein-mediated large-scale membrane remodeling.

1. Introduction

Biological membranes are multicomponent, self-assembled molecular sheets that surround the cells and its organelles. Besides separating the cell from the environment, compartmentalizing its components, and providing a mechanical protection, membranes play a crucial role in many biological processes that are vital for cell’s survival and function. Examples of such processes are cell adhesion, cell signaling, and the selective transport of ions and organic molecules in and out of the cell (Conner and Schmid, 2003; McMahon and Gallop, 2005). In order to perform such a diverse set of functions, membranes possess inherently multiscale material properties. While exhibiting fluid properties at molecular scales, membranes behave like elastic sheets at length scales that are large compared to their thickness (Helfrich, 1973). As a result, membranes can exhibit a remarkable variety of shapes and morphologies (Lipowsky, 1991) dictated by their composition and the surrounding environment (Johannes et al., 2014; Lipowsky and Sackmann, 1995).

Membrane remodeling is facilitated by the action of proteins that bind peripherally to the membrane, partially insert their domains, or are fully included into the bilayer (McMahon and Gallop, 2005). These proteins induce a local asymmetry between the layers of the membrane, which generates spontaneous curvature. It is believed that a cooperative behavior of multiple proteins gives rise to large-scale membrane remodeling (Gallop et al., 2006; Jao et al., 2010; Saarikangas et al., 2009; Zimmerberg and Kozlov, 2006). Perhaps the most studied membrane remodelers are Bin/Amphiphysin/Rvs (BAR) domain proteins. They play a crucial role in many cellular processes, including clathrin-mediated and clathrin-independent endocytosis (Boucrot et al., 2015; Doherty and McMahon, 2009; Renard et al., 2015; Slepnev and De Camilli, 2000), T-tubule morphogenesis (Lee et al., 2002; Peachey and Eisenberg, 1978), cytokinesis (Arasada and Pollard, 2015), and many others. BAR domain is a crescent-shaped dimer with positively charged residues on its membrane-interacting surface (Frost et al., 2007; Gallop and McMahon, 2005). It is believed to generate curvature by a combination of (1) adhesive interactions with the membrane surface, (2) insertion of amphipathic helices, and (3) by forming three-dimensional ordered structures that mold membrane tubules (Simunovic et al., 2015).

The inherently multiscale nature of membrane remodeling makes it quite challenging to study the mechanisms behind these phenomena. Due to a strong coupling between microscopic properties of the membrane (e.g., diffusion rate and packing defects) and its macroscopic characteristics (e.g., bending modulus and bulk compressibility), membrane remodeling cannot be studied using a single computational technique; rather, it requires a hierarchical approach. Atomistic simulations can provide invaluable insights into direct protein-membrane interactions, see, e.g., (Blood and Voth, 2006; Blood et al., 2008; Cui et al., 2009; Lyman et al., 2010). However, the high computational cost limits their applicability beyond single protein simulations. Coarse-grained (CG) simulations, on the other hand, can reach biologically relevant time and length scales, owing to a reduction in the number of degrees of freedom achieved by grouping lipid and protein atoms into CG sites and, often, by an implicit treatment of the bulk solvent. The effective interactions between CG sites can be derived, at least mostly, from atomistic simulations (the so-called bottom-up approach) (Ayton and Voth, 2009b; Ayton et al., 2010; Izvekov and Voth, 2009; Srivastava and Voth, 2012; Srivastava and Voth, 2014). The resulting CG models can be very valuable for studying complex behavior of protein cooperation during membrane remodeling.

In recent years, a number of mesoscopic membrane models have also been developed. Those models are beyond the resolution of individual molecules, but rather employ quasi-particle description of the membrane, often complimented with the use of vector as well as other continuum or semi-continuum fields that can represent the inhomogeneity of membrane composition or protein concentration on the membrane (Ayton et al., 2007; Ayton et al., 2009; Shiba and Noguchi, 2011; Sreeja et al., 2015).

This Review will survey the multiscale computational methods developed in our group for studying membrane-protein interactions and membrane remodeling (Ayton and Voth, 2009a; Ayton and Voth, 2010b). The remainder of this article is organized as follows: Section 2 shortly presents different CG models of lipids and proteins and discusses the main results of the CG approach. Section 3 is dedicated to mesoscopic modeling. We present the Elastic Membrane Version 2 (EM2) model and recapitulate the key results that this model predicts. We also draw a brief comparison with other mesoscopic models that have been developed by other groups. Section 4 contains the concluding remarks.

2. CG simulations of membrane remodeling by BAR proteins

Large-scale atomistic simulations have provided valuable insights into mechanisms of protein-membrane interactions and curvature coupling, especially by BAR proteins such as endophilin (Blood and Voth, 2006; Blood et al., 2008; Cui et al., 2009; Lyman et al., 2010). However, at present it is too challenging to expand those simulations to treat many proteins bound to the membrane. To reach the sub-cellular length and time scales (~μm and ~ms, respectively) that can be examined experimentally, various CG approaches have been developed in our group in recent years to model lipids (Ayton and Voth, 2009b; Izvekov and Voth, 2009; Lu and Voth, 2009; Srivastava and Voth, 2012; Srivastava and Voth, 2014) and proteins (Ayton and Voth, 2010a; Ayton et al., 2010; Srivastava and Voth, 2014). Those models rely on effective interactions between CG sites that represent the average interactions between the underlying atoms and the effect of the solvent. Moreover, the CG interactions are derived from the corresponding atomistic forces in a systematic way that ensures the consistency between CG and more detailed atomistic models.

While earlier CG lipid models were of relatively high resolution (10–15 CG sites per lipid (Izvekov and Voth, 2009; Lu and Voth, 2009)), lower-resolution models, namely, the hybrid analytic-systematic (HAS) model (Ayton and Voth, 2009b), the hybrid coarse-grained (HCG) model (Srivastava and Voth, 2012), and the charged hybrid coarse-grained (cHCG) model (Srivastava and Voth, 2014), were more successful in overcoming the barrier between simulations and experiments.

In the HAS approach each lipid is modeled as a single ellipsoid of revolution (see Fig. 1a), whose CG interactions with the surrounding lipids consist of an analytical and a systematic component. The systematic part gives the in-plane interaction potential that is derived using the multiscale coarse-graining (MS-CG) method (Izvekov and Voth, 2005; Noid et al., 2008a; Noid et al., 2008b). MS-CG provides a rigorous framework for constructing CG models from data acquired in atomistic simulations using a variational principle. The analytical part models the lipid-lipid interactions for distances closer than 0.5 nm and for out-of-plane interactions, where the all-atom simulations do not provide a sufficient sampling. This part is given by a liquid-crystal Gay-Berne potential with a 3:1 ratio (Gay and Berne, 1981). Its parameters are determined empirically in order to obtain the desired elastic properties of the membrane (e.g., bending modulus and area compressibility), while the MS-CG potential captures the correct local properties (e.g., lateral diffusion and radial distribution function) (Ayton and Voth, 2009b). When combined with CG protein models (see below), an extra CG site is added, representing the lipid head group (see Fig. 1a), which only interacts with the protein (Ayton et al., 2010; Cui et al., 2013).

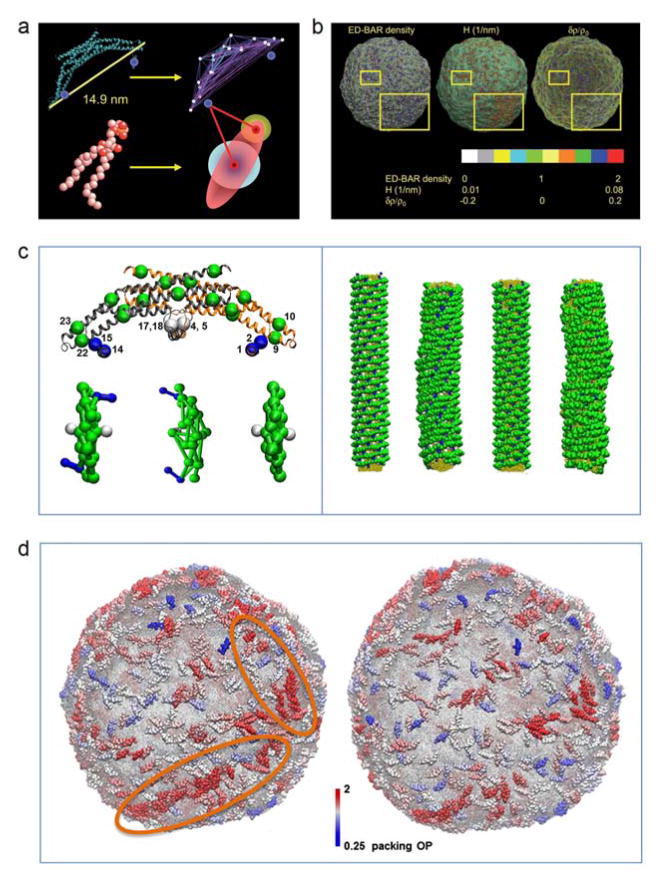
Figure 1.

a) Schematics of heteroENM CG model of N-BAR domain (top) and HAS CG lipid model (bottom) as employed in (Ayton et al., 2010) for liposome simulations. The CG model of the N-BAR domain is derived using the ED-CG approach (Zhang et al., 2008) from atomistic simulations. Two sites are introduced to represent each amphipathic helices (highlighted by blue spheres). In the membrane the lipids are modeled as Gay-Berne ellipsoid of revolution, while the additional headgroup sites interact with all CG sites of N-BAR domain. b) The panel demonstrates the correlation between N-BAR density, mean curvature, H, and relative membrane density change, δρ/ρ₀, for a selected snapshot of liposome simulations from (Ayton et al., 2010). The yellow squares point to the areas of the membrane where this correlation is most evident. c) The left side shows the schematic representation of ED-CG model of endophilin N-BAR (top) and top view of zigzag N-BAR, triad N-BAR, and BAR domain models, respectively. The zigzag and triad models correspond to different amphipathic helices orientations, while BAR lacks the amphipathic helices. The amphipathic helices are highlighted in blue, and the insert helices in white. The right side shows initial and final snapshots of CG simulations of N-BAR coated tubes. In the case of zigzag orientation (the two most left snapshots) the protein lattice remains more organized, while triad orientation (the two most right snapshots) destabilizes the lattice. d) Representative snapshots of N-BAR-coated (left) and BAR-coated (absent the amphipathic helices) (right) liposome simulations. The highlighted region shows the string-like organization of N-BAR domains that is not observed for BAR domain. Panels a) and b) are adapted from (Ayton et al., 2010) with permission from The Royal Society of Chemistry. Panels c) and d) are adapted from (Cui et al., 2013), © 2013 by the Biophysical Society.

In the case of the HCG and cHCG methods, each lipid is represented by either three or four spherical CG sites (Fig. 2a). The general idea behind the parameterization of these models is similar to the HAS approach. At short distances, poorly sampled by all-atom simulations, an analytical Lennard-Jones potential is used. At longer distances, where the atomistic simulations provide good sampling, the MS-CG method is used to find the interactions between the CG sites. The cHCG method explicitly represents screened electrostatic interactions between the CG sites. The electrostatic potential is derived using the MS-CG method, by dividing the non-bonded interactions into electrostatic and van der Waals (vdW) contributions. Also, a more general Lennard-Jones-like function is used for the analytical potential in the case of the cHCG method. HCG and cHCG models of single or multicomponent lipid membranes successfully capture both the short-range properties, namely, the radial distribution function and the z-density, and the long-range properties, such as area compressibility, bending modulus, and the lateral stress profile (Srivastava and Voth, 2012; Srivastava and Voth, 2014).

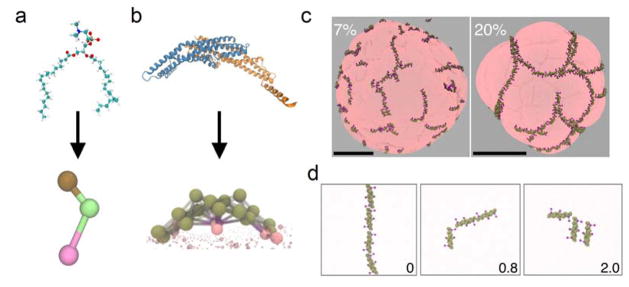
Figure 2.

Atomistic (top) and coarse-grained (CG) (bottom) representations of a) 1,2-dilauroylsn-glycero-3-phosphocholine (DLPC) lipid and b) the endophilin N-BAR domain. c) N-BAR domains form linear assemblies and meshes on the surface of liposomes inducing bud-like instabilities. The panels illustrate the remodeling of liposomes 200–300 nm in diameter at 7% (left) and 20% (right) protein surface coverages. Scale bars, 100 nm. Adapted from (Simunovic et al., 2013a), © 2013 National Academy of Sciences, USA. d) Membrane tension affects the assembly of N-BAR domains on the membrane. Shown are snapshots from simulations at different surface tensions (indicated in bottom right corner, units: mN/m) at 4% protein surface coverage. Taken from (Simunovic and Voth, 2015), © 2015 Nature Publishing Group.

Area compressibility and bending modulus are key indicators of the quality of a membrane model. For HCG model described above, the area compressibility modulus of pure DLPC and DOPC lipid systems have values of 310 ± 6 dyn/cm and 254 ± 9 dyn/cm, respectively. The DLPC value is consistent with 461 ± 6 dyn/cm value obtained from all-atom simulations that are known to overestimate the area compressibility modulus (Poger and Mark, 2009), and the DOPC result is within 188 – 265 dyn/cm experimental range (Rawicz et al., 2000; Tristram-Nagle et al., 1998). While the pure DLPC and DOPC values are nearly comparable, much smaller value is obtained for mix DLPC/DOPC lipid system 165 ± 12 dyn/cm, consistent with recent experiments (Rodowicz et al., 2010). This reduction of area compressibility modulus for mixed systems is also consistent with values of 97 dyn/cm and 121 dyn/cm obtained for 1:1 and 3:1 DOPC/DOPS systems, respectively, from the cHCG model. The bending modulus for pure DLPC, pure DOPC, and mixed DLPC/DOPC systems are estimated to be approximately 15k_BT, 18 – 19 k_BT, and 7 k_BT, respectively, from HCG system. For the mixed DOPC/DOPS system values of 15.5k_BT and 15.9k_BT are obtained for 1:1 and 3:1 compositions. Those values are generally consistent with expected range from a few k_BT to tens of k_BT for lipid bilayer (Marsh, 2007). Moreover, the individual values are typically within 1 – 2 k_BT of known experimental measurements, as detailed in correspond HCG and cHCG papers (Srivastava and Voth, 2012; Srivastava and Voth, 2014).

The lipid models described above can be used to carry out long time scale simulations of membrane sheets or liposomes that can contain even millions of lipids. Here, we will highlight the application of these models in studying membrane remodeling induced by BAR proteins. Similar approaches can be used to study the mechanism of other membrane-curving proteins.

The CG sites within BAR domains can be modeled using essential dynamics coarse-graining (ED-CG) (Zhang et al., 2008), an approach that captures the dominant long-wavelength motions in the CG model (Fig. 2b). The interactions between the CG sites within the protein are typically calculated by applying the heterogeneous elastic network model (HeteroENM), cast in the form of effective harmonic springs (Chu and Voth, 2006; Haliloglu et al., 1997; Lyman et al., 2008). The strength of various springs are derived by fitting the thermal fluctuations of corresponding CG distances to the ones observed in atomistic MD simulations (Lyman et al., 2008). A Lennard-Jones potential is then often used for various protein-lipid cross-interactions, whose parameters are obtained by a combination of empirical and systematic approaches (Ayton et al., 2010; Cui et al., 2013; Simunovic et al., 2013b). The interactions between all protein CG sites (except the amphipathic helices in the case of BAR domains) with lipid head groups are derived from atomistic pair distribution functions of phosphorus atoms in lipid head groups and the center of masses of protein CG sites. The interactions between the CG sites on amphipathic helices and the lipid are obtained by matching observables of either atomistic MD simulations (e.g., the insertion depth) or experimental observations (e.g., binding energy obtained from fluorescence measurements).

The resulting CG models have been used to shed light on the mechanism of BAR-mediated membrane remodeling. In Ayton et al. (2010) a model employing HAS lipids and heteroENM CG N-BAR domains (BAR domain + N-terminal amphipathic helices, see Fig. 1a) was used to simulate the early stages of liposome remodeling. It was found that the N-BAR domain density strongly correlates with the magnitude of local curvature and lipid area density (Fig. 1b). This observation is well aligned with the “wedge” mechanism of N-BAR-domain-mediated remodeling, where the N-BAR domain senses the regions of the membrane of reduced lipid density where it inserts its helix and generates curvature. A study by Cui et al. (2013) explored the role of N-terminal amphipathic helices (H0) of the N-BAR domain of endophilin on the organization of N-BAR domains on membrane tubes and liposomes. This work also employed the combination of the HAS lipid (Fig 1a) and the heteroENM protein models (Fig 1c), but with the addition of screened electrostatic potentials for lipid-protein and protein-protein interactions (Ayton and Voth, 2010a). The CG MD simulations of membrane tubules, fully coated by an N-BAR lattice, resolved the orientation of H0s, which was inaccessible by cryo-electron microscopy likely because they are too dynamic. This work also demonstrated the importance of H0 in the stability of the protein coat. Apparently, the removal or an incorrect orientation of H0 destabilizes the protein lattice (Fig 1c). Finally, the simulations of liposome bound by N-BAR domains, representing the initial stages of membrane remodeling, showed correlation between the density of N-BAR and a local membrane curvature, attributed to a local organization of N-BAR into strings (Fig. 1d).

In a subsequent series of papers (Simunovic and Voth, 2015; Simunovic et al., 2013a; Simunovic et al., 2013b), the HCG lipid model (see Fig. 2a) and the heteroENM model of the N-BAR domain (see Fig. 2b) were employed to study how N-BAR proteins assemble on the membrane to couple with membrane curvature. The nature of the cooperative behavior among proteins and its effect on membrane shape and topology was found to be strongly dependent on the protein density. At protein coverage up to 10 %, N-BAR domains were discovered to form linear aggregates on the surface of planar membranes or large vesicles (~300 nm in diameter) (Fig. 2c). As the protein density is increased (10–30%), the proteins form a percolated network, i.e., a meshwork. At the same time, the protein aggregation induces bud-like instabilities on the surface of the membrane at the centers of protein meshes (Fig. 2c). This interesting linear organization on the membrane is an increasingly emerging assembly pattern and recently, a linear oligomerization of F-BAR proteins on membranes has been captured with electron microscopy, confirming our theoretical predictions (McDonald et al., 2015; Traub, 2015).

CG MD simulations, free energy calculations, and analytical scaling arguments have also demonstrated an interesting membrane tension-dependence of protein association on the membrane. Apparently, increasing membrane tension dramatically alters the protein aggregation. While proteins quickly form stable linear aggregates on a tensionless membrane, an increase in tension inhibits the protein oligomerization and the interaction dynamics. At the same time, tension alters the angle at which two BAR proteins interact, thus affecting the large-scale geometry of the protein assemblies (Fig. 2d) (Simunovic and Voth, 2015).

At higher protein coverage (~ 50%), the linear organization is obscured by protein crowding. Large-scale instabilities in the membrane can then be seen (Simunovic et al., 2013b), with a striking resemblance to vesicle deformations induced by amphipathic nanoparticles (Czogalla et al., 2015).

At near-full packing densities, the N-BAR domains form a nematic assembly that breaks the bilayer topology and transforms an entire vesicle into an interconnected tubular or “reticulated” network, a structure demonstrated by a 3D reconstruction of an electron microscopy tomogram (Simunovic et al., 2013b).

3. Mesoscopic simulations of protein-induced membrane remodeling

The global membrane remodeling is a very slow process that occurs on the order of microseconds to even seconds. The CG simulations make it possible to study the early stages of membrane remodeling. While the CG models described before can simulate systems containing millions of lipids, simulating cellular-scale vesicles at microsecond or longer time scales is still too challenging for CG MD. A mesoscopic approach that operates beyond the resolution of individual molecules can model the dynamics of micron-sized membrane systems under various conditions that can be observed experimentally. The theoretical basis for this approach comes from the continuum elastic membrane models formulated by Helfrich (1973), Canham (1970), and Evans (1973), and extended by many others to capture the symmetry breaking that can be induced by membrane inclusions (see, e.g., Refs (Fischer, 1992; Fournier, 1996; Iglič et al., 2007; Kralj-Iglič et al., 2000)).

Our elastic membrane version 2 (EM2) approach employs a discretized solution to this continuum elastic model. It is based on the “smooth particle” approach (Hoover and Hoover, 2003; Hoover et al., 2006; Lucy, 1977) that defines an adaptive spatial grid making it possible to build a flexible and an efficient computational framework that can accommodate large-scale changes of the membrane topology. The full details of the EM2 model are given elsewhere (Ayton et al., 2006; Ayton et al., 2007; Ayton et al., 2005; Ayton et al., 2009). Here, we will briefly describe the key features of this approach.

EM2 models the membrane and the surrounding solvent using two types of quasiparticles. One type represents the solvent and it carries a protein composition field, while the other type represents the membrane and it carries both the protein and the lipid composition fields. The latter quasi-particles are characterized by a normal and an inplane vector (Fig. 3a). The normal vector defines the local orientation of the membrane and is used to calculate the local curvature, while the in-plane vector gives the local direction along which the spontaneous curvature is applied and is dictated by the organization of the BAR domains in that area of the membrane. The protein composition field describes the local BAR domain density, while the lipid composition gives the local charge density of negatively charged lipids. The spatial dynamics of the quasiparticles is controlled by the smooth-particle applied mechanics (SPAM) (Hoover and Hoover, 2003), where the dynamics of the composition fields is given by the Landau-Ginzburg equations (McWhirter et al., 2004; Metiu et al., 1976). The normal and the in-plane vectors are treated as dynamic variables and evolve according to torques arising from interactions with nearby particles. In the model, BAR domain density locally alters the membrane stiffness and it couples to either the local curvature of the membrane (intrinsic curvature coupling, IC) or the lipid charge density (composition coupling, CC).

Figure 3.

a) Left: initial configuration of a mesoscopic liposome immersed in a mesoscopic solvent. Right: each membrane quasi-particle is characterized by a normal and an in-plane vector (Ω and n^T, respectively), as well as lipid and protein composition fields (ϕ_m and ϕ_b, respectively). The principal component of the local curvature (1/R) along the in-plane vectors is computed on the fly based on the angles between the normal vectors (δθ) and distances between the quasi-particles. b) Final configurations of mesoscale simulations of liposomes (250 nm in diameter) fully coated by proteins for cases of various spontaneous curvatures (indicated in bottom right corner, units: 1/nm). When the spontaneous curvature is sufficiently high, the liposome undergoes a topological transition into a tubular network, with the diameter of the tubules decreasing with increasing spontaneous curvature. Scale bars, 100 nm.

In Ayton et al. (2007), the simulations of a small liposome (about 140 nm in diameter) and tubules showed that an isotropic vs. an anisotropic spontaneous curvature can have a dramatic effect on the resulting membrane geometry. A subsequent study (Ayton et al., 2009) significantly extended the EM2 model by introducing a dependence of the membrane bending modulus and the spontaneous curvature on the BAR domain density, as well as introducing a different protein-membrane coupling mechanisms (namely IC and CC). Consequently, simulations of a large liposome (up to 500 nm in diameter) with protein parameters mimicking N-BAR and F-BAR domains were carried out to explore the membrane remodeling under various coupling mechanisms and values of protein-induced spontaneous curvature parameter (that corresponds to the value of spontaneous curvature induced by maximal protein concentration). In the case of the N-BAR (modeled by a spontaneous curvature parameter values in the range from 0.08 to 0.15 nm⁻¹), a large variety of reticulated, tubulated, and fully or partially vesiculated structures occurred. There is a good agreement with electron microscopy experiments imaging liposomes covered with N-BAR proteins endophilin and amphiphysin when using IC coupling and a spontaneous curvature parameter value of 0.08 nm⁻¹ (Ayton et al., 2009). On the other hand, the tubulation by an F-BAR domain (modeled by a 0.034 nm⁻¹ spontaneous curvature parameter value) is only seen when using an explicit oligomerization term that favors a nematic protein assembly, possibly implying a distinct remodeling mechanism by F-BAR domains.

In a recent work by Simunovic et al. (2013b), remodeling of liposomes 200–250 nm in diameter was explored by varying several parameters, namely bending stiffness, spontaneous curvature, protein-induced membrane stiffening, and the strength of protein oligomerization. The simulations showed three distinct structures: 1) bud formations, 2) irregular reticules, and 3) fully formed reticular structures (Fig. 3b).

Other discretized mesoscale models have also been developed in recent years. The dynamically triangulated membrane model (Ramakrishnan et al., 2012; Ramakrishnan et al., 2013; Sreeja et al., 2015) employs an in-plane nematic field that couples with membrane curvature to represent the anisotropic membrane inclusions. In work by Noguchi et al. (Noguchi, 2014; Noguchi, 2016; Shiba and Noguchi, 2011) a solvent-free meshless membrane model combined with banana-shaped protein rods also demonstrated the mesh formation by BAR proteins and how it leads to the formation of tubules. Interestingly, it was also demonstrated that the intermediate step in tubule formation depends on the direction of local curvature imposed by the proteins (Noguchi, 2016).

While mesoscopic simulations provide important insights into longer length and time scales, they are devoid of molecular-scale information. Theories and models that correctly extract the molecular information from mesoscopic simulations would be highly valuable, however it remains an extremely challenging task. A step in that direction was taken in a study by Lyman et al. (2011) where a method was developed that makes a connection between the CG and the EM2 models. In short, the method maps CG lipids and proteins atop a quasi-particle membrane configuration obtained in a mesoscopic simulation. This approach allows one to first run a mesoscopic simulation to induce large-scale changes of liposomes, then to continue simulating the same system, but using CG MD simulations, thus exploring the molecular details at much larger scales than accessible by MD. It provides an important step towards a truly multiscale approach, where information from different scales can be propagated in both directions.

4. Conclusions and Perspectives for the Future

In this Review, we focused on CG and mesoscopic approaches developed in our group that allowed us to study membrane remodeling by proteins at high resolution, but also at long length and time scales. To successfully model a complex cellular process such as membrane remodeling, in which the molecular and the macroscopic levels are innately connected, a careful consideration of all the scales is needed.

For the future, advances in modeling large biological systems will require us to derive a theoretical framework and a related computational approach that will make a systematic “bottom-up” connection between the CG and mesoscopic scale models, as well to more directly connect the simulations with experiments. Real cell membranes are highly complex, involving many lipids and proteins, an so the combined CG and mesoscopic modeling methods must steadily push toward a description of that level of real complexity. Moreover, the coupling of membranes and membrane proteins to the actin-based cytoskeleton is a critical phenomenon that must also be addressed. The future presents many challenges, but it also holds many opportunities for creative new theory and simulation approaches.