Abstract
The superior temporal gyrus (STG) and neighboring brain regions play a key role in human language processing. Previous studies have attempted to reconstruct speech information from brain activity in the STG, but few of them incorporate the probabilistic framework and engineering methodology used in modern speech recognition systems. In this work, we describe the initial efforts toward the design of a neural speech recognition (NSR) system that performs continuous phoneme recognition on English stimuli with arbitrary vocabulary sizes using the high gamma band power of local field potentials in the STG and neighboring cortical areas obtained via electrocorticography. The system implements a Viterbi decoder that incorporates phoneme likelihood estimates from a linear discriminant analysis model and transition probabilities from an n-gram phonemic language model. Grid searches were used in an attempt to determine optimal parameterizations of the feature vectors and Viterbi decoder. The performance of the system was significantly improved by using spatiotemporal representations of the neural activity (as opposed to purely spatial representations) and by including language modeling and Viterbi decoding in the NSR system. These results emphasize the importance of modeling the temporal dynamics of neural responses when analyzing their variations with respect to varying stimuli and demonstrate that speech recognition techniques can be successfully leveraged when decoding speech from neural signals. Guided by the results detailed in this work, further development of the NSR system could have applications in the fields of automatic speech recognition and neural prosthetics.
Keywords: neural speech recognition, speech perception, electrocorticography, high gamma, superior temporal gyrus, human auditory cortex
1. Introduction
A region of the human auditory cortex called the superior temporal gyrus (STG) is essential for understanding spoken language [1–6]. Previous studies have attempted to reconstruct the acoustics of speech using STG activity [5] and to understand how phonetic features, which are building blocks of spoken language, are encoded in this high-level region of auditory cortex [6].
A major focus in the field of automatic speech recognition (ASR) is to develop systems that replicate the human brain’s ability to convert acoustic signals into words and sentences. These systems, which have been successfully implemented in multiple industries [7, 8], typically involve the use of probabilistic frameworks and language modeling to decode speech from acoustic signals. Many of the well-established algorithms commonly used in ASR research are reasonably suited for continuous speech decoding tasks using non-acoustic speech-related time series data, such as neural response time series.
A few studies have attempted to use these approaches to decode continuous speech from cortical activity. One group used neural activity recorded during speech production tasks to perform speech decoding with a restricted vocabulary [9]. Another group focused primarily on decoding speech in a multi-speaker setting using neural activity during speech perception tasks [10]. Both of these works are examples of an emerging field of study we refer to as neural speech recognition (NSR). We use the term NSR to denote performing continuous speech recognition using neural responses as features. However, to the best of our knowledge, no published work has described the potential benefits of using ASR techniques to decode perceived continuous speech from neural signals in a single-speaker environment. This research direction could add to the field of NSR research by informing the development of a speech decoder that uses neural activity in auditory cortical areas (including the STG) and providing insight on effective representations of neural activity for the purpose of speech decoding.
For these reasons, we developed an initial version of a new NSR system. In its current state, our NSR system uses electrocorticography (ECoG) arrays to decode phoneme sequences from neural populations that respond to perceived speech. Compared to many state-of-the-art ASR systems, which typically incorporate neural network modeling techniques [11, 12], we designed our NSR system using simple modeling approaches. Relative to the acoustic features typically used in ASR, neural signals that encode speech information are poorly understood, noisy, and available in limited amounts. These factors influenced our decision to use models that are easier to train and interpret and involve fewer tunable parameters. Similarly, our decision to use phoneme-level (as opposed to word-level) decoding in this study, which is a commonly used approach in ASR research, was made for simplicity and in an attempt to gain a better understanding of the limitations of our system. Our primary goal is to help establish an informative foundation for future NSR research by contributing to existing literature in this field. By using optimization techniques to determine effective spatiotemporal feature representations and assessing the impact that individual model components have on the overall performance of the system, we provide novel insights to guide the development of more sophisticated NSR systems.
Future work involving the decoding of speech from neural activity could lead to the development of a speech prosthetic that restores communicative capabilities to impaired individuals, such as those with locked-in syndrome. Locked-in patients are awake and aware of their surroundings but are unable to communicate verbally due to paralysis [13], and only a few methods exist to restore basic communicative functions to locked-in patients [14]. These patients could benefit substantially from a device that interprets intended speech based on neural activity and, perhaps through a coupled speech synthesis system, allows more natural communication with others. Although the ideal control paradigm for a successful speech prosthetic is currently unknown, it could rely on covert speech production [15,16], covert speech perception [17], or an alternative method that has not been described yet. However, because such a device would almost certainly involve processing of neural response time series and probabilistic decoding of speech, we are confident that the approaches and results described in this work would be relevant to its design.
An overview of the current NSR system is depicted in figure 1. First, cortical local field potentials recorded from electrodes over the cortex of multiple subjects (which all include STG coverage) are preprocessed and restructured into high gamma window (HGW) feature vectors, which are spatiotemporal representations of the cortical responses. A phoneme likelihood model, trained using HGWs in conjunction with phonemic class labels, estimates, for each phoneme, the probability of observing an HGW given that it represents a neural response evoked during perception of that phoneme. A separately trained phonemic language model (LM) describes the a priori probabilities of different phoneme sequences. Finally, a Viterbi decoder, implementing the well-known hidden Markov model (HMM) architecture, incorporates probabilities from both of these models to yield the maximum a posteriori (MAP) phoneme sequence estimate given the input features.
Figure 1.

A schematic depiction of the NSR system (similar to Figure 9.3 in [18]). The rectangles signify processing steps and model components, and the circles signify data and computed probability distributions.
2. Materials and methods
2.1. Data collection and manipulation
2.1.1. Subjects
The three volunteer subjects (subjects A–C) who participated in this study were human epilepsy patients undergoing treatment at the UCSF Medical Center. ECoG arrays (Ad-Tech, Corp.) were surgically implanted on the cortical surface of each subject for the clinical purpose of localizing seizure foci. Each subject exhibited left hemisphere language dominance, which was determined by clinicians using either the Wada test or fMRI analysis. Prior to surgery, each of these patients gave their informed consent to be a subject for this research. The research protocol was approved by the UCSF Committee on Human Research.
2.1.2. Speech stimuli
For the experimental tasks, each subject listened to multiple speech stimuli. All stimuli were sampled at 16 kHz and presented aurally via loudspeakers at the subject’s bedside. Each stimulus contained a speech sample from a single speaker, and the stimuli were separated from each other by at least 500 ms of silence during presentation to each subject. We computed 39-element mel-frequency cepstral coefficient (MFCC) vectors (including energy, velocity, and acceleration features) for each stimulus [19–21]. We used two sets of speech stimuli: the TIMIT set and the Gump set. Information about the number of stimuli presented to and the amount of neural data collected from each subject is given in table 1.
Table 1.
The amount of neural data collected from each subject during perception of the stimuli from the TIMIT and Gump sets. The TIMIT and Gump sets comprised of 499 and 382 unique stimuli, respectively. The table specifies both durations excluding silence samples and total durations in minutes (after rounding). In addition, the total number of stimulus presentations and the mean number of presentations per unique stimulus for each set and each subject are given.
| Data set | Subject | Non-silence duration (min) | Total duration (min) | Total stimulus presentations | Mean presentations per stimulus |
|---|---|---|---|---|---|
| TIMIT | A | 29 | 54 | 1092 | 2.19 |
| B | 31 | 59 | 1197 | 2.40 | |
| C | 11 | 21 | 412 | 0.83 | |
| Gump | A | 47 | 87 | 847 | 2.22 |
| B | 50 | 92 | 868 | 2.27 | |
| C | 50 | 92 | 867 | 2.27 |
The TIMIT set consisted of phonetically transcribed stimuli from the Texas Instruments / Massachusetts Institute of Technology (TIMIT) database [22]. It contained 499 samples (1.9–3.6 s duration) that had a combined length of approximately 25 minutes and consisted of utterances from 402 different speakers. 354 of the stimuli were each generated by one of the 286 male speakers, and the remaining 145 stimuli were each generated by one of the 116 female speakers. The full stimulus set was not presented to subject C due to external constraints associated with experimentation in a clinical setting (such as clinical interventions and subject fatigue). Most stimuli were presented to each subject multiple times, although the number of presentations of each stimulus varied by subject due to these external constraints. As described in later sections, we used this data set to perform parameter optimization for various components of the NSR system.
The Gump set consisted of re-enacted natural speech samples from Robert Zemeckis’s Forrest Gump by two speakers (one male and one female). It contained 91 single word (0.3–1 s duration), 175 phrase (0.4–2.4 s duration), and 116 dialog (4.5–19.9 s duration) speech samples, with each speaker producing 191 of the samples. The combined length across all 382 samples was approximately 43 minutes, with a total of only about 24 minutes when ignoring silence sample points. Each stimulus was presented at least one time to each subject, although the number of presentations of each stimulus varied by subject due to the aforementioned external constraints. We obtained a phonetic transcription for each sample via forced alignment, which was performed using the Penn Phonetics Lab Forced Aligner [23], followed by manual segmentation, which was done in Praat [24]. As explained in section 3, we primarily used this data set to evaluate the performance of the system.
We used a set of 39 phonemic labels in both data sets: 38 phonemes from the Arpabet and /sp/, a silence phoneme used to label non-speech data points [25]. Some phonetic labels from the TIMIT transcriptions were converted into one of the 39 phonemic labels used in this work. For example, we converted all three of the different silence tokens used in TIMIT transcriptions (“pau”, “epi”, and “h#”) to /sp/. We also converted each occurrence of /zh/ in the TIMIT set to /sh/ due to its low occurrence rate in the TIMIT set (fewer than 0.15% of time points) and its absence from the Gump set. For analytical purposes, we separated these phonemes into 8 disjoint phonemic categories using descriptive phonetic features [26]. The 39 phonemes and their respective categorizations are shown in table 2.
Table 2.
The phonemes used in this work and their respective categorizations. For visual convenience, the coloring and ordering of the phonemes in this table are used in later figures.
| Category | Phoneme |
|---|---|
| Silence | sp |
| Stop | b d g p t k |
| Affricate | ch jh |
| Fricative | f v s z sh th dh hh |
| Nasal | m n ng |
| Approximant | w y l r |
| Monophthong | iy aa ae eh ah uw ao ih uh er |
| Diphthong | ey ay ow aw oy |
2.1.3. Neural recordings
Each implanted ECoG array contained 256 disc electrodes with exposure diameters of 1.17 mm arranged in a square lattice formation with a center-to-center electrode spacing of 4 mm. We used these arrays to record cortical local field potentials at multiple cortical sites from each subject during the speech perception tasks. The analog ECoG signals were amplified and quantized using a pre-amplifier (PZ2, Tucker-Davis Technologies), preprocessed using a digital signal processor (RZ2, Tucker-Davis Technologies), and streamed to a separate computer for storage. We acquired and stored the data at a sampling rate of approximately 3052 Hz. Each subject’s 3-D pial reconstruction, extracted from T1-weighted MRI data using FreeSurfer [27], was co-registered to his or her post-operative computerized tomography scan to determine the ECoG electrode positions on the cortical surface [28]. All subjects had unilateral coverage that included the STG; subjects A and B had left hemisphere coverage and subject C had right hemisphere coverage. The reconstruction and electrode positions for each subject appear in figure 2.
Figure 2.
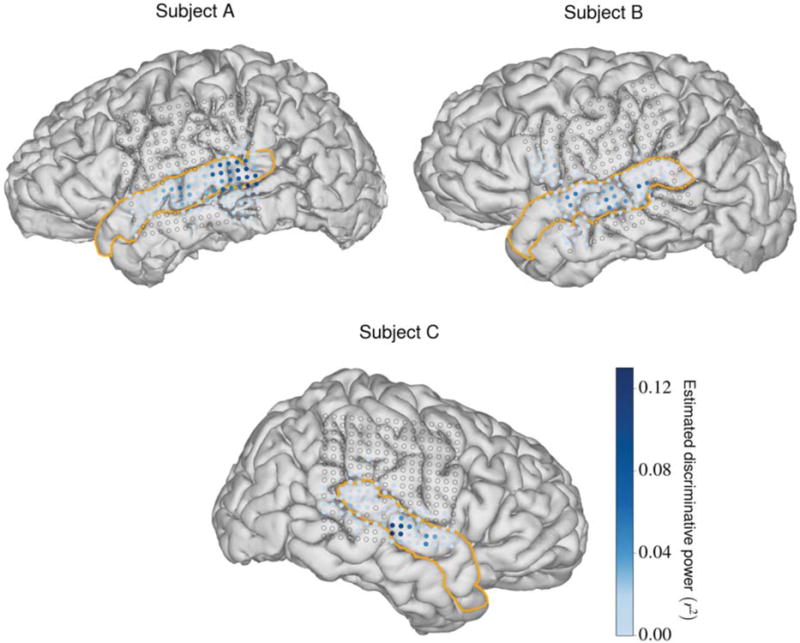
MRI reconstructions for each subject with electrode positions superimposed as dots. The sizes of the dots represent the relative sizes of the electrode contacts with respect to the brain. The STG is outlined in orange for each subject. Electrodes that were not deemed relevant appear as circular outlines (electrode relevance is discussed in section 2.1.4). Relevant electrodes are colored according to their estimated discriminative power (described in section 2.2.1), depicting the relative importance of each electrode for phoneme discrimination.
2.1.4. Preprocessing
We used MATLAB for preprocessing [29] and Python for all subsequent analyses (unless otherwise specified) [30]. After data collection, we first down-sampled the raw neural signals to 400 Hz and implemented notch filtering to reduce the mains hum noise at 60 Hz and its harmonics. Next, we qualitatively identified (via visual inspection) channels with severe artifacts and/or significant noise and rejected them. These rejected channels contained time segments that differed greatly in magnitude from the channels that were deemed normal, which is often caused by non-physiological factors (poor electrode contact with the cortical surface, electromagnetic interference from hospital equipment, defective electrodes or wires, etc.). We performed common average referencing on the remaining channels in an attempt to obtain a more favorable spatial representation of the ECoG data [31, 32].
Previous research has shown that high gamma band activity (70–150 Hz) correlates strongly with multi-unit firing processes in the brain [33] and is an effective representation of brain activity during speech processing [5,6,16,34]. For these reasons, we applied eight bandpass Gaussian filters with logarithmically increasing center frequencies between 70–150 Hz and semi-logarithmically increasing bandwidths to the neural responses from each electrode channel [34]. These center frequencies, rounded to the nearest decimal place and given in Hz, were 73.0, 79.5, 87.8, 96.9, 107.0, 118.1, 130.4, and 144.0. We then used the Hilbert transform to extract the time-varying analytic amplitudes from each of these eight filtered signals [35, 36]. We down-sampled these eight analytic amplitude signals to 100 Hz and individually z-scored each channel across each experimental session. We used a hyperbolic tangent function to perform soft de-spiking (similar to the methodology used in AFNI’s 3dDespike program) on each analytic amplitude signal, which reduced the magnitude of data points more than 10 standard deviations from the mean. We performed singular value decomposition on all eight analytic amplitude signals simultaneously (treating each signal as a single feature) and extracted the first principal component, which we then used to project the eight signals into a one-dimensional space. We used the resulting projection as the representation of high gamma activity in all subsequent analyses.
Since many electrodes for each subject recorded from areas of the cortex that are not associated with speech processing, we decided to only use activity from relevant electrodes during development and testing of the NSR system. Guided by a previously used method to find speech-responsive electrodes [37], we divided each subject’s high gamma activity during perception of the Gump set into speech and silence subsets using the phonemic transcriptions of the stimuli. For each channel, we conducted a t-test that compared all of the samples from each of these two subsets. We considered a channel relevant if the magnitude of the resulting t-value was greater than 2.54, which indicated that the channel was significantly modulated by the presence of a speech stimulus. This threshold value was qualitatively chosen after visual inspection of the high gamma activities for each channel. After these steps, subjects A, B, and C had 95, 89, and 74 relevant channels, respectively. The fewer number of relevant channels for subject C could be a result of electrode coverage over the language non-dominant hemisphere, although existing literature indicates that phonetic processing occurs bilaterally [38]. Over 50% of the relevant channels for each subject were located in the STG. In figure 2, the relevant electrode locations for each subject are depicted as colored dots and the remaining electrode locations are depicted as circular outlines.
2.1.5. Data reorganization
After preprocessing, a phonemic transcription and associated time sequences of high gamma activity from the relevant electrodes for each subject were available for each acoustic stimulus. An example of one such set of experimental task data is given in figure 3. This figure includes a visual representation of the phonemic transcription, which is referred to as an “actual posteriogram”.
Figure 3.
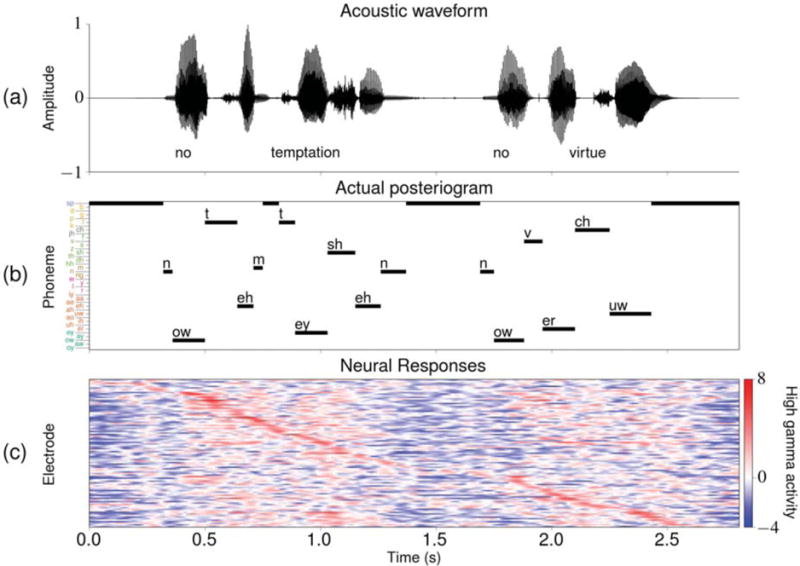
Sample task data associated with the utterance “No temptation, no virtue” from the TIMIT set. Some of the silence data points at the start and end of the stimulus were excluded from the visualizations. (a) The acoustic waveform along with the associated word transcription. (b) The actual posteriogram, which is a visualization of the phonemic transcription associated with this stimulus that depicts which phoneme is specified at each time point in the task. The ordering and coloring of the phoneme labels on the vertical axis are consistent with what was presented in table 2. (c) The preprocessed high gamma activity at each of the 95 relevant electrodes for subject A during perception of a single presentation of the stimulus. The electrodes are sorted from top to bottom in ascending peak activity time (i.e. the time at which the electrode exhibited its highest value during this task).
We created 10-fold cross-validation folds for the Gump and TIMIT sets. Each fold contained approximately 90% of the stimuli from the corresponding data set as training data and the remainder as test data. Each stimulus appeared in the test data for exactly one of the folds. In an attempt to increase homogeneity between folds, we constructed the folds for each of the two data sets such that the numbers of each type of stimuli present in the test data of each fold were approximately equal across all folds. For the 10 TIMIT folds, the two types of stimuli were characterized as being generated by either a male or female speaker. For the 10 Gump folds, the six types of stimuli were characterized as either a word, phrase, or dialog speech sample generated by either the male or female speaker. We performed the majority of our analyses using one or more of these folds.
2.1.6. Feature selection
Auditory speech stimuli evoke complex spatiotemporal cortical responses that can start tens of milliseconds after the acoustic onset and last hundreds of milliseconds after the acoustic offset [3,6,39–41]. In an attempt to more accurately model these activation patterns in our NSR system, we used high gamma windows (HGWs) as feature vectors. Each HGW contains multiple data points of high gamma activity within a pre-specified time window across all of the relevant electrodes. Thus, HGWs represent the responses both spatially (by using multiple electrodes) and temporally (by including multiple points in time). Using HGWs as features contradicts a key conditional independence assumption of the HMM architecture utilized by the Viterbi decoder which states that yt ╨ yt−1 | qt, where qt and yt are the phonemic label and feature vector, respectively, at time t. Despite this, we hypothesized that our NSR system would benefit by using these spatiotemporal feature vectors, similar to how performance gains are observed in some ASR systems when velocity and acceleration components are included in the feature vectors [21].
The HGWs are parameterized by three values: (1) initial delay, which is the amount of time between the phoneme time point and the first HGW data point, (2) duration, which is the time length of the HGW, and (3) size, which is the number of evenly spaced time points within the time window specified by the first two parameters to include. For example, an HGW parameterized by an initial delay of 50 ms, a duration of 60 ms, and a size of 4 would consist of the data points occurring 50, 70, 90, and 110 ms after the corresponding phoneme time point. We performed grid searches to choose the optimal values for these parameters for each subject. The search included initial delay values between 0–490 ms, durations between 0–490 ms, and sizes between 1–25 points. Because the sampling rate of the high gamma activity was 100 Hz, we evaluated the initial delay and duration parameters in 10 ms increments and used rounding when necessary to find indices within the data sequences that most closely corresponded to their related time values. We ignored invalid parameterizations, such as those that used sizes above 4 when the duration was 30 ms. We also ignored parameterizations that included data points occurring 500 ms or more after the corresponding phoneme time point. Any parameterization in which the size was 1 point, which results in a spatial feature vector using the activity at each electrode for a single time point, is referred to as a high gamma slice (HGS). Phoneme likelihood models, which are discussed in section 2.2.1, were trained and tested with feature vectors constructed using each parameterization. For each subject, we performed a grid search using the neural responses recorded from that subject during each stimulus presentation specified by one arbitrarily-chosen TIMIT cross-validation fold. The performance metric used in each grid search was the average posteriogram accuracy computed from the estimated posteriograms generated for the test data, which is a measure of the frame-by-frame prediction accuracy (see section 3.1.2 for more details).
The results of these grid searches are given in table 3. The time offsets represent which time points are used when constructing each feature vector. For example, the grid search results for subject A indicate that the optimal HGW for a phoneme occurring at time t contains the high gamma activity values for each relevant electrode at the time points occurring 70, 130, 190, and 250 milliseconds after t. For later comparison against the system’s performance when using the optimal HGW, we also determined the optimal HGS for each subject. For subject A, this occurred at a delay of 100 ms, meaning that the optimal HGS for a phoneme at time t contains the high gamma values for each relevant electrode at t + 100 ms. Although the optimal HGS time offsets were relatively consistent across subjects, the optimal HGW parameterizations were more varied. This observation could be explained by differences in one or more subject-specific factors, such as electrode coverage, number of relevant electrodes, and cortical structure. The optimal parameterizations for subject A are depicted in figure 4 along with sample neural response patterns. The results of these grid searches resemble findings reported in related literature [42].
Table 3.
The results of the feature selection grid searches for each subject. The optimal values for the three HGW parameters found in each grid search are given along with the time offsets calculated from these parameters. The optimal HGS time offset value found in each search is also given.
| Subject | High Gamma Window (HGW)
|
High Gamma Slice (HGS)
|
|||
|---|---|---|---|---|---|
| Initial delay (ms) | Duration (ms) | Size (points) | Time offsets (ms) | Time offset (ms) | |
| A | 70 | 180 | 4 | {70, 130, 190, 250} | 100 |
| B | 10 | 230 | 6 | {10, 60, 100, 150, 190, 240} | 90 |
| C | 0 | 210 | 5 | {0, 50, 100, 160, 210} | 120 |
Figure 4.
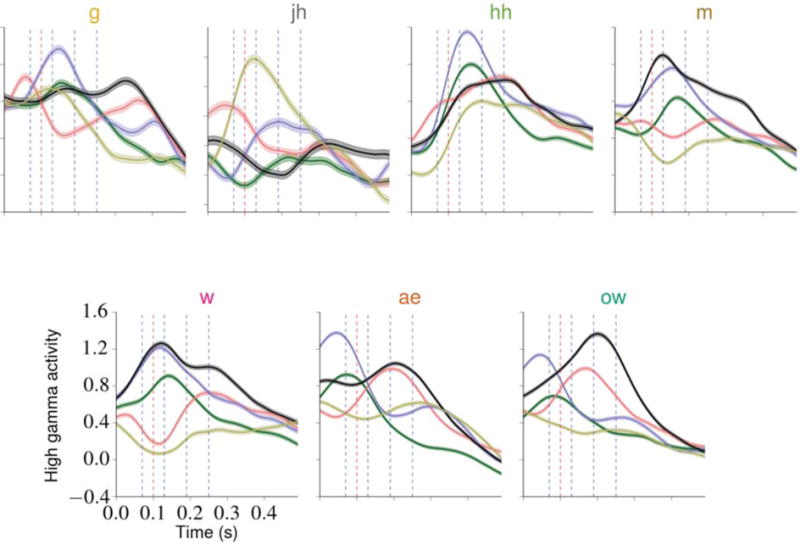
A depiction of evoked spatiotemporal response patterns and the computed optimal HGW and HGS parameterizations. At each time point in the TIMIT set specifying one of seven hand-selected phonemes, the high gamma activities recorded from the relevant electrodes for subject A during the succeeding 490 ms were obtained, resulting in approximately 3400 time series per phoneme (on average). From these, the mean response time series for each electrode and phoneme was computed. Each plot contains, for one phoneme, the mean time series for the five electrodes that exhibited the highest estimated discriminative power (as described in section 2.2.1), depicted as colored curves (the coloring is consistent across the individual plots). One standard error of the mean above and below each electrode curve is included. This subset of seven phonemes contains at least one phoneme from each of the non-silence phonemic categories, and the coloring of the phoneme labels is consistent with the phonemic category coloring introduced in table 2. The optimal HGW contains the values for each electrode at each time point marked with a blue vertical dashed line, and the optimal HGS contains the value for each electrode at the time point marked with a red vertical dashed line at t = 100 ms. These plots illustrate the complex spatiotemporal dynamics exhibited by the evoked responses and how these response patterns vary across the phonemes, suggesting that modeling these dynamics (by using HGWs, for example) is beneficial during discrimination tasks.
2.2. NSR system design
2.2.1. Phoneme likelihood model
The phoneme likelihood model used in this NSR system implemented the linear discriminant analysis (LDA) method [43]. Although LDA is commonly used as a dimensionality reduction technique, we used it as a classifier trained on the continuous-valued feature vectors (y) and the associated phonemic classes (q). The model fits multivariate Gaussian densities to each class using labeled training data. It assumes that the feature data are normally distributed and that the covariance matrix used to parameterize each class’s Gaussian distribution is equal across all classes. An LDA model was chosen due to its simplicity (it has a closed-form solution and no parameters to tune) and its performance in early ASR systems [44]. Additionally, previous work has shown that the STG linearly encodes some phonetic features in the high gamma band [6], which helps to motivate the choice of a linear model such as LDA. We implemented this model using the scikit-learn Python package [45].
For an unseen feature vector yt at some time t, the trained LDA model computes likelihood estimates p (yt|qt = k) using the fitted Gaussian density associated with each class (phoneme) k. From this, we can use Bayes’ rule to compute the phoneme posteriors p (qt = k|yt):
where p (qt = k) is the prior probability distribution over the phonemic classes. We computed these priors from the relative frequency of each phonemic class in the training data. Note that these priors do not change over time within a single task, but they can change between cross-validation folds. To obtain phoneme posterior probability distributions that sum to one at each time point, we used the following formula:
where Q is the set of all possible phonemic classes.
We also used the LDA model to estimate the discriminative power provided by each electrode channel. For each subject, we trained an LDA model using HGWs and all of the data in the Gump set. Then, for each feature in the LDA model, we computed the variance of the class means, representing a measure of between-class variance for that feature. The values along the diagonal of the shared covariance matrix represented a measure of the within-class variances for each feature (this is only an approximation of within-class variance because we did not force diagonal covariance matrices in the LDA model). The discriminative power for each feature was estimated using the following formula:
where , , and are the estimated discriminative power, within-class variance, and between-class variance, respectively, for the ith feature. For each electrode, the r2 values for each feature that specified a time point for that electrode in the HGW were averaged, yielding an estimated discriminative power for that electrode. For each subject, the relevant electrodes in the STG accounted for more than two-thirds of the total estimated discriminative power across all relevant electrodes. The r2 values for each relevant electrode for each subject are depicted in figure 2.
2.2.2. Phonemic language model
The language model (LM) used in the NSR system provides estimates for the a priori probabilities of phonemic sequences. Phoneme LMs are typically trained on large corpora containing phoneme sequences. We decided to construct a phoneme corpus by phonemically transcribing English sentences contained in the SUBTLEX-US corpus, which was created using the subtitles from many American films and television series [46]. The Festival speech synthesis system was used to convert the sentences into phoneme sequences [47]. Some sentences were excluded, such as short sentences with fewer than 6 phonemes and sentences that the Festival system was not able to phonetize. All /ax/ and /zh/ phoneme tokens were converted to /ah/ and /sh/ tokens, respectively. Any phoneme sequence which exactly matched the phoneme sequence associated with any of the Gump stimuli was excluded in an effort to keep the LM more generalized. A silence phoneme (/sp/) token was inserted at the end of the phoneme sequence transcribed from each sentence so that the sequences could be combined into one large corpus. Approximately 4.3 million sentences were included, resulting in a phoneme corpus with about 76.9 million non-silence phonemes (a total of about 81.2 million phoneme tokens when /sp/ is included).
Because of the relatively simple implementation and robust performance of n-gram LMs, we decided to choose between one of two different types of interpolated n-gram LMs for use in the NSR system: a basic n-gram LM using additive smoothing [48,49] and a modified Kneser-Ney n-gram LM [49, 50]. Although the modified Kneser-Ney n-gram LM typically outperforms other n-gram LMs when used in word-level ASR systems, it might not be as suitable for phoneme-level decoding because of the relatively small number of tokens (the 39 phoneme tokens) we use in our NSR system. We compared the performance of these two types of LMs using orders of n ∈ {1, 2, 3, 4, 5}. Each LM was trained using the aforementioned corpus and tested on a phoneme corpus constructed by concatenating the phonemic transcriptions of the 499 stimuli in the TIMIT set (including a silence phoneme between stimuli). We used the perplexity of the LM on the test corpus as the evaluation metric (a lower perplexity indicates better performance) [49]. Given the results of this analysis, which are depicted in figure 5, we decided to use the basic 4-gram LM (trained on the previously described phoneme corpus) in our NSR system.
Figure 5.
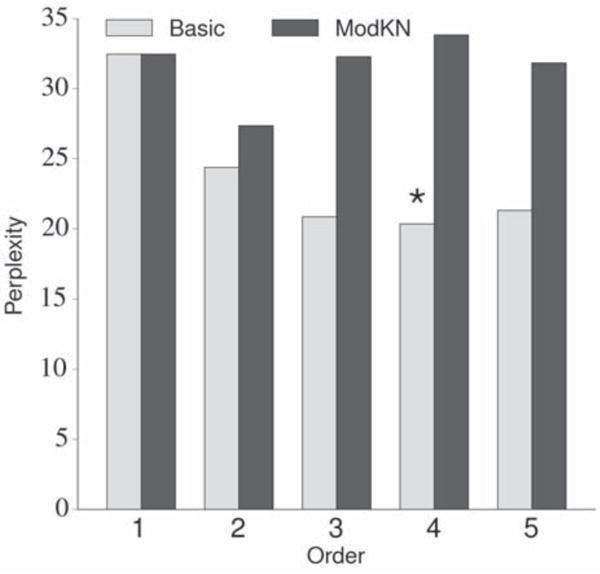
A comparison of the basic and modified Kneser-Ney n-gram phonemic language models using multiple orders. The labels “Basic” and “ModKN” refer to the basic additive smoothing and modified Kneser-Ney n-gram LMs, respectively. The same training and testing corpora were used for each LM. A lower perplexity value indicates better performance. The basic additive smoothing 4-gram model (marked with an asterisk) exhibited the best performance, with a perplexity of 20.33.
For a given sequence of phonemes, the basic 4-gram LM provides conditional probability estimates of for each phonemic class k at each index i within the sequence, where the notation denotes the ath through the bth phonemes in the sequence. The phonemic sequences used in LMs contain no information about phoneme durations; a phoneme that spans any number of time points will be represented as a phoneme at a single index in these phonemic sequences. For notational simplicity, these conditional probabilities are sometimes represented as p (qt), which suppresses their implicit dependence on the three distinct phonemes that precede the phoneme at time t. These probabilities should not be confused with the priors discussed in the previous section. In general, the conditional probabilities for a basic additive smoothing n-gram LM are computed recursively using the following formula [49]:
Here, is the count of the number of times the n-gram occurs in the corpus, δ is the additive smoothing factor that is added to the count of each n-gram (typically 0 ≤ δ ≤ 1), Q is the set of all possible phonemes, and λn is the interpolation weight for the order n. In our NSR system, we used n = 4, δ = 0.1, and .
2.2.3. Viterbi decoder
We implemented a Viterbi decoding algorithm to provide MAP phoneme sequence estimates given a sequence of likelihood estimates (from the likelihood model) and phoneme transition probabilities (from the LM) [18, 51]. The algorithm uses Viterbi path probabilities, which are computed recursively using the following formula:
Here, vt (j) is the jth Viterbi path’s log probability at time t, vt−1 (i) is the ith Viterbi path’s log probability at time t−1, p (yt|qt) is the likelihood of observing the feature vector yt given qt (provided by the phoneme likelihood model), p (qt) is the prior probability of observing phoneme qt at time t (provided by the LM), L is the language model scaling factor (LMSF), P is the phoneme insertion penalty, and nt is an indicator variable that is 1 if and only if qt for path j is not equal to qt−1 for path i. At every time point, the likelihoods p (yt|qt) are normalized such that they sum to one across all phonemes.
Paths are computed for each combination of i ∈ {1, 2, …, It−1} and qt ∈ Q, where It−1 is the total number of paths at time t − 1 and Q is the set of all possible phonemic classes. This results in a new path for each j ∈ {1, 2, …, |Q| It−1} at time t. For example, if there are 12 paths at time t − 1 and 39 phonemes, then there will be 468 paths at time t (prior to pruning). We used log probabilities for computational efficiency and numerical stability. To initialize the recursion, we forced each decoding to start at time t = 0 with q0 = /sp/ and a possible Viterbi path set of {v0 (1) = 0}. After computation of all of the vt (j) log probabilities for each t, we performed two steps of pruning. First, we performed a beam search to prune unlikely paths between iterations by discarding paths that did not satisfy
Here, z indexes over all paths available at time t and c is the beam search criterion, which we set equal to 50. Afterwards, we only retained a maximum of 100 of the most likely paths between iterations. The decoded MAP phoneme sequence is specified by the path at index m at time T, where m = arg maxu vT (u), T is the final time point, and u indexes over all paths available at time T.
The three main tunable parameters of this Viterbi decoding algorithm are the LMSF, the phoneme insertion penalty, and the self-transition probabilities. The LMSF controls the relative strength of the LM (as compared to the strength of the phoneme likelihood model). Because the normalized likelihoods p (yt|qt) and LM probabilities p (qt) each sum to one at every time point, the LMSF represents the ratio of the strength of the LM to the strength of the likelihood model. The phoneme insertion penalty (P) controls the preference for decoding short vs. long phoneme sequences. The self-transition probability (s) specifies the probability at each time point that a self-transition will occur, which is important because phonemes typically last for more than one time point. This probability replaces the probabilities given by the LM for p (qt) when qt = qt−1. Note that in the context of phoneme-level decoding (as opposed to word-level decoding), the self-transition probability is similar to the phoneme insertion penalty in that it also controls the preference for decoding short vs. long phoneme sequences.
We used grid searches to determine the optimal values for these three parameters. For each subject, we obtained likelihood estimates at each time point for each TIMIT stimulus presentation. These likelihoods were obtained from likelihood models trained with HGW feature vectors using the TIMIT cross-validation scheme. We also obtained likelihood estimates using feature vectors from all subjects simultaneously (as described in section 3) and using MFCC features. Using these likelihood estimates, we evaluated the performance of the decoder when parameterized by all possible combinations of , and . The performance metric used was the value of the expression (1 − ε) + γ, where ε and γ are the average phoneme error rate and posteriogram accuracy, respectively, across all of the results for a given parameterization (these metrics are explained in section 3.1). The results of this grid search for each subject, for all subjects simultaneously, and for the acoustic features are given in table 4.
Table 4.
The optimal values for the three Viterbi parameters found by the grid searches using MFCC features, neural features for each subject, and neural features for all subjects simultaneously.
| Subject | LMSF (L) | Phoneme insertion penalty (P) | Self-transition probability (s) |
|---|---|---|---|
| MFCC | 2 | −1 | 0.4 |
| A | 2 | −1 | 0.3 |
| B | 2 | −1 | 0.9 |
| C | 3 | −1 | 0.1 |
| All | 2 | −2 | 0.4 |
3. Results
We evaluated the performance of the NSR system using multiple feature sets and metrics. Each evaluation used all 10 of the Gump cross-validation folds. We conducted evaluations using either HGSs or HGWs as feature vectors. For each subject, we performed evaluations with single-trial data (using high gamma activity from each stimulus presentation individually) and averaged data (using high gamma activity averaged across all of the presentations of each stimulus). In addition to these analyses using responses from individual subjects, we also performed evaluations using concatenated feature vectors from all of the subjects; because the neural response data are time-aligned to the stimuli and the stimuli are identical across subjects, we were able to generate feature vector time sequences using data from all of the subjects simultaneously for each stimulus by concatenating the feature vectors (averaged across stimulus presentations) from each subject during perception of the stimulus.
For each evaluation, we obtained results using two types of predictions: “estimations” and “decodings”. Here, estimations refer to the phoneme sequences constructed by choosing the most likely phoneme at each time point from the phoneme posterior probabilities provided by the LDA model, and decodings refer to the MAP phoneme sequences provided by the Viterbi decoder. Continuing with the notation introduced in section 2.2.1, we computed the estimated phoneme sequences using = arg maxk p (qt = k|yt) at each time point, where is the estimated phoneme at time t in one of the stimuli. By comparing the estimation and decoding results, it is possible to measure the impact that language modeling and Viterbi decoding had on the performance of the system.
We performed a separate evaluation that used MFCCs as features to assess how well a similarly-designed ASR system would perform on the stimuli. Additionally, we evaluated chance performance by decoding the non-silence phoneme with the most time points in the training set, which was always /s/, at each time point. When considering frame-by-frame accuracy, this is a more conservative method of chance performance than simply using 1 divided by the number of classes (which would be about 2.6% for the 38 non-silence phonemes). We assessed the performance of the NSR system using three evaluation metrics to measure the similarities between the predicted and actual phoneme sequences: phoneme error rate, posteriogram accuracy, and confusion accuracy.
3.1. Evaluation metrics
3.1.1. Phoneme error rate
In ASR research, the word error rate evaluation metric is commonly used to assess the performance of a speech recognition system [7]. One of the main advantages of using this metric is that it evaluates performance by directly using predicted word sequences, which are what end users of many ASR systems interact with. The analog of this metric when used in the context of phoneme-level recognition is the phoneme error rate (PER), which is a measure of the Levenshtein distance between actual and predicted phoneme sequences. The PER for a predicted phoneme sequence can be computed using the following formula:
Here, S, D, and I specify the minimum number of substitutions, deletions, and insertions (respectively) required to transform the predicted phoneme sequence into the reference (actual) sequence, and N denotes the number of phonemes in the reference sequence. A lower PER value signifies better performance. Note that it is possible for PER values to exceed 1.0; for example, if the predicted sequence was /ay n ow/ and the reference sequence was /ay/, the PER value would be 2.0, with S = I = 0, D = 2, and N = 1.
The PER metric uses sequences that have been “compressed” by removing all silence phonemes from the sequences and then traversing each sequence in order and removing any phoneme that occurs immediately after an identical phoneme. Therefore, compressed sequences do not contain information about the time durations of any item in the sequence, which is typically not relevant for the end users of ASR systems. Note that the PERs for estimation results tend to be relatively large and are primarily included in the results for completeness; typically, PERs are only informative for decoding results.
3.1.2. Posteriogram accuracy
We constructed estimated and decoded posteriograms, which use estimated and decoded phoneme sequences, respectively, to visually represent predicted phoneme sequences. Sample posteriograms, along with the related time sequence of phoneme posteriors, are given in figure 6. The posteriogram accuracy is a measure of the frame-by-frame accuracy of a predicted posteriogram; it represents the fraction of time points within a given stimulus for which the predicted phoneme was equal to the actual phoneme. This metric does not use compressed sequences and is sensitive to the time durations of the predicted phonemes. For this metric, we excluded any data points for which the actual phoneme was the silence phoneme; although detecting the absence of speech will likely be an important aspect of an applied NSR system, including these points led to performance overestimation due to increased posteriogram accuracy for each prediction. For alternative evaluations that included silence time points, refer to table S1 and table S2.
Figure 6.
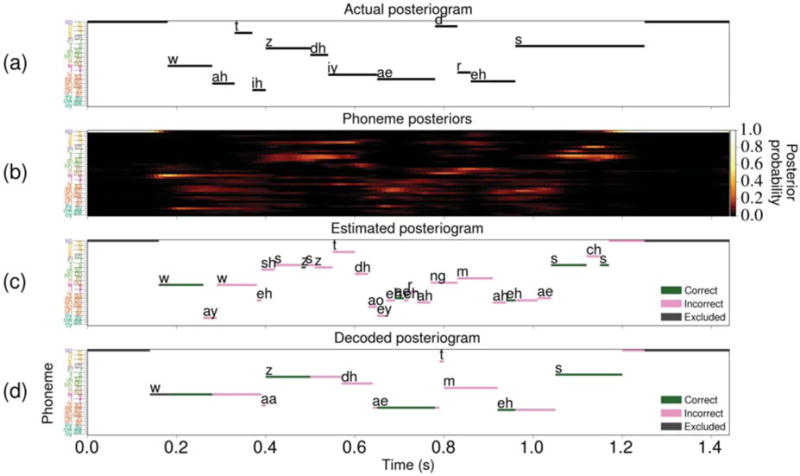
A sample set of results obtained using HGWs from subject A during perception of the utterance “What is the address?” by a female speaker in the Gump set. In all four visualizations, the ordering and coloring of the phoneme labels given in table 2 are used. Some of the data points specifying silence at the start and end of the stimulus were excluded from the visualizations. (a) The actual posteriogram showing the phonemic transcription of the stimulus. (b) The phoneme posterior probability distribution at each time point during the task. (c) The estimated posteriogram constructed by classifying the phoneme posteriors in (b) using the most likely phoneme at each time point. Here, the green and pink points signify classifications that were considered correct and incorrect, respectively. Dark gray points signify data that were excluded from the calculation of the posteriogram accuracy. (d) The decoded posteriogram computed by the Viterbi decoder, which is represented using the same coloring scheme as the estimated posteriogram. For this specific decoding result, the posteriogram accuracy is 48.6% and the phoneme error rate is 50.0%.
3.1.3. Confusion accuracy
We computed phoneme confusion matrices, such as the ones shown in figure 7, for each evaluation using the confusions between the actual and predicted phonemes for each time point in each stimulus. We normalized the confusion matrices by row such that the confusion values for any actual phoneme would sum to 1 across all of the predicted phonemes. The values along the diagonal of the matrix are measures of the model’s ability to correctly classify each phoneme. The confusion accuracy is defined as the mean of these values, which is effectively a re-scaled measure of the matrix’s trace. Consequently, this metric does not directly depend on the number of available time points for each phoneme; it weighs the classification accuracy for each phoneme equally. This metric can be used to identify whether or not the system only successfully predicts common phonemes, which would negatively affect the confusion accuracy more drastically than posteriogram accuracy. We also excluded the value along the diagonal for the silence phoneme when computing this metric to prevent performance overestimation. For alternative evaluations that include this silence value, refer to table S1 and table S2. Confusion matrices for all of the HGW results and comparisons between these confusion matrices and the ones for MFCCs are provided in figure S1.
Figure 7.
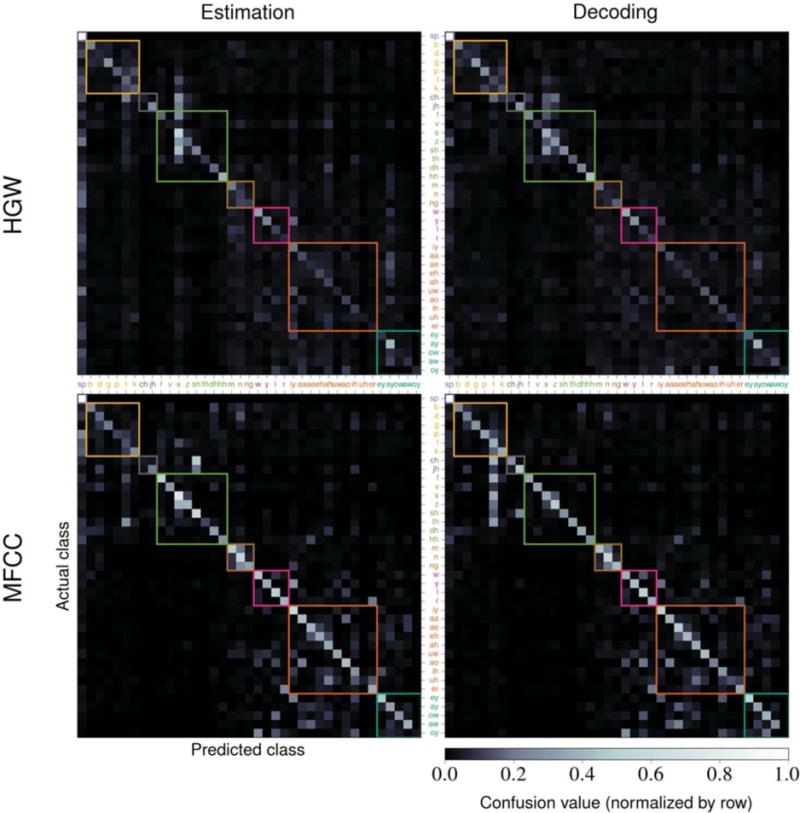
A sample set of confusion matrices computed using the performance evaluation results. The top row contains results using averaged HGWs from subject A and the bottom row contains results using MFCCs. The left column contains estimation results and the right column contains decoding results. The color-value mapping is identical across all matrices and uses row-normalized confusion values. The colored square outlines signify phonemic categories and correspond to the ordering and coloring of the phonemes on both axes (which match what was given in table 2). Confusion accuracies were computed by taking the mean value along the diagonal (excluding the silence phoneme value).
3.2. System performance
The performance of the NSR system for subject A and for the concatenated feature vectors is depicted in figure 8. The results of the system’s full performance evaluation are summarized in table 5.
Figure 8.
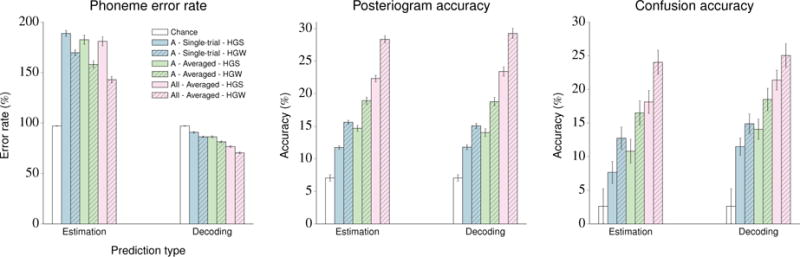
Visualization of the performance evaluation of the NSR system on the stimuli within the Gump set using single-trial and averaged HGSs and HGWs from subject A and concatenated feature vectors across all subjects. Chance performance is also included. Error bars indicate standard error of the mean. The results for all of the subjects with standard deviations are given in table 5.
Table 5.
Performance evaluation of the NSR system on the stimuli within the Gump set using three different types of feature vectors (MFCCs, HGSs, and HGWs) across four different subject sets (the three individual subjects and one combination of all subjects). Both single-trial and averaged neural response feature vectors were evaluated. Chance performance, which involves predicting the most likely phoneme /s/ at each time point, is also included. The phoneme error rate, posteriogram accuracy, and confusion accuracy metrics are used to assess the estimation and decoding results. All results are given as percentages in the following form: mean ± standard deviation.
| Feature set
|
Results
|
||||||
|---|---|---|---|---|---|---|---|
| Estimation
|
Decoding
|
||||||
| Feature type | Subject(s) | Phoneme error rate (%) | Posteriogram accuracy (%) | Confusion accuracy (%) | Phoneme error rate (%) | Posteriogram accuracy (%) | Confusion accuracy (%) |
| Chance | − | 97.12 ± 5.34 | 7.06 ± 9.77 | 2.63 ± 16.01 | 97.12 ± 5.34 | 7.06 ± 9.77 | 2.63 ± 16.01 |
| MFCC | − | 208.16 ± 67.45 | 40.45 ± 10.76 | 34.51 ± 16.15 | 60.60 ± 25.16 | 41.88 ± 17.30 | 36.30 ± 10.86 |
| Single-trial HGS | A | 188.73 ± 90.28 | 11.74 ± 7.98 | 7.67 ± 10.03 | 90.84 ± 25.00 | 11.79 ± 10.88 | 11.49 ± 7.94 |
| B | 176.91 ± 114.31 | 7.72 ± 6.02 | 4.79 ± 4.96 | 92.31 ± 26.43 | 10.23 ± 11.06 | 9.63 ± 5.52 | |
| C | 173.83 ± 92.48 | 9.00 ± 6.76 | 4.80 ± 7.22 | 87.67 ± 17.36 | 10.70 ± 11.58 | 8.16 ± 6.23 | |
| Single-trial HGW | A | 169.68 ± 84.89 | 15.62 ± 9.21 | 12.76 ± 10.12 | 86.34 ± 22.07 | 15.06 ± 11.73 | 14.89 ± 9.01 |
| B | 151.70 ± 78.01 | 12.69 ± 8.18 | 9.58 ± 5.89 | 90.63 ± 26.28 | 12.71 ± 11.49 | 11.80 ± 5.96 | |
| C | 152.48 ± 75.98 | 12.93 ± 8.77 | 8.09 ± 8.22 | 85.71 ± 17.30 | 12.62 ± 12.10 | 9.84 ± 6.40 | |
| Averaged HGS | A | 182.53 ± 89.81 | 14.68 ± 8.87 | 10.81 ± 10.80 | 86.37 ± 20.83 | 14.03 ± 11.72 | 14.07 ± 9.28 |
| B | 182.80 ± 99.75 | 11.95 ± 7.82 | 8.21 ± 6.92 | 87.13 ± 18.01 | 13.51 ± 11.30 | 12.59 ± 7.26 | |
| C | 181.75 ± 78.74 | 12.22 ± 8.01 | 7.08 ± 9.01 | 85.36 ± 13.67 | 12.41 ± 11.45 | 10.01 ± 6.56 | |
| All | 180.87 ± 84.47 | 22.34 ± 9.94 | 18.14 ± 10.47 | 76.68 ± 15.82 | 23.41 ± 13.85 | 21.39 ± 9.12 | |
| Averaged HGW | A | 158.00 ± 69.86 | 18.93 ± 10.39 | 16.49 ± 10.99 | 81.39 ± 18.85 | 18.79 ± 12.57 | 18.49 ± 10.30 |
| B | 149.66 ± 65.27 | 17.35 ± 9.46 | 13.80 ± 7.30 | 82.84 ± 21.02 | 17.64 ± 13.31 | 15.30 ± 6.99 | |
| C | 157.35 ± 73.80 | 16.42 ± 9.84 | 11.20 ± 8.79 | 83.65 ± 19.18 | 15.36 ± 13.02 | 12.27 ± 7.99 | |
| All | 142.96 ± 61.31 | 28.36 ± 10.47 | 24.02 ± 10.99 | 70.47 ± 16.77 | 29.26 ± 14.88 | 25.03 ± 10.69 | |
In the figure and the table, the statistics for the phoneme error rate and posteriogram accuracy metrics are computed using the individual results from each stimulus, and the statistics for the confusion accuracy metric are computed using the values along the diagonal of the overall confusion matrix.
We performed a variety of statistical significance tests on these results, using the one-tailed Wilcoxon signed-rank test (abbreviated to Wilcoxon) for paired comparisons and the one-tailed Welch’s t-test (abbreviated to Welch’s) for unpaired comparisons. We use a significance level of α = 0.01 during assessment of our results.
All of the HGW decoding results were significantly better than the HGS estimation results for all subject sets (each individual subject and the concatenated features) and metrics (Wilcoxon, p < 10−6).
All of the HGW results were significantly better than the HGS results for all subject sets and metrics (Wilcoxon, p < 0.005).
The decoding results were significantly better than the estimation results when evaluated with the PER metric for all subject sets (Wilcoxon, p < 10−11). Similarly, confusion accuracies were significantly better for decoding results than for estimation results (Wilcoxon, p < 0.01) for all evaluations except the ones using averaged HGWs from subject C and concatenated HGWs. However, significant improvements were not observed for many of the evaluations when using the posteriogram accuracy metric, and in some instances the mean decoding posteriogram accuracies were lower than the estimation posteriogram accuracies.
Averaged neural feature vectors outperformed their single-trial counterparts for each subject when using the posteriogram accuracy metric (Welch’s, p < 0.01). Except when HGWs from subject C are used, this was also observed for comparisons involving decoding PERs (Welch’s, p < 0.01). This was not observed for the majority of the confusion accuracy or estimation PER comparisons.
The concatenated feature vectors performed significantly better than individual subject feature vectors when evaluated with each metric other than the estimation PER metric (Wilcoxon for averaged results, Welch’s for unaveraged results, p < 10−5).
MFCC features significantly outperformed neural features when evaluated with each metric other than the estimation PER metric (Wilcoxon for averaged results, Welch’s for unaveraged results, p < 10−5).
Neural features performed better than chance in most situations (Wilcoxon for averaged results, Welch’s for unaveraged results, p < 0.01). The exceptions comprised of all estimation PER comparisons, a subset of the single-trial confusion accuracy results, and the single-trial estimation posteriogram accuracy result with HGSs for subject B.
3.3. Phoneme time position effects
Previous research has shown that transient responses to the onset of an acoustic stimulus are exhibited by some neurons in the auditory cortex of rats [52, 53] and humans [54, 55]. If similar response patterns are present in our ECoG data, we can expect the performance of our phoneme likelihood estimator to vary throughout the duration any given utterance. Specifically, we hypothesize that NSR performance degrades over the course of an utterance due to temporal complexities present in the evoked neural response patterns, such as sensitivity to stimulus onsets. Additionally, we expect that these same effects are not present in the acoustic features.
To assess this hypothesis, we analyzed the impact that phoneme time position had on posteriogram accuracy for both acoustic and neural features. Here, the time position of a phoneme is equal to the amount of elapsed time between the utterance onset and the phoneme time point. We defined the onset of an utterance to be the onset of any non-silence phoneme that occurs immediately after a period of silence lasting 500 ms or longer (we did not simply use the first non-silence phoneme in each stimulus because some of the longer Gump stimuli contained multiple sentences). For each feature type, we used the estimated posteriograms generated for the 382 Gump stimuli to constructed a data set using each time point in the corresponding actual posteriograms specifying a non-silence phoneme. Each datum in this new data set specified the stimulus identity, the phoneme time position, and a binary indicator that was 1 if that time point was correctly classified in the estimated posteriogram and 0 otherwise. A depiction of these data sets for MFCCs and averaged HGWs from subject B is provided in figure 9.
Figure 9.
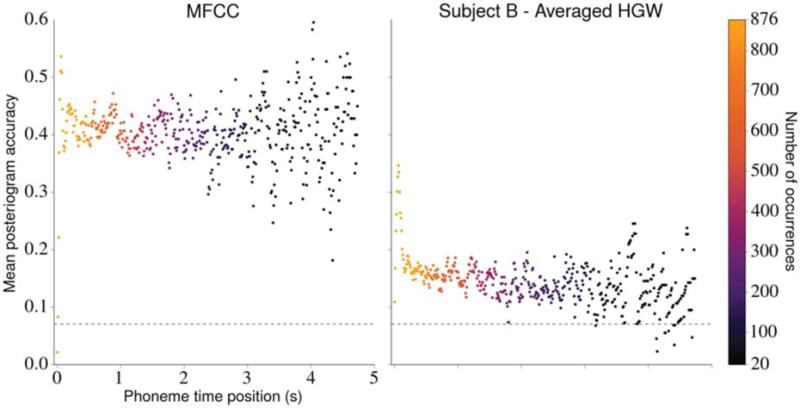
The effect of phoneme time position on posteriogram accuracy. Utterance onsets occur when a non-silence phoneme occurs after a silence duration lasting 500 ms or longer. The mean posteriogram accuracies were computed using estimated posteriograms associated with each stimulus in the Gump set generated with MFCCs (left) and averaged HGWs from subject B (right). Each dot represents the mean posteriogram accuracy associated with a phoneme time position, and the color of the dot indicates how many utterances contained a non-silence phoneme at that position. Phoneme time positions that were present in fewer than 20 of the stimuli and all silence phonemes were excluded from the figure. The horizontal dashed line in each plot depicts chance posteriogram accuracy. The apparent heteroscedasticity in each plot is most likely caused by the decreased number of occurrences of non-silence phonemes in the latter part of the utterances (because the utterances differ in duration), which led to less confident predictions of the mean accuracy at those time points. Testing with mixed effects logistic regression models revealed statistically significant negative relationships between phoneme time position and classification accuracy for neural features but not for MFCC features.
For each feature type, we used the lme4 package within the R programming language [56, 57] to fit a mixed effects logistic regression model with the associated data set to assess the effect that phoneme time position had on classification accuracy [58, 59]. In addition to the fixed effect of phoneme time position, random intercepts and slopes were utilized for each stimulus [60], which allowed the fits for each stimulus to vary in terms of overall classification accuracy and extent to which accuracy changes as a function of phoneme time position.
For MFCC features, we did not find evidence that phoneme time position influenced classification accuracy (β = 0.051, p = 0.225). Here, β is the regression coefficient for the phoneme time position variable. However, for averaged HGWs from subject B, the analysis revealed a significant effect in which accuracy diminished as a function of phoneme time position (β = −0.792, p < 10−10). After performing this analysis using the remaining feature types described in section 3.2, we observed a similar negative effect for every evaluation involving neural features (each β < −0.4, p < 10−5) and no statistically significant effect for the chance evaluation (β = −0.589, p = 0.085).
3.4. Speaker gender effects
In ASR research, it has been shown that the gender of a speaker affects the features used to train a speech recognition system, which can ultimately affect the system’s ability to decode speech from speakers of the opposite gender [61]. Because of this, we assessed the effect that speaker gender had on the performance of our NSR system. We performed separate evaluations on the 191 Gump stimuli produced by the male speaker and the 191 produced by the female speaker. We also performed an evaluation using 191 Gump stimuli chosen from both genders. These three evaluations used 10-fold cross-validation schemes with attempts to maintain homogeneity between folds (as described in section 2.1.5). We performed two additional evaluations by training on 90% of the stimuli from the male speaker and testing on all of the stimuli from the female speaker and then repeating this evaluation with the gender roles (training versus testing) swapped. All of these evaluations were performed using single-trial and averaged HGWs for each subject, concatenated HGWs, and MFCCs.
For MFCC features, this analysis revealed significant differences between evaluations for each metric (Welch’s ANOVA, p < 0.01). For each metric other than the estimation PER metric, post-hoc analyses revealed that the two evaluations involving training on the stimuli from one speaker and testing on the stimuli from the other speaker performed significantly worse than the other three evaluations (Welch’s t-test with Bonferonni correction, p < 0.001).
For the neural features, most analyses revealed no significant differences between evaluations for each metric (Welch’s ANOVA, p > 0.01). There were three exceptions: (1) the estimation PER for single-trial HGWs from subject A (Welch’s ANOVA, p = 8.28 × 10−3), (2) the estimation PER for averaged HGWs from subject A (Welch’s ANOVA, p = 1.30 × 10−3), and (3) the estimation posteriogram accuracy for single-trial HGWs from subject B (Welch’s ANOVA, p = 6.57 × 10−3). Overall, the differences between evaluations for each neural feature were negligible compared to the differences observed for acoustic features.
4. Discussion
Using relatively simple feature extraction techniques and model components, our NSR system was able to perform, to a limited extent, continuous speech decoding using neural signals. The novel results presented in this work quantitatively indicate that spatiotemporal modeling and ASR techniques, specifically language modeling and Viterbi decoding, can be used to improve phoneme recognition when using neural response features and continuous speech stimuli.
Feature selection had a significant impact on the performance of our NSR system. Unlike ASR, which contains well-established representations of audio waveforms such as MFCC vectors, the ideal representations of cortical surface recordings for the purpose of decoding speech remain unknown. We used HGWs as a relatively simple way to explore this realm of potential representations, guided by our hypothesis that including temporal information in the feature vectors would improve decoding in our system. The results of the feature window grid searches suggested using information contained in the neural responses occurring between 0–250 ms after an acoustic stimulus (within a continuous context) for maximum discriminative ability. However, the certainty of this conclusion is limited by the HGW parameterization constraints, the linearity assumption implicit in the LDA model used to evaluate the HGWs, and the relatively small amount of data used during the grid search. One reason why the HGW parameterization constraints are particularly troublesome arises from the fact that previous research has shown that different sub-populations of cortical neurons in the STG have different response properties [42], which suggests that forcing the same HGW parameters to be used for each electrode restricts the capability of HGWs to accurately represent the neural activity. It is also possible that the temporal dynamics are better represented implicitly within the models, through techniques such as sub-phone modeling [18, 21] or recurrent neural network (RNN) modeling [62], than explicitly in feature vectors. Additionally, despite the fact that power in the high gamma band has been used effectively in related research, the results of other research efforts indicate that it might be beneficial to evaluate the efficacy of using measures of the raw ECoG signal, power in other frequency bands, and phase information in feature vectors [63]. Furthermore, previous research suggests that speech sequence statistics are encoded in the human temporal cortex [64], suggesting that modeling the phonotactic information encoded directly in the neural signals can potentially be incorporated into an NSR system to improve performance. Although representations that are more powerful than these simple HGWs could be uncovered in future research, our results emphasize the importance of modeling spatiotemporal dynamics of neural activity when attempting to discriminate between responses evoked by varying continuous stimuli (at least within the context of speech perception analysis).
As described in section 3.2, the use of HGWs over HGSs and the use of language modeling and decoding tended to improve performance. HGWs consistently provided improvements when compared to HGSs, but the use of a phonemic LM and Viterbi decoding typically provided improvements only for the PER and confusion accuracy metrics and not for the posteriogram accuracy metric. The similarity in the posteriogram accuracy values for estimation and decoding results suggest that the basic phoneme priors used in the estimation results (as described in section 2.2.1) were as effective at frame-by-frame classification as the phonemic LM used in the decoding results. Altogether, these results indicate that temporal smoothing of the phoneme likelihoods is the primary benefit of incorporating a phoneme-level LM and performing Viterbi decoding. This claim is also supported by the sensitivity of the PER metric to temporal jitter in the predicted phoneme sequence (and the fact that decoding PERs were more favorable than estimation PERs), the apparent smoothing in many of the decoded posteriograms (such as the one depicted in figure 6), and the similarity between the estimation and decoding confusion matrices (such as the ones depicted in figure 7). From comparisons between the estimated and decoding confusion matrices in figure 7 and figure S1, the decoding techniques also seem to reduce the confusability of non-silence phonemes with /sp/. This is most likely a result of the impact that the high occurrence frequency of /sp/ had on the priors described in section 2.2.1 used when computing the phoneme posteriors. We anticipate that the use of a word-level LM would have a much more significant impact on the differences between estimation and decoding results because predicted phoneme sequences would be restricted to those that comprise word sequences. Additionally, future research could assess the effect that stimulus length has on decoding performance; because the Viterbi parameters affect decoded sequence length, decoding performance could be improved if stimuli of similar lengths were used throughout the development of an NSR system.
Averaging across stimulus presentations typically lessened the negative impact that large trial-by-trial variabilities in the neural responses had on our LDA model. Also, performance was improved using combined features across multiple subjects, which implies that the system could be limited by the spatial resolution of the ECoG arrays, the cortical response properties of individual subjects, or the inherent noise present in recorded ECoG signals. The results using concatenated feature vectors illustrate the upper limits on system performance and the amount of information available in recorded neural signals given the current physical and methodological limitations of our system. However, averaging and combining features across multiple subjects are relatively infeasible approaches for a speech prosthetic application. Future research efforts could explore alternative modeling and preprocessing techniques to obtain more accurate and less variable results using single-trial data from a single subject.
As expected, the MFCC features proved more effective than any of the neural features. However, we were able to observe similarities between the confusion matrices generated using neural and acoustic data (as shown in figure 7 and figure S1). In both cases, confusions typically occurred amongst stops, affricates, and fricatives or amongst the vowels, although for neural data the vowels were more confusable with the nasals and approximants than for acoustic data. These confusion matrices also suggest that prediction accuracy for stops was similar for neural and acoustic features. Additionally, for both feature types, our system was extremely effective at predicting silence, as made evident by the large phoneme confusion values for /sp/ in these confusion matrices and the performance improvements observed when silence data points are included during evaluation assessments (as described in table S1 and table S2).
We found a negative correlation between the time position of a phoneme in an utterance and our system’s ability to correctly predict that phoneme when neural (and not acoustic) features are used (as discussed in section 3.3). One factor that could be contributing to this observation is the existence of transient neural responses to acoustic onsets that might encode phonetic information in fundamentally different ways than sustained responses [54, 55]. This correlation could also indicate that response patterns evoked by a phoneme, which can last hundreds of milliseconds, are overlapping with response patterns of subsequent phonemes, resulting in observed responses that grow increasingly complex as an utterance progresses. Another possibility is that the cortical responses used in our analyses also contain representations of higher-order information related to the perceived speech, such as word identity [65] or phonotactic information [64], which could affect the accuracy of the phoneme likelihood model. Because the observed degradation of prediction quality over time is particularly problematic for continuous speech decoding approaches, attempts to directly model these effects could lead to performance improvements in future iterations of our NSR system.
As described in section 3.4, we showed that the gender of the speakers that generated the stimuli typically had no effect on the performance of our system when using neural features. As expected, speaker gender did have a significant effect on the system’s performance when using MFCCs. Because gender is one of the most influential sources of speaker-attributed acoustic variability during speech production [61], we conclude that speaker identity does not significantly affect our system when using neural features. This conclusion is consistent with the theory that phonetic information is encoded more strongly in the STG than other information that is more variable between genders (such as fundamental frequency) [6] and suggests that data from multiple speakers can be used to effectively train an NSR system.
To further assess the potential of using our NSR system in a speech prosthetic application, we can repeat our analyses using neural signals recorded during covert speech. Research groups have shown that covert and overt speech share partially overlapping neural representations in the auditory cortex and that it is feasible to reconstruct continuous auditory speech features from ECoG data recorded during a covert speech task [16, 17]. A future NSR system capable of intelligibly decoding covert speech could lead to the development of a speech prosthetic that allows impaired individuals to communicate more naturally with others. In addition, it could be beneficial to repeat our analyses using speech production tasks and neural activity from motor areas. Two research groups have reported favorable results by decoding produced speech using ECoG signals recorded in the motor cortex, although these groups did not perform continuous speech decoding [66, 67]. Also, by expanding on the approaches described in this work, stimuli containing speech from multiple speakers simultaneously could be used to add to the current knowledge of how the brain handles encoding of speech information in a multi-speaker setting [37] and to further ongoing research efforts aimed at gaining insights applicable to ASR systems that operate in multi-speaker environments [10]. Future NSR research should also include comparisons that address whether or not a discrete-state decoder (such as our system) that predicts sequences of speech tokens can effectively leverage language modeling and probabilistic decoding to increase performance over continuous-valued reconstruction methods that predict acoustics (such as spectrograms) [5].
The progress described in this work is primarily a proof-of-concept and should provide useful insights for future research in the field of NSR. The relatively simple model components and feature representations used in our system leave much room for improvement. For example, one of many recent advances in the ASR field has shown that modeling the spatiotemporal dynamics of the feature space non-linearly using deep recurrent neural network models can significantly improve decoding performance over more traditional methods [12]. The PERs reported in these studies are much lower than what we achieved with our system when using acoustic features, which implies that the incorporation of more sophisticated models from modern ASR systems could improve the performance of our NSR system. In addition, we intend to use word-level language modeling and decoding in future iterations of our system to make it more suitable for speech prosthetic applications.
Supplementary Material
Acknowledgments
DAM thanks Gopala Anumanchipalli, Neal Fox, and Nelson Morgan for project guidance and feedback, Liberty Hamilton and Benjamin Dichter for help during data organization and preprocessing, and Zachary Greenberg for the brain reconstruction images and electrode localizations. All of the authors thank the various members of EFC’s lab for help during data recording and the patients who volunteered to be subjects in this work.
This work was supported by the National Institutes of Health National Research Service Award F32-DC013486 and Grants R00-NS065120, DP2-OD00862, and R01-DC012379, the Ester A. and Joseph Klingenstein Foundation, and the National Science Foundation Grant No. 1144247. Additionally, this research effort used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231.
Footnotes
PACS numbers: 87.19.L, 43.71.An, 43.71Es, 43.71.Qr, 43.71.Sy, 43.72.Ne, 87.85.D, 87.85.E, 87.85.Wc
Author contributions
DAM developed and tested the NSR system, performed all analyses, and wrote the manuscript. NM started the project, collected the Gump data, performed most of the preprocessing, and provided project guidance. MKL provided project guidance. EFC led the research project. All authors edited the manuscript.
Conflict of interest
The authors declare no conflicts of interest.
Contributor Information
David A Moses, Email: David.Moses@ucsf.edu.
Nima Mesgarani, Email: nima@ee.columbia.edu.
Matthew K Leonard, Email: Matthew.Leonard@ucsf.edu.
References
- 1.Boatman Dana F, Hall Charles B, Goldstein Moise H, Lesser Ronald P, Gordon Barry J. Neuroperceptual differences in consonant and vowel discrimination: as revealed by direct cortical electrical interference. Cortex. 1997;33:83–98. doi: 10.1016/s0010-9452(97)80006-8. [DOI] [PubMed] [Google Scholar]
- 2.Binder Jeffrey R, Bellgowan Julie Anne Frost, Hammeke Thomas A, Bellgowan Patrick, Springer Jane, Kaufman Jacqueline N. Human temporal lobe activation by speech and nonspeech sounds. Cerebral Cortex. 2000;10(5):512–528. doi: 10.1093/cercor/10.5.512. [DOI] [PubMed] [Google Scholar]
- 3.Canolty Ryan T, Soltani Maryam, Dalal Sarang S, Edwards Erik, Dronkers Nina F, Nagarajan Srikantan S, Kirsch Heidi E, Barbaro Nicholas M, Knight Robert T. Spatiotemporal dynamics of word processing in the human brain. Frontiers in Neuroscience. 2007;1(1):185–196. doi: 10.3389/neuro.01.1.1.014.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Rauschecker Josef P, Scott Sophie K. Maps and streams in the auditory cortex: nonhuman primates illuminate human speech processing. Nature neuroscience. 2009 Jun;12(6):718–724. doi: 10.1038/nn.2331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Pasley Brian N, David Stephen V, Mesgarani Nima, Flinker Adeen, Shamma Shihab A, Crone Nathan E, Knight Robert T, Chang Edward F. Reconstructing speech from human auditory cortex. PLoS biology. 2012 Jan;10(1):e1001251. doi: 10.1371/journal.pbio.1001251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mesgarani Nima, Cheung Connie, Johnson Keith, Chang Edward F. Phonetic feature encoding in human superior temporal gyrus. Science. 2014 Feb;343(6174):1006–1010. doi: 10.1126/science.1245994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.BenZeghiba Mohamed Faouzi, De Mori Renato, Deroo Olivier, Dupont Stéphane, Erbes Teodora, Jouvet Denis, Fissore Luciano, Laface Pietro, Mertins Alfred, Ris Christophe, Rose Richard C, Tyagi Vivek M, Wellekens Christian J. Automatic speech recognition and speech variability: a review. Speech Communication. 2007;49(10–11):763–786. [Google Scholar]
- 8.Kurian Cini. A review on technological development of automatic speech recognition. International Journal of Soft Computing and Engineering. 2014;4(4):80–86. [Google Scholar]
- 9.Herff Christian, Heger Dominic, de Pesters Adriana, Telaar Dominic, Brunner Peter, Schalk Gerwin, Schultz Tanja. Brain-to-text: decoding spoken phrases from phone representations in the brain. Frontiers in Neuroscience. 2015;9(June):1–11. doi: 10.3389/fnins.2015.00217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chang Shuo-yiin, Edwards Erik, Morgan Nelson, Ellis Dan, Mesgarani Nima, Chang Edward. Phone recognition for mixed speech signals: comparison of human auditory cortex and machine performance. International Computer Science Institute; Berkeley, CA: 2015. (Technical report). [Google Scholar]
- 11.Hinton Geoffrey, Deng Li, Yu Dong, Dahl George E, Mohamed Abdel-rahman, Jaitly Navdeep, Senior Andrew, Vanhoucke Vincent, Nguyen Patrick, Sainath Tara N, Kingsbury Brian. Deep neural networks for acoustic modeling in speech recognition. IEEE Signal Processing, (November) 2012 Nov;:82–97. [Google Scholar]
- 12.Graves Alex, Mohamed Abdel-rahman, Hinton Geoffrey. Speech recognition with deep recurrent neural networks. International Conference on Acoustics, Speech, and Signal Processing. 2013;(3) [Google Scholar]
- 13.Laureys Steven, Pellas Frédéric, Van Eeckhout Philippe, Ghorbel Sofiane, Schnakers Caroline, Perrin Fabien, Berré Jacques, Faymonville Marie-Elisabeth, Pantke Karl-Heinz, Damas Francois, Lamy Maurice, Moonen Gustave, Goldman Serge. The locked-in syndrome: what is it like to be conscious but paralyzed and voiceless? Progress in brain research. 2005;150(5):495–511. doi: 10.1016/S0079-6123(05)50034-7. [DOI] [PubMed] [Google Scholar]
- 14.Sellers Eric W, Ryan David B, Hauser Christopher K. Noninvasive brain-computer interface enables communication after brainstem stroke. Science translational medicine. 2014 Oct;6(257):257re7. doi: 10.1126/scitranslmed.3007801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pei Xiaomei, Leuthardt Eric C, Gaona Charles M, Brunner Peter, Wolpaw Jonathan R, Schalk Gerwin. Spatiotemporal dynamics of electrocorticographic high gamma activity during overt and covert word repetition. NeuroImage. 2011;54(4):2960–2972. doi: 10.1016/j.neuroimage.2010.10.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Martin Stéphanie, Brunner Peter, Holdgraf Chris, Heinze Hans-Jochen, Crone Nathan E, Rieger Jochem, Schalk Gerwin, Knight Robert T, Pasley Brian N. Decoding spectrotemporal features of overt and covert speech from the human cortex. Frontiers in neuroengineering. 2014 May;7:14. doi: 10.3389/fneng.2014.00014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Tian Xing, Poeppel David. Mental imagery of speech and movement implicates the dynamics of internal forward models. Frontiers in Psychology. 2010 Oct;1:1–23. doi: 10.3389/fpsyg.2010.00166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Jurafsky Daniel, Martin James H. Speech and language processing: an introduction to natural language processing, computational linguistics, and speech recognition. 2nd. Pearson Education Inc; Upper Saddle River, New Jersey: 2009. [Google Scholar]
- 19.Davis Steven B, Mermelstein Paul. Comparison of parametric representations for monosyllabic word recognition in continuously spoken sentences. IEEE Transactions on Acoustics, Speech, and Signal Processing. 1980;28(4):357–366. [Google Scholar]
- 20.Huang Xuedong, Acero Alex, Hon Hsiao-Wuen. Spoken language processing: a guide to theory, algorithm and system development. 1st. Prentice Hall; Upper Saddle River, New Jersey: 2001. [Google Scholar]
- 21.Gold Ben, Morgan Nelson, Ellis Dan. Speech and audio signal processing: processing and perception of speech and music. John Wiley & Sons; 2011. [Google Scholar]
- 22.Garofolo John, Lamel Lori, Fisher William, Fiscus Jonathan, Pallett David, Dahlgren Nancy, Zue Victor. TIMIT acoustic-phonetic continuous speech corpus. 1993 [Google Scholar]
- 23.Yuan Jiahong, Liberman Mark. Speaker identification on the SCOTUS corpus. Journal of the Acoustical Society of America. 2008;123:3878. [Google Scholar]
- 24.Boersma Paul, van Heuven Vincent. Praat, a system for doing phonetics by computer. Glot International. 2001;5(9):341–347. [Google Scholar]
- 25.Rabiner Lawrence R, Juang Biing-Hwang. Fundamentals of speech recognition. Prentice-Hall; 1993. [Google Scholar]
- 26.Davenport Mike, Hannahs SJ. Introducing phonetics and phonology. third. Routledge; New York, NY: 2010. [Google Scholar]
- 27.Dale Anders M, Fischl Bruce, Sereno Martin I. Cortical surface-based analysis. NeuroImage. 1999;9:179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- 28.Hermes Dora, Miller Kai J, Noordmans Herke Jan, Vansteensel Mariska J, Ramsey Nick F. Automated electrocorticographic electrode localization on individually rendered brain surfaces. Neuroscience Methods. 2010;185(2):293–298. doi: 10.1016/j.jneumeth.2009.10.005. [DOI] [PubMed] [Google Scholar]
- 29.The MathWorks Inc. MATLAB, version 8.1.0. 2013 [Google Scholar]
- 30.Python Software Foundation. Python language reference, version 2. 2010;7 [Google Scholar]
- 31.Crone Nathan E, Boatman Dana, Gordon Barry, Hao Lei. Induced electrocorticographic gamma activity during auditory perception. Clinical Neurophysiology. 2001 Apr;112(4):565–582. doi: 10.1016/s1388-2457(00)00545-9. [DOI] [PubMed] [Google Scholar]
- 32.Ludwig Kip A, Miriani Rachel M, Langhals Nicholas B, Joseph Michael D, Anderson David J, Kipke Daryl R. Using a common average reference to improve cortical neuron recordings from microelectrode arrays. Journal of neurophysiology. 2009 Mar;101(3):1679–89. doi: 10.1152/jn.90989.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Crone Nathan E, Miglioretti Diana L, Gordon Barry, Lesser Ronald P. Functional mapping of human sensorimotor cortex with electrocorticographic spectral analysis. II. Event-related synchronization in the gamma band. Brain. 1998;121:2301–2315. doi: 10.1093/brain/121.12.2301. [DOI] [PubMed] [Google Scholar]
- 34.Bouchard Kristofer E, Mesgarani Nima, Johnson Keith, Chang Edward F. Functional organization of human sensorimotor cortex for speech articulation. Nature. 2013 Mar;495(7441):327–32. doi: 10.1038/nature11911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Marple S Lawrence. Computing the discrete-time analytic signal via FFT. IEEE Transactions on Signal Processing. 1999;47(9) [Google Scholar]
- 36.Oppenheim Alan V, Schafer Ronald W, Buck John R. Discrete-time signal processing. 2nd. Upper Saddle River, New Jersey: 1999. [Google Scholar]
- 37.Mesgarani Nima, Chang Edward F. Selective cortical representation of attended speaker in multi-talker speech perception. Nature. 2012 May;485(7397):233–6. doi: 10.1038/nature11020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hickok Gregory, Poeppel David. The cortical organization of speech processing. Nature Reviews Neuroscience. 2007 May;8:393–402. doi: 10.1038/nrn2113. [DOI] [PubMed] [Google Scholar]
- 39.Engineer Crystal T, Perez Claudia A, Chen Yeting H, Carraway Ryan S, Reed Amanda C, Shetake A, Jakkamsetti Vikram, Chang Kevin Q, Kilgard Michael P. Cortical activity patterns predict speech discrimination ability. Nature Neuroscience. 2008;11(5):603–608. doi: 10.1038/nn.2109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Buonomano Dean V, Maass Wolfgang. State-dependent computations: spatiotemporal processing in cortical networks. Nature reviews Neuroscience. 2009 Feb;10:113–125. doi: 10.1038/nrn2558. [DOI] [PubMed] [Google Scholar]
- 41.Chang Edward F, Rieger Jochem W, Johnson Keith, Berger Mitchel S, Barbaro Nicholas M, Knight Robert T. Categorical speech representation in human superior temporal gyrus. Nature neuroscience. 2010 Nov;13(11):1428–32. doi: 10.1038/nn.2641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Steinschneider Mitchell, Nourski Kirill V, Kawasaki Hiroto, Oya Hiroyuki, Brugge John F, Howard Matthew a. Intracranial study of speech-elicited activity on the human posterolateral superior temporal gyrus. Cerebral Cortex. 2011;21(10):2332–2347. doi: 10.1093/cercor/bhr014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hastie Trevor, Tibshirani Robert, Friedman Jerome. The elements of statistical learning: data mining, inference, and prediction. 2nd. Springer; New York: 2009. [Google Scholar]
- 44.Haeb-Umbach Reinhold, Ney Hermann J. IEEE International Conference on Acoustics, Speech, and Signal Processing. Ieee; 1992. Linear discriminant analysis for improved large vocabulary continuous speech recognition; pp. 13–16. [Google Scholar]
- 45.Pedregosa Fabian, Varoquaux Gael, Gramfort Alexandre, Michel Vincent, Thirion Bertrand, Grisel Olivier, Blondel Mathieu, Prettenhofer Peter, Weiss Ron, Dubourg Vincent, Vanderplas Jake, Passos Alexandre, Cournapeau David, Brucher Matthieu, Perrot Matthieu, Duchesnay Edouard. Scikit-learn: machine learning in Python. Machine Learning Research. 2011;12:2825–2830. [Google Scholar]
- 46.Brysbaert Marc, New Boris. Moving beyond Kucera and Francis: A critical evaluation of current word frequency norms and the introduction of a new and improved word frequency measure for American English. Behavior research methods. 2009;41(4):977–90. doi: 10.3758/BRM.41.4.977. [DOI] [PubMed] [Google Scholar]
- 47.Black Alan W, Taylor Paul, Caley Richard. The Festival Speech Synthesis System. 1997 [Google Scholar]
- 48.Lidstone George James. Note on the general case of the Bayes-Laplace formula for inductive or a posteriori probabilities. Transactions of the Faculty Actuaries. 1920;8:182–192. [Google Scholar]
- 49.Chen Stanley F, Goodman Joshua. An empirical study of smoothing techniques for language modeling. Computer Science Group, Harvard University; 1998. (Technical Report August). [Google Scholar]
- 50.Kneser Reinhard, Ney Hermann. Improved backing-off for m-gram language modeling. Proceedings of the IEEE, International Conference on Acoustics, Speech, and Signal Processing. 1995;1:181–184. [Google Scholar]
- 51.Viterbi Andrew J. Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Transactions on Information Theory. 1967;13(2):260–269. [Google Scholar]
- 52.DeWeese Michael R, Wehr Michael, Zador Anthony M. Binary spiking in auditory cortex. Journal of Neuroscience. 2003;23(21):7940–7949. doi: 10.1523/JNEUROSCI.23-21-07940.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Ogawa Takeshi, Riera Jorge, Goto Takakuni, Sumiyoshi Akira, Nonaka Hiroi, Jerbi Karim, Bertrand Olivier, Kawashima Ryuta. Large-scale heterogeneous representation of sound attributes in rat primary auditory cortex: from unit activity to population dynamics. Journal of Neuroscience. 2011;31(41):14639–14653. doi: 10.1523/JNEUROSCI.0086-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Tiitinen Hannu, Miettinen Ismo, Alku Paavo, May Patrick J C. Transient and sustained cortical activity elicited by connected speech of varying intelligibility. BMC neuroscience. 2012;13(1):157. doi: 10.1186/1471-2202-13-157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Okamoto Hidehiko, Kakigi Ryusuke. Neural adaptation to silence in the human auditory cortex: a magnetoencephalographic study. Brain and Behavior. 2014;4(6):858–866. doi: 10.1002/brb3.290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.R Core Team. R: A language and environment for statistical computing Technical report. R Foundation for Statistical Computing; Vienna, Austria: 2015. [Google Scholar]
- 57.Bates Douglas, Mächler Martin, Bolker Ben, Walker Steve. Fitting linear mixed-effects models using lme4. Journal of Statistical Software. 2015;67(1):1–48. [Google Scholar]
- 58.Baayen R Harald, Davidson Doug J, Bates Douglas M. Mixed-effects modeling with crossed random effects for subjects and items. Journal of Memory and Language. 2008;59(4):390–412. [Google Scholar]
- 59.Jaeger Tim Florian. Categorical data analysis: Away from ANOVAs (transformation or not) and towards logit mixed models. Journal of Memory and Language. 2008;59(4):434–446. doi: 10.1016/j.jml.2007.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Barr Dale J, Levy Roger, Scheepers Christoph, Tily Harry J. Random effects structure for confirmatory hypothesis testing: Keep it maximal. Journal of Memory and Language. 2013;68(3):255–278. doi: 10.1016/j.jml.2012.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Abdulla Waleed H, Kasabov Nikola K. Improving speech recognition performance through gender separation. Artificial Neural Networks and Expert Systems. 2001:218–222. [Google Scholar]
- 62.Elman Jeffrey L. Finding structure in time. Cognitive science. 1990;14(2):179–211. [Google Scholar]
- 63.Luo Huan, Poeppel David. Phase patterns of neuronal responses reliably discriminate speech in human auditory cortex. Neuron. 2007;54(6):1001–1010. doi: 10.1016/j.neuron.2007.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Leonard Matthew K, Bouchard Kristofer E, Tang Claire, Chang Edward F. Dynamic encoding of speech sequence probability in human temporal cortex. Journal of Neuroscience. 2015;35(18):7203–7214. doi: 10.1523/JNEUROSCI.4100-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Cibelli Emily S, Leonard Matthew K, Johnson Keith, Chang Edward F. The influence of lexical statistics on temporal lobe cortical dynamics during spoken word listening. Brain and Language. 2015;147:66–75. doi: 10.1016/j.bandl.2015.05.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Kellis Spencer, Miller Kai, Thomson Kyle, Brown Richard, House Paul, Greger Bradley. Decoding spoken words using local field potentials recorded from the cortical surface. Journal of neural engineering. 2010;7(5):56007. doi: 10.1088/1741-2560/7/5/056007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Mugler Emily M, Patton James L, Flint Robert D, Wright Zachary a, Schuele Stephan U, Rosenow Joshua, Shih Jerry J, Krusienski Dean J, Slutzky Marc W. Direct classification of all American English phonemes using signals from functional speech motor cortex. Journal of neural engineering. 2014;11(3):035015. doi: 10.1088/1741-2560/11/3/035015. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


