Diversification rates and species richness across the Tree of Life

Abstract

Species richness varies dramatically among clades across the Tree of Life, by over a million-fold in some cases (e.g. placozoans versus arthropods). Two major explanations for differences in richness among clades are the clade-age hypothesis (i.e. species-rich clades are older) and the diversification-rate hypothesis (i.e. species-rich clades diversify more rapidly, where diversification rate is the net balance of speciation and extinction over time). Here, we examine patterns of variation in diversification rates across the Tree of Life. We address how rates vary across higher taxa, whether rates within higher taxa are related to the subclades within them, and how diversification rates of clades are related to their species richness. We find substantial variation in diversification rates, with rates in plants nearly twice as high as in animals, and rates in some eukaryotes approximately 10-fold faster than prokaryotes. Rates for each kingdom-level clade are then significantly related to the subclades within them. Although caution is needed when interpreting relationships between diversification rates and richness, a positive relationship between the two is not inevitable. We find that variation in diversification rates seems to explain most variation in richness among clades across the Tree of Life, in contrast to the conclusions of previous studies.

1. Introduction

The unevenness in species richness across the Tree of Life is striking. For example, animal phyla [1] can range from one described species (Placozoa) to 1.3 million (Arthropoda). Plant families [2] can range from approximately 22 750 species (Asteraceae) to one (Ginkgoaceae). Explaining the variation in species richness among clades is a major goal of both evolutionary biology and ecology (e.g. [3]). Numerous studies have attempted to determine the evolutionary and ecological causes of species richness patterns across habitats and regions, such as the higher richness of tropical regions relative to temperate regions [4–6]. However, the causes of variation in richness patterns among clades remains surprisingly unresolved, especially at the largest phylogenetic scales.

The number of species in a clade is directly controlled by the addition of species through speciation and their subtraction through extinction over time. Given this, two major hypotheses to explain differences in richness among clades are the clade-age and diversification-rate hypotheses [7]. Under the clade-age hypothesis, some clades have higher richness because they are older, and therefore have had more time to accumulate species through speciation. Alternatively, under the diversification-rate hypothesis, higher richness in some clades is explained by faster rates of net diversification (speciation minus extinction over time). Thus, high species richness is associated with clades that have accumulated many species in a relatively short period of time. Old clades with low richness will have low net rates, and younger clades with higher richness will have higher rates. These net rates depend only on clade age and extant richness, and not constant rates within clades over time. ‘Ecological limits’ are therefore not a separate explanation for richness patterns (e.g. [5,8]), as limited resources can only influence clade richness by impacting diversification (speciation minus extinction), and ecological impacts on diversification are subsumed within the diversification-rate hypothesis [9].

Only two recent studies have attempted to test the relative importance of the clade-age and diversification-rate hypotheses at large phylogenetic scales. McPeek & Brown [7] investigated this question in animals using 163 species-level phylogenies from Arthropoda, Mollusca and Chordata, as well as data on richness and crown-group ages of higher taxa (orders) from major animal clades (e.g. vertebrates, insects). They concluded that variation in species richness among animal clades is explained primarily by clade age and not diversification rates. In contrast, Rabosky et al. [10] found that stem-group clade ages did not predict richness patterns across eukaryote clades (emphasizing comparisons among families). They also concluded that diversification rates and richness are decoupled across eukaryotes [10]. However, they did not directly test the relationship between these two variables. Instead, they rejected the diversification-rate hypothesis because their simulations of variable diversification rates supported a positive relationship between clade age and richness (although this may have been an artefact of overly simple simulations [11]). Neither McPeek & Brown [7] nor Rabosky et al. [10] considered protists or groups outside eukaryotes.

More broadly, it is unclear how diversification rates vary across the Tree of Life. For example, are diversification rates faster in animals than plants, given the greater species richness of animals? Are diversification rates in bacteria lower than in plants, animals or other groups? Similarly, it is unclear if diversification rates at higher ranks are related to diversification rates of the clades within them. For example, are kingdoms with fast diversification rates composed of families with fast diversification rates? Or does strong variation in diversification rates among these subclades erase any such trends within a higher-level clade?

Furthermore, the relationship between diversification rates and richness across the Tree of Life remains largely unexplored. Some authors have implied that a positive relationship between richness and diversification rate is basically inevitable, as a statistical artefact [12]. This may explain why some authors have not even tested this relationship, despite addressing whether diversification rates explain richness patterns [10]. Kozak & Wiens [11] used simulations to show that diversification rates and richness will be correlated when rates underlie richness patterns, but faster rates in younger clades can decouple rates and richness (showing that diversification rates and richness are not inevitably related). However, it remains unclear how often younger clades tend to have faster rates in real datasets, and whether the relationship between clade ages and diversification rates is related to the relationship between richness and diversification. Overall, the empirical relationships between clade age, richness and diversification rates have not been adequately explored. More generally, it is an open question whether or not diversification rates explain richness patterns across the Tree of Life.

Here, we examine variation in diversification rates among higher taxa across the Tree of Life for the first time. We assemble time-calibrated phylogenies and species richness data from the literature, and estimate diversification rates and ages of clades at different ranks (kingdom, phylum, class, order and family) for all major groups across the Tree of Life (i.e. bacteria, archaeans, protists, fungi, plants, animals). We describe patterns of variation among these major groups and test whether rates for these major groups are related to the rates of subclades within them. We also address the relationships among species richness, clade age and diversification rates. Specifically, we test whether patterns of species richness among clades are explained primarily by clade ages, diversification rates or neither. We also explore whether relationships between richness and diversification rates are inevitable or a statistical artefact.

2. Material and methods

(a). Data assembly

Our analyses were based on clades ranked as kingdoms, phyla, classes, orders and families (electronic supplementary material, table S1). We acknowledge that taxonomic ranks are arbitrary. However, these ranks were also used in the previous studies of this topic [7,10]. Most importantly, the use of these higher taxa allows assignment of species to clades without a complete phylogeny that includes all species. Furthermore, because we focus on monophyletic taxa, clades of a given rank can be compared without the complication of having some clades nested inside others. We address potential biases associated with using ranks in the Discussion.

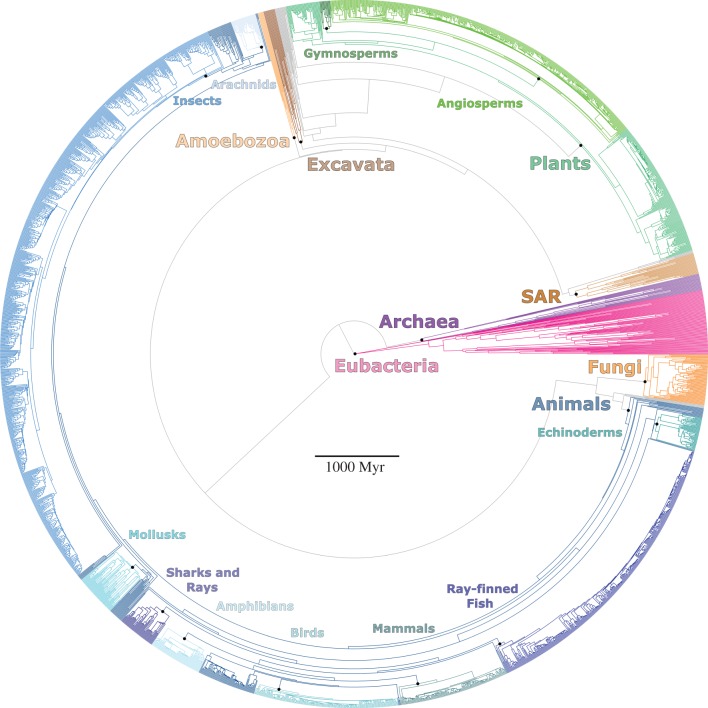
Taxonomy was based on various databases (for details see the electronic supplementary material, appendix S1). For kingdoms, we used the well-established monophyletic groups Animalia, Plantae, Fungi and Eubacteria [13]. We treated Archaea as a kingdom, although some rank it as a superkingdom instead [14]. Protists are not monophyletic in the higher-level tree used here [15], and instead consist of several clades that form successive outgroups to plants (figure 1). However, recent studies suggest that Amoebozoa, Excavata and the SAR clade (including Stramenopila, Alveolata and Rhizaria) are each major monophyletic groups of protists that are equivalent to other eukaryotic kingdoms [15–17], or at least similar in age. Therefore, we treated these three clades as kingdoms in our analyses, yielding a total of eight kingdom-level clades (along with animals, plants, fungi, eubacteria and archaeans). We did not analyse protists outside of these clades at the kingdom level, but we did include these other protist subclades in other analyses (e.g. analyses across all phyla, classes, orders, families).

Figure 1.

Chronogram including all sampled clades across the Tree of Life. The eight kingdom-level clades used are indicated by large type. Selected subclades are indicated with smaller type: these are merely shown for navigating the tree. The oldest part of the tree is the crown age of Eubacteria (4188 Ma): a separate root is not shown.

Species richness within each major clade was based primarily on the Catalogue of Life database [18], along with additional sources (see electronic supplementary material, table S1). For example, for animal phyla, we used the study of Zhang [1], which gave larger numbers of described species (and thus should be more accurate, given that actual richness almost certainly exceeds described richness). Protist richness was poorly represented in the Catalogue of Life database [18], and therefore we used Pawlowski et al. [17] for Amoebozoa and Excavata, and the NCBI Taxonomy database [19,20] for the SAR clade and for other protists not in these three clades.

We searched the literature for the most recent and comprehensive time-calibrated trees for major clades across the Tree of Life (electronic supplementary material, appendix S1 and table S2). We did not include any chronograms published after 2014. We collected data on stem-group age for each clade for the taxonomic ranks of kingdom, phylum, class, order and family. We also assembled the trees into an overall phylogeny spanning the Tree of Life, for comparative analyses (figure 1). For the backbone of the tree, we used a time-calibrated phylogeny of Eubacteria [21] and an estimate for the age of origin of Archaea [22]. To this backbone, we then added a time-calibrated phylogeny of major eukaryote clades [15]. We then added more detailed phylogenies for major clades across this tree (e.g. animals, plants and fungi). Trees were combinable because they all used time as a common currency for their branch lengths.

We used estimates of clade ages based on the stem-group age of each clade (the time when the clade first splits from its sister group). Stem-group ages require only a single species within each clade to be estimated correctly. In contrast, crown-group ages (age of the oldest split among extant lineages within a clade) require more complete taxon sampling of species within a clade [23], and are not usable when a clade contains a single species or only one sampled species [24]. Stem-group ages also reflect the entire history of the clade, rather than the age of the clade of extant species (which could be substantially younger).

Only a single species is needed to represent the stem age of a clade, but estimated stem ages could be biased if only a limited number of clades within a group are sampled (i.e. the stem age is the age of the split between a given taxon and its sister group, and will be overestimated if the actual sister group is not included in the tree). As our criterion, we included clades only if at least 30% of the ranked taxa within their group were included (e.g. we included a family only if at least 30% of the families within its order were represented in the tree). This value is somewhat arbitrary, but is partially addressed by Sanderson [23] and our own subsampling experiments (see below). A summary of the sampling of ranked clades within major groups is provided in electronic supplementary material, table S1. Many major clades were sampled completely at each rank. However, seemingly paraphyletic higher taxa were excluded. Note that our estimates of species richness within each higher taxon included all described species, not simply those subclades included in our tree (i.e. if our tree included only 5 of 10 families in a given phylum, our analyses of species richness for that phylum would include all 10 families, not just 5).

Our subsampling experiments with relatively well-sampled groups suggest that including only 30% of the higher taxa leads to overestimates of clade ages, but typically only by approximately 10–20%. Most importantly, reducing taxon sampling by 70% has relatively little impact on the relationships between richness and diversification rates, and richness and clade age (for details see electronic supplementary material, appendix S2).

(b). Data analysis

Net-diversification rates were estimated using the method-of-moments estimator for stem-group ages [24]. This estimator requires only stem-group ages and species richness of clades to estimate their net-diversification rates, along with an assumed ratio of extinction to speciation (relative extinction fraction or ɛ) intended to correct for the failure to include clades that are completely unsampled due to extinction [24]. We followed standard practice and assumed three values of ɛ (zero, intermediate and high relative extinction: ɛ = 0, 0.5 and 0.9). Each analysis assumed a single value of ɛ across all clades (again, ɛ merely corrects for unsampled clades, and is not an estimate of extinction rates within clades). Different values had relatively little impact on the results (electronic supplementary material, figure S1); therefore, we present results only from the intermediate value (ɛ = 0.5). Data on species richness, clade age and diversification rates for each clade at each rank are provided in electronic supplementary material, database S1. Phylogenies for comparisons across each rank are provided in electronic supplementary material, database S2.

Many other approaches for estimating diversification rates have been developed. However, all (or most) would be inapplicable at the broad phylogenetic scales analysed here, as they use species-level phylogenies within clades. Furthermore, we are specifically interested in net-diversification rates at different taxonomic ranks.

To analyse relationships between variables, we used phylogenetic generalized least-squares regression [25] to account for phylogenetic non-independence of clades, using the R package caper v. 0.5.2 [26]. Following standard practice, δ and κ were set to 1 while the maximum-likelihood value of λ [27] was estimated for each analysis and used to transform branch lengths. Richness and clade age were ln-transformed to improve linearity.

We analysed pairwise relationships between clade age and richness, diversification rate and richness, and also clade age and diversification rate. We conducted analyses across all clades of a given rank across the Tree of Life, and then repeated analyses within each kingdom.

We explored the potential statistical artefacts associated with the relationship between richness and diversification rates in several different ways (all analyses and randomizations were conducted in R). First, we tested whether weak relationships between diversification rates and richness are related to strong negative relationships between diversification rates and clade ages, as predicted [9] and shown in simulations [11]. We performed this test across the 29 comparisons listed above (phyla, classes, orders and families, among the eight kingdoms, excluding three comparisons with too few relevant clades).

Second, we explored three ways of randomizing the data to address the relationship between diversification rates and richness. (i) We randomized ages among clades while holding richness constant, recalculated diversification rates based on the new ages and then tested if the new diversification rates were significantly related to richness. Note that randomizing richness instead of clade ages in this case should yield identical results. (ii) We randomized richness among clades while holding clade ages constant, and then tested whether the original diversification rates were significantly related to the new richness values. (iii) We randomized the original diversification rates among clades, and then tested whether richness and diversification rates were significantly related. Importantly, if there is little non-random variation in clade ages, then the first randomization should actually yield values similar to those in the original dataset (i.e. diversification rates will still be related to richness). The second and third randomization should break up any relationships between species richness and diversification. We conducted these analyses at the level of kingdom, phylum, class and order (the large number of families was very unwieldy), using 1000 replicates each. We then summarized the mean r² and p-values across replicates.

Third, we performed simple experiments to explore how relationships between clade age and richness influenced relationships between diversification rates and richness. For these analyses, we first ordered the observed values (for a given rank) of richness and clade ages positively (higher richness in older clades) and then negatively (higher richness in younger clades). For each of these two scenarios, we then recalculated diversification rates based on the new ages and richnesses, and retested the relationship between diversification rates and richness.

3. Results

We assembled a phylogeny (figure 1), and analysed data on clade ages, species richness and diversification rates for 71 phyla, 122 classes, 434 orders, 2558 families and eight kingdom-level clades (electronic supplementary material, table S1).

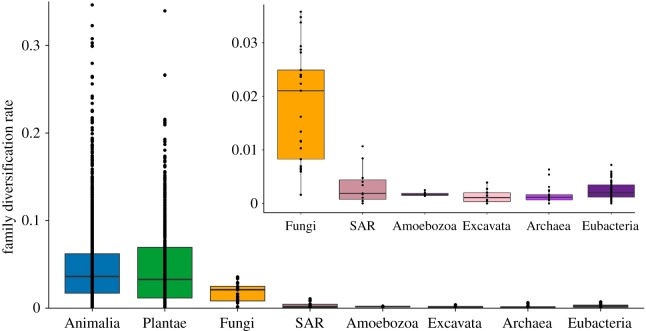
Our results show major differences in diversification rates across the Tree of Life. At the kingdom level, net-diversification rates (table 1) are almost twice as high in plants (0.0278 species per Myr) as in animals (0.0141), even though animals have many more species (1 525 728 species versus 345 501 of plants [1,2]). In turn, diversification rates in fungi (0.0085) are approximately half of those in animals. Diversification rates of the protist kingdoms are then lower than in fungi (Amoebozoa = 0.0040; Excavata = 0.0034; SAR = 0.0062). Those of eubacteria (0.0020) and archaeans (0.0014) are approximately one-tenth of those in plants and animals.

Table 1.

Average (avg) and maximum (max) diversification rates for higher taxa of different ranks (columns) within each major clade (rows), where diversification rates are in species per Myr. Amoebozoa, Excavata and the SAR clade are not recognized kingdoms but are major clades of protists treated as kingdoms here. Each kingdom has a single estimate for the net-diversification rate (no maximum or average). Diversification rates are estimated using ɛ = 0.5.

	family		order		class		phylum		kingdom
	avg	max	avg	max	avg	max	avg	max
Plantae	0.0492	0.8823	0.0317	0.1273	0.0126	0.0446	0.0186	0.0228	0.0278
Animalia	0.0485	0.5109	0.0297	0.0983	0.0157	0.0343	0.0161	0.0189	0.0141
Fungi	0.0184	0.0358	0.0107	0.0258	0.0207	0.0364	0.0132	0.0221	0.0085
Amoebozoa	0.0017	0.0025	0.0020	0.0024	0.0027	0.0035	0.0031	0.0031	0.0040
Excavata	0.0012	0.0039	0.0019	0.0045	0.0021	0.0034	0.0026	0.003	0.0034
SAR	0.0033	0.0107	0.0088	0.0323	0.0082	0.0245	0.0073	0.0109	0.0062
Eubacteria	0.0025	0.0072	0.0024	0.0086	0.0019	0.0076	0.0013	0.0028	0.0020
Archaea	0.0015	0.0063	0.0012	0.0024	0.0012	0.0024	0.0012	0.0014	0.0014

These large-scale patterns of net-diversification rates are generally mirrored at lower ranks (table 1; figure 2). For example, clades of plants, animals and fungi have much faster rates of mean net diversification than clades of protists, eubacteria and archaeans at nearly every rank (table 1). The net-diversification rates of kingdoms are strongly related to the mean diversification rates of families within each kingdom (r² = 0.70, p < 0.01). More generally, the net-diversification rate of each higher-level taxon is strongly related to the mean diversification rates of the families within it (phylum: r² = 0.62, p < 0.0001; class: r² = 0.52, p < 0.0001; order: r² = 0.74; p < 0.0001). Thus, rapidly diversifying higher-level clades are largely composed of rapidly diversifying subclades.

Figure 2.

Diversification rates at the family level (for ɛ = 0.5), in units of species per Myr. Sample sizes (families per kingdom) are Animalia (n = 1710), Plantae (n = 682), Fungi (n = 25), SAR clade (n = 11), Amoebozoa (n = 7), Excavata (n = 12), Eubacteria (n = 61) and Archaea (n = 21). The y-axis was cut off at 0.35 to increase the visibility of differences between groups. Values from two families of plants and four families animals are therefore not shown, but the quartiles and median are not affected. The inset shows the details of the slower rates in fungi, protists, eubacteria and archaeans (note the 10-fold change in scale).

Across all clades and taxonomic ranks, we found no case in which variation in species richness of clades was explained by a positive relationship with clade ages (electronic supplementary material, table S3 and figure S2). Instead, many comparisons showed a significant negative relationship between richness and clade ages (kingdom, phylum, class). This pattern is maintained when clades of the same rank are compared within each of the eight kingdom-level clades; only rarely are clade age and richness significantly related, and in those cases the relationship is negative (i.e. among animal phyla, fungi classes, SAR orders and orders and families of Eubacteria).

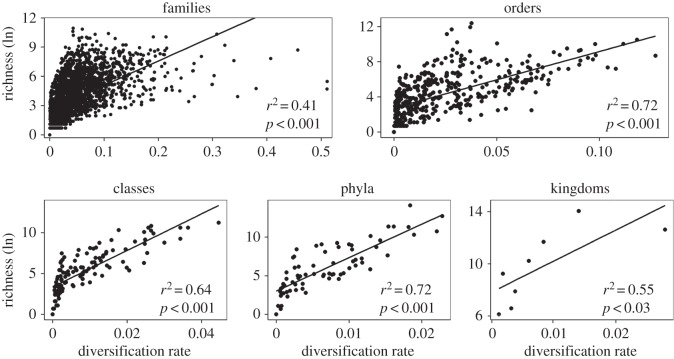
In contrast, we found that variation in diversification rates explained substantial variation in species richness among clades (figure 3), from almost half (kingdoms, families) to approximately two-thirds (phyla, classes, orders). Diversification rates explained most variation in species richness among clades of the same rank within kingdoms also (electronic supplementary material, table S3). However, there were a few cases in which the relationship was weak and non-significant (e.g. phyla of the SAR clade of protists; r² = 0.22). Diversification rates were negatively related to clade ages across the tree (kingdom: r² = 0.90; phylum: r² = 0.19; class: r² = 0.33; order: r² = 0.07; family: r² = 0.15; p < 0.01 in all cases), and in many cases within kingdoms.

Figure 3.

Phylogenetically corrected linear regression analyses of clade species richness (ln-transformed) versus diversification rate (species per Myr, ɛ = 0.5) compared across all clades of a given taxonomic rank across the tree. For families, the x-axis was cut off at 0.55 to increase the visibility of differences between groups. Thus, one data point from plants was excluded (in the figure only), but the analysis was unaffected.

We found that strong, positive relationships between richness and diversification rate are not inevitable (see also [7,11]). First, strong relationships between diversification rates and richness were sometimes absent (i.e. phyla of the SAR clade). Second, we found that variation in the strength of the relationship between diversification rates and richness is explained (at least in part) by variation in the relationship between diversification rates and clade ages (i.e. r² = 0.253; p = 0.0066; based on regression of r² values across the 29 cases in electronic supplementary material, table S3). In short, a stronger negative relationship between diversification rates and ages (i.e. faster rates in younger clades) leads to weaker positive relationships between diversification rates and richness, as predicted [9] and shown in simulations [11]. For example, among kingdoms, there is a strong negative relationship between diversification and clade age (r² = 0.90), and a relatively weak positive relationship between diversification and richness (r² = 0.55). A strong, negative diversification–age relationship and a non-significant diversification–richness relationship were also found by McPeek & Brown [7, fig. 1].

We also conducted additional randomizations and experiments on the relationship between diversification rates and richness (see electronic supplementary material, appendix S3 and tables S4–S7). Our results show that considerable caution is needed when interpreting randomizations of richness and diversification (see also [11]). Specifically, some randomization methods can yield strong diversification–richness relationships, but this does not mean that all diversification–richness relationships are therefore artefactual. We also find that strong, positive relationships between clade age and species richness can weaken diversification–richness relationships (as can strong negative age–diversification relationships; see above and [11]). Again, we emphasize that strong diversification–richness relationships are not inevitable.

4. Discussion

In this study, we analyse patterns of variation in diversification rates across the Tree of Life. We find three major results. First, we find substantial variation in diversification rates at the broadest scales, including faster rates in plants than animals (by almost twofold), faster rates in predominantly multicellular eukaryote clades (plants, animals, fungi) than in protists and prokaryotes, and faster rates in eukaryotes than prokaryotes (by almost 10-fold, depending on the eukaryote clade). Second, patterns of variation at the deepest scales (i.e. kingdoms) are generally mirrored in the rates of the subclades they contain (i.e. families). Third, diversification rates seem to explain much of the variation in species richness among clades. To our knowledge, none of these patterns have been documented or widely discussed in the previous literature.

A major pattern in our results is the difference in net-diversification rates between plants and animals, with plants having net rates approximately twice those of animals. This pattern is strongest at the level of kingdoms, but is reduced at lower levels (table 1). The higher net-diversification rate of plants is doubtless driven by the well-known rapid diversification of angiosperms. Many animal clades are older than angiosperms and have substantially less richness (e.g. major terrestrial vertebrate clades have approx. 10 000 species or fewer and are approx. 250–390 Myr old, whereas angiosperms have approx. 345 501 species and are approx. 150 Myr old [28]). This is intriguing because angiosperms and terrestrial vertebrates occur syntopically throughout the world, and often show parallel spatial patterns of richness (e.g. more topical species [29]). Future research should test for ecological or evolutionary drivers of rapid diversification in plants that are absent in animals. An essential piece of the puzzle may be to understand why angiosperms are so diverse among plants, an important but unresolved question [30,31].

Our study reveals other intriguing patterns of variation in rates among clades, and a major challenge for future studies will be to understand the causes of these patterns (e.g. traits that are related to diversification). For example, across the deepest levels of the tree, multicellularity and sexuality might be important traits that help explain the higher diversification rates of plants, animals and fungi relative to eubacteria, archaeans and many protists. However, tests so far have been limited in taxonomic scope and have yielded mixed support for the importance of these two traits [32,33]. Within animals and plants, the transition from aquatic to terrestrial habitats might be an important driver of variation in diversification rates. For example, terrestrial habitat use explains approximately 65% of the variation in diversification rates among major vertebrate clades [34]. Similarly, occurrence in marine versus non-marine habitats explains approximately 30–37% of the variation in diversification rates among animal phyla [35], and may explain even more variation within some phyla (approx. 90% in molluscs). Herbivory is demonstrably important for insect diversification [36,37], and complete metamorphosis and wings may also be important [37–39]. Furthermore, climatic distribution may be important in explaining patterns of diversification among families within clades (e.g. higher tropical diversification rates in amphibians and mammals [40,41]). Numerous other ecological factors and intrinsic traits may also be important.

Our results also show that at higher taxonomic levels, younger clades often show a strong tendency to have higher diversification rates (electronic supplementary material, table S3). There are several potential explanations for this pattern. One is that diversification rates slow over time (e.g. [8,9]), possibly due to density dependence or a general tendency for rates to increase when measured over shorter time scales. However, another explanation (not mutually exclusive) is that many younger clades have novel traits that help explain their rapid diversification (e.g. invasion of land among animal phyla).

We also show that patterns of variation in diversification rates among higher-level clades (i.e. kingdoms, phyla, classes, orders) are strongly related to the mean diversification rates of families they contain. Thus, the patterns that we describe at higher levels are not simply due to a few outlier subclades with exceptionally high rates, but rather seem to generally reflect broad-scale trends extending to lower ranks within each clade.

We find that patterns of species richness among major clades (family level and above) are explained primarily by variation in net-diversification rates. This result is intriguing in that two previous studies that addressed large-scale richness patterns among clades both concluded that richness patterns were not explained by diversification rates [7,10]. Although some variation in richness among clades remains unexplained at the family and kingdom level (approx. 50%), most variation is explained by diversification rates alone for orders, classes and phyla (more than 63%).

Why was the importance of diversification rates not found in previous studies of large-scale richness patterns? McPeek & Brown [7] examined several animal clades (especially vertebrates, molluscs and arthropods) and concluded that time explained their richness patterns. However, many of the clades they examined were much younger than those included here, with most clade ages in their species-level phylogenies <20 Myr old [7, fig. 1]. For orders, they focused on crown-group ages, and most were 100 Myr old or less, with none more than 250 Myr old (their fig. 2). There is increasing evidence that time may dominate richness patterns at smaller temporal scales, whereas diversification rates dominate at deeper scales (e.g. [35]). Rabosky et al. [10] examined stem-group ages of clades (primarily of families), and found no relationship between clade ages and species richness, in agreement with our results here. However, Rabosky et al. [10] did not directly test for a relationship between diversification rates and richness. Instead, they dismissed the relevance of diversification rates because their simulations of variable diversification rates yielded strong, positive relationships between clade ages and richness (in contrast with the patterns they observed). Interestingly, we find here that diversification rates tend to be faster in younger clades (see Results), a pattern that can weaken or reverse positive age–richness relationships (see also [11]) and that was not included in simulations of variable diversification rates by Rabosky et al. [10].

Our results also suggest that there may be important pitfalls in analysing the richness–diversification relationship. First, this relationship should be analysed empirically, rather than assuming that any relationship is inevitable or artefactual. We found that strong diversification–richness relationships are not universal (and therefore not inevitable; see also [7,11]). Instead, several patterns can disrupt this relationship, especially faster diversification rates in younger, species-poor clades (e.g. plants). Importantly, the lack of a positive age–richness relationship does not guarantee that diversification rates will explain richness instead of age. Again, negative age–diversification relationships are common (and often occur when positive age–richness relationships are absent), and can weaken the diversification–richness relationship (see Results and [11]). Second, randomizations of clade ages and richness can also lead to significant richness–diversification relationships, if diversification rates are re-estimated from the randomized data (and given limited or random variation in clade ages). However, this does not make observed relationships incorrect or meaningless (contra [12]), as significant richness–diversification relationships occur in randomizations of simulated datasets in which diversification rates are known to determine richness patterns [11]. In contrast, if we randomize observed diversification rates (or richness) among clades, we find no significant relationships between species richness and diversification rates. We strongly caution against dismissing all observed diversification–richness relationships based on a priori assumptions or randomizations.

Our results show that clade ages do not explain richness patterns among the higher taxa examined here, but our results should not be used to entirely dismiss the importance of clade ages to species richness patterns. In our study, we compared clades of the same rank (as have similar studies [7,10]). Thus, the clades compared are biased to be of comparable age, which may strongly bias the results in favour of the importance of diversification rates [9]. However, it is clear that clades at lower ranks (e.g. families) must be younger and have lower richness than those at higher ranks (e.g. phyla, kingdoms), simply because these lower-ranked clades are nested inside the higher-ranked clades (electronic supplementary material, figure S3). Therefore, differences in ages of clades might still be critically important for explaining patterns of species richness, especially in cases when the clades compared can be of any rank or age (as in biogeographic studies of the time-for-speciation effect [9]).

We acknowledge numerous sources of error that might influence specific results, but should not overturn our major conclusions. First, only a small fraction of all species have been described, even though the actual number of species remains uncertain [42,43]. However, the results should remain similar if new species increase the richness of clades in similar proportions to their current richness. Second, even if some clades increased disproportionately relative to their current size, this need not overturn our conclusions. For example, given the very old age of Eubacteria, they would need to have more than 100 sextillion species to have diversification rates of the same magnitude as animals and plants (electronic supplementary material, table S8). However, we note that scenarios with extremely high bacterial richness might also imply greater overall importance of clade age for richness patterns in the kingdom-level comparisons. Third, some divergence dates may be incorrect, which may influence estimated clade ages and diversification rates [44]. However, our inferences rest primarily on the relative ages of clades, rather than their absolute ages (e.g. do older clades have more species?). Additionally, our inferences are based on dozens, hundreds and thousands of clades (for phyla, classes, orders and families), which should minimize impacts of errors in individual date estimates on our overall conclusions. We also show that our age estimates and the relationships between richness, diversification and clade ages are relatively robust to incomplete taxon sampling, even though the age estimates are biased to be somewhat older (electronic supplementary material, appendix S2). Fourth, the phylogenies used here may not be fully correct. Nevertheless, this may be a more minor source of error in our study. Branch lengths (e.g. clade ages) may be more important than topology for comparative analyses, and may remain similar even as topologies change (especially as most topological uncertainty may be associated with short branch lengths [45,46]). However, non-monophyly of clades might influence some results. Fifth, species richness may not be directly comparable between some groups. For example, an asexual bacterial species may not be fully equivalent to sexual plant and animal species, in which speciation and species boundaries are determined (ultimately) by gene flow and reproductive isolation (e.g. [47]). Species delimitation in bacteria and archaeans remains debated, and other criteria may be considered in asexuals that are similar to sexual species, such as adaptive divergence and phenotypic clustering (e.g. [48,49]). The comparability of asexual and sexual species cannot be resolved here, but it should impact relatively few of our comparisons (e.g. eukaryotes and prokaryotes). Quantitative analyses do suggest that animal and plant species are comparable, and that plant species may be more likely to be reproductively isolated from each other than are animal species [50]. Therefore, the higher diversification rates of plants relative to animals observed here should not be an artefact of taxonomic oversplitting of plant species.

Some authors have stated that the net-diversification-rate estimators used here [24] require ‘constant’ diversification rates within clades (e.g. [8,10]). However, this requirement of constant rates within clades appears to be conflated with the idea that rates are constant among clades. Specifically, these authors have stated that these estimators are valid only if clade age and richness are positively related (e.g. [10]). Clade age and richness should be positively related when diversification rates are constant among clades, such that clade ages explain richness, not diversification rates [9,11]. In contrast, variation in diversification rates among clades can disrupt a positive age–richness relationship [9,11], especially when younger clades have faster diversification rates, as we find here. Indeed, we find that clade ages generally do not explain richness patterns among higher taxa, but diversification rates do. Furthermore, recent simulations show that the age–richness relationship is irrelevant to the accuracy of net-diversification-rate estimators [11]. Previous studies arguing that these estimators were inaccurate without a positive age–richness relationship (e.g. [10]) did not actually address their accuracy. New simulation results suggest that these estimators are reasonably accurate (e.g. strong relationships between true and estimated rates), especially when clades are relatively old [11].

Here, we analyse major patterns of variation in diversification rates and species richness across the Tree of Life. Our results show major differences in diversification rates among clades, such as the higher rates in plants than animals, and higher rates in plants, animals and fungi relative to protists, eubacteria and archaeans. We also show that the dramatic differences in species richness among clades across the Tree of Life are largely explained by variation in diversification rates, especially at the phylum, class and ordinal ranks.

Data accessibility

All data are available in the electronic supplementary material.

Authors' contributions

J.J.W. conceived the study. J.P.S. collected, compiled and analysed the data. J.P.S. and J.J.W. interpreted the results and wrote the manuscript. Both the authors gave final approval for publication.

Competing interests

The authors declare no competing interests.

Funding

J.P.S. thanks the US National Science Foundation Graduate Research Fellowship Program for support.