Spatially cascading effect of perturbations in experimental meta-ecosystems

Abstract

Ecosystems are linked to neighbouring ecosystems not only by dispersal, but also by the movement of subsidy. Such subsidy couplings between ecosystems have important landscape-scale implications because perturbations in one ecosystem may affect community structure and functioning in neighbouring ecosystems via increased/decreased subsidies. Here, we combine a general theoretical approach based on harvesting theory and a two-patch protist meta-ecosystem experiment to test the effect of regional perturbations on local community dynamics. We first characterized the relationship between the perturbation regime and local population demography on detritus production using a mathematical model. We then experimentally simulated a perturbation gradient affecting connected ecosystems simultaneously, thus altering cross-ecosystem subsidy exchanges. We demonstrate that the perturbation regime can interact with local population dynamics to trigger unexpected temporal variations in subsidy pulses from one ecosystem to another. High perturbation intensity initially led to the highest level of subsidy flows; however, the level of perturbation interacted with population dynamics to generate a crash in subsidy exchange over time. Both theoretical and experimental results show that a perturbation regime interacting with local community dynamics can induce a collapse in population levels for recipient ecosystems. These results call for integrative management of human-altered landscapes that takes into account regional dynamics of both species and resource flows.

1. Introduction

The importance of allochthonous subsidies for biological community persistence and functioning in recipient ecosystems has been long recognized [1–3]. Ecosystems are linked to neighbouring ecosystems through their shared boundaries by the spatial movement of resources, despite wide variations in magnitude and type of inputs (e.g. movement of prey, detritus and nutrient). Allochthonous inputs to the recipient ecosystem subsidize primary producer biomass, consumer biomass [4–6], and strongly modulate the dynamics and structure of food webs [7,8]. These spatial flows may even trigger complex dynamical feedbacks between ecosystems (meta-ecosystem dynamics), acting at different trophic levels. Over the last decade, extensive conceptual and theoretical work has suggested that meta-ecosystem dynamics, by integrating spatial flows of energy, material and organisms, may have important implications for the stability of biological communities [9,10] and the unfolding of ecosystem processes [9,11–14]. As a direct consequence of such a coupling of energy/resource release and spatial transport between ecosystems, perturbations in one ecosystem will probably affect community structure and functioning in neighbouring ecosystems via increased or decreased subsidies.

Such a scenario is expected to be common in natural systems under recurrent perturbation dynamics [15]. For instance, spatial flows of nutrients and detritus from a forest to a lake or a river are greatly affected following a fire due to increased erosion and nutrient run-off [16–18]. Because perturbation pressure is usually intensified in human-managed regions, the dependence of spatial flows on perturbations is expected to be even stronger. This is well exemplified by the effect of biomass harvesting and fertilization in agricultural systems leading to higher resource run-offs in streams, which in turn leads to higher primary production in downstream lakes and potentially to eutrophication issues [19]. Such changes in ecosystem budgets (carbon and nutrient) following fire, overgrazing or intensive agricultural practices have been widely studied by ecosystem and forest ecologists for their direct impacts on neighbouring ecosystems [18–21]. However, rather than directly impacting subsidies (e.g. by leaching of agricultural fertilizers), perturbations can also trigger indirect effects between communities by modifying local community dynamics such that outflowing subsidies are increased or decreased. This can occur if some specific traits of the local community or population interact with perturbation frequency or intensity to increase or decrease local detritus production, generating variations in spatial subsidies to connected ecosystems. The historical divide between community and ecosystem ecology impeded a unification of these perspectives despite its potential significance for understanding connected-ecosystem dynamics and the cascading effect of perturbations across the landscape [22]. In the context of global changes, many perturbations are likely to affect resource exchanges between ecosystems, either directly (e.g. agricultural nutrient loads) or indirectly with impacts on communities triggering modifications of outflowing subsidies (e.g. habitat fragmentation and resource exploitation). This suggests that spatial variations in ecosystem processes and services in human-altered landscapes will be at least partly determined by meta-ecosystem dynamics [23], and their alteration following community response to perturbations.

In this study, we propose a demonstration of meta-ecosystem dynamics under perturbations by studying the effects of perturbation-induced cross-ecosystem subsidy exchanges on each ecosystem's biological community and function over time. First, we used a mathematical model inspired from general harvesting theory that couples population demographics to recurrent perturbations, from which we extracted the analytical prediction that detritus levels closely depend on the interaction between local species dynamics and the perturbation regime, and that they follow a hump-shaped relationship with perturbation intensity. We then experimentally tested this prediction and analysed its spatial consequences on neighbouring community dynamics using two-patch meta-ecosystems containing contrasting protist communities: one heterotrophic and one autotrophic community. Such a configuration is commonly seen in many natural ecosystems such as the coupling found between lake benthic (or stream) and forest (or cropland) ecosystems. We simulated a perturbation gradient affecting both ecosystems simultaneously and altering cross-ecosystem subsidy exchanges. The perturbation consisted of the sampling of a certain volume corresponding to the perturbation intensity/subsidy diffusion level (0, 5, 30 and 80% of total volume) from each ecosystem. Living protists were subsequently turned into dead biomass and the sample transferred to the recipient ecosystem. Perturbations and subsidy diffusion events occurred repeatedly at controlled intervals, over a three-week period. In parallel, we monitored changes in protist and bacteria density, and percentage oxygen availability as a proxy for ecosystem functioning in each ecosystem.

2. Material and methods

(a). Model description

Resource subsidies are often linked to perturbations. Mortality triggered by perturbations fuels the detritus pool that can serve as new resources for organisms, which can be transferred to other ecosystems as subsidies. For instance, during a storm, there may be increased leaf litter input from the riparian vegetation into rivers, or in marine fisheries discarded by-catch may feed benthic marine ecosystems [24]. We analysed a simple population model, derived from classic harvesting theory, to understand how subsidies depend on population growth rate (r) and carrying capacity (K), as well as on the frequency (f) and intensity (I) of perturbations. We describe the dynamics of a population density N with a simple logistic model

2.1

The population, initially at carrying capacity, is subjected to recurrent perturbations. At a frequency f, a perturbation provokes the death of a fraction I of the population, which characterizes the intensity of the perturbation. This fraction is removed from N and is considered as a subsidy. This leads to the following equation to characterize subsidy dynamics:

2.2

with T = 1/f the time between two perturbations (period), n the number of the perturbation, and 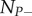the biomass of the population at the time nT just before the perturbation. We analytically derived the solution of S(nT), the level of subsidy at equilibrium, and the conditions under which the system is not crashing.

(b). Experimental design

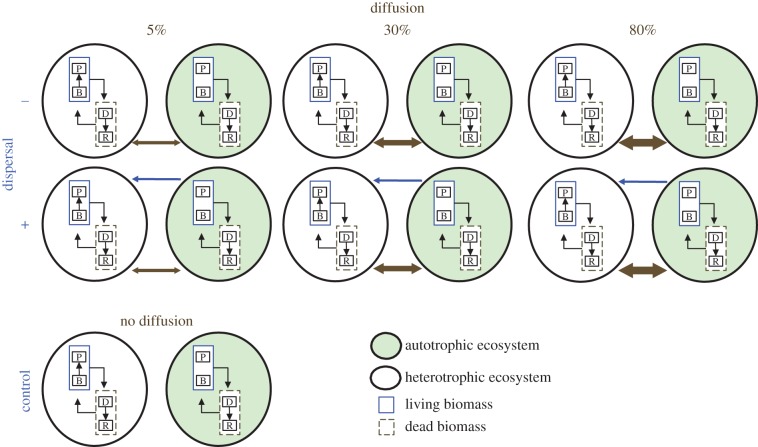
Our general model showed that the amount of perturbation-induced subsidy produced locally is strongly dependent on the interaction between demography parameters (e.g. growth rate) and perturbation regime (e.g. intensity, see ‘Results’ section). We propose to test these predictions and their consequences at the landscape level. To do so, we built a factorial protist microcosm experiment composed of two-patch meta-ecosystems linked by different intensity of perturbation-induced subsidy pulse (0, 5, 30 and 80%, thereafter referred to as diffusion treatment) and by species dispersal (with/without dispersal; figure 1). We had four replicates of each treatment combination at the meta-ecosystem level, resulting in a total of 24 meta-ecosystems, each composed of two connected patches and four unconnected controls (56 microcosms; figure 1). The experiment lasted 21 days and took place in a controlled culture room at 20°C and constant light. The position of replicate groups was randomized across the shelves in the culture room to control for possible micro-condition differences.

Figure 1.

Each meta-ecosystem was composed of two ecosystems with contrasting protist communities: one heterotrophic (white background) and one autotrophic community (green background). The two microcosms within each meta-ecosystem were either linked by diffusion alone (movement of the brown compartment; brown line), or diffusion and dispersal (movement of the blue compartment; blue line). The diffusion of detritus was generated by a gradient of perturbation intensity (0, 5, 30, 80%) and occurred by reciprocal transfer of medium without living organisms. With four replicates per treatment combination, the experiment was composed of 24 meta-ecosystems and four unconnected pairs as controls for a total of 56 microcosms. P, protist community; B, bacteria community; D, detritus; R, resource. (Online version in colour.)

In order to study effects of subsidy exchanges between contrasting ecosystem types in a representative way, we built two-patch meta-ecosystems consisting of one heterotrophic protist community (ecosystem 1) and one autotrophic protist community (ecosystem 2). The heterotrophic community was composed of four bacteriophagous ciliate protist species: Colpidium sp., Paramecium aurelia, Spirostomum sp. and Tetrahymena pyriformis. The autotrophic community was composed of the photosynthetic flagellate Euglena gracilis. This autotrophic species has a slow growth rate relative to most species in the heterotrophic community (except for Spirostomum sp.). These contrasting growth rates between the two ecosystems are essential to test the spatial consequences of our model predictions on the interaction between demography and perturbation intensity (see above). For details on culture conditions and experimental procedures, see [25,26].

Each microcosm consisted of a 250 ml Schott bottle filled to 100 ml. Microcosms were assembled by first filling each Schott bottle with 75 ml of pre-autoclaved standard protist medium (Carolina Biological Supply, Burlington NC, USA), and 5 ml of a bacteria solution composed of three species (Serratia fonticola, Bacillus subtilis and Brevibacillus brevis). After 24 h, to allow time for bacteria growth, we added 20 ml of protist solution with each protist species at carrying capacity (5 ml per species for heterotrophic communities and 20 ml of Euglena gracilis for autotrophic communities). Thus, protist communities were added at 20% of their carrying capacity and were allowed to grow for 24 h before the first diffusion event.

(c). Diffusion and dispersal procedures

For each diffusion level (0, 5, 30 and 80%), a corresponding volume (0, 5, 30, and 80 ml) was sampled from each microcosm and microwaved to turn living cells into detritus. After a 3 h cooling period at ambient temperature (20°C), the microwaved samples were poured into the respective neighbouring recipient ecosystems. Dispersal was unidirectional, from the autotrophic to the heterotrophic community, to test whether the introduction of an autotroph species could interact synergistically with subsidy diffusion and enhance microbial activity and ecosystem functioning. Dispersal was performed simultaneously with the diffusion procedure. It was done by sampling 5 ml (corresponds to an average of 1450 Euglena cells) from the autotrophic microcosm that was then poured directly into the heterotrophic microcosm of the corresponding meta-ecosystem. Because detritus and nutrient were also dispersed at the same time via the medium, the 5 ml was subtracted from the volume taken for subsidy diffusion from the autotrophic community. The logistical difficulty to disperse species without also diffusing medium (i.e. nutrient and detritus) did not permit having a ‘no-diffusion with dispersal’ treatment (see below for statistical implications and figure 1). The dispersal rate used herein (i.e. 5%) corresponds to levels of dispersal rates that have been successfully applied in related experiments (e.g. [27,28]), and is arguably an intermediate to high value even for many natural systems (e.g. [29]). Experimentally, much lower dispersal rates (less than 0.01%) have been shown to significantly affect metacommunity dynamics (e.g. [30]).

(d). Measurements

Measurements were synchronized with diffusion/dispersion procedures, with the measurements occurring every Tuesday (experimental days 0, 7, 14, 21) and Friday (experimental days 3, 10, 17), and diffusion/dispersion occurring every Wednesday and Saturday (see experimental calendar on the electronic supplementary material, figure S1). The last diffusion event was performed on day 15 to allow ecosystems to reach near equilibrium by day 21 (last measurement), and thus to evaluate the long-term impacts of our different diffusion treatments without its mortality effect.

On each measurement day, we quantified oxygen concentration, protist and bacteria densities in each microcosm. Oxygen concentration was measured using sensors that were mounted in the microcosm bottles at a medium depth of 2 cm. The information from the sensors was collected through an optical fibre cable connected to an oxygen meter device (PreSens Fibox 4 Optical Oxygen Meters, Germany) controlling for water pressure and temperature. On each measurement day, two 0.5 ml samples were taken: one for protist and one for bacteria density analysis. Protist density was measured by using a standardized video procedure [25,31]. In brief, a constant volume (17.6 µl) of each sample was placed under a dissecting microscope connected to a camera and a computer for the recording of videos (5 s per video). Then, using image processing software (ImageJ, National Institute of Health, USA) we extracted the number of moving organisms per video frame along with a suit of different traits for each occurrence (e.g. speed, shape and size) that were used to filter out background movement noise (e.g. particles from the medium, [31,32]). Finally, bacteria density was measured using standard flow cytometry on fresh SYBR green fixated cells using a BD Accuri^TM C6 cell counter (1/1000 dilution, following [25]).

As detritus spatial flows varied through time with species densities, we estimated the effective amount of detritus transferred from the autotroph ecosystem by simulating the logistic growth of Euglena from measured densities at each sampling day (approx. 48 h before each diffusion treatment). Parameters for the growth curve were extracted from control time series. We used the predicted numbers of Euglena individuals multiplied by the diffusion intensity as a proxy for realized subsidy (see also model description above, results section below and the analysis of the general model).

(e). Statistical analyses

To test for the reciprocal effects of cross-ecosystem subsidy exchanges on protist and bacteria densities, and ecosystem oxygen level, we first ran one generalized linear model (GLM) for each variable, testing for the main and interacting effects among all treatments and time. We used standardized residuals versus fitted values plots, residuals distribution, variance over-dispersion and log-likelihood information to select the most appropriate variance and link functions for each GLM model (i.e. gamma for oxygen concentration, and Gaussian on log-transformed data for bacteria and protist densities). The level of significance and the effect size of each factor and their interactions were then assessed using a standard F-test (type II analysis of deviance) on each GLM model. Finally, we used post-hoc pairwise comparisons (with Tukey adjusted p-values) on sub-models to extract the different contrasts of interest from significant terms in the main model. We used sub-models to avoid inflations of type II error [33] given the high number of potential pairwise comparisons in each main model. Because there was by definition no direct control for the dispersal effect (no dispersal only treatment; figure 1), this treatment was removed from the main GLM models to avoid contrast imbalance. Instead, we tested for dispersal effects using log-response ratios for each diffusion level with 95% confidence intervals (see the electronic supplementary material, figure S2).

In a few microcosms, we observed protist contaminations (e.g. Euglena individuals in heterotrophic communities without dispersal), though mostly occurring at low densities. To account for these contaminations, and to ensure that they did not bias our results, we evaluated their impact on our analyses. We ran all of our GLM models with and without the contaminated microcosms (see the electronic supplementary material, tables S1–S3). We show that retaining the replicates with contamination in the analysis did not affect the qualitative outputs of our models, and that in all cases they made our interpretations overall more conservative by increasing each model's residual variation. Therefore, we decided to retain all replicates in the main analyses.

All analyses were conducted with R v. 3.1.2 (R Development Core Team, 2014), using the ‘bemovi’ package [32] for video analyses, the ‘car’ package [34] for type II analysis of deviance and the ‘lsmeans’ package for post-hoc pairwise comparisons [35]. All data and the R code to reproduce our main results and figures are available from the Dryad Digital Repository [36].

3. Results

(a). Model

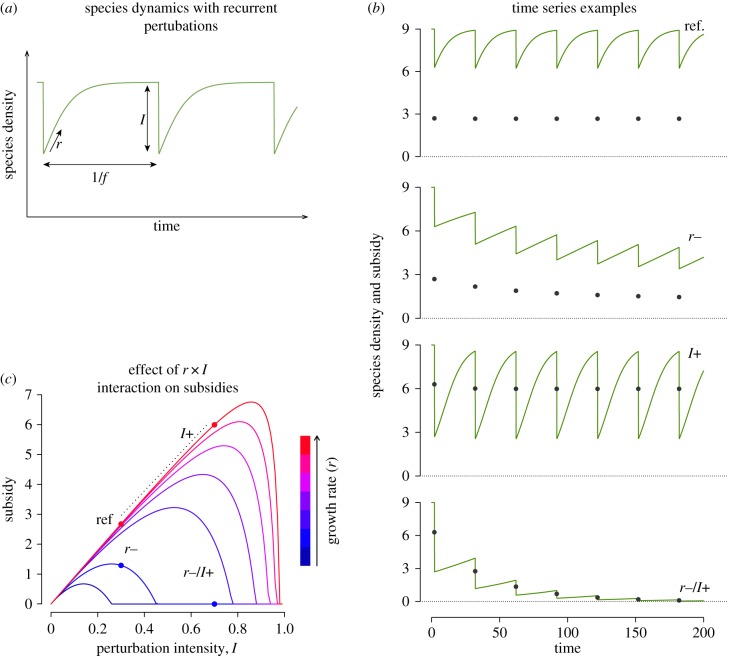
We examined how changes in perturbation intensity, frequency and specific demographic parameters (here intrinsic growth rate) can affect available subsidy levels. We found that when a population has enough time to reach its carrying capacity between perturbations, the level of subsidy remains almost constant (e.g. top dynamics in figure 2b). However, when the perturbations are too frequent, too intense or the population too slow to recover, the population and subsidies decrease over time (figure 2b, dynamics ‘r−’, ‘I+’, ‘r− /I+’). We can demonstrate (see the electronic supplementary material, appendix S1) that, assuming initial density at carrying capacity (N(0) = K), if the growth rate and perturbation regime satisfy the inequality:

3.1

the level of subsidies stabilizes to the following finite positive value:

3.2

with 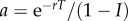. The amount of subsidy at equilibrium (equation (3.2)) decreases with decreasing r and increasing f, and follows a hump-shaped relationship with I (figure 2c). If inequality (3.1) is not satisfied, for instance with a combination of high perturbation intensity and low species growth rate, then both population and subsidies even tend to crash over time (figure 2b ‘r−/I+’ and 2c).

Figure 2.

Interaction between species dynamics, perturbations and subsidies. Results from a simple population model (defined in ‘Material and methods’) showing (a) the changes in density (green solid lines) through time of a species having a logistic growth rate r, submitted to recurrent perturbations of intensity I at a frequency f. The intensity of the perturbation is defined as the proportion of species dying suddenly and turned into subsidies. Panel (b) shows examples of species (green solid lines) and subsidy (grey points) dynamics for different parameter sets. In the top dynamics (‘ref.’), the species can reach its carrying capacity between two perturbations and subsidies are constant. Other dynamics illustrate, from top to bottom, cases with a lower growth rate (r−), a greater perturbation intensity (I+), or both (r−/I+), compared to the top dynamics. Panel (c) shows the variation of subsidies at equilibrium according to perturbation intensity I and for different growth rates r (blue colour refers to low growth rate while red to high ones). Points show the parameter couples used in panel (b). Values of parameters are: K = 9; f = 1/30; in panel (b) r = {0.13,0.02,0.13,0.02} and I = {0.3,0.3,0.7,0.7} from top to bottom; in panel (c) 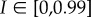and 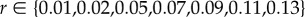. (Online version in colour.)

(b). Experiment

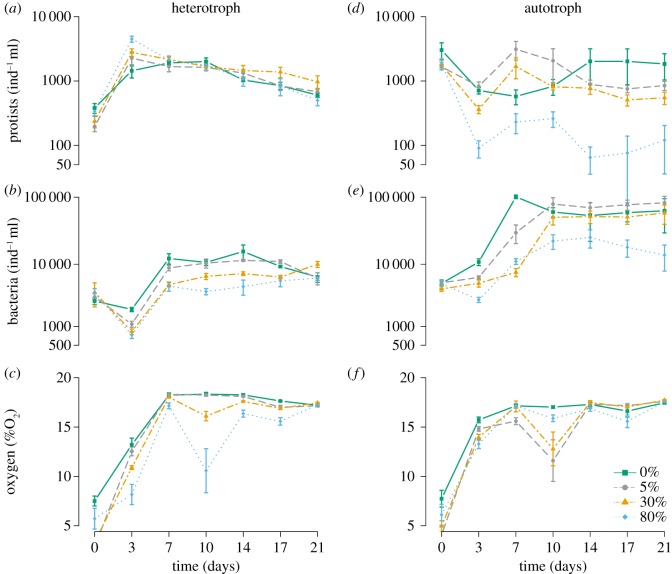
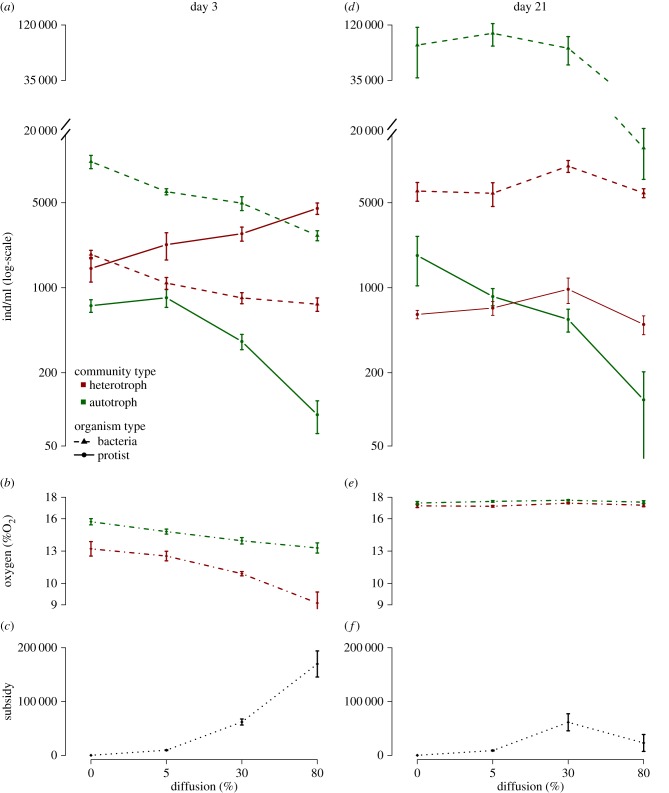
We found contrasting effects of the diffusion treatment in heterotroph versus autotroph ecosystems on protist density (F_3,333 = 61.24, p < 0.001; see the electronic supplementary material, table S1 for full GLM table), and bacteria density (F_3,333 = 3.65, p < 0.01; see the electronic supplementary material, table S2 for full GLM table). In the autotroph ecosystems, Euglena gracilis, which is characterized by a slower growth rate than the bacteriophagous species in the heterotroph ecosystems, was slow to recover from each diffusion-induced mortality event, especially at high levels of diffusion (figure 3d). The slow recovery at 80% diffusion level eventually resulted in a significant decline in population densities from the beginning to the end of the experiment (adjusted p-value of less than 0.0001; figure 3d). As predicted by the model, this decline fed back along time on subsidies coming from autotroph ecosystems (figure 4c–f): at the beginning of the experiment (figure 4: day 3), the 80% diffusion level generated a high amount of available subsidy (estimated dead Euglena cells) to the heterotroph ecosystems (figure 4c). In the heterotroph ecosystems, these subsidies sustained higher bacteriophagous protist densities (F_18,333 = 3.00, p < 0.001; figure 4a and electronic supplementary material, table S4 for all post-hoc multiple comparison results), paralleled by a decrease in bacteria density (F_18,333 = 1.74, p < 0.05; figure 4a and electronic supplementary material, table S4). As a consequence of this increase in bacteria consumption, and potentially bacteria turnover rates, oxygen concentration declined along the diffusion gradient (F_18,333 = 1.69 p < 0.05; figure 4b and electronic supplementary material, table S4). Over time, however, Euglena's difficulty to recover from the repeated 80% mortality (figure 3d) led to a drop in detritus production that disrupted the amount of subsidies available to the heterotrophic ecosystems (figure 4f). As a consequence, by the end of the experiment (figure 4: day 21), the intermediate 30% diffusion level provided more subsidies to the heterotrophic ecosystems than the 80% diffusion (figure 4f, adjusted p-value of less than 0.05) thus mirroring the model prediction of a hump-shaped relationship between perturbation intensity and detritus production. This resulted into a significant peak of bacteria densities at 30% (adjusted p-value of less than 0.05; figure 4d and electronic supplementary material, table S4) followed by a decline at 80% diffusion (adjusted p-value of less than 0.05; figure 4d and electronic supplementary material, table S4).

Figure 3.

Temporal dynamics for each diffusion level of protist densities in (a) heterotroph and (d) autotroph ecosystems, bacteria densities in (b) heterotroph and (e) autotroph ecosystems, oxygen concentration in (c) heterotroph and (f) autotroph ecosystems. Panels a, b, d and e are presented on a log-scale. Bars represent ±s.e. for each experimental day. Dispersal and no dispersal treatments were lumped together to produce the figure. (Online version in colour.)

Figure 4.

Effect of diffusion at the beginning (a–c) and at the end (d–f) of the experiment. The upper panels illustrate the effect of diffusion on protist and bacteria densities at day 3 (a) and 21 (d). The middle panels illustrate the effect of diffusion on oxygen concentration at day 3 (b) and 21 (e). The lower panels illustrate the estimated amount of detritus moved from the autotrophic to the heterotrophic ecosystem at the last diffusion procedure before sampling day 3 (c) and 21 (f). Panels (a,d) are presented on a log-scale. Bars represent ±s.e. for each diffusion level. (Online version in colour.)

In contrast to initial dynamics (figure 4a), protist and bacteria densities were positively rather than negatively associated by the end of the experiment (figure 4d). This temporal change probably occurred because of an overall enrichment of the heterotroph communities at 30% compared to 80% diffusion, owing to Euglena photosynthesis over the course of the experiment. By the end of the experiment, and in the absence of recent diffusion-induced perturbations (we stopped the diffusion treatment 6 days before the last measurement—see ‘Material and methods’), all heterotrophic and autotrophic ecosystems converged to similar oxygen concentrations (figure 4e). This convergence in oxygen level, in the absence of perturbations, probably developed because of similar overall biological rate averaging between Euglena producing oxygen, but sustaining a high density of oxygen-consuming bacteria in autotroph ecosystems, and low level of bacteria but likely with a high turnover due to the higher level of protist density in heterotroph ecosystems.

The negative effect of diffusion-induced mortality on Euglena densities also meant that in treatments where it dispersed to heterotrophic ecosystems its density was systematically too low to have significant contributions on oxygen concentration or protist density at 80% diffusion level (see the electronic supplementary material, figure S2); however, it did significantly contribute to increase protist density in heterotrophic ecosystems at low and intermediate diffusion levels (day 21 only; electronic supplementary material, figure S2b).

4. Discussion

We experimentally showed how perturbation-induced cross-ecosystem subsidy exchanges affect the local biological communities of two connected ecosystems with contrasting demographic and natural history parameters. Our experimental results that perturbations can lead to a decline of subsidy over time also matched the outcome of our theoretical model, which indicates that high levels of perturbations lead to collapsing subsidies after initial positive effects. Thus, we found the first experimental evidence of meta-ecosystem effects on biological communities and ecosystem function (figures 3 and 4), and of spatially cascading effect of perturbations via a disruption of spatial flows (figures 2 and 4).

Exploring theoretical scenarios, we first derived the general conditions under which local perturbations lead to the collapse of the local detritus pool (‘Material and methods’, equation (3.2)), disrupting regional dynamics through the flow of detritus. Similar dynamics have been studied in harvesting theory with a general focus on determining the optimal harvest effort (i.e. perturbation intensity and frequency) for a maximal profit [37]. Here, we stress the indirect consequences of recurrent perturbations on connected ecosystems. In the particular context of global changes, perturbations that kill part of a population (e.g. insect outbreaks, fires, storms) may occur in a more frequent or intense way [38]. Our model shows that this may decrease subsidies to other systems (e.g. litter inputs into rivers), more severely as the intensity and frequency of focal perturbations increase if populations are slow to recover. This change in subsidy levels may affect deeply the structure and functioning of the recipient community [39]. Previous empirical work had shown the importance of directional resource spatial flows between ecosystems for the maintenance of community structure and stability [2,7,40]. However, the temporal feedback that can occur over time had only been investigated in theoretical terms, using the meta-ecosystem framework [9,10,41]. Thus, in a second step we experimentally demonstrated that meta-ecosystem dynamics have implications for natural ecosystems under perturbation pressure because the way neighbouring ecosystems respond can directly affect community dynamics and functioning in connected ecosystems. The link between subsidy flow and perturbations, however, was not trivial because the direction of the effect was completely reversed over time. Initially, the high level of diffusion-induced mortality in the autotrophic ecosystem generated a peak in available subsidy for the heterotrophic neighbour. By the end of the experiment, this high mortality level fed back to generate an overall impoverishment in subsidy exchange, which significantly impacted community composition and ecosystem dynamics in both ecosystems.

The analysis of the demographic mathematical model revealed the circumstances that can lead (or not lead) to the observed temporal feedback in detritus exchanges (figure 2). Slow species growth rates in a neighbouring ecosystem in combination with high perturbation frequency and intensity generated the conditions for a collapse of the amount of detritus exchanged over time (figure 2c, bottom panel). For instance, slow-growing woody plants of riparian forests exposed to recurrent fires are progressively replaced by alien annuals of higher growth rates in Mediterranean areas [39,42]. Such high perturbation regimes will both deforest and re-structure the autotrophic riparian community towards a lower biomass system, and decline macro-invertebrate densities in streams by reducing leaf litter inputs [43]. Here we show that, more generally, a habitat- or ecosystem-specific response to any kind of perturbation can strongly impact neighbouring ecosystems through the disruption of detritus flows.

Subsidy quality can also have important impacts on recipient ecosystems [44–46]. In our experiment, the autotrophic protist species was not only a key species because of its inability to recover from perturbation over time, but also because it could increase the total level of resource in each ecosystem through photosynthetic activities. Thus, spatial flows from autotroph ecosystems would have contained higher levels of resources than flows from heterotrophic ecosystems. Over time such local enrichment would have increased the overall level of energy in the meta-ecosystems where autotrophs remained abundant (e.g. 30% as opposed to 80% diffusion). Therefore, the feedback between perturbation intensity and the slow recovery rate of autotrophs impoverished the meta-ecosystem under high perturbation pressure. This led to the observed change in the relationship between heterotrophic bacteria and protist density from initially negative to positive at the end. This interpretation also led to the important, but yet untested hypothesis, that local species identity might play an essential role in mediating the quantity and quality of among-ecosystems spatial flows.

Our results have important implications for the management of human-altered landscapes because conservation targets, such as in forest or grasslands, are usually localized in their actions, focusing on the most sensitive habitats or ecosystems. Our findings show that these management-induced disturbances (or preventions thereof) can directly affect dynamics in spatially coupled ecosystems, such as rivers or lakes, which are fed by resources from these ‘green’ ecosystems [7,46–49]. We experimentally demonstrated, and showed also in a mathematical model, that the direction of the effects depend on the temporal unfolding, the magnitude of disturbance and the type of connected ecosystems (autotrophic versus heterotrophic dominated). Increasing dispersal rate by maintaining habitat connections can mitigate the deleterious effects of perturbation on local communities [50], however, our results suggest that high perturbation pressure can hinder rescue effects when the dispersing populations are too slow to recover. Our study calls for more integrative management that takes into account regional dynamics related to species and resource flows [51], and spatial variations in ecosystem functions [52,53]. For instance, watershed conservation approaches could help to better integrate spatial flows within river networks [23], and a better understanding of spatial flows between forest and agricultural habitats would greatly improve agroforestry landscape management, maximizing the delivery of ecosystem services.

We have demonstrated that cross-ecosystem subsidy exchanges can have far-reaching implications for community dynamics and ecosystem processes beyond the generally well recognized one-way allochthonous input of detritus [2,3]. The actual prevalence of meta-ecosystems in natural landscapes is currently unknown but evidence suggests that they might be ubiquitous to certain ecosystem boundaries [7,23]. The feedback between demography, perturbations and changes in cross-ecosystem subsidy exchanges that we demonstrated here suggests that meta-ecosystem dynamics might be even more significant within fragmented and altered landscapes [54]. Yet our empirical understanding of meta-ecosystems is strikingly insufficient, and more experiments are needed to fully understand the potentially complex feedback triggered by spatial flows that theory predicts [10–13], and to forecast how local perturbations can spread across space in spatially structured landscapes [55,56].

Data accessibility

R code and data are available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.hm041 [36].

Authors' contributions

E.H., I.G. and F.A. designed the research; E.H., I.G. and P.G. conducted the research and processed the data; E.H. analysed the data and wrote the first draft of the manuscript. All authors edited the manuscript.

Competing interests

We declare we have no competing interests.

Funding

 Funding is from the Swiss National Science Foundation grant no. PP00P3_150698, University of Zurich and Eawag.