Abstract
In multidimensional cancer omics studies, one subject is profiled on multiple layers of omics activities. In this article, the goal is to integrate multiple types of omics measurements, identify markers, and build a model for cancer outcome. The proposed analysis is achieved in two steps. In the first step, we analyze the regulation among different types of omics measurements, through the construction of linear regulatory modules (LRMs). The LRMs have sound biological basis, and their construction differs from the existing analyses by modeling the regulation of sets of gene expressions (GEs) by sets of regulators. The construction is realized with the assistance of regularized singular value decomposition. In the second step, the proposed cancer outcome model includes the regulated GEs, “residuals” of GEs, and “residuals” of regulators, and we use regularized estimation to select relevant markers. Simulation shows that the proposed method outperforms the alternatives with more accurate marker identification. We analyze the The Cancer Genome Atlas data on cutaneous melanoma and lung adenocarcinoma and obtain meaningful results.
Keywords: Integrated analysis, Multidimensional data, Regularized estimation and selection
1. Introduction
Profiling studies have been extensively conducted in cancer research. The early studies are often limited by being “1D” and collecting a single type of omics data. In recent research, multidimensional studies are gaining significant popularity. In such studies, multiple types of omics data are collected on the same subjects. A representative example is The Cancer Genome Atlas (TCGA; http://cancergenome.nih.gov/), which has generated gene expression (GE), copy number variation (CNV), DNA methylation (DM), microRNA expression (ME), protein expression (PE), and other types of data for multiple cancer types. Multidimensional data provide valuable insights beyond 1D data (Cancer Genome Atlas Network, 2012).
For presentation clarity, we consider data with GE, CNV, and DM measurements, which match the data analyzed in Section 4. Methodological development in this article has been guided by the findings generated in biological studies (Kristensen and others, 2014), which include the following: (C1) GE is regulated by CNV, DM, and other regulators. Compared with its regulators, GE has a more direct effect on cancer outcomes. (C2) CNV and DE can have indirect effects on cancer outcomes mediated through GE. They may also have direct effects not captured by GE, for example through post-transcriptional regulations. (C3) The regulation relationship is more complicated than one (regulator) to one (GE). Instead, it is expected that sets of regulators, each of which is composed of multiple CNVs and/or DMs, regulate sets of GEs. This has been the basis of regulatory network analysis, gene co-expression analysis, and others. (C4) Among a large number of profiled GEs, CNVs, and DMs, only a small subset is associated with cancer.
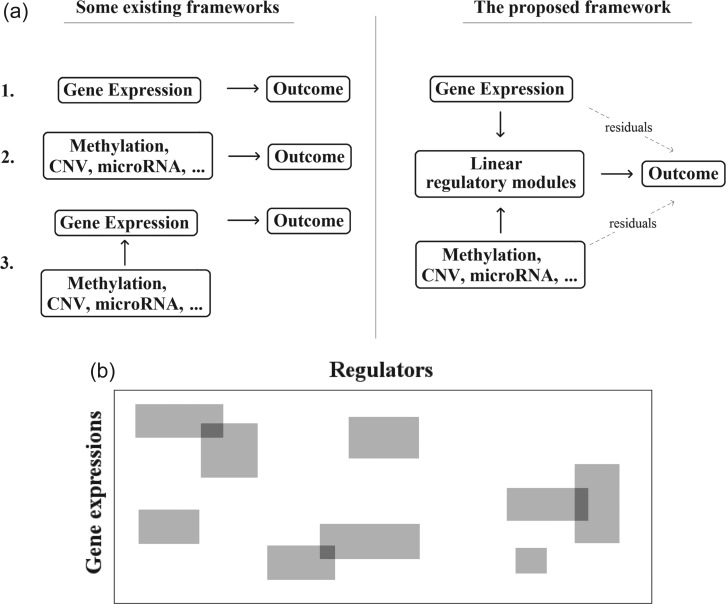
The analysis of multidimensional data has been conducted in the literature. The frameworks of some existing studies are summarized in Figure 1. van Iterson and others (2013) and Li and others (2012) analyze the regulations among GE, CNV, DM, and ME. Such studies address (C1), however, do not associate genetic variants with cancer outcomes. Daemen and others (2009) selects important features from each individual data type and models cancer outcomes using integrated information. Witten and Tibshirani (2009) proposes to jointly select GEs and array CGH measurements by conducting sparse canonical correlation analysis (CCA). However, in such studies, the information across different types of measurements is treated equally, without accounting for the fact that GE is the downstream product. Under more comprehensive frameworks that accommodate the gene regulation, Wang and others (2013) and Jennings and others (2013) analyze the regulation of GE by CNV, DM, and ME and then link GE with cancer outcomes. However, such a strategy does not accommodate the direct effects of regulators on cancer.
Fig. 1.
Modeling strategies. (a) Upper panel: the existing and proposed analysis frameworks. (b) Lower panel: representation of the LRMs. The entire rectangle represents the transition matrix from a variety of regulators to GEs. Each gray block represents an LRM that consists of a set of GEs and a set of regulators. The white areas represent no detectable regulations.
To address the limitations of existing studies, we propose a new analysis framework (Figure 1). Our approach addresses (C1) and (C3) by constructing the linear regulatory modules (LRMs) that link different types of omics measurements. (C2) is addressed by allowing for “residual” signals that cannot be captured by the LRMs. And we further consider sparse models to address (C4). Compared with the existing frameworks, our approach is unique in accommodating both GE and regulator signals, and the interconnections between the two are modeled using the LRMs. Our approach includes several of the existing ones as special cases and is more flexible. In what follows, the proposed method is described in Section 2. In Section 3, we conduct simulations and comparisons with the alternatives. The analysis of TCGA data is presented in Section 4. The article concludes with discussions in Section 5. Additional numerical results are provided in the Supplementary Materials (available at Biostatistics online).
2. Methods
For a subject, let 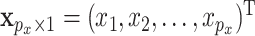 denote the
denote the  GE levels and
GE levels and 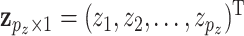 denote the
denote the 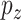 regulators. With for example
regulators. With for example 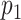 CNV and
CNV and 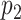 DM measurements,
DM measurements, 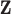 is the vector obtained by stacking the measurements together with
is the vector obtained by stacking the measurements together with 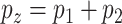 . Denote
. Denote  as the outcome variable. The analysis goal is to model
as the outcome variable. The analysis goal is to model 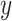 using
using 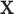 and
and 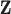 while properly accommodating their regulation relationship. Assume
while properly accommodating their regulation relationship. Assume 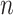 iid subjects. Denote the design matrices of GEs and regulators as
iid subjects. Denote the design matrices of GEs and regulators as  and
and 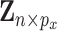 , respectively, and the outcome vector as
, respectively, and the outcome vector as 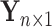 .
.
2.1. Analysis framework and rationale
We start with a simple regression model that describes the additive effects of GEs and regulators, that is, 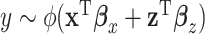 , where the form of
, where the form of 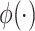 is known, and
is known, and  and
and 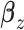 are the regression coefficients. This model includes the first and second existing analysis frameworks in Figure 1 as special cases. To better describe cancer biology, we need to accommodate the regulation between
are the regression coefficients. This model includes the first and second existing analysis frameworks in Figure 1 as special cases. To better describe cancer biology, we need to accommodate the regulation between 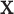 and
and  . Under the extreme scenario where
. Under the extreme scenario where 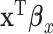 and
and 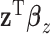 explain the same variation in
explain the same variation in 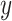 ,
, 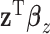 can be viewed as a “mega regulator” of
can be viewed as a “mega regulator” of 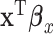 , and the above model suffers from an identifiability problem. It is possible that
, and the above model suffers from an identifiability problem. It is possible that 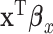 and
and 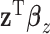 contain largely overlapping information, which has motivated the development of the collaborative regression method (Gross and Tibshirani, 2015). Our strategy differs from the collaborative regression and others as follows. Genes (Regulators) form functional sets, and the regulation relationship is “localized”. This motivates us to consider multiple connections in the form of
contain largely overlapping information, which has motivated the development of the collaborative regression method (Gross and Tibshirani, 2015). Our strategy differs from the collaborative regression and others as follows. Genes (Regulators) form functional sets, and the regulation relationship is “localized”. This motivates us to consider multiple connections in the form of 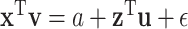 , where
, where 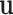 and
and 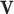 are (sparse) parameter vectors,
are (sparse) parameter vectors, 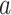 is a constant representing a stable state of a set of genes, and
is a constant representing a stable state of a set of genes, and 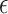 consists of “random noises” occurred during the transcription from DNA to mRNA that are not controlled by the measured regulators. We refer to each linear connection as an LRM. A graphical representation is provided in the lower panel of Figure 1, where each block represents one LRM that links a set of GEs and a set of regulators.
consists of “random noises” occurred during the transcription from DNA to mRNA that are not controlled by the measured regulators. We refer to each linear connection as an LRM. A graphical representation is provided in the lower panel of Figure 1, where each block represents one LRM that links a set of GEs and a set of regulators.
With the LRMs, an integrated model consists of three parts that possibly contribute to cancer outcomes: (i) a collective representation of the GEs that are regulated, 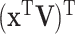 , where each column of
, where each column of 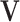 corresponds to a loading vector
corresponds to a loading vector 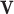 . This part is linked to the regulators through the LRMs; (ii)
. This part is linked to the regulators through the LRMs; (ii) 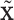 , which corresponds to the “residual” GE signals regulated by other mechanisms; and (iii)
, which corresponds to the “residual” GE signals regulated by other mechanisms; and (iii) 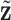 , which corresponds to the “residual” regulator signals that may affect outcomes through channels other than GE. Overall, we propose the model
, which corresponds to the “residual” regulator signals that may affect outcomes through channels other than GE. Overall, we propose the model
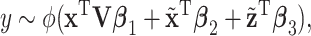 |
(2.1) |
where 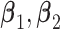 , and
, and 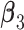 are the regression coefficients.
are the regression coefficients.
With different values of the regression coefficients, model (2.1) includes the following as special cases: the model with GE (or CNV, DM) only (Kim and others, 2013), the model with decomposed GEs (Wang and others, 2013), and the additive model of GEs and regulators (Zhao and others, 2015). It is thus more flexible and more comprehensive. With (C4), the regression coefficients are sparse with a small number of non-zero components. Note that the regulated GEs (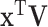 ) are linked to the regulators. The proposed method is thus able to achieve simultaneous marker selection across multiple types of omics measurements, which is not feasible with the alternative methods described in Figure 1, and generates more interpretable results. In the following subsections, we provide details on components of the proposed method. An outline is available in Table 1.
) are linked to the regulators. The proposed method is thus able to achieve simultaneous marker selection across multiple types of omics measurements, which is not feasible with the alternative methods described in Figure 1, and generates more interpretable results. In the following subsections, we provide details on components of the proposed method. An outline is available in Table 1.
Table 1.
Outline of the proposed method
Step 1. Estimate 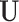 and and 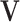 , the loading matrices of LRMs , the loading matrices of LRMs | |
| (a) | Estimate 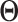 , the transition matrix from , the transition matrix from 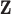 to to 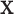
|
For the  th row of th row of 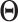 , , 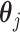 , its estimate , its estimate 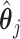 is obtained by fitting a penalized linear model for is obtained by fitting a penalized linear model for 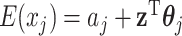
|
|
| (b) | Compute the LRM loading matrices 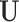 and and 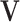 by conducting regularized SVD on by conducting regularized SVD on  . Pre-specify . Pre-specify 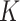 , the total number of LRMs. Initialize , the total number of LRMs. Initialize 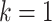 . Repeat (i) and (ii) for . Repeat (i) and (ii) for 
|
(i)Apply rank-1 sparse SVD on 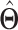 , and obtain the singular vectors , and obtain the singular vectors 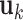 and and 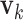 and singular value and singular value 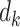
|
|
(ii)Update 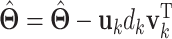 and and 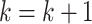
|
|
Step 2. Estimate the regression coefficients  , , 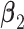 , and , and 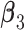
| |
| (a) | Calculate 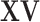 , , 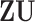 , and the residuals , and the residuals 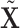 and and 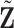
|
| (b) | Fit the regression model 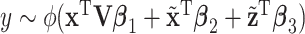 with the Lasso penalization with the Lasso penalization |
2.2. Estimating the LRMs
We first write all of the LRMs collectively as
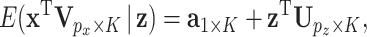 |
(2.2) |
where 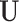 and
and 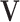 both contain
both contain 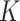 columns of loading vectors,
columns of loading vectors, 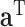 is a vector of constants, and
is a vector of constants, and 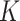 is the number of LRMs. Here, the grouping structure of genes in an LRM is defined using one column of
is the number of LRMs. Here, the grouping structure of genes in an LRM is defined using one column of 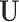 and the corresponding column of
and the corresponding column of 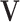 . We impose two conditions on the columns of
. We impose two conditions on the columns of 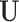 and
and 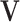 (the loading vectors
(the loading vectors 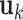 and
and 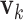 for
for 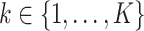 ). First,
). First, 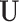 and
and 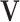 have orthogonal columns. That is,
have orthogonal columns. That is, 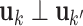 for
for 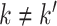 , and similarly for
, and similarly for 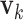 's. Loosely speaking, this condition postulates that the regulation relationships do not have overlap with each other. GEs and their regulators in different LRMs are expected to have different functionalities. Similar weak or no overlap assumptions have been considered in the literature (Ciriello and others, 2012). The second is that both
's. Loosely speaking, this condition postulates that the regulation relationships do not have overlap with each other. GEs and their regulators in different LRMs are expected to have different functionalities. Similar weak or no overlap assumptions have been considered in the literature (Ciriello and others, 2012). The second is that both 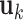 's and
's and 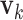 's are sparse. One GE is regulated by at most a small number of regulators, and a regulator affects at most a small number of GEs.
's are sparse. One GE is regulated by at most a small number of regulators, and a regulator affects at most a small number of GEs.
Under the above conditions, we construct the LRMs with the assistance of singular value decomposition (SVD). If we multiply 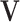 to both sides, Equation (2.2) becomes a regression problem with
to both sides, Equation (2.2) becomes a regression problem with 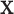 as outcomes and
as outcomes and 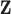 as predictors. Hence we can consider the linear model that regresses each single GE onto the entire vector of regulators. That is,
as predictors. Hence we can consider the linear model that regresses each single GE onto the entire vector of regulators. That is, 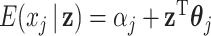 for
for 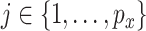 , where
, where 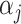 is an intercept, and
is an intercept, and 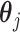 is a vector of regression coefficients. Under the sparsity condition, we estimate
is a vector of regression coefficients. Under the sparsity condition, we estimate 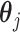 with penalized regression
with penalized regression
 |
(2.3) |
where 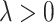 is the data-dependent tuning parameter. Here the Lasso penalization (Tibshirani, 1996) is adopted for its computational simplicity and satisfactory performance. We impose the same
is the data-dependent tuning parameter. Here the Lasso penalization (Tibshirani, 1996) is adopted for its computational simplicity and satisfactory performance. We impose the same 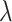 on all
on all 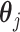 's to ensure comparability. Denote
's to ensure comparability. Denote 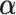 as the vector of
as the vector of 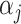 's and
's and 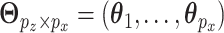 . The above regression models can be collectively written as
. The above regression models can be collectively written as 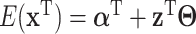 . With the orthogonality condition and Equation (2.2), we perform SVD on the transition matrix
. With the orthogonality condition and Equation (2.2), we perform SVD on the transition matrix 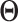 :
:
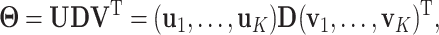 |
(2.4) |
where 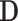 is a diagonal matrix with
is a diagonal matrix with 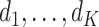 as the first
as the first  diagonal elements. The loading vectors defined here may differ from those in (2.2) by scaling factors, which can be absorbed into
diagonal elements. The loading vectors defined here may differ from those in (2.2) by scaling factors, which can be absorbed into 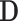 .
.
With SVD, we decompose the estimated regression coefficient matrix 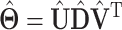 . Without the sparsity condition, the LRMs correspond to the first
. Without the sparsity condition, the LRMs correspond to the first 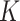 columns of
columns of 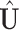 and
and 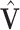 . With the sparsity condition, regularization needs to be incorporated in SVD. Specifically, we adopt the sparse SVD (SSVD, Lee and others, 2010) which recursively solves for rank-1 sparse singular vectors, i.e., the sparse vectors corresponding to the largest singular values. For the first singular vectors and singular value
. With the sparsity condition, regularization needs to be incorporated in SVD. Specifically, we adopt the sparse SVD (SSVD, Lee and others, 2010) which recursively solves for rank-1 sparse singular vectors, i.e., the sparse vectors corresponding to the largest singular values. For the first singular vectors and singular value 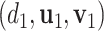 , we use the Lasso penalized estimation to obtain a sparse solution
, we use the Lasso penalized estimation to obtain a sparse solution
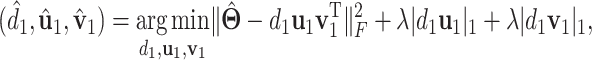 |
(2.5) |
where 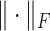 denotes the Frobenius norm. We then update
denotes the Frobenius norm. We then update 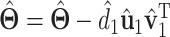 . The rest of the singular values and singular vectors can be obtained recursively in a similar manner.
. The rest of the singular values and singular vectors can be obtained recursively in a similar manner.
Remark 2.1. —
Multiple methods can perform SSVD (Lee and others, 2010; Witten and others, 2009; Yang and others, 2014). However, when the dimensions of
and
are large, the rank-1 approximation procedures need to be recursively performed for a large number of times, and the existing methods may fail to produce sparse solutions and/or run into convergence problems. To deal with this issue and also to reduce computer time, it is beneficial to focus on a smaller sub-matrix of
for each rank-1 approximation. To obtain this sub-matrix, we first conduct a non-sparse SVD and then apply a hard thresholding to
and
to reduce the numbers of non-zero elements to a manageable level (say, a few hundred). We then perform SSVD on this sub-matrix of
where the columns and rows correspond to the non-zero elements of
's and
's after thresholding. Note that this strategy is not essential and does not have a significant impact when
and
are not very large (in our simulation,
).
2.3. Modeling the cancer outcomes
With the LRMs, we can partition the effects of GEs and their regulators into three parts: (i) the 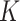 sets of regulated GEs
sets of regulated GEs 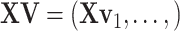 , or equivalently,
, or equivalently, 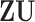 , the
, the 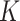 sets of regulators. Note that as
sets of regulators. Note that as 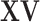 and
and 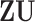 carry the same information, only one is needed. We choose using
carry the same information, only one is needed. We choose using 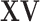 as GE is more closely related to cancer outcomes; (ii)
as GE is more closely related to cancer outcomes; (ii)  , which consists of the residual GE signals; and (iii)
, which consists of the residual GE signals; and (iii) 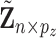 , which consists of the residual regulators signals.
, which consists of the residual regulators signals.
We implement the following procedure to calculate  and
and 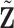 . Take
. Take 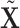 as an example, and
as an example, and 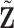 can be computed in the same manner. For the
can be computed in the same manner. For the 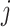 th GE, denote the residual effect as
th GE, denote the residual effect as 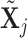 . Define
. Define 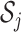 as the index set of all LRMs that contain the
as the index set of all LRMs that contain the 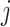 th GE; that is,
th GE; that is, 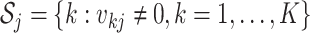 , where
, where 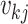 is the
is the 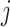 th entry of
th entry of  . If
. If 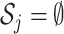 , the empty set, then the
, the empty set, then the 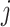 th GE is not regulated, and
th GE is not regulated, and 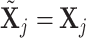 . When
. When 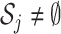 , let
, let 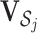 be the sub-matrix of
be the sub-matrix of 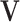 that contains columns with indices in
that contains columns with indices in 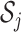 . Then
. Then 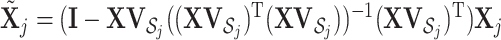 , which is the projection of
, which is the projection of 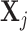 onto the orthogonal space of
onto the orthogonal space of  . This projection removes all the GE information contained in the LRMs. Note that this procedure yields a
. This projection removes all the GE information contained in the LRMs. Note that this procedure yields a 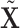 with which the column space of
with which the column space of 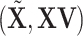 preserves exactly the column space of
preserves exactly the column space of  . However, it is also noted that the column space of
. However, it is also noted that the column space of 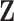 is not exactly preserved since the column space of
is not exactly preserved since the column space of 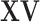 is not exactly equal to that of
is not exactly equal to that of 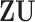 . A small proportion of information in
. A small proportion of information in 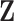 may be sacrificed with the expectation that similar information can be captured in
may be sacrificed with the expectation that similar information can be captured in 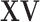 .
.
With the above decomposition, we consider model (2.1) for the cancer outcome. With 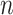 iid observations, denote by
iid observations, denote by 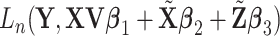 the loss function. To accommodate the high dimensionality and (C4), we estimate the unknown regression coefficients by minimizing the penalized loss function
the loss function. To accommodate the high dimensionality and (C4), we estimate the unknown regression coefficients by minimizing the penalized loss function
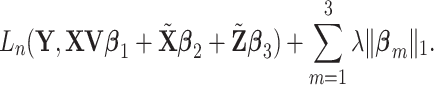 |
(2.6) |
Lasso is adopted again for the consistency of analysis. Note that it is possible to use different tunings for different terms. However, this may significantly increase computational cost. In addition, it may not be entirely necessary since the three terms are on a relatively similar scale.
2.4. Connections with the existing methods
A key step of the proposed method is the reconstruction of the column spaces of 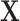 and
and 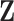 . It is noted that both
. It is noted that both 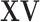 and
and  belong to the column space of
belong to the column space of  , and similarly for
, and similarly for 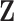 . Thus the naive additive linear model (Zhao and others, 2015) is a special case of the proposed method. The construction of
. Thus the naive additive linear model (Zhao and others, 2015) is a special case of the proposed method. The construction of  has a connection with some of the existing dimension reduction techniques, for example principal component analysis. The linear combination form also shares a certain similarity with the (sparse) CCA (Witten and others, 2009) and partial least squares (PLS, Geladi and Kowalski, 1986). However, the proposed method has unique properties and advantages. First, it accommodates the natural order of omics measurements, with GE at the downstream of its regulators. Thus it is more sensible to use regression as opposed to correlation analysis for the present problem. The loading vectors of PLS are obtained through maximizing covariance. The existing theories for sparse PLS require that the covariance matrix of
has a connection with some of the existing dimension reduction techniques, for example principal component analysis. The linear combination form also shares a certain similarity with the (sparse) CCA (Witten and others, 2009) and partial least squares (PLS, Geladi and Kowalski, 1986). However, the proposed method has unique properties and advantages. First, it accommodates the natural order of omics measurements, with GE at the downstream of its regulators. Thus it is more sensible to use regression as opposed to correlation analysis for the present problem. The loading vectors of PLS are obtained through maximizing covariance. The existing theories for sparse PLS require that the covariance matrix of 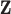 has a latent eigenstructure (Chun and Keleş, 2010), which not necessarily holds for the gene regulators. In contrast, the proposed method derives the loading vectors directly from regression coefficients and may better suit the need and interpretation of multidimensional omics data analysis.
has a latent eigenstructure (Chun and Keleş, 2010), which not necessarily holds for the gene regulators. In contrast, the proposed method derives the loading vectors directly from regression coefficients and may better suit the need and interpretation of multidimensional omics data analysis.
2.5. Heuristic theoretical justifications
Consistency of the proposed method relies on several key estimation procedures and conditions. First,  needs to be consistently estimated. For a specific GE, under mild regularity conditions on the design matrix
needs to be consistently estimated. For a specific GE, under mild regularity conditions on the design matrix 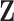 and signal strengths, with probability
and signal strengths, with probability 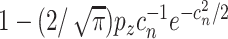 , consistency can be achieved, where
, consistency can be achieved, where 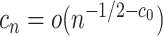 is a diverging sequence (Fan and Lv, 2010). The dimension
is a diverging sequence (Fan and Lv, 2010). The dimension 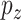 can grow with
can grow with 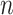 as long as
as long as 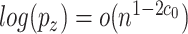 , and
, and 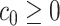 is a constant. Note that the proposed method for estimating
is a constant. Note that the proposed method for estimating 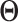 essentially performs
essentially performs 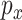 penalized estimations. With the Bonferroni approach, to ensure the overall consistency, we require that
penalized estimations. With the Bonferroni approach, to ensure the overall consistency, we require that 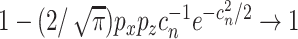 . If
. If 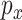 and
and 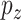 are of the same order, then
are of the same order, then 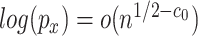 ensures the overall consistency in the estimation of
ensures the overall consistency in the estimation of 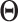 . The consistency of
. The consistency of 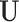 and
and 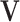 is ensured under the orthonormality and sparsity conditions on the true loading vectors. Estimating the
is ensured under the orthonormality and sparsity conditions on the true loading vectors. Estimating the 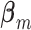 's is a “standard” penalization problem. Special attention may be needed on the design matrix
's is a “standard” penalization problem. Special attention may be needed on the design matrix 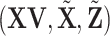 as different components are interconnected.
as different components are interconnected.
3. Simulation study
We conduct simulation to assess performance of the proposed method (referred to as Integrated). In addition, we are interested in comparing against alternatives. To the best of our knowledge, there is no approach in the literature that searches for the LRM (or similar forms that identify sets of linked GEs and regulators). The following alternatives, which can also link omics measurements with outcomes, are considered. (a) The Lasso-Separate approach regresses the outcome on 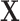 and
and 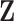 separately using Lasso and then combines results. (b) The Lasso-Joint approach regresses the outcome on
separately using Lasso and then combines results. (b) The Lasso-Joint approach regresses the outcome on 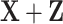 using Lasso. (c) The iterative sure independence screening approach (ISIS, Fan and Lv, 2008) marginally searches for candidate features of
using Lasso. (c) The iterative sure independence screening approach (ISIS, Fan and Lv, 2008) marginally searches for candidate features of  and
and 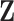 and iteratively performs variable selection. (d) The collaborative regression approach (CollReg, Gross and Tibshirani, 2015) models
and iteratively performs variable selection. (d) The collaborative regression approach (CollReg, Gross and Tibshirani, 2015) models 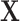 and
and 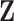 jointly and also encourages them to explain similar variation in
jointly and also encourages them to explain similar variation in 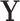 . With the proposed method, the rank-1 SSVD is realized using the R code provided by Lee and others (2010) with default settings. Approaches (a) and (b) are conducted using the R package glmnet. ISIS is conducted using the SIS package. The collaborative regression is conducted with manipulation of the data matrix, following Gross and Tibshirani (2015).
. With the proposed method, the rank-1 SSVD is realized using the R code provided by Lee and others (2010) with default settings. Approaches (a) and (b) are conducted using the R package glmnet. ISIS is conducted using the SIS package. The collaborative regression is conducted with manipulation of the data matrix, following Gross and Tibshirani (2015).
Data are generated as follows. First, the rows of 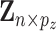 are independently generated from a multivariate normal distribution with covariance matrix
are independently generated from a multivariate normal distribution with covariance matrix 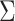 , where
, where 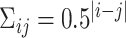 . Then
. Then 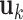 and
and 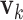 for
for 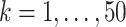 are generated. Each
are generated. Each 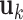 or
or 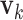 contains five randomly selected non-zero entries, with values generated from uniform (0.5, 1). We compute
contains five randomly selected non-zero entries, with values generated from uniform (0.5, 1). We compute 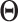 as
as  ;
; 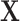 is generated as
is generated as 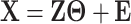 , where the rows of
, where the rows of 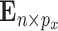 are iid and follow a multivariate normal distribution with covariance matrix
are iid and follow a multivariate normal distribution with covariance matrix  . Finally
. Finally 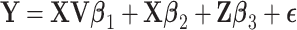 , with the components of
, with the components of 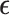 iid and following a normal distribution. Note that we use
iid and following a normal distribution. Note that we use 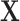 and
and 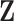 , as opposed to
, as opposed to 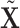 and
and  , in the residual parts because the construction and identification of the residuals should be up to the method.
, in the residual parts because the construction and identification of the residuals should be up to the method.
We simulate four scenarios which represent different complexity of LRMs and individual effects. (Scenario 1) The locations of non-zero components in 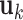 's (
's (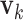 's) are mutually exclusive. This makes the LRMs having no overlap and
's) are mutually exclusive. This makes the LRMs having no overlap and 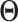 having a blockwise structure. The individual effects in
having a blockwise structure. The individual effects in 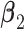 and
and  are not involved in any LRM. This scenario is standard for the proposed method, and the next three scenarios add more complexity to demonstrate a certain degree of robustness of the proposed method. (Scenario 2) The locations of non-zero components in
are not involved in any LRM. This scenario is standard for the proposed method, and the next three scenarios add more complexity to demonstrate a certain degree of robustness of the proposed method. (Scenario 2) The locations of non-zero components in 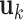 's and
's and 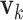 's are randomly selected without reinforcing exclusiveness. With a chance of overlapping non-zero entries, this creates a violation of the orthogonality condition. (Scenario 3) The locations of non-zero individual effects are randomly generated from those of genes in the non-zero LRMs to force overlapping signals. Under the above three scenarios, there are five non-zero entries in
's are randomly selected without reinforcing exclusiveness. With a chance of overlapping non-zero entries, this creates a violation of the orthogonality condition. (Scenario 3) The locations of non-zero individual effects are randomly generated from those of genes in the non-zero LRMs to force overlapping signals. Under the above three scenarios, there are five non-zero entries in 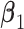 and also five non-zero individual effects in both
and also five non-zero individual effects in both 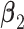 and
and 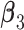 . (Scenario 4) We generate two non-zero entries in
. (Scenario 4) We generate two non-zero entries in 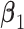 and twenty non-zero entries in both
and twenty non-zero entries in both 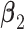 and
and 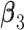 . Under all scenarios, the non-zero components of
. Under all scenarios, the non-zero components of 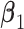 are generated uniformly from
are generated uniformly from 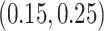 or
or 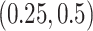 to represent weak or strong signals. The non-zero components of
to represent weak or strong signals. The non-zero components of 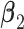 and
and  are generated uniformly from
are generated uniformly from 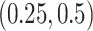 . We set
. We set 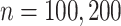 and
and 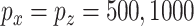 .
.
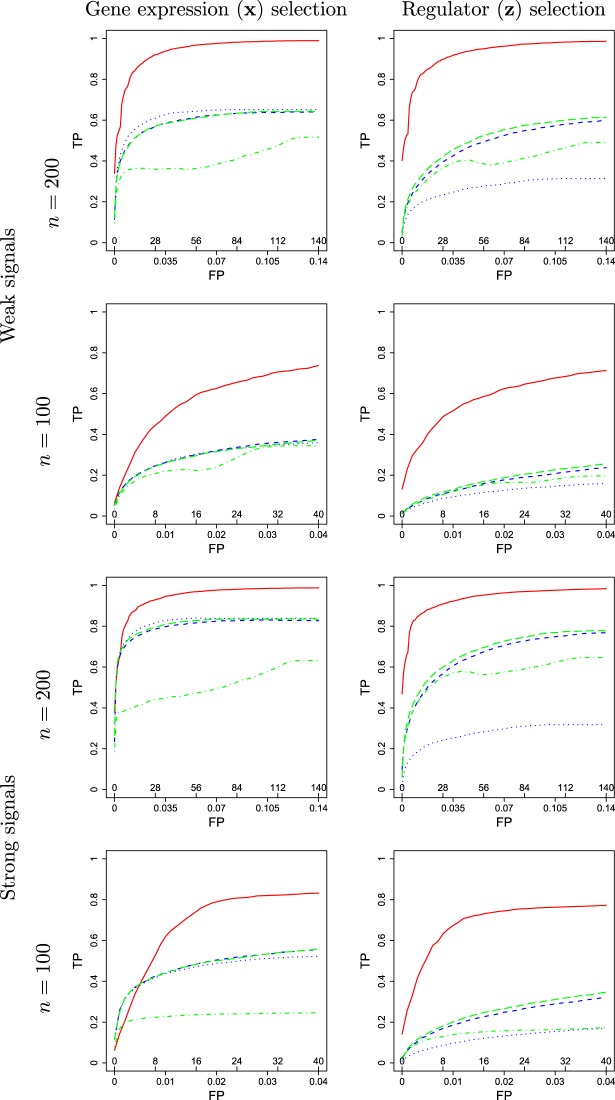
The proposed and alternative methods involve tuning parameters. For a comprehensive evaluation, we consider a sequence of tuning parameter values and use the receiver operating characteristic (ROC) curve and partial area under the ROC curve (PAUC) to compare different methods. Since Lasso can select at most 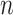 non-zero variables, and the total number of truly associated GEs and regulators is 60 (except for Scenario 3 which has 50), we compute the partial AUC up to
non-zero variables, and the total number of truly associated GEs and regulators is 60 (except for Scenario 3 which has 50), we compute the partial AUC up to 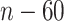 falsely selected variables. Simulation results for
falsely selected variables. Simulation results for 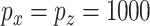 are summarized in Table 2. The ROC plots for Scenario 1 with
are summarized in Table 2. The ROC plots for Scenario 1 with 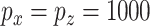 are shown in Figure 2. More simulation results are provided in the Supplementary Materials (available at Biostatistics online).
are shown in Figure 2. More simulation results are provided in the Supplementary Materials (available at Biostatistics online).
Table 2.
Simulation. PAUC: mean (SD) based on 200 replicates. 
GE (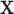 ) selection ) selection |
Regulator ( ) selection ) selection |
|||||||
| Signal level | Weak | Strong | Weak | Strong | ||||
 |
100 | 200 | 100 | 200 | 100 | 200 | 100 | 200 |
| Scenario 1 | ||||||||
| Integrated | 0.57 (0.13) | 0.94 (0.03) | 0.68 (0.09) | 0.95 (0.03) | 0.58 (0.15) | 0.93 (0.04) | 0.68 (0.11) | 0.94 (0.03) |
| Lasso-Separate | 0.30 (0.08) | 0.60 (0.07) | 0.48 (0.07) | 0.80 (0.06) | 0.16 (0.06) | 0.48 (0.09) | 0.23 (0.07) | 0.66 (0.08) |
| Lasso-Joint | 0.30 (0.08) | 0.62 (0.07) | 0.46 (0.07) | 0.82 (0.06) | 0.12 (0.05) | 0.27 (0.05) | 0.12 (0.05) | 0.28 (0.05) |
| ISIS | 0.26 (0.08) | 0.41 (0.08) | 0.23 (0.08) | 0.51 (0.06) | 0.15 (0.07) | 0.40 (0.09) | 0.15 (0.07) | 0.57 (0.08) |
| CollReg | 0.29 (0.08) | 0.60 (0.08) | 0.48 (0.08) | 0.81 (0.06) | 0.17 (0.07) | 0.51 (0.09) | 0.25 (0.07) | 0.68 (0.08) |
| Scenario 2 | ||||||||
| Integrated | 0.51 (0.13) | 0.87 (0.05) | 0.66 (0.10) | 0.89 (0.04) | 0.51 (0.13) | 0.86 (0.06) | 0.68 (0.09) | 0.88 (0.03) |
| Lasso-Separate | 0.34 (0.08) | 0.64 (0.06) | 0.53 (0.09) | 0.83 (0.07) | 0.22 (0.07) | 0.58 (0.07) | 0.30 (0.07) | 0.74 (0.07) |
| Lasso-Joint | 0.32 (0.08) | 0.65 (0.07) | 0.51 (0.09) | 0.84 (0.06) | 0.16 (0.05) | 0.33 (0.06) | 0.17 (0.05) | 0.34 (0.06) |
| ISIS | 0.18 (0.08) | 0.42 (0.06) | 0.27 (0.09) | 0.55 (0.07) | 0.15 (0.07) | 0.48 (0.08) | 0.21 (0.07) | 0.65 (0.07) |
| CollReg | 0.33 (0.08) | 0.63 (0.06) | 0.53 (0.09) | 0.83 (0.07) | 0.23 (0.07) | 0.61 (0.08) | 0.32 (0.07) | 0.76 (0.07) |
| Scenario 3 | ||||||||
| Integrated | 0.58 (0.16) | 0.86 (0.13) | 0.78 (0.12) | 0.97 (0.07) | 0.56 (0.18) | 0.87 (0.11) | 0.73 (0.20) | 0.98 (0.05) |
| Lasso-Separate | 0.34 (0.10) | 0.52 (0.11) | 0.54 (0.11) | 0.73 (0.10) | 0.27 (0.08) | 0.56 (0.09) | 0.33 (0.08) | 0.70 (0.09) |
| Lasso-Joint | 0.33 (0.10) | 0.50 (0.11) | 0.53 (0.11) | 0.72 (0.10) | 0.20 (0.07) | 0.37 (0.07) | 0.20 (0.07) | 0.38 (0.07) |
| ISIS | 0.19 (0.11) | 0.36 (0.12) | 0.26 (0.11) | 0.48 (0.10) | 0.18 (0.08) | 0.49 (0.09) | 0.24 (0.09) | 0.64 (0.09) |
| CollReg | 0.35 (0.11) | 0.53 (0.12) | 0.54 (0.11) | 0.75 (0.10) | 0.28 (0.08) | 0.58 (0.09) | 0.35 (0.09) | 0.73 (0.09) |
| Scenario 4 | ||||||||
| Integrated | 0.22 (0.11) | 0.66 (0.09) | 0.34 (0.08) | 0.70 (0.07) | 0.16 (0.11) | 0.56 (0.11) | 0.30 (0.10) | 0.62 (0.08) |
| Lasso-Separate | 0.17 (0.06) | 0.48 (0.09) | 0.23 (0.07) | 0.57 (0.08) | 0.14 (0.06) | 0.43 (0.07) | 0.16 (0.06) | 0.51 (0.08) |
| Lasso-Joint | 0.16 (0.06) | 0.51 (0.08) | 0.22 (0.07) | 0.60 (0.08) | 0.14 (0.07) | 0.43 (0.06) | 0.13 (0.05) | 0.44 (0.07) |
| ISIS | 0.10 (0.06) | 0.36 (0.08) | 0.12 (0.06) | 0.39 (0.08) | 0.09 (0.06) | 0.34 (0.07) | 0.10 (0.06) | 0.40 (0.08) |
| CollReg | 0.17 (0.06) | 0.46 (0.08) | 0.23 (0.06) | 0.56 (0.08) | 0.14 (0.06) | 0.42 (0.07) | 0.17 (0.06) | 0.51 (0.08) |
Fig. 2.
ROC curves under simulation Scenario 1. 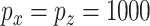 . Integrated, solid; Lasso-Separate, dashed; Lasso-Joint, dotted; ISIS, dot-dashed; CollReg, long-dashed; TP, true positive; FP, false positive.
. Integrated, solid; Lasso-Separate, dashed; Lasso-Joint, dotted; ISIS, dot-dashed; CollReg, long-dashed; TP, true positive; FP, false positive.
Under all simulation settings, the proposed method has higher PAUCs than the competing alternatives for both GE and regulator selection. Consider for example Scenario 1 with strong signals, which is the easiest setting for identifying the important  variables. For
variables. For 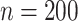 , the proposed method has mean PAUC 0.95, while Lasso-Separate, Lasso-Joint, ISIS, and CollReg have PAUCs 0.80, 0.82, 0.51, and 0.81, respectively. For
, the proposed method has mean PAUC 0.95, while Lasso-Separate, Lasso-Joint, ISIS, and CollReg have PAUCs 0.80, 0.82, 0.51, and 0.81, respectively. For 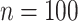 , all methods have smaller PAUC values: 0.68 (Integrated), 0.48 (Lasso-Separate), 0.46 (Lasso-Joint), 0.23 (ISIS), and 0.48 (CollReg). Similar conclusion can be drawn for Scenario 3. An interesting pattern is observed here: Integrated may start with a lower ROC curve when false positive rates are small, with about four false non-zero variables. This is because that the estimated LRM may contain false variables, and selecting a module forces these variables to enter the model. The alternative methods, based on individual selection, are less likely to make mistakes early on since only variables with very strong signals are selected. However, as we allow slightly higher false positive rates, the proposed method quickly surpasses the other methods in terms of true positive rate. The variables with weaker signals can still be picked up by the LRMs due to the stronger combined signals, while the alternatives have a substantial chance to miss these individual ones completely. This pattern is also observed under other settings especially for Scenario 2. Scenario 4 represents another interesting situation where there is little room for the proposed method to take advantage of, since most of the important effects contribute individually. Constructing LRMs brings less benefit especially to the regulator selection, although the proposed method has a higher selection rate under large models. Overall, across the whole spectrum, Integrated has higher identification accuracy. For regulator selection, Integrated completely dominates in both PAUCs and ROC curves with its capability of correctly identifying the LRMs. Since the indirect contribution from
, all methods have smaller PAUC values: 0.68 (Integrated), 0.48 (Lasso-Separate), 0.46 (Lasso-Joint), 0.23 (ISIS), and 0.48 (CollReg). Similar conclusion can be drawn for Scenario 3. An interesting pattern is observed here: Integrated may start with a lower ROC curve when false positive rates are small, with about four false non-zero variables. This is because that the estimated LRM may contain false variables, and selecting a module forces these variables to enter the model. The alternative methods, based on individual selection, are less likely to make mistakes early on since only variables with very strong signals are selected. However, as we allow slightly higher false positive rates, the proposed method quickly surpasses the other methods in terms of true positive rate. The variables with weaker signals can still be picked up by the LRMs due to the stronger combined signals, while the alternatives have a substantial chance to miss these individual ones completely. This pattern is also observed under other settings especially for Scenario 2. Scenario 4 represents another interesting situation where there is little room for the proposed method to take advantage of, since most of the important effects contribute individually. Constructing LRMs brings less benefit especially to the regulator selection, although the proposed method has a higher selection rate under large models. Overall, across the whole spectrum, Integrated has higher identification accuracy. For regulator selection, Integrated completely dominates in both PAUCs and ROC curves with its capability of correctly identifying the LRMs. Since the indirect contribution from 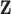 to the outcome may be partially explained by
to the outcome may be partially explained by 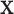 , collinearity occurs between the two types of covariates. Hence Lasso-Joint usually performs the worst. CollReg is often the second best since it is able to simultaneously identify both
, collinearity occurs between the two types of covariates. Hence Lasso-Joint usually performs the worst. CollReg is often the second best since it is able to simultaneously identify both 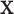 and
and 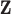 . However, some individual variables can be missed due to the miss-match of the two spaces since the individual
. However, some individual variables can be missed due to the miss-match of the two spaces since the individual 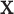 signals cannot be explained by the individual
signals cannot be explained by the individual 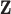 signals.
signals.
4. Analysis of TCGA data
We analyze the TCGA data on skin cutaneous melanoma (SKCM) and lung adenocarcinoma (LUAD). Data were obtained in October of 2015. Measurements are available on GE (obtained using the Illumina HiSeq 2000 RNA Sequencing Version 2 analysis platform), DM (obtained using the Illumina Infinium HumanMethylation450 platform), and CNV (obtained using the Genome-Wide Human SNP Array 6.0 platform). For GE and DM, we use the level 3 processed data downloaded from the TCGA website. For CNV, we calculate and map using the raw SNP Array data and TCGA-Assembler (Zhu and others, 2014). Beyond the omics measurements, we also collect data on two clinical variables: age and gender. The cancer outcome of interest is overall survival. Below we describe the SKCM data analysis results. Additional details are provided in the Supplementary Materials (available at Biostatistics online). Results for LUAD are also provided in the Supplementary Materials (available at Biostatistics online).
With standard data processing, we obtain measurements on 469 subjects (with 156 failures) and 20 531 GEs, 21 231 DMs, and 24 958 CNVs. In principle, the proposed method can be directly applied. Given the small sample size, we conduct screening to reduce dimensionality and improve stability. Specifically, we conduct marginal screening, select the top 200 measurements (of each type) with the largest marginal variances, and then pool all the screened measurements. This leads to 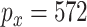 unique GEs and
unique GEs and 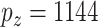 (DM and CNV) regulators. This marginal screening combines the most active measurements from each type and is suitable for the purpose of data integration. For linking the omics measurements with survival, we adopt the accelerated failure time (AFT, Stute, 1993) model. For details on fitting the AFT model, we refer the reader to Liu and others (2013).
(DM and CNV) regulators. This marginal screening combines the most active measurements from each type and is suitable for the purpose of data integration. For linking the omics measurements with survival, we adopt the accelerated failure time (AFT, Stute, 1993) model. For details on fitting the AFT model, we refer the reader to Liu and others (2013).
When applying the proposed method, we choose the tuning parameters for Lasso penalties using cross-validation. The proposed method also involves the number of LRMs and sub-matrix size. Although they can be determined based on subjective judgment, we explore a more data-driven approach, which can also serve the purpose of sensitivity analysis. Specifically, we randomly select 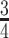 of the subjects to form the training data. A model is generated using the proposed method and training data and used to make prediction for the remaining
of the subjects to form the training data. A model is generated using the proposed method and training data and used to make prediction for the remaining 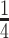 subjects. As the outcome is subject to censoring, the Harrell's concordance index (C-index, Harrell and others, 1982) is adopted to evaluate prediction performance. This procedure is repeated 200 times, and the summary C-index results are provided in Table 5 of the Supplementary Materials (available at Biostatistics online). We consider the number of
subjects. As the outcome is subject to censoring, the Harrell's concordance index (C-index, Harrell and others, 1982) is adopted to evaluate prediction performance. This procedure is repeated 200 times, and the summary C-index results are provided in Table 5 of the Supplementary Materials (available at Biostatistics online). We consider the number of 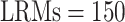 and 300 and sub-matrix
and 300 and sub-matrix 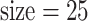 , 50, and 100 and observe that prediction performance is not sensitive to those choices. The dual (number of LRMs, sub-matrix size) = (300, 25) slightly outperforms and is used in downstream analysis.
, 50, and 100 and observe that prediction performance is not sensitive to those choices. The dual (number of LRMs, sub-matrix size) = (300, 25) slightly outperforms and is used in downstream analysis.
The proposed method identifies 9 LRMs as well as 6 GE and 21 regulator residual effects. A total of 68 unique omics measurements are involved, including 16 GEs, 33 CNVs, and 19 DMs. More detailed results are provided in Table 3. The identification results are meaningful. Specifically, we identify CDKN2B, which has been identified for multiple cancer types. A recent study shows that the depletion of p15, which is encoded by CDKN2B, in benign nevi promotes progression to melanoma (McNeal and others, 2015). The human leukocyte antigen (HLA) class II genes, including HLA-DRB1 and HLA-DRB5, can regulate cytokine production in melanoma patients, and this mechanism may also help determine the risk of disease recurrence (Campoli and Ferrone, 2008). Another marker, the eukaryotic translation elongation factor 1-alpha 1, has been found to inhibit p53-, p73-, and chemotherapy-induced apoptosis. Wit and others (2002) reported high levels of eEF1A1 in melanomas. Zinc-finger proteins, such as ZNF630, function as interaction modules that bind DNA, RNA, and others to alter the binding specificity of a particular protein. A variety of zinc-finger proteins have been found to be associated with melanoma. RGS1 in module 4 is a molecular prognostic marker for melanoma. A significant association has been found between increased RGS1 expression and poorer relapse-free survival (Rangel and others, 2008). TYRP1 in module 4 is correlated with distant metastasis-free survival, overall survival, and Breslow thickness (Journè and others, 2011). This association has been independently validated.
Table 3.
Analysis of the TCGA SKCM data: markers identified using the proposed method. Values in “()” are the estimated regression coefficients or loadings
| LRMs |
|||||
|---|---|---|---|---|---|
| LRM | #1 ( 1.02) 1.02) |
#2 (0.85) | #3 (0.16) | #4 ( 0.08) 0.08) |
#5 ( 0.04) 0.04) |
| GE | DDX3Y (0.98) | XIST (0.96) | CA8 ( 0.62) 0.62) |
GCDKN2B (0.88) | VGF (0.46) |
HIST1H2AE ( 0.22) 0.22) |
LOC146481 (0.12) | DNAH9 (0.19) | SLC1A1 (0.48) | CHRFAM7A (0.36) | |
| ZNF630 (0.25) | C6orf57 (0.42) | SAMHD1 ( 0.35) 0.35) |
|||
APEX2 ( 0.64) 0.64) |
CA5B ( 0.74) 0.74) |
||||
| DM | PRKY ( 0.73) 0.73) |
PRKY (0.14) | IGSF5 ( 1.00) 1.00) |
RGS1 (0.11) | ZBED2 (1.00) |
APEX2 ( 0.68) 0.68) |
APEX2 (0.98) | ABCA6 ( 0.67) 0.67) |
|||
| HERC2P4 (0.06) | TYRP1 (0.66) | ||||
| FCGR3B (0.09) | MUC15 (0.31) | ||||
| LRM | #6 ( 0.24) 0.24) |
#7 (0.18) | #8 (0.04) | #9 (0.02) | |
| GE | C6orf57 ( 1.00) 1.00) |
PCSK2 ( 1.00) 1.00) |
RSF1 (0.55) | XAGE1D (0.22) | |
| CLNS1A (0.84) | LOC146481 (0.11) | ||||
| UBQLNL (0.97) | |||||
| CNV | GSTM1 (0.05) | SERPINB3 (0.66) | CLNS1A (1.00) | ||
C6orf57 ( 0.91) 0.91) |
SERPINB4 ( 0.74) 0.74) |
||||
COL9A1 ( 0.38) 0.38) |
LGALS7B (0.16) | ||||
| C14orf39 (0.08) | |||||
| DM | LOC100128675 (0.12) | UBQLNL (0.98) | |||
DDX3Y ( 0.18) 0.18) |
|||||
| Residual effects | |||||
| GE | ZNHIT2 ( 0.06) 0.06) |
GPR150 ( 0.06) 0.06) |
GGT3P ( 0.03) 0.03) |
LOC647859 (0.03) | NARS2 (0.09) |
EIF3IP1 ( 0.03) 0.03) |
|||||
| CNV | NCRNA00185 ( 0.12) 0.12) |
HLA.DRB5 ( 0.11) 0.11) |
BTNL3 ( 0.05) 0.05) |
LOC146481 (0.06) | RNLS ( 0.09) 0.09) |
GOLGA8B ( 0.07) 0.07) |
DLGAP2 ( 0.05) 0.05) |
LOC349196 ( 0.03) 0.03) |
COL21A1 (0.08) | SFRP1 (0.00) | |
| GNMT (0.01) | ABCB5 ( 0.09) 0.09) |
CFTR ( 0.11) 0.11) |
CTSW (0.04) | NELL1 (0.12) | |
FAM178B ( 0.02) 0.02) |
|||||
| DM | GSTT2 (0.32) | VENTX ( 0.03) 0.03) |
SDHAP2 (0.00) | TMSB4Y ( 0.07) 0.07) |
RPS4Y1 (0.07) |
The identified LRMs are also meaningful. We observe several pairs of different measurements of the same gene in the LRMs (e.g., modules 6, 8, and 9), which provides a natural interpretation of the LRMs. We note that such a structure may not be identified by the simple joint modeling. In addition, measurements involved in module 7 are highly enriched with genes down-regulated in metastases (from malignant melanomas) compared with primary tumors with an FDR adjusted p-value 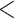 0.002 using the MSigDB curated by the Broad Institute. A panel of novel melanoma markers has been identified including the two Serpin peptidase inhibitors (SERPINB3 and SERPINB4 in module 2), which are both linked to MAPK signaling (Mauerer and others, 2011).
0.002 using the MSigDB curated by the Broad Institute. A panel of novel melanoma markers has been identified including the two Serpin peptidase inhibitors (SERPINB3 and SERPINB4 in module 2), which are both linked to MAPK signaling (Mauerer and others, 2011).
Beyond the proposed, we also apply the alternative methods described in simulation as well as the random survival forest (RSF) method (Ishwaran and others, 2008). Detailed results are provided in the Supplementary Materials (available at Biostatistics online). Different methods lead to different identification and estimation. In addition, we also compute the C-index summary statistics (except for the ISIS method, which does not generate predictive models). The proposed method has slightly better prediction.
5. Discussion
Multidimensional data, with their unique comprehensiveness, are gaining significant popularity in cancer research. A regularized marker selection and estimation method has been developed, linking multiple types of omics measurements with cancer outcome. The development has been guided by the regulation of GE by multiple mechanisms and effectively accommodates the underlying biology. The proposed method advances from some of the GE decomposition alternatives by considering the grouping of GEs. The inclusion of residual effects is also innovative and has sound biological interpretations. It is possible that the construction of the LRMs can be achieved by alternative approaches, such as the sparse CCA, sparse PLS, and others. Developing and comparing with such alternatives are of interest, however, beyond the scope of this paper. In simulation, the proposed method shows superior marker identification performance over several much relevant alternatives. In data analysis, it identifies markers different from those using the alternatives. The identified markers have important biological implications and satisfactory prediction.
This study inevitably has limitations. The modeling of regulations among omics measurements may not be comprehensive and accurate enough. However, the current modeling provides a reasonable and computationally manageable solution. The outcome model describes the three effects in an equal manner, which has been motivated by Zhao and others (2015). Potentially, this model can be improved to reflect the “unequal” status of GE and regulators. Moreover, it is possible to extend and accommodate non-linear effects by considering 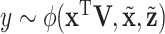 . The proposed method involves multiple parameters, which may need to be determined in a somewhat subjective manner. The sensitivity analysis described in data analysis and penalized selection in the last step can reduce this subjectiveness to a large extent. Heuristic theoretical justifications have been provided. More rigorous justification may follow in future studies. In data analysis, the proposed method leads to meaningful findings. A validation study may be needed to support the findings.
. The proposed method involves multiple parameters, which may need to be determined in a somewhat subjective manner. The sensitivity analysis described in data analysis and penalized selection in the last step can reduce this subjectiveness to a large extent. Heuristic theoretical justifications have been provided. More rigorous justification may follow in future studies. In data analysis, the proposed method leads to meaningful findings. A validation study may be needed to support the findings.
Supplementary material
Supplementary Material is available at http://biostatistics.oxfordjournals.org.
Funding
This study has been partly supported by a startup grant from the Department of Statistics at University of Illinois at Urbana-Champaign, CA142774, CA182984, CA016359, and CA121974 from NIH, and 13&ZD148 and 13CTJ001 from the National Social Science Foundation of China.
Supplementary Material
Acknowledgements
The authors thank the editor and reviewers for their careful review and insightful comments. Conflict of Interest: None declared.
References
- Campoli M., Ferrone S. (2008). Hla antigen changes in malignant cells: epigenetic mechanisms and biologic significance. Oncogene 2745, 5869–5885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cancer Genome Atlas Network. (2012). Comprehensive molecular portraits of human breast tumors. Nature 4907418, 61–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chun H., Keleş S. (2010). Sparse partial least squares regression for simultaneous dimension reduction and variable selection. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 721, 3–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ciriello G., Cerami E., Sander C., Schultz N. (2012). Mutual exclusivity analysis identifies oncogenic network modules. Genome Research 222, 398–406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daemen A., Gevaert O., Ojeda F., Debucquoy A., Suykens J. A., Sempoux C., Machiels J.-P., Haustermans K., De Moor B. (2009). A kernel-based integration of genome-wide data for clinical decision support. Genome Medicine 14, 39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Wit N. J. W., Burtscher H. J., Weidle U. H., Ruiter D. J., Van Muijen G. N. P. (2002). Differentially expressed genes identified in human melanoma cell lines with different metastatic behaviour using high density oligonucleotide arrays. Melanoma Research 121, 57–69. [DOI] [PubMed] [Google Scholar]
- Fan J., Lv J. (2008). Sure independence screening for ultrahigh dimensional feature space. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 705, 849–911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan J., Lv J. (2010). A selective overview of variable selection in high-dimensional feature space. Statistica Sinica 201, 101–148. [PMC free article] [PubMed] [Google Scholar]
- Geladi P., Kowalski B. R. (1986). Partial least-squares regression: a tutorial. Analytica Chimica Acta 185, 1-–17. [Google Scholar]
- Gross S. M., Tibshirani R. (2015). Collaborative regression. Biostatistics 162, 326–338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrell F. E, Califf R. M, Pryor D. B, Lee K. L, Rosati R. A. (1982). Evaluating the yield of medical tests. Journal of the American Medical Association 24718, 2543–2546. [PubMed] [Google Scholar]
- Ishwaran H., Kogalur U. B., Blackstone E. H., Lauer M. S. (2008). Random survival forests. The Annals of Applied Statistics 2, 841–860. [Google Scholar]
- Jennings E. M., Morris J. S., Carroll R. J., Manyam G., Baladandayuthapani V. (2013). Bayesian methods for expression-based integration of various types of genomics data. EURASIP Journal on Bioinformatics and Systems Biology 2013, 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Journè F., Boufker H. I., Van Kempen L., Galibert M. D., Wiedig M., Salès F., Theunis A., Nonclercq D., Frau A., Laurent G.. and others (2011). TYRP1 mRNA expression in melanoma metastases correlates with clinical outcome. British Journal of Cancer 10511, 1726–1732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim Y. W., Koul D., Kim S. H., Lucio-Eterovic A. K., Freire P. R., Yao J., Wang J., Almeida J. S., Aldape K., Yung W. A. (2013). Identification of prognostic gene signatures of glioblastoma: a study based on TCGA data analysis. Neuro-oncology 157, 829–839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kristensen V. N., Lingjærde O. C., Russnes H. G., Vollan H. K. M., Frigessi A., Børresen-Dale A. L. (2014). Principles and methods of integrative genomic analyses in cancer. Nature Reviews Cancer 145, 299–313. [DOI] [PubMed] [Google Scholar]
- Lee M., Shen H., Huang J. Z., Marron J. S. (2010). Biclustering via sparse singular value decomposition. Biometrics 664, 1087–1095. [DOI] [PubMed] [Google Scholar]
- Li W., Zhang S., Liu C. C., Zhou X. J. (2012). Identifying multi-layer gene regulatory modules from multi-dimensional genomic data. Bioinformatics 2819, 2458–2466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J., Huang J., Zhang Y., Lan Q., Rothman N., Zheng T., Ma S. (2013). Identification of gene-environment interactions in cancer studies using penalization. Genomics 1024, 189–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mauerer A., Roesch A., Hafner C., Stempfl T., Wild P., Meyer S., Landthaler M., Vogt T. (2011). Identification of new genes associated with melanoma. Experimental Dermatology 206, 502–507. [DOI] [PubMed] [Google Scholar]
- McNeal A. S., Liu K., Nakhate V., Natale C. A., Duperret E. K., Capell B. C., Dentchev T., Berger S. L., Herlyn M., Seykora J. T.. and others (2015). CDKN2B loss promotes progression from benign melanocytic nevus to melanoma. Cancer Discovery 510, 1072–1085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rangel J., Nosrati M., Leong S. P. L., Haqq C. III, Miller J. R., Sagebiel R. W., Kashani-Sabet M. (2008). Novel role for RGS1 in melanoma progression. The American Journal of Surgical Pathology 328, 1207–1212. [DOI] [PubMed] [Google Scholar]
- Stute W. (1993). Consistent estimation under random censorship when covariables are present. Journal of Multivariate Analysis 451, 89–103. [Google Scholar]
- Tibshirani R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B (Methodological) 581, 267–288. [Google Scholar]
- van Iterson M., Bervoets S., de Meijer E. J., Buermans H. P., 't Hoen P. A. C., Menezes R. X., Boer J. M. (2013). Integrated analysis of microRNA and mRNA expression: adding biological significance to microRNA target predictions. Nucleic Acids Research 4115, e146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang W., Baladandayuthapani V., Morris J. S., Broom B. M., Manyam G., Do K. A. (2013). iBAG: integrative bayesian analysis of high-dimensional multiplatform genomics data. Bioinformatics 292, 149–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witten D. M., Tibshirani R. (2009). Extensions of sparse canonical correlation analysis with applications to genomic data. Statistical Applications in Genetics and Molecular Biology 81, 1–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witten D. M., Tibshirani R., Hastie T. (2009). A penalized matrix decomposition, with applications to sparse principal components and canonical correlation analysis. Biostatistics 103, 515–534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang D., Ma Z., Buja A. (2014). A sparse singular value decomposition method for high-dimensional data. Journal of Computational and Graphical Statistics 234, 923–942. [Google Scholar]
- Zhao Q., Shi X., Xie Y., Huang J., Shia B., Ma S. (2015). Combining multidimensional genomic measurements for predicting cancer prognosis: observations from TCGA. Briefings in Bioinformatics 162, 291–303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu Y., Qiu P., Ji Y. (2014). TCGA-assembler: open-source software for retrieving and processing TCGA data. Nature Methods 116, 599–600. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.