A new frontier in CO₂ flux measurements using a highly portable DIAL laser system

Abstract

Volcanic CO₂ emissions play a key role in the geological carbon cycle, and monitoring of volcanic CO₂ fluxes helps to forecast eruptions. The quantification of CO₂ fluxes is challenging due to rapid dilution of magmatic CO₂ in CO₂-rich ambient air and the diffuse nature of many emissions, leading to large uncertainties in the global magmatic CO₂ flux inventory. Here, we report measurements using a new DIAL laser remote sensing system for volcanic CO₂ (CO₂DIAL). Two sites in the volcanic zone of Campi Flegrei (Italy) were scanned, yielding CO₂ path-amount profiles used to compute fluxes. Our results reveal a relatively high CO₂ flux from Campi Flegrei, consistent with an increasing trend. Unlike previous methods, the CO₂DIAL is able to measure integrated CO₂ path-amounts at distances up to 2000 m using virtually any solid surface as a reflector, whilst also being highly portable. This opens a new frontier in quantification of geological and anthropogenic CO₂ fluxes.

Quantifying CO₂ emissions from geological and anthropogenic sources is a key objective for Earth and environmental scientists. The geological carbon cycle¹ buffers the CO₂ content of the atmosphere and thereby global temperatures, through a balance between CO₂ emissions from volcanoes and geological sources, and CO₂ take-up by temperature-dependent silicate rock weathering. This balance has maintained relatively stable atmospheric CO₂ concentrations for the last 600 kyr², thereby helping to stabilize temperatures on Earth³. Current estimates of global geological CO₂ emissions have a large uncertainty⁴. The IPCC determine a geological CO₂ flux of 370 Mt/yr⁵, while recent assessments of global CO₂ flux indicate 540 Mt/yr⁴, neglecting potentially enormous but largely unquantified diffuse CO₂ emission sources, such as that of the East African Rift, which alone may produce 71 Mt/yr⁶. Improving our quantitative understanding of geological CO₂ emissions is therefore a fundamental goal for Earth scientists.

Geological CO₂ emissions are the product of a complex exchange of CO₂ between primordial mantle, mantle mixed with subducted material, continental crust and the exosphere. The degree to which CO₂ emissions from arc volcanism reflects recycling of crustal CO₂ or degassing of primordial mantle is an open question with large uncertainties⁷. Further measurements of the magnitudes of such fluxes can shed light on the CO₂ recycling budget. Monitoring of gas emissions from volcanic areas is also useful for hazard assessment, as eruptive activity may be heralded by variations in gas composition and flux. CO₂ is particularly useful as it is exsolved from magma at greater depths than other volatile species, and therefore can reflect deep processes⁸,⁹,¹⁰,¹¹.

It is clear, therefore, that volcanic CO₂ flux measurement is of great importance in the Earth sciences, however, performing this is by no means straightforward. To quantify gas fluxes, concentration profiles are needed. Owing to the often moderate magmatic CO₂ signal compared with the ambient CO₂ concentration volcanic CO₂ fluxes are usually derived indirectly. In-situ point samples of CO₂/SO₂ ratios using MultiGAS¹², or remote sensing gas composition measurement with COSPEC¹³,¹⁴,¹⁵,¹⁶, or open path FTIR spectrometry (OP-FTIR)¹⁷,¹⁸ are combined with measurements of SO₂ flux using ultraviolet remote sensing¹⁹,²⁰. CO₂ fluxes may also be determined using airborne in-situ CO₂ sensors and flying vertical grids through volcanic plume cross-sections⁸,²¹,²². Diffuse soil degassing CO₂ efflux is typically measured in situ as well, using accumulation chambers²³,²⁴,²⁵, LICOR analysers²⁶ or the eddy covariance method²⁷,²⁸. Degassing of magmatic CO₂ often occurs over large areas (10 s to 100 s of m). This includes vented and diffuse releases, such as soil leakage and volcano flank degassing²⁹,³⁰. Such fluxes are typically highly variable in space and time³¹, which poses a challenge to sporadically applied measurement techniques. Estimating gas fluxes from in-situ point measurements may thus lead to large uncertainties³². Moreover, in situ acquisitions require significant time and effort, especially for time-lapse studies. Even if they can be performed rather swiftly, such as by airborne sampling, in situ measurements often bear risk, e.g. when flying or hiking near volcanic craters.

Remote sensing techniques are usually safer to deploy than in-situ techniques and can offer attractive spatial coverage, yielding 1-D (path averaged) or 2-D concentration profiles from which more robust flux estimates can be retrieved. OP-FTIR³³,³⁴,³⁵, hyperspectral imagers³⁶,³⁷ and differential absorption spectroscopy (DOAS)³⁸,³⁹ have all been used to measure magmatic gas compositions and fluxes. Passive remote sensing approaches, however, depend on light coming from the end of the measurement path. This may limit their flexibility, e.g. to clear sky conditions. Moreover, one risks to sense photons that have not penetrated the volcanic plume⁴⁰.

Active remote sensing techniques, including open path laser absorption spectrometers⁴¹,⁴², carry their own light source and overcome these difficulties. Ideally, such instruments would not require designed retroreflectors, as this severely limits the flexibility of the measurement setup, in particular for airborne acquisitions. Active remote sensing approaches without the need for retroreflectors, such as LIDAR, overcome all previously mentioned drawbacks. Instruments based on differential absorption LIDAR (DIAL) have been performing pioneering measurements of SO₂ at volcanoes over 20 years ago⁴³,⁴⁴, yet have not become a standard approach to measure volcanic gases. DIAL is increasingly used in global warming science to measure path averaged, ambient CO₂ concentrations⁴⁵,⁴⁶,⁴⁷,⁴⁸ and has even been used to map a CO₂ plume at an industrial site⁴⁹. Recently, a range-resolving DIAL has successfully measured 2-D volcanic CO₂ concentration profiles in the Campi Flegrei volcanic zone (Italy) from which CO₂ fluxes have been inferred⁵⁰.

Perhaps the main reasons why LIDAR based active remote sensing has not established itself as a standard for volcanic gas measurement is that LIDAR systems are not readily portable, due to their size and power requirements⁴⁶,⁴⁷,⁴⁹, and require extensive operational resources (personal, expertise, setup time, logistics, maintenance)⁴⁴,⁴⁷. A versatile volcanology tool, instead, requires high portability and flexibility, since many volcanoes are in remote and difficult to access locations. Quick setup times and efficient data acquisition are also highly beneficial to minimise exposure to hazards. In the last decade, technology has moved sufficiently far forward to allow for the development of systems that fulfil these requirements.

We have developed an active remote sensing instrument based on the differential absorption principle, called CO₂DIAL, which is specifically designed to detect volcanic CO₂ emissions. This article presents results of an experiment in which the CO₂DIAL was used to sense volcanic CO₂ at the Solfatara crater and the Pisciarelli fumaroles in the active volcanic area of Campi Flegrei (CF) in Italy (Fig. 1a). CF is a nested caldera, resulting from two large collapses that occurred ~39 ka BP and ~15 ka BP⁵¹,⁵². Being close to the city of Naples, CF poses a direct threat to approximately one million people⁵³. During the measurements at CF the CO₂DIAL demonstrated its key capabilities, quickly acquiring profiles of CO₂ path-amounts both near (~100 m) and far (~1 km) from the source after only ~15 min setup, for both diffuse and vented emissions, whilst being highly portable and operated by a single person. The retrieved CO₂ fluxes from CF confirm the unusually strong degassing activity previously observed²⁶,⁵⁴.

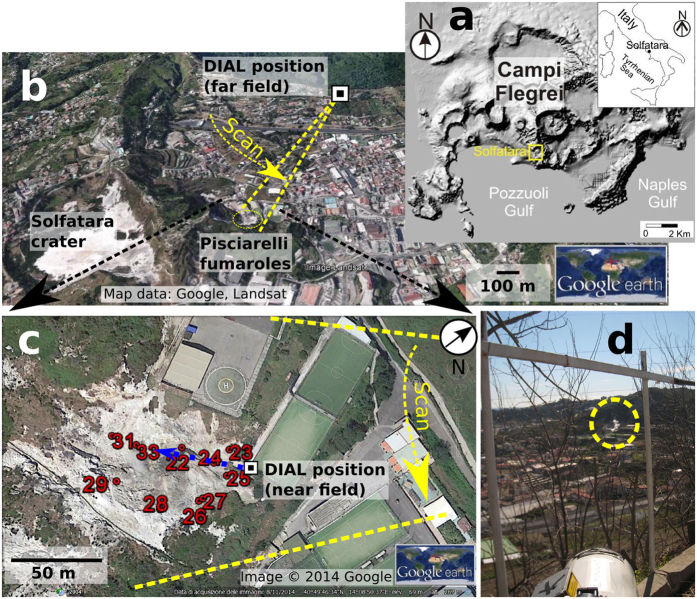
Figure 1. Geography of Campi Flegrei and overview of measurement sites.

(a) Location of Campi Flegrei (CF) close to Naples in Italy. Both maps were obtained using the open-access digital elevation model of Italy, TINITALY/01⁶⁵. (b) Overview of the measurement geometry of this study showing the Solfatara crater and the Pisciarelli fumaroles (within dotted circle). The angular extension of the scan for the measurement of the Pisciarelli fumaroles is indicated as well as the scan direction (arrow). (c) Close up nadir view of the Pisciarelli fumarole field depicting the numbered locations were CO₂ concentrations have been measured in situ using a LICOR analyser. The blue dotted line marks the path of the fixed angle acquisition with length 55 m. (d) Photo taken from the DIAL position showing the telescope aligned with the Pisciarelli fumarole (dotted circle).

These results demonstrate how the CO₂DIAL could provide effortless monitoring of magmatic CO₂ fluxes for eruption monitoring purposes at a volcanic area at unrest such as CF. The CO₂DIAL is rugged and has been transported on passenger airplanes as ordinary carry-on luggage, which makes rapid international deployment uncomplicated. The CO₂DIAL is platform independent and can, for instance, be operated airborne, e.g., from a helicopter, airplane and eventually a UAV. As such the CO₂DIAL fills a key operational gap in volcanic CO₂ sensing techniques and opens a new, exciting route to knowledge about volcanic systems, in particular regarding magma dynamics and the geological carbon cycle.

Results

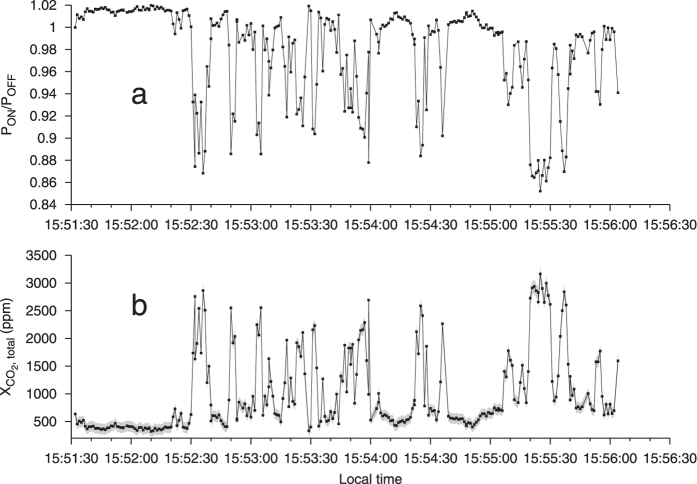
The area of Pisciarelli encompasses a fault-related, fumarolic area, vigorously degassing water vapour and CO₂, featuring a prominent, hot (90 to 110 °C) main vent and various smaller vents, including mud pools exhibiting gas bubbling. The Pisciarelli fumaroles therefore offer an optimal context for the CO₂DIAL. The measurement geometry (Fig. 1b, see also Methods) mimics airborne acquisition and hence demonstrates the system’s capability for systematic airborne scanning of volcanic chains. The CO₂DIAL was first placed in the vicinity of the Pisciarelli fumaroles (~60 m distance). During the measurement the optical axis of the instrument was pointing to the right of the centre of the plume (Fig. 1c) at a fixed angle. Strong, transient decreases in the grand ratio (GR, normalised intensity ratio, see Methods) are apparent (Fig. 2a), indicating the presence of considerable amounts of volcanic CO₂ (Fig. 2b). The CO₂ concentration at this angle was rapidly varying in a pulse like manner, which may be related to small scale wind eddies flushing in CO₂ from a nearby vent. The path averaged CO₂ concentrations (Equation (4), Methods) acquired with the CO₂DIAL (between ~400 and 3163 ppm) agree well with those measured in situ during the acquisition of the data using a LICOR CO₂ analyser (between 650 and 3000 ppm along the CO₂DIAL path). Note that, in the following, CO₂ concentrations measured by the CO₂ DIAL always refer to path averaged concentrations. We found that working at a small distance between the instrument and the plume was impractical, since, due to the limited radial scanning velocity, scans took too much time. Depending on local, small-scale wind eddies in the plume area, opaque, condensed water vapour occasionally covered the measurement path. Sunlight scattered by these cloud then saturated the detector and made a repetition of the scan necessary. By moving further away we were able to perform a more rapid scanning of the plume area, reducing the chance of scattered sunlight interfering with the scan.

Figure 2. Near field static measurement at Pisciarelli.

The range was 55 m. (a) Normalized intensity ratio (GR, Methods). Decrease indicates presence of excess CO₂. The strong, pulse-like modulation of the GR is indicating the presence of large amounts of CO₂. (b) Total path averaged CO₂ concentrations obtained from CO₂ path length concentration products (path-amounts) after dividing by the range (path length). At times they are over 3000 ppm. As in all of the following figures, the grey envelope depicts precision (1 SD, Equation (9) in Methods). Each point corresponds to 784 ms integration time.

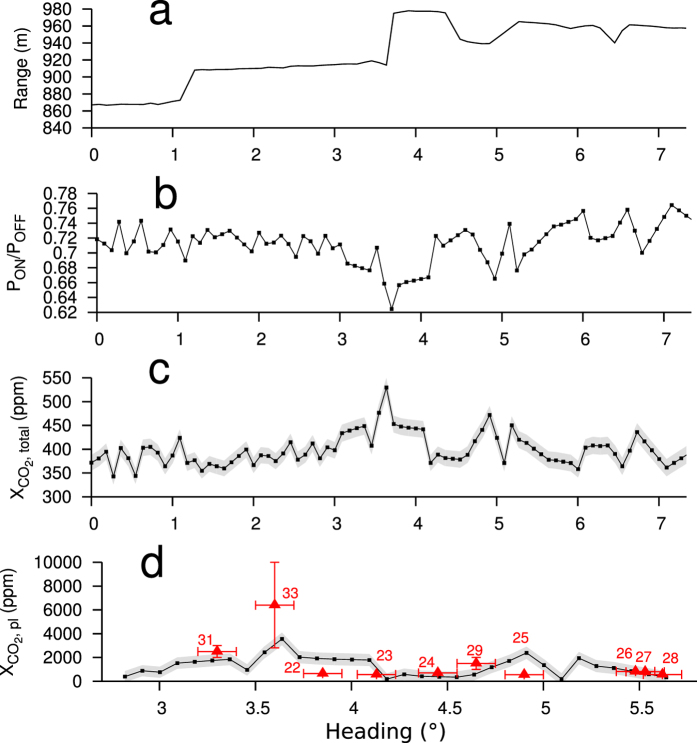
The CO₂DIAL was located in a small parking lot located at an exposed part of a slope ~940 m northeast of Pisciarelli (Fig. 1b,d). The telescope was visually aligned with the Pisciarelli plume by means of a 90° flip mirror in the ocular tube of the telescope. The angular coverage of the scans was chosen generously at 7.5°, in order to include surroundings free of plume CO₂ into the scan, to help unambiguously identify the plume. The optical power was set to 1 W (66% of maximum). Scans were performed by means of a step motor that pivoted the complete transmitter and telescope unit around the region of interest (Fig. 3a). The angular velocity of the scan was fixed at 0.525 mrad/s. A single scan took ~4 min out of which the plume itself was traversed in ~100 s. The CO₂DIAL detected a strong increase in column integrated CO₂ path length concentration product (hereafter called CO₂ path-amount, Equation (3) in Methods). The latter varied from ~4 × 10⁵ ppm.m up to 4.8 × 10⁵ ppm.m near the centre of the plume, which, after dividing by the target range (measured by an onboard laser range-finder), corresponds to a path averaged concentration of up to 530 ppm (Fig. 3c). Assuming that this excess CO₂ was contained entirely in the plume, and estimating the plume diameter, permits us to estimate the in-plume concentration of CO₂ as 3600 ± 530 ppm (1 SD, see Equation (5) in methods for derivation of the in-plume concentration), in good agreement with the LICOR in situ data (Fig. 3d).

Figure 3. Example of far field scan at Pisciarelli.

(a) Range measurements versus scan angle (heading). The ranges were measured using a range finder LIDAR (Methods). They defined the path length. (b) Grand ratio (GR) versus heading. (c) Total path averaged CO₂ concentration. Also shown is the measurement precision (1 SD) in grey. (d) In-plume CO₂ concentrations. They were derived from data in c) using Equation 4 (Methods). The numbered triangles depict the values and ranges as well as lateral position uncertainties of the in situ measurements (Fig. 1c). Note that these have been acquired ~20h earlier. Thus, they serve as approximate reference only. Moreover, concentrations in d) from the CO₂DIAL represent path averages with contributions from across the plume, while the in situ values show concentrations measured at a single point in the plume.

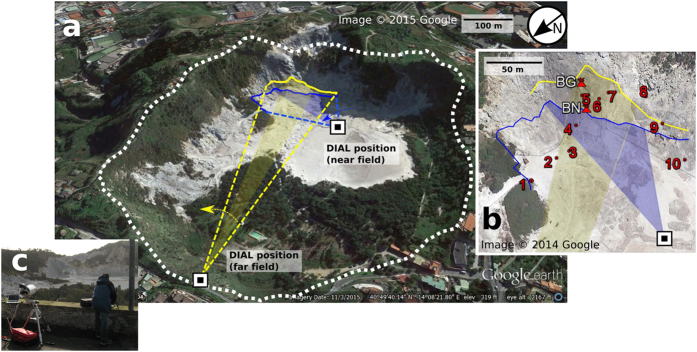
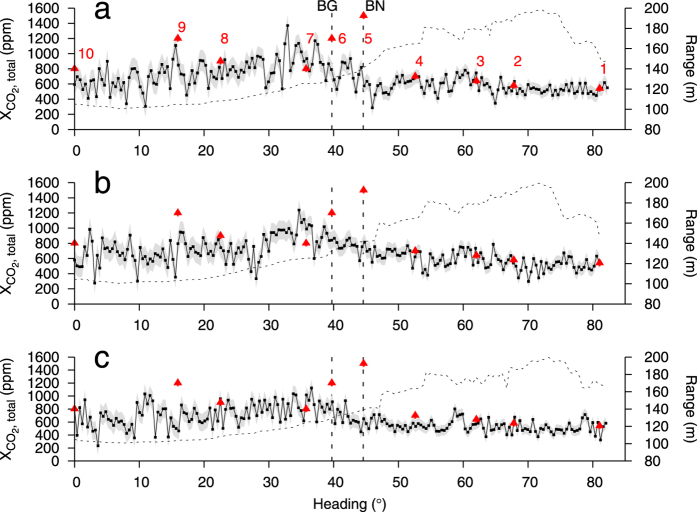
Solfatara is a tuff cone associated with intense hydrothermal activity, manifesting fumaroles, hot soils and diffuse CO₂ degassing. The Solfatara crater therefore offered an excellent possibility to probe a mixture between fumarole and diffuse degassing. An overview of the setup is given in Fig. 4a. The scanning angular velocity was 2.1 mrad/s. The two main fumarole vents, Bocca Nuova (BN) and Bocca Grande (BG), are located near the edge of the crater (Fig. 4b). In-situ measurements using the LICOR analyser that took place during the CO₂DIAL scans confirmed high CO₂ concentrations in their vicinity, as expected. Solfatara furthermore features zones of weaker degassing strength and an extensive diffuse soil CO₂ output. The corresponding CO₂ concentrations were clearly detectable with the LICOR analyser. A relatively high scanning inclination angle would have been necessary to scan over the main vents. This would, however, likely have missed excess CO₂ concentrations in the centre of the crater (towards the instrument location) and further south along the rim (in situ points 1 to 4), in particular the weaker zones of anomalous CO₂ release, both vented and diffuse. In addition, since we could visually observe that the plume water vapour movement was a superposition of vertical flow and a horizontal component towards south/southeast, it was clear that the plume CO₂ would be advected away from BN and BG towards the southeast (roughly along the crater rim). We therefore chose a scanning inclination such that the scan altitude at BN was 2 m above the ground, which while missing the direct observation of the BG vent, would capture the CO₂ emissions from the BG vent downwind. From Fig. 5 it can be seen that the CO₂DIAL detected high CO₂ concentrations near 35° that are compatible with the LICOR in situ values, both having a symmetric profile. However, with respect to the in situ values these CO₂ concentrations are shifted by 9°, i.e. ca. 20 m further south. This can be explained by the fact that the in situ measurements at points 5 to 8 were performed at slightly higher elevation (Fig. 4b) and were not covered by the CO₂DIAL measurement path during the near field scans. At 60° another zone of higher CO₂ concentrations can be identified in all three scans (Fig. 5a–c), which reveals the presence of a diffuse CO₂ source. Given the associated position, the increase in CO₂ concentration near 50° (Fig. 5a–c) could be related to BC, a vent that appeared recently²⁶. Lastly, there are numerous, persistent small-scale fluctuations in the profiles (Fig. 5a–c), such as near 16°, confirming widespread CO₂ degassing activity.

Figure 4. Overview of the measurement geometry at Solfatara.

(a) Solfatara crater. The crater area is marked by the white dotted line. The extension of the far and near field scans and scan is indicated by dotted lines. The curved arrows mark the scan direction. Shaded areas depict regions of interest, i.e. the sectors for which flux results are reported in Table 1 (blue near field, yellow far field). The target distances versus heading are indicated for the near and far field scans (blue and yellow lines). (b) Nadir photo showing a zoom around the main fumaroles. Shown are the in situ measurement points and the locations of the main fumaroles Bocca Nuova (BN) and Bocca Grande (BG). (c) Photo of the CO₂DIAL while measuring from the far field position.

Figure 5. Time lapse near field scans across the diffuse degassing area in the Solfatara crater.

See also Fig. 4b. The dashed curve shows the measured range per heading. The headings corresponding to the positions of BN and BG are indicated. Since the acquisition was done within the degassing area, the total concentrations instead of the in-plume concentrations are shown. The triangles depict the LICOR in situ values acquired during acquisition of these scans, identified by the numbers (Fig. 4b). All three scans were carried out on March 3, 2016. (a) Scan performed between 11:31:39 and 11:43:06. (b) Scan performed between 11:52:48 and 12:04:27. (c) Scan performed between 12:07:20 and 12:19:05. The short scanning interval makes it possible to resolve fluctuations in the CO₂ concentration on a minute scale. By comparing the magnitude of the main peak near 35° it becomes evident that at places the average CO₂ concentration fluctuated by more than 20%.

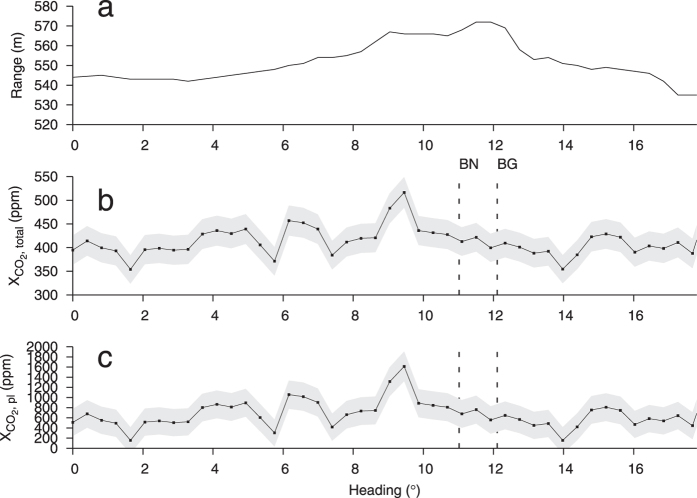
To further test the results from the CO₂LIDAR, we scanned the same degassing feature from a location further away, with the instrument installed ~550 m northwest of the main vents (Fig. 4a). The inclination for these measurements included both BN and BG (Fig. 4b). The detected CO₂ concentration versus the heading angle appears smoother (Fig. 6). This could be partly due to the slightly higher inclination (beam travelled ~5 m above ground near BN) and larger atmospheric contribution which both tend to diminishes the relative contribution of CO₂ from weaker vents. Moreover, using the same angular scan velocity of 2.1 mrad/s as before the probed sector size was ~1.2 m/s compared with 30 cm/s for the near field scan. As a result, the effect of the CO₂ is averaged, contributing to a smoother profile. Out of all scans performed from the Solfatara far field position, the maximum in-plume volcanic CO₂ concentration detected with the CO₂DIAL was 1900 ± 303 ppm.

Figure 6. Result of a far field scan across the area around BN and BG at Solfatara crater.

The scan was performed between 18:32:29 and 18:35:13 on March 2, 2016, i.e. ca. 18 h prior to the acquisition in Fig. 5. (a) Measured ranges per heading. (b) Total path averaged CO₂ concentrations. (c) Average in-plume CO₂ concentrations. The heading of the peak near 9.5° corresponds to 35° in Fig. 5.

CO₂ fluxes

Our CO₂ path-amount profiles together with estimated vertical plume transport speeds were used to retrieve CO₂ fluxes as described in the Methods section. Table 1 summarizes the results for the scans carried out at Pisciarelli and Solfatara during the complete duration of the experiment. For Solfatara the sectors considered for flux retrieval include the area around the main vents as shown in Fig. 4b. As already suggested by the CO₂ concentrations (Fig. 5), the CO₂ fluxes vary strongly during the course of even tens of minutes (Table 1). The time-averaged CO₂ flux estimated for Pisciarelli is 3.1 ± 2.5 kg/s (1 SD) or 266 ± 212 tons/day. The average over subsequent scans yields a mean CO₂ flux for Solfatara of 9.3 ± 4.7 kg/s (805 ± 408 tons/day) for the near field and 7.7 ± 4.5 kg/s (664 ± 386 tons/day) for the far field scans, associated with a total average of 715 ± 394 tons/day for Solfatara.

Table 1. Results of selected scans performed at Solfatara and Pisciarelli.

Acquisition date and time	Transport speed vpl (m/s)	Flux (kg/s)
	Far field Solfatara
02/03/2016 18:11	1. 53 ± 0.5	5.8 ± 3.5
02/03/2016 18:19	1. 53 ± 0.5	7.9 ± 4.0
02/03/2016 18:29	1. 53 ± 0.5	5.9 ± 3.5
02/03/2016 18:32	1. 53 ± 0.5	5.1 ± 3.4
02/03/2016 18:38	1. 53 ± 0.5	6.4 ± 3.5
03/03/2016 10:19	3.12 ± 1.1	12.5 ± 6.4
03/03/2016 10:24	3.12 ± 1.1	10.2 ± 7.1
Mean ± 1 SD		7. 7 ± 4.5 (664 ± 386 tons/day)
	Near field Solfatara
03/03/2016 11:31	1.68 ± 0.6	11.7 ± 5.8
03/03/2016 11:52	1.68 ± 0.6	10.7 ± 5.1
03/03/2016 12:07	1.68 ± 0.6	8.1 ± 4.4
03/03/2016 12:39	1.68 ± 0.6	6.8 ± 3.6
Mean ± 1 SD		9.3 ± 4.7 (805 ± 408 tons/day)
	Far field Pisciarelli
04/03/2016 13:18	1.69 ± 0.8	2.1 ± 2.2
04/03/2016 13:33	1.69 ± 0.8	3.6 ± 2.4
04/03/2016 13:50	1.69 ± 0.8	3.6 ± 2.7
Mean ± 1 SD		3.1 ± 2.5 (266 ± 212 tons/day)

The experiment lasted between 02/03/2016 evening and 04/03/2016 afternoon. Shown are the vertical plume transport speeds as derived from video analysis and the values of the CO₂ fluxes . Scans presented in the figures have their time marked in bold. For details on the error calculation please see Methods.

Discussion

We have used the newly developed CO₂DIAL to sense volcanic CO₂ at the restless Campi Flegrei volcanic zone in Italy. The CO₂ concentrations measured with the CO₂DIAL are in good agreement with in situ values acquired with a LICOR CO₂ analyser. Care has to be taken when comparing in situ values with those from the CO₂DIAL, since the in situ measurements detect contributions from a point-like volume around the instrument, whereas concentrations detected by the CO₂DIAL correspond to contributions from points all along the column between instrument and hard target (Methods). The most robust comparison is produced when the CO₂ concentration in the column is governed by the same CO₂ source sensed by the in situ device. For Solfatara, this was the more the case for near field scans (Fig. 5) than for the far field scans (Fig. 6).

CO₂ path-amount profiles have been converted into fluxes using the vertical plume transport speed estimated from video footage (Methods). The precision of the CO₂ concentration along with error of the vertical CO₂ transport speed propagate to an error of the CO₂ flux (Equation (12), Methods), which is on average 60% (mean over relative errors of all computed fluxes). The system has yet not reached its full potential, mainly in terms of precision. Future work will focus on increasing precision to be able to sense more subtle volcanic CO₂ signals and increase confidence of the retrieved CO₂ fluxes. Further, the plume speed measurement technique will be improved to reduce the related uncertainty.

While much variability in the measured CO₂ path amounts is the product of local fluctuations in transport speed and direction within the plume, the varying CO₂ path-amount detected at Pisciarelli (Fig. 2) may reflect a varying fumarole degassing rate on a timescale of tens of seconds⁴². A further, more systematic investigation, including a frequency analysis, would enable improved identification of the origin of the variability. This represents one of the doors opened by new active remote sensing tools with high temporal resolution, such as the CO₂DIAL. A longer time-scale variability in CO₂ flux is observed at both Pisciarelli and Solfatara. Table 1 suggests that strong variations of the CO₂ flux by 20 to 76% may occur within less than an hour, which is consistent with previous observations⁵⁰ which found average degassing rates at Pisciarelli of 227 tons/day (mean of all measurements) in late 2014. That result is slightly lower than the average of 266 ± 212 tons/day found in this study. Results from more previous years are significantly lower (e.g., ~180 tons/day in 2012⁴²). The high quality dataset of CO₂ fluxes captured by the Osservatorio Veusiviano geochemistry team has revealed that fluxes have risen by ~40% every year between 2008 and 2014⁵⁵. The present finding suggests an increase in CO₂ flux by a factor of 266/227 (17%) in 1.5 years, which is reasonably consistent with previous observations, and certainly indicates a general trend of increasing CO₂ efflux from Pisciarelli. This contributes to the general picture of increased degassing associated with enhanced ground uplift observed in the area²⁶,⁵⁴.

For the mixed degassing (vented and diffuse) at Solfatara it is more challenging to compare with in-situ fluxes as the boundaries of the area investigated are generally not exactly the same. This is already the case for the near and far field Solfatara scans of the present study, which span different areas. Yet, the CO₂ fluxes for the far and the near field agree within error. Note that the CO₂DIAL measures path-amounts, (Methods) with contributions from vented and diffuse CO₂ emissions all across the measurement line. Therefore, differences between the fluxes from the far and near field measurement are very likely due to the different integrated soil areas covered by the near and the far field scans. The average flux of 715 tons/day found in this study is considerably larger than CO₂ fluxes from previous measurements between 2012 and 2013 at the main vents (BN and BG), which yielded between 251 and 300 tons/day²⁶,⁴². However, these values account for the fumarole degassing, excluding diffuse degassing. The fumarole emissions near BG and BN were estimated to correspond to roughly 40% of the total soil CO₂ output²⁶, resulting in a total flux of ~1560 tons/day, however, for the whole Solfatara/ Pisciarelli area. In line with this value, a diffuse degassing rate of ~1500 tons/day for a 0.5 km² area of Solfatara has been reported previously⁵⁶. It is hard to scale the calculated flux in this study up to the size of the whole degassing area of CF as there are areas with a very low flux and areas with a very high flux. We can, however, provide an estimation for the Solfatara crater alone, excluding the area of the Pisciarelli fumaroles. For the Solfatara far field scans, the sector accounted for in the flux computation of this work corresponds to a surface of ~20000 m² inside the Solfatara crater (region of interest, shaded area in Fig. 4a,b). When integrating over all headings (dashed triangle, Fig. 4a), as opposed to the region of interest only, the flux doubles on average, amounting to ~1400 tons/day. This larger region has an area of ~43000 m², which corresponds to ~14% of the crater area of ~300000 m², approximately bounded by the dashed white line in Fig. 4a. Flux maps of previous in situ studies⁵⁷,⁵⁸ suggest that the area covered in our study accounts for 31% (=43000/140000) to 61% (=43000/70000) of the anomalous degassing area inside the crater. Assuming a consistent flux per unit area throughout the crater implies a CO₂ flux between 2300 and 4600 t/day for the Solfatara crater alone, including the contribution of the main fumaroles (BN and BG) and other minor vented emissions on the southeast wall of the crater. In the future, a more spatially comprehensive flux measurement is envisaged, scanning the whole of Solfatara cater, which will allow to compare fluxes of the Solfatara area with greater confidence.

Whilst smaller than at Pisciarelli, Solfatara has seen a steady increase in CO₂ degassing rate in the last decade or so⁵⁵. Recent findings⁵⁹,⁶⁰ indicate that apart from the vented degassing area near BN and BG there is a “hot spot” zone of approximately rectangular shape along the south-eastern edge of the Solfatara crater (between 0 and 36° in Fig. 5), featuring high anomalous CO₂ release, in line with the LICOR data of this study. It underpins the high CO₂ concentrations detected in that zone by the CO₂DIAL and furthermore supports that the associated CO₂ amounts largely correspond to diffuse emissions and minor vents with formerly unknown CO₂ output.

In summary, the CO₂ fluxes found with the CO₂DIAL are compatible with previous results, indicating strong, increasing CO₂ degassing at CF. To the best of our knowledge, it is the first time that a man-portable active remote sensing system has been used to acquire volcanic CO₂ profiles. The outcomes show the tremendous potential of a portable gas remote sensing system. The ease and flexibility with which the presented data has been attained represents a breakthrough in the measurement of volcanic CO₂. The results show that the CO₂DIAL is a powerful tool to overcome the aforementioned drawbacks of in situ measurement techniques by offering a faster, safer and comprehensive acquisition (spatial coverage yields CO₂ concentration profiles). The platform demonstrated its capability to execute effortless time-lapse acquisitions within minutes or tens of minutes, depending on the area covered and the target range. This is a very desirable feature to analyse correlation between CO₂ degassing and uplift at inhabited volcanic zones, such as CF, where days can be a crucial time scale.

In conclusion, a man-portable active remote sensing tool as the CO₂DIAL represents a step change in volcanology by opening completely new measurement possibilities. One of these prospects is uncomplicated, systematic probing of arc volcanoes to populate the global volcanic CO₂ flux data inventory and help constraining the geological carbon cycle and deliver new insights in the magmatic plumbing system of subaerial volcanoes. Applications of the CO₂DIAL also include more general areas of environmental and Earth system science.

Methods

DIAL principle

The CO₂DIAL is based on continuous wave, hard target differential absorption LIDAR (DIAL), measuring path averaged CO₂ concentrations. A DIAL transmits and receives photons at two wavelengths, one corresponding to a rotational-vibrational transition of CO₂ where photons are being absorbed (λ_ON) and one where there is no associated absorption (λ_OFF). λ_ON and λ_OFF are closely spaced to each other so that atmospheric propagation effects other than absorption by the probed molecule can assumed to be negligible. By taking the ratio of the optical powers associated with the received signals for λ_ON and λ_OFF one arrives at⁴⁷

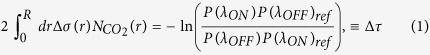where R is distance between the instrument and the hard target (e.g. the soil), Δσ is the difference between the molecular absorption cross sections of CO₂ associated with λ_ON and λ_OFF, P(λ) is the received power (hereafter referred to as science signal as it carries the information of scientific interest) and P(λ)_ref is the transmitted optical power (referred to as reference signal). The latter is measured as a reference to normalize fluctuations of the transmitted power. Δτ is the differential optical depth. The ratio of the normalized powers in Equation (1) is referred to as the grand ratio (GR). The presence of excess CO₂ leads to a decrease in GR (Fig. 2a). By measuring the GR as well as R one may obtain the path averaged CO₂ number density 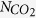, which for a horizontal measurement path (as in this work) can be converted to a concentration (in ppm) as

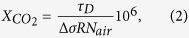where N_air is the (moist) air number density computed with knowledge of specific humidity, air pressure and temperature.

The CO₂DIAL

Supplementary Fig. S1 presents an overview of the CO₂DIAL instrument as used for this work, which is an all-fiber optic instrument. The instrument is a prototype with development costs of the order of 100 k €. A next generation commercial prototype is planned with associated costs roughly a third of that. The CO₂DIAL is designed to measure path averaged CO₂ concentrations for path lengths up to 2000 m. The instrument has been developed to acquire volcanic CO₂ concentration profiles from which CO₂ fluxes can be deduced. The complete system weighs ~26 kg and uses a power of ~20 W in idle mode and ~70 W when the laser is emitting at its full optical power. The CO₂DIAL can operate for ~1 h on a single 600 g, 5000 mAh lithium polymer battery. The laser consists of two continuous wave distributed feedback (DFB) fiber seed lasers emitting at λ_ON = 1572.992 nm and λ_OFF = 1573.173 nm⁶¹. The seed laser beams are amplitude modulated using two LiNbO₃ electro-optical modulators (EOM) at a respective sine tone near 5 kHz and simultaneously amplified by an Erbium doped fiber amplifier (EDFA) before being transmitted. Light backscattered by a hard target is received by a commercial 200 mm diameter Schmidt-Cassegrain Telescope with a focal length of 1950 mm. The analogue to digital converter (ADC) operates at 250 kSamples s⁻¹ and has a resolution of 16-bit. The integration time per scan angle was set to 4000 EOM modulation periods, which corresponds to chunks of length 784 ms for both science and reference channel. Each of these chunks of data is demodulated using a digital lock-in routine (or through performing a FFT for diagnostic purposes) written in National Instruments LabVIEW. This is done in real-time for quality control purposes (e.g. to check for abnormal baseline drift) and again in the post processing of the data to compute CO₂ concentrations. After the lock-in operation one arrives at four DC signals associated with P(λ_ON), P(λ_OFF), P(λ_ON)_ref and P(λ_OFF)_ref. The GR and Δτ are calculated using the right hand side of Equation (1) after taking the mean of each of the four signals. Each point in Figs 2, 3, 5 and 6 is associated with an integration time of 784 ms. The target distance R is measured by a range finder (DLEM, Jenoptik, Germany), based on a 1550 nm LIDAR with pulse energy of 500 μJ and accuracy <1 m. The working principle of the range finder is the time of flight measurement. The integration time was set to 500 ms.

CO₂ concentration retrieval

DIAL instruments generally have an offset, i.e. Δτ(R = 0) ≠ 0. In addition, due to the fact that the metastable state lifetime of the erbium atoms is comparable to the period of the seed laser amplitude modulation, the EDFA distorts the amplitudes of the seed laser signals. Demodulation of the distorted science and reference signals creates an offset that depends on the signal power, but which is repeatable. As a result, the measured GR are shifted with respect to those expected from Equation (1). Therefore, to retrieve path averaged CO₂ concentrations a calibration is performed using the ambient CO₂ at the measurement site, away from any CO₂ degassing (Supplementary Fig. S2). To this end, GR were measured in the well-mixed ambient atmosphere for various ranges, converted to differential optical depths using Equation (1) and plotted against the CO₂ path length concentration product (path-amount, product of ambient CO₂ concentrations and ranges). A straight line,

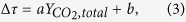was fitted to the ensemble of points using a least square algorithm. Equation (3) was used as the calibration curve, with slope a (in ppm.m⁻¹) and instrumental off set b. Employing the calibration curve the measured Δτat CF were converted to CO₂ path-amounts 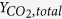(in ppm.m), which were used for further computations as detailed below.

Conversion of CO₂ path-amounts to in-plume CO₂ concentrations

Figure 7 shows a simplified sketch of a typical measurement geometry at Campi Flegrei. Since the CO₂DIAL yields CO₂ path-amounts (ppm.m), volume CO₂ concentrations measured in situ (in the plume area) cannot be compared directly with the result from the CO₂DIAL. If the plume extension approximately equals the CO₂DIAL path length, dividing column amounts by the path length may be done, i.e.

Figure 7. Sketch of a typical measurement geometry.

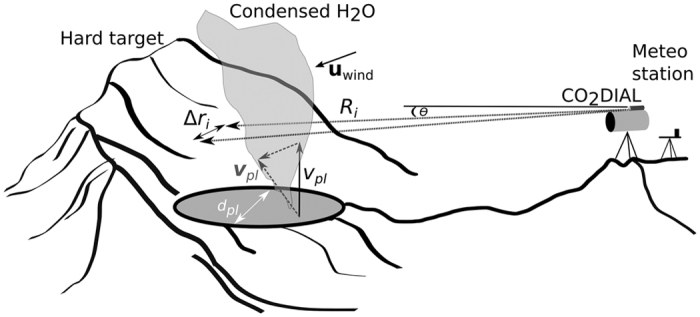
The hard target can be any surface. The transmitter/telescope unit is pivoted around the degassing feature (lateral extension 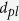, Equation 7), R_idepicts the range, Δr_i the lateral distance increment (in m) at angular step i. The wind is indicated as a velocity vector u_wind (in bold). The vertical plume transport speed v_pl is shown here as a vector resulting from superposition of the inherent velocity of the ejected CO₂ and the wind speed. For the flux computation the magnitude of its vertical component v_pl is needed (also shown in the figure).

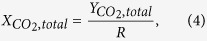such as shown in Figs 2b and 5, yielding path averaged CO₂ concentrations. Of course, for path lengths much longer than the plume extension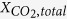 cannot be compared with in situ values taken in the plume. In these cases CO₂ column amounts were converted to in-plume concentrations 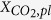, which account for the volcanic and the ambient CO₂ (such as detected by the LICOR analyser). They were obtained using

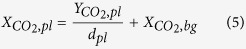where 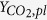is the volcanic excess CO₂ path-amount (in ppm.m), obtained as

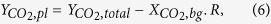where 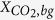 = 380 ppm (ambient CO₂ concentration at CF from in situ measurement) and R is the target range.d_pl is the lateral dimension of the plume, calculated as

where Δr_i is the lateral distance increment (in m) per angular step i. 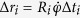with the range per angle R_i (see Fig. 7), the angular scan velocity 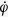and the time interval Δt_i between points (angles), retrieved from the time stamps of the data chunks.

Identifying the plume

An increase in volcanic CO₂ would lead to an increased column averaged amount of CO₂ and would thus decrease the GR (increase Δτ). When performing a scan across a sufficiently strong CO₂ emission this behaviour occurs as a function of scanning angle. By repeatedly scanning across the emission feature, artefacts can be ruled out and the decrease in GR as well as the angle where this happens can be unambiguously attributed to CO₂ originating from anomalous degassing activity. Of course, this assumes that the plume extension is sufficiently stable between subsequent scans. For vented degassing, the position of the telescope (and hence the angle) when it entered an anomalously degassing zone could be determined visually using the telescope. This procedure works well when the scanned horizon also contains areas with ambient atmosphere only. This was not the case for the near field Solfatara scans since the instrument was placed inside the anomalous degassing (i.e. the main plume) itself already. Nonetheless, one could identify a rather stable symmetric increase in CO₂ concentration, which was chosen as the region of interest to integrate over to arrive at the CO₂ flux.

Flux retrieval

To compute the mass flux of CO₂ (in kg/s) the volcanic excess CO₂ path-amounts (Equation 6) were integrated over the lateral plume extension as

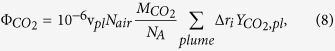where v_pl is the plume transport speed (m/s), more precisely the component of the transport speed vector perpendicular to the scanned cross section. It was assumed constant during the scan and across the plume cross sectional area (see section plume speed estimation). Since the scans were performed horizontally, here it refers to the magnitude of the vertical component of the transport speed vector (Fig. 7). N_air is the number density of moist air, computed using meteorological data (pressure, temperature, humidity) acquired by a portable meteo station close to the instrument (Fig. 7). 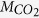is the molar mass of CO₂ (kg mol⁻¹) and N_A is Avogadro’s constant (mol⁻¹). For a vented emission, as at Pisciarelli, the integration boundaries were determined by the angles between which there was a steady increase followed by steady decrease in CO₂ concentration above the background. For Solfatara, the integration was carried out for the region of interest around the main vents, that is, between in situ measurement points 8 and 4 (near field) and 8 and 2 (far field) (Fig. 4a,b, and section identifying the plume). This interval was chosen since the scans indicated that it contained the CO₂ from the main fumaroles as well as CO₂ from along the crater edge between in situ point 5 and 8, discernible by a repeatable feature (Fig. 5).

Plume speed estimation

v_pl may be estimated from the wind vector. However, particularly close to the ground or close to reliefs, such as at Solfatara, the topography gives rise to a complicated wind vector field. The wind speed may thus be quite different from the actual transport speed of the plume. Further, the meteo station was not measuring the wind field components, but the true wind direction. For the near field Solfatara measurements the wind veered around 285° (mean of wind speeds for all scans). For the Solfatara far field measurement on 02/03/2016 there was no wind direction data available as the compass was not calibrated. For the Solfatara far field measurements on 03/02/2016 the mean wind direction was 168°. For the scans at Pisciarelli the wind direction measured was on average 200°, which means the Pisciarelli fumaroles were in the wind shadow of the Solfatara crater rim. v_pl was estimated therefore directly from the plume movement. It was assumed that the movement of the visible condensed plume water vapour aerosol propagated with the same velocity as the volcanic CO₂. Video footage with a resolution of 480 × 640 pixels² was acquired from the plume using a commercial digital camera placed next to the CO₂DIAL telescope. During each set of scans a video clip of the plume was produced (4 in total). A video analysis program (Tracker from Open Source Physics) was used to analyse the video footage. At a given video frame a pixel of the plume was picked (Supplementary Fig. S3a). The pixel (which corresponds to a parcel of gas) was moving with each frame until it eventually experienced a decrease in brightness, usually after 3 to 13 seconds, due to associated water droplets evaporating. The analysis focused on pixels within and near the telescope field of view. Transformation from pixel into real world coordinates was carried out via distance calibration using the size of a real world feature (e.g. a house). These features were chosen such that they were aligned approximately parallel to the plane of the plume. In cases where these features were not perpendicular to the telescope line of sight (for Pisciarelli) their projected size was used, employing Google Earth software. The camera line of sight was usually quasi perpendicular to the (on average vertical) plume transport direction (for Pisciarelli, cos θ = 0.997 in Fig. 7). For the Solfatara scans (both near and far field) the plume speed had a horizontal component, which was, however, quasi perpendicular to the telescope viewing direction. This resulted therefore in a negligible length projection error. Frames were converted to time using the frame rate of the camera (30 Hz). The tracking software enabled to extract the relative vertical position of a pixel (y-position). v_pl was derived from the slope of the regression line fitted on the y-positions (Supplementary Fig. S3b). The error was extracted from the root mean square error of the fit (RMSE of observed minus modelled y-coordinates). For a tracked parcel of gas this error accounts for fluctuations in transport speed due to a complex, perhaps turbulent wind field. Note that v_pl derived in that fashion represents an average speed over the course of the measurement. The RMSE represents an uncertainty over time, but for only a part of the plume. The procedure was therefore repeated for various parcels across the plume. The retrieved speeds and their RMSEs are summarized in Supplementary Table S1. Comparing the derived speeds provided a way to assess fluctuations in vertical transport speed across the plume as viewed by the CO₂DIAL telescope. Assuming normally distributed plume speeds the associated standard deviation was computed using Student’s t distribution⁶², developed for small number of samples, which are, however, statistically meaningful. Here, 8 tracks have been performed per video (Supplementary Table S1). Note that each of the 8 plume speeds per video is based on a fit of >100 points and thus exhibit a certain robustness. The uncertaintyΔv_pl of v_pl was estimated as the maximum out of the Student’s SD and the mean of the RMSEs (Supplementary Table S1). For the scans carried out at far field Solfatara at the evening of 02/03/2016, y-positions versus time were usually quite steady, suggesting a rather laminar plume flow, which resulted in a lower RMSE (Supplementary Fig. S3b and Table S1). Supplementary Fig. S3c,d show two less steady y-tracks of parcels of the far field Solfatara scans the morning after, suggesting a higher degree of turbulence and hence a higher associated uncertainty of the plume transport speed.

Estimating measurement precision

The total relative uncertainty of the CO₂ path-amount was evaluated as

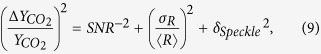with the signal-to-noise-ratio (SNR)

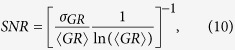where 〈GR〉 and σ_GR are the mean and standard deviation of the grand ratio values, respectively. They were estimated from time series acquired at fixed angles in between the scans at CF. The SNR accounts for all noise sources occurring during acquisition, including instrumental noise, non-stationary baseline drift, solar background noise, atmospheric noise (mostly air turbulence) and perturbation by aerosol scattering. It is therefore an indicator of the instrument’s true measurement performance in the field⁶³. The second term quantifies the relative range error (standard deviation of ranges σ_R over mean of ranges 〈R〉), which is typically ~1 m. The relative uncertainty due to hard target speckle was estimated as⁶⁴

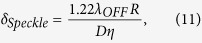where D is the spot diameter on the hard target (in m) and η is the dimension of the telescope FOV (in m) on the hard target.

The total relative error of the CO₂ flux was computed as

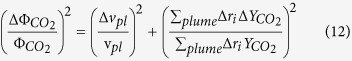Additional Information

How to cite this article: Queiβer, M. et al. A new frontier in CO₂ flux measurements using a highly portable DIAL laser system. Sci. Rep. 6, 33834; doi: 10.1038/srep33834 (2016).