Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2016 Sep 22.
Published in final edited form as: J Biomech. 2010 Aug 3;43(14):2785–2791. doi: 10.1016/j.jbiomech.2010.06.009

A mechanistic study for strain rate sensitivity of rabbit patellar tendon

John Clemmer a,b, Jun Liao a,b,*, Debbie Davis a, Mark F Horstemeyer a,b, Lakiesha N Williams a,b,*
PMCID: PMC5032624  NIHMSID: NIHMS255462  PMID: 20678772

Abstract

The ultrastructural mechanism for strain rate sensitivity of collagenous tissue has not been well studied at the collagen fibril level. Our objective is to reveal the mechanistic contribution of tendon's key structural component to strain rate sensitivity. We have investigated the structure of the collagen fibril undergoing tension at different strain rates. Tendon fascicles were pulled and fixed within the linear region (12% local tissue strain) at multiple strain rates. Although samples were pulled to the same percent elongation, the fibrils were noticed to elongate differently, increasing with strain rate. For the 0.1, 10, and 70%/s strain rates, there were 1.84±3.6%, 5.5±1.9%, and 7.03±2.2% elongations (mean±S.D.), respectively. We concluded that the collagen fibrils underwent significantly greater recruitment (fibril strain relative to global tissue strain) at higher strain rates. A better understanding of tendon mechanisms at lower hierarchical levels would help establish a basis for future development of constitutive models and assist in tissue replacement design.

Keywords: Collagen fibril, D-Period, Tendon microstructure, Fibril recruitment

1. Introduction

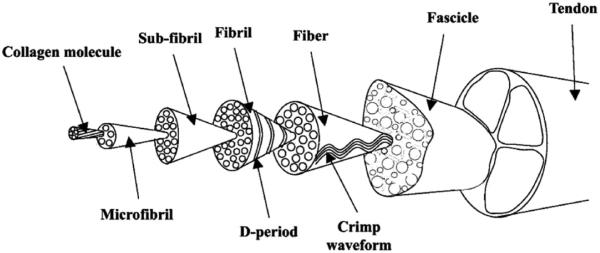
Tendons are soft connective tissue exhibiting nonlinear viscoelastic properties, with a hierarchical structure ranging from the entire tendon to fascicle to collagen fiber to collagen fibril to the collagen molecule (Fig. 1)(Butler et al., 1978; Wang, 2006; Kastelic et al., 1978; Screen et al., 2004). This intricate structural hierarchy gives tendon the viscoelastic characteristics of most soft tissues, i.e., strain rate sensitivity, stress relaxation, and creep. Many mechanistic studies have been carried out to understand the underlying mechanisms of these viscoelastic tissue behaviors (Butler et al., 1978; Wang, 2006; Cohen et al., 1976; Woo, 1982; Yamamoto et al., 1992; Johnson et al., 1994; Duenwald et al., 2009).

Fig. 1.

Fig. 1

Open in a new tab

Tendon's hierarchical structure adopted in current study. (Adapted from Kastelic et al. (1978) and Screen et al. (2004).

In tendon mechanics, the central role is played by Collagen Type I, which is the major component of tendon and makes up approximately 70–80% of the tissue dry mass(Kannus, 2000; Yamamoto, 1999). Collagen fibril diameter distribution changes with age and affects the stiffness of tendon (Derwin and Soslowsky, 1999). As the key structural protein component, the collagen molecule consists of a triple helix formed by three poly-peptide a-chains with a length of ~300 nm and a diameter of ~ 1.5 nm(Petruska and Hodge, 1964). Quarter staggering of the collagen molecules gives rise to the collagen fibril with a banding appearance also known as the D-period(Petruska and Hodge, 1964).

There have been previous studies on kinematics of collagen fibrils under uniaxial loading (Sasaki and Odajima, 1996a,b; Graham et al., 2004; Shen et al., 2008; van der Rijt et al., 2006; Yang et al., 2008, 2007 Hansen et al., 2009). Fibril mechanisms have been studied mainly using X-ray diffraction techniques and TEM. Increasing load has been shown to result in elongated collagen fibrils, demonstrated by an increased D-period (Sasaki and Odajima, 1996a,b; Folkard et al., 1987; Fratzl et al., 1998; Liao et al., 2005). When collagen fibrils undergo load, the D-period elongates due to intrinsic fibril mechanisms of molecular elongation and slippage (Sasaki and Odajima, 1996a). Recently, combining multi-scale measurements (inter-fiber sliding and intra-fiber elongation along with fibril elongation), Gupta et al. (2009) created a novel multiscale model to describe how tendon distributes load between its fiber and fibril hierarchies during stress-relaxation. Recently, fascicle viscoelastic models were proposed by Lucas et al. (2009); Elliott et al. (2003).

Noncollagenous components in tendon are proteoglycans, elastin, water, and fibroblasts. Tendon's proteoglycan (PG) network is composed of highly negatively charged glycosaminoglycans (GAGs), which are matrix components that regulate fluid flow and attribute to viscoelasticity within the tendon (Elliott et al., 2003; Puxkandl et al., 2002; Screen et al., 2005; Robinson et al., 2004; Yin and Elliott 2004; Weiss et al., 2002). There has been theoretical modeling and experimental observations supporting the interfibrillar mechanical role of PG bridges (Liao and Vesely 2007; Redaelli et al., 2003; Scott, 2003). Some question the noncollagenous matrix's mechanical role, stating collagen fibrils span the whole tissue and load is not transferred to PGs (Provenzano and Vanderby, 2006). Note that mechanical role of PGs is still debatable and in need of research.

In the present study, our objective is to reveal the mechanistic contribution of tendon structural component to tissue strain rate sensitivity, specifically to examine the collagen fibril elongation in tendon tissues that were loaded at various strain rates. The interruption mechanical testing (IMT) and scanning electron microscopy (SEM) were applied to assess the collagen fibrils in the chemically fixed tendon fascicles that have been loaded to the same strain level at various ramping rates. A better understanding of tendon mechanisms at lower hierarchical levels can help us better to understand tissue structure–function relation and shed light on biomimic design of tissue replacements that are optimized in strength and robustness (Ackbarow and Buehler, 2009).

2. Methods

2.1. Sample preparation

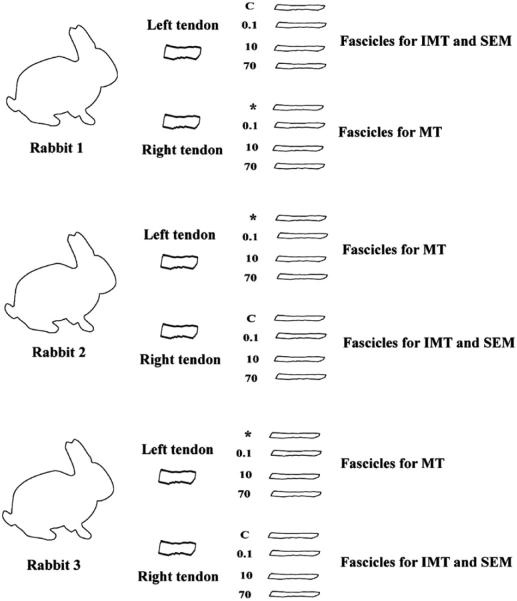
Three mature Japanese white rabbits were used in this study. The procedures of sacrifice and experiment were approved by the MSU Institutional Animal Care and Use Committee (IACUC). Animals were humanely euthanatized by administration of Beuthanasia solution (100 mg/ml perntabarbitol, 1 ml/10 lbs) intravenously in the ear vein or by intracardiac injection. Prior to euthanasia, each rabbit was sedated with an intramuscular injection of ketamine (10 mg/kg) and medetomidine (0.5 mg/kg). Immediately after euthanasia, both hind limbs were harvested using sharp dissection. Each limb was wrapped in gauze soaked in a phosphate saline solution and sealed in an airtight plastic bag. These were then stored at –30 °C until testing procedures were executed. Prior to testing, the legs were thawed at room temperature for 2 h fully hydrated with PBS. Three tendons, all from different animals, were used in the study for interrupted mechanical testing and SEM analysis (D-period measurement). The remaining patellar tendon samples were used for mechanical testing only (Fig. 2).

Fig. 2.

Fig. 2

Open in a new tab

Number of animals and fascicles for both mechanical testing (MT) for calculations of tangent modulus and interruption mechanical testing (IMT) for calculations of D-period with SEM. Stress–strain data of IMT samples were also used for the calculation of the tangent modulus. Fascicles are labeled either control (C) or their corresponding strain rate (%/s). * indicates extra fascicle not used in the study.

Both the proximal and distal insertion portions of the patellar tendon and the fascia surrounding the tendon were removed. The middle portion of the tendon was carefully extracted and then trimmed into four fascicles with the patella end attached to a holder and the other end grasped tightly with forceps (cut with an approximate width of 1 mm (Yamamoto, 1999)). All fascicles used in the study were cut from the inner portions (the central 4 mm) of the tendon to prevent location variability within the tendon (Williams et al., 2008). One tendon from each animal yielded 4 fascicles (extracted from the inner portion of tendon), among which 3 fascicles were used for tensile testing and 1 was used as a control sample. The specimens were kept moistened with PBS during the sample extraction procedure and testing.

2.2. Interruption tensile mechanical testing

Tendon fascicles were mounted onto the Biomomentum Mach-1 mechanical testing system (Biomomentum Inc., Canada). Special grips were designed to secure the specimen and minimize slippage (Fig. 3). The fascicles were then measured for their cross-sectional areas in the midsubstance using NIH Image J digital imaging program. All tested fascicles had grips initially at 7 mm apart giving a ratio of the samples’ dimensions to be around 7:1 (length vs. width), with each sample slightly varying in diameter. Fascicles were more elliptical in shape than assuming a completely round cross-sectional area. Area was defined as A=(π/4) × a × b, where a and b are the width and depth of the fascicle.

Fig. 3.

Fig. 3

Open in a new tab

(A) Fascicles were subjected to mechanical testing with 7 mm clamp-to-clamp initial length with the region of interest (ROI) between markers of 2 mm apart. (B) Midsubstance was processed for SEM analysis for D-period measurement. Scale bar=100 nm.

The fascicles were preconditioned in order to provide the specimens with similar loading histories and reduce variations in response to loading. Each sample was preloaded at 0.01 N at 0.01 mm/s; and zero strain (gauge length) was defined at this load. Each specimen was then preconditioned to a strain of 2%, for 10 cycles at 1 Hz (Yamamoto, 1999). The mechanical data were recorded in engineering stress and engineering strain. Control samples were subjected to the same preconditioning protocol and then fixed at a zero load in the fixative bath for the same amount of time (4 h). For the 4 fascicles yielded from each tendon, one was used as load free control and three were loaded to 20% clamp-to-clamp strain at 0.1, 10, and 70%/s strain rates. This corresponded to a 12% local strain in the midsubstance. Immediately after the test, the tendon was fixed in 1.25% glutaraldehyde for 4 h. The tangent modulus was taken from the linear portion of the curve at approximately 5% strain. Because of the inhomogeneous nature of tissue strain field from clamp-to-clamp, we monitored the local strain of midsubstance by placing two markers using permanent ink vertically on the fascicle surface and imaging the marker movement before and after the elongation. The local strain was calculated by measuring the distances between the centroids of two markers.

Each rabbit used in the study yielded one leg for interruption tensile testing and D-period analysis and one leg devoted just for mechanical testing for modulus calculations. Mechanical data from the interruption testing fascicles were also used in calculating the modulus (n=6).

2.3. Scanning electron microscopy

Samples for SEM were fixed in 1.25% glutaraldehyde in 0.1 M phosphate buffer (pH 7.2), rinsed with 0.1 M phosphate buffer, and post-fixed with 2% osmium tetraoxide in 0.1 M phosphate buffer. Samples were dehydrated in a graded ethanol series and then were critical point dried in a Polaron E 3000 CPD. They were then mounted on aluminum stubs and sputter coated with gold–palladium. Specimens were imaged using a JEOL JSM-6500 FE scanning electron microscope.

2.4. D-period analysis

After imaging, the samples were analyzed using Image J software (Image J 1.41, National Institutes of Health, USA). SEM photographs were taken from × 20,000 to × 30,000 magnification. The average number of D-periods for each fibril (40±9) was averaged by Image J using the image's scale bar and a scale factor calculated by SF=(distance in pixels)/(known distance (nm)). The elongation of collagen fibrils were compared among different strain rates to show the differences in fibril recruitment. Note that, in this study, fibril recruitment was defined as the amount of fibril strain relative to the global tissue strain.

For each interruption tensile test, five images randomly located in the specimen's midsubstance were used to measure the fibril periodicity (Fig. 4). However, in order to avoid stereological bias, the imaging areas needed to have collagen fibrils predominately aligned along the image plane. Obviously, collagen fibrils with a large oblique orientation (out of plane) could potentially underestimate the D-period.

Fig. 4.

Fig. 4

Open in a new tab

Image analysis for 2 fibrils after a 70%/s test. SEM image shows 50 D-periods measuring 2755 and 2760 nm (correlating to a 55.1 and 55.2 nm D-period, respectively). Scale bar=100 nm.

Six fibrils from each image were selected for D-period measurement. Again, collagen fibrils within plane orientation were picked for an accurate measurement. The sample size was 90 fibrils for each strain rate (Fig. 5), while the total number of fibrils analyzed for the control group was 50. This was due to the crimping nature of load free tendon and the difficulty of locating in-plane undistorted fibrils (Fig. 6-a).

Fig. 5.

Fig. 5

Open in a new tab

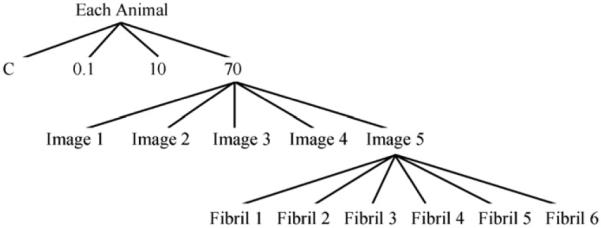
Sample tree for fascicles undergoing D-period analysis. A sample size of n=90 was the total number of fibrils coming from all 3 animals (3 animals × 5 images × 6 fibrils). Each fibril measurement represented an average of 40 ± 9 D-periods.

Fig. 6.

Fig. 6

Open in a new tab

SEM images of control sample (A), 0.1 (B), 10 (C), and 70%/s (D) tests.

2.5. Statistical analysis

The data in this study were presented as mean±standard deviation (S.D.). One way Analysis of Variances (ANOVA) was used for statistical analysis. The differences in D-period elongations were considered to be statistically significant when p is less than 0.05. Holm–Sidak test was used for post-hoc pair-wise comparisons and comparisons vs. the control group (SigmaStat 3.0, SPSS Inc., Chicago, IL). Tangent modulus values were found to be significantly different using post-hoc pair-wise comparisons vs. the quasistatic rate when p is less than 0.05.

3. Results

The stress–strain curves showed strain rate sensitivity of tendon fascicles (Fig. 7). Strain rate sensitivity was verified by an increase in tangent modulus with a strain rate increase. The tangent moduli in the linear region were found to have values of 102±42, 195±58, and 251±116 MPa for 0.1, 10, and 70%/s, respectively (Fig. 8). Tangent modulus values were found to be significantly different using post-hoc pair-wise comparisons vs. the quasistatic rate (p < 0.05). There was no difference found between 10 and 70%/s strain rates (p = 0.32) although there was an increase in trend.

Fig. 7.

Fig. 7

Open in a new tab

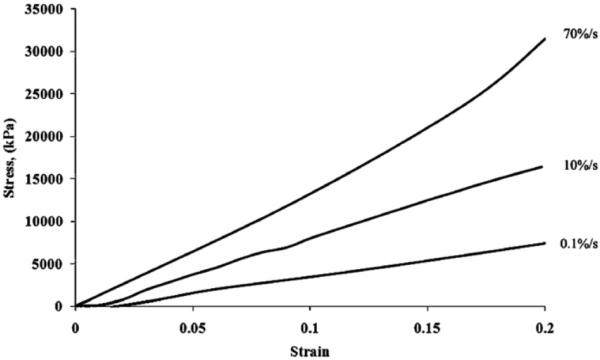
Tensile testing to 20% clamp-to-clamp strain with 3 different rates showing rate sensitivity (engineering stress vs. engineering strain).

Fig. 8.

Fig. 8

Open in a new tab

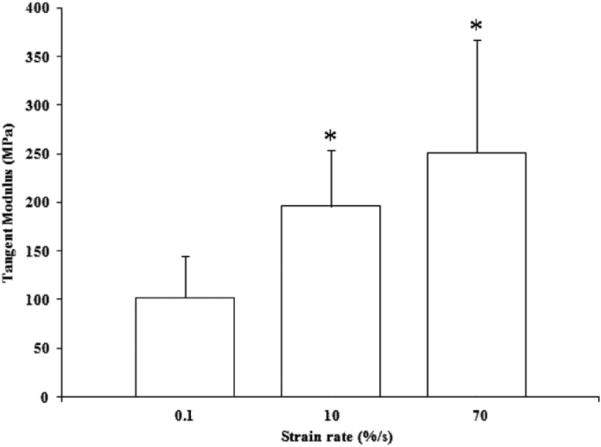
Average tangent modulus of tendon fascicles (n=6), taken from 5% strain. * indicates p<0.05 vs. 0.1%/s.

The fixed fascicles were found to maintain their elongation after the removal of the tendon from the grips. SEM images showed a straightening of fibrils in strained fascicles compared with the less orderly control samples (Fig. 6). Elongation of the D-period was found to increase with strain rate increase (Fig. 9). For the control, 0.1, 10, and 70%/s fascicles, the average D-period lengths were found to be 51.3±1.4, 52.2±1.9, 54.1±1.0, and 54.9±1.2 nm, respectively. Statistical analysis found that all strain rates to be statistically significant from the control (p < 0.005). Each rate was also compared with each other and also was found to be significant (p < 0.001).

Fig. 9.

Fig. 9

Open in a new tab

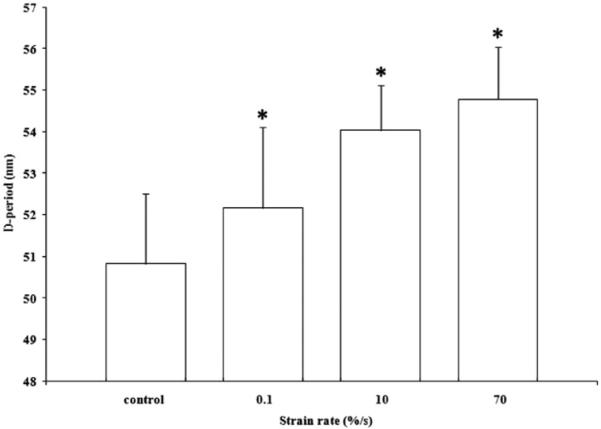
D-period analysis of 3 strain rates (n=90) with measurements normalized to control (n=50). n indicates significant difference between all groups (p<0.005).

As expected, the analysis of the local midsubstance strain revealed a non-homogeneous strain field from clamp-to-clamp. However, our analysis showed that midsubstance strains for all 3 tests were around 12% in each strain rate group (10–14% local strain). Differences in local midsubstance strains were found to be insignificant among different strain rate groups. Mechanical data revealed fascicles were not pulled past the linear region.

4. Discussion

Our data proves Puxkandl et al. (2002) and his speculation of an increasing fibril strain to tissue strain ratio relative to strain rate (Liao et al., 2007). To our knowledge, this study is the first to reveal statistically significant data of increasing fibril elongation relative to the applied strain rate. PGs have been known to participate in load transferring/bearing among a collagen fibril network. Screen et al. (2005) suggests that extracellular matrix is stiffer at higher strain rates due to its affinity for water. Elliott et al. (2003) proved a larger and faster relaxation in matrix deficient fascicles. Based on the dissipative theory, at relatively slow rates, the water and proteoglycan matrix have time to disperse and distribute forces, respectively (Ciarletta and Ben Amar, 2008). We speculate that at higher strain rates, fluid has less time to dissipate through the extracellular matrix and there is less time to distribute forces from collagen fibril to noncollagenous components (Yin and Elliott, 2004; Atkinson et al., 1999).

Previous collagen fibril studies have used X-ray diffraction to monitor fibril recruitment during elongation of various tissue types. These studies are compared with the current patellar tendon study in Table 1. In this study, the quasistatic rate yielded a 1.84% strain in the fibril, correlating a 15% fibril strain to tissue strain ratio (єF/єT). The ratio of fibril strain to tissue strain is a definitive way of looking at mechanical function of the tissue. Heart valve showed low fibril strain to tissue strain, which possibly related to its mechanics and design to resist creep in lifelong cyclic loading (Liao et al., 2007). Although there are no direct comparisons with the patellar tendon model, our study falls in between heart valve and tissues less likely to undergo regular occurring tensile strain like the antler (Krauss et al., 2009) and bone (Gupta et al., 2005). There are differences in sample preparation and testing methods between the present SEM study and the X-ray diffraction studies in Table 1. We believe the difference in єF/єT is mostly attributed to biological variability and the compositional variation within those collagenous tissues.

Table 1.

Comparison of the ratio of fibril strain to tissue strain (єF/єT). Collagenous tissues were from different animal models using X-ray differaction for the D-period measurement. Tissue samples were loaded with similar quasistatic rates.

Primary author, year Animal model Quasistatic rate, %/s Fibril strain, єF Tissue strain, єT Fibular ratio strain (єF/єT) (%)
Current study Rabbit patellar 0.1 1.8 12 15
Liao et al. (2007) Porcine mitral valve 0.6 0.5 12 4
Liao et al. (2005) Bovine pericardium 1 3.2 30 11
Puxkandl et al. (2002) Rat tail 0.08 3.3 9.5 34
Mosler et al. (1985) Rat tail 0.1 1.8 5 36
Gupta et al. (2005) Mineralized tendon 0.1 3.37 7.46 45
Krauss et al. (2009) Deer antler 0.005 1.23 2.46 50
Gupta et al. (2005) Bovine femur N/A 0.44 0.69 64
Open in a new tab

All data compared were analyzed from graphs in X-ray diffraction studies.

The fascicle mechanical properties we reported in this paper were indirectly similar with previous studies. Yamamoto et al. (2007) reported a tangent modulus for 0.3 mm2 rabbit patellar fascicles to be 180 MPa for a strain rate of 0.1%/s, higher than the 102 MPa for the 1 mm2 fascicles found in the current study. Although not a direct comparison, smaller cross-sectional area fascicles have been shown to have a higher modulus (Atkinson et al., 1999). Human patellar tendon allografts (~50 mm2) have shown a 239–306 MPa modulus at 100%/s (Haut and Powlison, 1990; Noyes et al., 1984). The current study calculated a value of 251 MPa for a 70%/s strain rate.

It is notable that the unstressed D-period reported in this paper was 51 nm, which is smaller than the typical 64–67 nm quantified in research but comparable with D-periods measured by SEM and TEM technologies (53–54 nm) (Prostak and Lees, 1996; Kukreti and Belkoff, 2000; Yamaguchi et al., 2003). A shrinking of fibrils takes place as a regular occurring effect due to the fixation and processing required for electron microscopy (Gusnard and Kirschner, 1977; Charulatha and Rajaram, 1997). We assumed the degree of collagen shrinkage due to chemical fixation and SEM processing was consistent throughout the sample and the change in the D-period length was disregarded as variability in the experiment.

Fascicle mechanics in this study were more linear, less stiff, and more extensible than bulk tendon while also having a reduced toe region as seen in Fig. 7 (Elliott et al., 2003; Atkinson et al., 1999). Previous studies report a wide fascicle failure strain range from 8% to 21% (Yamamoto, 1999; Derwin and Soslowsky, 1999; Lucas et al., 2009; Yamamoto et al., 2007; Butler et al., 1986; Haraldsson et al., 2005). This wide range is most likely due to species/biological variability and experimental setup. Failure strains of fascicles in the present study were found to be approximately 15–20% local strain (data not shown). The local strain in the study (12%) was chosen to be close to peak stress and still within the linear region (to avoid aggressive subfailure damage). The current study did not investigate fibril failure. With the highest strain rate used in this study, the fibril underwent an average of 7% strain. Isolated collagen fibrils have shown to be linear from 4–7% strain (van der Rijt et al., 2006; Svensson et al., 2010; Eppell et al., 2006). We believe that fibril failure did not occur during our tensile testing. If fibril failure had occurred, substantial damage would have been evident with the presence of relaxed fibrils in the SEM images (Arnoczky et al., 2007).

Relaxation data were recorded after every test. Initial relaxation of tendon happens almost instantly after the ramping and to our knowledge is unpreventable. This may have led to an underestimation of fibril elongation. Although the samples underwent relaxation before fully cross-linked, the relaxation took place in a shorter period of time due to fast fixative infiltration and had more residual stress compared with fascicles submerged in hydrating buffer (data not shown.) Without fixative, our fascicles showed a ~40% relaxation that showed equilibrium at 1300 s. Our data showed that, in the glutaralde-hyde fixative, the stress in the fascicle relaxed approximately 15% and reached equilibrium at 200–300 s, showing the effect of glutaraldehyde and the speed of the cross-linking.

The number of animals in this study was small compared with our fibril sample number. We decided to follow the procedure of Kukreti and Belkoff, 2000 to exhaustively analyze D-period measurements throughout the midsubstance of 3 separate animals rather than fewer image analysis and greater number of animals. Our SEM analysis averaged fibrils throughout the midsubstance and not in one localized area. This different method represents what is happening throughout the sample and accounts for errors likely caused by local variability (Williams et al., 2008; Haraldsson et al., 2005; Lake et al., 2009).

In conclusion, our finding unfolds the underlying mechanism of tendon strain rate sensitivity. We conclude that collagen fibrils undergo a significantly greater degree of elongation, relative to the tissue strain, at higher strain rates. This mechanistic finding provides insight into the behavior of the tendon at the micro-scale and establishes a basis for future development of constitutive models. Future studies will also be focused on tendonitis and chronic collagen disorders that effect fibril kinematics.

Acknowledgements

This material is based upon work supported by the National Nuclear Security Administration, Department of Energy, under award number [DE-FC26-06NT42755]. The authors would like to thank Center for Advanced Vehicular Systems, Department of Defense, Southern Regional Center for Lightweight materials, Dr. Jennifer Wardlaw, Amanda Lawrence, the MSU Electron Microscope Center, and our Department of Agricultural and Biological Engineering.

Footnotes

Publisher's Disclaimer: This article appeared in a journal published by Elsevier. The attached copy is furnished to the author for internal non-commercial research and education use, including for instruction at the authors institution and sharing with colleagues. Other uses, including reproduction and distribution, or selling or licensing copies, or posting to personal, institutional or third party websites are prohibited. In most cases authors are permitted to post their version of the article (e.g. in Word or Tex form) to their personal website or institutional repository. Authors requiring further information regarding Elsevier's archiving and manuscript policies are encouraged to visit: http://www.elsevier.com/copyright

Conflict of interest statement

The authors listed on manuscript entitled “A mechanistic study for strain rate sensitivity of rabbit patellar tendon” declare that we have no affiliations or relationships (personal, financial, and professional) with other people or organizations that can inappropriately influence this work.

Disclaimer

This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.

References

  1. Ackbarow T, Buehler MJ. Alpha-helical protein domains unify strength and robustness through hierarchical nanostructures. Nanotechnology. 2009;20(7):75103. doi: 10.1088/0957-4484/20/7/075103. [DOI] [PubMed] [Google Scholar]
  2. Atkinson TS, Ewers BJ, Haut RC. The tensile and stress relaxation responses of human patellar tendon varies with specimen cross-sectional area. J. Biomech. 1999;32(9):907–914. doi: 10.1016/s0021-9290(99)00089-5. [DOI] [PubMed] [Google Scholar]
  3. Arnoczky SP, Lavagnino M, Egerbacher M. The mechanobiological aetiopathogenesis of tendinopathy: is it the over-stimulation or the under-stimulation of tendon cells? Int. J. Exp. Pathol. 2007;88(4):217–226. doi: 10.1111/j.1365-2613.2007.00548.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Butler DL, Grood ES, Noyes FR, Zernicke RF. Biomechanics of ligaments and tendons. Exerc. Sport. Sci. Rev. 1978;6:125–181. [PubMed] [Google Scholar]
  5. Butler DL, Kay MD, Stouffer DC. Comparison of material properties in fascicle-bone units from human patellar tendon and knee ligaments. J. Biomech. 1986;19(6):425–432. doi: 10.1016/0021-9290(86)90019-9. [DOI] [PubMed] [Google Scholar]
  6. Cohen RE, Hooley CJ, McCrum NG. Viscoelastic creep of collagenous tissue. J. Biomech. 1976;9(4):175–184. doi: 10.1016/0021-9290(76)90002-6. [DOI] [PubMed] [Google Scholar]
  7. Ciarletta P, Ben Amar M. A finite dissipative theory of temporary interfibrillar bridges in the extracellular matrix of ligaments and tendons. J. R. Soc. Interface. 2008 doi: 10.1098/rsif.2008.0487. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Charulatha V, Rajaram A. Crosslinking density and resorption of dimethyl suberimidate-treated collagen. J. Biomed Mater Res. 1997;36(4):478–486. doi: 10.1002/(sici)1097-4636(19970915)36:4<478::aid-jbm5>3.0.co;2-b. [DOI] [PubMed] [Google Scholar]
  9. Duenwald SE, Vanderby R, Jr., Lakes RS. Viscoelastic relaxation and recovery of tendon. Ann. Biomed. Eng. 2009;37(6):1131–1140. doi: 10.1007/s10439-009-9687-0. [DOI] [PubMed] [Google Scholar]
  10. Derwin KA, Soslowsky LJ. A quantitative investigation of structure–function relationships in a tendon fascicle model. J. Biomech. Eng. 1999;121(6):598–604. doi: 10.1115/1.2800859. [DOI] [PubMed] [Google Scholar]
  11. Elliott DM, Robinson PS, Gimbel JA, Sarver JJ, Abboud JA, Iozzo RV, Soslowsky LJ. Effect of altered matrix proteins on quasilinear viscoelastic properties in transgenic mouse tail tendons. Ann. Biomed. Eng. 2003;31(5):599–605. doi: 10.1114/1.1567282. [DOI] [PubMed] [Google Scholar]
  12. Eppell SJ, Smith BN, Kahn H, Ballarini R. Nano measurements with micro-devices: mechanical properties of hydrated collagen fibrils. J. R. Soc. Interface. 2006;3(6):117–121. doi: 10.1098/rsif.2005.0100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Folkard W, Geercken W, Knorzer E, Mosler E, Nemetschek-Gansler H, Nemetschek T, Koch MH. Structural dynamic of native tendon collagen. J. Mol. Biol. 1987;193(2):405–407. doi: 10.1016/0022-2836(87)90228-2. [DOI] [PubMed] [Google Scholar]
  14. Fratzl P, Misof K, Zizak I, Rapp G, Amenitsch H, Bernstorff S. Fibrillar structure and mechanical properties of collagen. J. Struct. Biol. 1998;122(1–2):119–122. doi: 10.1006/jsbi.1998.3966. [DOI] [PubMed] [Google Scholar]
  15. Graham JS, Vomund AN, Phillips CL, Grandbois M. Structural changes in human type I collagen fibrils investigated by force spectroscopy. Exp. Cell Res. 2004;299(2):335–342. doi: 10.1016/j.yexcr.2004.05.022. [DOI] [PubMed] [Google Scholar]
  16. Gupta HS, Seto J, Krauss S, Boesecke P, Screen HR. In situ multi-level analysis of viscoelastic deformation mechanisms in tendon collagen. J. Struct. Biol. 2009 doi: 10.1016/j.jsb.2009.10.002. [DOI] [PubMed] [Google Scholar]
  17. Gupta HS, Wagermaier W, Zickler GA, Raz-Ben Aroush D, Funari SS, Roschger P, Wagner HD, Fratzl P. Nanoscale deformation mechanisms in bone. Nano Lett. 2005;5(10):2108–2111. doi: 10.1021/nl051584b. [DOI] [PubMed] [Google Scholar]
  18. Gusnard D, Kirschner RH. Cell and organelle shrinkage during preparation for scanning electron microscopy: effects of fixation, dehydration, and critical point drying. J. Microsc. 1977;110(1):51–57. doi: 10.1111/j.1365-2818.1977.tb00012.x. [DOI] [PubMed] [Google Scholar]
  19. Hansen P, Hassenkam T, Svensson RB, Aagaard P, Trappe T, Haraldsson BT, Kjaer M, Magnusson P. Glutaraldehyde cross-linking of tendon—me chanical effects at the level of the tendon fascicle and fibril. Connect. Tissue Res. 2009;50(4):211–222. doi: 10.1080/03008200802610040. [DOI] [PubMed] [Google Scholar]
  20. Haut RC, Powlison AC. The effects of test environment and cyclic stretching on the failure properties of human patellar tendons. J. Orthop. Res. 1990;8(4):532–540. doi: 10.1002/jor.1100080409. [DOI] [PubMed] [Google Scholar]
  21. Haraldsson BT, Aagaard P, Krogsgaard M, Alkjaer T, Kjaer M, Magnusson SP. Region-specific mechanical properties of the human patella tendon. J. Appl. Physiol. 2005;98(3):1006–1012. doi: 10.1152/japplphysiol.00482.2004. [DOI] [PubMed] [Google Scholar]
  22. Johnson GA, Tramaglini DM, Levine RE, Ohno K, Choi NY, Woo SL. Tensile and viscoelastic properties of human patellar tendon. J. Orthop. Res. 1994;12(6):796–803. doi: 10.1002/jor.1100120607. [DOI] [PubMed] [Google Scholar]
  23. Kastelic J, Galeski A, Baer E. The multicomposite structure of tendon. Connect. Tissue Res. 1978;6(1):11–23. doi: 10.3109/03008207809152283. [DOI] [PubMed] [Google Scholar]
  24. Kannus P. Structure of the tendon connective tissue. Scand. J. Med. Sci. Sports. 2000;10:312–320. doi: 10.1034/j.1600-0838.2000.010006312.x. [DOI] [PubMed] [Google Scholar]
  25. Krauss S, Fratzl P, Seto J, Currey JD, Estevez JA, Funari SS, Gupta HS. Inhomogeneous fibril stretching in antler starts after macroscopic yielding: indication for a nanoscale toughening mechanism. Bone. 2009;44(6):1105–1110. doi: 10.1016/j.bone.2009.02.009. [DOI] [PubMed] [Google Scholar]
  26. Kukreti U, Belkoff SM. Collagen fibril D-period may change as a function of strain and location in ligament. J. Biomech. 2000;33(12):1569–1574. doi: 10.1016/s0021-9290(00)00150-0. [DOI] [PubMed] [Google Scholar]
  27. Liao J, Yang L, Grashow J, Sacks MS. Molecular orientation of collagen in intact planar connective tissues under biaxial stretch. Acta Biomater. 2005;1(1):45–54. doi: 10.1016/j.actbio.2004.09.007. [DOI] [PubMed] [Google Scholar]
  28. Lucas SR, Bass CR, Crandall JR, Kent RW, Shen FH, Salzar RS. Viscoelastic and failure properties of spine ligament collagen fascicles. Biomech. Model. Mechanobiol. 2009 doi: 10.1007/s10237-009-0152-7. [DOI] [PubMed] [Google Scholar]
  29. Liao J, Vesely I. Skewness angle of interfibrillar proteoglycans increases with applied load on mitral valve chordae tendineae. J. Biomech. 2007;40(2):390–398. doi: 10.1016/j.jbiomech.2005.12.011. [DOI] [PubMed] [Google Scholar]
  30. Liao J, Yang L, Grashow J, Sacks MS. The relation between collagen fibril kinematics and mechanical properties in the mitral valve anterior leaflet. J. Biomech. Eng. 2007;129(1):78–87. doi: 10.1115/1.2401186. [DOI] [PubMed] [Google Scholar]
  31. Lake SP, Miller KS, Elliott DM, Soslowsky LJ. Effect of fiber distribution and realignment on the nonlinear and inhomogeneous mechanical properties of human supraspinatus tendon under longitudinal tensile Loading. J. Orthop. Res. 2009 doi: 10.1002/jor.20938. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Mosler E, Folkhard W, Knorzer E, Nemetschek-Gonsler H, Nemetschek H, Koch MHJ. Stress-induced molecular rearrangement in tendon collagen. J. Mol. Biol. 1985;182:589–596. doi: 10.1016/0022-2836(85)90244-x. [DOI] [PubMed] [Google Scholar]
  33. Noyes FR, Butler DL, Grood ES, Zernicke RF, Hefzy MS. Biomechanical analysis of human ligament grafts used in knee-ligament repairs and reconstructions. J. Bone Joint Surg. Am. 1984;66(3):344–352. [PubMed] [Google Scholar]
  34. Petruska JA, Hodge AJ. A Subunit model for the tropocollagen macromolecule. Proc. Natl. Acad. Sci. USA. 1964;51:871–876. doi: 10.1073/pnas.51.5.871. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Puxkandl R, Zizak I, Paris O, Keckes J, Tesch W, Bernstorff S, Purslow P, Fratzl P. Viscoelastic properties of collagen: synchrotron radiation investigations and structural model. Philos. Trans. R. Soc. London, Ser. B: Biological Sciences. 2002;357(1418):191–197. doi: 10.1098/rstb.2001.1033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Provenzano PP, Vanderby R., Jr. Collagen fibril morphology and organization: implications for force transmission in ligament and tendon. Matrix Biol. 2006;25(2):71–84. doi: 10.1016/j.matbio.2005.09.005. [DOI] [PubMed] [Google Scholar]
  37. Prostak KS, Lees S. Visualization of crystal-matrix structure. In situ demineralization of mineralized turkey leg tendon and bone. Calcif. Tissue Int. 1996;59(6):474–479. doi: 10.1007/BF00369213. [DOI] [PubMed] [Google Scholar]
  38. Robinson PS, Lin TW, Reynolds PR, Derwin KA, Iozzo RV, Soslowsky LJ. Strain-rate sensitive mechanical properties of tendon fascicles from mice with genetically engineered alterations in collagen and decorin. J. Biomech. Eng. 2004;126(2):252–257. doi: 10.1115/1.1695570. [DOI] [PubMed] [Google Scholar]
  39. Redaelli A, Vesentini S, Soncini M, Vena P, Mantero S, Montevecchi FM. Possible role of decorin glycosaminoglycans in fibril to fibril force transfer in relative mature tendons—a computational study from molecular to microstructural level. J. Biomech. 2003;36(10):1555–1569. doi: 10.1016/s0021-9290(03)00133-7. [DOI] [PubMed] [Google Scholar]
  40. Screen HR, Lee DA, Bader DL, Shelton JC. An investigation into the effects of the hierarchical structure of tendon fascicles on micromechanical properties. Proc. Inst. Mech. Eng. H. 2004;218(2):109–119. doi: 10.1243/095441104322984004. [DOI] [PubMed] [Google Scholar]
  41. Sasaki N, Odajima S. Elongation mechanism of collagen fibrils and force-strain relations of tendon at each level of structural hierarchy. J. Biomech. 1996a;29(9):1131–1136. doi: 10.1016/0021-9290(96)00024-3. [DOI] [PubMed] [Google Scholar]
  42. Shen ZL, Dodge MR, Kahn H, Ballarini R, Eppell SJ. Stress–strain experiments on individual collagen fibrils. Biophys. J. 2008;95(8):3956–3963. doi: 10.1529/biophysj.107.124602. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Sasaki N, Odajima S. Stress–strain curve and Young's modulus of a collagen molecule as determined by the X-ray diffraction technique. J. Biomech. 1996b;29(5):655–658. doi: 10.1016/0021-9290(95)00110-7. [DOI] [PubMed] [Google Scholar]
  44. Screen HR, Shelton JC, Chhaya VH, Kayser MV, Bader DL, Lee DA. The influence of noncollagenous matrix components on the micromechanical environment of tendon fascicles. Ann. Biomed. Eng. 2005;33(8):1090–1099. doi: 10.1007/s10439-005-5777-9. [DOI] [PubMed] [Google Scholar]
  45. Scott JE. Elasticity in extracellular matrix shape modules of tendon, cartilage, etc. A sliding proteoglycan-filament model. J. Physiol. 2003;553(Pt 2):335–343. doi: 10.1113/jphysiol.2003.050179. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Svensson RB, Hassenkam T, Hansen P, Peter Magnusson S. Viscoelastic behavior of discrete human collagen fibrils. J. Mech. Behav. Biomed. Mater. 2010;3(1):112–115. doi: 10.1016/j.jmbbm.2009.01.005. [DOI] [PubMed] [Google Scholar]
  47. van der Rijt JA, van der Werf KO, Bennink ML, Dijkstra PJ, Feijen J. Micromechanical testing of individual collagen fibrils. Macromol. Biosci. 2006;6(9):697–702. doi: 10.1002/mabi.200600063. [DOI] [PubMed] [Google Scholar]
  48. Wang JH. Mechanobiology of tendon. J. Biomech. 2006;39(9):1563–1582. doi: 10.1016/j.jbiomech.2005.05.011. [DOI] [PubMed] [Google Scholar]
  49. Woo SL. Mechanical properties of tendons and ligaments. I. Quasi-static and nonlinear viscoelastic properties. Biorheology. 1982;19(3):385–396. doi: 10.3233/bir-1982-19301. [DOI] [PubMed] [Google Scholar]
  50. Weiss JA, Gardiner JC, Bonifasi-Lista C. Ligament material behavior is nonlinear, viscoelastic, and rate-independent under shear loading. J. Biomech. 2002;35(7):943–950. doi: 10.1016/s0021-9290(02)00041-6. [DOI] [PubMed] [Google Scholar]
  51. Williams LN, Elder SH, Horstemeyer MF, Harbarger D. Variation of diameter distribution, number density, and area fraction of fibrils within five areas of the rabbit patellar tendon. Ann. Anat. 2008;190(5):442–451. doi: 10.1016/j.aanat.2008.05.003. [DOI] [PubMed] [Google Scholar]
  52. Yamamoto N, Hayashi K, Kuriyama H, Ohno K, Yasuda K, Kaneda K. Mechanical properties of the rabbit patellar tendon. J. Biomech. Eng. 1992;114(3):332–337. doi: 10.1115/1.2891392. [DOI] [PubMed] [Google Scholar]
  53. Yamamoto Mechanical properties of collagen fascicles form the rabbit patellar tendon. Trans. ASME. 1999;121:124–131. doi: 10.1115/1.2798033. [DOI] [PubMed] [Google Scholar]
  54. Yang L, van der Werf KO, Fitie CF, Bennink ML, Dijkstra PJ, Feijen J. Mechanical properties of native and cross-linked type I collagen fibrils. Biophys. J. 2008;94(6):2204–2211. doi: 10.1529/biophysj.107.111013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Yang L, van der Werf KO, Koopman BF, Subramaniam V, Bennink ML, Dijkstra PJ, Feijen J. Micromechanical bending of single collagen fibrils using atomic force microscopy. J. Biomed. Mater Res. A. 2007;82(1):160–168. doi: 10.1002/jbm.a.31127. [DOI] [PubMed] [Google Scholar]
  56. Yin L, Elliott DM. A biphasic and transversely isotropic mechanical model for tendon: application to mouse tail fascicles in uniaxial tension. J. Biomech. 2004;37(6):907–916. doi: 10.1016/j.jbiomech.2003.10.007. [DOI] [PubMed] [Google Scholar]
  57. Yamamoto E, Kogawa D, Tokura S, Hayashi K. Biomechanical response of collagen fascicles to restressing after stress deprivation during culture. J. Biomech. 2007;40(9):2063–2070. doi: 10.1016/j.jbiomech.2006.10.007. [DOI] [PubMed] [Google Scholar]
  58. Yamaguchi I, Kogure T, Sakane M, Tanaka S, Osaka A, Tanaka J. Microstructure analysis of calcium phosphate formed in tendon. J. Mater. Sci. Mater. Med. 2003;14(10):883–889. doi: 10.1023/a:1025634710453. [DOI] [PubMed] [Google Scholar]

RESOURCES