Coinfection Dynamics of Two Diseases in a Single Host Population

Abstract

A susceptible-infectious-susceptible (SIS) epidemic model that describes the coinfection and cotransmission of two infectious diseases spreading through a single population is studied. The host population consists of two subclasses: susceptible and infectious, and the infectious individuals are further divided into three subgroups: those infected by the first agent/pathogen, the second agent/pathogen, and both. The basic reproduction numbers for all cases are derived which completely determine the global stability of the system if the presence of one agent/pathogen does not affect the transmission of the other. When the constraint on the transmissibility of the dually infected hosts is removed, we introduce the invasion reproduction number, compare it with two other types of reproduction number and show the uniform persistence of both diseases under certain conditions. Numerical simulations suggest that the system can display much richer dynamics such as backward bifurcation, bistability and Hopf bifurcation.

1 Introduction

Different infectious agents may infect or colonize a host at the same time [21]. Many examples can be found, these involving HIV [30, 37] (for example, HIV and TB [19], HIV and Hepatitis B [12, 26], HIV and Hepatitis C [23], and HIV and malaria [2]), as well as some not involving HIV (for example, Hepatitis B and C coinfection [11], gonorrhea and Chlamydia [13], and herpes simplex viruses 1 and 2 [41, 59]) Moreover, simultaneous infection may occur with multiple strains or serotypes of the same organism, as is the case for influenza [20, 49], human papilloma virus [9], and HIV [55, 63, 22], for just three of many examples. However, simultaneous colonization or infection may occur even when there appears to be little or no interaction between the two agents, as in the case of infection by ocular strains of chlamydia and nasopharyngeal colonization by pneumococcus [24]. The dynamics of coinfection is important in this case, because antimicrobials used to treat one infection may affect the other (e.g., [51, 24]).

A variety of mathematical models for coinfections with multiple specific diseases, such as HIV/TB [43, 48, 6, 47], HIV/gonorrhea [40], HIV/malaria [1, 39], malaria and meningitis [29], general diseases [5, 7, 35, 28], and microparasites (viruses, bacteria, protozoa, fungi) [54, 10, 3, 4, 61], have been developed and analyzed in the past few years. Ferguson et al. [16] and Kawaguchi et al. [27] presented models to describe the coinfection of two serotypes of dengue virus in a human community. With respect to the interaction between nonspecific agents or pathogens, Blyuss and Kyrychko [7] studied a two-disease SIS model with equal transmission efficiency for both susceptible and singly infected individuals; Allen et al. [5] studied an SI model for a single host population with two viral infections, in which one is vertically transmitted and the other is horizontally transmitted; Zhang et al. [60] proposed an ODEs coinfection model with two strains of parasites and two host types to study the influence of heterogeneities in parasite virulence and host life history on the persistence and spread of parasite strains; Martcheva and Pilyugin [35] considered an epidemic model of two diseases: a primary disease and a secondary disease, structured by time since infection structure (for the primary disease); in the monograph of Keeling and Rohani [28], the interaction of two pathogens spreading through a host population was discussed in four cases: complete cross-immunity, no cross-immunity, enhanced susceptibility and partial cross-immunity. Among these models either the uninfected hosts cannot become infected with both diseases/strains directly [38, 35, 28, 10], or there is no recovery and an infection is lifelong [54, 5, 4], or both [60, 3].

In this paper, we develop and analyze a simple model of multiple infections; this model includes the possibility that the two agents are simultaneously transmitted with aspects of Chlamydia trachomatis and pneumococcus, though we do not restrict the analysis to this setting (see [31, 46] for examples of cotransmission in vector-borne disease ecology and human case report, respectively), thereby inaugurating a dual infection. Our model will also include the possibility that an individual who is currently infected with one agent will become dually infected as a result of an exposure to the second agent. In this paper, the condition of being simultaneously infected by multiple agents will be referred to simply as coinfection. Our model is similar to the model of Blyuss and Kyrychko [7] where the disease induced mortality is included, the doubly infected hosts recover from both diseases simultaneously and strong restrictions on transmission parameters are required, and to the models for coinfection by different species in Tanaka and Feldman [54] and Alizon [4] where disease-induced mortality may occur, but no recovery is possible (and the forces of infection follow a different rule).

We will assess a two-disease SIS model with no immunity or cross-immunity. For simplicity, we will refer to the first and second disease, recognizing that the model applies equally well to colonization or to subclinical infections. In Section 3, we carry out a complete global stability analysis of the model for the case where the force of infection of one disease is not affected by the presence of the other (i.e., no interaction between two infections). In Section 4, when the two infections interact with each other, we calculate the invasion reproduction numbers and obtain their epidemiologically meaningful lower and upper bounds, and show that the interaction outcome could be extinction of one or both diseases or persistence of both diseases. In Section 5, four numerical examples are provided to support the existence of competitive exclusion, backward bifurcation, bistability and Hopf bifurcation, respectively.

2 The model

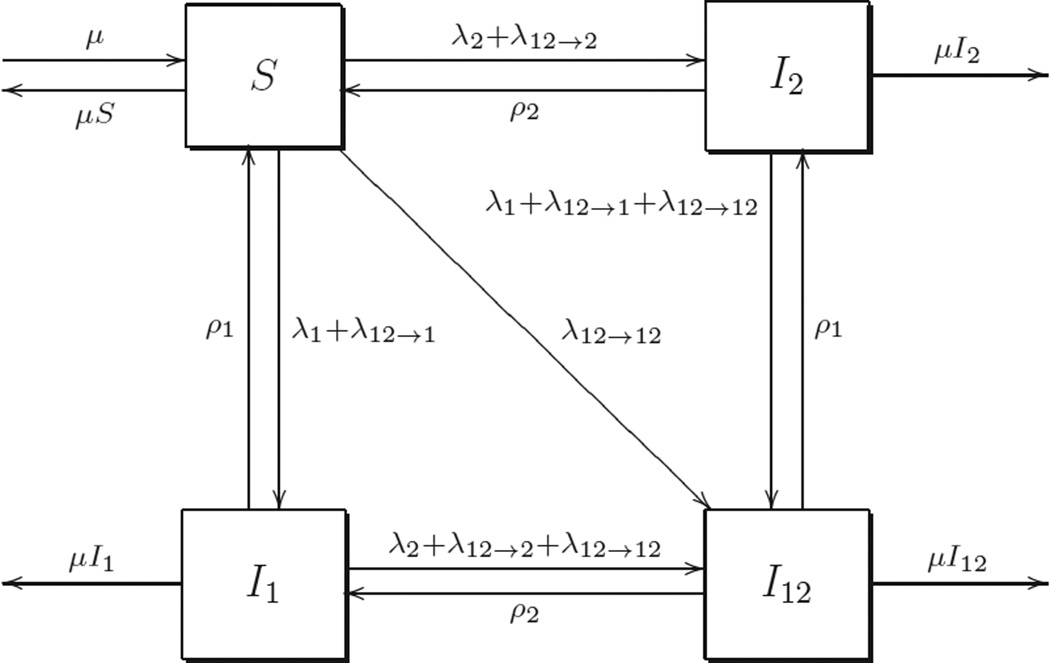
We propose a simple SIS epidemic model with two infectious agents (or strains of the same agent) spreading through one host species. Let S(t), I₁(t), I₂(t) and I₁₂(t) be the fractions of the population infected with no infectious agent, the first agent, the second agent and both agents at time t, respectively. A susceptible individual who contacts coinfected persons can be infected with either one or both disease agents as a result of a single contact. Using ocular strains of Chlamydia trachomatis and nasopharyngeal pneumococcus as an example, transmission of either or both organisms could occur as a result of a single contact. This process is illustrated in Figure 1. The model is then described by a system of four ordinary differential equations as follows:

$$\frac{dS}{dt}=\mu -({\lambda }_1+{\lambda }_2+{\lambda }_{12\to 1}+{\lambda }_{12\to 12}+{\lambda }_{12\to 2})S+({\rho }_1{I}_1+{\rho }_2{I}_2)-\mu S,$$

$$\frac{d{I}_1}{dt}=({\lambda }_1+{\lambda }_{12\to 1})S-({\lambda }_2+{\lambda }_{12\to 2}+{\lambda }_{12\to 12})I_1+({\rho }_2{I}_{12}-{\rho }_1{I}_1)-\mu I_1,$$

$$\frac{d{I}_2}{dt}=({\lambda }_2+{\lambda }_{12\to 2})S-({\lambda }_1+{\lambda }_{12\to 1}+{\lambda }_{12\to 12})I_2+({\rho }_1{I}_{12}-{\rho }_2{I}_2)-\mu I_2,$$ (2.1)

$$\frac{d{I}_{12}}{dt}={\lambda }_{12\to 12}S+({\lambda }_2+{\lambda }_{12\to 2}+{\lambda }_{12\to 12})I_1+({\lambda }_1+{\lambda }_{12\to 1}+{\lambda }_{12\to 12})I_2-({\rho }_1+{\rho }_2)I_{12}-\mu I_{12},1=S+I_1+I_2+I_{12},$$

where the forces of infection are proportional to disease prevalence, i.e.,

$${\lambda }_1={\beta }_1{I}_1,{\lambda }_2={\beta }_2{I}_2,{\lambda }_{12\to 12}={\beta }_{12}{I}_{12},{\lambda }_{12\to 1}={\beta }_{10}{I}_{12},{\lambda }_{12\to 2}={\beta }_{02}{I}_{12}.$$

Figure 1.

Flowchart of a two-disease coinfection model. S, I₁, I₂ and I₁₂ represent the fractions of population infected with no infectious agent, the first agent, the second agent and both agents, respectively.

Parameters ρ₁ and ρ₂ represent the recovery rate of the first and second diseases, respectively. The disease induced death rate is ignored. We assume that the natural birth and death rates are balanced and equal to μ, so that the total population size is constant. All parameters are assumed to be positive, except that β₁₂ ≥ 0. As stated earlier, the possibility of simultaneous transmission from a single contact with a dually infected individual, which we model according to the assumption β₁₂ > 0. An underlying assumption in the model is that individuals in all disease states have the same contact rate; we do not assume that individuals have fewer contacts if they are infected. The rates/probabilities of transmission of the model in Blyuss and Kyrychko [7] satisfy β₁₂ + β₁₀ = β₁, β₁₂ + β₀₂ = β₂, β₁₂ = β₁β₂, which is a special case of ours.

Following the method and notations of van den Driessche and Watmough [58] and Diekmann et al. [14, 15], we have

$$F=\left(\begin{array}{ccc}\hfill {\beta }_1\hfill & \hfill 0\hfill & \hfill {\beta }_{10}\hfill \\ \hfill 0\hfill & \hfill {\beta }_2\hfill & \hfill {\beta }_{02}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\beta }_{12}\hfill \end{array}\right)\text{ and }V=\left(\begin{array}{ccc}\hfill {\rho }_1+\mu \hfill & \hfill 0\hfill & \hfill -{\rho }_2\hfill \\ \hfill 0\hfill & \hfill {\rho }_2+\mu \hfill & \hfill -{\rho }_1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\rho }_1+{\rho }_2+\mu \hfill \end{array}\right).$$

The basic reproduction number associated with the model (2.1) is defined as the spectral radius of the next generation matrix FV⁻¹, i.e., ℛ₀ = max{ℛ₁₀, ℛ₂₀, ℛ₃₀}, where

$${ℛ}_{10}=\frac{{\beta }_1}{{\rho }_1+\mu },{ℛ}_{20}=\frac{{\beta }_2}{{\rho }_2+\mu },{ℛ}_{30}=\frac{{\beta }_{12}}{{\rho }_1+{\rho }_2+\mu }.$$

Let $\mathrm{\Omega }=\{(S,I_1,I_2,I_{12})\in {ℝ}_{+}^4:S+I_1+I_2+I_{12}=1\}$. Clearly, the set Ω is positively invariant for system (2.1), so we will always set initial values within Ω. It is immediate that system (2.1) has up to three boundary equilibria as follows.

Proposition 2.1

For system (2.1), we have

1. the disease-free equilibrium E₀ = (1, 0, 0, 0) always exists;

2. the equilibrium with the presence of only the first disease E₁ = (1/ℛ₁₀, 1 − 1/ℛ₁₀, 0, 0) exists if and only if ℛ₁₀ > 1;

3. the equilibrium with the presence of only the second disease E₂ = (1/ℛ₂₀, 0, 1 − 1/ℛ₂₀, 0) exists if and only if ℛ₂₀ > 1.

3 Noninteracting transmission

We begin with the simpler case where the presence of each disease does not affect the transmission of the other; throughout this section, we assume that a doubly infected individual has the same total infectivity as a singly infected person, which translates to

$${\beta }_{12}+{\beta }_{10}={\beta }_1\text{ and }{\beta }_{12}+{\beta }_{02}={\beta }_2.$$ (H)

Under the assumption (H), the persistence and extinction of one disease, and the total fraction of people infected by that disease are not affected by the presence of the other disease. The ability of a disease to invade an uninfected population is completely determined by its own basic reproduction number.

Theorem 3.1

Let Ω₀ = {E₀}, Ω₁ = {(S, I₁, 0, 0) ∈ Ω : I₁ > 0} and Ω₂ = {(S, 0, I₂, 0) ∈ Ω : I₂ > 0}. For system (2.1) under assumption (H), we have

1. if ℛ₀ ≤ 1 then the disease-free equilibrium E₀ is globally asymptotically stable in Ω;

2. if ℛ₁₀ > 1 ≥ ℛ₂₀ (or ℛ₂₀ > 1 ≥ ℛ₁₀), then E₁ (or E₂) is globally asymptotically stable in Ω\(Ω₀ ∪ Ω₂) (or Ω\(Ω₀ ∪ Ω₁)) where Ω₀ ∪ Ω₂ (or ( Ω₀ ∪ Ω₁)) is the attractor of E₀;

3. if ℛ₁₀ > 1 and ℛ₂₀ > 1, then there exists a unique coexistence equilibrium, denoted by $E_{12}=(S^{*},I_1^{*},I_2^{*},I_{12}^{*})$, which is globally asymptotically stable in

   $$\mathrm{\Omega }\backslash ({\mathrm{\Omega }}_0\cup {\mathrm{\Omega }}_1\cup {\mathrm{\Omega }}_2)=\{(S,I_1,I_2,I_{12})\in \mathrm{\Omega }:I_{12}>0\mathit{\text{ or }}{I}_1{I}_2>0\}.$$

   Here Ω₀, Ω₁ and Ω₂ are the attractor of E₀, E₁ and E₂, respectively.

Proof

The summations of the second and fourth equations of (2.1) and the third and fourth equations of (2.1) give

$$\frac{d(I_1+I_{12})}{dt}=-({\rho }_1+\mu -{\beta }_1(S+I_2))(I_1+I_{12})$$

and

$$\frac{d(I_2+I_{12})}{dt}=-({\rho }_2+\mu -{\beta }_2(S+I_1))(I_2+I_{12}),$$

respectively. It follows from S + I₁ + I₂ + I₁₂ = 1 that the above two logistic equations satisfy

$$I_1(t)+I_{12}(t)\to \text{max }\{0,1-\frac{1}{{ℛ}_{10}}\}\text{ and }{I}_2(t)+I_{12}(t)\to \text{max }\{0,1-\frac{1}{{ℛ}_{20}}\}\text{ as }t\to \infty ,$$

respectively, if both diseases present initially. If, for example, ℛ₁₀ ≤ 1, then I₁(t) + I₁₂(t) → 0 which implies $\underset{t\to \infty }{\text{lim}}{I}_1(t)=\underset{t\to \infty }{\text{lim}}{I}_{12}(t)=0$. Thus, the first two arguments are established.

Now we assume that ℛ₁₀ ≥ ℛ₂₀ > 1 and the symmetric case ℛ₂₀ ≥ ℛ₁₀ > 1 can be proved similarly. If $E_{12}=(S^{*},I_1^{*},I_2^{*},I_{12}^{*})$ exists, then it must satisfy

$$I_1^{*}=\frac{1}{{ℛ}_{20}}-S^{*},I_2^{*}=\frac{1}{{ℛ}_{10}}-S^{*}\text{ and }{I}_{12}^{*}=S^{*}+1-\frac{1}{{ℛ}_{10}}-\frac{1}{{ℛ}_{20}}$$ (3.1)

and substituting them into the first equation of (2.1) yields

$$\frac{d{S}^{*}}{dt}={\beta }_{12}{(S^{*})}^2-\left(\right(\frac{1}{{ℛ}_{10}}+\frac{1}{{ℛ}_{20}}-1){\beta }_{12}+({\beta }_1+{\beta }_2)-\mu )S^{*}+\frac{{\rho }_1}{{ℛ}_{20}}+\frac{{\rho }_2}{{ℛ}_{10}}+\mu =0.$$ (3.2)

Meanwhile, solving $I_{12}^{*}$ in terms of S* from the first equation of (2.1) gives

$$I_{12}^{*}=\frac{{\beta }_1(\frac{1}{{ℛ}_{10}}-S^{*})I_1^{*}+{\beta }_2(\frac{1}{{ℛ}_{20}}-S^{*})I_2^{*}}{({\beta }_{10}+{\beta }_{02}+{\beta }_{12})S^{*}-\mu }=\frac{({\beta }_1+{\beta }_2)(\frac{1}{{ℛ}_{10}}-S^{*})(\frac{1}{{ℛ}_{20}}-S^{*})}{({\beta }_1+{\beta }_2-{\beta }_{12})S^{*}-\mu }\ge \frac{I_1^{*}{I}_2^{*}}{S^{*}}.$$

Claim 1

If β₁₂ = 0, then $S^{*}=(\frac{{\rho }_1}{{ℛ}_{20}}+\frac{{\rho }_2}{{ℛ}_{10}}+\mu )/({\beta }_1+{\beta }_2-\mu )$ and there exists a unique endemic equilibrium

$$E_{12}=\frac{1}{{\beta }_1+{\beta }_2-\mu }(\frac{{\rho }_1}{{ℛ}_{20}}+\frac{{\rho }_2}{{ℛ}_{10}}+\mu ,(1-\frac{1}{{ℛ}_{10}}\left)\right(\frac{{\beta }_1+{\beta }_2}{{ℛ}_{20}}-\mu ),(1-\frac{1}{{ℛ}_{20}}\left)\right(\frac{{\beta }_1+{\beta }_2}{{ℛ}_{10}}-\mu ),(1-\frac{1}{{ℛ}_{10}}\left)\right(1-\frac{1}{{ℛ}_{20}})({\beta }_1+{\beta }_2)).$$

If β₁₂ > 0, then (3.2) has two roots, labeled by $S_1^{*}$ and $S_2^{*}$, satisfying $0<\Re S_1^{*}\le \Re S_2^{*}$. Here ℜ(z) is the real part of a complex number z. Dividing both sides of (3.2) by β₁₂ yields

$$F(S^{*})\equiv {(S^{*})}^2-({\upsilon }_1+{\upsilon }_2-1+g-h)S^{*}+g{\upsilon }_1{\upsilon }_2+(1-{\upsilon }_1-{\upsilon }_2)h=0,$$

where ${\upsilon }_1=\frac{1}{{ℛ}_{10}},{\upsilon }_2=\frac{1}{{ℛ}_{20}},g=\frac{{\beta }_1+{\beta }_2}{{\beta }_{12}}$ and $h=\frac{\mu }{{\beta }_{12}}$. Clearly, υ₁ ≤ υ₂ < 1, g > 2 and g > 2h.

Claim 2

$0<S_1^{*}<{\upsilon }_1\le {\upsilon }_2<1<S_2^{*}$. It follows from $F(0)=S_1^{*}{S}_2^{*}>0$ and

$$F({\upsilon }_1)={\upsilon }_1^2-({\upsilon }_1+{\upsilon }_2-1+g-h){\upsilon }_1+g{\upsilon }_1{\upsilon }_2+(1-{\upsilon }_1-{\upsilon }_2)h=-({\upsilon }_2-1+g-g{\upsilon }_2){\upsilon }_1+(1-{\upsilon }_2)h=(1-{\upsilon }_2)(h-{\upsilon }_1(g-1))=(1-{\upsilon }_2)(\frac{\mu }{{\beta }_{12}}-\frac{{\rho }_1+\mu }{{\beta }_1}(\frac{{\beta }_1+{\beta }_2}{{\beta }_{12}}-1\left)\right)=(1-{\upsilon }_2)(\frac{\mu }{{\beta }_{12}}-\frac{{\rho }_1+\mu }{{\beta }_{12}}-\frac{{\rho }_1+\mu }{{\beta }_1}(\frac{{\beta }_2}{{\beta }_{12}}-1\left)\right)<0$$

that both $S_1^{*}$ and $S_2^{*}$ are positive real numbers and $S_1^{*}<{\upsilon }_1$. In addition,

$$S_2^{*}={\upsilon }_1+{\upsilon }_2-1+g-h-S_1^{*}>{\upsilon }_2-1+g-h=\frac{{\rho }_2+\mu }{{\beta }_2}-1+\frac{{\beta }_1+{\beta }_2}{{\beta }_{12}}-\frac{\mu }{{\beta }_{12}}\ge (\frac{\mu }{{\beta }_2}-1+\frac{{\beta }_2}{{\beta }_{12}}-\frac{\mu }{{\beta }_{12}})+\frac{{\beta }_1}{{\beta }_{12}}=(\frac{{\beta }_2}{{\beta }_{12}}-1)(1-\frac{\mu }{{\beta }_2})+\frac{{\beta }_1}{{\beta }_{12}}>\frac{{\beta }_1}{{\beta }_{12}}>1.$$

When $S^{*}=S_1^{*}$, the positivities of $I_1^{*}$ and $I_2^{*}$ follow from $S_1^{*}<{\upsilon }_1\le {\upsilon }_2$ and $I_{12}^{*}>0$ is equivalent to $S_1^{*}>\mu /({\beta }_1+{\beta }_2-{\beta }_{12})=h/(g-1)\in (0,1)$, which is guaranteed by

$$F\left(\frac{h}{g-1}\right)=\frac{g(h-(g-1){\upsilon }_1)(h-(g-1){\upsilon }_2)}{{(g-1)}^2}>0=F(S_1^{*})\text{ and }h<(g-1){\upsilon }_1\le (g-1){\upsilon }_2.$$

Consequently, if ℛ₁₀ > 1 and ℛ₂₀ > 1, then (2.1) has a unique endemic equilibrium

$$E_{12}=(S^{*},I_1^{*},I_2^{*},I_{12}^{*})=(S^{*},\frac{1}{{ℛ}_{20}}-S^{*},\frac{1}{{ℛ}_{10}}-S^{*},S^{*}+1-\frac{1}{{ℛ}_{10}}-\frac{1}{{ℛ}_{20}}),$$

where S* ∈ (0, 1) is the unique feasible solution to (3.2).

The spectrum of the Jacobian matrix of system (2.1) at E₁₂ is

$$\{-\mu ,-{\beta }_1+{\rho }_1+\mu ,-{\beta }_2+{\rho }_2+\mu ,-{\beta }_1-{\beta }_2+\mu +{\beta }_{12}-{\beta }_{12}(I_1^{*}+I_2^{*})\}.$$

which means the endemic equilibrium is locally asymptotically stable. It follows from the result on asymptotically autonomous differential equations [56] that E₁₂ is globally attractive. Hence the endemic equilibrium is globally asymptotically stable when it exists.

Remark 3.2

When coinfection is impossible, the competitive exclusion principle holds and the disease with a larger reproduction number must exclude the other [8]. Thus coinfection is a mechanism for the coexistence of multiple agents or pathogens [35].

Remark 3.3

It follows from S* + (υ₁ − S*) + (υ₂ − S*) + (υ₁ − S*)(υ₂ − S*)/S* ≤ 1 and (3.1) that min{υ₁, υ₂} > S* ≥ υ₁υ₂,$I_1^{*}\le (1-{\upsilon }_1){\upsilon }_2,I_2^{*}\le (1-{\upsilon }_2){\upsilon }_1$, and $I_{12}^{*}\ge (1-{\upsilon }_1)(1-{\upsilon }_2)$. Both the uninfected population and the coinfected population are increasing in the cotransmission rate. Indeed, differentiating F(S*) = 0 with respect to β₁₂ gives

$$\frac{\partial S^{*}}{\partial {\beta }_{12}}=\frac{g{\upsilon }_1{\upsilon }_2+(1-{\upsilon }_1-{\upsilon }_2)h-(g-h)S^{*}}{(2S^{*}-({\upsilon }_1+{\upsilon }_2+g-1-h)){\beta }_{12}}=\frac{{(S^{*})}^2-({\upsilon }_1+{\upsilon }_2-1)S^{*}}{(({\upsilon }_1-S^{*})+({\upsilon }_2-S^{*})+(g-1-h)){\beta }_{12}}>\frac{({\upsilon }_1{\upsilon }_2-({\upsilon }_1+{\upsilon }_2-1))S^{*}{\beta }_{12}^{-1}}{({\upsilon }_1-S^{*})+({\upsilon }_2-S^{*})+(g-1-h)}=\frac{(1-{\upsilon }_1)(1-{\upsilon }_2)S^{*}{\beta }_{12}^{-1}}{({\upsilon }_1-S^{*})+({\upsilon }_2-S^{*})+(g-1-h)}>0.$$

and $I_{12}^{*}=S^{*}+1-{\upsilon }_1-{\upsilon }_2$ implies that $\frac{\partial I_{12}^{*}}{\partial {\beta }_{12}}=\frac{\partial S^{*}}{\partial {\beta }_{12}}>0$.

In the setting of multiple diseases, we may treat the entire population (mass treatment, ρ_i → ρ_i + θ for any i), or only a fraction of people infected by a specific disease (targeted treatment, ρ_i → ρ_i + θ_i for some i). Under both treatment strategies, it is shown that for model (2.1) with the restriction (H) the uninfected population is always increased by choosing a higher treatment rate; this differs from the two-disease model we studied in [17].

Corollary 3.4

For system (2.1) under assumption (H), the fraction of susceptible, S*, is always increasing in the mass treatment rate θ (or targeted treatment rate θ_i).

Proof

If β₁₂ = 0, then under the mass treatment and targeted treatment we have

$$\frac{\partial S^{*}}{\partial \theta }=\frac{({\beta }_1+{\beta }_2)({\rho }_1+{\rho }_2+2\theta +\mu )}{{\beta }_1{\beta }_2({\beta }_1+{\beta }_2-\mu )}\text{ and }\frac{\partial S^{*}}{\partial {\theta }_i}=\frac{{\beta }_i({\rho }_j+\mu )+{\beta }_j{\rho }_j}{{\beta }_1{\beta }_2({\beta }_1+{\beta }_2-\mu )},i\ne j,i,j=1,2,$$

respectively. Now assume that β₁₂ > 0 and υ₁ ≥ υ₂, it follows from the differentiation of F(S*) = 0 with respect to targeted treatment rate θ_i or mass treatment rate θ that

$$\frac{\partial S^{*}}{\partial {\theta }_i}=\frac{(S^{*}-g{\upsilon }_j+h){\beta }_i^{-1}}{2S^{*}-({\upsilon }_1+{\upsilon }_2+g-1-h)}=\frac{(({\upsilon }_j-S^{*})+({\upsilon }_j(g-1)-h)){\beta }_i^{-1}}{({\upsilon }_1-S^{*})+({\upsilon }_2-S^{*})+(g-1-h)}>0$$

and

$$\frac{\partial S^{*}}{\partial \theta }=\frac{S^{*}-g({\rho }_1+\theta +\mu +{\rho }_2+\theta +\mu )/({\beta }_1+{\beta }_2)+h}{2S^{*}-({\upsilon }_1+{\upsilon }_2+g-1-h)}·(\frac{1}{{\beta }_1}+\frac{1}{{\beta }_2})>\frac{S^{*}-g{\upsilon }_1+h}{2S^{*}-({\upsilon }_1+{\upsilon }_2+g-1-h)}·(\frac{1}{{\beta }_1}+\frac{1}{{\beta }_2})>0.$$

The last inequality holds because of S* − gυ₁ + h < 0 and 2S* − (υ₁ + υ₂ + g − 1 − h) < 0.

4 Interacting transmission

In the rest of the paper, we remove the requirement (H), namely, β₁₂ + β₁₀ ≠ β₁ or β₁₂ + β₀₂ ≠ β₂. Biologically, this means that a dually-infected individual may transmit each agent either more or less efficiently than a person infected with each agent singly. Three possible scenarios are listed as follows:

1. Mutual enhancement: β₁₂ + β₁₀ > β₁ and β₁₂ + β₀₂ > β₂;

2. Enhancement and inhibition: β₁₂ + β₁₀ > β₁ and β₁₂ + β₀₂ < β₂, or β₁₂ + β₁₀ < β₁ and β₁₂ + β₀₂ > β₂;

3. Mutual inhibition: β₁₂ + β₁₀ < β₁ and β₁₂ + β₀₂ < β₂.

The dynamics are simple equilibrium if the double infection has mild impact on the transmission of one of the two infections. The following proof utilizes the theory of monotone dynamical systems [52], simplfying the proof of Theorem 3.1.

Proposition 4.1

Assume that dual infection has no impact on the transmission of the first disease, i.e., β₁₂ + β₁₀ = β₁. For system (2.1), every orbit with initial value in Ω converges to an equilibrium.

Proof

The assumption β₁₂ + β₁₀ = β₁ implies that I₁(t) + I₁₂(t) → max{0, 1 − 1/ℛ₁₀} as t → ∞ for I₁(0) + I₁₂(0) > 0. If ℛ₁₀ ≤ 1, then either E₀ or E₂ is globally stable. If ℛ₁₀ > 1, then I₁(t) + I₁₂(t) → 1 − 1/ℛ₁₀ and S(t) + I₂(t) → 1/ℛ₁₀ as t → ∞. Thus, the 4-dimensional system (2.1) can be reduced to a 2-dimensional system in I₁ and I₂. Denote the Jacobian matrix of this two-dimensional system by J₂ = (a_ij)_2×2, where

$$a_{12}=-({\beta }_1-{\beta }_{12})(1-1/{ℛ}_{10})-({\beta }_2+{\beta }_{12})I_1<0\text{ and }{a}_{21}=-{\rho }_1-(1/{ℛ}_{10}-I_2){\beta }_{02}<0.$$

Thus, the reduced 2-dimensional system is competitive. By Theorem 3.2.2 in Smith [52], every orbit converges to an equilibrium.

The stability analysis for system (2.1) now becomes more complicated, and we need to introduce a new threshold parameter—the invasion reproduction number, which is used to measure the ability of one disease to invade an equilibrium of the other disease [42, 35, 60]. We now assume that the equilibrium E₁ exists, or equivalently, ℛ₁₀ > 1. Using the next generation matrix method [14, 15, 58], the vectors for the rate of the appearance of new infections by disease two and the rate of transfer of individuals are, respectively,

$${ℱ}_2(I_2,I_{12})=\left(\begin{array}{c}\hfill ({\lambda }_2+{\lambda }_{12\to 2})\overline{S}\hfill \\ \hfill {\lambda }_{12\to 12}\overline{S}+{\lambda }_2{Ī}_1+({\lambda }_{12\to 2}+{\lambda }_{12\to 12}){Ī}_1\hfill \end{array}\right),$$

$${𝒱}_2(I_2,I_{12})=\left(\begin{array}{c}\hfill ({\lambda }_1+{\lambda }_{12\to 1}+{\lambda }_{12\to 12}){Ī}_2-({\rho }_1{Ī}_{12}-{\rho }_2{Ī}_2)+\mu {Ī}_2\hfill \\ \hfill -{\lambda }_1{Ī}_2-({\lambda }_{12\to 1}+{\lambda }_{12\to 12}){Ī}_2+({\rho }_1+{\rho }_2){Ī}_{12}+\mu {Ī}_{12}\hfill \end{array}\right),$$

where (S̄, Ī₁) = (1/ℛ₁₀, 1 − 1/ℛ₁₀). The derivatives of ℱ₂ and 𝒱₂ at (I₂, I₁₂) = (0, 0) are, respectively,

$$F_2=D{ℱ}_2(0,0)=\left(\begin{array}{cc}\hfill {\beta }_2\overline{S}\hfill & \hfill {\beta }_{02}\overline{S}\hfill \\ \hfill {\beta }_2{Ī}_1\hfill & \hfill {\beta }_{12}\overline{S}+({\beta }_{12}+{\beta }_{02}){Ī}_1\hfill \end{array}\right),$$

$$V_2=D{𝒱}_2(0,0)=\left(\begin{array}{cc}\hfill {\beta }_1{Ī}_1+{\rho }_2+\mu \hfill & \hfill -{\rho }_1\hfill \\ \hfill -{\beta }_1{Ī}_1\hfill & \hfill {\rho }_1+{\rho }_2+\mu \hfill \end{array}\right).$$

The characteristic polynomial of the matrix $F_2{V}_2^{-1}$ is A₂λ² + A₁λ + A₀ = 0, where

$$A_2=({\beta }_1+{\rho }_2)({\rho }_2+\mu ),A_0={\beta }_2{\beta }_{12}({\rho }_1+\mu )/{\beta }_1,$$

$$A_1=-({\beta }_2\overline{S}({\rho }_1+{\rho }_2+\mu )+{\beta }_{02}\overline{S}{\beta }_1{Ī}_1+{\beta }_2{Ī}_1{\rho }_1+({\beta }_{12}\overline{S}+({\beta }_{12}+{\beta }_{02}){Ī}_1)({\beta }_1{Ī}_1+{\rho }_2+\mu ))=-({\beta }_{12}+{\beta }_{02}){\beta }_1+(({\beta }_{12}+{\beta }_{02})({\rho }_1-{\rho }_2)-{\beta }_2{\rho }_1)+({\beta }_{02}-{\beta }_2)({\rho }_1+\mu )({\rho }_2+\mu )/{\beta }_1<0.$$

The invasion reproduction number of disease 2, denoted by ${ℛ}_2^1$, is given by the spectral radius of the non-negative matrix $F_2{V}_2^{-1}$, i.e.,

$${ℛ}_2^1=\rho (F_2{V}_2^{-1})=\frac{-A_1+\sqrt{A_1^2-4A_0{A}_2}}{2A_2}>0.$$

It follows from A₀ > 0 that the characteristic equation has two positive roots as β₁₂ > 0. If β₁₂ = 0 then A₀ = 0 and ${ℛ}_2^1=-A_1/A_2$.

Similarly, we can derive a formula for the invasion reproduction number of disease 1, denoted by ${ℛ}_1^2$. By Theorem 2 in van den Driessche and Watmough [58], disease 1 can invade disease 2 if ${ℛ}_1^2>1$ and disease 2 can invade disease 1 if ${ℛ}_2^1>1$ (see Appendix A for a direct proof).

Proposition 4.2

For system (2.1), when the equilibrium E₁ exists (i.e., ℛ₁₀ > 1), it is locally asymptotically stable if ${ℛ}_2^1<1$ and unstable if ${ℛ}_2^1>1$. Symmetrically, the equilibrium E₂ is locally asymptotically stable if ${ℛ}_1^2<1$ and unstable if ${ℛ}_1^2>1$.

Define ℛ̃₂₀ = (β₁₂ + β₀₂)/(ρ₂ + μ); this quantity, analogous to a basic reproduction number, is the number of cases of disease 2 resulting from the introduction of a dually infected person into a wholly susceptible population. We can establish the lower and upper bounds for the invasion reproduction number ${ℛ}_2^1$.

Proposition 4.3

Assume that E₁ exists, or equivalently, ℛ₁₀ > 1. Then the following statements are valid:

1. ${\widetilde{ℛ}}_{20}<{ℛ}_2^1<{ℛ}_{20}$ if and only if β₂ > β₁₂ + β₀₂;

2. ${\widetilde{ℛ}}_{20}>{ℛ}_2^1>{ℛ}_{20}$ if and only if β₂ < β₁₂ + β₀₂;

3. ${\widetilde{ℛ}}_{20}={ℛ}_2^1={ℛ}_{20}$ if and only if β₂ = β₁₂ + β₀₂.

Proof

${ℛ}_{20}-{ℛ}_2^1$ has the same sign as β₂ − β₁₂ − β₀₂. In fact, we can rewrite ${ℛ}_{20}<{ℛ}_2^1$ as

$$\frac{{\beta }_2}{{\rho }_2+\mu }<\frac{-A_1+\sqrt{A_1^2-4A_0{A}_2}}{2A_2}\iff 2{\beta }_2{A}_2+({\rho }_2+\mu )A_1<({\rho }_2+\mu )\sqrt{A_1^2-4A_0{A}_2}.$$

If G ≡ 2β₂A₂ + (ρ₂ + μ)A₁ ≥ 0, then ${ℛ}_{20}<{ℛ}_2^1$ is equivalent to

$$4{\beta }_2^2{A}_2^2+4{\beta }_2({\rho }_2+\mu )A_1{A}_2+{({\rho }_2+\mu )}^2{A}_1^2<{({\rho }_2+\mu )}^2{A}_1^2-4{({\rho }_2+\mu )}^2{A}_0{A}_2\iff 4A_2(A_2{\beta }_2^2+A_1{\beta }_2({\rho }_2+\mu )+A_0{({\rho }_2+\mu )}^2)<0\iff {\beta }_2({\beta }_2-{\beta }_{12}-{\beta }_{02})({\beta }_1-{\rho }_1-\mu )({\rho }_2+\mu )({\beta }_1+{\rho }_2+\mu )<0\iff {\beta }_2<{\beta }_{12}+{\beta }_{02}.$$

If G < 0, then G = (ρ₂ + μ)(G₀ + (β₂ − β₁₂ − β₀₂)G₁) where

$$G_0=[{\beta }_1{\beta }_{02}({\beta }_1+{\rho }_2)+{\beta }_{12}({\beta }_1({\beta }_1+{\rho }_2)-({\rho }_1+\mu )({\rho }_2+\mu ))]/{\beta }_1,$$

$$G_1=2({\beta }_1+{\rho }_2)-{\rho }_1-({\rho }_1+\mu )({\rho }_2+\mu )/{\beta }_1.$$

Note that G₀ > 0 and G₁ > 0 when ℛ₁₀ > 1. If β₂ ≥ β₁₂ + β₀₂ then G > 0, a contradiction.

On the other hand, ${\widetilde{ℛ}}_{20}<{ℛ}_2^1$ is equivalent to

$$A_2{({\beta }_{12}+{\beta }_{02})}^2+A_1({\beta }_{12}+{\beta }_{02})({\rho }_2+\mu )+A_0{({\rho }_2+\mu )}^2<0\iff ({\beta }_{12}+{\beta }_{02}-{\beta }_2)({\rho }_2+\mu )({\mu }^2{\beta }_{02}+\mu {\beta }_{02}({\rho }_1+{\rho }_2)+{\rho }_1({\beta }_1({\beta }_{12}+{\beta }_{02})+{\beta }_{02}{\rho }_2))<0\iff {\beta }_{12}+{\beta }_{02}<{\beta }_2.$$

This completes the proof.

Therefore, it is possible that ${ℛ}_{20}<1<{ℛ}_2^1$ as β₂ < β₁₂ + β₀₂. Moreover, we will show that the second disease may be able to invade in the presence of the first disease even if it cannot persist alone. That is, the presence of the first disease promotes persistence of the second disease. Similar to the model in Martcheva and Pilyugin [35], we can obtain the following result about the consequence of competition.

Proposition 4.4

For system (2.1), if ℛ̃₁₀ ≤ 1 or ℛ̃₂₀ ≤ 1 and ℛ₁₀ ≤ 1, ℛ₂₀ ≤ 1, then both diseases go extinct and the disease-free equilibrium is globally stable; if max{ℛ₁₀, ℛ̃₁₀} ≤ 1 (or max{ℛ₂₀, ℛ̃₂₀} ≤ 1) then disease 1 (or 2) goes extinct; if min{ℛ₁₀, ℛ̃₁₀} > 1 (or min{ℛ₂₀, ℛ̃₂₀} > 1) then disease 1 (or 2) persists.

Proof

It follows from the second and fourth equations of system (2.1) that

$$\frac{d(I_1+I_{12})}{dt}=-({\rho }_1+\mu )(I_1+I_{12})+({\beta }_{12}{I}_{12}+{\beta }_{10}{I}_{12}+{\beta }_1{I}_1)(S+I_2)$$

and hence

$$\frac{d(I_1+I_{12})}{dt}\le (\text{max}\{{\beta }_{12}+{\beta }_{10},{\beta }_1\}-({\rho }_1+\mu ))(I_1+I_{12})-\text{max}\{{\beta }_{12}+{\beta }_{10},{\beta }_1\}{(I_1+I_{12})}^2,$$

$$\frac{d(I_1+I_{12})}{dt}\ge (\text{min}\{{\beta }_{12}+{\beta }_{10},{\beta }_1\}-({\rho }_1+\mu ))(I_1+I_{12})-\text{min}\{{\beta }_{12}+{\beta }_{10},{\beta }_1\}{(I_1+I_{12})}^2.$$

By a simple comparison principle [53], we get

$$\underset{t\to \infty }{\text{lim sup}}(I_1+I_{12})\le \text{max}\{1-\frac{{\rho }_1+\mu }{\text{max}\{{\beta }_1,{\beta }_{12}+{\beta }_{10}\}},0\},$$

$$\underset{t\to \infty }{\text{lim inf}}(I_1+I_{12})\ge \text{max}\{1-\frac{{\rho }_1+\mu }{\text{min}\{{\beta }_1,{\beta }_{12}+{\beta }_{10}\}},0\}$$

if I₁(0) + I₁₂(0) > 0.

Remark 4.5

A necessary condition for the existence of a coexistence equilibrium $E^{*}=(S^{*},I_1^{*},I_2^{*},I_{12}^{*})$ is that max{ℛ_i0, ℛ̃_i0} > 1 for i = 1, 2. When E* exists, it satisfies

$$1-\frac{{\rho }_1+\mu }{\text{min}\{{\beta }_1,{\beta }_{12}+{\beta }_{10}\}}\le I_1^{*}+I_{12}^{*}\le 1-\frac{{\rho }_1+\mu }{\text{max}\{{\beta }_1,{\beta }_{12}+{\beta }_{10}\}},$$

$$1-\frac{{\rho }_2+\mu }{\text{min}\{{\beta }_2,{\beta }_{12}+{\beta }_{02}\}}\le I_2^{*}+I_{12}^{*}\le 1-\frac{{\rho }_2+\mu }{\text{max}\{{\beta }_2,{\beta }_{12}+{\beta }_{02}\}}.$$

The above result indicates that the two diseases coexist whenever min{ℛ_i0, ℛ̃_i0} > 1, i = 1, 2. By a similar argument to that of Theorem 2.5 in Gao and Ruan [18], we will show that it remains true under a weaker condition: $\text{min}\{{ℛ}_{i0},{ℛ}_i^j\}>1$, i ≠ j, i, j = 1, 2.

Theorem 4.6

For model (2.1), if

$${ℛ}_{10}>1,{ℛ}_{20}>1,{ℛ}_1^2>1\mathit{\text{ and }}{ℛ}_2^1>1,$$ (4.1)

then (2.1) admits at least one coexistence equilibrium and both diseases are uniformly persistent, i.e., there is a constant κ > 0 such that each solution φ_t(x₀) ≡ (S(t), I₁(t), I₂(t), I₁₂(t)) of system (2.1) with x₀ ≡ (S(0), I₁(0), I₂(0), I₁₂(0)) ∈ Ω₀ ≡ {(S, I₁, I₂, I₁₂) ∈ Ω : I₁I₂ > 0 or I₁₂ > 0} satisfies

$$\underset{t\to \infty }{\text{lim inf }}{I}_1(t)>\kappa ,\underset{t\to \infty }{\text{ lim inf }}{I}_2(t)>\kappa \mathit{\text{ and }}\underset{t\to \infty }{\text{lim inf }}{I}_{12}(t)>\kappa .$$

Proof

Denote ∂Ω₀ = Ω\Ω₀ = {(S, I₁, I₂, I₁₂) ∈ Ω : I₁ = 0 or I₂ = 0, I₁₂ = 0}. It is sufficient to show that system (2.1) is uniformly persistent with respect to (Ω₀, ∂Ω₀). Obviously, ∂Ω₀ is relatively closed in Ω. It is clear that Ω and Ω₀ are positively invariant and system (2.1) is point dissipative.

Let M_∂ = {x₀ ∈ ∂Ω₀ : φ_t(x₀) ∈ ∂Ω₀ for t ≥ 0}. Therefore, M_∂ = ∂Ω₀. The boundary equilibria E₀, E₁ and E₂ are in M_∂. Let W^s(E_i) be the stable manifold of E_i for i = 0, 1, 2. We will show that W^s(E_i) ∩ Ω₀ = ∅ whenever (4.1) holds.

Define

$${ℛ}_1^{\epsilon }=\frac{(1-\epsilon ){\beta }_1}{({\beta }_2+{\beta }_{12}+{\beta }_{02})\epsilon +{\rho }_1+\mu }.$$

It follows from ℛ₁₀ > 1 that there is an ε₀ > 0 such that ${ℛ}_1^{\epsilon }>1$ for ε ∈ [0, ε₀]. Select η₀ small enough such that

$$S(0)\ge 1-{\epsilon }_0\text{ for }\Vert {\mathbf{x}}_0-E_0\Vert \le {\eta }_0.$$

We claim that $\underset{t\to \infty }{\text{lim sup}}\Vert {\varphi }_t({\mathbf{x}}_0)-E_0\Vert >{\eta }_0$ for x₀ ∈ Ω₀, where ‖ · ‖ is the Euclidean norm. Supposing not, then by translation, we have ‖φ_t(x₀) − E₀‖ ≤ η₀ for all t ≥ 0 and hence

$$\frac{d{I}_1}{dt}\ge {\beta }_1(1-{\epsilon }_0)I_1-({\beta }_2+{\beta }_{12}+{\beta }_{02}){\epsilon }_0{I}_1-{\rho }_1{I}_1-\mu I_1=({\beta }_1(1-{\epsilon }_0)-({\beta }_2+{\beta }_{12}+{\beta }_{02}){\epsilon }_0-{\rho }_1-\mu )I_1.$$

By a comparison theorem, I₁(t) → ∞ as t → ∞; the contradiction establishes the result.

To show W^s(E₁) ∩ Ω₀ = ∅, we define

$$\mathrm{\Delta }=\left(\begin{array}{cc}\hfill {\beta }_2+{\beta }_1+2{\beta }_{12}+2{\beta }_{10}\hfill & \hfill {\beta }_{02}\hfill \\ \hfill {\beta }_1+{\beta }_2\hfill & \hfill 2{\beta }_{12}+{\beta }_{02}\hfill \end{array}\right)\text{ and }{M}_{\epsilon }=F_2+V_2-\epsilon \mathrm{\Delta }.$$

Since s(F₂ − V₂) > 0 if and only if ${ℛ}_2^1>1$, there is an ε₁ > 0 such that s(M_ε) > 0 for ε ∈ [0, ε₁]. Recall that (S̄, Ī₁) = (1/ℛ₁₀, 1 − 1/ℛ₁₀). Choose η₁ small enough such that

$$\overline{S}-{\epsilon }_1\le S(0)\le \overline{S}+{\epsilon }_1\text{ and }{Ī}_1-{\epsilon }_1\le I_1(0)\le {Ī}_1+{\epsilon }_1\text{ for }\Vert {\mathbf{x}}_0-E_1\Vert \le {\eta }_1.$$

We claim that $\underset{t\to \infty }{\text{lim sup}}\Vert {\varphi }_t({\mathbf{x}}_0)-E_1\Vert >{\eta }_1$ for x₀ ∈ Ω₀. Supposing not, then again by translation, we have ‖φ_t(x₀) − E₁‖ ≤ η₁ for all t ≥ 0 and hence

$$\frac{d{I}_2}{dt}\ge ({\beta }_2{I}_2+{\beta }_{02}{I}_{12})(\overline{S}-{\epsilon }_1)-({\beta }_1({Ī}_1+{\epsilon }_1)+({\beta }_{12}+{\beta }_{10})2{\epsilon }_1)I_2+({\rho }_1{I}_{12}-{\rho }_2{I}_2)-\mu I_2,$$

$$\frac{d{I}_{12}}{dt}\ge {\beta }_{12}{I}_{12}(\overline{S}-{\epsilon }_1)+({\beta }_1+{\beta }_2)({\overline{I}}_1-{\epsilon }_1)I_2+({\beta }_{12}+{\beta }_{02})I_{12}({\overline{I}}_1-{\epsilon }_1)-({\rho }_1+{\rho }_2+\mu )I_{12}.$$

Notice that M_ε1 has a positive eigenvalue s(M_ε1) associated to a positive eigenvector. It follows from a comparison theorem that I₂(t) → ∞ and I₁₂(t) → ∞ as t → ∞, a contradiction.

Since W^s(E₀) = {E₀}, W^s(E₁) = {(S, I₁, I₂, I₁₂) ∈ Ω : I₁ > 0, I₂ = I₁₂ = 0}, W^s(E₂) = {(S, I₁, I₂, I₁₂) ∈ Ω : I₂ > 0, I₁ = I₁₂ = 0} and M_∂ = W^s(E₀)∪W^s(E₁)∪W^s(E₂), {E₀}, {E₁} and {E₂} are isolated invariant sets and acyclic in M_∂. By Theorem 4.6 in Thieme [57], system (2.1) is uniformly persistent with respect to (Ω₀, ∂Ω₀). Moreover, by Theorem 2.4 in Zhao [62], we know that system (2.1) has an equilibrium $E^{*}=(S^{*},I_1^{*},I_2^{*},I_{12}^{*})$. It is easy to check that E* is a positive equilibrium of system (2.1).

Remark 4.7

Similarly, we can show the uniform persistence of both diseases and the existence of a coexistence equilibrium under the assumption ℛ₁₀ > 1 and ${ℛ}_{20}<1<{ℛ}_2^1$, or ℛ₂₀ > 1 and ${ℛ}_{10}<1<{ℛ}_1^1$. In this case, one disease goes extinct in the absence of the other and the presence of the other disease mediates the coexistence. Control strategies toward a reduction of both infections are favored.

A more detailed classification for the transmission dynamics of the coinfection model (2.1) based on its basic reproduction numbers and invasion reproduction numbers [35] is beyond the scope of current paper. For example, we are particularly interested in the local/global stability of the coexistence equilibrium under conditions in Theorem 4.6, but numerical examples in the next section show that an unstable coexistence equilibrium could present in case of backward bifurcation, bistability or a Hopf bifurcation. This suggests that it is hard to use the well-known Routh-Hurwitz criterion to determine the local stability of the coexistence equilibrium.

5 Numerical Simulations

In this section, we illustrate, by numerical examples, possible phenomena the model of coinfection may exhibit.

Example 5.1. Competitive exclusion

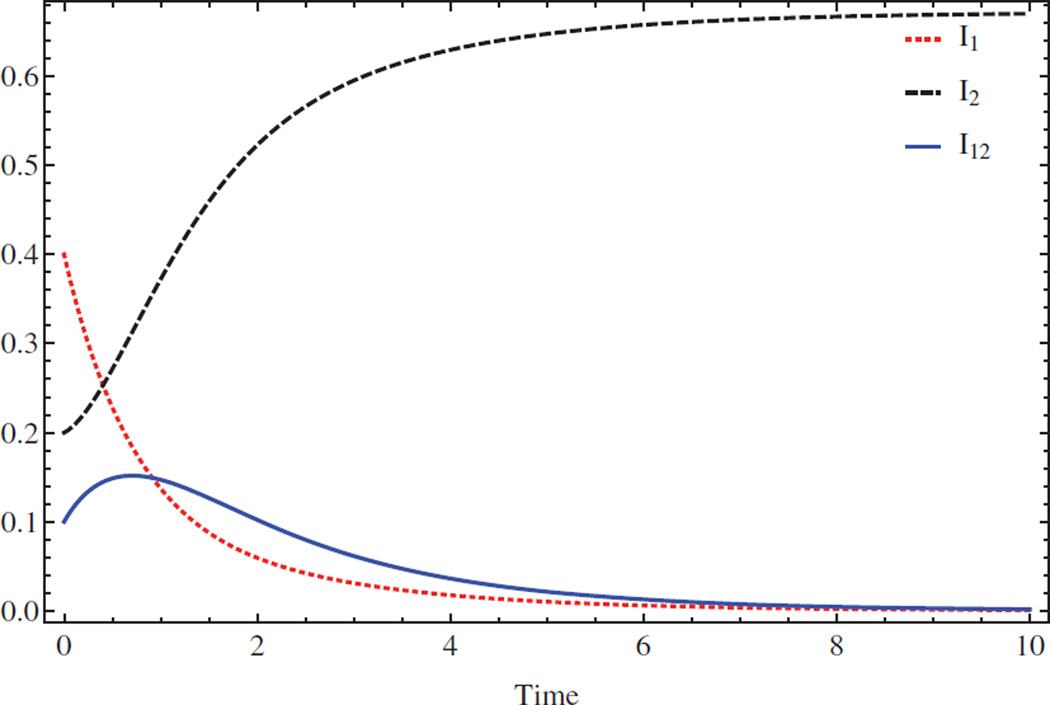
Two diseases cannot coexist even if each one can persist independently. Parameter values: β₁ = 1.05, β₂ = 2.5, ρ₁ = 1, ρ₂ = 0.8, μ = 0.02, β₁₂ = 0.05, β₁₀ = 0.2, β₀₂ = 2. The respective basic reproduction numbers are ℛ₁₀ = 1.0294 > 1 and ℛ₂₀ = 3.0488 > 1. Figure 2 shows that the first disease goes extinct while the second persists. It provides a theoretically plausible treatment strategy for some pathogens: suppose that 1 < ℛ₁₀ < ℛ₂₀, β₁₂ + β₁₀ < β₁ and β₁₂ + β₀₂ < β₂; there is an effective way to treat pathogen 2, but not for pathogen 1. Here, one could in principle introduce pathogen 2 to eradicate pathogen 1.

Figure 2.

Numerical solution of system (2.1) with initial condition (S(0), I₁(0), I₂(0), I₁₂(0)) = (0.3, 0.4, 0.2, 0.1). Red dotted line-I₁, black dashed line-I₂ and solid blue line-I₁₂. Two infections cannot coexist even if each one can survive independently.

Moreover, consider a scenario in which β₁ = 2.9, β₂ = 3, ρ₁ = ρ₂ = μ = 1, β₁₂ = 0.5, β₁₀ = 2, β₀₂ = 0.1; we have ℛ₁₀ = 1.45, ℛ₂₀ = 1.5, ${ℛ}_1^2=1.3612$ and ${ℛ}_2^1=0.9860$. Thus, E₁ is locally stable but E₂ is unstable and there is no coexistence equilibrium. Interestingly, in this case the competitive exclusion principle still holds, but the disease with a higher reproduction number dies out while the other one persists (in contrast with [8]).

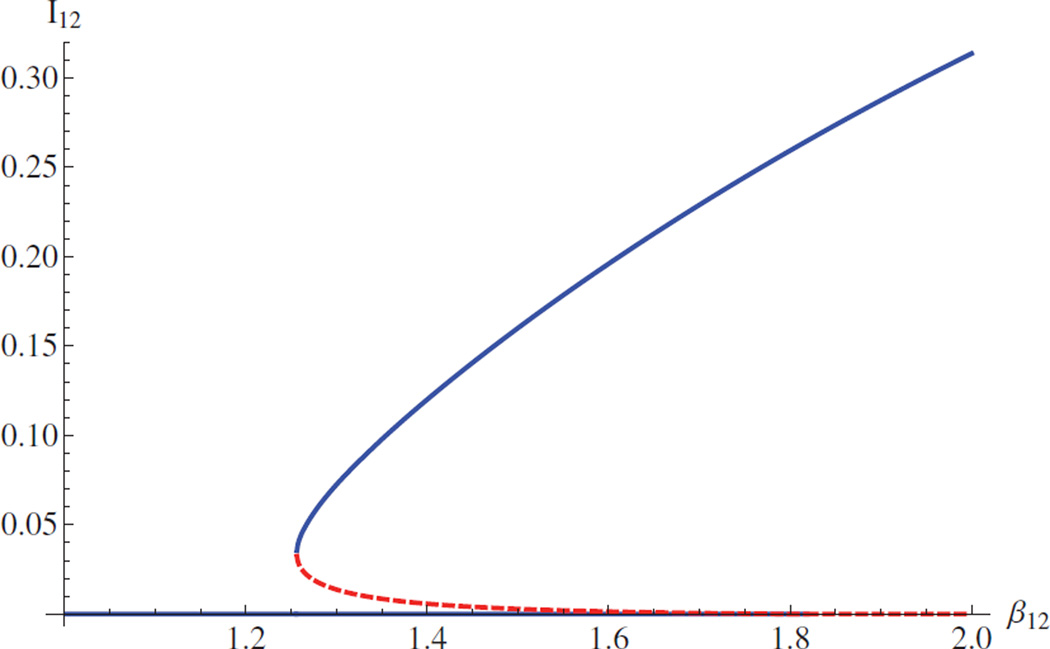
Example 5.2. Backward bifurcation

Assume that ℛ₁₀ < 1 and ℛ₂₀ < 1. If β₁₂ + β₁₀ > β₁ and β₁₂ + β₀₂ > β₂, then it is possible that both diseases become persistent. Parameter values: β₁ = 0.9, β₂ = 0.7, ρ₁ = 1, ρ₂ = 0.8, μ = 0.02, β₁₀ = β₀₂ = 0.6. A bifurcation diagram for model (2.1) shows that the endemic equilibrium value of I₁₂ with respect to β₁₂ is presented in Figure 3. In this setting, there is one stable coexistence equilibrium and one unstable coexistence equilibrium for β₁₂ ∈ (1.256, 1.82). Biologically, this means that a small perturbation in model parameters or initial conditions may lead to a large difference in the dynamic behavior of the disease. The occurrence of backward bifurcation precludes, in general, the global stability of the disease-free equilibrium as ℛ₀ < 1. Note that backward bifurcation still exists even if there is no cotransmission (β₁₂ = 0).

Figure 3.

Backward bifurcation arising from the change of β₁₂. Blue solid line-stable, red dashed line-unstable. Two diseases can coexist even if each one dies out independently.

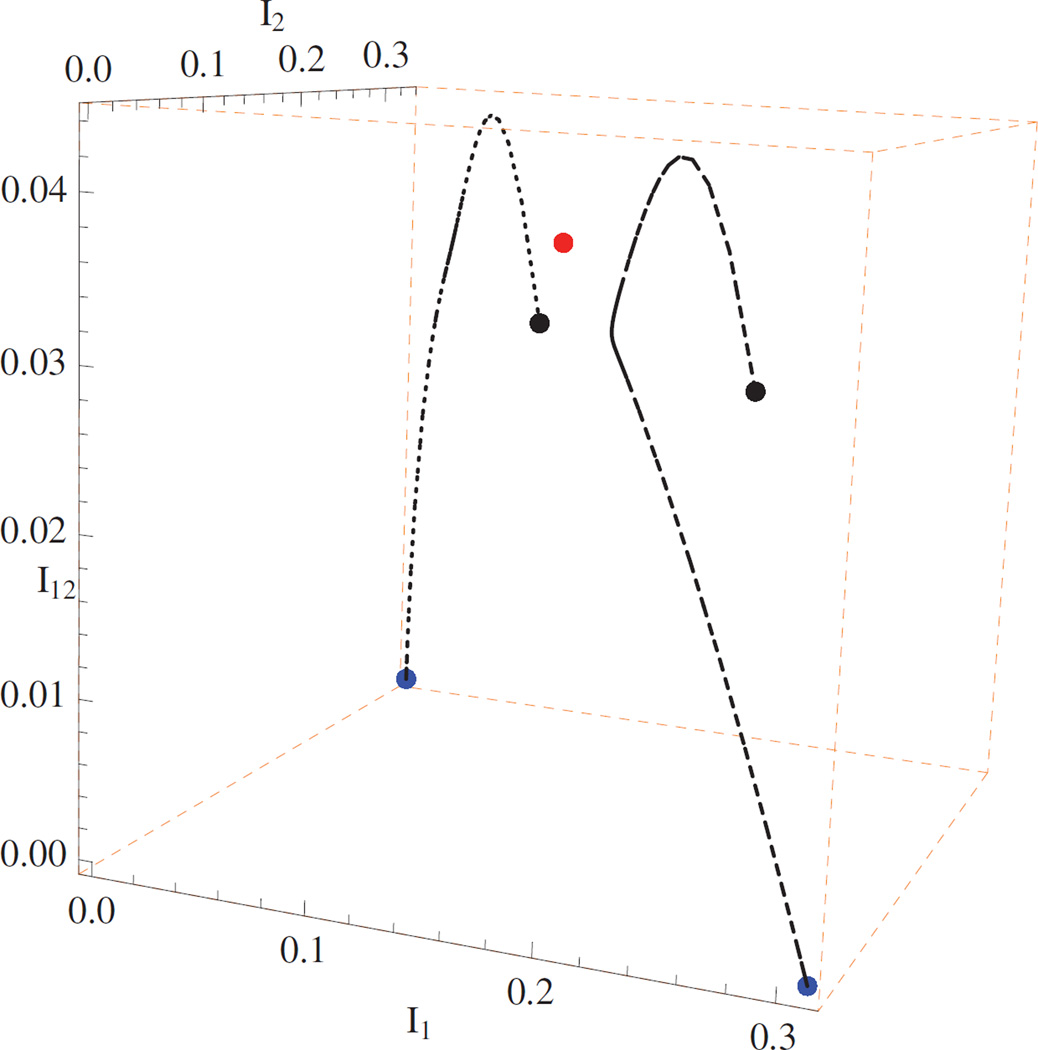
Example 5.3. Bistability (ℛ₁₀ > 1, ℛ₂₀ > 1, ${ℛ}_1^2<1$ and ${ℛ}_2^1<1$)

The two boundary equilibria E₁ and E₂ are locally stable, while the coexistence equilibrium E* is unstable. Parameter setting: β₁ = 2.9, β₂ = 3, ρ₁ = ρ₂ = μ = 1, β₁₂ = 0.5, β₁₀ = 0.3, β₀₂ = 0.05. Direct calculations yield the basic reproduction numbers ℛ₁₀ = 1.45, ℛ₂₀ = 1.5 and the invasion reproduction numbers ${ℛ}_1^2=0.9714,{ℛ}_2^1=0.9747$. A bistability phenomenon is observed in Figure 4. The disease outcome depends on initial conditions and there exists a smooth surface separating the feasible region into two domains.

Figure 4.

Numerical solutions of system (2.1) with initial conditions: (0.62, 0.25, 0.1, 0.03) and (0.62, 0.1, 0.25, 0.03) (black dots). Bistability: the two boundary equilibria E₁ = (20/29, 9/29, 0, 0) and E₂ = (2/3, 0, 1/3, 0) (blue dots) are locally stable, and the coexistence equilibrium E* ≈ (0.701, 0.165, 0.096, 0.038) (red dot) is unstable.

The occurrence of bistability also implies that the infection with a higher reproduction number is not necessarily the winner, so to speak, of the competition. In addition, there is no bistability phenomenon when the mortality rate μ is small enough (see Appendix B for a proof). Namely, if ℛ₂₀ > max{ℛ₁₀, 1}, then the second disease always persists as μ → 0.

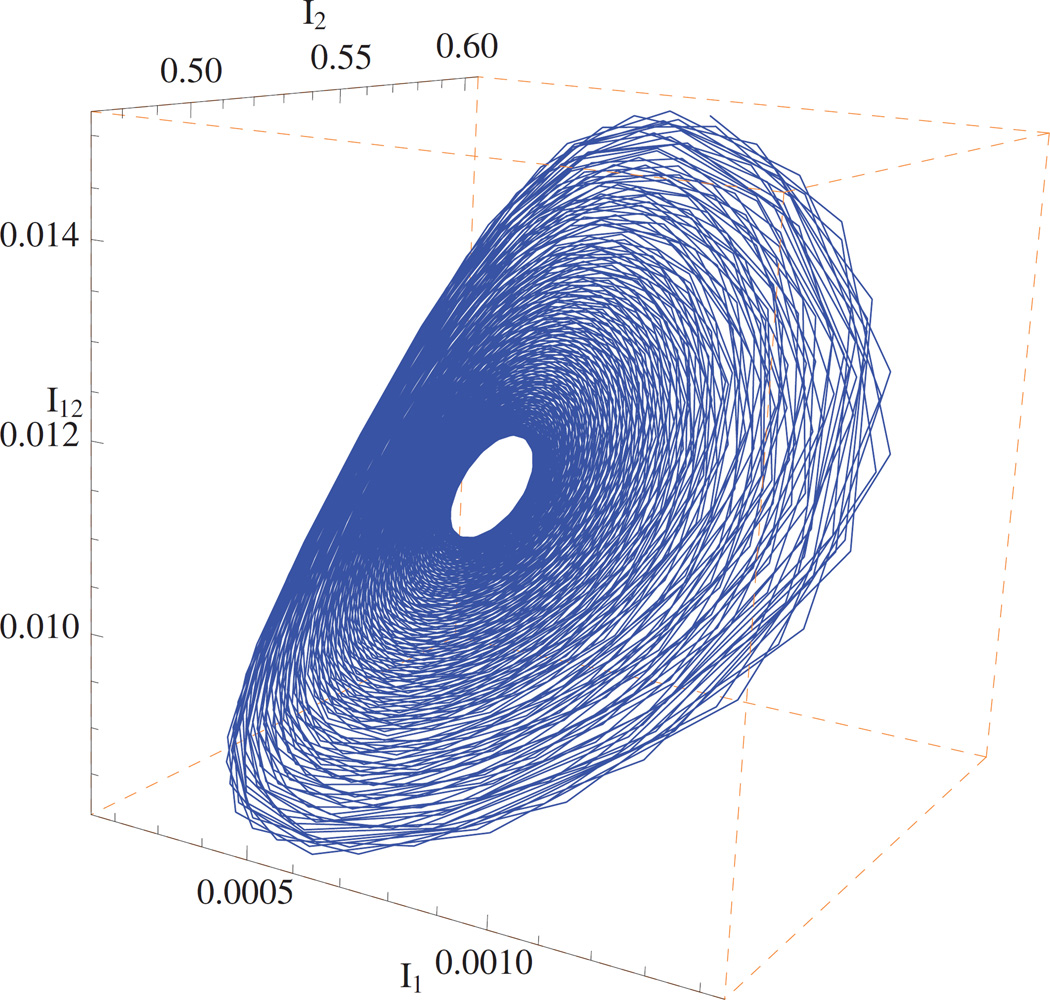
Example 5.4. Hopf bifurcation

The model can exhibit non-equilibrium dynamical behavior—periodic oscillations under certain conditions. Set β₁ = 5, β₂ = 0.2, ρ₁ = ρ₂ = 0, μ = 1, β₁₂ = 0.805, β₁₀ = 0 and β₀₂ ∈ [70, 100]. It follows from ℛ₁₀ = 5 > 1 > ℛ₂₀ = 0.2 and ${ℛ}_2^1\gg 1$ that both diseases are uniformly persistent and there is a coexistence equilibrium (see Remark 4.7). The Jacobian matrix at the coexistence equilibrium has a pair of complex eigenvalues with negative real parts as β₀₂ ∈ [70, 84.74), a pair of purely imaginary eigenvalues as β₀₂ ≈ 84.74, and a pair of complex eigenvalues with positive real parts as β₀₂ ∈ (84.74, 100]. Therefore, the coexistence equilibrium loses its stability and a Hopf bifurcation appears (see Figure 5). For sufficiently small but nonzero ρ₁, ρ₂ and β₁₀, the system still has a Hopf bifurcation.

Figure 5.

Hopf bifurcation-two diseases coexist in an oscillatory mode.

6 Discussion

In this paper, we proposed a simple two-disease SIS coinfection model featuring simultaneous transmission of infection due to contacts with dually infected individuals, as well as superinfection leading to dual infection. In our model, there are four epidemiological classes: susceptible to both diseases, susceptible to disease 2 but infectious for disease 1, susceptible to disease 1 but infectious for disease 2, and infectious for both diseases. It is a simplified version of the two-disease three-strain model in Gao et al. [17] in which the first disease exhibits both drug sensitive and resistant strains. The cotransmission dynamics of two diseases modeled as a SIS process is of interest as a simplified model of, for instance, ocular chlamydia [33, 32, 34] and respiratory pneumococcal colonization [36]. In hyperendemic trachoma regions, both organisms are common and both are affected by trachoma control programs [24].

We considered the case for which the transmission of the first disease is completely unaffected by the presence of the second; that is, when coinfected people transmit infection to the same degree as singly infected people, disease dynamics are completely determined by the basic reproduction numbers of each. The two diseases coexist at an endemic level as long as they can persist independently. However, if the assumption does not hold, then we calculated the invasion reproduction number to measure the ability of one disease to invade the other at its steady state. The relation between the basic reproduction number and the invasion reproduction number was investigated, and sufficient conditions for the persistence of both diseases were obtained. Using numerical methods, more complicated dynamics including backward bifurcation, bistability and Hopf bifurcation were found. The disease with smaller reproduction number may be able to invade and competitively exclude the other disease even if there is no coexistence steady state. It is noteworthy that some of these dynamical behaviors have been observed in previous studies based on different models [7, 35, 60, 61]. Our study provides some more advanced theoretical results on the stability and persistence of a reasonable coinfected model. The results throughout this paper for one disease also holds for the other due to the symmetry of the model. Note that some of our analytical results are applicable to models of coinfection by different parasites (e.g. [54, 4, 3]) where there is no recovery (ρ₁ = ρ₂ = 0).

It is well known that, for a simple SIS epidemic model, the disease goes extinct if the basic reproduction number is less than unity and persists at a unique endemic equilibrium otherwise. Our analysis shows that the disease dynamics become more complicated in the presence of a second disease. For instance, the presence of coinfection could mediate coexistence despite that fact that one or both diseases could not survive independently. Different types of interaction in dually infected hosts can yield different outcomes. These findings emphasize the importance of understanding the interactions among pathogens and developing a multi-disease approach in the treatment of coinfected patients.

A complete classification of the model studied here is not yet available. For example, we would like to know how to rigorously prove the existence of Hopf bifurcations and whether a Hopf bifurcation is impossible for small death rate. It will be interesting to analyze our model from the perspective of evolutionary epidemiology [45, 10, 3, 4]. The current model may be extended to other natural history models, such as the SEIR assumption, or include three or more agents/strains [61]. There may be partial cross-immunity or enhanced susceptibility to either of the two infections [28]. Coinfected patients may have more serious illness and take a longer time to recover. In general, treatment of one infection in a doubly infected person may affect the other infection directly or indirectly (e.g. [50, 25, 44, 51]). We will leave these for future consideration.

Appendix

A. The equivalence between s(F₂ − V₂) < 0 and ${ℛ}_2^1<1$

As we know, the boundary equilibrium E₁ is locally asymptotically stable if and only if all eigenvalues of the Jacobian matrix F₂ − V₂ have negative real parts. This is also equivalent to ${ℛ}_2^1<1$ by Theorem 2 in van den Driessche and Watmough [58]. Here we provide a direct proof. For simplicity, we consider two matrices

$$F_2=\left(\begin{array}{cc}\hfill a\hfill & \hfill b\hfill \\ \hfill c\hfill & \hfill d\hfill \end{array}\right)\text{ and }{V}_2=\left(\begin{array}{cc}\hfill h\hfill & \hfill -i\hfill \\ \hfill -j\hfill & \hfill k\hfill \end{array}\right)$$

satisfying a, b, c, d, h, i, j, k ≥ 0 and hk − ij > 0. The characteristic polynomial of the matrix F₂ − V₂ is

$${\lambda }^2+(h-a+k-d)\lambda +(h-a)(k-d)-(b+i)(c+j)=0.$$

By the Routh-Hurwitz criterion, the spectral bound s(F₂ − V₂) < 0 if and only if

$$h-a+k-d>0,$$ (6.1a)

$$(h-a)(k-d)-(b+i)(c+j)>0.$$ (6.1b)

Meanwhile, the characteristic polynomial of the matrix $F_2{V}_2^{-1}$ is A₂λ² + A₁λ + A₀ = 0, where

$$A_2=hk-ij>0,A_1=-(ak+bj+ci+dh),A_0=ad-bc.$$

Then ${ℛ}_2^1=\rho (F_2{V}_2^{-1})<1$ if and only if

$$2A_2+A_1=2(hk-ij)-(ak+bj+ci+dh)>0,$$ (6.2a)

$$A_2+A_1+A_0=(hk-ij)+(ad-bc)-(ak+bj+ci+dh)>0.$$ (6.2b)

Note that (6.1b) is the same as (6.2b). It suffices to show that (6.1) implies (6.2a) and (6.2) implies (6.1a), respectively.

It follows from (6.1) that h > a and k > d. Thus

$$2A_2+A_1=hk+(h-a+a)(k-d+d)-2ij-(ak+bj+ci+dh)=hk+(h-a)(k-d)+(h-a)d+a(k-d)+ad-2ij-(ak+bj+ci+dh)>hk+(b+i)(c+j)+(h-a)d+a(k-d)+ad-2ij-(hk-ij)-(ad-bc)=bj+ci+(h-a)d+a(k-d)\ge 0.$$

On the other hand, suppose that h − a + k − d ≤ 0, then (6.1b) or (6.2b) implies that h < a and k < d. We obtain

$$2A_2+A_1<2(hk-ij)-(hk+bj+ci+kh)=-2ij-bj-ci\le 0,$$

a contradiction. The proof is complete.

B. The nonexistence of bistability for small μ

If ℛ₂₀ > max{ℛ₁₀, 1}, then the second disease always persists for sufficiently small μ. We only need to show the instability of the equilibrium E₁ when it exists. In fact, E₁ is locally asymptotically stable if and only if s(F₂ −V₂) < 0. The characteristic equation of F₂ − V₂ is β₁λ² + C₁(β₁)λ + C₀(β₁) = 0, where

$$C_1({\beta }_1)={\beta }_1^2+{\beta }_1(2{\rho }_2+\mu -{\beta }_{12}-{\beta }_{02})-({\beta }_2-{\beta }_{02})({\rho }_1+\mu )\text{ and }{C}_0({\beta }_1)=a_2{\beta }_1^2+a_1{\beta }_1+a_0.$$

Here a₂ = ρ₂ + μ − β₁₂ − β₀₂, $a_1=-{\beta }_2{\rho }_1+({\beta }_{12}+{\beta }_{02})({\rho }_1-{\rho }_2)+\mu {\rho }_2+{\rho }_2^2$, and a₀ = −(ρ₁ + μ)(β₂(ρ₂ + μ − β₁₂) − β₀₂(ρ₂ + μ)).

Thus, by the Routh-Hurwitz stability criterion, E₁ is locally stable if C₁ > 0 and C₀ > 0. In particular, if β₁₂ = 0 then E₁ is locally stable if C₀ > 0 (by Appendix A). For the instability of the equilibrium E₁, It suffices to show that C₀ < 0 in case of ℛ₁₀ > 1 and β₁₂ + β₀₂ < ρ₂ + μ by Remark 4.5. This follows from a₂ > 0, a₀ < 0, β₁ < (ρ₁ + μ)ℛ₂₀ and

$$C_0(({\rho }_1+\mu ){ℛ}_{20})={({\rho }_2+\mu )}^{-2}({\rho }_1+\mu )({\beta }_2-{\rho }_2-\mu )\times ({\beta }_2\mu ({\rho }_2+\mu -{\beta }_{12}-{\beta }_{02})-{\beta }_2{\rho }_1({\beta }_{12}+{\beta }_{02})-{\beta }_{02}{({\rho }_2+\mu )}^2)<0$$

for small enough μ > 0.